HYSTERETIC PERFORMANCE OF JOINT CONNECTING BOUNDARY ELEMENT OF STEEL CORRUGATED-PLATE COMPOSITE WALL AND I-BEAM
-
摘要:
多高层住宅钢结构建筑中，采用剪力墙边缘构件与钢梁连接的等宽度设计，可避免室内凸柱现象，能获得整洁的室内空间，但使墙边缘构件-梁连接节点设计的难度增加。为此，该文结合波形钢板-混凝土组合墙构成特点，提出了墙边缘构件与梁连接采用上翼缘环板节点、下翼缘贴板节点的组合型式，并进行了2个不同轴压比组合节点的滞回加载试验，研究其承载性能、破坏模式、滞回性能、骨架曲线、强度和刚度退化等。试验发现，两个试件的屈服位移角平均值为1/136，极限位移角为1/42，均能满足《建筑抗震设计规范》(GB 50011−2010)中弹性和弹塑性层间位移角的要求；下翼缘贴板节点弱于上翼缘外环板节点的变形能力，而且贴板节点连接焊缝易于开裂；一旦贴板节点达到承载力极限，之后强度和刚度迅速退化。该文建立了组合节点的实体-壳单元的精细化有限元模型，进行了试验加载全过程分析。比较了节点试验与有限元分析结果，利用该文建立的有限元模型开展分析，为贴板节点设计提供了依据。
Abstract:In residential steel building structures, the identical depth design among joints and, the boundary element of steel plate shear wall and I-beam can lead to a required interior space, but it makes the joint design more difficult. A combination type of the joint connecting the boundary element with the I-beam was proposed, with an external-diaphragm connection on the upper flange and with a flitch plate connection on the lower flange of I-beam. The hysteretic tests of two specimens with different axial compression ratios were carried out to study their load-bearing performance, failure mode, hysteretic performance, skeleton curve and, strength and stiffness degradation. The test results indicated that: The average yield displacement angle of 1/136 and limit displacement angle of 1/42 both could meet the specified requirements in Chinese Code for the seismic design of buildings GB 50011−2010; The deformability of the flitch plate connection on the lower flange is weaker than that of the external-diaphragm connection on the upper flange; The cracking is prone to occur in the weld seam of the flitch plate connection, resulting in the strength and stiffness degrade rapidly. A refined finite element model including all details of connecting joints was established and the tests are simulated numerically. A good agreement between the test and finite element results was reached, and the investigation of the validated finite element model could provide fundamentals for establishing the design methods of the flitch plate connection.
-
在多高层钢结构住宅设计中，钢管混凝土柱作为剪力墙两侧的竖向边缘构件被广泛使用。为了避免室内凸柱现象、获得整洁的室内空间，采用剪力墙边缘构件与钢梁等宽度的设计，是结构节点设计的最好方式之一。
在公共建筑框架结构中，柱截面尺寸大于梁翼缘宽度，梁柱连接节点常采用外环板节点和内隔板式节点。在柱截面尺寸较大的情况下，这两类梁柱连接节点不仅传力可靠，也能使柱内混凝土浇筑顺畅、密实。外环板节点的构造简单，便于加工安装，且能保持钢管混凝土柱竖向贯通；而内隔板式节点传力直接，节点具有更好的承载能力和刚度。学者们对这两种类型节点进行了大量的试验研究和数值分析工作[1-9]，相关规范[10]也给出了这两种类型节点的构造要求和设计方法。
但在住宅钢结构建筑中，为了获得整洁的室内空间，无论对于框架结构还是剪力墙结构，墙厚度、柱沿墙厚度方向的截面尺寸、梁翼缘宽度三者的设计趋于相同。柱梁截面宽度随墙的厚度，通常控制在150 mm~350 mm。这样小的柱截面尺寸，梁上、下翼缘与墙边缘构件或框架柱连接，无论采用外环板和内隔板节点都很难满足建筑功能和施工质量要求。对于外环板节点，过大的外环板尺寸会影响使用效果，而过小的尺寸会影响受力性能；对于内隔板式节点，隔板灌浆孔过小会影响混凝土的浇筑的密实性，灌浆孔过大会影响受力性能，因而内隔板难以兼顾受力性能和混凝土浇筑质量。
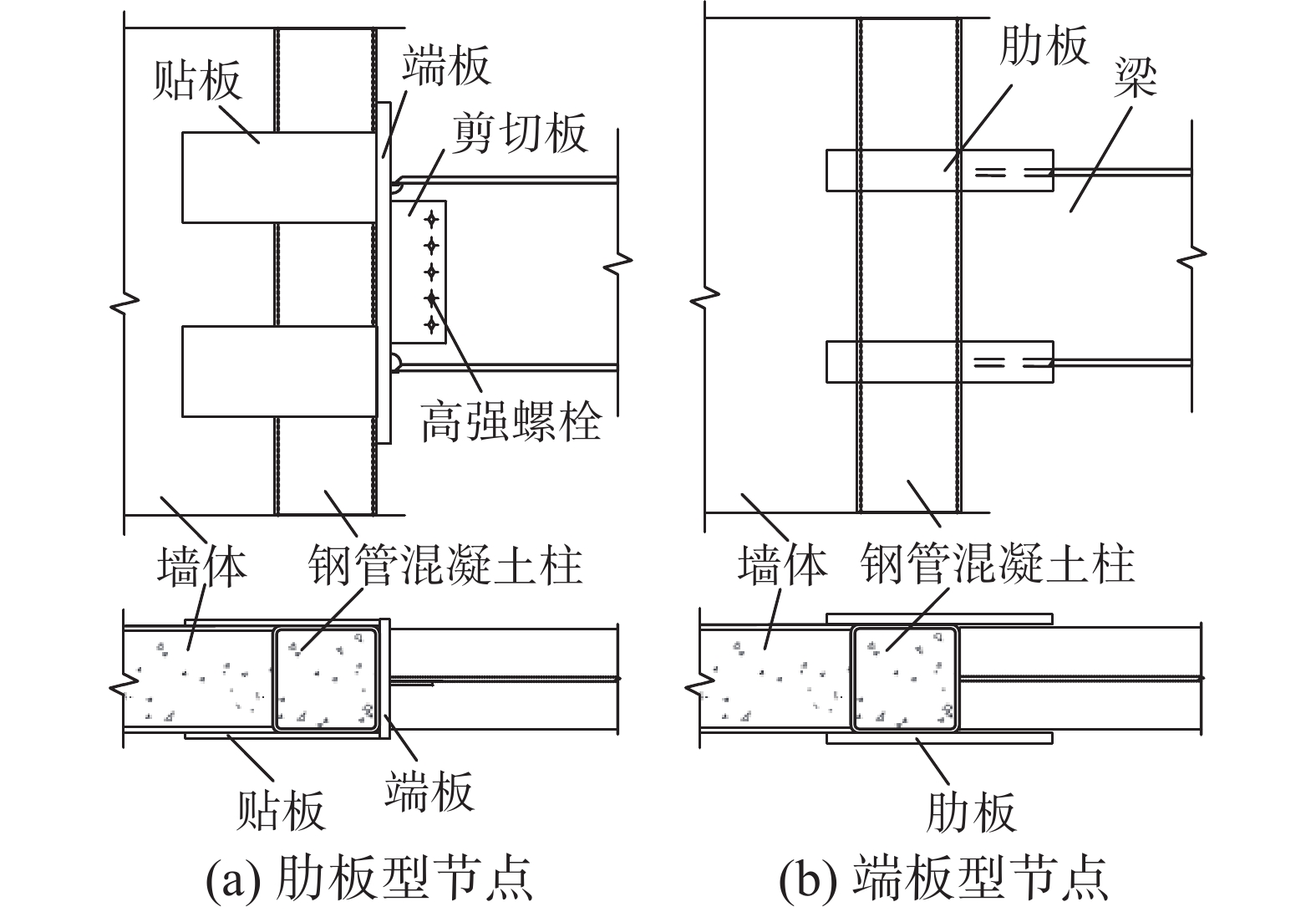
针对上述提到的问题，学者们提出了肋板型节点和端板型节点，并对其受力性能进行了研究。肋板型节点如图1(a)所示，在梁上、下翼缘的侧面设置肋板并通过角焊缝连接，肋板和钢管侧壁也通过角焊缝连接。对于肋板型梁柱节点和墙梁节点，多名学者进行了抗震性能的试验研究和数值分析[11-16]，研究表明肋板型节点具有较高的耗能性能和延展性。端板型节点如图1(b)所示，在钢管混凝土柱的正面焊接一块端板，在梁上、下翼缘高度处的钢管侧壁上焊接贴板，贴板用于传递端板和柱之间的荷载，梁翼缘和端板焊接，梁腹板和端板上的剪切板通过螺栓连接。对于端板型墙梁节点，李杰等[17]进行了抗震性能试验研究，TONG等[18]建立了有限元数值分析并提出了节点的抗弯承载力的设计方法，胡立黎等[19]采用塑性极限分析方法，推导了端板厚度设计方法，赵均海等[20]对带单边螺栓的端板式节点开展了理论研究，并提出节点极限弯矩计算方法。无论是肋板型节点还是端板型节点，节点的延性系数、层间位移角均满足抗震设计要求，适合用在柱截面较小的墙梁节点和梁柱节点中。不过，在梁翼缘位置设置竖向肋板，会增加楼板与梁连接的复杂程度，多少会影响楼板的安装。
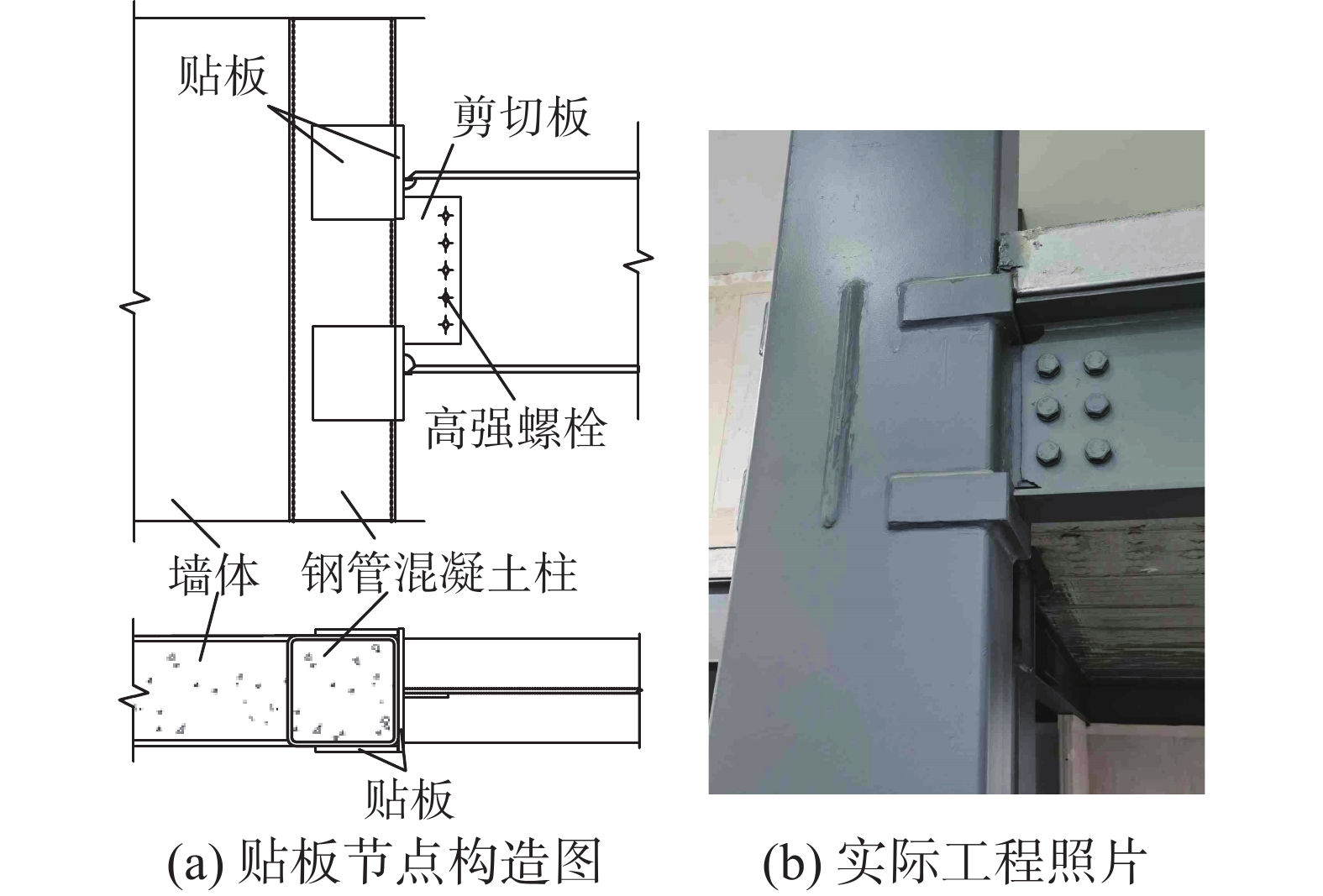
付波等[21-22]将端板型节点的端板和贴板换成带状贴板，提出了贴板节点。贴板式连接节点的构造形式如图2所示，梁翼缘板与贴板采用熔透焊缝，贴板与柱壁采用角焊缝连接，梁腹板和剪切板通过高强螺栓连接。相比前述其他连接节点，贴板节点构造更简单、施工效率更高，但受力机理更加复杂：梁翼缘拉/压力通过贴板传递到钢管混凝土柱柱壁，贴板起到类似于外环板的作用，同时梁剪力通过剪切板传递给钢管混凝土柱柱壁。
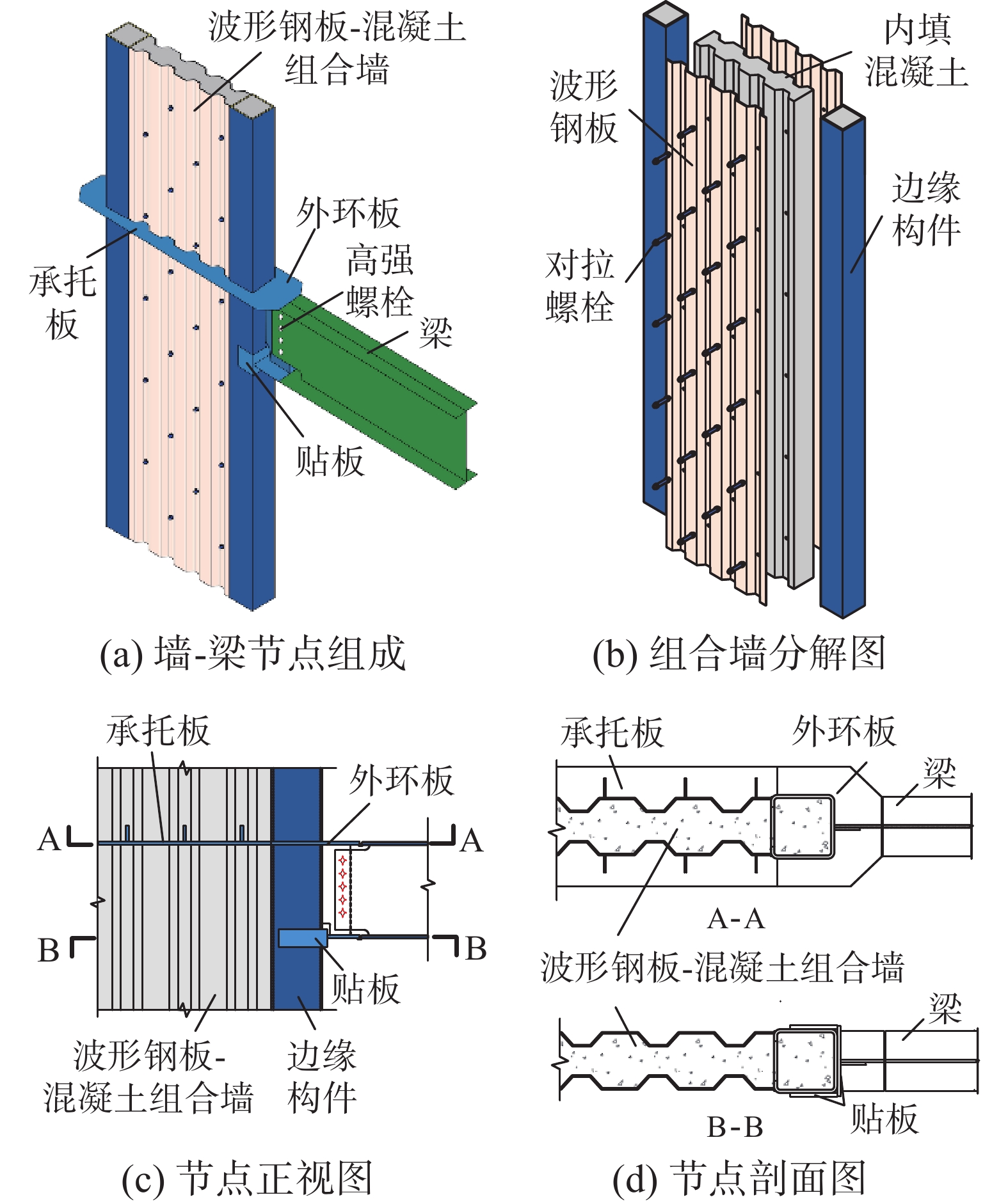
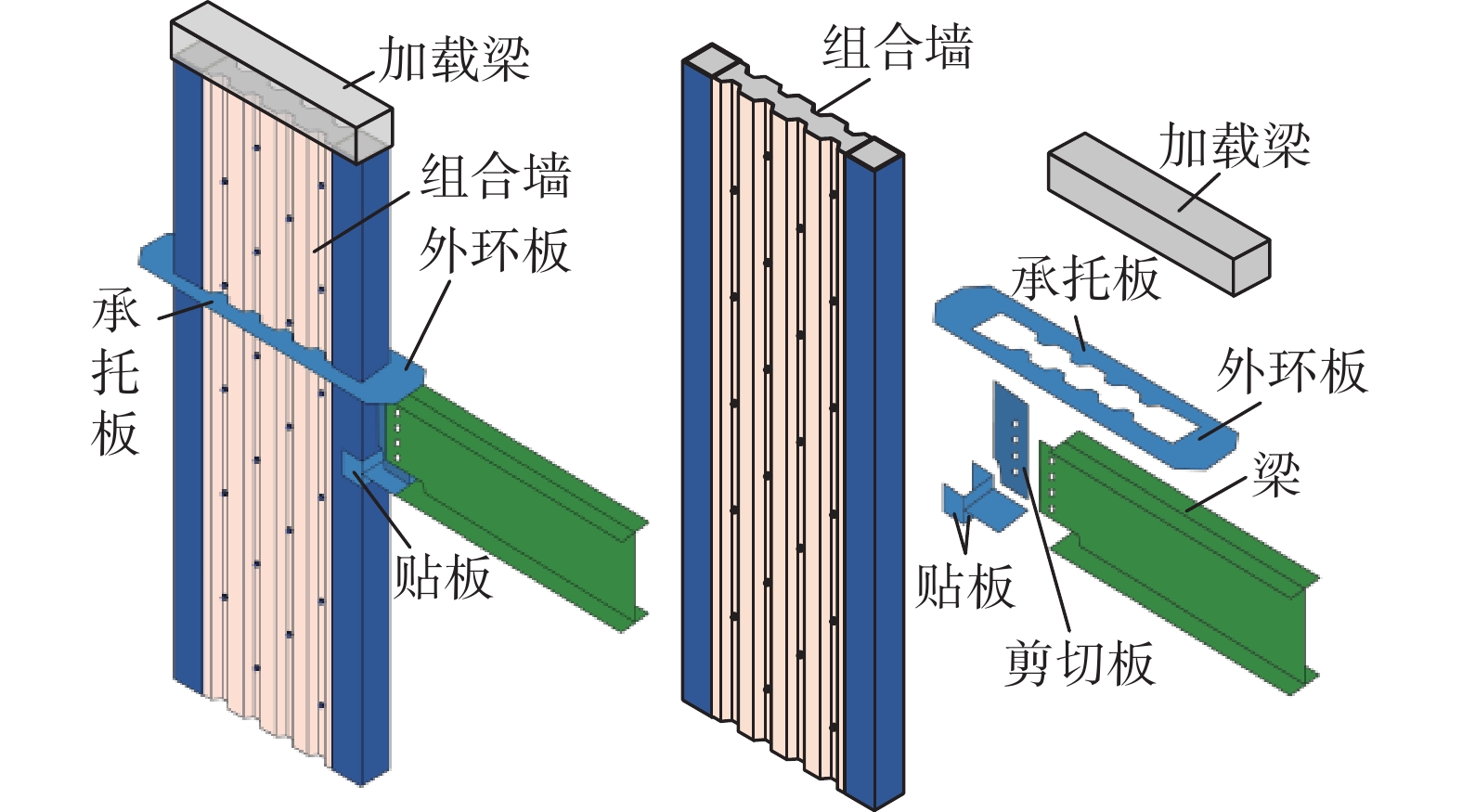
尽管贴板节点具有构造简单和不占用室内空间等优点，但是墙边缘构件-梁连接的贴板节点还缺少相关抗震试验研究数据，尚没有形成配套的设计方法。本文主要结合波形钢板-混凝土组合墙设置托板支承叠合板的构造特点(图3)，将贴板节点运用到墙边缘构件与梁下翼缘的连接中，同时考虑到水平托板紧贴楼板下表面，墙边缘构件与梁上翼缘仍采用外环板节点，不会形成对室内空间的遮挡。本文设计了2个不同轴压比的墙边缘构件-梁连接节点的足尺试验试件，主要研究贴板节点的破坏模式和抗震性能，同时建立了精细化有限元模型对试验过程进行模拟，进而通过有限元算例的参数化分析，为该类节点设计提供设计依据。
![]()
图 3 墙边缘构件与梁连接节点及细部构造Figure 3. Connections and details of wall boundary element-beam joint1 试验方案
1.1 试件设计
本文设计了2个墙边缘构件-梁连接组合节点试件用于试验研究，试验试件及细部构造如图3所示。试件墙体采用波形钢板-混凝土组合墙，墙边缘构件为钢管混凝土柱。波形钢板-混凝土组合墙采用双层波形钢板内注混凝土组成，通过对穿螺栓连接成整体[23]。在墙-梁节点设计中，梁与墙边缘构件则采用上翼缘环板节点连接、下翼缘采用U形贴板节点连接的组合型式；梁上翼缘与环板、下翼缘与贴板均采用对接熔透焊接连接，而U形贴板与墙边缘构件壁板采用角焊缝连接。
试件将梁上翼缘外环板节点与下翼缘贴板节点构造形式组合，主要基于以下3方面的原因：一是因为波形钢板-混凝土组合墙贯通的构成特点，会在墙外侧设置承托板来支承楼板，外环板和承托板能连接形成一个加强环板，既有利于传递节点拉力/压力，又能与混凝土楼板融为一体，不影响室内空间的使用；二是梁下翼缘与墙边缘构件采用贴板节点连接正好规避了遮挡室内空间的缺陷；三是能在滞回试验中对比这两种节点的承载性能和破坏模式。
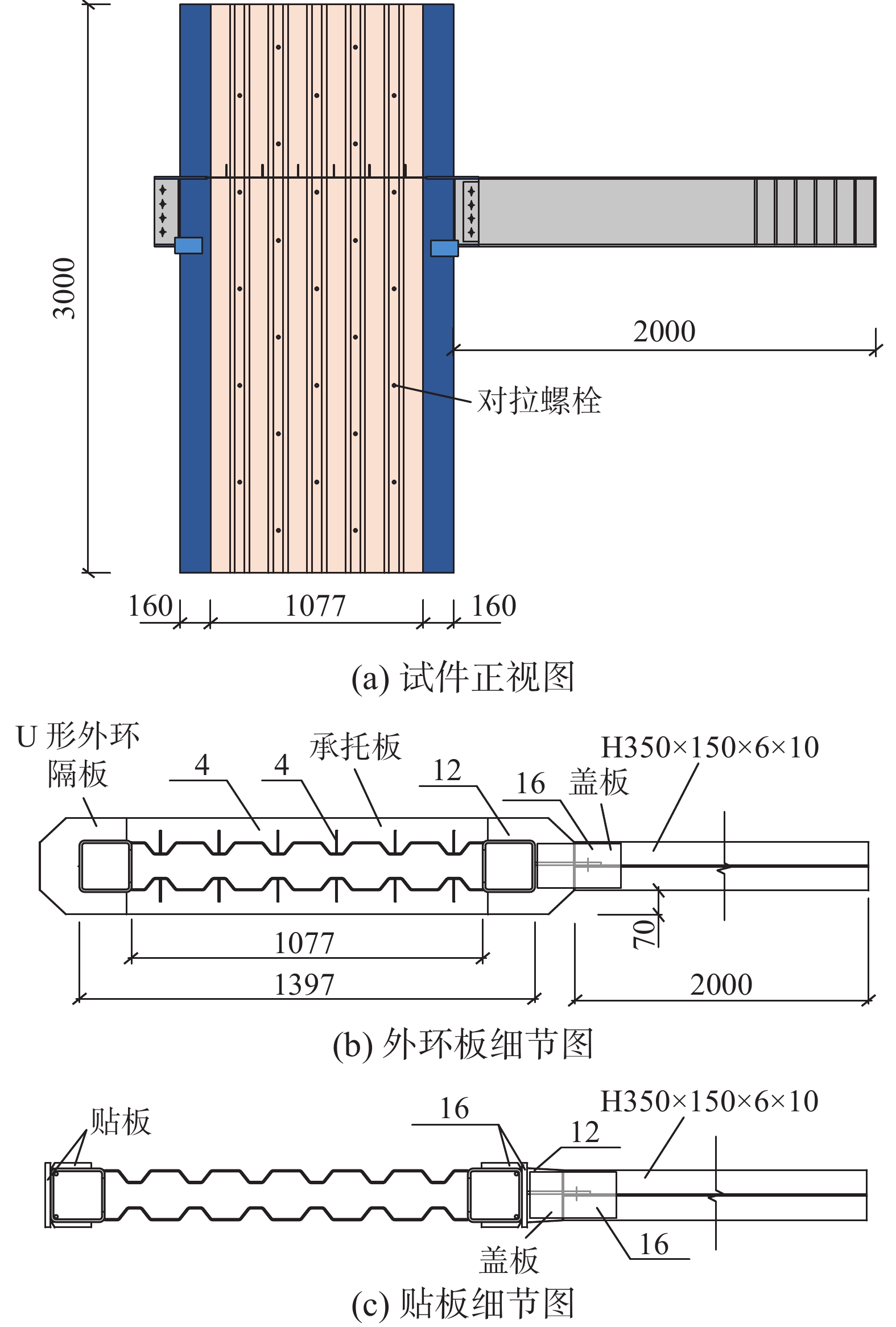
试件的整体尺寸如图4(a)所示，两个试件的尺寸参数完全一致，但试验采用不同的轴压比。波形钢板组合墙高3.0 m，组合墙波形部分宽度为1077 mm、墙厚为150 mm，波形钢板厚度为4 mm，边缘构件的截面边长均为160 mm，钢管的板件厚度为8 mm；对穿螺栓采用错列式的布置形式，其纵向间距为280 mm。试件的细部尺寸如图4(b)、图4(c)所示：与梁上翼缘相连的外环板厚度为12 mm、外伸宽度为70 mm，组合墙上的承托板厚度取4 mm，并与外环板相连形成一个整体；贴板高度为80 mm、厚度为16 mm；梁截面统一取为H350×150×6×10，梁长度为2000 mm。
在梁往复加载过程中，为了重点考察节点的破坏机理，避免梁会先于节点破坏，故对试件的梁翼缘进行加强，即在梁上、下翼缘靠近节点位置处焊接了盖板，防止梁翼缘提前屈曲退出工作，盖板的厚度统一取16 mm。
节点区域的轴压比对节点的强度和延性都有影响，通常认为节点区域的轴压比和组合墙的轴压比保持一致。本文按照式(1)计算轴压比[24]，式中：N为试验中施加的轴压荷载；As和Ac分别为组合墙钢板和混凝土的截面积；fs和fc分别为钢板和混凝土的单轴抗压强度设计值。采用的钢材标号都为Q345，混凝土强度等级为C40。两个试件的设计轴压比分别为0.35和0.5，将两个试件分别称为试验试件1和试验试件2。
nd=Nfs,dAs+fc,dAc (1) 1.2 试验加载装置
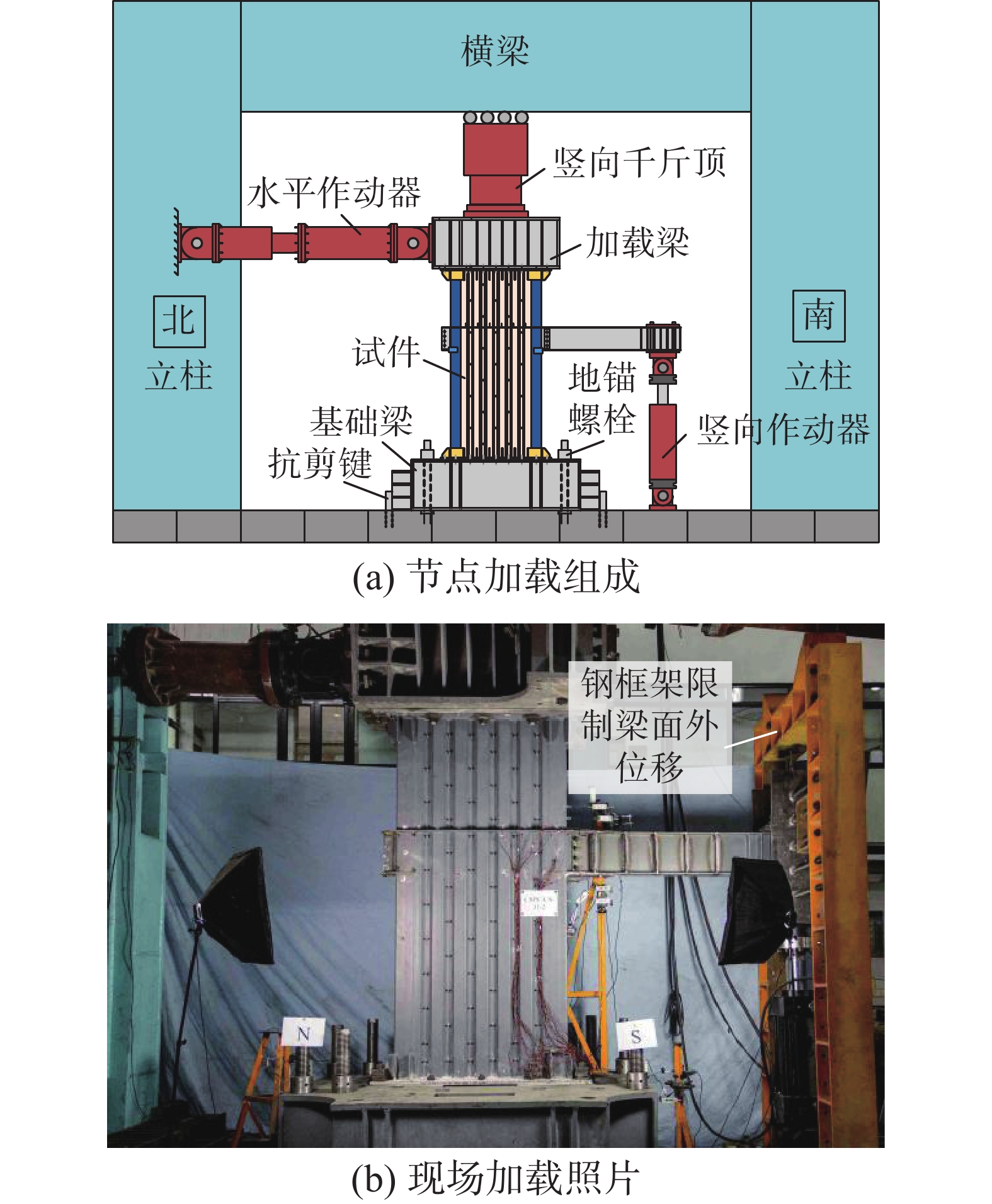
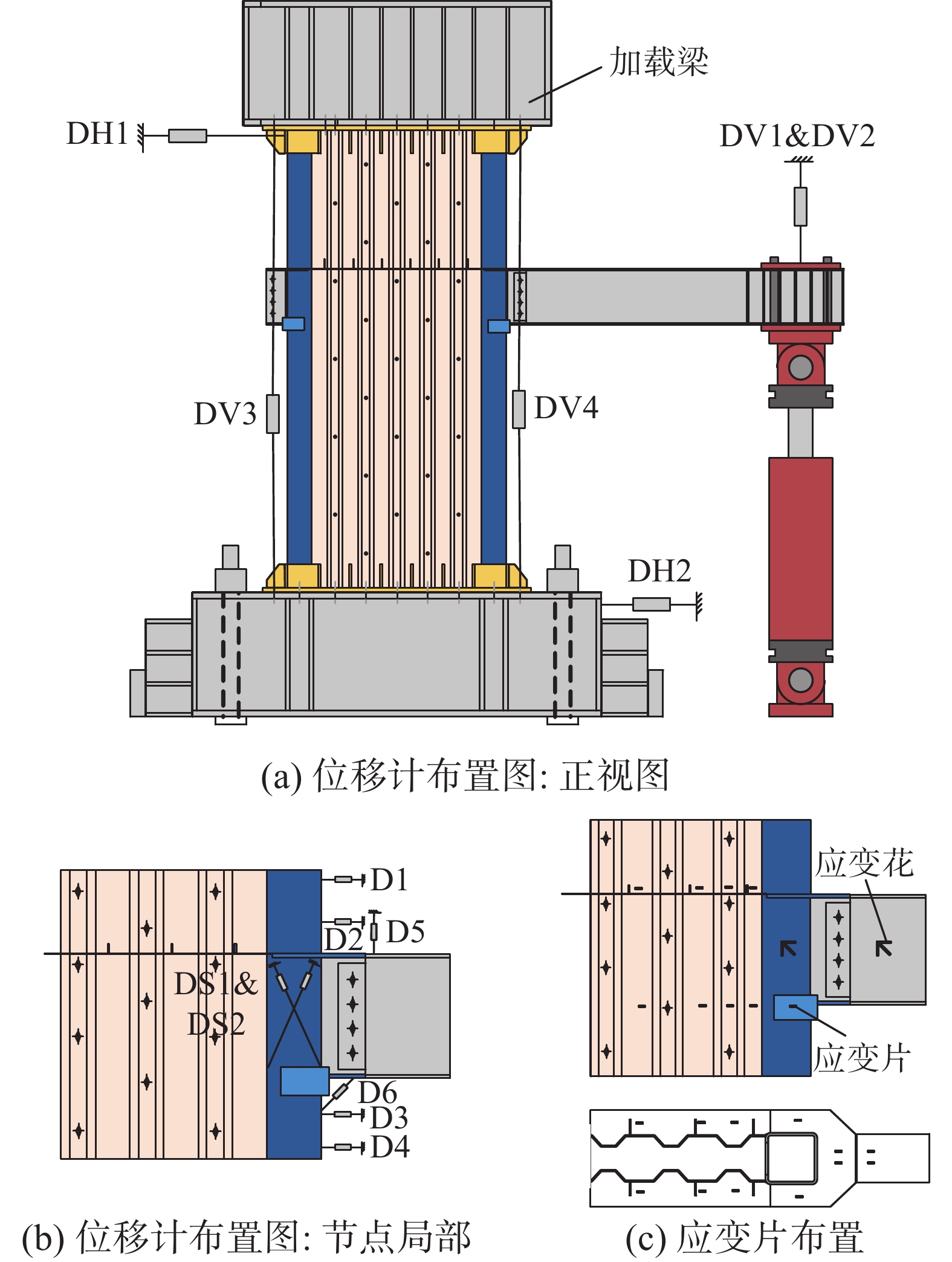
本试验利用多功能加载装置进行加载，加载装置立面如图5所示。加载装置的两根立柱分别位于南北方向，在试验中规定南北方向为试件的面内方向，东西方向为试件面外方向。加载装置包括竖向千斤顶和两个作动器：竖向千斤顶吨位为20 000 kN，通过液压稳定系统控制，作用在组合墙顶面的加载梁上，用于为组合墙提供固定的轴压力。竖向千斤顶可以随着水平作动器在面内水平移动，作动器的内部包含一个球铰，通过球铰可以保证竖向千斤顶的荷载始终垂直于加载梁的顶面；吨位为2000 kN的水平作动器通过螺栓连接固定在加载梁的北侧，用于限制组合墙顶部在面内的水平位移以及绕水平作动器的扭转；而吨位同样为2000 kN的竖向作动器用于在梁端提供往复荷载，为了防止在加载过程中梁端产生较大的面外位移或者扭转变形，在靠近千斤顶加载点的位置，如图5(b)所示，采用钢框架限制梁的面外变形和扭转变形。组合墙的顶面和底面分别与加载梁和基础梁通过螺栓连接，而基础梁又通过地锚螺栓和抗剪键固定在地面上。
1.3 测量装置及测点布置
试验过程中主要测量了作动器施加的荷载、组合墙和节点的位移以及应变，测点的布置如图6所示，试验过程中发生的钢板屈曲、钢板或者焊缝开裂以及其他破坏现象均通过人工观察拍照记录。竖向千斤顶和作动器上都设置了力传感器，可以测量施加的荷载大小。竖向位移计DV1和DV2用于测量梁端加载点的竖向位移，竖向位移计DV3和DV4用于测量在整个加载过程中组合墙的竖向位移；墙肢顶部的水平位移计DH1用于测量组合墙在面内是否出现较大的水平位移，而水平位移计DH2用于测量基础梁在水平方向上是否发生滑移；在墙梁节点区域还设置了行程较短的多个位移计D1~D6、DS1和DS2用于测量节点区域的变形发展。同时在节点区域及附近的钢板上设置了22个应变片和4个应变花，用于观察节点区域钢板应变或应力变化。
1.4 加载方案
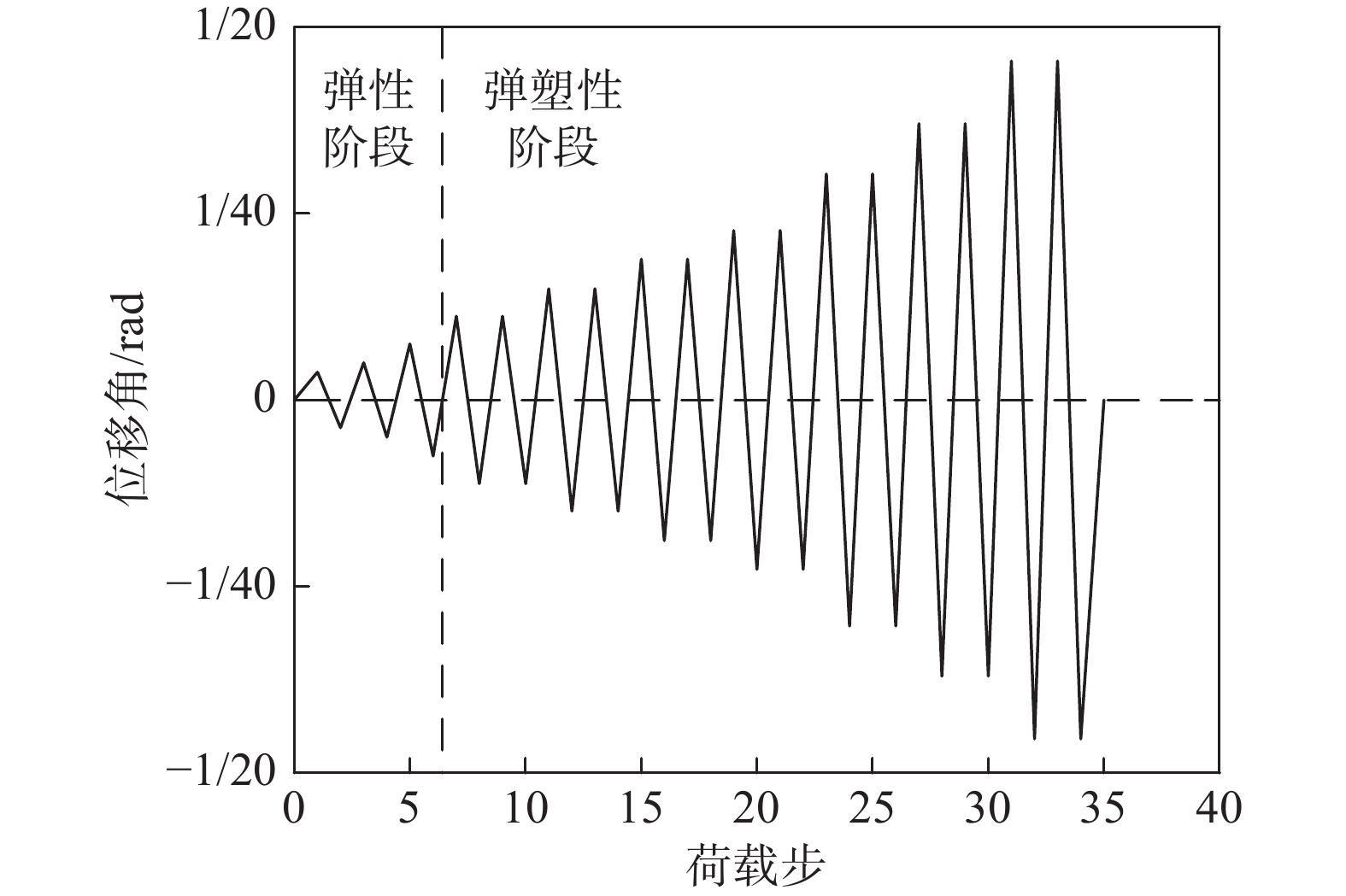
试验的加载过程分为施加组合墙竖向荷载和梁端往复加载2个步骤。首先通过竖向千斤顶在组合墙上施加恒定的竖向荷载，竖向荷载由材性试验测得的材料强度、试件的截面面积及轴压比共同决定。对于轴压比等于0.35的试件，施加的竖向荷载为2606 kN，对于施加的轴压比等于0.5的试件，施加的竖向荷载为3723 kN。然后在梁端通过竖直作动器施加竖向的往复荷载。荷载往复加载制度[25]如图7所示，在位移角较小的前三级，每个加载级循环1圈，梁端加载点位移分别控制在7.5 mm、10 mm、15 mm，位移角分别为1/267、1/200、1/133；接着按梁端加载点位移依次为22.5 mm、30 mm、37.5 mm、45 mm、60 mm、75 mm和90 mm，对应的位移角分别为1/89、1/67、1/53、1/44、1/33、1/27和1/22，每级循环2圈。直到试件出现明显破坏无法继续加载，或者承载力下降到极限承载力的85%以下时，试验停止。
2 试验结果与讨论
2.1 材性试验结果
首先进行了钢材和混凝土的材性试验。根据《普通混凝土力学性能试验方法标准》(GB/T 50081−2002)[26]中的方法测量了混凝土的立方体抗压强度fcu,m和混凝土弹性模量Ec，测量的结果如表1所示。混凝土的立方体抗压强度平均值为42.8 MPa，而根据混凝土立方体抗压强度和轴心抗压强度的换算关系(fc,m=0.76fcu,m)，可以得到混凝土轴心抗压强度的实测值为32.5 MPa。根据《金属材料室温拉伸试验方法》(GB/T 228.1−2021)[27]中的方法对试验中使用的厚度分别为4 mm、6 mm、10 mm的钢板进行了材性试验，试验结果如表2所示。钢材弹性模量的平均值在202 GPa~207 GPa，屈服强度在404 MPa~442 MPa，极限强度在530 MPa~569 MPa。材性试验的结果将用于试验有限元模拟和理论分析。
表 1 混凝土材性试验结果Table 1. Concrete material property test results材性试验
编号混凝土立方块
抗压强度fcu,m/MPa混凝土
弹性模量Ec/MPaC-1 40.96 − C-2 47.55 − C-3 45.95 − C-4 42.53 17693 C-5 37.14 18390 平均值 42.83 18042 表 2 钢材材性试验结果Table 2. Steel material property test results材性试验
编号钢材弹性
模量Es/GPa屈服强度
fy/MPa抗拉强度
fu/MPa抗拉应变
εu/(%)S4-1 193.9 386.6 525.6 14.33 S4-2 208.3 419.6 568.7 13.96 S4-3 202.6 406.4 554.2 13.33 S4-4 216.7 400.8 554.6 16.62 S4-5 212.7 405.3 551.1 13.86 平均值 206.8 403.7 550.8 14.39 S6-1 201.6 438.0 567.9 16.24 S6-2 199.3 445.1 569.2 13.38 S6-3 204.4 444.3 569.0 13.59 平均值 201.8 442.4 568.7 14.40 S10-1 207.1 410.5 530.9 19.40 S10-2 207.2 410.1 531.7 18.57 S10-3 203.6 410.4 528.9 18.67 平均值 205.9 410.3 530.5 18.88 2.2 试验过程及破坏模式
规定当梁上翼缘受拉、下翼缘受压时为正向加载，梁上翼缘受压、下翼缘受拉时为负向加载。各试件的破坏过程如下所述：
对于试验试件1：在位移角分别为1/267、1/200和1/133的前3级加载中，试件处于弹性阶段，试验过程中没有观察到明显的位移。当位移角增加达到1/89时，通过观察节点区梁翼缘的应变可以发现，节点区梁上、下翼缘都进入屈服，节点区域的刚度开始下降。增加位移角到1/53，在负向加载的第二圈，如图8(a)所示，贴板底侧角焊缝开始开裂，负向承载力下降。继续增大位移角，当进行位移角1/44第一圈负向加载时，如图8(b)所示，即当加载到梁端位移为36 mm时，贴板底侧角焊缝完全开裂，此时已不适合继续进行负向加载。之后进行单调正向加载，在正向位移约85 mm时，如图8(c)所示，此时外环板和柱之间的焊缝开裂，梁腹板的螺栓发生滑移，正向承载力达到极限值。在正向位移约105 mm时，如图8(d)所示，节点区矩形钢管开裂，加载结束。试验试件1最终的破坏形式为贴板和柱之间的焊缝开裂、节点区外环板和柱之间的焊缝开裂以及柱钢管开裂。
对于试验试件2：在位移角分别为1/267、1/200和1/133的前3级加载中，试件处于弹性阶段，试验过程中没有观察到明显的位移。当位移角增加达到1/89时，通过观察节点区梁翼缘的应变可以发现，节点区梁上、下翼缘都进入屈服。增加位移角到1/53，在正向加载的第一圈，外环板和柱之间的焊缝开裂，在负向加载的第二圈，如图9(a)所示，贴板和下翼缘连接板之间的焊缝开裂，负向承载力略微下降。继续增大位移角，当进行位移角1/44第一圈负向加载时，贴板底侧角焊缝开裂；当进行位移角1/44第二圈负向加载时，如图9(b)所示，即加载到梁端位移为36 mm时，贴板底侧角焊缝完全开裂，此时已不适合继续进行负向加载。之后进行单调正向加载，在正向位移约75 mm时，正向承载力达到极限值；在正向位移约100 mm时，如图9(c)所示，节点区矩形钢管开裂，加载结束。试件2与试件1最终的破坏形式类似，贴板和柱之间的焊缝完全开裂、节点区外环板和柱之间的焊缝开裂，且柱钢管开裂。
2.3 试件滞回曲线
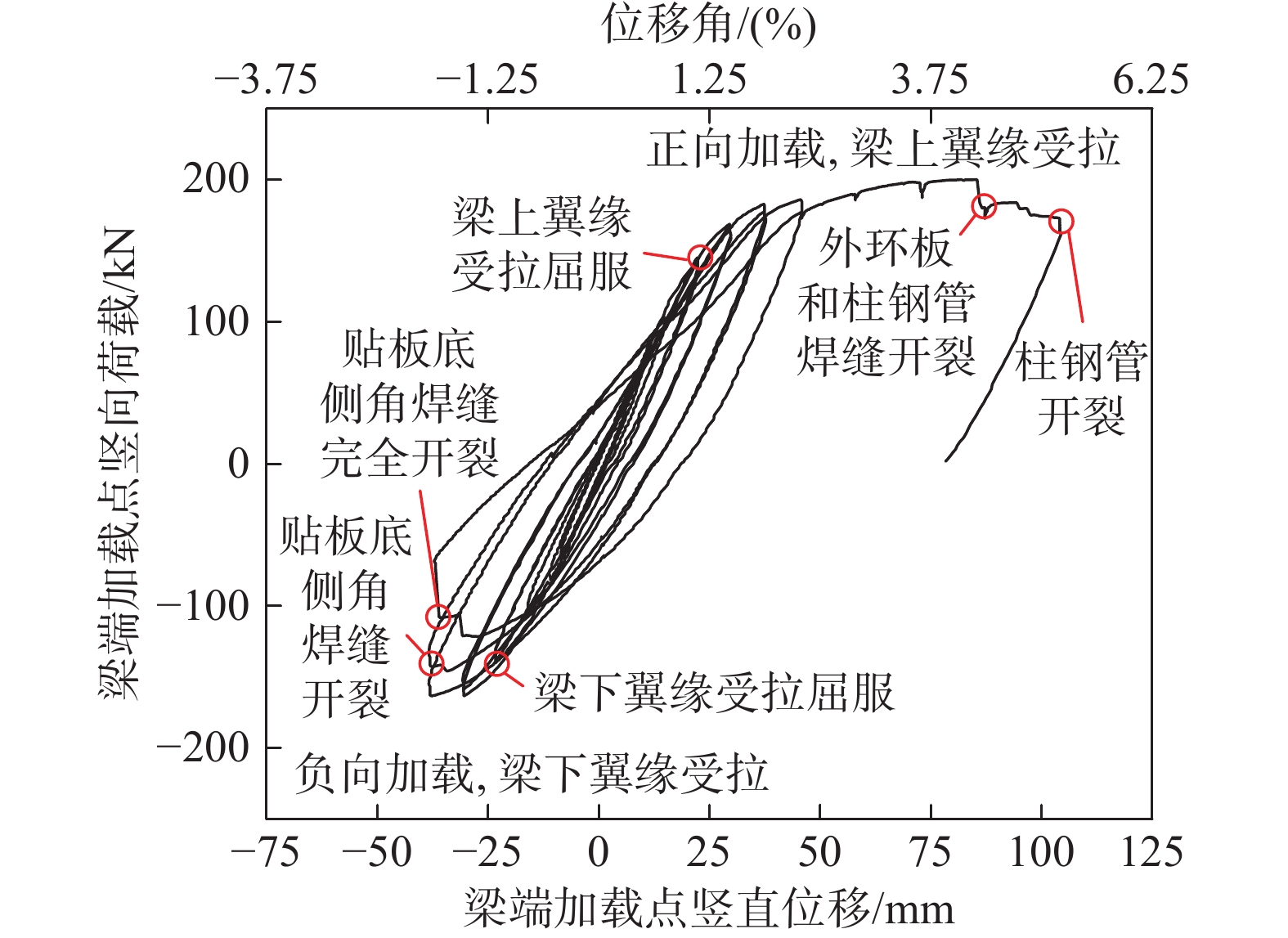
试件1的梁端加载点竖向荷载-梁端加载点竖向位移滞回曲线如图10所示。由于外环板没有发生开裂，滞回曲线在正向加载时始终较为饱满；在负向加载的过程中节点区贴板焊缝受拉破坏，负向加载的曲线在贴板焊缝开裂之后曲线下降明显，每一级荷载都可以看到明显的刚度和强度的退化。从试验的破坏现象可以看到，相比于外环板节点，贴板节点更容易发生焊缝的开裂，在设计过程中有必要单独对贴板节点的焊缝承载性能进行验算，或者加强焊缝的构造措施。
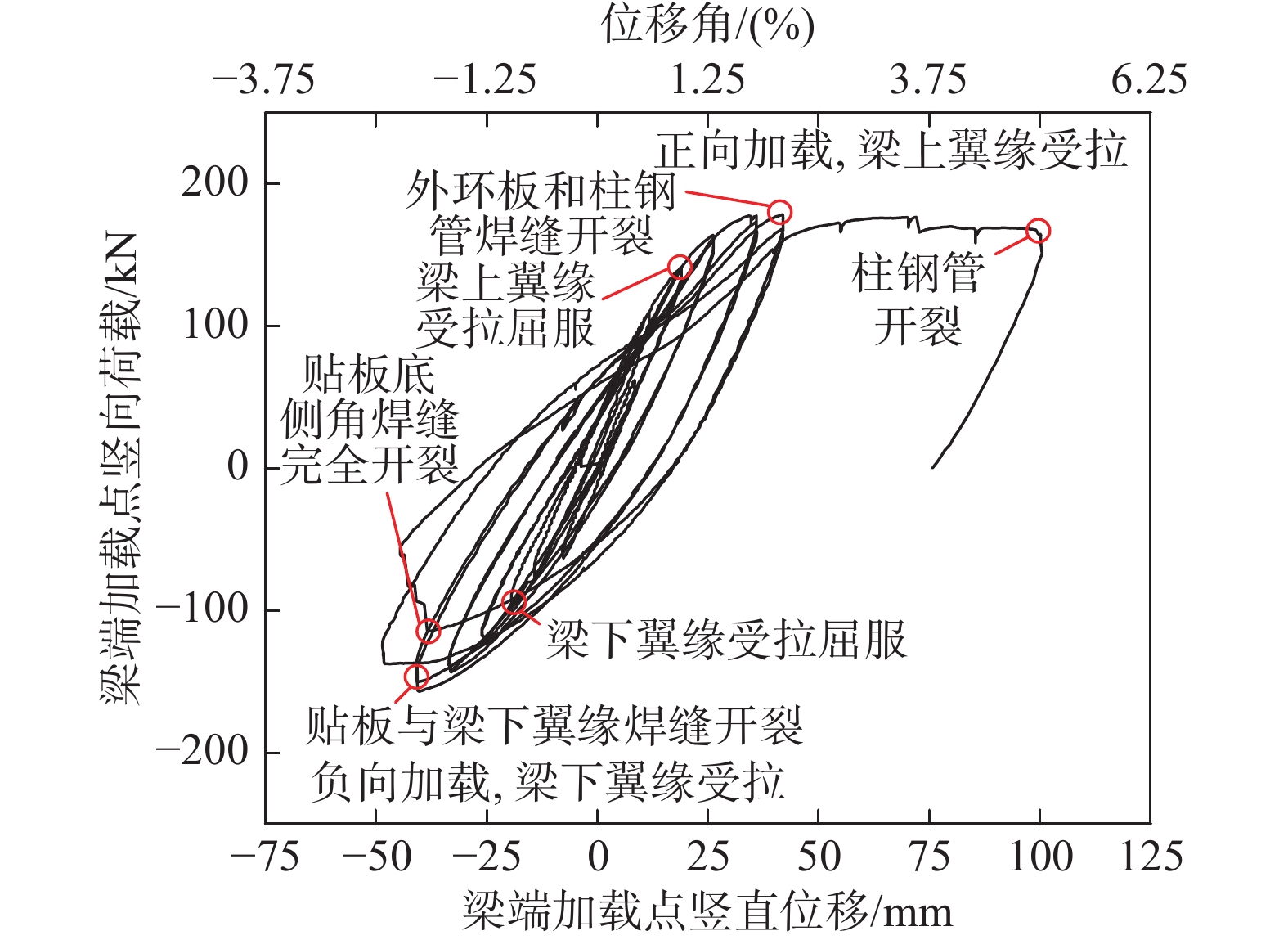
试件2的梁端加载点竖向荷载-梁端加载点竖向位移滞回曲线如图11所示。试件2和试件1的滞回曲线形状非常相似，同样是正向加载时曲线始终较为饱满，而负向加载的曲线在贴板焊缝开裂之后曲线下降明显，每一级荷载都可以看到明显的刚度和强度的退化。对比两个试件的滞回曲线可以发现，随着组合墙轴压比增大，外环板节点和贴板节点的极限承载力都有所下降。
2.4 试件骨架曲线、承载力和变形能力
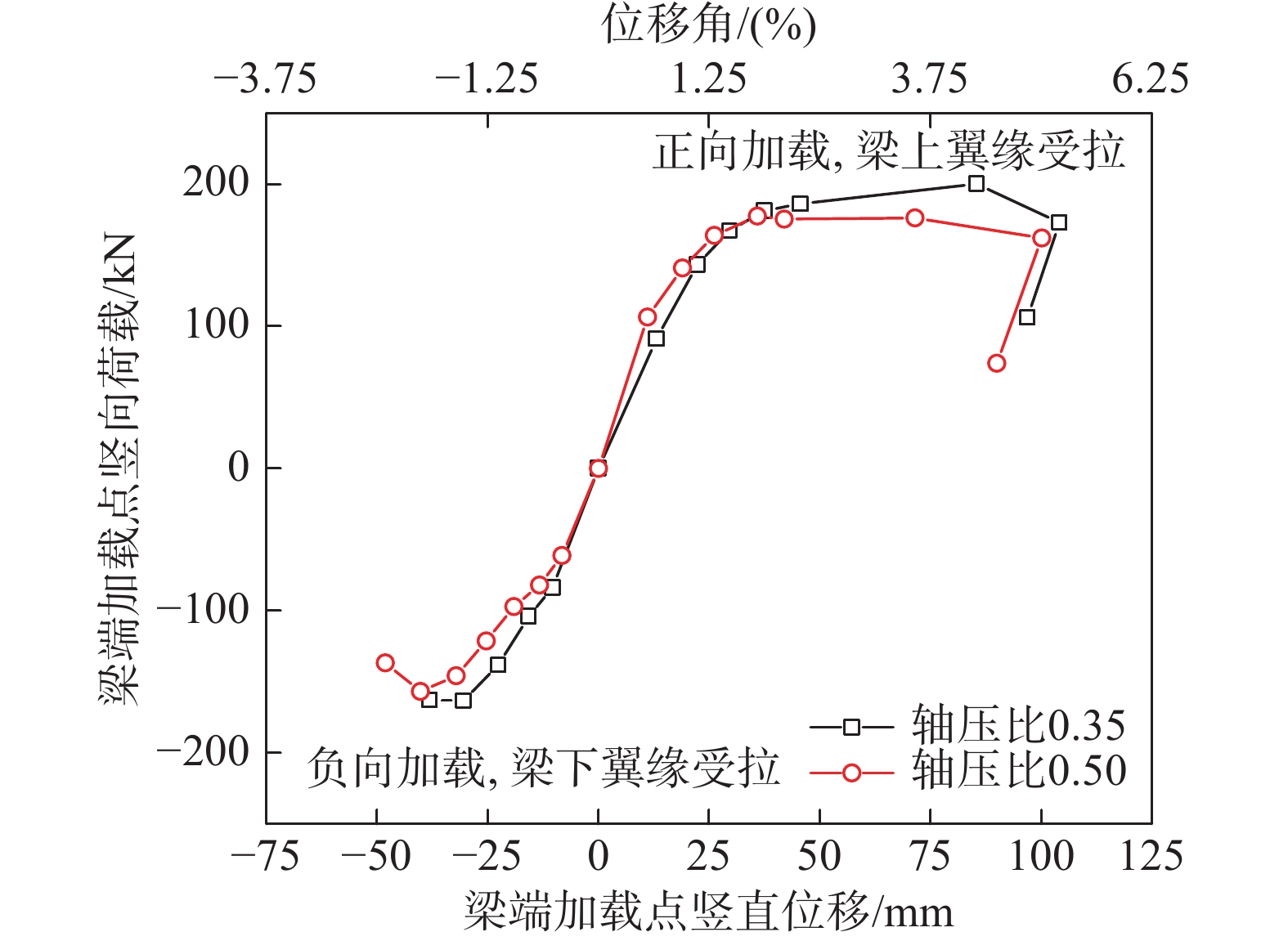
从滞回曲线提取出各级位移角加载时的荷载峰值点，并将峰值点依次相连，可以得到试件的荷载-位移骨架曲线，两个试件的骨架曲线如图12所示。在不同轴压比下，骨架曲线的形态基本相同，而随着轴压比的增大，在正向加载和负向加载时的节点承载力都有不同程度的下降。结合试验现象可以发现，无论是正向加载还是负向加载，在达到极限状态时都是在节点受拉侧发生破坏，由节点受拉侧的承载力决定整个节点的极限承载力。在正向加载时环板式节点受拉，节点的极限承载力下降12%，这主要是由于外环板节点在受到竖向压力时，其抗拉承载力被削弱。而在负向加载时贴板节点受拉，节点承载力仅下降4%，下降幅度较小并不是由于轴压力对贴板节点的抗拉承载性能没有影响，而是由于在两次试验中都发生了贴板和柱的焊缝开裂，组合墙轴压比对于焊缝强度影响较小，才导致极限承载力变化较小。
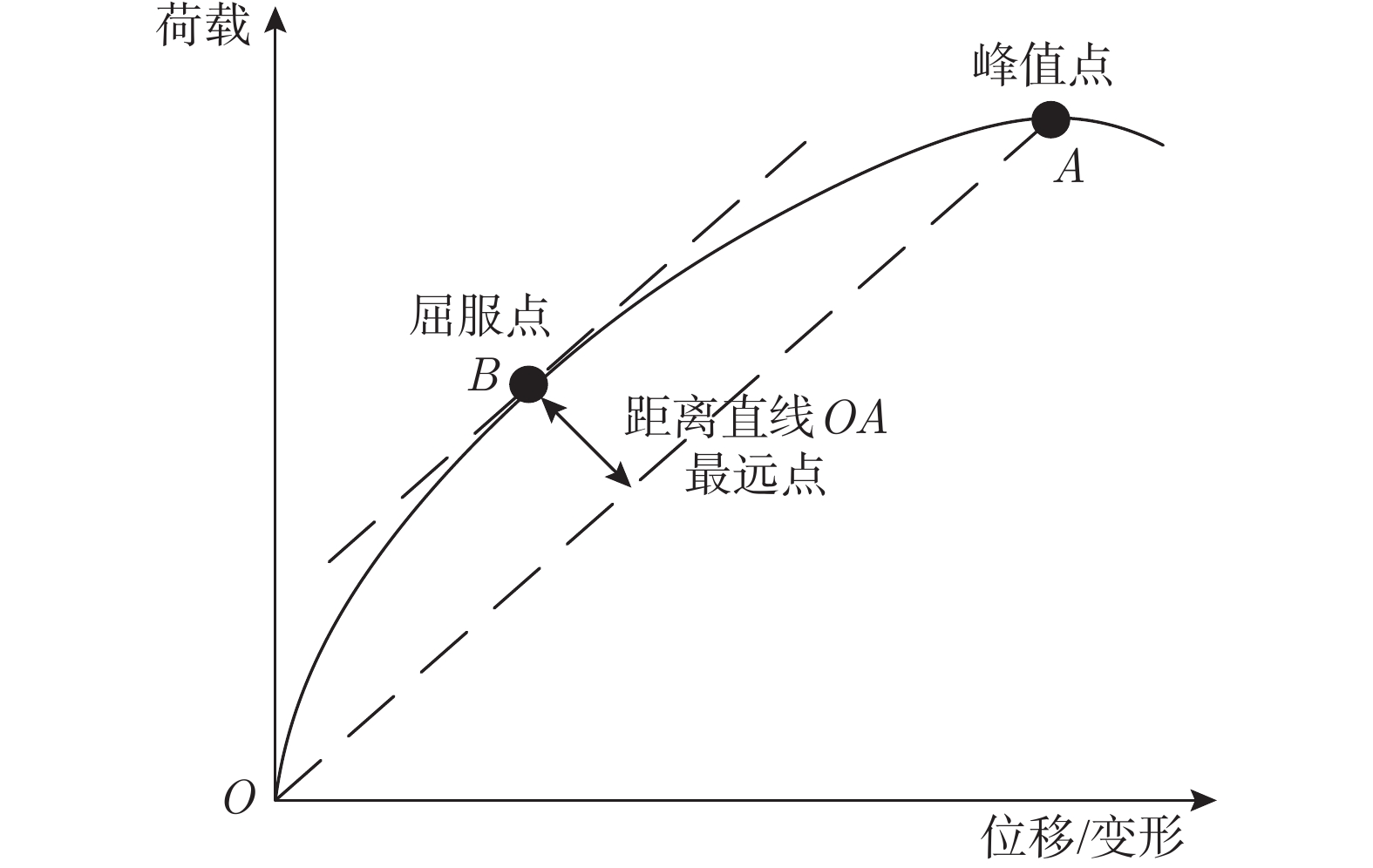
根据试件的骨架曲线确定试件的屈服点、峰值点及最终破坏点，可以作为试件的承载力指标。峰值点即为加载过程中梁端加载点竖向荷载最大点，最终破坏点取荷载下降到峰值荷载为85%左右的时刻，屈服点有多种定义方式，采用“最远点”法确定屈服点[28]：如图13所示，将原点和曲线峰值点连线，曲线上距离这条线最远的点即为构件的屈服点。试件在正向加载和负向加载过程中的屈服点、峰值点和最终破坏点的荷载和位移如表3所示，负向加载时节点的承载力明显低于正向加载时节点的承载力，即贴板节点受拉时承载力较低，且极限状态对应的节点位移角较小，反映出贴板节点的延性较弱于外环板节点。贴板节点受拉时，试件的屈服位移角为1/105~1/192，而外环板节点受拉时，试件的屈服位移角为1/68~1/76，均满足弹性层间位移角不小于1/300的限值要求[10, 29]；而贴板节点和外环板节点的极限位移角分别为1/42和1/20，也都能满足弹塑性层间位移角不小于1/50的要求[10, 29]。将本文试件的位移角与其类型节点的位移角进行对比，如表4所示，外环板式节点的变形能力与隔板贯通式节点接近，而贴板式节点变形能力弱于这两种类型的节点，综合而言虽然贴板节点变形能力弱于外环板节点，但仍能满足规范要求。
表 3 试件在达到屈服、峰值和破坏时的荷载和位移Table 3. Loads and displacement angles of specimens at yield, peak and failure stages试件编号 加载方向 屈服 峰值 破坏 位移角/rad 荷载/kN 位移角/rad 荷载/kN 位移角/rad 荷载/kN 试件1 正向 1/68 167.3 1/23 200.2 1/19 173.1 负向 1/192 83.9 1/66 163.4 − − 试件2 正向 1/76 164.0 1/28 176.3 1/20 162.2 负向 1/105 97.2 1/50 156.89 1/42 136.9 表 4 对比不同类型节点的弹性和弹塑性层间位移角Table 4. Comparison of elastic and elastoplastic interlayer displacement angles of different types of joints2.5 节点刚度退化和强度退化
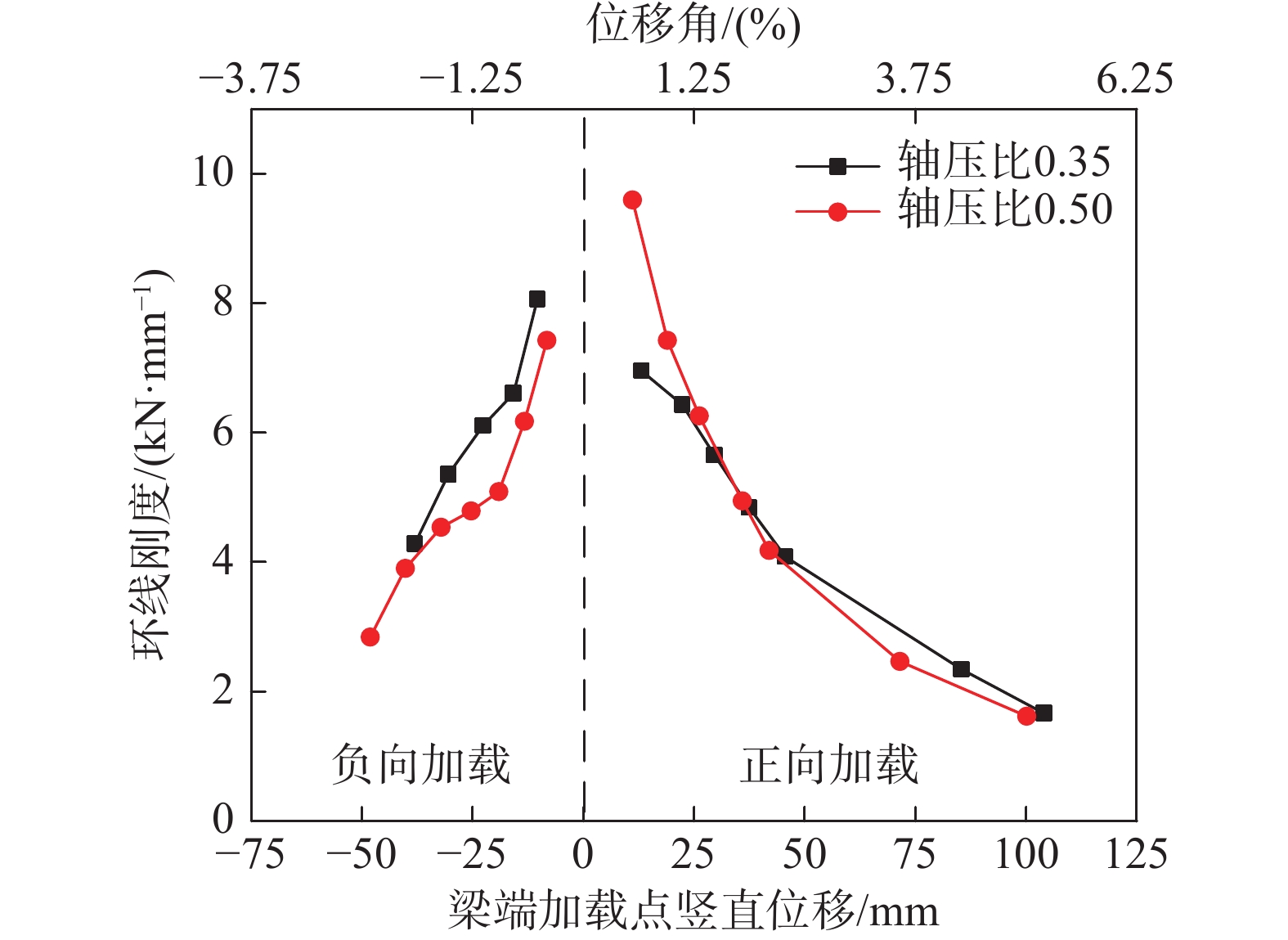
节点在往复荷载下的刚度可以通过环线刚度来衡量，环线刚度定义为在每一圈循环中荷载的峰值和与之对应的位移绝对值的比值。环线刚度-梁端位移曲线如图14所示，在整个加载过程中环线刚度不断下降，综合来看当轴压比更大时，环线刚度下降的速率更快；在负向加载时，轴压刚度一开始下降速度很快，在钢板屈服后下降速率减缓，而在贴板焊缝接近开裂时环线刚度加速下降；在正向加载时，轴压比较小时环线刚度下降速率比较均匀，轴压比较大时下降速率先快后慢。
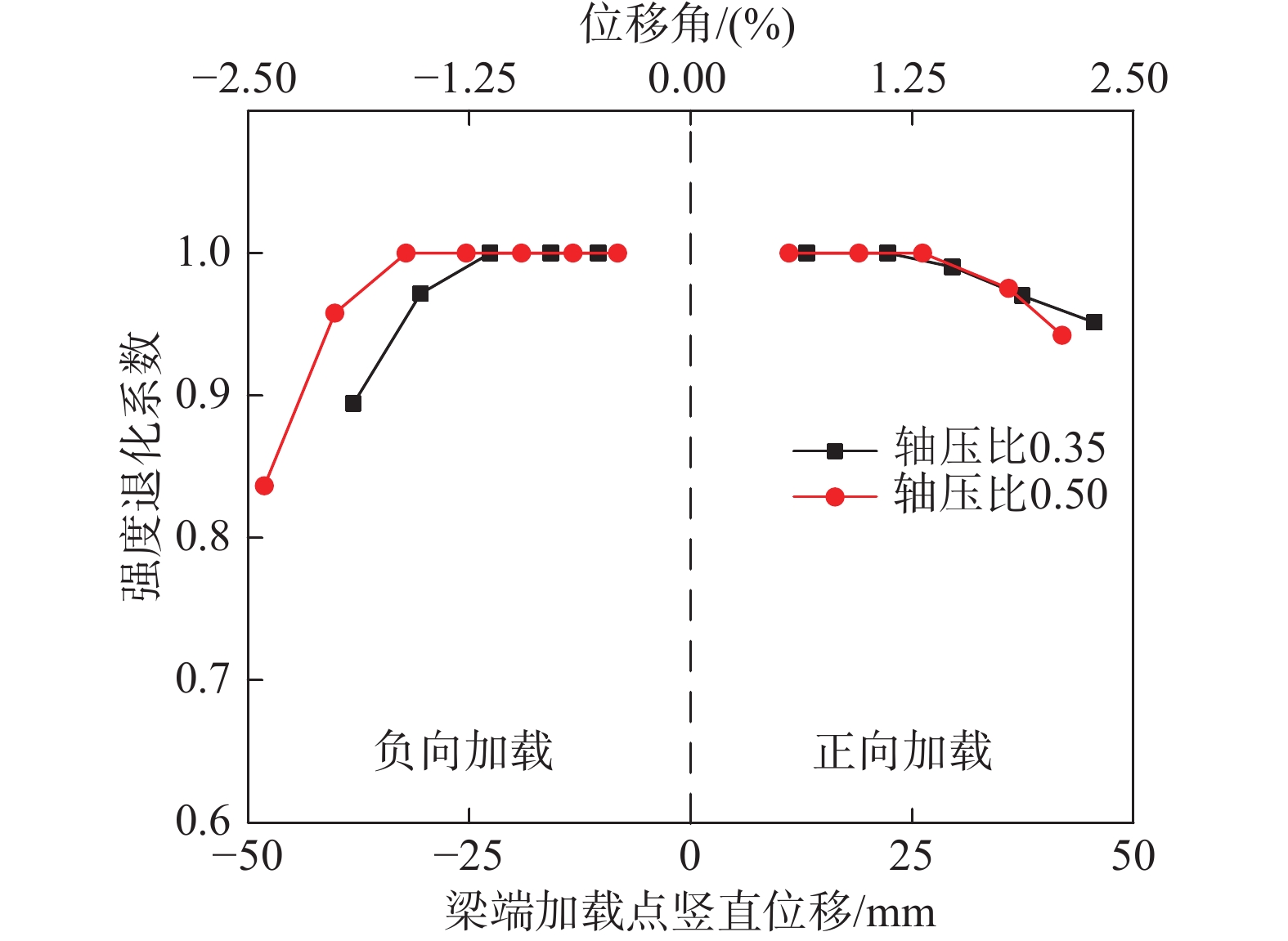
节点的强度退化系数定义为某级荷载下第i次循环荷载的峰值和第一次循环荷载的峰值的比值，试件的强度退化曲线如图15所示。在弹性阶段和弹塑性阶段的初期，无论是正向加载还是负向加载，强度退化系数基本等于1，节点强度的退化程度很小。当梁端位移较大时，正向加载时外环板节点受拉，强度退化系数缓慢减小，从图10和图11的滞回曲线也可以看到，即使在外环板开裂之后，随着梁端位移不断增加，节点承载力缓慢下降，节点的延性较好；而在负向加载时，梁端加载点竖直位移加载到36 mm时贴板焊缝开裂，贴板焊缝开裂后节点的强度退化系数迅速减小，从图10和图11的滞回曲线也可以看到，节点的强度和刚度都迅速退化。综合来看，当轴压比更大时，焊缝或钢板开裂后强度退化程度更大；同时，相比于外环板的钢板开裂，贴板节点的焊缝开裂对强度退化的影响更加显著。
3 试验有限元模拟计算
3.1 有限元模型
采用通用有限元软件ABAQUS 6.14建立精细化的实体-壳单元有限元模型，对滞回试验的全过程进行模拟。首先对有限元模型的单元选取、材料本构、相互作用关系、边界条件、荷载施加以及网格划分进行介绍。
有限元模型包含的部件如图16所示，主要包含波形钢板-混凝土组合墙和节点2部分。波形钢板-混凝土组合墙有较多的研究成果[24, 31-37]，在其精细化有限元模型中，波形钢板和钢管采用S4R壳单元，内填混凝土采用C3D8R实体单元，而对拉螺栓采用T3D2桁架单元。节点部分包含U形外环板、承托板、贴板、剪切板以及梁，均用S4R壳单元模拟，其中剪切板和梁之间通过摩擦型高强螺栓相连。由于在本文的研究中螺栓位置的应力不是研究重点，试验过程中也没有在螺栓所在区域发生破坏，故在此区域不单独建立螺栓的精细化模型，而是在螺栓孔的位置将剪切板和梁绑定在一起，用于模拟摩擦型螺栓带来的约束作用。板件厚度、几何尺寸均与试件测量结果保持一致。除此之外，还用C3D8R实体单元模拟试验过程中试件顶端的加载梁。
有限元模型中材料本构关系是滞回试验模拟关注的重点，混凝土采用损伤塑性模型，钢材选取双折线模型，具体数值依据材性试验的结果进行设置。混凝土采用ABAQUS中的损伤塑性模型，定义混凝土的弹性模量为30.6 GPa，泊松比为0.2，混凝土轴心抗压强度为32.5 MPa，损伤塑性模型中的基本参数采用默认值[34]，具体数值见表5。组合墙内填的混凝土在外侧波形钢板的约束下，承载性能有一定程度的提高。波形钢板对内部混凝土的约束效应，以及节点区钢管混凝土柱的壁板对内部混凝土的约束效应，在模型中都通过在混凝土本构关系中定义合理的屈服面，以及在钢板和混凝土之间建立合理的的相互作用关系来实现。由于组合墙中内填的混凝土无钢筋约束，同时根据已有研究结果[24, 34]，采用素混凝土的本构模型能够很好地模拟组合墙中的混凝土，所以在有限元模型中采用过镇海曲线来模拟混凝土的应力-应变关系[24, 34]，损伤因子的选取参考《混凝土结构设计规范》(GB 50010−2010)[38-39]。钢材的本构关系采取双折线弹塑性模型，为考虑在循环荷载作用下钢材的包辛格效应[40]，强化方式选取随动强化，按照材性试验结果进行取值，根据钢板厚度的不同钢材弹性模量的取值在202 GPa~207 GPa，屈服强度在404 MPa~442 MPa，极限强度在530 MPa~569 MPa。在不考虑材料的损伤时，材料在塑性阶段的强度会缓慢增加，而实际上钢材在往复荷载的作用下会发生强度和刚度的退化。为了模拟这一现象，在钢材的本构关系中还叠加了金属的延性损伤(ductile damage)模型。延性损伤模型包含损伤起始准则和损伤演化准则2个部分：将损伤起始准则中的等效塑性损伤应变εpl与应力三轴度η之间的关系进行简化[41]，简化后二者的关系见式(2)，将损伤演化准则的类型定义为线性损伤，在模型中需要输入钢材拉伸断裂时的等效塑性应变，其值采用钢材拉伸材性试验的试验结果：
{\varepsilon ^{{\text{pl}}}} = \left\{ \begin{aligned} & \infty, \;\;\qquad\qquad\qquad\qquad {\eta \leqslant - 1/3}\\ & {{C_1}/\left( {1 + 3\eta } \right)},\;\;\qquad\qquad {1/3 \leqslant \eta \leqslant 0} \\ & {{C_1} + \left( {{C_2} - {C_1}} \right){{\left( {\eta /{\eta _0}} \right)}^2}},\;\;{0 \leqslant \eta \leqslant {\eta _0}} \\ & {{C_2}{\eta _0}/\eta } ,\;\;\;\qquad\qquad\qquad{{\eta _0} \leqslant \eta } \end{aligned} \right. (2) {C_1} = {C_2}{\left( {\frac{{\sqrt 3 }}{2}} \right)^{1/n}} 式中：C1为钢材平板纯剪切状态下的等效塑性损伤应变；C2为钢材开口圆棒单轴拉伸时的等效塑性损伤应变；η0为一常数，取为1/3[42]；n为钢材的硬化参数，C2和n分别取0.63和0.18[41]。
表 5 混凝土损伤塑性模型基本参数Table 5. Basic parameters of concrete damage plasticity model剪胀角\psi /(^\circ) 流动势
偏移量 \varepsilon双轴受压与单轴受压
极限强度比 {f_{{\rm b}0}}/{f_{{\rm c}0}}不变量
应力比K粘滞
系数 \eta30 0.1 1.16 0.6667 0.0005 试验试件中各个部件之间的相互作用关系如图17所示。钢板和混凝土之间采取接触单元，钢材和混凝土、钢材和钢材之间切向相互作用定义为库仑摩擦，摩擦系数分别为0.6和0.45[38]。U形外环板、剪切板与一字形组合墙的钢板通过合并(merge)形成一个整体，用于模拟彼此之间的焊接连接；贴板和组合墙边缘构件的钢管柱之间通过8条角焊缝连接，通过绑定(tie)来模拟这8条角焊缝；梁的上翼缘与外环板之间通过绑定的方式模拟二者之间的焊接连接；在摩擦型高强螺栓所在位置，利用绑定约束剪切板和梁腹板，简化模拟高强螺栓带来的约束效应。
![]()
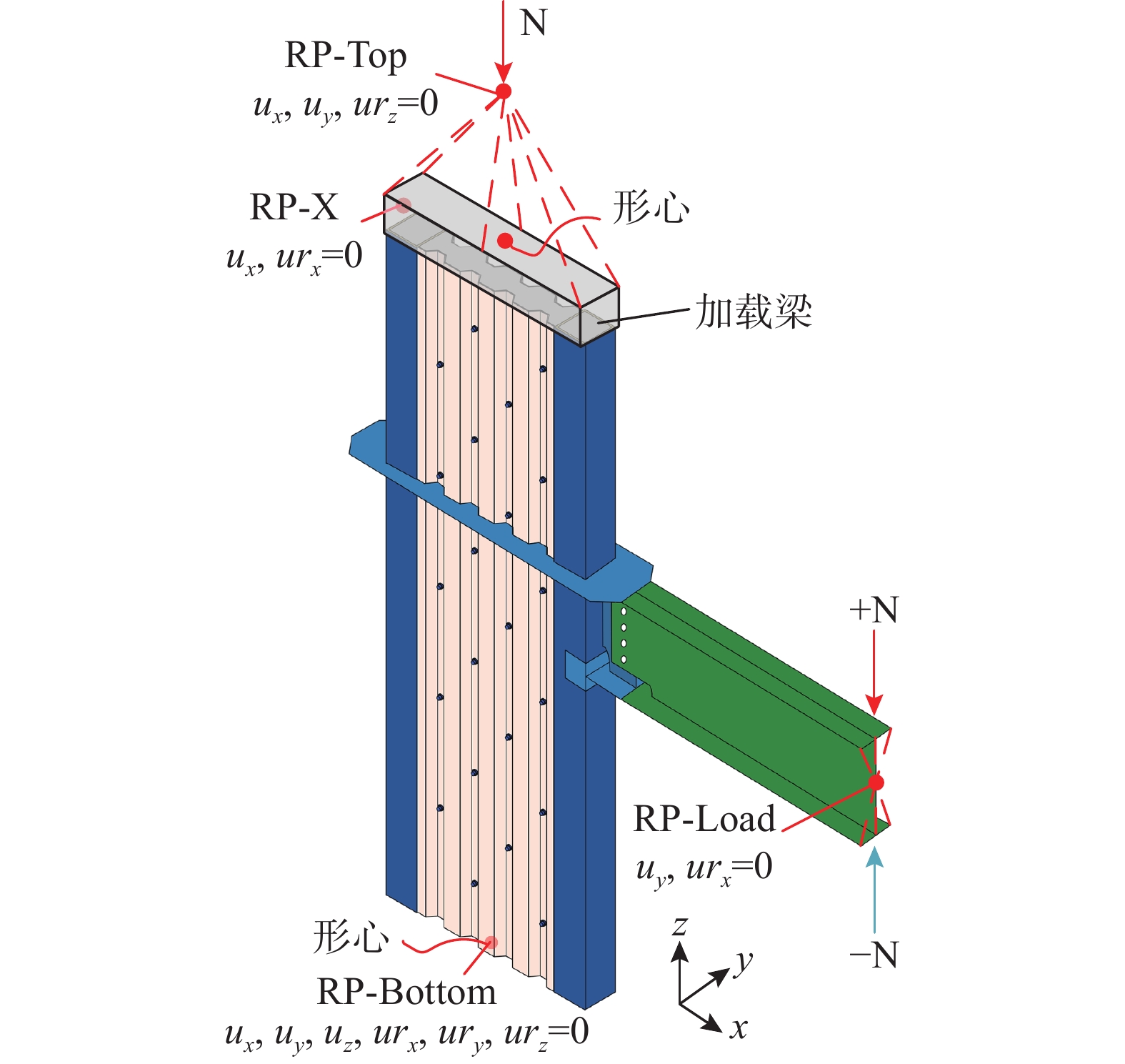
图 17 墙梁节点模型各部件相互连接与作用图Figure 17. Schematic diagram of the interaction between the components of the wall-beam joint model有限元模型的边界条件如图18所示。组合墙的底面和参考点RP-Bottom通过 耦合绑定在一起，通过参考点来实现边界条件的施加。试验发现试件的刚性底座在水平方向上位移几乎为0，可以实现组合墙底部固接的边界条件，故约束RP-Bottom所有平动和转动自由度；组合墙的顶面和加载梁的底面绑定在一起，加载梁的北侧和水平作动器相连，水平作动器用于约束组合墙顶面在面内水平方向的移动，故将加载梁的北侧面和参考点RP-X绑定，约束RP-X的平动自由度ux和转动自由度urx；试验通过竖向千斤顶向组合墙施加竖向轴压力N，将参考点RP-Top设置在球铰的中心点，RP-Top距离组合墙顶面1.15 m，将RP-Top与加载梁顶面绑定，同时约束RP-Top水平平动自由度ux、uy以及转动自由度urz，并在试验过程中施加恒定竖向轴压力N；在加载点的梁截面中心设置参考点RP-Load，将RP-Load和梁截面绑定。由于用钢框架在梁的加载点位置约束梁的面外位移和转动，约束RP-Load的面外水平平动自由度uy和转动自由度urx，通过在RP-Load上施加沿竖直方向(uz方向)的位移，来实现节点处荷载的加载，其中规定RP-Load向下移动(uz负方向)为正向加载，RP-Load向上移动(沿着uz正方向)为负向加载，加载制度则和试验过程中的实际加载制度保持一致。
![]()
图 18 有限元模型边界条件示意图Figure 18. Schematic diagram of the boundary conditions of the FE model有限元模型网格划分采用结构化网格划分。当组合墙部分的网格划分取最小边长为50 mm、节点区域单元网格边长取20 mm时，继续加密网格计算结果变化不超过5%，认为此时的网格尺寸能够满足精度和计算效率的要求。有限元分析方法采用弹塑性大挠度非线性分析方法。
3.2 有限元计算结果
利用建立的组合墙-梁连接节点的有限元模型，模拟整个试验加载过程。主要对试件的荷载-位移曲线、骨架曲线以及加载过程中的破坏现象进行对比，考察有限元模型模拟试验过程的准确性。
1) 试验试件1(设计轴压比0.35)
对比试验和有限元模拟得到的梁端荷载-梁端竖向位移滞回曲线和骨架曲线，如图19(a)、图19(b)所示。有限元和试验的骨架曲线、滞回曲线在达到极限状态前都基本重合，但由于有限元模型无法模拟钢板的开裂，试验滞回曲线在贴板角焊缝开裂后强度和刚度不断退化，而有限元模型滞回曲线始终较为饱满，最终有限元模型在正、负向加载时计算得到的极限承载力都略高于试验值。
![]()
图 19 试件1有限元模拟试件破坏过程Figure 19. The FE simulation of specimen failure process of the specimen 1对比试验和有限元模拟结果发现，在试验加载过程，在负向加载到位移角为1/53时，贴板底侧角焊缝的两端开裂，而在位移角增大到1/44时，如图8 (b)所示，贴板底侧整条角焊缝完全开裂，而在有限元模拟中，如图19(c)有限元应力云图所示，红色区域表示钢板应力接近屈服应力，可以看到贴板底侧角焊缝位置应力较大、钢板基本屈服，但无法模拟焊缝开裂；在试验加载过程，正向加载到极限状态时，如图8(c)、图8(d)所示，外环板和柱钢管之间的焊缝开裂、节点区柱钢管开裂，而从图19(d)、图19(e)有限元应力云图上可以看到在这两个位置钢板的应力较大，但同样无法模拟焊缝和钢板的开裂。试件最终破坏时整体的应力云图如图19(f)所示，可以看到应力较大区域集中在节点区域以及与节点相连的钢管混凝土柱，节点加载对组合墙波形部分的应力影响较小。
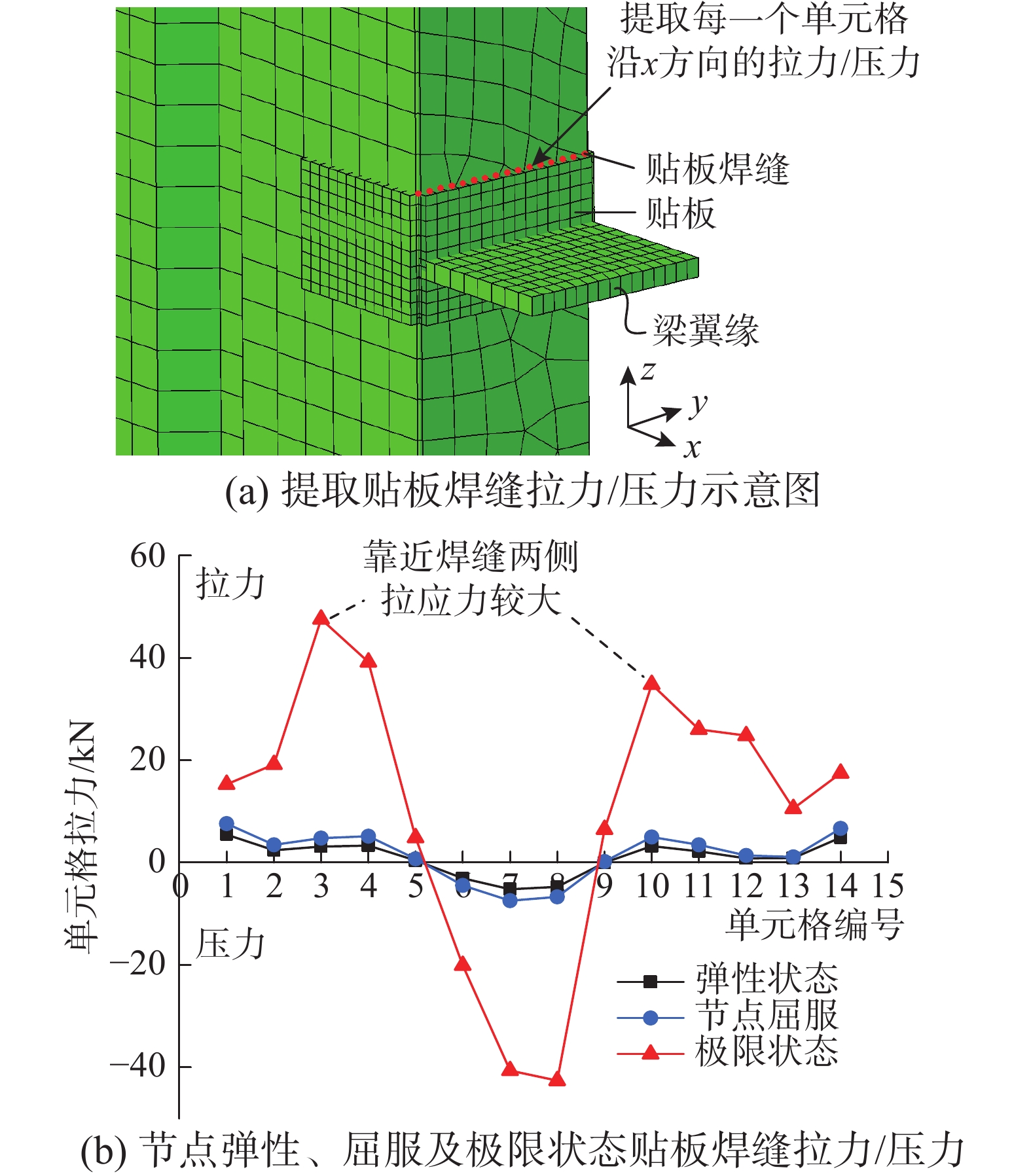
在梁下翼缘位置，提取贴板与边缘构件壁板之间水平焊缝的拉力，其拉力分布及幅值可以反映出贴板角焊缝的应力集中程度。如图20所示，在节点屈服之前，贴板焊缝拉力沿焊缝宽度分布比较均匀，应力集中程度不明显；当荷载加载到节点抗弯极限状态，其焊缝拉力分布严重不均匀，靠近焊缝两侧的拉力较大，焊缝拉应力集中程度更加严重，这说明了焊缝拉应力峰值是导致图8(a)中试件贴板水平角焊缝两端区域最先开裂的原因。
![]()
图 20 试件1贴板焊缝拉力/压力分布及幅值Figure 20. Tension/compression distribution and amplitude of the weld of the specimen 12) 试验试件2(设计轴压比0.50)
对比试验和有限元模拟得到的梁端荷载-梁端竖向位移滞回曲线和骨架曲线，如图21(a)、图21(b)所示。骨架曲线基本重合，极限承载力与试验值吻合得很好；有限元模拟得到的滞回曲线与试验滞回曲线在贴板底侧焊缝开裂前基本吻合，焊缝开裂后，试验滞回曲线在负向加载时的刚度和强度退化更显著。
![]()
图 21 试件2有限元模拟试件破坏过程Figure 21. The FE simulation of specimen failure process of the specimen 2对比试验加载和有限元模拟结果发现，在试验加载过程，当负向加载到位移角为1/53时，如图9(b)所示，贴板底侧整条角焊缝完全开裂，在角焊缝开裂后，节点的刚度不断退化；而在有限元模拟中，如图21(c)有限元应力云图所示，红色区域表示钢板应力接近屈服应力，灰色区域表示应力超过屈服应力，可以看到贴板底侧角焊缝位置应力较大、周围钢板大于屈服应力440 MPa，节点区域塑性区的扩展造成了节点刚度和强度的下降，但仍然比不上试验中焊缝开裂导致的退化。试件最终破坏时整体的应力云图如图21(d)所示，应力较大区域集中在节点区域以及与节点相连的钢管混凝土柱，节点加载对组合墙波形部分的应力影响较小。
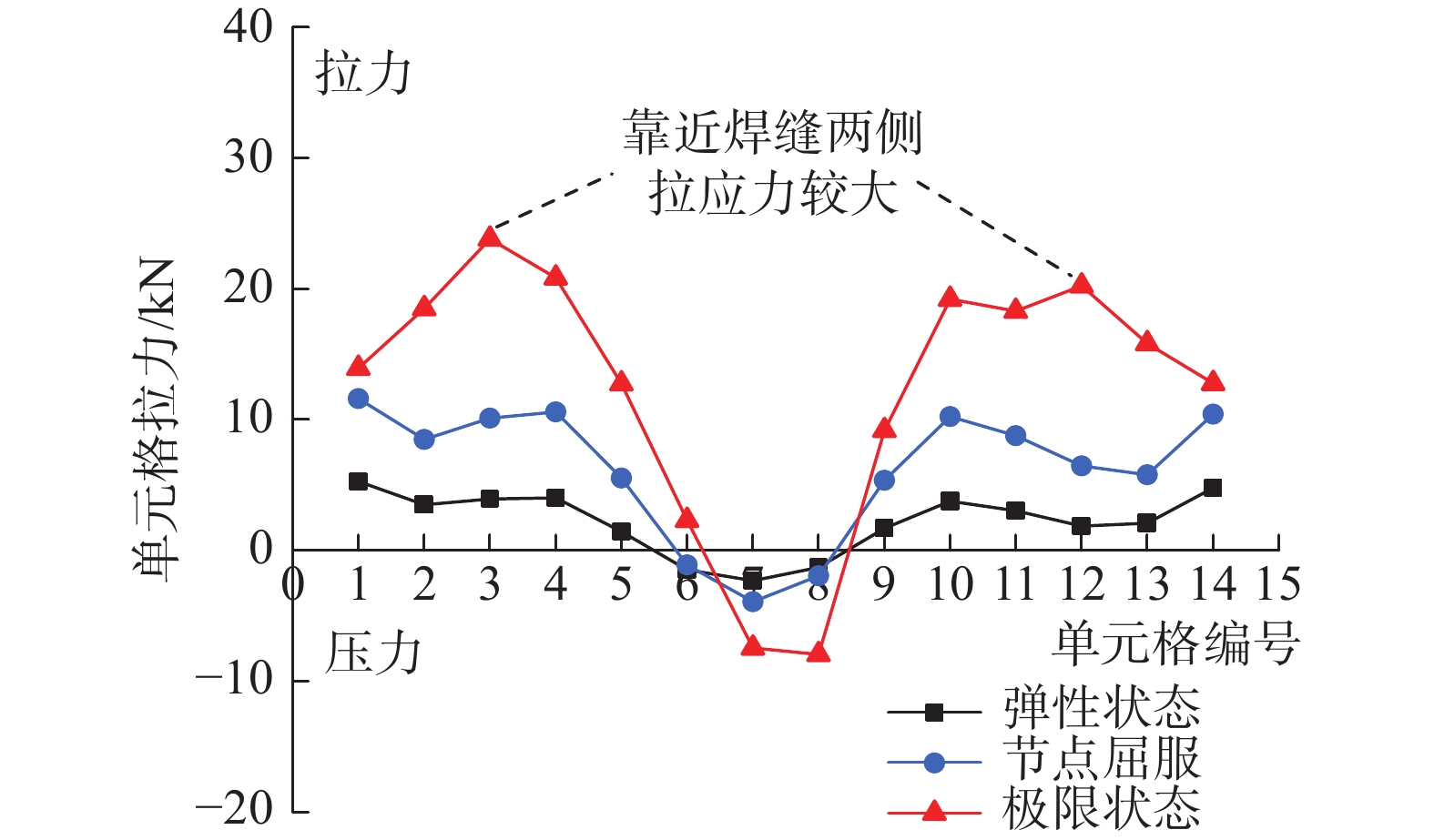
在梁下翼缘位置提取贴板与边缘构件壁板之间的焊缝拉力如图22所示。在靠近焊缝两侧的位置，焊缝拉力最大。在节点加载到极限状态时，焊缝拉力沿其宽度分布更不均匀。此时，焊缝两侧峰值拉力是导致焊缝最先开裂破坏的主要原因。
![]()
图 22 试件2贴板焊缝拉力/压力分布及幅值Figure 22. Tension/compression distribution and amplitude of the weld of the specimen 2对比试验结果和有限元模拟结果如表6所示。有限元能较好地预测试件屈服时的承载力，误差在5%以内；但是在部分情况下会高估节点的峰值承载力，最大误差为13.5%，误差主要是由于有限元模型无法模拟焊缝的开裂。
表 6 对比试验和有限元在节点屈服和达到峰值时的结果Table 6. Comparing tests and FE results at yield and peak stages试件
编号加载
方向屈服 峰值 试验/
kN有限元/
kN相对
误差/(%)试验/
kN有限元/
kN相对
误差/(%)试件1 正向 167.3 161.8 −3.3 200.2 211.2 5.5 负向 83.9 83.2 −0.8 163.4 185.4 13.5 试件2 正向 164.0 156.0 −4.9 176.3 176.7 0.2 负向 97.2 96.8 −0.4 156.9 162.6 3.6 3.3 小结
从有限元模拟和试验结果对比可以看到，在试件的钢板和焊缝发生开裂前，有限元模型能非常好的模拟节点区的应力状态、节点承载力以及节点的刚度；而当钢板或者焊缝开裂之后，试件通常达到极限状态，之后继续加载会导致节点承载力下降以及节点刚度退化。有限元模型目前无法模拟焊缝开裂这一破坏现象，导致在某些情况下有限元计算得到节点承载力高于试验结果，滞回曲线也比试验更加饱满。但是，有限元模型仍能够很好地评估节点的极限承载力，同时能够很好地模拟试验过程中节点的应力和变形发展。有限元模拟计算结果也揭示了节点焊缝应力集中程度的严重性，焊缝峰值应力是焊缝早先开裂破坏的真实原因。因此，后续研究工作建议，对影响焊缝应力集中程度的因素进行研究与分析，建立焊缝峰值应力的计算方法，确保焊缝强度设计安全。
4 结论
本文对不同轴压比的波形钢板-混凝土组合墙边缘构件-梁连接节点进行了滞回试验，试件梁采用上翼缘外环板节点和贴板节点的组合形式。试验研究了节点的承载性能、滞回性能、破坏模式，建立了有限元模型并模拟了整个试验过程，获得结论如下：
(1) 滞回加载过程中节点剪切变形较小，非剪切变形为主要变形，无论是外环板式节点还是贴板式节点，破坏模式均为节点受拉侧发生钢板或焊缝的断裂破坏。当贴板节点受拉时，破坏形式主要表现为贴板和边缘构件之间的焊缝开裂；而当外环板节点受拉时，主要发生外环板和边缘构件之间焊缝开裂，以及节点区柱钢板开裂。梁翼缘节点受拉侧的承载力决定整个节点的抗弯承载力，且随着轴压比的增大，节点的抗弯承载力会降低，但是不会改变节点的破坏模式。
(2) 两个试件破坏时，贴板节点屈服位移角平均值为1/136，极限位移角为1/42，满足规范规定的弹性和弹塑性层间位移角的要求。试验发现，贴板节点的变形能力弱于外环板节点，贴板节点在贴板焊缝开裂后强度和刚度迅速退化。在对贴板节点的承载力计算时，需要考虑焊缝应力集中对焊缝承载力的影响，并采取其他加强焊缝的措施。
(3) 利用有限元软件ABAQUS建立了精细化的实体-壳单元的墙边缘构件-梁连接节点有限元模型。有限元计算结果和试验数据对比验证了有限元模型的有效性，虽然有限元模型尚不能模拟钢板的开裂，但仍然能够精确地预测节点的极限承载力和破坏模式。本文有限元计算结果和试验结果表明，为防止贴板节点焊缝断裂破坏，需要进一步建立相应焊缝强度的设计计算方法。
-
![]()
图 3 墙边缘构件与梁连接节点及细部构造
Figure 3. Connections and details of wall boundary element-beam joint
![]()
图 17 墙梁节点模型各部件相互连接与作用图
Figure 17. Schematic diagram of the interaction between the components of the wall-beam joint model
![]()
图 18 有限元模型边界条件示意图
Figure 18. Schematic diagram of the boundary conditions of the FE model
![]()
图 19 试件1有限元模拟试件破坏过程
Figure 19. The FE simulation of specimen failure process of the specimen 1
![]()
图 20 试件1贴板焊缝拉力/压力分布及幅值
Figure 20. Tension/compression distribution and amplitude of the weld of the specimen 1
![]()
图 21 试件2有限元模拟试件破坏过程
Figure 21. The FE simulation of specimen failure process of the specimen 2
![]()
图 22 试件2贴板焊缝拉力/压力分布及幅值
Figure 22. Tension/compression distribution and amplitude of the weld of the specimen 2
表 1 混凝土材性试验结果
Table 1 Concrete material property test results
材性试验
编号混凝土立方块
抗压强度fcu,m/MPa混凝土
弹性模量Ec/MPaC-1 40.96 − C-2 47.55 − C-3 45.95 − C-4 42.53 17693 C-5 37.14 18390 平均值 42.83 18042 
下载: 导出CSV
表 2 钢材材性试验结果
Table 2 Steel material property test results
材性试验
编号钢材弹性
模量Es/GPa屈服强度
fy/MPa抗拉强度
fu/MPa抗拉应变
εu/(%)S4-1 193.9 386.6 525.6 14.33 S4-2 208.3 419.6 568.7 13.96 S4-3 202.6 406.4 554.2 13.33 S4-4 216.7 400.8 554.6 16.62 S4-5 212.7 405.3 551.1 13.86 平均值 206.8 403.7 550.8 14.39 S6-1 201.6 438.0 567.9 16.24 S6-2 199.3 445.1 569.2 13.38 S6-3 204.4 444.3 569.0 13.59 平均值 201.8 442.4 568.7 14.40 S10-1 207.1 410.5 530.9 19.40 S10-2 207.2 410.1 531.7 18.57 S10-3 203.6 410.4 528.9 18.67 平均值 205.9 410.3 530.5 18.88
下载: 导出CSV
表 3 试件在达到屈服、峰值和破坏时的荷载和位移
Table 3 Loads and displacement angles of specimens at yield, peak and failure stages
试件编号 加载方向 屈服 峰值 破坏 位移角/rad 荷载/kN 位移角/rad 荷载/kN 位移角/rad 荷载/kN 试件1 正向 1/68 167.3 1/23 200.2 1/19 173.1 负向 1/192 83.9 1/66 163.4 − − 试件2 正向 1/76 164.0 1/28 176.3 1/20 162.2 负向 1/105 97.2 1/50 156.89 1/42 136.9
下载: 导出CSV
表 4 对比不同类型节点的弹性和弹塑性层间位移角
Table 4 Comparison of elastic and elastoplastic interlayer displacement angles of different types of joints
下载: 导出CSV
表 5 混凝土损伤塑性模型基本参数
Table 5 Basic parameters of concrete damage plasticity model
剪胀角\psi /(^\circ) 流动势
偏移量 \varepsilon双轴受压与单轴受压
极限强度比 {f_{{\rm b}0}}/{f_{{\rm c}0}}不变量
应力比K粘滞
系数 \eta30 0.1 1.16 0.6667 0.0005
下载: 导出CSV
表 6 对比试验和有限元在节点屈服和达到峰值时的结果
Table 6 Comparing tests and FE results at yield and peak stages
试件
编号加载
方向屈服 峰值 试验/
kN有限元/
kN相对
误差/(%)试验/
kN有限元/
kN相对
误差/(%)试件1 正向 167.3 161.8 −3.3 200.2 211.2 5.5 负向 83.9 83.2 −0.8 163.4 185.4 13.5 试件2 正向 164.0 156.0 −4.9 176.3 176.7 0.2 负向 97.2 96.8 −0.4 156.9 162.6 3.6
下载: 导出CSV
-
[1] CAO S, SHU G, LIN K, et al. Experimental seismic behaviour of bottom-through-diaphragm and top-ring connection to SST columns [J]. Journal of Constructional Steel Research, 2018, 150: 249 − 260.
[2] DOUNG P, SASAKI E. Load-deformation characteristics and performance of internal diaphragm connections to box columns [J]. Thin-Walled Structures, 2019, 143: 106221.
[3] RONG B, LIU S, YAN J B, et al. Shear behaviour of panel zone in through-diaphragm connections to steel tubular columns [J]. Thin-Walled Structures, 2018, 122: 286 − 299.
[4] 樊健生, 周慧, 聂建国, 等. 空间钢-混凝土组合节点抗震性能试验研究[J]. 土木工程学报, 2014, 47(4): 47 − 55. FAN Jiansheng, ZHOU Hui, NIE Jianguo, et al. Experimental study on seismic performance of three-dimensional composite beam-to-column joints [J]. China Civil Engineering Journal, 2014, 47(4): 47 − 55. (in Chinese)
[5] 何子奇, 胡盛文, 李彬洋, 等. 钢管混凝土异形柱-H型钢梁框架节点抗震性能研究[J]. 建筑结构学报, 2021, 225: 1 − 12. HE Ziqi, HU Shengwen, LI Binyang, et al. Research on seismic behavior of interior joint between special-shaped CFST column and H-section steel beam [J]. Journal of Building Structures, 2021, 225: 1 − 12. (in Chinese)
[6] 林彦, 周学军, 姜伟, 等. 方钢管混凝土柱-外包钢混凝土组合梁连接节点滞回性能分析[J]. 土木工程学报, 2015, 48(12): 72 − 81. LIN Yan, ZHOU Xuejun, JIANG Wei, et al. Analysis on hysteretic behavior of concrete-filled square steel tubular column to steel-encased concrete composite beam connections [J]. China Civil Engineering Journal, 2015, 48(12): 72 − 81. (in Chinese)
[7] 刘用, 郭兰慧, 张素梅. 方钢管混凝土柱-外包U形钢混凝土组合梁节点抗震性能试验研究[J]. 建筑结构学报, 2018, 39(6): 131 − 140. LIU Yong, GUO Lanhui, ZHANG Sumei. Cyclic loading tests of composite joints between concrete-filled square steel tubular column and composite beam with U-shaped steel girder [J]. Journal of Building Structures, 2018, 39(6): 131 − 140. (in Chinese)
[8] 王文达, 陈润亭. 方钢管混凝土柱-外环板式组合梁节点在地震损伤后的耐火性能分析[J]. 工程力学, 2021, 38(3): 73 − 85. doi: 10.6052/j.issn.1000-4750.2020.04.0259 WANG Wenda, CHEN Runting. Analysis on the fire resistance of square concretefilled steel tubular column to composite beam with outer ring plate connections after earthquake damage [J]. Engineering Mechanics, 2021, 38(3): 73 − 85. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.04.0259
[9] 徐桂根, 聂建国. 方钢管混凝土柱内隔板贯通式节点核心区抗震性能的试验研究[J]. 土木工程学报, 2011, 44(8): 25 − 32. XU Guigen, NIE Jianguo. Experimental study of connections of concrete-filled square steel tubular columns with continuous diaphragms [J]. China Civil Engineering Journal, 2011, 44(8): 25 − 32. (in Chinese)
[10] CECS 159: 2004, 矩形钢管混凝土结构技术规程 [S]. 北京: 中国计划出版社, 2004. CECS 159: 2004, Technical specification for structures with concrete-filled rectangular steel tube members [S]. Beijing: China Planning Press, 2004. (in Chinese)
[11] GHOBADI M S, GHASSEMIEH M, MAZROI A, et al. Seismic performance of ductile welded connections using T-stiffener [J]. Journal of Constructional Steel Research, 2009, 65(4): 766 − 775. doi: 10.1016/j.jcsr.2008.05.007
[12] KANG C H, SHIN K J, OH Y S, et al. Hysteresis behavior of CFT column to H-beam connections with external T-stiffeners and penetrated elements [J]. Engineering Structures, 2001, 23(9): 1194 − 1201. doi: 10.1016/S0141-0296(00)00119-X
[13] KANG C H, KIM Y J, SHIN K J, et al. Experimental investigation of composite moment connections with external stiffeners [J]. Advances in Structural Engineering, 2013, 16(10): 1683 − 1700. doi: 10.1260/1369-4332.16.10.1683
[14] SHIN K J, KIM Y J, OH Y S. Seismic behaviour of composite concrete-filled tube column-to-beam moment connections [J]. Journal of Constructional Steel Research, 2008, 64(1): 118 − 127. doi: 10.1016/j.jcsr.2007.04.001
[15] SHIN K J, KIM Y J, OH Y S, et al. Behavior of welded CFT column to H-beam connections with external stiffeners [J]. Engineering Structures, 2004, 26(13): 1877 − 1887. doi: 10.1016/j.engstruct.2004.06.016
[16] 付波, 王彦超, 童根树. 矩形钢管混凝土柱-H形钢梁外顶板式节点抗震性能试验研究[J]. 工程力学, 2020, 37(7): 125 − 137. doi: 10.6052/j.issn.1000-4750.2019.08.0474 FU Bo, WANG Yanchao, TONG Genshu. Experimental study on the seismic behavior of cfst rectangular column to H-section steel beam connections with external stiffeners [J]. Engineering Mechanics, 2020, 37(7): 125 − 137. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.08.0474
[17] 李杰, 陈志华, 张晓萌, 等. 无边缘构件钢管束剪力墙的墙梁节点抗震性能试验研究[J]. 振动与冲击, 2016, 35(21): 159 − 165. LI Jie, CHEN Zhihua, ZHANG Xiaomeng, et al. Tests for aseismic performance of connections between bundled lipped channel-concrete (BLC-C) composite walls and steel beams [J]. Journal of Vibration and Shock, 2016, 35(21): 159 − 165. (in Chinese)
[18] TONG G, HU Z, CHEN Y. Study on the moment capacity of a connection joining an I-beam to concrete-filled multicellular steel tube walls [J]. Journal of Constructional Steel Research, 2021, 182: 106643. doi: 10.1016/j.jcsr.2021.106643
[19] 胡立黎, 尹卫泽. 钢梁与钢管混凝土束剪力墙端板式刚接节点[J]. 工程力学, 2020, 37(6): 60 − 64. doi: 10.6052/j.issn.1000-4750.2019.05.ST03 HU Lili, YIN Weize. A rigid joint of steel beam-to-shear wall formed by concrete-filled multicellular steel tubes [J]. Engineering Mechanics, 2020, 37(6): 60 − 64. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.05.ST03
[20] 赵均海, 樊军超, 高伟琪. H型钢梁与矩形钢管混凝土柱平齐式端板单边螺栓连接节点弯矩-转角分析模型[J]. 工程力学, 2021, 38(6): 91 − 102. doi: 10.6052/j.issn.1000-4750.2020.07.0436 ZHAO Junhai, FAN Junchao, GAO Weiqi. Moment-rotation analysis model of flush end-plate bolted connections between H-shaped steel beams and rectangular cfst columns [J]. Engineering Mechanics, 2021, 38(6): 91 − 102. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.07.0436
[21] 付波, 童根树. 一种基于加强板厚度设计的带状加强式节点 [P/OL]. 中国: CN109779038B, 2019. FU Bo, TONG Genshu. A ribbon-reinforced node designed based on the thickness of the reinforcement plate [P/OL]. China: CN109779038B, 2019. (in Chinese)
[22] 王彦超, 付波, 周耀彬, 等. H型钢梁与宽钢管混凝土柱短边连接的带状加强式节点 [P/OL]. 中国: CN207314550U, 2017. WANG Yanchao, FU Bo, ZHOU Yaobin, et al. Ribbon reinforced joint connecting H-shaped steel beam and short side of wide CFST column [P/OL]. China: CN207314550U, 2017. (in Chinese)
[23] 郭彦林, 朱靖申. 剪力墙的型式、设计理论研究进展[J]. 工程力学, 2020, 37(6): 19 − 33. doi: 10.6052/j.issn.1000-4750.2019.08.0432 GUO Yanlin, ZHU Jingshen. Research progress of shear walls: Types and design methods [J]. Engineering Mechanics, 2020, 37(6): 19 − 33. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.08.0432
[24] ZHU J S, GUO Y L, WANG M Z, et al. Seismic performance of concrete-infilled double steel corrugated-plate walls: Experimental research [J]. Engineering Structures, 2020, 215: 110601-1 − 110601-18. doi: 10.1016/j.engstruct.2020.110601
[25] JGJ/T 101−2015, 建筑抗震试验规程 [S]. 北京: 中国建筑工业出版社, 2015. JGJ/T 101−2015, Specification for seismic test of buildings [S]. Beijing: China Architecture & Building Press, 2015. (in Chinese)
[26] GB/T 50081−2002, 普通混凝土力学性能试验方法标准 [S]. 北京: 中国建筑工业出版社, 2003. GB/T 50081−2002, Standard for test method of mechanical properties on ordinary concrete [S]. Beijing: China Architecture & Building Press, 2003. (in Chinese)
[27] GB/T 228.1−2021, 金属材料 拉伸试验 第1部分: 室温试验方法 [S]. 北京: 中国标准出版社, 2022. GB/T 228.1−2021, Metallic materials—Tensile testing—Part 1: Method of test at room temperature [S]. Beijing: Standards Press of China, 2022. (in Chinese)
[28] 冯鹏, 强翰霖, 叶列平. 材料、构件、结构的“屈服点”定义与讨论[J]. 工程力学, 2017, 34(3): 36 − 46. doi: 10.6052/j.issn.1000-4750.2016.03.0192 FENG Peng, QIANG Hanlin, YE Lieping. Discussion and definition on yield points of materials, members and structures [J]. Engineering Mechanics, 2017, 34(3): 36 − 46. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.03.0192
[29] GB 50011−2010, 建筑抗震设计规范 [S]. 北京: 中国建筑工业出版社, 2016. GB 50011−2010, Code for seismic design of buildings [S]. Beijing: Standards Press of China, 2016. (in Chinese)
[30] 徐礼华, 凡红, 刘胜兵, 等. 方钢管混凝土柱-钢梁节点抗震性能试验研究与有限元分析[J]. 工程力学, 2008, 25(2): 122 − 131. XU Lihua, FAN Hong, LIU Shengbing, et al. Experimental studies on aseismic behavior of connection between concrete-filled steel square tubular column and steel beam [J]. Engineering Mechanics, 2008, 25(2): 122 − 131. (in Chinese)
[31] GUO Y L, ZHU J S, WANG M Z, et al. Overall instability performance of concrete-infilled double steel corrugated plate wall [J]. Thin-Walled Structures, 2018, 130: 372 − 394. doi: 10.1016/j.tws.2018.05.026
[32] WANG M Z, GUO Y L, YANG X, et al. Interaction equations of composite walls with T-section under axial compression and biaxial bending [J]. Engineering Structures, 2021, 229: 111667-1 − 111667-21. doi: 10.1016/j.engstruct.2020.111667
[33] WANG M Z, GUO Y L, ZHU J S, et al. Flexural-torsional buckling and design recommendations of axially loaded concrete-infilled double steel corrugated-plate walls with T-section [J]. Engineering Structures, 2020, 208: 110345.1 − 110345.13. doi: 10.1016/j.engstruct.2020.110345
[34] WANG M Z, GUO Y L, ZHU J S, et al. Flexural buckling of axially loaded concrete-infilled double steel corrugated-plate walls with T-section [J]. Journal of Constructional Steel Research, 2020, 166: 105940.1 − 105940.17. doi: 10.1016/j.jcsr.2020.105940
[35] WANG M Z, GUO Y L, ZHU J S, et al. Sectional strength design of concrete-infilled double steel corrugated-plate walls with T-section [J]. Journal of Constructional Steel Research, 2019, 160: 23 − 44. doi: 10.1016/j.jcsr.2019.05.017
[36] WANG Y, GUO Y, WANG M. Research progress of concrete-infilled double steel corrugated-plate composite walls with T-section [J]. Industrial Construction, 2021, 51(4): 181 − 8.
[37] ZHU J S, GUO Y L, WANG M Z, et al. Strength design of concrete-infilled double steel corrugated-plate walls under uniform compressions [J]. Thin-Walled Structures, 2019, 141: 153 − 174. doi: 10.1016/j.tws.2019.02.021
[38] 李威. 圆钢管混凝土柱-钢梁外环板式框架节点抗震性能研究 [D]. 北京: 清华大学, 2011. LI Wei. Study on the seismic performance of circular concrete-filled steel tubular column to steel beam joint with external diaphragm [D]. Beijing: Tsinghua University, 2011. (in Chinese)
[39] GB 50010−2010, 混凝土 结构设计规范 [S]. 北京: 中国建筑工业出版社, 2011. GB 50010−2010, Code for design of concrete structures [S]. Beijing: China Architecture & Building Press, 2011. (in Chinese)
[40] 李红孝. 延性金属弹塑性损伤模型研究与应用 [D]. 西安: 西安建筑科技大学, 2014. LI Hongxiao. Ductile metal elastic-plastic damage model research and application [D]. Xi’an: Xi’an University of Architecture and Technology, 2014. (in Chinese)
[41] 周天华, 李文超, 管宇, 等. 基于应力三轴度的钢框架循环加载损伤分析[J]. 工程力学, 2014, 31(7): 146 − 155. doi: 10.6052/j.issn.1000-4750.2013.01.0090 ZHOU Tianhua, LI Wenchao, GUAN Yu, et al. Damage analysis of steel frames under cyclic load based on stress triaxiality [J]. Engineering Mechanics, 2014, 31(7): 146 − 155. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.01.0090
[42] BAO Y, WIERZBICKI T. On fracture locus in the equivalent strain and stress triaxiality space [J]. International Journal of Mechanical Sciences, 2004, 46: 81 − 98.
-
期刊类型引用(2)
1. 刘磊，贾苑松. 波纹腹板钢梁及节点的研究现状及展望. 大众标准化. 2024(12): 43-45 . 
百度学术
2. 周凌宇，刘家豪，方蛟鹏，刘晓春，石敬州，戴超虎. 装配式双槽钢拼合PEC柱受压性能试验研究. 天津大学学报(自然科学与工程技术版). 2024(06): 642-653 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 386
- HTML全文浏览量: 298
- PDF下载量: 83
- 被引次数: 2
