REPRESENTATION AND RECONSTRUCTION OF FLOW AROUND BRIDGE DECK USING TIME HISTORY DEEP LEARNING
-
摘要: 流场特性的研究是结构风工程的核心问题，而高分辨率的流场数据对解决风致振动问题、探索流固耦合机理具有着重要意义。受测量方法、计算效率等因素限制，高空间分辨率的流场时程数据的直接获取仍有一定困难。该文基于流场时程数据的表征模型，提出了桥面非定常流动时程重构的深度学习方法。基于一维卷积方法建立了非定常桥面绕流场的表征模型，得到了物理空间与表征模型的编码空间之间的映射关系，最后利用表征模型的解码器生成未知测点处的流场时程数据。对较低雷诺数桥梁主梁的非定常绕流流场进行了研究与验证，实现了桥面绕流的时程数据重构，验证了方法的准确性与可行性。该文所提方法基于流场的时程数据进行表征与重构，可广泛应用于工程中基于一点的传感器数据处理，是一种桥面流场数据分析的新方法。Abstract: High-resolution flow field data has a great significance to the study of fluid induced vibration and vortex induced vibration mechanism. Limited by measurement methods and calculation efficiency, it is still difficult to obtain high-resolution flow fields. Thusly, the low-dimensional representation model of flow time history data is adopted, and a deep learning method is proposed for the reconstruction of unsteady flow time history data. A low-dimensional representation model is established for the unsteady flow field based on the one-dimensional convolution method; The mapping relationship is developed between the physical space and the encoding space; The decoder in the representation model is utilized to generate the flow field time history data at any position. The problem of unsteady flow around bridge deck is verified, and the accuracy of the method is proved. The method proposed is a high-precision flow field data reconstruction method in the time dimension, and it is an unsupervised training method. It is a brand-new method that can be widely used in point-based sensor data processing.
-
Keywords:
- flow reconstruction /
- flow time history /
- deep learning /
- feature extraction /
- unsupervised model
-
流致振动是工程中常见的现象[1]，工程结构周围的绕流可能会引起结构破坏[2]，流动的能量也可加以利用[3]，因此对绕流流场的分析是研究流致振动等问题的重要方法[4]。然而高分辨率流场的获取仍存在一些困难：在数值模拟方面，高分辨率的流场数据依赖于更多的计算网格，导致求解的效率降低；在流体实验方面，流场中的某些位置可能无法布设传感器，而PIV方法仍难以实现大范围的三维全场测量。针对这些问题，本文基于流场时程的深度学习模型提出了一种具有较高精度的高分辨率流场重构方法。
深度学习方法由于其强大的功能，在流体力学研究中得到了越来越广泛的应用[5]。在计算流体力学湍流模型建模方面，已成为湍流模拟、乃至高维复杂动力系统领域的重要研究方法之一[6]。在流场特征识别的研究中，MURATA等[7]用深度学习方法实现了瞬态流场的模态分解，借助深度学习方法的非线性表征能力，得到了比传统模态分解法方法精度更高的结果。FUKAMI等[8]提出了基于卷积神经网络的流场自动编码模型分析方法，对流场的非线性特征实现了自动表征，且能够保持各流动模态的贡献排序。在守恒控制方程的求解方面，使用嵌入控制方程的深度学习方法为偏微分方程的求解提供了思路。如RAISSI等[9]提出了基于物理信息的深度神经网络方法，建立了求解偏微分方程的全新数值计算框架，同时应用该方法进行了涡激振动圆柱所受升力和阻力的计算预测[10]。
另外，基于深度学习方法的高分辨率流场重构也成为了研究的热点，使得通过部分数据或者低分辨率数据来获取时空的高分辨率结果成为可能。如有监督方法的单层前馈人工神经网络[11]实现了从低分辨率和包含噪声的数据中还原得到真实的流场信息；混合下采样多尺度模型[12]实现了从低分辨率图像重建高分辨率的湍流流场，并能较准确地保留湍流动能谱；多时间路径卷积神经网络[13]以流场速度时程作为输入，可从连续的流体场中提取流场的时变特征；基于无监督学习的循环生成对抗网络[14]使用未配对的湍流数据进行训练来进行超分辨率重建，大大降低了模型对已知训练样本信息的依赖。
上述基于深度学习的流场研究中，面向的数据均为试验或计算的整场瞬态快照(snapshot)[15-16]。然而，实验中的数据采集、特征提取和分析等方面存在着诸多困难。同时，上述研究更多的将流场看作“图片”，采用各种图片重构技术进行处理。而流动规律受NS方程控制，这种复杂的时空耦合效应导致流场的重构应与普通的图像重构有着本质的区别，因此，本文从时程数据的重构角度出发，构建具有时间维度高精度的流动数据。目前，关于流场时程的深度学习研究较少，其中文献[17-18]提出了基于时程数据深度学习的方法对流场特征提取进行研究，为本文的研究提供了依据。
综上，采用深度学习方法对复杂流场进行高分辨率重构是一种极具潜力的方法，而目前基于一维时程数据的流场特征鲜有研究。本文基于一维无量纲时程数据的流场特征低维表征模型，建立了桥面流场时程数据的重构计算框架，并以桥面绕流流场为案例，验证方法的可行性。
1 主梁绕流时程数据
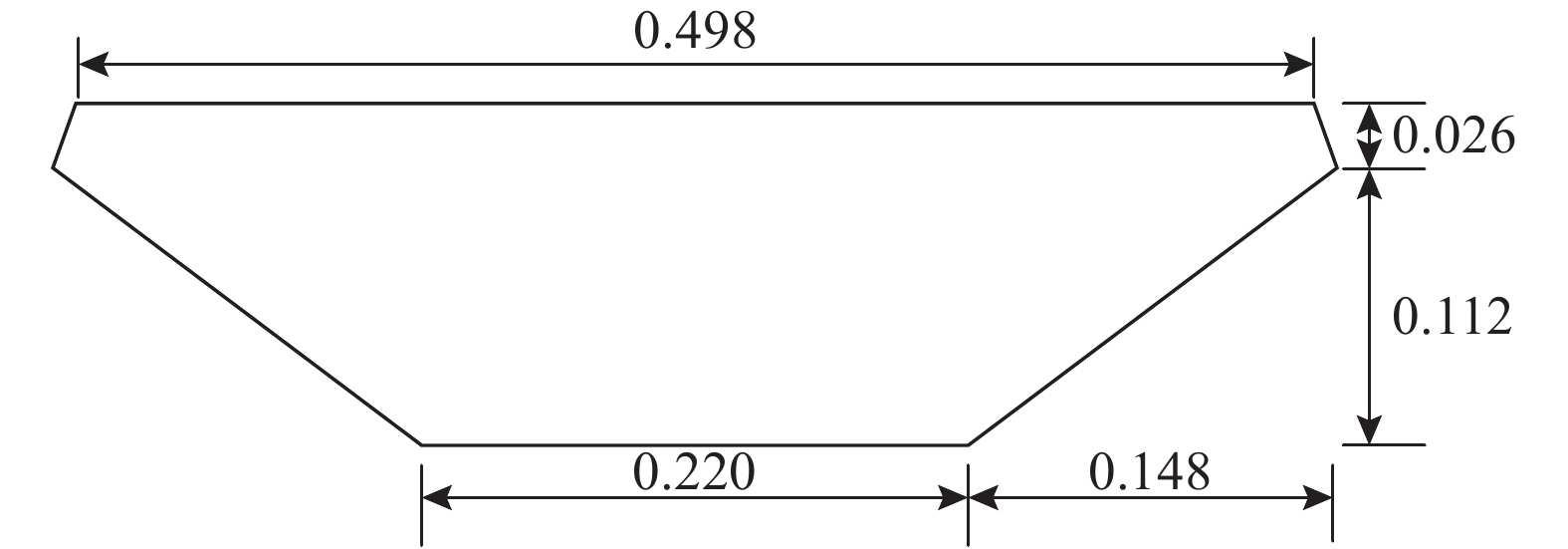
本文所提出的方法以空间测点处的流场时程信号为研究参数，数据的获取可以采用实验获得，也可使用数值方法计算得到。本文采用数值模拟方法获得流场时程数据，以某桥梁主梁为研究对象，其断面形状与尺寸如图1所示，没有考虑栏杆等附属构件对流场的影响。以桥梁高度为特征长度定义的雷诺数Re=1300。
构造如图2所示的绕流计算域，流向长度20L，横向长度20L，其中L为断面的顺流向长度。上游来流区域流向长度10L，下游区域流向长度为10L。为保证计算的准确性，壁面处及尾流区域使用结构化网格。流场左侧边界条件为速度入口，右侧边界条件为出口，上下侧的边界条件为速度入口。在主梁表面附近和尾部流场区域内进行了网格加密，保证大尺度流动模拟的准确，平面内的单层网格约包含29 000个网格。
流场采用自主研发的有限体积桥面绕流软件zFlower[19]获取，其中包含了流场深度学习数据提取模块，实现计算过程中的流场时程数据监测与存储。本算例中在顺流方向(−0.3, 1.3)范围、横向方向(−0.14, 0.12)范围内分别等间距选取180与40排测点，组合成测点集合(去除主梁断面内部的点)，测点集中共包含6269个测点，具体分布如图3所示。
通过数值模拟，得到了桥面绕流时程数据集，各数据集中共6269个时程样本。参考文献[20]对尾流流场的深度学习研究结论，无量纲化的流动时程中包含了尾流的特征，且有利于深度学习模型的训练，因此本文对计算所得到的时程样本进行了归一化处理。同时，选取计算平稳段的时程数据，并随机列出6个压力时程与速度时程样本，见图4。由图4中的时程样本可知，桥面绕流的流场无统一规律可寻，难以采用传统方法准确而全面地描述其特征，因而对稀疏数据的重构具有不小的挑战性。
2 流场时程的降维模型与训练
基于文献[21]等研究，本文建立了适用于桥面绕流流场降维的深度学习模型。模型采用基于卷积的时程自编码模型(FTH-AE)对复杂桥面绕流系统进行降维表征。网络各层卷积核大小为41，可以感受到更多的局部视野。第一层卷积层的卷积核数为64，而后每层卷积核数依次缩小2倍，临近中间层的卷积核数为10，之后展平成向量形式，最后通过Dense层完成输入数据的降维。自编码器模型具有对称性，解码部分的卷积核数与编码部分对等。网络各层的激活函数均为ReLU(Rectified Linear Units)函数，该函数为分段线性函数，在梯度下降和反向传播中具有更快的计算速度。具体参数如表1。
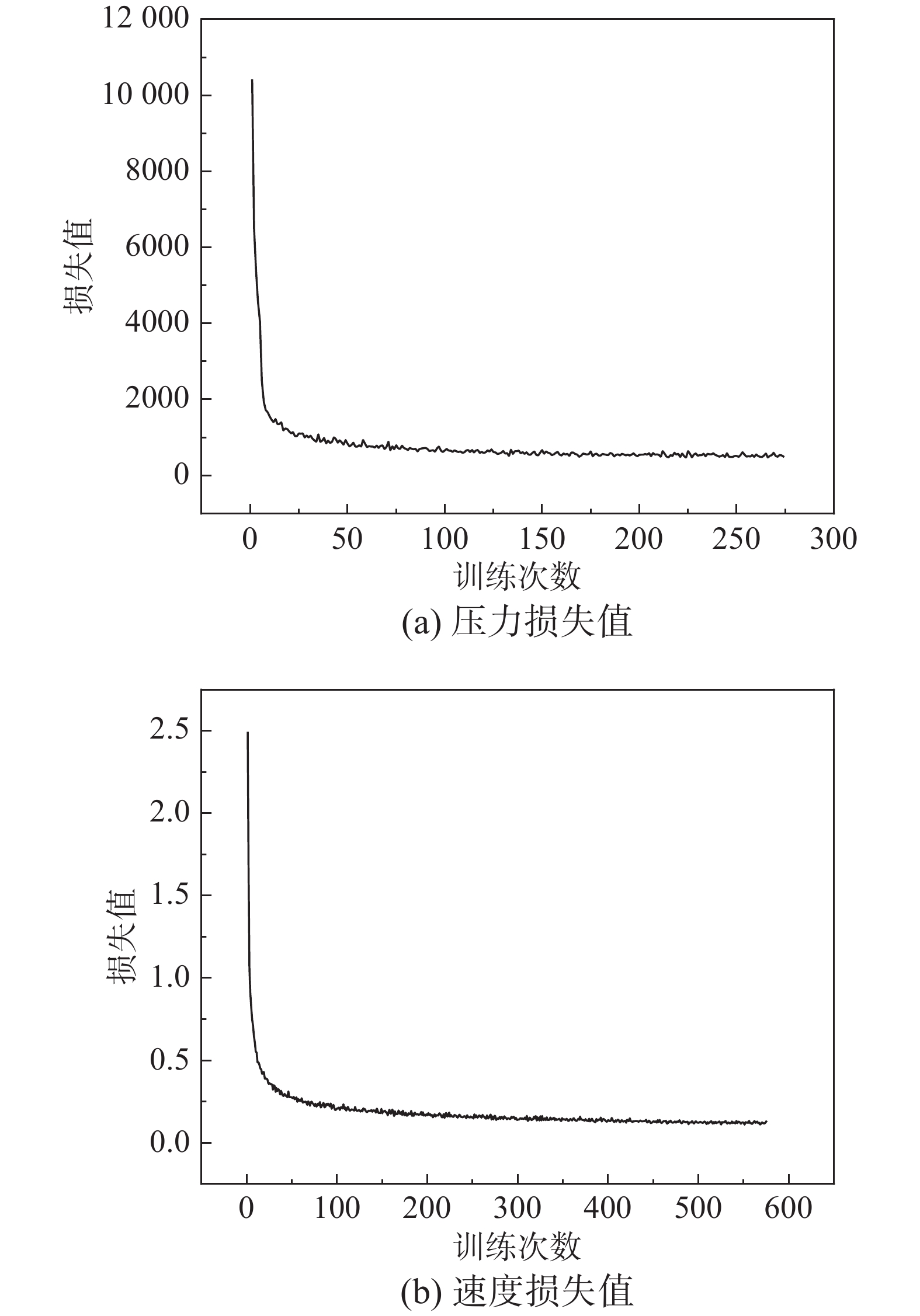
表 1 流动时程自动编码特征分类模型参数Table 1. FTH-AE model parameters网络层 通道数 激活函数 参数个数 Input − − 0 Conv 1 64 ReLU 2688 Conv 2 32 ReLU 84000 Conv 3 10 ReLU 13130 Code 10 ReLU 185710 Dense 18570 ReLU 204270 Conv_T 1 10 ReLU 4110 Conv_T 2 32 ReLU 13152 Conv_T 3 64 ReLU 84032 Output 1 ReLU 2625 本次训练所选损失函数为均方误差函数，均方误差是指参数估计值与参数值之差平方的平均值，记为MSE。本文通过数值模拟计算了2组数据集，分别为流场压力数据集、流场速度数据集，每组数据集中包含6269个时程曲线样本。为确保网络训练结果的准确性及泛化性，训练时从各数据集中随机选取50%数据样本作为训练集，另50%作为测试集，其中测试集验证模型的拟合精度不参与网络的训练。得到压力与速度数据集在训练中的损失函数曲线如图5所示。MSE是衡量平均误差的一种较方便的方法，MSE可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度。由图5可知，本文的FTH-AE模型准确地对桥面绕流系统进行了降维表征。
为直观验证降维模型对训练集的拟合精度，在训练集中随机选取的4个采样点处的压力时程与速度时程，并采用最佳模型参数进行拟合，得到的结果见图6。观察图6，可以看出虽然桥面绕流场的时程曲线无法用明确的流动特征进行描述，但本文的FTH-AE模型准确提取到了不同测点位置处的流动特征，并对流场进行了较准确的还原。
将预测样本的物理坐标与误差相结合，得到可视化的误差散点图。相对误差计算公式如下：
MAE(y,y′)=|∑ni=1(yi−y′i)Ai⋅n| (1) 式中：y为真实样本曲线，为y′预测样本曲线；A为样本时程曲线的振幅。该残差是一个相对的无量纲残差，可以定量给出模型还原曲线的整体误差。将各训练测点位置处的无量纲误差进行计算，可得到误差散点图，结果如图7所示。
由图7可知，本文桥面绕流系统的降维表征模型对整体流场时程的拟合较好，仅在来流上游区有稍大的误差。由于上游区的流场未受桥面干扰，引起时程的振幅较小，例如图6(c)中的时程样本3，该区域内测点时程的脉动较小，导致相对误差的计算值偏大。尾部区域的时程曲线相较于迎风侧脉动大，导致相对误差较小。
3 时程预测与流场重构
由于流场时程的降维模型可以准确表征已知测点位置处的流场时程，因此可以用其近似表征训练数据空间范围内的未知测点时程。对除模型训练用到的剩余3169个验证测点集进行了模型计算，并与输入时程进行结果比较，列于图8。
由图8的计算结果可知，虽然降维模型在训练过程中并没有验证集中测点位置处的时程输入，然而其依然准确地进行了时程的预测，证明了降维模型同样可用于计算域其他测点位置处的时程信号拟合，大大提升了降维模型的应用范围。
同样研究了降维模型在验证集上的误差分布，见图9。根据结果可知，本文的降维模型用于未知测点处的时程预测是可行的，但低于训练数据集的精度，这是合乎逻辑的。相对误差较大的区域位于来流区，时程脉动较小导致了大的相对误差计算值。同时在桥面壁面附近的精度也受到了复杂的壁面流动影响导致精度较低。根据图8与图9总体来看，本文方法在整个流场范围内的计算都是稳定的，可以在一定程度上预测未知测点处的时程特征。
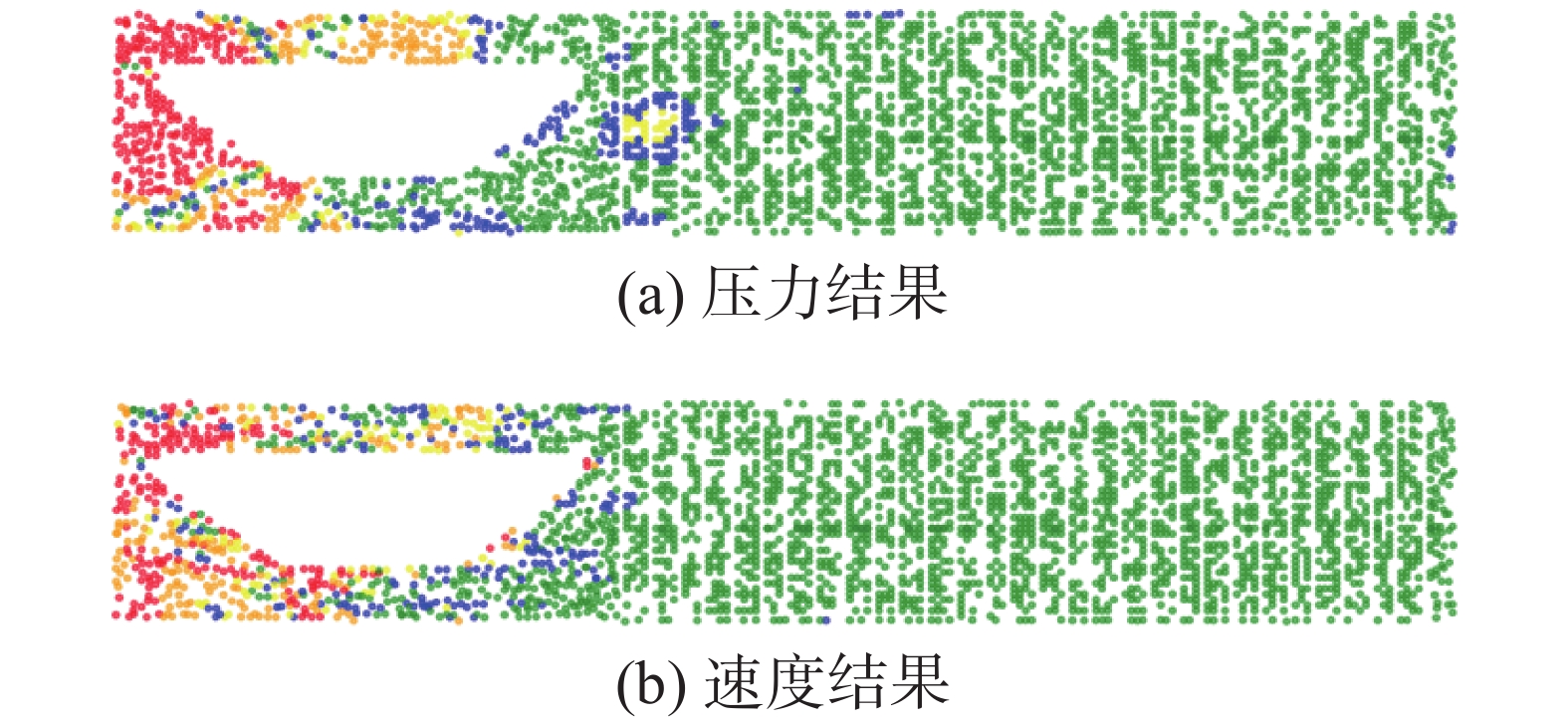
为了进一步验证该方法的有效性，本文在图3范围内随机选取了10万个坐标点，并使用降维模型进行了流场时程预测。对得到的时程数据集取同一时刻的时程量值，得到了瞬态流场云图，结果见图10和图11。
由图10与图11可知，对于较稀疏的输入数据，本文方法较准确地进行了桥面绕流流场的重构。值得注意的是，这些云图只是重构时程数据集的一个瞬态结果，对于其他流场时刻，本文仍可得到同样的重构结果。对于压力时程的预测，在桥面上部没能成功重构下游位置处的低压区，在桥面下表面位置处的重构也明显出现了不合理的压力分布。对比图9的误差分布，发现两处的误差较大，这是由于变量梯度较大处训练样本过于稀疏所致。速度重构结果精度较高，得到了与CFD同样的速度分布云图。
4 结论
针对工程中常见的稀疏流场时程数据，本文采用基于深度学习的流场重构方法进行了桥面绕流的流场时程高分辨率重构，可得到以下结论：
(1)基于时程的FTH-AE流场表征模型不仅适用于训练样本点的流动特征表征，同样也适用于没有参与模型训练的测点处流动表征。
(2)本文方法可对稀疏的流场时程数据进行高空间分辨率的重构，且重构结果在时间维度上依旧有高精度，是一种适用于工程时程数据重构的新方法。
-
表 1 流动时程自动编码特征分类模型参数
Table 1 FTH-AE model parameters
网络层 通道数 激活函数 参数个数 Input − − 0 Conv 1 64 ReLU 2688 Conv 2 32 ReLU 84000 Conv 3 10 ReLU 13130 Code 10 ReLU 185710 Dense 18570 ReLU 204270 Conv_T 1 10 ReLU 4110 Conv_T 2 32 ReLU 13152 Conv_T 3 64 ReLU 84032 Output 1 ReLU 2625 
下载: 导出CSV
-
[1] 葛耀君. 大跨度桥梁抗风的技术挑战与精细化研究[J]. 工程力学, 2011(增刊 2): 11 − 23. GE Yaojun. Technical challenges and refinement research on wind resistance of long-span bridges [J]. Engineering Mechanics, 2011(Suppl 2): 11 − 23. (in Chinese)
[2] 李永乐, 陈星宇, 汪斌, 等. 扁平箱梁涡激共振阻塞效应及振幅修正[J]. 工程力学, 2018, 35(11): 45 − 52. doi: 10.6052/j.issn.1000-4750.2017.07.0576 LI Yongle, CHEN Xingyu, WANG Bin, et al. Blockage-Effects and amplitude conversion of vortex- induced vibration for flat-box girder [J]. Engineering Mechanics, 2018, 35(11): 45 − 52. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.07.0576
[3] 刘剑寒, 马文勇. 旋转圆柱气动力特性风洞试验研究[J]. 工程力学, 2021, 38(增刊): 89 − 92. doi: 10.6052/j.issn.1000-4750.2020.05.S016 LIU Jianhan, MA Wenyong. Wind tunnel test on aerodynamic characteristics of a rotating cylinder [J]. Engineering Mechanics, 2021, 38(Suppl): 89 − 92. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.05.S016
[4] 刘庆宽, 孙一飞, 张磊杰, 等. 凹痕对斜拉桥斜拉索气动性能影响研究[J]. 工程力学, 2019, 36(增刊): 272 − 277. doi: 10.6052/j.issn.1000-4750.2018.05.S053 LIU Qingkuan, SUN Yifei, ZHANG Leijie, et al. Study on the influence of dent on aerodynamic performance of stay cables of cable-stayed bridge [J]. Engineering Mechanics, 2019, 36(Suppl): 272 − 277. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.05.S053
[5] 金晓威, 赖马树金, 李惠. 物理增强的流场深度学习建模与模拟方法[J]. 力学学报, 2021, 53(10): 2616 − 2629. doi: 10.6052/0459-1879-21-373 JIN Xiaowei, LAIMA Shujin, LI Hui. Physics-enhanced deep learning methods for modelling and simulating flow fields [J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(10): 2616 − 2629. (in Chinese) doi: 10.6052/0459-1879-21-373
[6] KUTZ J N. Deep learning in fluid dynamics [J]. Journal of Fluid Mechanics, 2017, 814: 1 − 4. doi: 10.1017/jfm.2016.803
[7] MURATA T, FUKAMI K, FUKAGATA K. Nonlinear mode decomposition with convolutional neural networks for fluid dynamics [J]. Journal of Fluid Mechanics, 2019, 882: 1 − 15. doi: 10.1017/jfm.2019.822
[8] FUKAMI K, NAKAMURA T, FUKAGATA K. Convolutional neural network based hierarchical autoencoder for nonlinear mode decomposition of fluid field data [J]. Physics of Fluids, 2020, 32(9): 095110. doi: 10.1063/5.0020721
[9] RAISSI M, KARNIADAKIS G E. Hidden physics models: Machine learning of nonlinear partial differential equations [J]. Journal of Computational Physics, 2018, 357: 125 − 141. doi: 10.1016/j.jcp.2017.11.039
[10] RAISSI M, WANG Z, TRIANTAFYLLOU M S, et al. Deep learning of vortex-induced vibrations [J]. Journal of Fluid Mechanics, 2019, 861: 119 − 137. doi: 10.1017/jfm.2018.872
[11] MAULIK R, SAN O. A neural network approach for the blind deconvolution of turbulent flows [J]. Journal of Fluid Mechanics, 2017, 831: 151 − 181. doi: 10.1017/jfm.2017.637
[12] FUKAMI K, FUKAGATA K, TAIRA K. Super-resolution reconstruction of turbulent flows with machine learning [J]. Journal of Fluid Mechanics, 2019, 870: 106 − 120. doi: 10.1017/jfm.2019.238
[13] LIU B, TANG J, HUANG H, et al. Deep learning methods for super-resolution reconstruction of turbulent flows [J]. Physics of Fluids, 2020, 32(2): 025105. doi: 10.1063/1.5140772
[14] KIM H, KIM J, WON S, et al. Unsupervised deep learning for super-resolution reconstruction of turbulence [J]. Journal of Fluid Mechanics, 2021, 910: 1 − 14. doi: 10.1017/jfm.2020.1028
[15] 叶舒然, 张珍, 宋旭东, 等. 自动编码器在流场降阶中的应用[J]. 空气动力学学报, 2019, 37(3): 498 − 504. YE Shuran, ZHANG Zhen, SONG Xudong, et al. Applications of autoencoder in reducedGorder modeling of flow field [J]. Acta Aerodynamica Sinica, 2019, 37(3): 498 − 504. (in Chinese)
[16] 惠心雨, 袁泽龙, 白俊强, 等. 基于深度学习的非定常周期性流动预测方法[J]. 空气动力学学报, 2019, 37(3): 462 − 469. HUI Xinyu, YUAN Zelong, BAI Junqiang, et al. A method of unsteady periodic flow field prediction based on the deep learning [J]. Acta Aerodynamica Sinica, 2019, 37(3): 462 − 469. (in Chinese)
[17] 战庆亮, 葛耀君, 白春锦. 基于尾流时程目标识别的流场参数选择研究[J]. 力学学报, 2021, 10(53): 2692 − 2702. ZHAN Qingliang, GE Yaojun, BAI Chunjin. Study on flow field parameters of wake time history target recognition [J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 10(53): 2692 − 2702. (in Chinese)
[18] 战庆亮, 白春锦, 张宁, 等. 基于时程卷积自编码的机翼绕流特征识别方法[J]. 航空学报, 2022, 43(11): 126531. doi: 10.7527/S1000-6893.2021.26531 ZHAN Qingliang, BAI Chunjin, ZHANG Ning, et al. Feature extraction method of flow around wing based on time history convolutional autoencoder [J]. Acta Aeronauticaet Astronautica Sinica, 2022, 43(11): 126531. (in Chinese) doi: 10.7527/S1000-6893.2021.26531
[19] 战庆亮, 周志勇, 葛耀君. Re=3900圆柱绕流的三维大涡模拟[J]. 哈尔滨工业大学学报, 2015, 47(12): 75 − 79. ZHAN Qingliang, ZHOU Zhiyong, GE Yaojun. 3-Dimensional large eddy simulation of circular cylinder at Re=3900 [J]. Journal of Harbin Institute of Technology, 2015, 47(12): 75 − 79. (in Chinese)
[20] 战庆亮, 葛耀君, 白春锦. 流场特征识别的无量纲时程深度学习方法[J]. 工程力学, 2023, 40(2): 17 − 24. doi: 10.6052/j.issn.1000-4750.2021.08.0638 Zhan Qingliang, Ge Yaojun, Bai Chunjin. Deep learning method for flow field feature recognition based on dimensionless time history [J]. Engineering Mechanics, 2023, 40(2): 17 − 24. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.08.0638
[21] 战庆亮, 白春锦, 葛耀君. 基于时程深度学习的流场特征分析方法[J]. 力学学报, 2022, 54(3): 822 − 828. ZHAN Qingliang, BAI Chunjin, GE Yaojun. Fluid feature analysis based on time history deep learning [J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(3): 822 − 828. (in Chinese)
-
期刊类型引用(1)
1. 战庆亮，刘鑫，张冠华，白春锦，葛耀君. 桥面风场时程重构的机器学习方法. 中国公路学报. 2023(08): 22-31 . 
百度学术
其他类型引用(2)
计量
- 文章访问数: 487
- HTML全文浏览量: 82
- PDF下载量: 124
- 被引次数: 3
