基于深度神经网络代理模型的盾构隧道密封垫断面优化

张纯; 何君儒; 周宇轩; 林莹

doi:10.6052/j.issn.1000-4750.2021.11.0923

基于深度神经网络代理模型的盾构隧道密封垫断面优化

南昌大学工程建设学院，江西，南昌 330031

基金项目: 国家自然科学基金项目(52268050，51968047)；江西省自然科学基金项目(20202BAB204029)；江西省研究生教改项目(JXYJG-2019-018)

详细信息

作者简介:
何君儒(1985−)，男，湖北黄梅人，博士生，主要从事工程结构力学分析研究(E-mail: 598799722@qq.com)

周宇轩(1997−)，男，江西南昌人，硕士生，主要从事隧道结构力学分析研究(E-mail: 1159309807@qq.com)

林　莹(1998−)，女，福建福州人，硕士生，主要从事工程结构力学分析研究(E-mail: yl1099042527@qq.com)

通讯作者:
张　纯(1976−)，男，江西九江人，教授，博士，主要从事结构健康检测与损伤识别研究(E-mail: zhangchun@ncu.edu.cn)

中图分类号: U454
计量
- 文章访问数: 383
- HTML全文浏览量: 62
- PDF下载量: 72
出版历程
- 收稿日期: 2021-11-24
- 修回日期: 2022-03-23
- 录用日期: 2022-04-07
- 网络出版日期: 2022-04-07
- 刊出日期: 2023-07-24

SHIELD TUNNEL GASKET SECTION OPTIMIZATION BASED ON DEEP NEURAL NETWORK SURROGATE MODEL

School of Infrastructure Engineering, Nanchang University, Nanchang, Jiangxi 330031, China

摘要

摘要: 合理的弹性橡胶密封垫断面形状是保障盾构隧道管片接缝防水设计性能的关键。密封垫断面优化设计时，需要反复进行材料大变形、接触分析等复杂的非线性计算，极大限制了优化效率。为此，以闭合压力与有效接触压力占比为双控目标，提出了一种结合深度神经网络代理模型的结构优化算法。在遗传算法框架下，深度神经网络代理模型可以实现由断面形状到接触应力场的快速映射。同时，迁移学习的引入实现了不同类型断面形状代理模型的知识复用，仅利用小样本即可建立高精度的接触应力预测模型，从而有效提高了闭合压力约束条件下的密封垫结构断面优化效率。
- 代理模型 /
- 迁移学习 /
- 遗传算法 /
- 结构优化 /
- 深度神经网络 /
- 密封垫
Abstract: The key to ensuring the waterproof design performance of a shield tunnel segment joint is a reasonable cross-sectional shape of an elastic rubber gasket. The frequent nonlinear calculations linked to large material deformation and contact analysis in the gasket section optimization design process limit the optimization efficiency. A structural optimization approach compiled with a deep neural network surrogate model is proposed, with the closure pressure and the ratio of effective contact pressure as the dual control objectives. The depth neural network surrogate model is utilized in the framework of the genetic algorithm to swiftly transform the section form into the contact stress field; Simultaneously, the use of transfer learning allows for the reuse of knowledge from surrogate models with variable sectional shapes, enabling for the creation of high-precision contact stress prediction models with few samples. As a result, the optimization efficiency of a sealing gasket structural section under its closure pressure constraint is significantly increased.
- surrogate model /
- transfer learning /
- genetic algorithm /
- sectionoptimization /
- deep neural network /
- gasket

HTML全文

图 1 弹性密封垫截面尺寸　/mm

Figure 1. Sectional dimension of elastic gasket

下载: 全尺寸图片幻灯片

图 2 弹性密封垫压缩变形与接触应力

Figure 2. Compression deformation and contact stress of elastic gasket

下载: 全尺寸图片幻灯片

图 3 弹性密封垫不同压缩工况

Figure 3. Different compression conditions of elastic gasket

下载: 全尺寸图片幻灯片

图 4 闭合压力、有效接触面积占比随压缩量变化曲线

Figure 4. Variation curve of closure pressure and effective contact area with compression value

下载: 全尺寸图片幻灯片

图 5 深度卷积神经网络代理模型结构

Figure 5. Agent model structure of deep convolution neural network

下载: 全尺寸图片幻灯片

图 6 损失函数曲线图

Figure 6. Curve of loss function

下载: 全尺寸图片幻灯片

图 7 弹性密封垫上表面接触应力预测样例

Figure 7. Example of contact stress prediction on the upper surface of elastic gasket

下载: 全尺寸图片幻灯片

图 8 不同断面的弹性密封垫(利用对称性显示一半断面)

Figure 8. Elastic gasket with different section forms (half section is shown due to symmetry)

下载: 全尺寸图片幻灯片

图 9 不同断面形状弹性密封垫的神经网络样本集输入及其标签

Figure 9. Neural network sample set input and label of elastic gaskets with different section shapes

下载: 全尺寸图片幻灯片

图 10 遗传算法流程图

Figure 10. Flow chart of genetic algorithm

下载: 全尺寸图片幻灯片

表 1 卷积神经网络具体参数

Table 1 Specific parameters of convolutional neural network

层名	输出尺寸	深度神经网络各层参数
Conv1	81×186	6×12, 20 stride 1	2×2, max pool stride 2
Conv2	40×93	3×6, 40 stride 1	2×2, max pool stride 2
Conv3	20×47	3×6, 80 stride 1	2×2, max pool stride 2
SEResNet	20×47	$\left[\begin{array}{c}3\times \mathrm{3, 80}\\ 3\times \mathrm{3, 80}\end{array}\right]\times 3$
Fc1	1×160	global mean pool 1×80
Fc2	1×371

下载: 导出CSV

表 2 不同断面形式密封垫的可优化参数变动范围

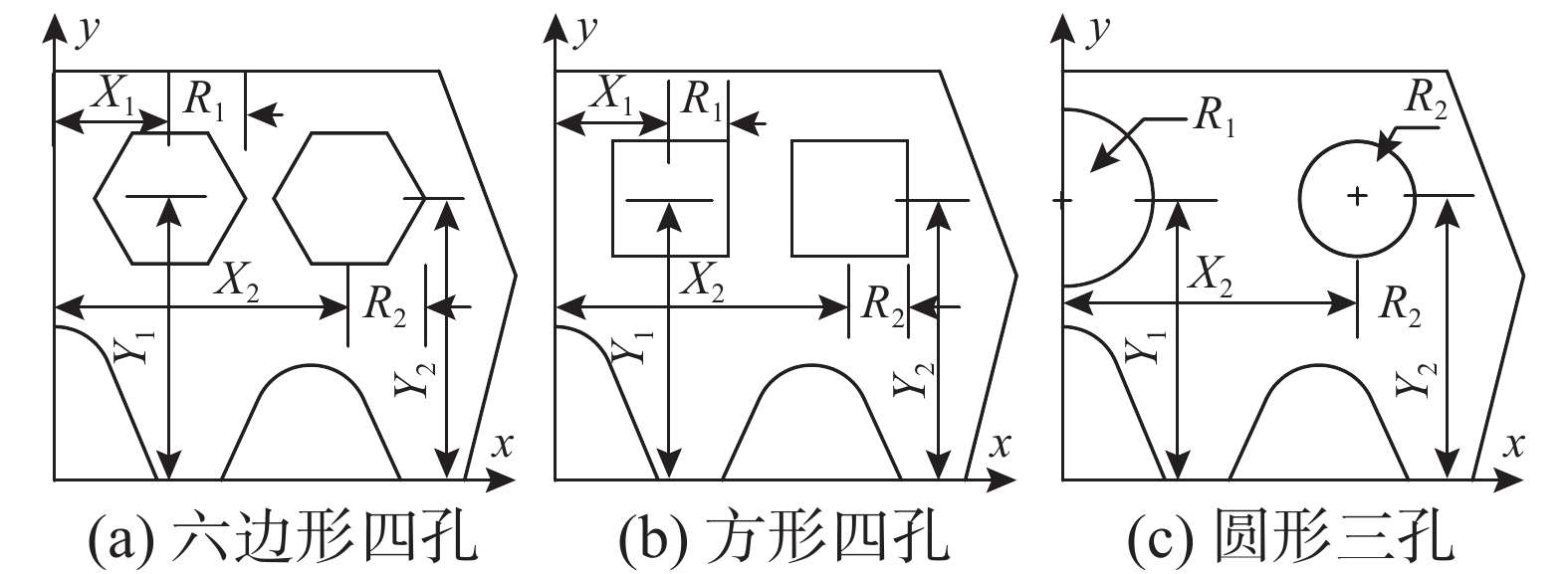
Table 2 Variation range of optimized parameters of gaskets with different section forms

参数	${X}_{1}/{\rm mm}$	${X}_{2}/{\rm mm}$	${Y}_{1},{Y}_{2}/{\rm mm}$	${R}_{1},{R}_{2}/{\rm mm}$
六边形四孔	$\left[\mathrm{2.5,5.5}\right]$	$\left[\mathrm{9.5,12.5}\right]$	$\left[\mathrm{9.5,13.5}\right]$	$\left[\mathrm{1.5,3}\right]$
方形四孔	$\left[\mathrm{2.5,5.5}\right]$	$\left[\mathrm{9.5,12.5}\right]$	$\left[\mathrm{9.5,13.5}\right]$	$\left[\mathrm{1.5,3}\right]$
圆形三孔	0	$\left[\mathrm{6.5,12.5}\right]$	$\left[\mathrm{9.5,13.5}\right]$	$\left[\mathrm{1.5,3}\right]$

下载: 导出CSV

表 3 弹性密封垫上表面接触应力

Table 3 Contact stress on upper surface of elastic gasket

训练工况及结果	六边形四孔断面	方形四孔断面	圆形三孔断面
断面形式
参数/ mm	${X}_{1}$ = $3.1,{Y}_{1}$ = $11.5,{R}_{1}$ = $2.1$ ${X}_{2}$ = $10.7,{Y}_{2}$ = $12.7,{R}_{2}$ = $1.9$	${X}_{1}$ = $3.87,{Y}_{1}$ = $10.4,{R}_{1}$ = $1.6$ ${X}_{2}$ = $11.8,{Y}_{2}$ = $11.0,{R}_{2}$ = $2.0$	${X}_{1}$ = $0,{Y}_{1}$ = $11.7,{R}_{1}$ = $2.6$ ${X}_{2}$ = $11.9,{Y}_{2}$ = $11.5,{R}_{2}$ = $2.9$
迁移学习
直接训练

下载: 导出CSV

表 4 代理模型接触应力均方误差

Table 4 Mean square error of contact stress of surrogate model

压缩量/mm	开孔类型	直接训练	迁移学习
3	六边形四孔	$5.24\times {10}^{-4}$	$1.20\times {10}^{-4}$
	方向四孔	$2.90\times {10}^{-4}$	$1.13\times {10}^{-4}$
	圆形三孔	$8.74\times {10}^{-4}$	$2.67\times {10}^{-4}$
6	六边形四孔	$3.62\times {10}^{-3}$	$5.10\times {10}^{-4}$
	方向四孔	$3.41\times {10}^{-3}$	$1.07\times {10}^{-3}$
	圆形三孔	$2.64\times {10}^{-3}$	$7.08\times {10}^{-4}$

下载: 导出CSV

表 5 不同断面类型密封垫的优化结果

Table 5 Optimization results of different section types of gaskets

优化内容及结果	圆形四孔	六边形四孔	方形四孔	圆形三孔	圆形四孔(非优化解)
密封垫断面形状优化结果
密封垫断面参数优化结果/mm	${X}_{1}$ = $4.77,{Y}_{1}$ = $12.28$ ${X}_{2}$ = $11.06,{Y}_{2}$ = $9.55$ ${R}_{1}$ = $2.17,{R}_{2}$ = $2.09$	${X}_{1}$ = $4.11,{Y}_{1}$ = $11.20$ ${X}_{2}$ = $12.83,{Y}_{2}$ = $9.92$ ${{R}_{1}=2.41,R}_{2}$ = $1.97$	${X}_{1}$ = $4.25,{Y}_{1}$ = $11.85$ ${X}_{2}$ = $11.02,{Y}_{2}$ = $9.59$ ${R}_{1}$ = $2.81,{R}_{2}$ = $2.57$	${X}_{1}$ = $0,{Y}_{1}$ = $11.23$ ${X}_{2}$ = $12.63,{Y}_{2}$ = $9.56$ ${R}_{1}$ = $2.68,{R}_{2}$ = $2.15$	${X}_{1}$ = $4.60,{Y}_{1}$ = $11.00$ ${X}_{2}$ = $12.00,{Y}_{2}$ = $10.50$ ${R}_{1}$ = $2.40,{R}_{2}$ = $2.10$
有效接触面积占比	0.759	0.759	0.739	0.672	0.612
最大闭合压力/ (kN/m)	58.81	59.15	57.91	59.68	55.19

下载: 导出CSV

参考文献(19)

[1]	董林伟, 江玉生, 杨志勇, 等. 隧道管片接缝密封垫防水机理及试验研究[J]. 岩土工程学报, 2017(3): 128 − 132. DONG Linwei, JIANG Yusheng, YANG Zhiyong, et al. Experimental study and water-resistant mechanism of gaskets in joints of tunnel segments [J]. Chinese Journal of Geotechnical Engineering, 2017(3): 128 − 132. (in Chinese)
[2]	向科, 石修巍. 盾构管片弹性密封垫断面设计与优化[J]. 地下空间与工程学报, 2008, 4(2): 361 − 364. XIANG Ke, SHI Xiuwei. Design and optimization of elastic gasket section of shield tunnel lining [J]. Chinese Journal of Underground Space and Engineering, 2008, 4(2): 361 − 364. (in Chinese)
[3]	ZHANG G, ZHANG W, CAO W, et al. A novel test setup for determining waterproof performance of rubber gaskets used in tunnel segmental joints: Development and application [J]. Tunnelling and Underground Space Technology, 2021, 115(4): 104079.
[4]	拓勇飞, 舒恒, 郭小红, 等. 超高水压大直径盾构隧道管片接缝防水设计与试验研究[J]. 岩土工程学报, 2013, 35(增刊 1): 227 − 231. TUO Yongfei, SHU Heng, GUO Xiaohong, et al. Design and experimental study on waterproof gasket of large-diameter shield tunnel under ultra high water pressure [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(Suppl 1): 227 − 231. (in Chinese)
[5]	王湛. 水下盾构隧道弹性密封垫防水失效数值模拟研究[J]. 隧道建设, 2015, 35(11): 1164 − 1168. doi: 10.3973/j.issn.1672-741X.2015.11.008 WANG Zhan. Numerical study on waterproof failure mechanism of elastic sealing gasket of underwater shield-bored tunnel [J]. Tunnel Construction, 2015, 35(11): 1164 − 1168. (in Chinese) doi: 10.3973/j.issn.1672-741X.2015.11.008
[6]	雷震宇, 刘明. 具有随机参数的盾构管片弹性密封垫防水性能优化分析[J]. 应用数学和力学, 2017, 37(8): 899 − 910. LEI Zhenyu, LIU Ming. Waterproofness optimization for elastic rubber gaskets in shield tunnels with random parameters [J]. Applied Mathematics and Mechanics, 2017, 37(8): 899 − 910. (in Chinese)
[7]	陈云尧, 张军伟, 马士伟, 等. 盾构隧道管片密封垫防水失效模式及改善研究[J]. 隧道建设(中英文), 2019, 39(6): 946 − 952. CHEN Yunyao, ZHANG Junwei, MA Shiwei, et al. Waterproof failure mode and improvement for sealing gasket of shield tunnel segment [J]. Tunnel Construction, 2019, 39(6): 946 − 952. (in Chinese)
[8]	李拼, 谢宏明, 何川, 等. 基于有效接触应力的大张开量盾构隧道密封垫防水性能分析[J]. 隧道建设(中英文), 2019, 39(12): 1993 − 1999. LI Pin, XIE Hongming, HE Chuan, et al. Waterproof performance analysis of water sealing gasket of large open shield tunnel based on effective contact stress [J]. Tunnel Construction, 2019, 39(12): 1993 − 1999. (in Chinese)
[9]	GONG C, DING W, SOGA K, et al. Sealant behavior of gasketed segmental joints in shield tunnels: An experimental and numerical study [J]. Tunnelling and Underground Space Technology, 2018, 77: 127 − 141. doi: 10.1016/j.tust.2018.03.029
[10]	GONG C, DING W. A computational framework to predict the water-leakage pressure of segmental joints in underwater shield tunnels using an advanced finite element method [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2018, 42(16): 1957 − 1975. doi: 10.1002/nag.2839
[11]	季熠, 李彦斌, 杭晓晨, 等. 基于响应面代理模型的雷达天线阵面风载分析[J]. 工程力学, 2019, 36(11): 222 − 229. doi: 10.6052/j.issn.1000-4750.2018.12.0680 JI Yi, LI Yanbin, HANG Xiaochen, et al. Wind load analysis of radar antenna based on response surface model [J]. Engineering Mechanics, 2019, 36(11): 222 − 229. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.12.0680
[12]	高月华, 王希诚. 基于Kriging代理模型的多点加点序列优化方法[J]. 工程力学, 2012, 29(4): 90 − 95. GAO Yuehua, WANG Xicheng. A Sequential optimization method with multi-point sampling criterion based on Kriging surrogate model [J]. Engineering Mechanics, 2012, 29(4): 90 − 95. (in Chinese)
[13]	李正良, 彭思思, 王涛. 基于混合加点准则的代理模型优化设计方法[J]. 工程力学, 2022, 39(1): 27 − 33. doi: 10.6052/j.issn.1000-4750.2020.12.0925 LI Zhengliang, PENG Sisi, WANG Tao. A surrogate-based optimization design method based on hybrid infill sampling criterion [J]. Engineering Mechanics, 2022, 39(1): 27 − 33. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.12.0925
[14]	JIN R, CHEN W, SIMPSON T W. Comparative studies of metamodelling techniques under multiple modelling criteria [J]. Structural and Multidisciplinary Optimization, 2001, 23(1): 1 − 13. doi: 10.1007/s00158-001-0160-4
[15]	ZHANG J, CHEN Y, FENG Q. Characteristic parameters' optimization based on contact pressure of sealing gasket for segmental joints [J]. Advances in Mechanical Engineering, 2020, 12(7): 168781402094336.
[16]	张纯, 罗金, 李登鹏. 基于深度神经网络的力学场量代理计算模型研究[J]. 应用力学学报, 2021, 38(2): 552 − 559. ZHANG Chun, LUO Jin, LI Dengpeng. Research on surrogate calculation model of mechanical quantity field based on neural network [J]. Chinese Journal of Applied Mechanics, 2021, 38(2): 552 − 559. (in Chinese)
[17]	YU Z X, SHEN D, JIN Z G, et al. Progressive transfer learning [J]. IEEE Transactions on Image Processing, 2022, 31: 1340 − 1348. doi: 10.1109/TIP.2022.3141258
[18]	ZHONG H W, WANG C, TUO H Y, et al. Transfer learning based on joint feature matching and adversarial networks [J]. Journal of Shanghai Jiaotong University (Science), 2019, 24(6): 699 − 705. doi: 10.1007/s12204-019-2132-0
[19]	WU B X, YANG C G, ZHONG J P. Research on transfer learning of vision-based gesture recognition [J]. International Journal of Automation and Computing, 2021, 18(3): 422 − 431.

施引文献(25)

期刊类型引用(11)

1.	刘庆宽，韩鹏，孙一飞，褚泽楷，王滨璇，李凯文. 安装肋条斜拉索的涡激振动和气动力特性研究. 湖南大学学报(自然科学版). 2024(07): 95-110 . 百度学术
2.	马文荣，陈学江，胡超，徐勇. 毕节倒天河斜塔斜拉桥的总体设计. 公路与汽运. 2024(05): 113-118 . 百度学术
3.	刘建峰，王刚，段世铭，刘士岳，王其昂，刘冠良，周鹏. 考虑非线性的负刚度阻尼器拉索多模态减振优化研究. 自然灾害学报. 2024(06): 162-168 . 百度学术
4.	孙一飞，刘庆宽，王仰雪，常幸，邵林媛. O型套环对斜拉索涡激振动影响的试验研究. 工程力学. 2023(07): 239-248 . 本站查看
5.	刘庆宽，邵林媛，孙一飞，常幸，韩鹏，王仰雪. 螺旋线对斜拉索涡激振动特性影响的试验研究. 湖南大学学报(自然科学版). 2023(11): 25-35 . 百度学术
6.	张为，刘庆宽，刘小兵. 长安街西延永定河大桥斜拉索风雨振及减振措施研究. 世界桥梁. 2020(03): 48-52 . 百度学术
7.	郑云飞，刘庆宽，战启芳，刘训臣，刘晓庆. 螺旋线参数对斜拉索气动特性影响的试验研究. 工程力学. 2020(S1): 301-306 . 本站查看
8.	陈学兵. 一种新型斜拉索防水罩制造技术研究. 公路交通技术. 2019(01): 59-63 . 百度学术
9.	张胤，周颖，龚硕. 基于负刚度支撑的拉索振动控制研究. 交通科技. 2019(02): 9-12 . 百度学术
10.	刘庆宽，卢照亮，田凯强，胡波，马文勇. 螺旋线对斜拉桥斜拉索高雷诺数风致振动影响的试验研究. 振动与冲击. 2018(14): 175-179 . 百度学术
11.	刘庆宽，李聪辉，郑云飞，刘小兵，马文勇. 缠绕螺旋线的斜拉桥斜拉索平均气动阻力特性的试验研究. 土木工程学报. 2017(05): 97-104 . 百度学术