钢-混凝土组合结构因充分发挥了两种材料的力学性能优势，提升了结构的刚度、承载力、延性性能和耗能能力而得到广泛应用。为推广钢-混凝土组合框架结构在强震地区的应用，KAWAGUCHI等^[1-3]、韩林海等^[4]、王文达等^[5]、聂建国等^[6]、丁发兴等^[7]、王冬花等^[8]、张继承等^[9]、王静峰等^[10]分别对不同形式的钢管混凝土柱组合框架结构进行了滞回性能试验研究和有限元分析，研究结果表明在往复荷载作用下钢-混凝土组合框架结构具有良好的塑性变形能力和抗震耗能能力。王静峰等^[11]、TSAI等^[12-13]对钢-混凝土组合框架结构开展了拟动力性能试验研究，王文达等^[14]、韩林海等^[15]对钢-混凝土组合框架结构的动力性能进行了理论分析和试验研究，试验结果表明组合框架结构在拟动力或振动台作用下最大可承受1.4 g的水平峰值加速度地震波。

既然钢-混凝土组合框架结构具有良好的抗震性能，能否利用其柱的抗震能力进行结构抗震设计是值得探讨的课题。此外，钢管内约束混凝土是在普通钢管混凝土内添加内约束部件以提高对混凝土的约束作用，改善组合构件受力特性，常见的内约束部件有加劲肋、内置栓钉、斜拉筋、约束拉杆以及对拉钢筋等，如图1所示。丁发兴等^[16-17]采用端部拉筋钢管混凝土技术，开展钢管混凝土柱滞回性能试验研究，研究结果表明：水平滞回荷载下柱端拉筋可提高钢管混凝土柱的刚度、承载力和延性，且当钢管含钢率低至0.05而实际轴压比高至0.8时，端部带拉筋矩形钢管混凝土柱仍具有良好的抗震性能指标。可见柱端拉筋强柱构造措施对于提升高烈度区建筑物的抗震能力，降低震害损失，保护人民生命财产安全具有十分积极的作用。

图  1  钢管混凝土柱的内约束构造形式

Figure  1.  The forms of stiffened concrete-filled steel tubular column

下载: 全尺寸图片 幻灯片

然而，以往学者对于组合框架结构的研究都是基于“强柱弱梁”的设计原则，但实际工程中跨度较大的多层建筑易表现为“强梁弱柱”框架。为实现组合框架中由钢管混凝土柱抗震耗能的设想，本文开展如下工作：开展低周往复荷载下两层两跨钢-混凝土组合框架结构的抗震性能试验研究，探讨柱端拉筋强柱构造对其抗震性能的影响；建立实体单元与壳单元为主的钢-混凝土组合框架结构有限元模型，在试验验证的基础上开展参数分析，探讨拉筋构造对组合框架刚度、承载力和耗能的影响规律。

1   试验概况

1.1   模型设计与制作

本试验以2层2跨方钢管混凝土柱-组合梁框架结构作为研究对象。笔者参考《钢管混凝土结构技术规程》 (GB 50936−2014)^[18]、《钢结构设计标准》 (GB 50017−2017)^[19]和《混凝土结构设计规范》 (GB50010−2010)^[20]等相关规范，考虑钢梁与混凝土楼板的组合作用，设计并制作了2榀缩尺比例为2/5的“强节点弱构件”和“梁柱共同耗能”方钢管混凝土柱-组合梁平面框架结构模型，其梁柱抗弯承载力比均大于1。为避免节点发生破坏，笔者参考文献[21-23]中组合节点设计方案和试验结果，采用外加强环+内隔板组合形式将钢梁和柱牢固焊接。试验参数为钢管混凝土柱端部是否有拉筋强柱构造措施，模型NCF为普通钢-混凝土组合框架，模型SCF为柱端带拉筋钢-混凝土组合框架。

图2所示两个平面框架模型具有相同的外观尺寸、施工工艺和加载方式。图2(b)分别给出了模型NCF和SCF的1-1截面布置形式，钢管壁厚3 mm，模型SCF中拉筋选用直径为6 mm的HPB235级钢筋，拉筋布置在柱底及梁柱节点处上下400 mm (2B)范围内，纵向间距为100 mm，柱端拉筋区域等效体积配箍率为0.42%；图2(c)为钢-混凝土组合梁截面详图，梁中布置双排直径为13 mm的普通圆柱头栓钉，栓钉数量根据《钢结构设计标准》 (GB 50017−2017)^[19]中完全剪力连接计算，钢梁与钢管柱采用四周围焊的方法形成可靠的梁柱节点；钢筋混凝土楼板尺寸及板内配筋如图2(c)和图2(d)所示，楼板与钢管混凝土柱壁间不做连接处理。各部件尺寸及柱顶受力情况见表1，其中：轴压比n=N₀/(f_cA_c+f_yA_s)，N₀ 为模型顶部施加的恒定轴压力，f_c为混凝土轴心抗压强度，A_c为核心混凝土截面积， f_y为钢管屈服强度，A_s为钢管截面积。

图  2  模型外形尺寸构造图　/mm

Figure  2.  Dimensions and constructions of models

下载: 全尺寸图片 幻灯片

表  1  模型参数表

Table  1.  Parameters of models

模型	钢梁截面 hb×bf×tw×tf/mm	梁长 L/mm	柱截面 B×t×H /mm	立方体抗压强度fcu/MPa	轴压比n(轴压力N0/kN)
					中柱	边柱
SCF	200×100×5.5×8	2000	200×3×4000	30.3	0.43(691)	0.26(417)
NCF	200×100×5.5×8	2000	200×3×4000	43.6	0.43(726)	0.26(439)

下载: 导出CSV 

| 显示表格

由于钢管尺寸较小，采用对拉穿孔焊的方法将拉筋与钢管壁焊接。钢管柱加工完成后，为方便观察变形，在钢管外表面粉刷红色油漆，并用白色油漆笔在其表面绘制50 mm×50 mm的网格。模型安装完成后，将钢管与模板内侧用水打湿，从钢管柱顶灌入混凝土，并用振捣棒振捣密实，同时制作2组6个150 mm×150 mm×150 mm的混凝土标准立方体试块，与模型在相同条件下养护。模板拆除后，钢管混凝土柱顶端用高强水泥砂浆(强度C60以上)进行填补，并用打磨机打磨平整后焊接厚度为10 mm的钢盖板，以期尽可能保证钢管与核心混凝土在模型加载初期共同受力，加工完成后模型如图2(e)所示。

等效配箍率ρ_sa定义如下：

式中：f_sv和f_y分别为拉筋和钢管的屈服强度；ρ_sv为拉筋加强区实际配箍率；V_sv为拉筋加强区拉筋总体积；V_c为拉筋加强区混凝土总体积。

1.2   材料性能

1.2.1   钢材

钢管采用普通钢板冷弯形成，钢梁采用普通商用H型钢，钢筋采用HPB235级和HRB335级。根据《钢及钢产品力学性能试验取样位置及试样制备》 (GB/T 2975−2018)^[24]的规定，各加工一组标准拉伸试件，并根据《金属材料拉伸试验第1部分：室温试验方法》 (GB/T 228−2010)^[25]的标准测试方法测其屈服强度f_y、拉伸强度f_u、弹性模量E_s等参数，测试结果列于表2。栓钉规格为Φ13×60 mm，材料强度根据厂家提供的检测报告取值，其屈服强度为350 MPa，极限强度为460 MPa。

表  2  钢材材料性能表

Table  2.  Material properties of steel

类别	厚度或直径t/mm		屈服强度 fy/MPa	拉伸强度 fu/MPa	弹性模量 Es/MPa
	设计值	实测值
钢管	3.0	3.24	290.3	390.5	1.89×105
HPB235	6.0	6.11	310.5	450.3	1.98×105
HRB335	8.0	7.89	430.3	639.5	1.98×105
钢梁翼缘	8.0	7.92	317.3	468.3	1.93×105
钢梁腹板	5.5	5.18	311.7	434.3	1.93×105

下载: 导出CSV 

| 显示表格

1.2.2   混凝土

混凝土采用商品细石混凝土，根据《混凝土物理力学性能试验方法标准》 (GB/T 50081−2019)^[26]对与模型同养护条件下的三块150 mm×150 mm×150 mm标准立方体试块进行测试，取测试结果(见表1)的平均值作为混凝土立方体抗压强度f_cu。由于试验场地限制，导致模型SCF与NCF无法同时浇筑，又因模型养护条件以及混凝土浇筑环境不同导致2榀组合框架模型混凝土强度不一致(设计混凝土强度均为C40)。

1.3   试验装置、加载制度和测试内容

1.3.1   试验装置

试验为拟静力试验，试验装置及加载设备如图3(a)和图3(b)所示。试验模型通过高强螺栓固定在钢筋混凝土底座上，并通过地锚杆与地锚相连；3个2000 kN液压千斤顶用于施加柱顶轴向恒定压力，为保证轴压力的稳定同时尽可能消除摩擦力的影响，通过两侧6根高强精轧螺纹钢使千斤顶与横梁组成传力体系；1台500 kN美国MTS液压伺服作动器通过连接板与模型二层梁端相连，以施加水平循环往复荷载。

图  3  试验装置与加载制度

Figure  3.  Test device and load pattern

下载: 全尺寸图片 幻灯片

1.3.2   加载制度

根据《建筑抗震试验规程》 (JGJ/T 101−2015)^[27]制定循环加载制度，采用荷载与位移共同加载控制，即弹性阶段采用荷载控制，模型开裂或屈服后改为位移加载。施加的水平位移相对原点为正时为正向加载，为负时为负向加载，每级位移循环加载三次，然后逐级增大直至水平承载力下降至最大承载力的85%或模型不适合继续加载时，循环加载制度如图3(c)所示。

1.3.3   测试内容

梁加载端位移和荷载数据分别通过布置在梁加载端的数显位移计LVDT 1与MTS加载系统采集，楼板与钢梁之间的界面滑移由位移计LVDT 3与LVDT 4测量，底座与地面间的相对滑移由位移计LVDT 5与LVDT 6测量，位移计的布置如图3(a)所示。直角应变花主要布置在钢管柱外表面，应变片主要布置在钢梁上下翼缘、腹板中心处以及混凝土楼板上表面，测点的布置如图4所示。另外在模型两侧各布置多个位移监测点，以监控加载过程中模型平面外变形情况。

图  4  应变片布置示意图

Figure  4.  Distribution of strain gauges

下载: 全尺寸图片 幻灯片

2   试验现象及结果分析

2.1   试验现象及破坏模式

试验过程平缓稳定，监测数据表明模型未发生明显平面外变形，底座基本无滑移，结构锚固良好，试验现象可大致描述如下：

1) 弹性阶段：当水平位移小于20 mm(2Δ)时，没有观察到明显的钢材屈曲与混凝土开裂现象，荷载随水平位移的增加平稳增加；

2) 弹塑性阶段：中柱柱脚钢管屈曲→节点处混凝土板开裂。当水平位移加载至20 mm~30 mm(对于模型NCF为2Δ，对于模型SCF为3Δ)时，由于中柱轴压比更大导致柱脚加劲肋上方出现局部轻微鼓曲，与此同时，中柱附近一层混凝土板下表面出现宽度约为0.15 mm的斜裂缝(图5(a))；随水平位移的增加，节点附近混凝土板出现数条横向裂缝，裂缝宽度较小，与此同时上述板裂缝不断向跨中方向延伸，且裂缝宽度不断增加；当水平位移达到30 mm~50 mm(1/127${\leqslant}\theta{\leqslant}$1/76)时，混凝土板裂缝越来越明显，且多集中在节点附近，最大裂缝宽度达到0.25 mm。此外边柱柱脚加劲肋上方钢管明显鼓曲(图5(b))；

图  5  模型典型破坏形态

Figure  5.  Typical damage mode of the models

下载: 全尺寸图片 幻灯片

3) 破坏阶段：中柱二层钢管鼓曲→中柱柱脚鼓曲加剧→混凝土板形成贯穿裂缝。当水平位移加载至70 mm(θ=1/54)时，中柱二层节点下方同样发现钢管局部鼓曲，随水平位移的增加少量混凝土板掉落；当水平位移增加到80 mm~90 mm(1/48${\leqslant} \theta{\leqslant}$1/42)时，模型承载力不再增加；当水平位移达到95 mm(θ=1/40)时，中柱柱脚出现较为严重的鼓曲现象(图5(c))，荷载随着位移的增加平缓变化；当水平位移临近最大量程100 mm(θ=1/38)时，混凝土板出现贯穿裂缝(图5(d))，此时伺服作动器达到最大加载限制，试验加载随即结束。

2榀组合框架模型表现出以“柱耗能为主”的破坏模式，即塑性铰首先出现在柱脚，随后依次出现在一层节点上方和二层节点下方。试验结束后，塑性铰分布如图6所示，其中图中数字表示柱铰形成时的位移幅值及相应的结构侧移角。与模型NCF相比，模型SCF中塑性铰不仅出现时间延后，而且数量增多，表明柱端拉筋强柱构造措施能够增大结构刚度，延缓塑性铰的出现，增强结构耗能能力。

图  6  塑性铰出现位置及顺序

Figure  6.  Appearance and sequence of plastic hinges

下载: 全尺寸图片 幻灯片

2.2   钢-混凝土组合梁界面滑移

根据钢梁上水平位移计采集数据得到的荷载-相对滑移曲线如图7所示，可知：

图  7  组合框架中钢-混凝土组合梁界面滑移曲线

Figure  7.  Interface slip curves of steel-concrete composite beam in frames

下载: 全尺寸图片 幻灯片

1)组合梁跨中，钢梁与楼板之间的滑移量较小，最大滑移量为0.6 mm左右；

2)组合梁梁端，由于荷载的增加使得组合梁负弯矩区混凝土板不断开裂而退出工作，导致两者间相对滑移增大，最大滑移量在4.4 mm左右。

2.3   抗震性能指标

2.3.1   滞回曲线

2榀模型加载端的滞回曲线如图8(a)所示，试验中每级荷载的三次循环曲线基本一致，为方便对比图中仅显示第三次循环曲线。将滞回曲线的各个峰值点相连即得到P-Δ骨架曲线，如图8(b)所示，其主要特征点数据列于表3，由图8与表3可知：

图  8  组合框架荷载-位移曲线和骨架曲线比较

Figure  8.  Load-displacement curves and skeleton curves of composite frames

下载: 全尺寸图片 幻灯片

表  3  荷载-位移曲线主要特征点

Table  3.  Main characteristic points of load-displacement curves

模型	加载 方向	屈服点			峰值点			结束点
		屈服荷载 Py /kN	屈服位移 Δy /mm		极限荷载 Pmax /kN	极限位移 Δmax /mm		破坏荷载 Pu /kN	破坏位移 Δu /mm
NCF	+	151.1	49.0		170.0	90.3		165.2	99.5
	−	−140.6	−49.7		−169.2	−90.5		−163.7	−95.0
SCF	+	144.5	35.5		183.0	93.1		177.1	102.6
	−	−129.0	−27.2		−159.0	−82.1		−148.5	−100.8

下载: 导出CSV 

| 显示表格

1) 2榀组合框架荷载-位移曲线形状相似，骨架曲线大致呈S形，表明组合框架模型在循环荷载作用下经历了弹性、弹塑性和破坏三个阶段，由于钢管混凝土柱的局部屈曲和混凝土板开裂导致2榀模型均具有明显捏拢现象，试验加载后期(Δ>70 mm)两个模型承载力变化幅度均在5%左右。

2)即使在混凝土强度较低的情况下，模型SCF较模型NCF仍拥有较大的滞回面积，且结构的弹性刚度提高了74.7%，极限承载力提高了7.67%，表明柱端拉筋强柱构造措施能显著提高钢-混凝土组合框架结构的弹性刚度和极限承载能力。

2.3.2   延性系数

本文采用位移延性系数μ来表征模型的延性，定义为破坏位移Δ_u与屈服位移Δ_y之比，即：

根据图8(b)模型荷载-位移骨架曲线，按“通用屈服弯矩法”(G.Y.M.M)^[28]可确定结构屈服位移Δ_y与屈服承载力P_y、破坏位移Δ_u与破坏承载力P_u，其中OC为P-Δ骨架曲线的弹性刚度，如图9所示。因受试验装置限制，本试验未能加载至承载力下降为最大承载力的85%，故取结束加载时的承载力作为破坏承载力P_u。

图  9  通用屈服弯矩法求延性系数

Figure  9.  Ductility index obtained from general yield

下载: 全尺寸图片 幻灯片

按上述计算方法得到模型NCF和SCF的位移延性系数μ均值分别是1.971和3.295，表明柱端拉筋强柱构造措施有效提高了钢-混凝土组合框架结构的延性。

2.3.3   刚度退化

刚度退化采用环线刚度K_i评价：

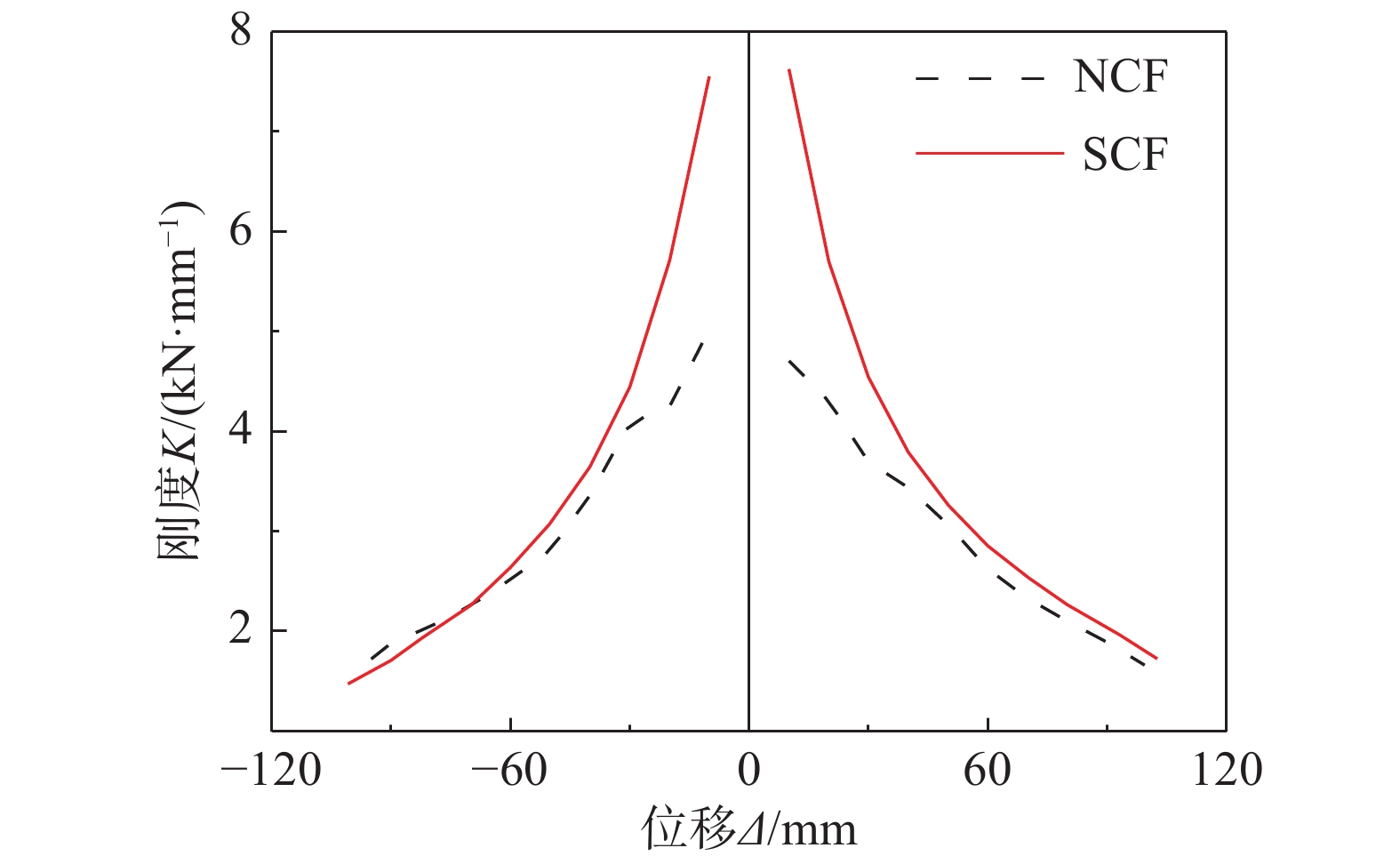
式中：$P_{ j}^i$为第j级加载位移(Δ/Δ_y=j)时，第i级加载循环的水平峰值点荷载；$\varDelta_{ j}^i$为第j级加载位移(Δ/Δ_y=j)时，第i级加载循环的峰值点位移；m为总滞回环数。

图10绘出了2榀模型环线刚度退化曲线，表4列出了模型的初始刚度及模型屈服时、达到峰值承载力时和结束加载时对应的割线刚度，可见拉筋对模型前期刚度有较大提升作用。

图  10  模型环线刚度退化曲线

Figure  10.  Loop stiffness degradation curves of models

下载: 全尺寸图片 幻灯片

表  4  各阶段刚度对比情况

Table  4.  Comparison of stiffness at various stages

加载方向	模型	初始刚度/(kN/mm)	提高比例/(%)	屈服刚度/(kN/mm)	提高比例/(%)	峰值刚度/(kN/mm)	提高比例/(%)	破坏刚度/(kN/mm)	提高比例/(%)
正向	NCF	4.71	62.0	3.09	31.8	1.88	4.4	1.66	3.8
	SCF	7.63		4.07		1.97		1.72
反向	NCF	5.02	50.6	2.83	67.6	1.87	3.6	1.72	−14.5
	SCF	7.55		4.74		1.94		1.47

下载: 导出CSV 

| 显示表格

2.3.4   等效阻尼粘滞系数和累积耗能

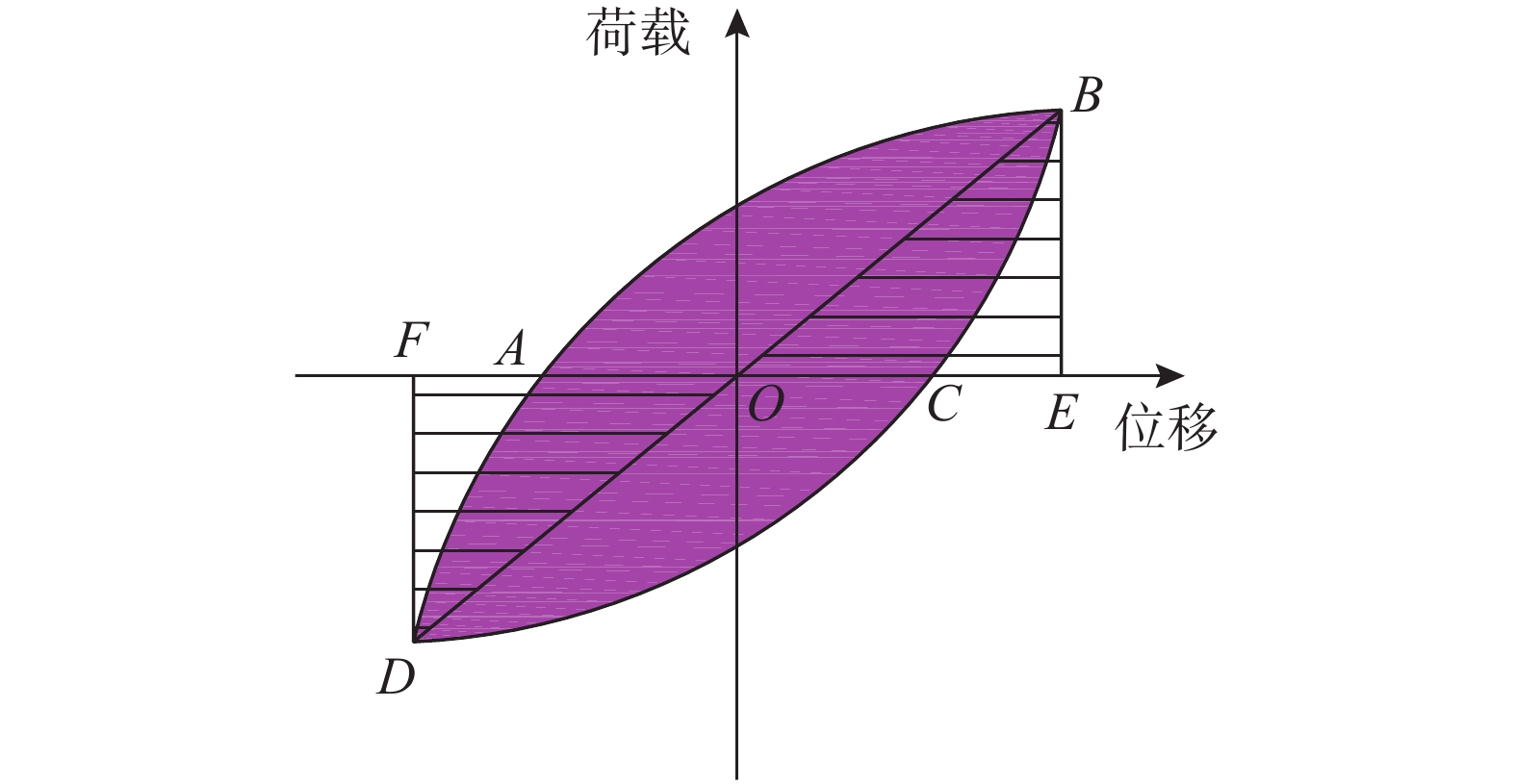
根据《建筑抗震试验规程》 (JGJ/T 101−2015)^[27]的规定，本文选用等效阻尼粘滞系数h_e来评定结构的耗能能力，定义如下：

式中：S_ABCDA为图11中所示填充滞回环ABCD的面积；S_{(△OBE+△ODF)}为△OBE和△ODF面积之和。累积耗能由每个滞回环的能量叠加而得到。

图  11  等效粘滞阻尼系数h_e计算图

Figure  11.  Calculation figure of equivalent viscous damping coefficient

下载: 全尺寸图片 幻灯片

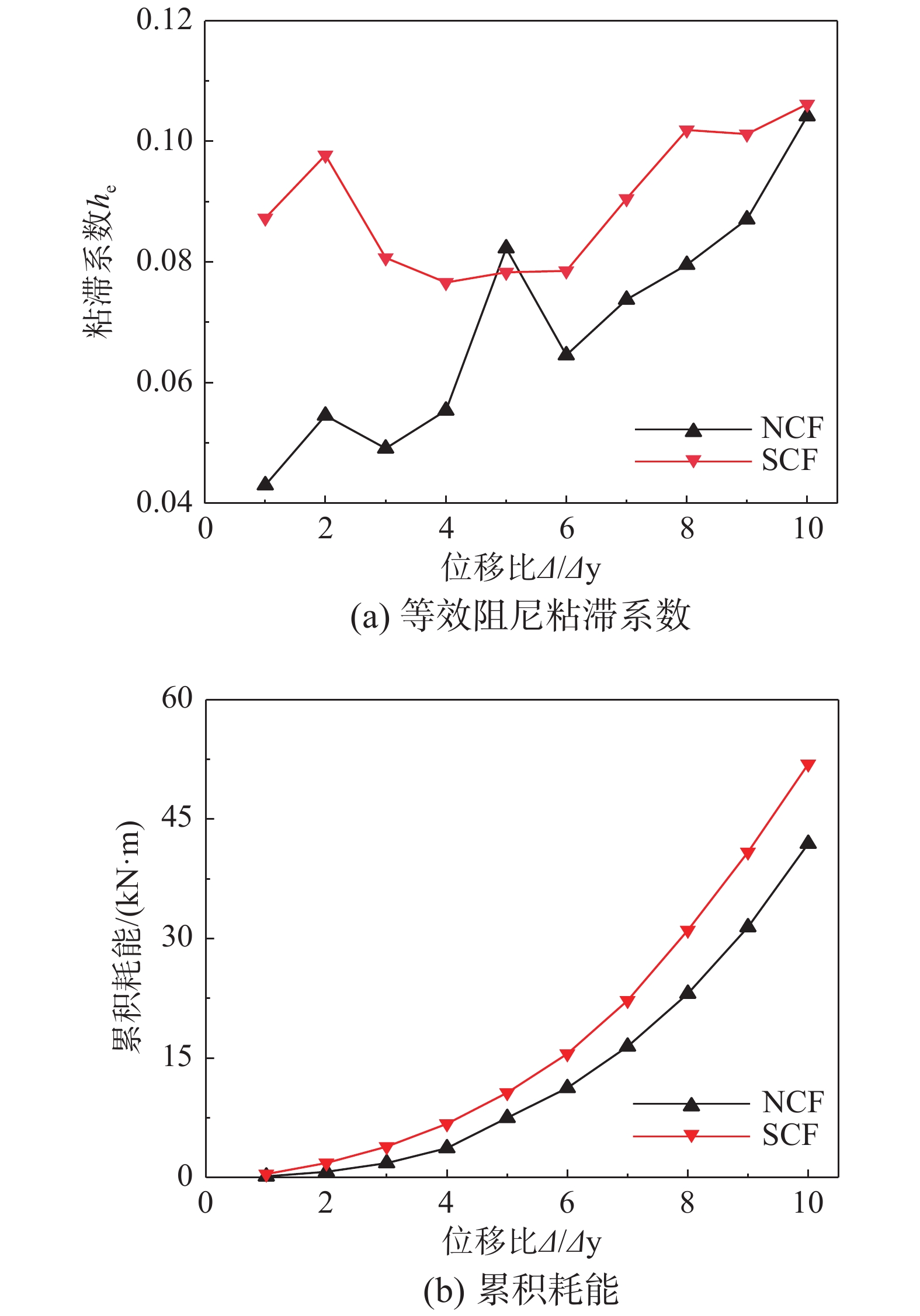
图12对比了两组模型等效阻尼粘滞系数变化规律和累积耗能变化规律，可知：1) 模型SCF在试验各个阶段的等效阻尼粘滞系数都普遍大于模型NCF；2)结束加载时模型SCF的累积耗能比模型NCF的累积耗能提高23.9%，表明柱端拉筋强柱构造措施使得结构的耗能能力显著提高。

图  12  拉筋对等效阻尼粘滞系数和累积耗能的影响

Figure  12.  Influence of stirrup on equivalent damping viscosity coefficient and cumulative energy dissipation

下载: 全尺寸图片 幻灯片

3   有限元模型验证及参数分析

3.1   有限元模型

本文采用有限元软件ABAQUS对2榀框架模型进行数值仿真。核心混凝土柱、混凝土楼板、钢盖板、加劲肋等均采用八节点减缩积分格式的三维实体单元；钢管、钢梁等可视为同性、薄壁构件，忽略其厚度方向的应力，均采用四节点减缩积分格式的壳单元，沿壳的厚度方向采用9积分点的Simpson积分；钢筋采用两节点线性三维桁架单元；栓钉近似简化为三维线性梁单元。

钢管与核心混凝土之间采用面-面摩擦型接触方式，将钢管内表面定义为主面，核心混凝土外表面定义为从面，采用有限滑移，离散化方法选择表面-表面。在接触属性选项中切向行为选用罚函数，其摩擦系数取0.5^[29]，法向行为设置为“硬”接触，允许接触后分离。栓钉采用梁单元嵌入式的方法能有效模拟钢-混凝土组合梁的力学性能^[30]，栓钉采用内置方法内嵌到混凝土楼板中。钢筋在混凝土楼板内锚固良好，试验结束后没有发现粘结破坏现象，钢筋与拉筋同样采用内置方法内嵌到混凝土楼板中。试验中未发现明显的焊接破坏，钢管柱与钢梁、钢盖板、钢底板和加劲肋共同受力，上述部件之间采用绑定约束。图13为模型的边界条件及加载点位置。

混凝土本构关系采用丁发兴等^[29]所提出的塑性-损伤模型，其中混凝土单轴应力-应变关系如下：

式中：当i=1时，y =σ/ f_c，x =ε/ε_c；σ和ε分别为混凝土的应力和应变；轴心抗压强度${f_{\rm{c}}}=0.4f_{{\rm{cu}}}^{7/6}$；ε_c为峰值应力对应的应变，${\varepsilon_{\rm{c}}}=291f_{{\rm{cu}}}^{7/15}\times10^{-6}$；弹性模量E_c=9500$f_{\rm{cu}}^{1/3}$；上升段参数$A_{1}=6.9 f_{\mathrm{cu}}^{-11 / 30}$，B₁=1.67(A₁−1)²；下降段参数a₁=0.15。当i=2时，y =σ/f_t， x =ε/ε_t；轴心抗拉强度f_t=0.24$f_{\rm{cu}}^{2/3}$；ε_t为峰值应力对应的应变，ε_t=33$f_{\rm{cu}}^{1/3}$×10⁻⁶；上升段参数A₂=1.3，B₂=0.15；下降段参数$a_{2}=0.8$。

图  13  模型网格划分及边界条件

Figure  13.  Model meshing and boundary condition setting

下载: 全尺寸图片 幻灯片

混凝土塑性-损伤本构模型中其他参数取值如下：混凝土的泊松比取为0.2，膨胀角取为40°，偏心率取为0.1，双轴等压强度与单轴强度之比取为1.277，拉、压子午线上的第二应力不变量比值为2/3，粘性系数取为0.0005。卸载时损伤因子取值采用丁发兴等^[31]提出的混凝土弹性模量损伤变量计算方法。

钢材选用混合强化模型，其准确性在课题组前期研究中^[32]进行了验证，其参数取值如下：屈服应力为实测屈服强度f_y，随动硬化参数C₁为750，Gamma为50，Q-无限为0.5f_y，硬化参数b为0.1。

栓钉的弹塑性应力-应变关系如下：

式中：σ为应力；ε为应变；ε_y为屈服应变；ε_u为极限应变，取为21ε_y；f_y为屈服强度；弹性模量E_s＝2.06×10⁵ N/mm²。

3.2   模型验证

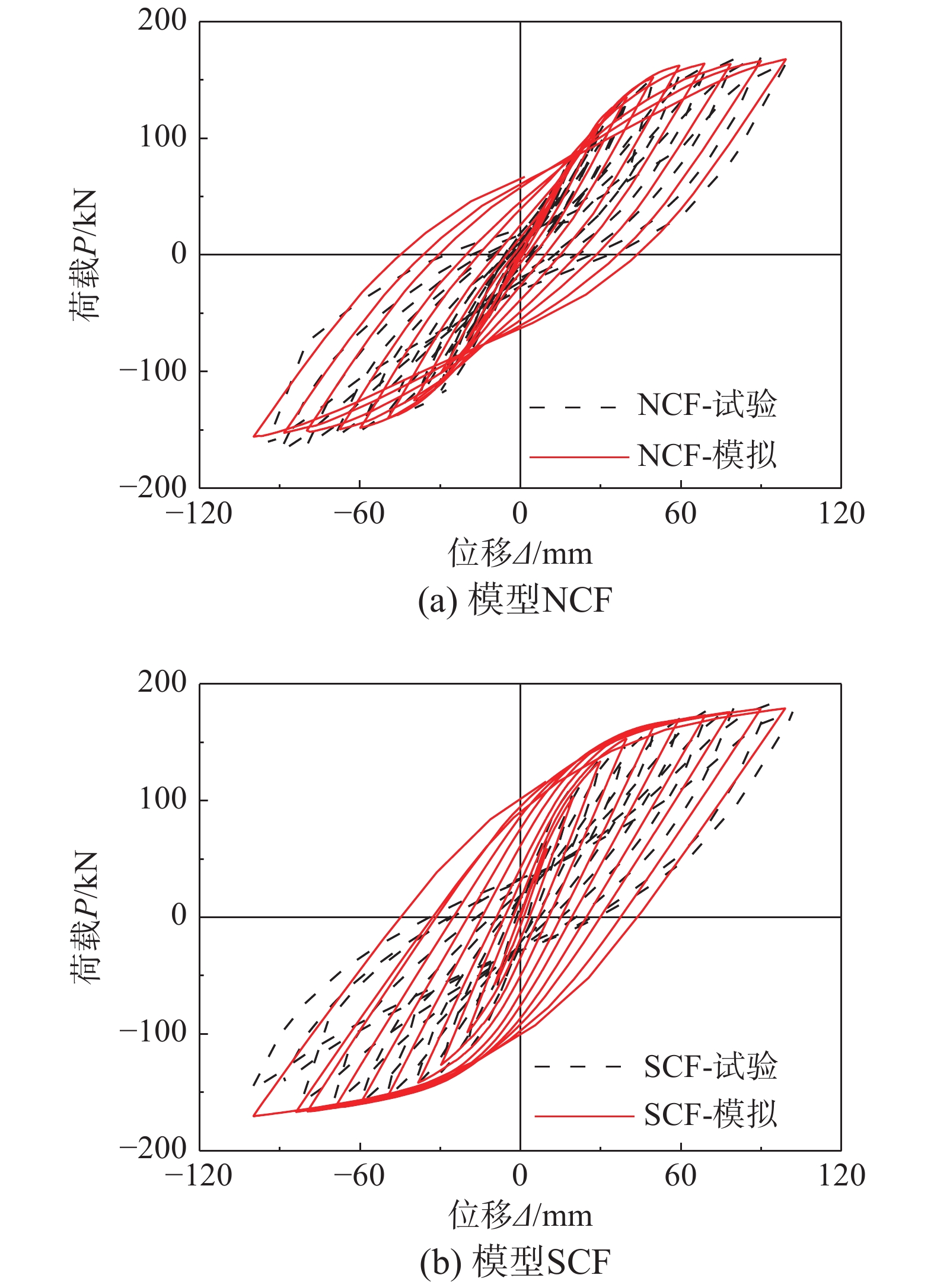
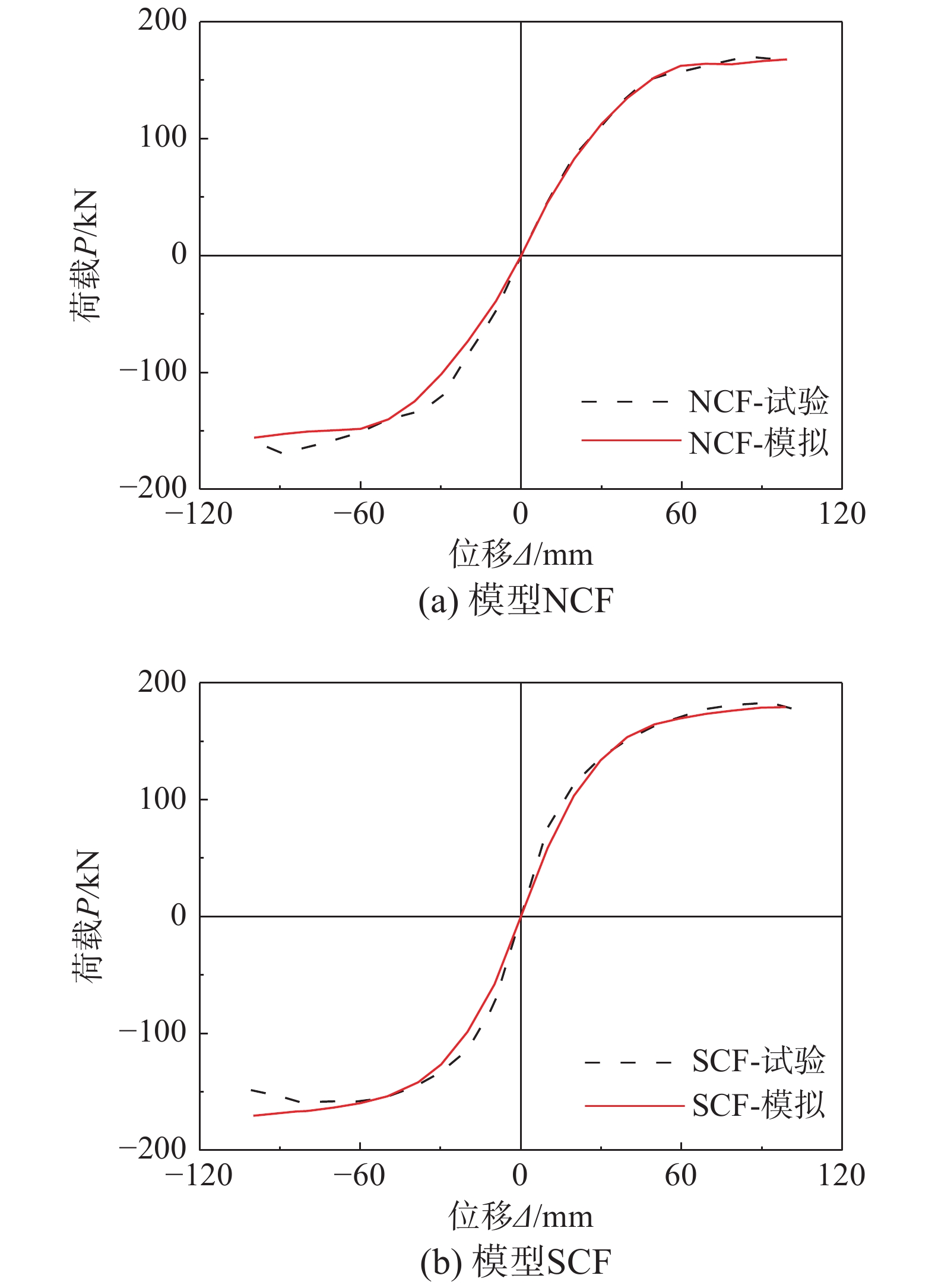
采用上述建模方法得到的滞回曲线与试验结果对比如图14所示，可知：1)有限元模拟所得滞回曲线能够较为准确地反映往复荷载作用下结构的荷载-位移变化趋势；2)由于有限元软件难以精确描述试验过程中钢材与混凝土的卸载和再加载曲线以及两者间的滑移现象，导致模拟所得滞回曲线较试验曲线饱满。

图  14  模型滞回曲线对比

Figure  14.  Load-displacement curves comparison

下载: 全尺寸图片 幻灯片

图15为有限元模拟骨架曲线与试验结果的比较，可见模拟所得骨架曲线与试验结果吻合良好；表5列出了有限元方法和试验得到的屈服荷载P_y、极限荷载P_max、屈服刚度K_y、延性系数μ，对比显示两者吻合较好，表明本文建模参数与方法能够满足进一步参数分析的精度要求。

图  15  模型骨架曲线对比

Figure  15.  Skeleton curves comparison

下载: 全尺寸图片 幻灯片

表  5  试验结果与有限元结果比较

Table  5.  Comparison of test results and finite element results

模型	NCF						SCF
	正向			反向			正向			反向
	试验	有限元		试验	有限元		试验	有限元		试验	有限元
屈服荷载 Py /kN	151.1	148.5		−140.6	−139.5		144.5	133.8		−129.0	−146.8
极限荷载 Pmax /kN	170.0	167.9		−169.2	−155.9		183.0	179.2		−159.0	−170.5
屈服刚度 Ky/(kN/mm)	3.1	3.1		2.8	2.9		4.1	3.3		4.7	3.7
延性 系数μ	2.0	2.1		1.9	2.0		2.9	2.4		3.7	2.5

下载: 导出CSV 

| 显示表格

3.3   等效配箍率的影响

为探讨柱端拉筋等效配箍率对组合框架结构滞回性能的影响，笔者共设计了3种工况：拉筋直径分别为6 mm、10 mm和14 mm，对应的等效配箍率分别为ρ_sa=0.42%、ρ_sa=1.18%与ρ_sa=2.33%，模型算例的尺寸、材料强度和轴压比等参数均与模型NCF相同，拉筋布置范围及间距与模型SCF相同。

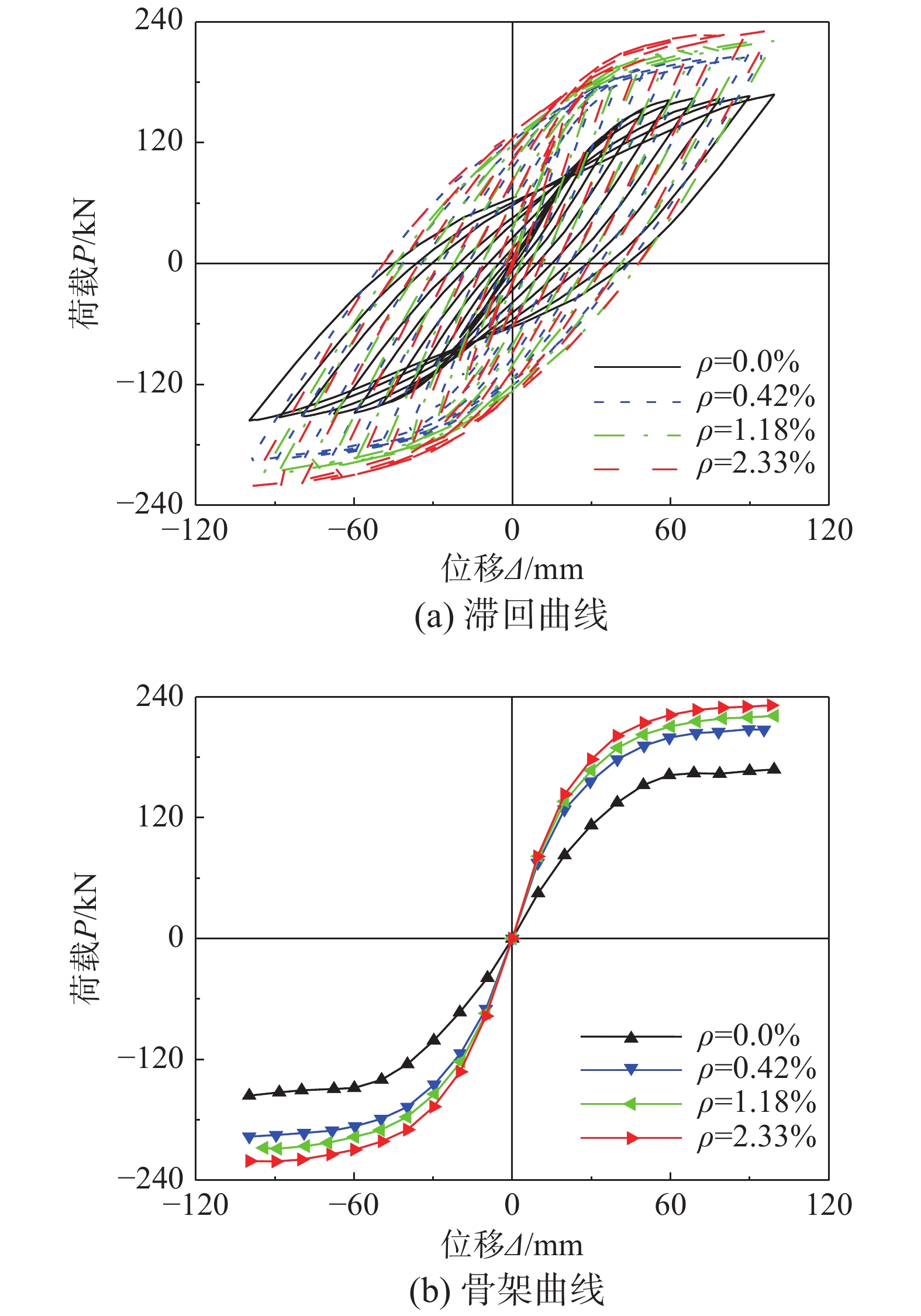
图16为模型NCF和上述3种工况下滞回曲线与骨架曲线的比较，图17(a)和图17(b)显示了弹性刚度和极限承载力的变化，可见随着等效配箍率的增加：1)滞回环面积增大，表明模型算例的耗能能力增强；2)模型算例的弹性刚度有明显提高，与模型NCF相比，等效配箍率ρ_sa=0.42%、ρ_sa=1.18%和ρ_sa=2.33%时模型的弹性刚度分别提高了76.3%、84.1%和94.0%；3)模型算例的极限承载力也有明显提高，与模型NCF相比，等效配箍率ρ_sa=0.42%、ρ_sa=1.18%和ρ_sa=2.33%时模型的极限承载力分别提高了23.6%、31.7%与38.0%。

图  16  等效配箍率对组合框架荷载-位移曲线的影响

Figure  16.  Influence of equivalent stirrup ratio on load-displacement curves and skeleton curves

下载: 全尺寸图片 幻灯片

下载: 全尺寸图片 幻灯片

图  17  拉筋对组合框架弹性刚度和极限承载力的影响

Figure  17.  Influence of stirrup on elastic stiffness and ultimate bearing capacity of composite frames

下载: 全尺寸图片 幻灯片

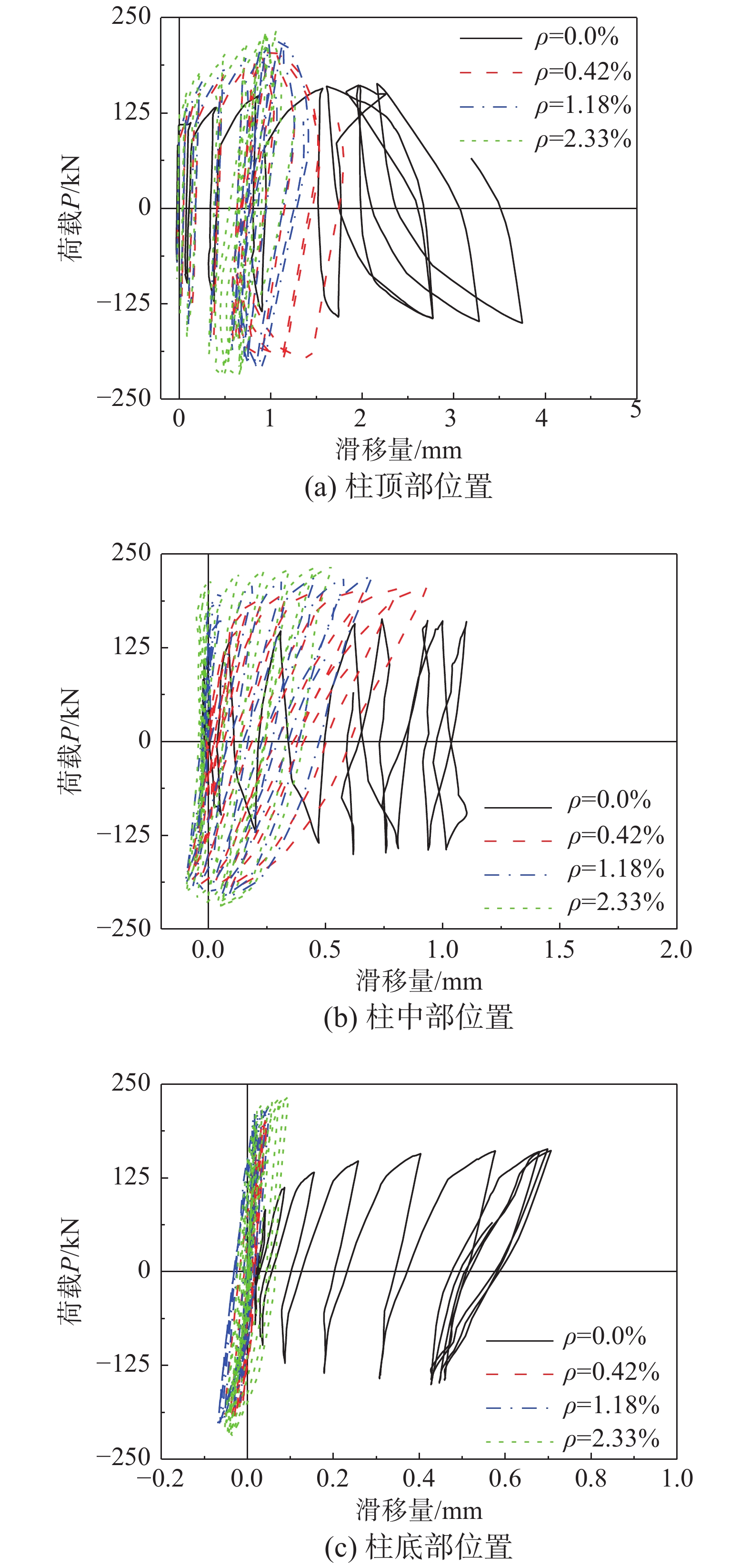
图18显示了不同配箍率下柱端拉筋对钢管与混凝土间滑移滞回曲线的影响规律，算例点分别位于加载侧一层柱顶部、中部和底部截面。未设置拉筋的算例最大滑移量约为4 mm，而配有拉筋的算例最大滑移量降低至1.8 mm，表明拉筋降低了核心混凝土与钢管壁间的滑移，且等效配箍率越大，界面滑移越小，组合框架结构模型算例刚度越大。

图  18  钢管混凝土柱界面滑移曲线对比

Figure  18.  Interface slip curves of concrete-filled steel tube

下载: 全尺寸图片 幻灯片

根据有限元模型计算结果，图19列出了4种工况下组合框架结构模型算例在相同侧移时的塑性耗能值，可见随着等效配箍率的增加：1)模型算例的塑性耗能值增加，但涨幅趋于平缓；2)组合梁的耗能一直在增加，主要表现为钢梁耗能增加；3)钢管混凝土柱的耗能先增加后减小，主要表现为混凝土和钢管的耗能先增加后减小，而拉筋的耗能一直增加。

图  19  等效配箍率对框架模型算例塑性耗能的影响

Figure  19.  Influence of equivalent stirrup ratio on plastic energy dissipation of composite frame models

下载: 全尺寸图片 幻灯片

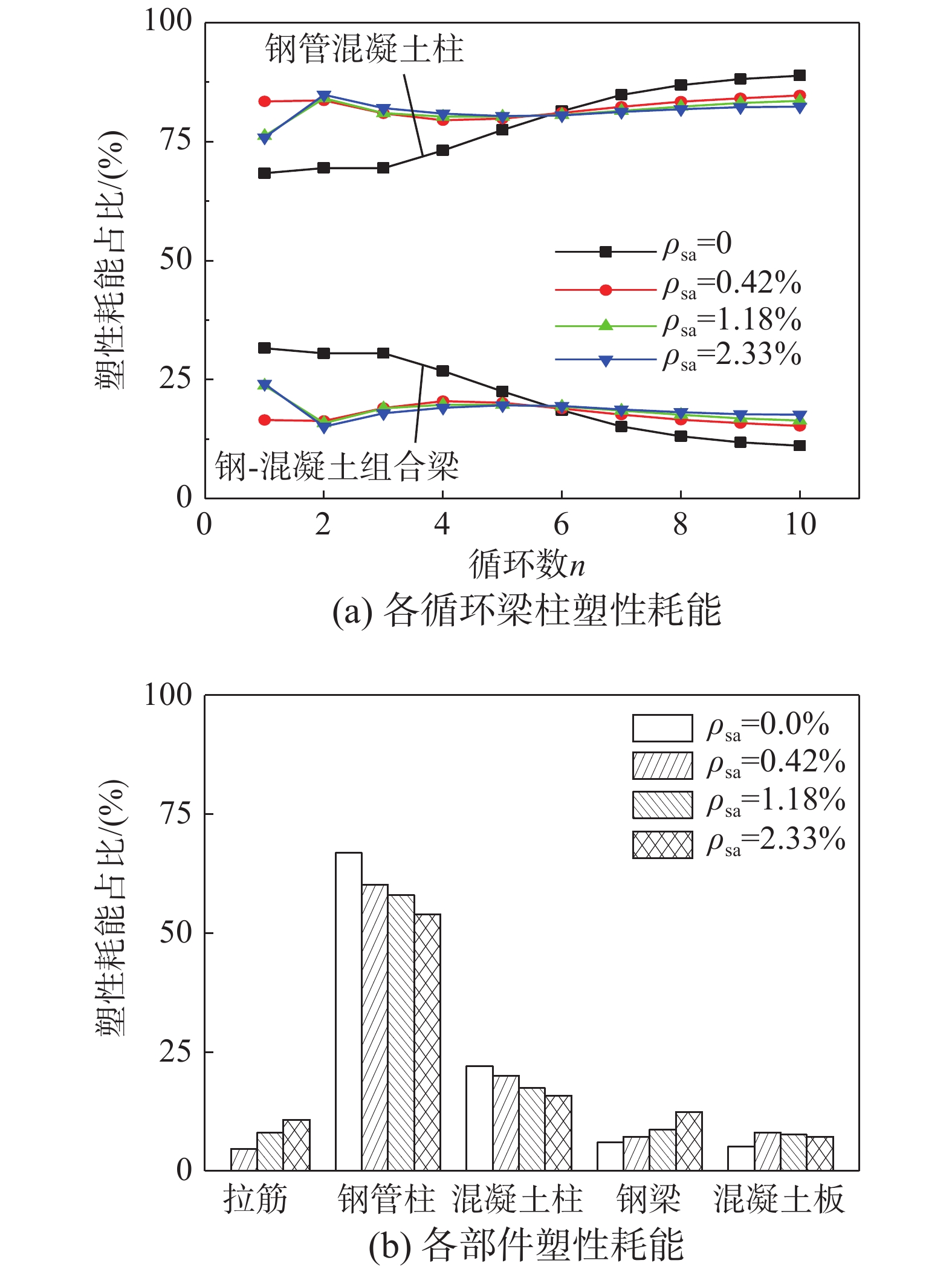
图20给出了4种工况下模型算例各主要部件的耗能百分比，其中栓钉耗能值很小，不予比较，可见：1)钢管混凝土柱为主要耗能部件，占总塑性耗能的70%以上；2)随着等效配箍率的增加，钢管混凝土柱的塑性耗能占比不断下降，组合梁的塑性耗能占比不断上升，表明由于柱端拉筋的存在，降低了钢管与混凝土之间的滑移、加强对混凝土的约束以及提高柱端抗弯承载力与耗能能力，间接改变梁柱线刚度比和抗弯承载力比，进一步利用钢梁的耗能潜力，有效改善模型算例各部件塑性耗能占比，使以“柱耗能为主”的组合框架中组合梁承担更多的塑性耗能；3)随着等效配箍率的增加，拉筋在组合框架结构算例中的耗能占比也不断增加。

图  20  等效配箍率对模型算例塑性耗能占比的影响

Figure  20.  Influence of equivalent stirrup ratio on plastic energy dissipation ratio composite frame models

下载: 全尺寸图片 幻灯片

4   结论

本文对2榀两层两跨钢-混凝土组合框架结构进行了滞回性能试验研究和有限元分析，结论如下：

(1)在水平低周往复荷载作用下以“柱耗能为主”的方钢管混凝土柱-组合梁框架结构因柱端形成塑性铰而使结构失效。在混凝土强度等级较低的情况下，柱端拉筋强柱构造措施不仅使组合框架结构具有较强的刚度、承载力和耗能能力，还使柱端塑性铰数量增多，出现时间延迟。这表明该构造措施能显著提高组合框架结构的抗震性能；

(2)有限元分析表明：柱端拉筋降低了钢管与混凝土之间的滑移，加强了钢管对混凝土的约束，同时提高了柱的抗弯承载力与耗能能力，间接改变了梁柱线刚度比和抗弯承载力比；

(3)有限元参数分析表明：该组合框架结构以柱耗能为主。随着等效配箍率的增加，柱端拉筋和组合梁的塑性耗能占比也逐渐增加，而钢管混凝土柱的塑性耗能占比却不断下降，这有利于进一步挖掘组合梁的耗能潜力，使以“柱耗能为主”的组合框架中组合梁承担更多的塑性耗能。