REDUCED-ORDER PROGRESSIVE COLLAPSE MODELING OF STEEL FRAME BUILDINGS WITH COMPOSITE SLABS
-
摘要: 该文借助经过校验的组合楼盖精细模型,建立了组合楼板钢框架结构连续倒塌有限元简化模型,通过与组合楼盖子结构试验对比验证了此简化模型的准确性。采用简化模型,分析了柱子失效位置、结构层数和组合楼板等参数对一个五层组合楼板钢框架原型结构抗连续倒塌性能的影响。分析结果表明:原型结构具有足够的承载力以避免由单个底层柱子失效所导致的结构连续倒塌;除了角柱失效工况外,原型结构的层数变化对结构抗连续倒塌性能的影响可以忽略,而在角柱失效工况下,层间桁架承载机制的贡献会使得原型结构比单层有楼板结构的抗连续倒塌承载力更高;在考虑组合楼板之后,原型结构的抗连续倒塌承载力提升了114%。Abstract: With the aid of a validated high-fidelity composite floor model, a reduced-order finite element model of steel-framed structures with composite slabs was established for analyzing the structural behavior under progressive collapse scenarios. The accuracy of the reduced-order model was validated by comparing it with a composite floor substructure test. The progressive collapse resistance of a five-story prototype building was analyzed using the reduced-order model. The analysis results indicate the prototype building has sufficient loading-carrying capacity to prevent the progressive collapse caused by the failure of a single ground floor column. Except for the corner loss scenario, the altering of floor number has an insignificant effect on the progressive collapse behavior of the prototype building. The predicted progressive collapse resistance of the prototype building is improved by 114% after considering the contribution of the composite slab.
-
Keywords:
- progressive collapse /
- composite slab /
- steel frame /
- composite structure /
- reduced-order modeling
-
真实或足尺整体结构的连续倒塌试验可以准确地反映结构在连续倒塌情况下的实际性能和真实响应[1-2],但是费用和耗时都极高。如今,广泛开展的节点子结构连续倒塌试验[3-8]能够很好地反映失效位置附近局部区域的破坏发展规律,但是其不能获知此局部失效所导致的后续破坏扩展和结构的整体失效模式。与试验研究相比,数值模拟研究可以用较低的成本开展大量工况的模拟计算,是结构连续倒塌研究的重要手段。现有的试验研究表明[9-10],钢-混凝土组合楼盖系统的连续倒塌主要由梁柱节点区域的钢材断裂或混凝土性能损伤退化引起。因此,为了获得较为可靠的数值结果,针对此类结构的连续倒塌数值模型必须要能够准确反映钢材断裂失效和混凝土损伤退化的影响。
在目前有关组合楼盖系统[11-14]或组合楼板钢框架整体结构[15-19]的连续倒塌数值模拟中,梁柱节点区域应力状态对钢材断裂行为的影响还未受到重视。根据足尺组合楼盖子结构连续倒塌试验[20]及与其对应的材性试验,作者利用有限元精细模型对比发现,在梁柱节点位置必须要同时考虑应力三轴度和罗德角等应力状态参数对钢材断裂行为的影响,否则将导致组合楼盖子结构数值模拟结果失真[21]。若要在有限元模型中直接考虑应力三轴度和罗德角等应力状态参数的影响,那么必须要在此有限元模型可能出现钢材断裂的节点区域划分足够细密的单元,以获得足够精度的应力状态参数。由于组合楼板钢框架结构在发生连续倒塌时通常伴随着材料的断裂失效,为了保证计算的收敛性,在对其进行有限元模拟时普遍采用显式算法。但是,采用较小的单元尺寸不仅会增加模型单元数量,也会限制显式算法的计算步长,这两个因素都会增加模型的计算时间。为了提高计算效率,组合楼板钢框架结构的连续倒塌模拟可以采用简化模型[18],即梁和柱等构件由梁单元代替,组合楼板由壳单元代替。但是,目前还未有能在整体结构简化模型中考虑应力三轴度和罗德角等应力状态参数对钢材断裂影响的模拟方法。
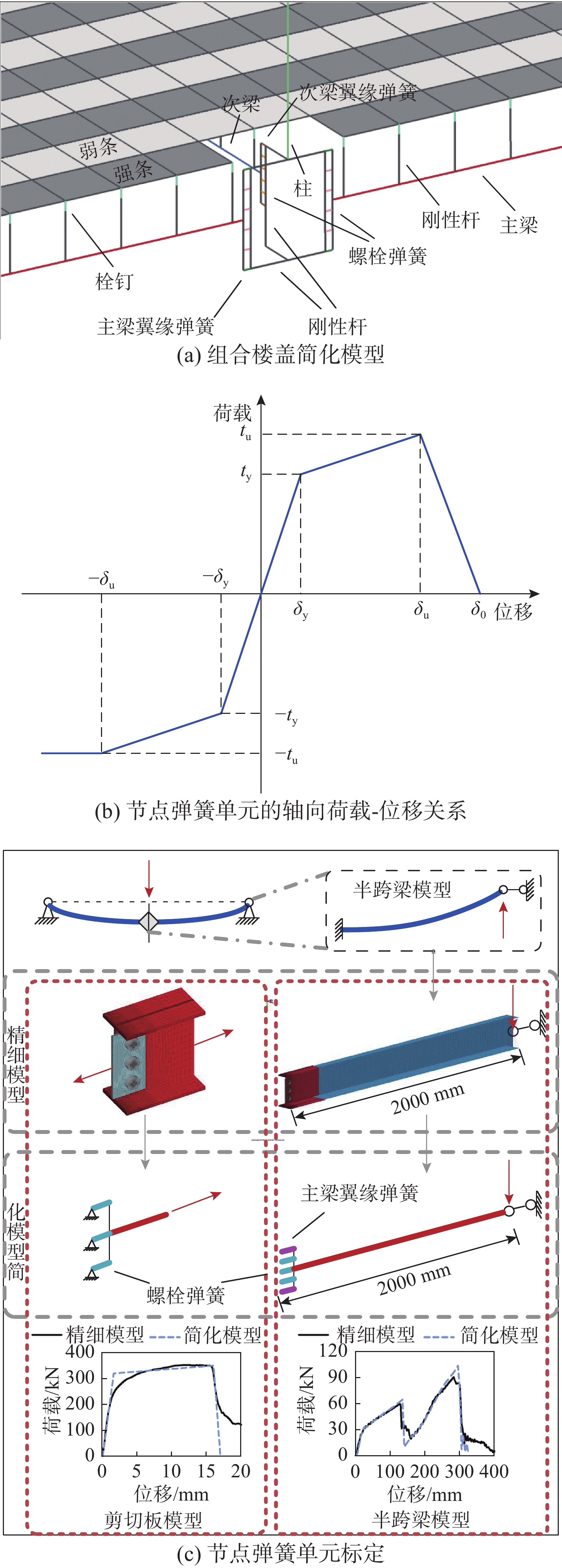
因此,本文借助经过足尺组合楼盖子结构试验[10, 20]校验的组合楼盖有限元精细模型[21],建立了适用于模拟组合楼板钢框架结构抗连续倒塌性能,且同时兼顾计算效率和计算精度的有限元简化模型。此简化模型的建模流程如图1所示。然后,借助简化模型,分析了柱失效位置、结构层数和组合楼板等参数对一个五层组合楼板钢框架原型结构抗连续倒塌性能的影响。
1 组合楼盖子结构试验
如图1所示,用于标定组合楼盖简化模型的精细模型是根据足尺组合楼盖子结构连续倒塌试验[10, 20]而建立的。此试验研究了组合楼盖子结构在移除边中柱工况下的抗连续倒塌性能,其试验装置和试件平面布置如图2所示。此试件的主梁和次梁跨度分别为4.2 m和3.6 m,柱子高度为层高的一半,即1.8 m。主梁截面为H200 mm×100 mm×5.5 mm×8 mm,次梁截面为H150 mm×75 mm×7 mm×10 mm,柱截面为H200 mm×200 mm×8 mm×12 mm,所有梁柱均采用Q345钢。组合楼板的总厚度为100 mm,其中开口型压型钢板高度为50 mm,上部的混凝土翼板厚度为50 mm。压型钢板强度等级为Q345,厚度为1.2 mm。压型钢板板肋布置方向与主梁轴线平行。混凝土翼板内布置网口尺寸为200 mm×200 mm的CRB550焊接钢筋网,钢筋直径为8 mm。组合楼板和钢梁通过直径为16 mm、长度为80 mm的5.6级栓钉连接。栓钉布置方式按完全抗剪设计,沿主梁方向每隔300 mm布置一个,沿次梁方向每个板肋(305 mm)布置一个。主梁-柱节点采用栓焊刚接节点;次梁-柱节点采用剪切板螺栓铰接节点;次梁-主梁节点采用剪切板螺栓铰接节点。如图2(b)所示,在试件水平边界处,组合楼板向外延伸900 mm,以考虑相邻跨所提供的约束作用。此外,框架梁在边界处亦向外延伸,其端部约束于水平约束支座。在试验过程中,与失效柱相连的主梁内发展了显著的悬链线拉力,导致其两端的水平约束支座出现明显的水平滑移。支座水平约束刚度可以通过将试验测得的水平力除以支座水平位移而得到,约为10 kN/mm[21]。在试验过程中,除了失效柱,其他所有柱子的柱底均被完全约束。在试验过程中,作动器施加的集中力通过4级分配梁系统均匀分配到楼板上的24个点,以实现较为理想的均布加载效果。由边长为150 mm的标准立方体混凝土试块所测得的混凝土抗压强度为33 MPa。在之后的模拟中,主要钢构件和混凝土所采用的应力-应变曲线如图2(c)所示。与此试验有关的更多细节可以参照文献[10, 20]。
2 组合楼盖子结构有限元精细模型
如图1所示,根据第1节所述的组合楼盖子结构试验,采用LS-DYNA软件建立了对应的有限元精细模型[21],本节将对此模型的建模方式进行简要介绍。在精细模型中,梁、柱和压型钢板采用壳单元建模,钢筋和栓钉分别采用桁架单元和梁单元建模,混凝土楼板采用实体单元建模。钢材延性断裂和混凝土塑性损伤等材料非线性行为根据材性试验的结果进行标定。栓钉与钢梁间的剪切滑移行为通过非线性弹簧单元模拟,其剪切-滑移曲线通过推出试验[10]获得。钢筋单元节点绑定于对应的混凝土实体单元,忽略其与混凝土之间的相对滑移。梁端水平约束支座的水平约束刚度通过在与失效柱相连的主梁梁端设置的水平弹簧单元来模拟。由于在试验中,未在其他外伸梁端测得明显的水平位移,因此,在模型中其他外伸梁的端部均被完全约束。在精细模型中,分配梁系统所施加的楼面荷载通过在与失效柱相邻的组合楼板上施加逐渐增大的竖向均布荷载来模拟。此精细模型已在文献[21]中验证,图2(d)为其计算得到的组合楼盖子结构荷载-位移曲线与试验结果的对比。接下来,将采用此精细模型来标定组合楼盖子结构的简化模型。
3 组合楼盖子结构有限元简化模型
尽管第2节已经建立了精度较高的精细模型,但其计算耗时较长而难以应用于整体结构的连续倒塌分析。因此,如图1所示,通过组合楼盖子结构试验和其对应的精细模型,采用LS-DYNA软件建立了其对应的有限元简化模型,以将其应用于之后的组合楼板钢框架整体结构的连续倒塌分析。
3.1 梁柱节点连接
如图3(a)所示,在组合楼盖简化模型中,主梁、次梁和柱都采用Hughes-Liu梁单元来模拟。在梁柱连接的翼缘和腹板螺栓位置,分别设置对应的翼缘弹簧单元和螺栓弹簧单元。在试验中,主梁-柱节点和次梁-柱节点的破坏都是受拉破坏,未出现竖向剪切破坏和面外破坏。因此,这些弹簧单元仅定义了轴向荷载-位移行为(图3(b)),在其他方向的变形被完全约束。如图3(b)所示,在受拉状态下,弹簧单元在达到极限受拉承载力(tu)之后,其承载力线性降低,在达到断裂位移(δ0)时承载力降为0;在受压状态下,弹簧单元在达到极限受压承载力(−tu)之后,其承载力保持不变。
如前所述,在对组合楼盖进行连续倒塌模拟时,必须考虑应力三轴度和罗德角等应力状态参数对节点连接断裂行为的影响[21]。虽然已经根据取自组合楼盖子结构的钢材材性试件标定了考虑应力三轴度和罗德角影响的钢材延性断裂模型[21],然而,由于梁单元并不能够精确反映节点区域的应力状态,因此不能将标定好的钢材断裂模型直接应用于简化模型。为了解决此问题,本文在简化模型建模时,采用间接方式来考虑应力状态对梁柱节点断裂行为的影响,其具体的建模流程如图3(c)所示。
首先,根据主梁-柱节点处的腹板剪切板螺栓连接,分别建立此剪切板连接的精细模型和简化模型,并在模型端部施加平行于梁轴线的单调受拉位移荷载。根据精细模型的计算结果[21],标定简化模型中螺栓弹簧单元参数,经过多次迭代,直至简化模型的荷载-位移曲线与精细模型相吻合。由于在单柱移除条件下,梁柱节点的抗连续倒塌性能可以通过如图3(c)所示的半跨梁模型来近似分析[21],故选取此半跨梁模型来标定翼缘弹簧单元参数。在此半跨梁模型中,柱子提供的约束被简化为完全约束,在约束梁端水平位移的同时在梁端施加竖向的单调位移荷载。根据此半跨梁模型,分别建立对应的精细模型和简化模型,将已经标定好的螺栓弹簧单元用于此半跨梁简化模型。对于翼缘弹簧单元来说,ty和tu分别等于主梁翼缘截面的受拉屈服承载力和极限受拉承载力,δy等于主梁翼缘全截面屈服时的受拉变形,因此,只有δu和δ0两个参数需要进行标定。根据精细模型的计算结果,标定翼缘弹簧单元的δu和δ0参数,直至简化模型的荷载-位移曲线与精细模型吻合时为止。由于次梁-柱连接的螺栓连接尺寸和材料均与主梁-柱连接相同,因此上述标定好的弹簧单元也被用于次梁-柱连接的简化模型中。表1为上述标定好的梁柱节点弹簧单元参数。
表 1 梁柱节点连接弹簧单元参数Table 1. Calibrated connection spring parameters弹簧单元 屈服位移
δy/mm屈服承载力
ty/kN极限位移
δu/mm极限承载力
tu/kN断裂位移
δ0/mm螺栓弹簧 1.60 107 16.0 117 17 翼缘弹簧 0.02 300 1.7 400 2 3.2 组合楼板
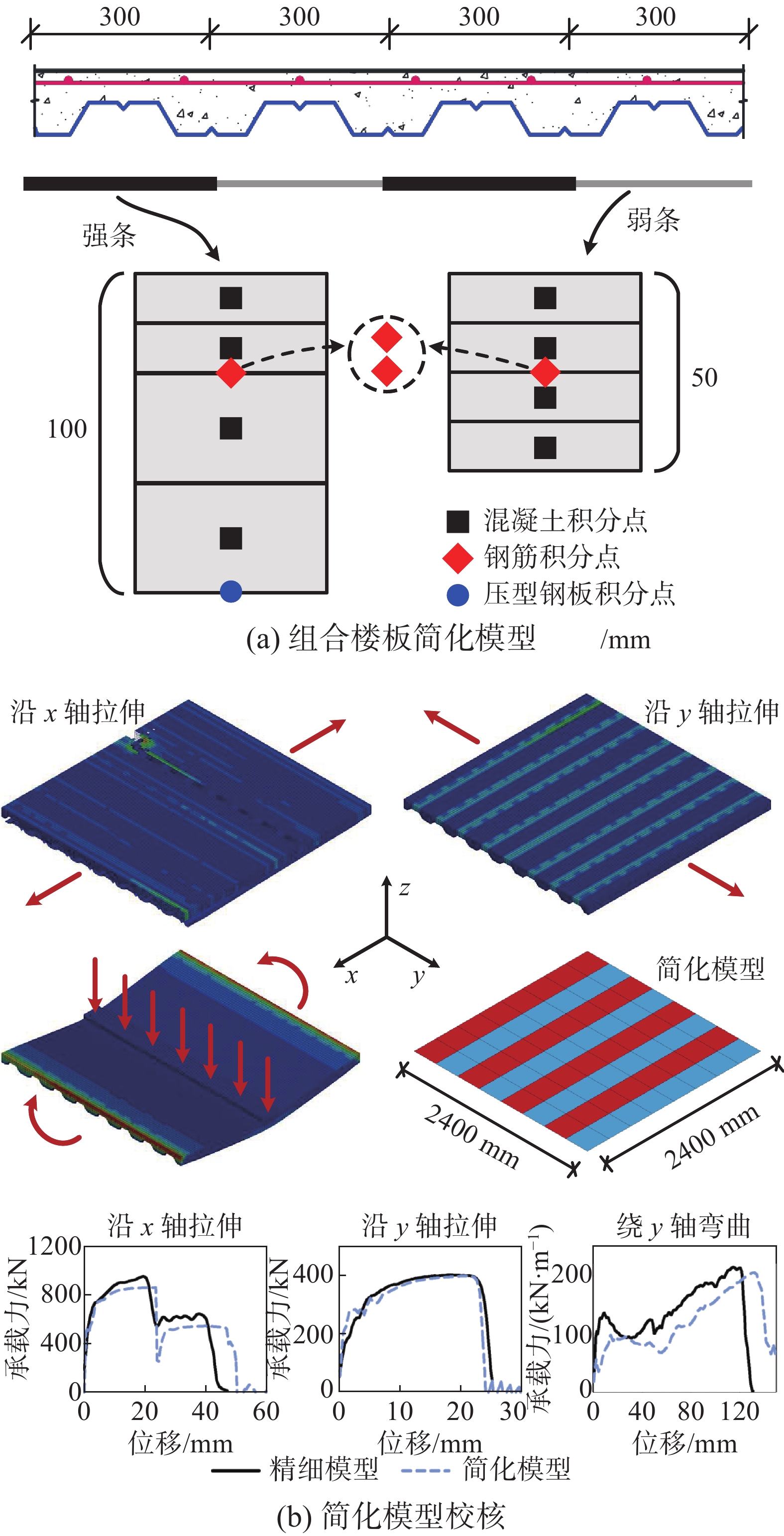
如图4(a)所示,为了减少计算时间,在简化模型中,组合楼板采用分层壳单元来建模,并且根据组合楼板截面厚度的变化将其划分为强条和弱条两种壳单元。强条对应组合楼板板肋位置,此处厚度为100 mm,而弱条对应组合楼板的翼板,其厚度为50 mm。每个强条壳单元沿厚度方向有七个积分点,包括四个混凝土积分点,两个钢筋积分点和一个压型钢板积分点。在分层壳模型中,忽略了压型钢板与混凝土之间的相对滑移。由于压型钢板只在板肋处通过栓钉固定于钢梁上翼缘,则只有板肋处的压型钢板才能有效发展受拉薄膜力;此外,板肋处组合楼板具有较高的截面高度,使得板肋底面的压型钢板对截面抗弯承载力的贡献明显高于翼缘底面的压型钢板。因此,在弱条壳单元中没有考虑压型钢板的贡献,即仅包括四个混凝土积分点和两个钢筋积分点。每个壳单元的边长为300 mm。为了保持模型的连续性,强条和弱条壳单元均设置在组合楼板翼板底面高度处,即强条壳单元位于板肋位置处组合楼板截面高度方向的中面,而弱条壳单元则位于组合楼板翼板底面。
在组合楼板壳单元中,混凝土、钢筋和压型钢板均采用LS-DYNA中的172号材料模拟,此材料模型可以通过改变配筋率来模拟素混凝土、钢筋或同时包含二者的钢筋混凝土,各材料的应力-应变关系如图2(c)所示。为了避免两个垂直方向钢筋断裂行为的互相影响,如图4(a)所示,两个方向的钢筋分别用两个独立的钢筋积分点表示。壳单元底部的压型钢板积分点仅定义了平行于板肋方向的应力-应变关系,以模拟压型钢板仅能在此方向发展受拉薄膜力的受力特征。为了避免因过大的单元扭曲变形而导致的计算收敛问题,组合楼板壳单元在塑性应变达到30%时会被强制删除。
在连续倒塌情况下,组合楼板的承载力主要由抗弯承载力和受拉薄膜承载力提供。如图4(b)所示,受限于开口型压型钢板组合楼板的截面特性,其表现为单向板的承载特征,即仅能绕y轴(垂直于板肋方向)发展抗弯承载力,不过,其仍可以沿x轴(平行于板肋方向)和y轴两个方向发展受拉承载力。沿x轴方向的受拉承载力由压型钢板和钢筋提供,而沿y轴方向的受拉承载力仅由钢筋提供。因此,如图4(b)所示,组合楼板简化模型的校核仅考虑了三种加载工况:沿x轴拉伸、沿y轴拉伸和绕y轴弯曲。以边长为2400 mm的正方形压型钢板组合楼板精细模型作为基准模型,来校核组合楼板简化模型的准确性。在精细模型中,考虑到压型钢板只在板肋底部被栓钉约束,因此,在模拟压型钢板水平边界条件时,只将水平拉力(沿x轴拉伸)或水平约束(绕y轴弯曲)施加在板肋底部的压型钢板单元节点上。如图4(b)所示,简化模型的计算结果与精细模型较为吻合,验证了组合楼板简化建模方法的准确性。
3.3 与试验结果对比
如图3(a)所示,在简化模型中,栓钉采用非线性弹簧单元模拟,并通过刚性杆将其连接于对应的主梁或次梁单元节点。栓钉连接的剪切滑移行为根据推出试验结果[10]定义。在组合楼盖子结构简化模型中(图1),在与失效柱相邻的组合楼板上施加逐渐增大的竖向均布荷载以模拟试验时分配梁系统所施加的楼面荷载。与试验一致,除了失效柱,此模型中各柱柱底均被完全约束。除了在与失效柱相连的主梁梁端设置10 kN/mm的水平弹簧外,其余外伸梁的梁端位移均被完全约束。将简化模型计算得到的所有柱底反力之和看作此楼盖子结构的竖向承载力。图2(d)为此简化模型计算得到的承载力-失效柱竖向位移曲线,其与组合楼盖子结构试验的荷载-位移曲线吻合较好。主梁-柱节点连接断裂失效所对应的两个荷载峰值点,均被简化模型准确模拟。这表明,此简化模型可以用于分析组合楼盖结构在柱子失效条件下的抗连续倒塌性能。
4 组合楼板钢框架结构连续倒塌分析
4.1 原型结构
为了研究组合楼板钢框架结构的抗连续倒塌性能,依照中国规范[22-27],设计了一栋5层组合楼板钢框架结构,其平面布置和立面布置如图5(a)所示。主梁跨度为9 m,次梁跨度为6 m,次梁间距为3 m,各层层高均为4.5 m。此结构的设计恒载和活载分别为5 kN/m2和2 kN/m2。方钢管柱子截面尺寸为400 mm×12 mm,H型主梁和次梁截面尺寸分别为H500 mm×200 mm×10 mm×16 mm和H300 mm×150 mm×6.5 mm×9 mm。如图5(b)所示,主梁-柱节点和次梁-柱节点均采用栓焊刚接节点,次梁-主梁节点为剪切板铰接节点。选用的压型钢板组合楼板与第1节组合楼盖子结构试验相同,压型钢板平行于主梁方向布置。组合楼板与钢梁通过直径为19 mm的栓钉相连,其数量按完全抗剪设计,每根主梁布置85个,每根次梁布置38个。原型结构中梁和柱的材性性能与图2(c)中主梁翼缘相同,而压型钢板、钢筋、栓钉及混凝土的材性性能均与第1节组合楼盖子结构试验相同。
4.2 模拟结果
采用3.1节所述的节点连接弹簧标定方法,分别标定了主梁-柱节点和次梁-柱节点简化模型的弹簧单元参数,其结果列于表2。次梁-主梁节点弹簧单元参数与次梁-柱节点相同。由于组合楼板与钢梁之间按完全抗剪设计,在原型结构简化模型中没有考虑栓钉的剪切破坏。
表 2 原型结构梁柱节点连接弹簧参数Table 2. Parameters of connection spring for prototype building节点 弹簧 屈服位移
δy/mm屈服承载力
ty/kN极限位移
δu/mm极限承载力
tu/kN断裂位移
δ0/mm主梁-
柱节点螺栓弹簧 1.50 280 20.00 340 39.00 翼缘弹簧 0.02 1354 2.05 1818 2.55 次梁-
柱节点螺栓弹簧 1.00 125 13.50 160 16.00 翼缘弹簧 0.02 571 2.00 760 2.50 如图5(a)所示,由于原型结构的对称性,其底层柱的单柱失效工况一共有九种,即A1、A2、A3、B1、B2、B3、C1、C2和C3。在失效柱移除之后,在与失效柱相邻跨度内的楼板上,施加从零开始逐渐增大的竖向均布荷载,直至整个结构达到极限承载力。此竖向均布荷载也同样施加在上部各层所对应的楼板位置。在9种柱失效工况下,原型结构的荷载-位移曲线如图6所示,其中,图6中的竖向荷载换算为单位面积受荷楼板上的等效均布荷载。此外,为了研究结构层数和组合楼板对结构抗连续倒塌性能的影响,抽取了原型结构中的第一层,分别在有楼板和无楼板两种情况下,模拟了其在9种柱失效工况下的结构响应,对应的荷载-位移曲线如图6所示。以上各结构在C1柱失效工况下的破坏模式亦示于图6。
通过简化模型可以得到如图6所示的组合楼板钢框架结构在连续倒塌情况下的非线性静力响应。采用基于能量守恒的方法[28](图7(a)),可以将非线性静力响应转化为等效动力响应。在达到静力响应极值Fsu后,结构的承载能力会变得不稳定,甚至出现较大的振荡,这可能会使得结构在动力荷载作用下出现突然破坏。因此,将静力响应极值Fsu对应的位移定为等效动力响应曲线的终止点[29],在此终止点之前,等效动力响应曲线的极值Fdu即可认为是结构在对应工况下的抗连续倒塌能力。采用此方法,可计算出图6中各非线性静力模拟所对应的Fdu,并绘于图7(b)。图7(b)中的水平虚线代表ASCE/SEI 7-16[30]规范规定的结构连续倒塌荷载组合Rd (1.2恒载 + 0.5活载),对于原型结构来说,Rd为7 kN/m2。
如图6和图7(b)所示,相对于其他六种柱子失效工况,原型结构在A1、B1和C1这三种柱失效工况下的极限承载力较高。这是因为在这三种工况下,与失效柱子相连主梁的楼板附属面积较小,仅为其它六种工况主梁楼板附属面积的一半。原型结构在各工况下的Fdu最小值为2.45Rd (17.12 kN/m2),这说明原型结构有足够的承载能力来避免由单个底层柱子失效所导致的结构连续倒塌。
如图6所示,除了A1柱(角柱)失效工况,原型结构与单层有楼板结构在其它柱失效工况下的荷载-位移曲线大致相同。这是因为在角柱失效工况下,原型结构借助连接各层的角柱发展了桁架承载机制[31],而单层有楼板结构无法发展此层间抗力机制;但在其他柱失效工况下,桁架承载机制对原型结构承载力的影响可以忽略。这说明,在原型结构中每层所承担的荷载是大致相同的,也就是说竖向荷载并没有向某一层集中。因此,如果组合楼板钢框架结构中每层的结构布置、构件尺寸和材料性能都相同,那么每层倾向于只承担施加于其上的竖向荷载。在此条件下,如果柱子有足够的承载力避免失稳破坏,则结构层数的变化不会显著改变结构的抗连续倒塌性能。单层有楼板结构在各工况下的Fdu最小值为17.05 kN/m2,与原型结构的Fdu最小值大致相等。
对于单层无楼板结构来说,A2、B3和C3柱失效工况的Fdu非常接近于Rd,这在柱子突然失效的动力情况下非常可能发生连续倒塌。因此,仅仅依靠未针对连续倒塌特殊设计的无楼板钢框架结构,可能很难避免由柱子突然失效所导致的结构连续倒塌。单层有楼板结构在各工况下的Fdu最小值是单层无楼板结构Fdu最小值7.96 kN/m2的2.14倍,这说明在考虑了组合楼板之后,本文所设计的钢框架结构的抗连续倒塌承载力被至少提高了一倍。
5 结论
本文建立了组合楼板钢框架结构连续倒塌有限元简化模型,通过与组合楼盖子结构试验结果对比验证了此简化模型的准确性。之后,设计了一幢5层组合楼板钢框架原型结构,采用简化模型分析了柱子失效位置、结构层数和组合楼板对其抗连续倒塌性能的影响。本文的主要结论归纳如下:
(1) 原型结构在各工况下的最小抗连续倒塌承载力为2.45Rd,表明其有足够的承载力以避免由单个底层柱子失效所导致的结构连续倒塌。
(2) 由于层间桁架承载机制的贡献,在角柱失效工况下,原型结构比单层有楼板结构的抗连续倒塌承载力更高。在除了角柱失效之外的其他柱失效工况下,原型结构的层数变化对抗连续倒塌性能的影响可以忽略。
(3) 单层有楼板结构比单层无楼板结构的抗连续倒塌承载力提高了114%。因此,在对组合楼板钢框架结构进行抗连续倒塌设计时,忽略组合楼板的贡献可能会极大地低估结构的抗连续倒塌能力。
-
表 1 梁柱节点连接弹簧单元参数
Table 1 Calibrated connection spring parameters
弹簧单元 屈服位移
δy/mm屈服承载力
ty/kN极限位移
δu/mm极限承载力
tu/kN断裂位移
δ0/mm螺栓弹簧 1.60 107 16.0 117 17 翼缘弹簧 0.02 300 1.7 400 2 表 2 原型结构梁柱节点连接弹簧参数
Table 2 Parameters of connection spring for prototype building
节点 弹簧 屈服位移
δy/mm屈服承载力
ty/kN极限位移
δu/mm极限承载力
tu/kN断裂位移
δ0/mm主梁-
柱节点螺栓弹簧 1.50 280 20.00 340 39.00 翼缘弹簧 0.02 1354 2.05 1818 2.55 次梁-
柱节点螺栓弹簧 1.00 125 13.50 160 16.00 翼缘弹簧 0.02 571 2.00 760 2.50 -
[1] SONG B I, SEZEN H. Experimental and analytical progressive collapse assessment of a steel frame building [J]. Engineering Structures, 2013, 56: 664 − 672. doi: 10.1016/j.engstruct.2013.05.050
[2] XIAO Y, KUNNATH S, LI F W, et al. Collapse test of three-story half-scale reinforced concrete frame building [J]. ACI Structural Journal, 2015, 112(4): 429 − 438.
[3] SADEK F, MAIN J A, LEW H S, et al. Testing and analysis of steel and concrete beam-column assemblies under a column removal scenario [J]. Journal of Structural Engineering, 2011, 137(9): 881 − 892. doi: 10.1061/(ASCE)ST.1943-541X.0000422
[4] CHEN S, CHEN K, TAN K H. Effect of profiled decking on composite beam-column joints with end-plate bolted connections under column-removal scenario [J]. Journal of Constructional Steel Research, 2021, 182: 106668. doi: 10.1016/j.jcsr.2021.106668
[5] GUO L, GAO S, FU F, et al. Experimental study and numerical analysis of progressive collapse resistance of composite frames [J]. Journal of Constructional Steel Research, 2013, 89: 236 − 251. doi: 10.1016/j.jcsr.2013.07.006
[6] LI L, WANG W, CHEN Y, et al. Experimental investigation of beam-to-tubular column moment connections under column removal scenario [J]. Journal of Constructional Steel Research, 2013, 88: 244 − 255. doi: 10.1016/j.jcsr.2013.05.017
[7] 余洋, 李治, 肖龙山, 等. 边柱失效后预应力拼接连接装配式结构抗连续倒塌机理研究[J]. 工程力学, 2021, 38(4): 159 − 168. doi: 10.6052/j.issn.1000-4750.2020.06.0366 YU Yang, LI Zhi, XIAO Longshan, et al. Load resisting mechanism of precast structure under exterior column failure [J]. Engineering Mechanics, 2021, 38(4): 159 − 168. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.0366
[8] 孟宝, 钟炜辉, 郝际平. 不同跨度比下栓焊刚性连接梁柱子结构抗倒塌性能试验研究[J]. 工程力学, 2018, 35(1): 79 − 87. doi: 10.6052/j.issn.1000-4750.2016.09.0672 MENG Bao, ZHONG Weihui, HAO Jiping. Experimental study on anti-collapse performance for beam-column assemblies with bolt and weld rigid connection based on different span ratio [J]. Engineering Mechanics, 2018, 35(1): 79 − 87. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.09.0672
[9] FU Q N. Structural behaviour of composite floor systems under column removal scenario [D]. Singapore: Nanyang Technological University, 2018.
[10] 王伟, 王俊杰. 大型钢-混凝土组合楼盖系统的连续倒塌试验与失效机理研究[J]. 建筑结构学报, 2021, 42(5): 82 − 91. WANG Wei, WANG Junjie. Progressive collapse tests and failure mechanism of large-scale steel-concrete composite floor system [J]. Journal of Building Structures, 2021, 42(5): 82 − 91. (in Chinese)
[11] ALASHKER Y, EL-TAWIL S, SADEK F. Progressive collapse resistance of steel-concrete composite floors [J]. Journal of Structural Engineering, 2010, 136(10): 1187 − 1196. doi: 10.1061/(ASCE)ST.1943-541X.0000230
[12] MAIN J A. Composite floor systems under column loss: Collapse resistance and tie force requirements [J]. Journal of Structural Engineering, 2014, 140(8): A4014003.
[13] FU Q N, TAN K H, ZHOU X H, et al. Numerical simulations on three-dimensional composite structural systems against progressive collapse [J]. Journal of Constructional Steel Research, 2017, 135: 125 − 136. doi: 10.1016/j.jcsr.2017.04.014
[14] DIMOPOULOS C A, FREDDI F, KARAVASILIS T L, et al. Progressive collapse resistance of steel self-centering MRFs including the effects of the composite floor [J]. Engineering Structures, 2020, 208: 109923.
[15] FU F. Progressive collapse analysis of high-rise building with 3-D finite element modeling method [J]. Journal of Constructional Steel Research, 2009, 65(6): 1269 − 1278. doi: 10.1016/j.jcsr.2009.02.001
[16] KWASNIEWSKI L. Nonlinear dynamic simulations of progressive collapse for a multistory building [J]. Engineering Structures, 2010, 32(5): 1223 − 1235. doi: 10.1016/j.engstruct.2009.12.048
[17] ALASHKER Y, LI H, EL-TAWIL S. Approximations in progressive collapse modeling [J]. Journal of Structural Engineering, 2011, 137(9): 914 − 924. doi: 10.1061/(ASCE)ST.1943-541X.0000452
[18] LI H, EL-TAWIL S. Three-dimensional effects and collapse resistance mechanisms in steel frame buildings [J]. Journal of Structural Engineering, 2014, 140(8): A4014017.
[19] LEE S Y, NOH S Y, LEE D. Comparison of progressive collapse resistance capacities of steel ordinary and intermediate moment frames considering different connection details [J]. Engineering Structures, 2021, 231: 111753. doi: 10.1016/j.engstruct.2020.111753
[20] WANG J J, WANG W, BAO Y H. Full-scale test of a steel–concrete composite floor system with moment-resisting connections under a middle-edge column removal scenario [J]. Journal of Structural Engineering, 2020, 146(5): 04020067. doi: 10.1061/(ASCE)ST.1943-541X.0002630
[21] WANG J, WANG W, QIAN X. Progressive collapse simulation of the steel-concrete composite floor system considering ductile fracture of steel [J]. Engineering Structures, 2019, 200: 109701. doi: 10.1016/j.engstruct.2019.109701
[22] GB 50017−2017, 钢结构设计标准 [S]. 北京: 中国建筑工业出版社, 2017. GB 50017−2017, Standard for design of steel structures [S]. Beijing: China Architecture & Building Press, 2017. (in Chinese)
[23] GB 50011−2010, 建筑抗震设计规范 [S]. 北京: 中国建筑工业出版社, 2010. GB 50011−2010, Code for seismic design of buildings [S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
[24] GB 50009−2012, 建筑结构荷载规范 [S]. 北京: 中国建筑工业出版社, 2012. GB 50009−2012, Load code for the design of building structures [S]. Beijing: China Architecture & Building Press, 2012. (in Chinese)
[25] GB 50010−2010, 混凝土结构设计规范 [S]. 北京: 中国建筑工业出版社, 2015. GB 50010−2010, Code for design of concrete structures [S]. Beijing: China Architecture & Building Press, 2015. (in Chinese)
[26] JGJ 114−2014, 钢筋焊接网混凝土结构技术规程 [S]. 北京: 中国建筑工业出版社, 2014. JGJ 114−2014, Technical specification for concrete structures reinforced with welded steel fabric [S]. Beijing: China Architecture & Building Press, 2014. (in Chinese)
[27] CECS 273−2010, 组合楼板设计与施工规范 [S]. 北京: 中国计划出版社, 2010. CECS 273−2010, Code for composite slabs design and construction [S]. Beijing: China Planning Press, 2010. (in Chinese)
[28] IZZUDDIN B A, VLASSIS A G, ELGHAZOULI A Y, et al. Progressive collapse of multi-storey buildings due to sudden column loss—part I: Simplified assessment framework [J]. Engineering Structures, 2008, 30(5): 1308 − 1318. doi: 10.1016/j.engstruct.2007.07.011
[29] BAO Y H, MAIN J A, SAM-YOUNG N. Evaluation of structural robustness against column loss: methodology and application to RC frame buildings [J]. Journal of Structural Engineering, 2017, 143(8): 04017066. doi: 10.1061/(ASCE)ST.1943-541X.0001795
[30] ASCE/SEI 7-16, Minimum design loads and associated criteria for buildings and other structures [S]. Reston, VA: ASCE, 2016.
[31] SAGIROGLU S. Analytical and experimental evaluation of progressive collapse resistance of reinforced concrete structures [D]. Boston: Northeastern University, 2012.
-
期刊类型引用(5)
1. 谭政,钟炜辉,郑玉辉,孟宝,段仕超,张驰,王洪臣. 考虑边界约束的多层组合框架抗倒塌性能研究. 建筑结构学报. 2025(02): 24-38 .  百度学术
百度学术
2. 谭政,钟炜辉,高垚,段仕超,曲泽宇,孟宝. 不对称跨度多层钢框架抗倒塌性能试验研究. 建筑结构学报. 2025(03): 117-129 .  百度学术
百度学术
3. 林楷奇,吴苏静,郑俊浩,李易,陈素文,陆新征. 地震灾害和意外事件下建筑结构抗倒塌研究:进展和展望. 工程力学. 2025(04): 1-24 .  本站查看
本站查看
4. 赵峥. 多层钢框架结构抗连续倒塌风险鲁棒性建模分析. 金属功能材料. 2024(01): 132-137 .  百度学术
百度学术
5. 陶慕轩,蒋骋昊,潘文豪. 复杂结构楼板面内力学行为研究综述与展望. 工程力学. 2024(12): 1-9 .  本站查看
本站查看
其他类型引用(4)




 下载:
下载: