钢-竹组合结构以冷弯薄壁型钢与重组竹材为主要材料，具有轻质高强、低碳环保^[1-2]等特性。近年来，研究者对钢-竹组合构件及界面的力学性能开展了理论与试验研究^[3-6]。结果表明，钢-竹组合构件中两种材料的组合效应突出、整体性好，但仍存在高强材料无法充分利用，竹材弹性模量低、结构变形大等缺点^[7]。随着预应力技术的不断发展与成熟，借鉴预应力混凝土结构^[8]和预应力木结构^[9]，设想通过施加预应力的方式，来提高钢-竹组合构件的刚度，改善钢-竹组合结构的受力性能。

目前，国内外对预应力木结构开展了一定的研究。宋彧等^[10]对预应力木梁的受弯性能开展了试验研究与分析，结果表明施加预应力后，在相同荷载作用下，木梁的挠度可降低近70%；而在相同挠度情况下，木梁的受弯承载力可提高近3倍。左宏亮等^[11-12]对一种新型预应力胶合木梁承载能力与抗弯刚度的影响因素开展了试验研究，结果表明配置预应力筋后，木梁的承载力与刚度均可提高30%以上。张晋等^[13-14]对体内预应力木梁短期受力特征的试验研究发现，与普通木梁相比较，预应力木梁的承载能力、抗弯刚度与变形能力等受弯性能均有明显提升。杨会峰等^[15]以张拉控制应力、张弦位置等为变量，通过对21根体外预应力木梁的试验研究，分析了未配置加强筋、配置非预应力筋和配置预应力筋胶合木梁的受弯承载力与截面抗弯刚度。结果表明，配置非预应力筋和预应力筋后，截面刚度可分别提高约18%和45%。此外，一些研究者对CFRP筋、FRP筋、GFRP筋增强木梁的受力性能与特征亦开展了一定试验研究与分析^[16-22]，结果均表明配置预应力筋对改良木梁性能具有显著作用。

在预应力结构的挠度验算方面，由于需综合考虑配筋特征、张弦方式、预应力增量、二次效应等因素影响，计算方法较为复杂。目前，已有研究针对预应力混凝土结构开展了一定的分析。贺志启等^[23]通过建立体外预应力梁在变形前后的几何关系，利用弹性理论推导得出了预应力筋应力增量与跨中挠度之间的统一关系式。刘钊等^[24]以体外预应力梁为对象，考虑布筋形式与荷载特征等因素，采用能量法建立了正常使用阶段应力增量的计算公式与简化方法。王宗林等^[25]根据体外预应力梁的受力平衡方程与变形协调条件，提出了从加载到破坏全过程中预应力筋应力增量、截面应力-应变关系，以及荷载-挠度曲线的计算方法，并进行了试验验证。

考虑制作难度与施工便捷性，本文采用体外预应力筋对钢-竹组合构件施加预应力。鉴于目前尚无预应力钢-竹组合梁的挠度计算方法，在设计12根组合梁试件并开展试验研究的基础上，借鉴预应力混凝土梁的挠度计算方法，考虑不同加载方式、不同张弦位置、不同预应力度，以及反拱挠度影响，提出钢-竹组合梁受弯挠度的统一计算公式，并与试验结果进行对比分析，从而为预应力钢-竹组合梁在正常使用阶段的挠度验算提供参考。

1   试验概况

1.1   试件设计

为分析钢-竹组合梁在正常使用阶段的挠度，考虑加载方式、张弦方式、预应力度等影响因素，设计制作了12根截面尺寸相同、长度均为3800 mm的工字形截面梁，试件照片及横截面尺寸如图1所示。各试件的设计参数如表1所示，其中试件L-1和L-2为未配置预应力筋的对照组，试件L-3~L-12为配置了体外预应力筋的试验组，但试件L-12未施加初始预应力。

图  1  钢-竹组合梁试件及横截面尺寸

Figure  1.  Specimens and cross-sectional dimensions of steel-bamboo composite beams

下载: 全尺寸图片 幻灯片

表  1  试件设计参数

Table  1.  Design parameters of specimens

编号	加载 方式	加载点至 梁端距离/mm	张弦方式	张弦点至 梁端距离/mm	预应 力筋	初始 预加力/kN
L-1	1	1900	—	—	—	—
L-2	2	1350	—	—	—	—
L-3	1	1900	1	1900	2ΦS15.2	40
L-4	1	1900	1	1900	2ΦS15.2	60
L-5	2	1350	1	1900	2ΦS15.2	40
L-6	2	1350	1	1900	2ΦS15.2	60
L-7	1	1900	2	1350	2ΦS15.2	40
L-8	1	1900	2	1350	2ΦS15.2	60
L-9	2	1350	2	1350	2ΦS15.2	40
L-10	2	1350	2	1350	2ΦS15.2	60
L-11	2	1350	2	1350	2ΦS15.2	80
L-12	2	1350	2	1350	2ΦS15.2	0
注：加载方式1和2分别表示跨中单点加载和两点对称加载；张弦方式1和2分别表示跨中一点张弦和两点对称张弦。

下载: 导出CSV 

| 显示表格

1.2   材料性能

钢-竹组合梁采用冷弯薄壁［形钢、重组竹两种主要材料经环氧树脂胶粘结而成，预应力筋采用预应力七股钢绞线。三种材料的主要物理力学性能指标见表2，其中薄壁钢板和重组竹的强度和弹性模量依据标准试验测定，并取各试样的算术平均值；钢绞线的力学性能指标由生产厂家提供。

表  2  材料的力学性能指标

Table  2.  Mechanical properties of materials

材料	规格尺寸	强度指标/MPa	弹性模量/MPa
重组竹	−140×20.0(翼缘) −160×20.0(腹板)	155.2(静曲强度) 93.47(抗压强度) 124.04(抗拉强度)	15673
薄壁钢板	［160×60×2.0	284(屈服强度) 378(极限强度)	2.0×105
钢绞线	1×7Φs15.2	1860(极限强度)	1.95×105

下载: 导出CSV 

| 显示表格

1.3   加载方案

1.3.1   预应力加载

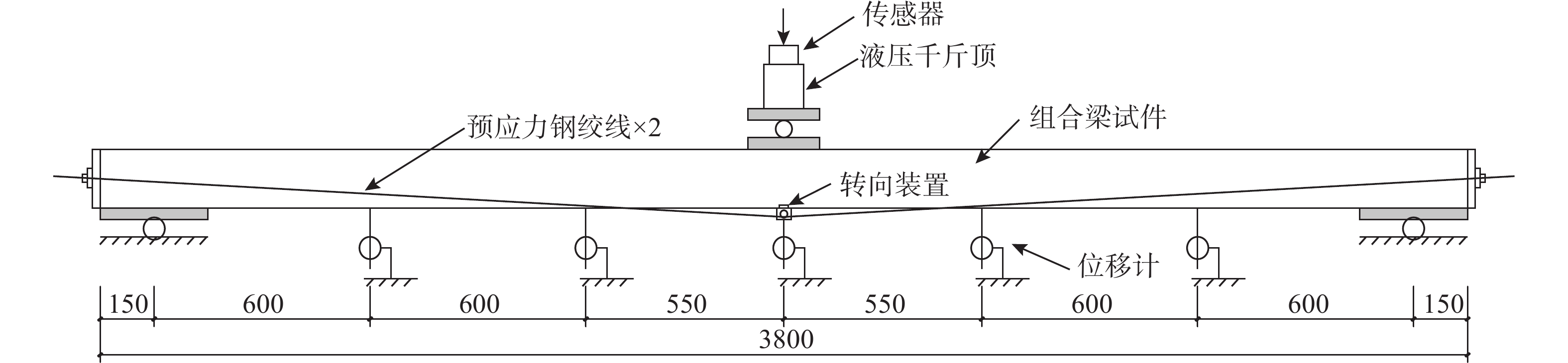
如图2所示，通过体外预应力钢绞线对钢-竹组合梁施加预应力，试验加载装置及主要方案如下：

图  2  预应力钢绞线锚固及转向装置

Figure  2.  Anchorage and steering devices for prestressed strands

下载: 全尺寸图片 幻灯片

1)组合梁试件采用工字形截面，为有效锚固预应力钢绞线，如图2(a)所示设计并制作了包含垫板、欧维姆M15型工作锚板、工作夹片，以及自行加工的转换钢板和防松盖板的端部锚具，并通过压力传感器控制预应力水平。

2)借鉴体外预应力混凝土结构，结合工字形组合梁的截面特征，预应力钢绞线沿梁纵轴线左右对称布置，并通过如图2(b)所示的转向装置，实现一点张弦与两点对称张弦。

3)施加预应力时，张拉端按次序布置传感器与锚固装置，以总预加力的10%为一级，对两根钢绞线采用两个穿心千斤实现力控制同步加载，直至传感器示数达到预设值。在张拉及放张时，穿心千斤顶的端头始终顶紧锚固装置，同时千斤顶加载与卸载前后，压力传感器示数无明显波动，即此过程中夹片未出现外移、回缩。

4)短期加载时，钢绞线可能由于锚具变形、摩擦等因素产生预应力损失。试验中采取了以下两项措施以减小预应力损失影响：① 对预应力筋与转向装置的接触面进行了涂油处理，以减小摩擦损失；② 在预应力筋的锚具与梁端部之间设置了事先标定的应力传感器，通过分级施加预应力使传感器示数稳定在预设值，以消除锚具变形的影响。因此，在后续分析中不再计入预应力损失。

1.3.2   竖向力加载

如图3(a)和图3(b)所示，竖向力加载通过100 t反力架及超高压千斤顶实现。一点加载时，竖向力直接通过滚轴施加于梁跨中截面上部；两点加载时通过设置分配梁实现对称加载，各加载点至跨中截面距离为550 mm。

图  3  竖向力加载方案

Figure  3.  Vertical loading scheme

下载: 全尺寸图片 幻灯片

加载过程中，以5 kN为一级进行力控制加载，并采集数据、观察试验现象。为分析组合梁在加载过程中的挠度变化，如图4所示布置了5个位移计，分别位于梁跨中截面、两点加载的竖向力作用截面，以及铰支座与竖向力作用截面的中点位置。

图  4  加载装置与位移计布置(一点加载、一点张弦) /mm

Figure  4.  Loading device and displacement meter arrangement (one-point loading and one-point prestressing scheme)

下载: 全尺寸图片 幻灯片

2   计算假定

2.1   计算简图

以工字形截面预应力钢-竹组合梁为对象，在分析正常使用阶段的受弯挠度时，根据加载与张弦方式不同共考虑了4种情况，相应的计算简图如图5。

图  5  预应力钢-竹组合梁的计算简图

Figure  5.  Computing model for prestressed steel-bamboo composite beam

下载: 全尺寸图片 幻灯片

如图5所示，12根组合梁试件的总跨度(L₀)均为3800 mm，计算跨度(支座中心距L)均为3500 mm，两端悬挑长度(λL₀)均为150 mm。所有试件设计为对称加载、对称张弦。一点和两点加载时，加载点到支座的距离(βL₀)分别为1750 mm和1200 mm；一点和两点张弦时，张弦点到梁端的距离(μL₀)分别为1900 mm和1350 mm。此外，张弦点到梁中心线的竖向距离e=130 mm。

2.2   基本假定

为简化计算过程，根据预应力钢-竹组合梁的力学特点与试验现象分析，在正常使用阶段的挠度计算中引入如下基本假设：

1)组合梁和预应力筋均处入弹性工作状态，不考虑梁体的塑性变形与刚度变化；

2)梁体受弯后，截面应变符合平截面假定，组合梁的整体变形近似符合正弦半波曲线；

3)忽略梁体剪切变形与粘结滑移的影响；

4)不计摩擦损失的影响，各截面上预应力筋的应力均相等。

2.3   基本公式

2.3.1   组合梁的弯曲刚度

弹性工作阶段，组合梁的弯曲刚度EI/(N·mm²)可根据叠加原理按下式计算：

式中：E_s/(N/mm²)和E_b/(N/mm²)分别为薄壁型钢和重组竹材的弯曲弹性模量；I_s/mm⁴和I_b/mm⁴分别为薄壁型钢和重组竹材对截面形心轴的惯性矩。

2.3.2   预应力等效荷载

对于折线形布置的预应力筋，预应力等效荷载可分解为预应力筋在锚固区对梁产生的压力和张弦点处对梁产生的等效竖向集中力两部分。

1)预应力筋在锚固区对梁产生的压力，大小近似等于预应力筋的总拉力值T_p/N，即：

式中：N_p/N为梁端锚固区的预应力水平分力；T₀/N为预应力筋的初始预拉力值；A_p/mm²为预应力筋的有效截面面积；Δσ_p/(N/mm²)为预应力筋的应力增量。

2)张弦点处，预应力筋对组合梁产生的等效竖向集中力满足以下平衡条件：

整理可得：

式中：N_e/N为预应力的总等效竖向荷载，两点张弦时，每个张弦点处的等效竖向荷载为0.5N_e；L₀/mm为组合梁的总长度，μ为张弦点至梁端距离与梁长度L₀的比值；e/mm为张弦点至截面形心轴的竖向距离。

2.3.3   挠度计算理论公式

以向下为正方向，在预应力等效竖向荷载作用下，两点张弦时，根据材料力学易知组合梁的反拱挠度曲线f_p(x)为：

式中，x/mm为沿梁长方向，计算截面与梁左端之间的水平距离。

x∈[0.5L₀, L₀]时的挠度曲线与x∈[0, 0.5L₀]时对称。对于一点张弦，可看作两张弦点重合于跨中的特例。故预应力等效竖向荷载作用下组合梁的反拱挠度仍可用式(5)描述，且此时μ=0.5，即仅按第一分段(0≤x≤μL₀)的挠曲线函数计算即可。

同理，一点加载或两点加载时，外荷载作用下组合梁的挠度曲线方程f_F(x)可统一为：

式中：λ为竖向支座到梁端距离与梁长L₀的比值；β为加载点到支座距离与梁长L₀的比值；F/N为竖向荷载的大小，两点加载时，每个加载点的竖向力取0.5F。

根据小变形时的挠度叠加原理，可得组合梁的实际挠度曲线f(x)可表示为：

鉴于预应力筋的应力增量与梁的挠度之间存在耦合关系，直接按上述公式分段计算过程繁琐。为简化分析过程，在后续理论计算中以梁左端为零点，跨中最大相对挠度$\Delta$f/mm按式(5)和式(6)计算，并假定一点/两点加载和一点/两点张弦时，在梁端与跨中截面之间梁的挠度均近似符合正弦半波曲线，且忽略梁的轴向变形，则：

式中，$\Delta$f(x)/mm为以梁左端做零点时，沿梁长方向x位置处的相对挠度。

3   挠度计算方法

3.1   钢-竹组合梁的挠度

3.1.1   预应力作用下梁的挠度

由式(5)易得，在预应力等效竖向荷载作用下，梁跨中与梁端截面的挠度差$\Delta$f_p/mm为：

式中，k_p/(N/mm)为组合梁产生单位反拱挠度所需的等效竖向荷载，易知${k_{\rm p}}{\text{ = }}\dfrac{{48EI}}{{( {3 - 4{\mu ^2}} )\mu L_0^3}}$。

3.1.2   外荷载作用下梁的挠度

由式(6)易得，在荷载F作用下，梁跨中截面挠度f_F0/mm与梁端截面挠度f_F1/mm分别为：

故梁跨中与梁端截面的挠度差Δf_F为：

式中，k_F/(N/mm)为组合梁产生单位挠度所需的竖向荷载，易知${k_{\rm F}}{\text{ = }}\dfrac{{48EI}}{{\beta ( {3 - 4{\beta ^2} - 12{\lambda ^2} - 12\lambda \beta } )L_0^3}}$。

3.1.3   梁的总挠度及调整系数

F和N_e共同作用下，组合梁跨中与梁端截面的挠度差$\Delta$f/mm可由下式计算：

在上述分析中，没有考虑预应力筋在锚固区对梁端压力N_p的影响，而是按单向弯曲梁进行挠度计算。而实际上，在N_p、N_e和F共同作用下，组合梁挠度计算属于纵横弯曲问题。参考钢结构设计方法，考虑N_p引起的附加弯矩，引入挠度近似放大系数(1−α)⁻¹，其中α按下式计算：

式中，N_cr/N为欧拉临界力。

3.2   预应力筋的应力增量

3.2.1   有效偏心距

由于钢-竹组合梁与体外预应力筋仅在锚固点和转向装置处保持竖向位移相等，二者的变形不协调，故梁产生挠度后预应力筋的有效偏心距e(x)会发生变化。以梁左端预应力筋的锚固点为原点(0, 0)，则张弦点的相对坐标为(μL₀, e+Δf₂)，其中Δf₂ /mm为张弦点的竖向相对挠度，由式(8)可得：

由张弦点和锚固点坐标易得左侧锚固点至中部截面范围内，预应力筋的竖向相对位置可由下述直线方程y(x)描述：

故有效偏心距e(x)可表示为：

3.2.2   预应力筋的应力增量

预应力筋弹性工作时，应力增量$\Delta {\sigma '_{\rm{p}}}$/(N/mm²)与伸长量$\Delta$L_p/mm满足如下关系：

式中：E_p/(N/mm²)为预应力筋的弹性模量；L_p/mm为预应力筋的总长度。

小变形条件下，预应力筋的伸长量ΔL_p可通过如下积分^[23]求得：

当张弦点、荷载与梁变形满足对称性条件时，可得：

将式(8)和式(17)代入式(20)并积分可得：

此外，在施加预应力阶段，以压力传感器示数作为预加力值的判断依据。此过程中，反拱挠度产生的预应力筋应力增量被穿心千斤顶不断补偿，故实际的应力增量Δσ_p/(N/mm²)为：

式中，Δf_p0/mm为施加外荷载前，组合梁在初始预加力T₀作用下的反拱挠度值。

3.3   迭代法求解过程

3.3.1   基本方程组

根据上述理论分析，联立公式可得以下关于挠度计算的方程组：

式中，f₀/mm为组合梁跨中截面相对于支座位置的竖向挠度。对于施加外荷载前的反拱挠度，采用f_p0替代f₀，以示区分。

上述方程组中，共有六个方程以及$\Delta$f、N_e、N_p、$\Delta$σ_p、α和f₀六个未知数，因此可求得唯一解。

3.3.2   加载前跨中反拱挠度

在施加预应力阶段，满足F=0，$\Delta$σ_p=0，N_p=T₀和$\Delta$f=$\Delta$f_p0，上述方程组可简化为：

此时，可按如下步骤计算：

1)按式(31)计算N_e；

2)按式(30)计算α；

3)将α和N_e代入式(29)求$\Delta$f_p0；

4)将$\Delta$f_p0代入式(32)求得跨中反拱挠度f_p0。特别地，对于未配置预应力筋或初始预应力为0的试件(L-1、L-2和L-12)有T₀=0，易得f_p0=0。

3.3.3   加载后跨中实际挠度

施加外荷载F后，基本方程组是关于未知参数的高次方程，可采用迭代法按如下步骤求解：

1)假定$\Delta$σ_p的初值，如令$\Delta$σ_p=0；

2)将$\Delta$σ_p代入式(24)计算N_p；

3)将N_p代入(25)式计算α；

4)将N_p代入(26)式计算N_e；

5)将α和N_e代入(23)求$\Delta$f；

6)将$\Delta$f代入(27)式计算$\Delta$σ_p；

7)重复步骤2)~步骤6)直至计算的Δf小于容许误差δ(如取δ=0.1 mm)；

8)将$\Delta$f代入式(28)计算跨中实际挠度${f_0}$。特别地，对未配置预应力筋的试件(L-1和L-2)有T₀=0和A_p=0，易得${f_0} = \dfrac{F}{{( {1 - \alpha } ){k_f}}}( {1 - \sin \lambda \pi })$；而对未施加初始预应力的试件(L-12)有T₀=0和$\Delta$f_p0=0，但$\Delta$σ_p≠0，仍需按上述迭代过程求解。

4   结果分析

4.1   主要试验现象描述

在短期荷载作用下，参考《木结构设计规范》(GB 50005−2017)和《工程竹结构技术规程》(征求意见稿)，以组合梁计算跨度的1/250作为跨中挠度限值，即组合梁的容许挠度[f]取为14 mm。此时，对应的竖向荷载即为挠度控制的荷载，记作[F]。在竖向荷载从0加载至[F]的过程中，主要试验现象分析如下：

1)梁的整体变形情况

对于有初始预应力的试件，在施加预应力阶段出现明显的反拱；施加竖向荷载后，整体变形基本符合正弦半波曲线，且在该阶段五个位移量测点处，梁截面竖向变形随荷载基本呈线性增长。

2)组合梁截面应变特征

各组梁试件在该阶段均未表现出明显的破坏现象(竹材未发生撕裂、钢板没有明显屈曲)，除试件L7~L9外，跨中截面的应变沿梁高度方向上呈现线性分布特征，试件基本处于弹性工作阶段。

3)预应力筋的应力变化

在加载过程中，各试件预应力筋的应力增量均不超过300 N/mm²，梁L-11中预应力筋的最大总应力在580 N/mm²左右，各试件中的预应力筋均处于弹性工作阶段。

4)钢-竹界面滑移情况

试验表明，荷载由0增加至[F]的过程中，钢-竹界面未发生明显的脱胶现象，二者可以较好的共同工作。当荷载增加至约80%破坏荷载时，试验梁钢-竹界面逐渐出现脱胶，并由于竹材撕裂、断裂，或界面脱胶后薄壁钢板严重屈曲而发生破坏。

4.2   荷载-挠度曲线对比

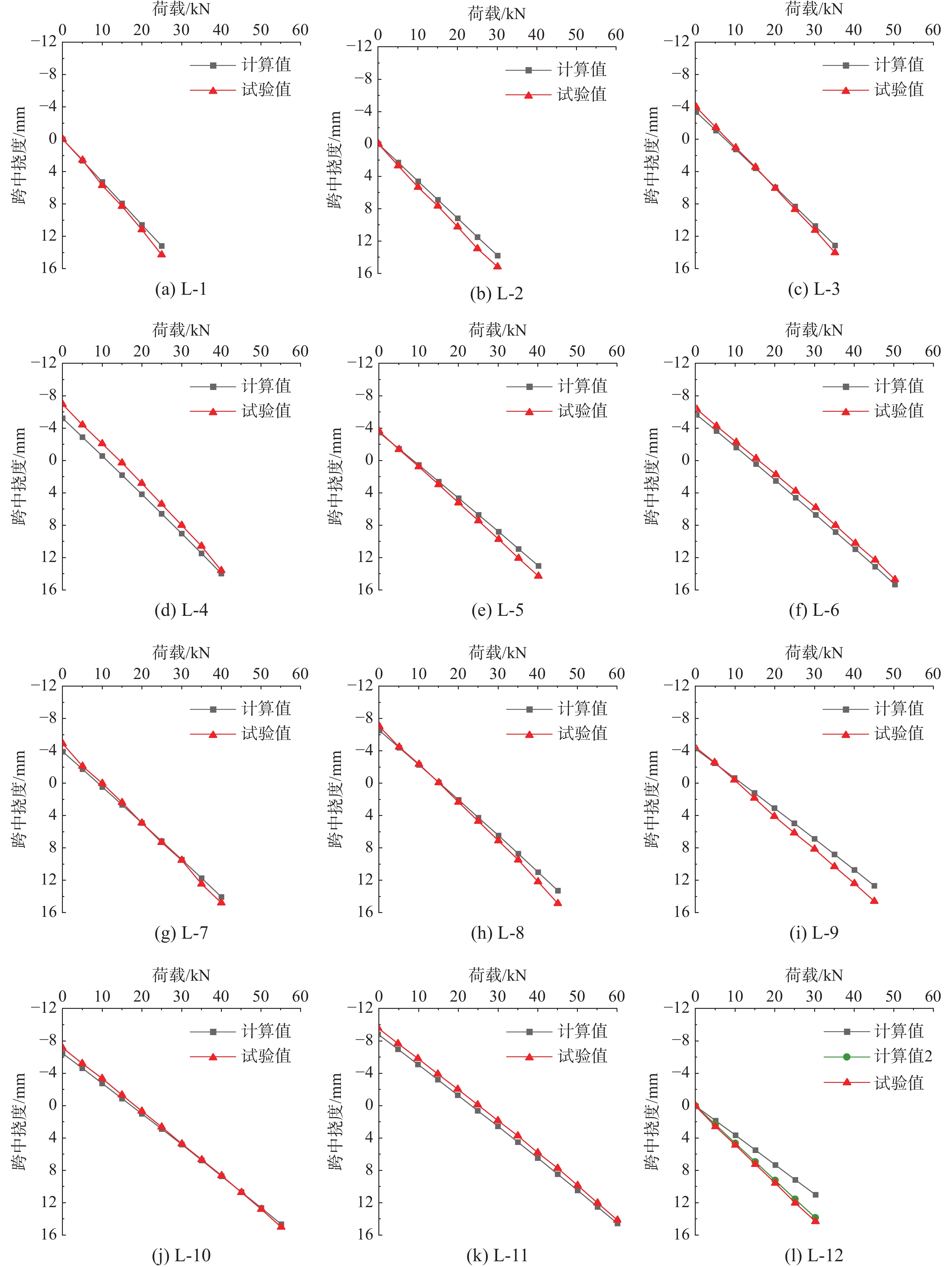
试验中采用力控制分级加载，无法精确对应至[f]，分析中以最接近[f]的一级荷载所对应的挠度值进行试验与理论计算结果的比较。

当竖向荷载F由0增大至挠度控制的荷载[F]时，荷载-跨中挠度变化情况的试验结果与计算结果对比见图6。如图所示，当F≤[F]时，各试件的跨中挠度随荷载增加呈现出线性变化规律，说明此时试件基本处于弹性工作阶段。进一步地，本文提供的挠度计算方法能够与大多数的试验结果较好吻合。达到挠度控制的荷载[F]时，多数试件跨中挠度的相对误差在10%以内，平均误差为4.9%。但个别试件的理论预测结果存在较大偏差，主要情况及原因说明如下：

图  6  荷载-跨中挠度曲线对比

Figure  6.  Comparison of load-mid-span-deflection curves

下载: 全尺寸图片 幻灯片

1)理论计算中，结合表2所示的竹材试样静曲模量和冷弯薄壁钢材的弹性模量取值，根据式(1)计算挠度时，将各组合梁试件的弯曲刚度统一取为1.673×10¹² N·mm²。而受到材料性能不定性与试验环境影响，实际各试件的弯曲刚度与上述数值可能存在一定偏差。

2)由于计算中假定组合梁处于弹性工作阶段，但实际加载中竖向荷载较大的试件在挠度达到[f]时，应变测试结果表明其翼缘薄壁钢板亦出现了一定的塑性变形。此外，理论计算中未考虑加载时的预应力摩擦损失，应力增量Δσ_p的计算结果可能偏高。因此，多数试件梁的理论计算挠度偏小。

3)施加预应力的试件L3~L11，在加载前的反拱挠度实测值与计算值存在14.3%的平均偏差，且反拱挠度的理论计算值偏小，对计算结果的准确性造成了一定影响。经分析，造成这一误差的主要原因可能是分级施加初始预应力过程中，受试件尺寸、形状缺陷，锚固、转向装置与试件的间隙等因素影响，预紧阶段产生了一定的初变形。

4)对于配置了预应力钢绞线，但未施加初始预应力的试件L-12，其容许挠度理论计算结果(图中“计算值1”)产生了高达23.2%的误差。进一步分析表明，不考虑L-12中预应力筋影响，按未配筋梁得出的荷载-跨中挠度计算结果(图中“计算值2”)能够与试验值高度吻合，其容许挠度的相对误差仅为3%。这一结果说明，试件L-12中的预应力筋尽管采用了一定的预紧措施，但显然未起到应有效果，加载后试件未能按预测建立预应力增量，预应力筋不能有效发挥作用。

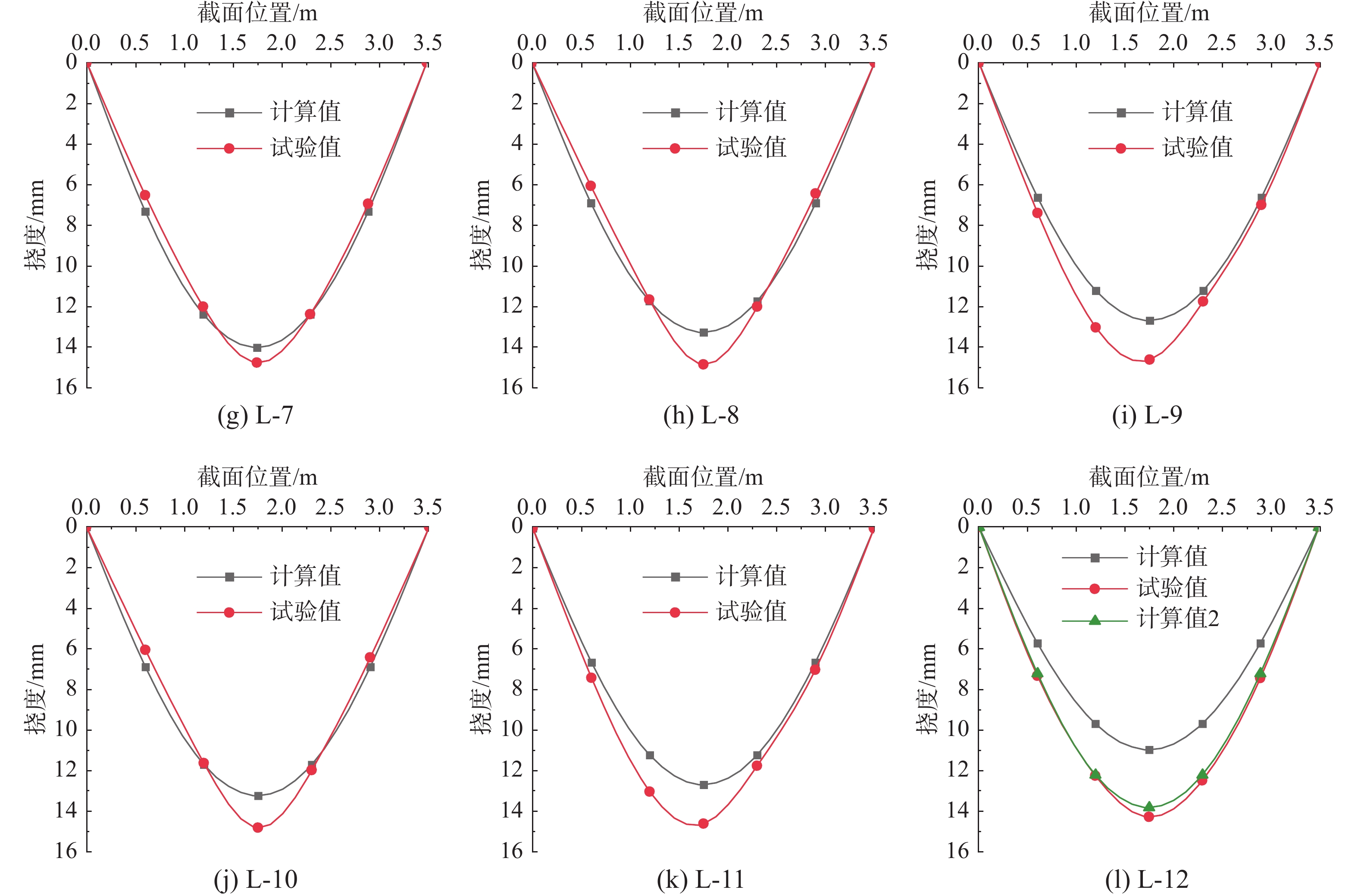
4.3   整体挠度对比

当跨中挠度达到容许挠度[f]时，各试件的整体挠度曲线试验结果与计算结果对比如图7所示。总体而言，理论计算能够较好的预测组合梁的整体挠曲线。具体对比情况如下：

下载: 全尺寸图片 幻灯片

图  7  整体挠度曲线对比

Figure  7.  Comparison of deflection curves

下载: 全尺寸图片 幻灯片

1)除L-2和L-9外，试验获得的各试件整体挠度曲线形状呈现出对称分布特征，与理论计算相符。但受到图6所示挠度计算误差影响，各控制截面的挠度存在一定相对偏差。

2)多数试件的整体挠度分布与理论计算中假定的正弦曲线形状接近，但部分试件(L-8和L-9)的跨中截面变形较为集中，可能是梁跨中截面产生了一定塑性变形造成的。

3)如4.1节分析所示，L-12的整体挠度曲线理论计算结果误差较大，但不考虑预应力筋作用时，挠度曲线的理论分析结果与试验结果十分吻合。这一现象再次说明，预应力筋在这一受力阶段未发挥明显的作用。

4.4   等效弯曲刚度对比

根据图6~图7所示组合梁挠度达到[f]时的荷载与跨中挠度关系，由式(25)可计算考虑预应力作用时的等效弯曲刚度$E'I'$(N·mm²)，结果如表3所示。

表  3  试件的等效弯曲刚度

Table  3.  Equivalent bending stiffness of specimens

编号	加载方式	张弦方式	初始预拉力值T0/N	竖向荷载F/N	跨中截面相对挠度f0/mm	等效弯曲刚度$E'I'$/(N·mm2)
L-1	1	—	0	25 000	14.286	1.563×1012
L-2	2	—	0	30 000	15.180	1.531×1012
L-3	1	1	40 000	35 000	13.993	1.729×1012
L-4	1	1	60 000	40 000	13.613	1.738×1012
L-5	2	1	40 000	40 000	14.280	1.705×1012
L-6	2	1	60 000	50 000	15.167	1.841×1012
L-7	1	2	40 000	40 000	14.773	1.818×1012
L-8	1	2	60 000	45 000	14.880	1.833×1012
L-9	2	2	40 000	45 000	14.647	1.796×1012
L-10	2	2	60 000	55 000	14.981	1.890×1012
L-11	2	2	80 000	60 000	14.168	1.961×1012
L-12	2	2	0	30 000	14.264	1.629×1012

下载: 导出CSV 

| 显示表格

由表3可知，施加预应力可有效提高组合梁的等效弯曲刚度，相比于对照组试件，等效弯曲刚度的最大提升幅度达28.1%，且存在以下变化规律：

1)加载与张弦方式相同时，随着初始预应力值的增加，预应力等效竖向荷载提高，应力增量亦呈现出增长趋势，故组合梁的等效弯曲刚度不断提高；

2)张弦方式与预应力大小相同时，采用不同加载方式对挠度控制的荷载有明显影响，两点加载时的[F]较一点加载有一定提高，但对达到[f]时的等效弯曲刚度影响不明显；

3)加载方式与预应力度相同时，相比于一点张弦，采用两点张弦可获得较大的预应力等效竖向荷载，从而使组合梁的等效弯曲刚度显著提高。

5   主要结论

本文通过对预应力钢-竹组合梁在正常使用阶段受弯挠度计算方法的推导，以及12根不同加载方式、不同张弦方式、不同预应力度组合梁试件的试验研究，得出以下主要结论：

(1)考虑体外预应力筋有效偏心与预应力反拱影响，提出了一点或两点加载、一点或两点对称张弦时，钢-竹组合梁受弯挠度计算的统一公式，适用于组合梁在正常使用阶段的挠度验算。

(2)正常使用阶段，钢-竹组合梁的受弯挠度分布大致符合正弦半波曲线，采用弹性方法得出的组合梁挠度计算理论公式与试验结果可以较好的吻合，但考虑材料性能和尺寸不定性、预应力摩擦损失，以及截面产生一定塑性变形等因素的影响，可偏于保守的对理论计算乘以1.05~1.10的放大系数。

(3)计算表明，预应力可有效提高组合梁的等效弯曲刚度、减小梁的变形，且随着预应力度提高，等效弯曲刚度呈现增长趋势。此外，采用两点张弦时可获得较高的预应力等效竖向荷载，在相同预应力度情况下，等效弯曲刚度亦可得到提高。

(4)试验与理论计算的对比表明，对于配置体外预应力筋，但不施加初始预应力的组合梁，需研究并采用可靠的预紧措施，否则预应力筋在后续加载过程中不能有效地建立应力增量与发挥作用。