随着科学技术的不断进步，现代工程结构正在向大型化、复杂化和智能化方向发展，如大跨度桥梁、高层建筑和大型风力机等。大型化将导致结构更加趋于柔性，基于传统小变形假设的有限元分析方法有时已不能满足计算需求，因此对结构进行几何非线性分析成为近年研究的热点问题，也是难点问题。关于几何非线性的有限元分析方法，最常用的是以结构变形前为参考建立平衡方程的完全Lagrange列式法(TL列式)和以结构变形后为参考建立平衡方程的更新Lagrange列式法(UL列式)^[1]。其中，TL列式法在求解大转动问题时，会因参考系的转动引起不可忽略的误差，甚至出现错误的解，而UL列式法虽然可以求解大转角问题，但非线性应变关系的计算非常复杂，导致计算量也随之偏大^[2]。近些年发展起来的共旋坐标法是对上述两种方法的一种改进，它具有建模简单，意义明确，并且能借用现有的有限元理论，求解效率和精度相对较高^[3]等特点，成为几何非线性研究的热点。

共旋坐标法的概念最早由WEMPNER等^[4]提出，即通过剔除结构的刚体位移来得到单元节点的真实位移。CRISFIELD^[5]使用共旋坐标法求解各种单元的几何非线性，提出了一致的单元平衡方程计算方法。AREIAS等^[6]将共旋坐标法用于分析材料失效破坏及断裂，证明共旋坐标法可以对更复杂的问题进行研究。STÄBLEIN等^[7]基于共旋坐标法，提出了各向异性的Timoshenko梁单元用于梁单元的几何非线性分析。邓继华等^[8]基于共旋坐标法和稳定函数提出了一种几何非线性平面梁单元，杨浩文等^[9]将能量守恒和共旋坐标法相结合对二维Timoshenko梁单元进行动力学分析，杜柯等^[10]利用共旋坐标法模拟框架结构的连续倒塌，ZIYUN等^[11]简化并开发了一种新的共旋分析框架，来避免非线性投影矩阵的复杂推导。在共旋坐标法中，材料非线性和结构纯变形等位于局部坐标系内，因此局部坐标系的选取对于精度的计算有显著的影响。通常梁单元局部坐标系的选择有以下几种方法：RANKIN法^[12]、BATTINI法^[13]、CRISFIELD法^[14]和HSIAO法^[15]。前三种方法都是通过左右两端总转角值线性插值构造刚体旋转矩阵，当变形较小时，计算结果较为精确；而当变形较大时，会产生较大的虚假应变。对于HSIAO法，可以得到比前面几种方法精确的刚体旋转矩阵，但对于大应变和大转动问题的误差仍然较大，并且计算更加复杂。同时Timoshenko梁单元的剪切自锁现象也会使得部分变形被放大，从而导致虚假的刚体转动被放大，误差较大。

为了解决上述方法中存在计算精度和效率较低的问题，需对现有的共旋坐标法进行改进。因此，本文在共旋坐标法的框架上，基于改进的空间Timoshenko梁单元^[16]，使用逆向运动方法，剔除结构刚体运动部分，再结合梁单元形函数和截面刚度矩阵得到整体坐标系下的单元切线刚度矩阵。最后，通过多种类型的算例对本文提出的方法和程序进行了较全面和严格的检验。

1   空间梁单元

使用共旋坐标法求解非线性问题时，首先需要求解单元的线刚度矩阵，分析时通常采用插值形函数法构造梁单元，但这些插值函数大多为位移的近似方程，计算往往存在截断误差，导致精度较低。本文采用一种改进的空间Timoshenko梁单元^[16]求解单元线刚度矩阵，具体推导过程如下。

1.1   梁单元横向位移的形函数

对于空间Timoshenko梁，截面横向位移包含弯曲位移和剪切位移两部分，可以表示为：

式中：$v$、$w$分别为梁两个方向总的横向位移；下标b为弯曲变形产生的位移；下标s为剪切变形产生的位移。

对式(1)求一阶导，可得：

式中：${\gamma }_{xy}$、${\gamma }_{x{\textit z}}$分别为x-y和x-z平面内的剪应变；${\theta }_{y}$、${\theta }_{\textit z}$为弯曲位移引起的转角。

把Timoshenko梁的本构关系和几何方程代入到梁截面内的平衡方程中，可得：

式中：E为弹性模量；${I}_{y}$为截面关于y轴的惯性矩；G为材料剪切模量；A为截面面积；${k}_{\textit z}$为z方向的截面不均匀系数。

将式(3)对x求一阶导，化简之后可得：

由式(5)可知，满足弯曲位移${w}_{b}$的解析解为三次多项式，同理可得到满足${v}_{b}$的解析解也为三次多项式。

根据弯曲位移与横向位移之间的关系，得到梁单元横向位移w的表达式为：

同理，横向位移$v$的表达式为：

式中：${I}_{\textit{z}}$为截面关于z轴的惯性矩；${k}_{y}$为y方向的截面不均匀系数。

1.2   梁单元刚度矩阵

与传统Timoshenko梁单元一样，梁轴方向的位移$u$及转角${\theta }_{x}$的形函数假设为线性插值，而弯曲位移的插值函数为三次多项式，表达式如下：

通常，Timoshenko梁单元的应变矢量可以表示为：

其中：

结合式(6)、式(7)和式(8)，得到梁的位移和旋转向量$\boldsymbol{u}\left(x\right)={\{u,v,w,{\theta }_{x},{\theta }_{y},{\theta }_{\textit{z}}\}}^{\rm T}$的表达式为：

式中：矩阵$\boldsymbol{A}\left(x\right)$是相对于形函数系数向量$\boldsymbol{c}={\left\{{c}_{1},{c}_{2},\cdots ,{c}_{12}\right\}}^{\rm T}$的位移旋转系数矩阵。对式(10)求导可得：

根据空间梁单元在$x=0,L$上的边界条件，可以得到形函数的系数与节点位移之间的关系，其矩阵表达式为：

式中：E(x)为形函数系数向量的系数矩阵；$\boldsymbol{d}$为节点位移，其表达式为：

把式(13)代入式(10)和式(11)，可得：

结合式(14)和式(15)，得到单元的应变与节点位移之间的关系为：

式中：$\boldsymbol{N}\left(x\right)=\boldsymbol{A}\left(x\right)\boldsymbol{E}{\left(x\right)}^{-1}$，${\rm d}\boldsymbol{N}\left(x\right)={\rm d}\boldsymbol{A}\left(x\right)\boldsymbol{E}{\left(x\right)}^{-1}$，B矩阵为应变位移矩阵，并且：

最后通过对梁长L的数值积分，得到Timoshenko梁单元的单元刚度矩阵${\boldsymbol{K}}_{\boldsymbol{e}}$的表达式为：

其中，${\boldsymbol{K}}_{cs}$为截面刚度矩阵，表达式为：

式中：${K}_{11}=EA\;,\;{K}_{22}={k}_{y}GA$，其余参数具体物理意义在HODGES等^[17]和GIAVOTTO等^[18]论文中做出了具体解释。

2   改进共旋坐标法

共旋坐标法的独特之处在于从总体位移中提取弹性变形位移来预先定义投影关系。将梁单元运动从初始状态到最终变形状态分解为刚体运动部分和纯变形部分，其中刚体运动部分包括局部参考坐标系的刚体平移和旋转。因此共旋坐标法的核心问题就是处理不同坐标之间的转换，从而建立纯变形与整体变形之间关系。

对于经典共旋坐标法，一般通过线性插值构造刚体旋转矩阵^[19]，当变形较小时，计算结果较为精确，但考虑大应变和大转动问题时则不可忽略计算产生的虚假刚体转动，本文通过使用逆向运动改进共旋坐标法从而减小这一部分所产生的误差。

2.1   空间梁单元的参考坐标系定义与转换

首先定义梁单元相关参考坐标系。

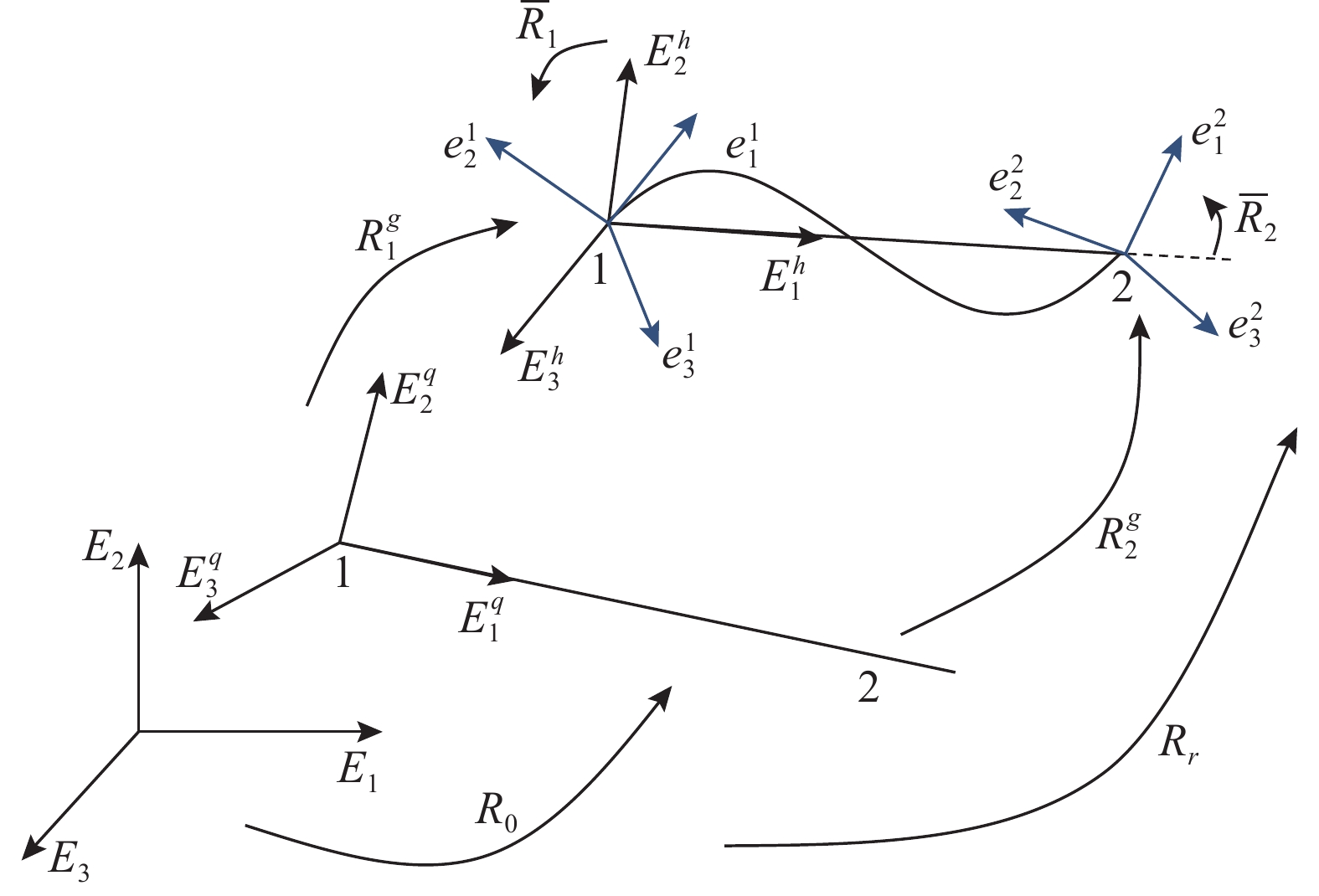
空间两节点梁单元定义的参考坐标系如图1所示，其中单位正交向量${\boldsymbol{E}}_{\boldsymbol{i}},i=\mathrm{1,2},3$表示梁单元的整体参考系，是固定不变的；单位正交向量${\boldsymbol{E}}_{i}^{h},i=\mathrm{1,2},3$表示梁单元刚体运动后的局部参考系，它是随梁单元不断平移和转动的；局部参考系${\boldsymbol{E}}_{i}^{q},i=\mathrm{1,2},3$表示梁单元变形前的原始坐标系，此外$\mathrm{定}\mathrm{义}{\boldsymbol{e}}_{i}^{1}$和${\boldsymbol{e}}_{i}^{2},i=\mathrm{1,2},3$为梁端两个节点1和2的截面参考系。

图  1  梁的运动及坐标系

Figure  1.  Beam kinematics and coordinate systems

下载: 全尺寸图片 幻灯片

首先解决局部坐标系${\boldsymbol{E}}_{i}^{h}$的刚体旋转问题，刚体旋转矩阵${\boldsymbol{R}}_{r}$表示参考系从${\boldsymbol{E}}_{i}$到${\boldsymbol{E}}_{i}^{h}$的变换矩阵，其表达式为：

其中，向量${\boldsymbol{r}}_{1}$由梁单元变形前后的节点1和节点2的连线计算可得：

式中：${\boldsymbol{S}}_{i}^{g}$为刚体旋转后 i节点整体参考系下的坐标；$l$为梁发生变形后的长度，可由$l = \| {\boldsymbol{S}}_2^g - {\boldsymbol{S}}_1^g \|$求得。

剩余两个轴的大小通过引入辅助向量q来确定。引入辅助向量主要有两个目的：一是通过辅助向量求解整体坐标系下的刚体旋转矩阵；二是通过辅助向量求解刚体旋转角度对结构总位移的微分关系。初始状态时，q的方向沿着局部坐标轴${\boldsymbol{E}}_{2}^{q}$，而当梁单元发生变形后，辅助向量q的求解与局部参考系的变换有关。

下面开始求解参考坐标系之间的转换。

定义局部参考系下的刚体旋转矩阵${\boldsymbol{R}}_{m}$表示局部参考系从${\boldsymbol{E}}_{i}^{q}$到${\boldsymbol{E}}_{i}^{h}$的变换矩阵。本文采用逆向运动方法^[20-21]求解${\boldsymbol{R}}_{m}$，图2给出了逆向运动图示。

图  2  逆向运动图示

Figure  2.  Diagram of reverse motion

下载: 全尺寸图片 幻灯片

将梁单元的逆向运动分解为两步：一是刚体旋转前后梁单元轴线的转动；二是刚体旋转前后绕着梁轴线的定轴转动。首先求得刚体旋转前后梁的轴向坐标：

式中，${\bar{\boldsymbol{e}}}_{x}^{a}$和${\bar{\boldsymbol{e}}}_{x}^{b}$定义了局部坐标系下，单元刚体旋转前后轴线方向的单位向量。

则两主轴间的转动向量${\boldsymbol{\varTheta }}_{ba}$的表达式为：

设单元左右两端绕着${\boldsymbol{E}}_{2}^{q}$(即y轴)总的旋转角度分别为${\theta }_{yl}$和${\theta }_{yr}$，绕着梁长方向(即x轴)总的旋转角度分别为${\theta }_{xl}$和${\theta }_{xr}$。绕着y轴的刚体旋转角度${\bar{\theta }}_{y}$容易求得：

式中：${\bar{\theta }}_{y}$为单元绕着y轴的刚体旋转角度；z为单元在整体坐标系下z方向的坐标。

根据y轴总旋转角度${\theta }_{yl}$和${\theta }_{yr}$与刚体旋转角度${\bar{\theta }}_{y}$的关系，通过经典共旋理论计算及算例分析验证，得到较为精确的梁轴向扭转刚体部分角度${\bar{\theta }}_{x}$的插值函数为：

由式(24)~式(29)，得到变形前后刚体旋转向量${{\boldsymbol{\phi}} _m}$为：

式中：旋转向量${{\boldsymbol{\phi}} _m}$的转角大小为$\gamma$，转轴方向为${\boldsymbol{e}}_{\gamma }={[{l}_{\gamma }\;\; {m}_{\gamma }\;\; {n}_{\gamma }]}^{\rm T}$；${l}_{\gamma }$、${m}_{\gamma }$、${n}_{\gamma }$分别为旋转单位向量的三个分量。

通过${{\boldsymbol{\phi}} _m}$的大小和方向，得到局部参考系下刚体旋转矩阵^[14]为：

式中，${\stackrel{~}{\boldsymbol{e}}}_{\gamma }$为向量${\boldsymbol{e}}_{\gamma }$对应的斜对称矩阵，即：

由式(32)，得到辅助向量的表达式如下：

式中：${\boldsymbol{q}}_{1}$和${\boldsymbol{q}}_{2}$分别为局部参考系${\boldsymbol{E}}_{2}^{q}$发生刚体旋转后的单元左右两端参考系方向；$\boldsymbol{q}$为局部参考系${\boldsymbol{E}}_{2}^{q}$刚体旋转后的方向。

结合式(23)、式(34)、式(35)，求得正交矩阵${\boldsymbol{R}}_{r}$剩余两个轴的表达式为：

坐标轴的局部旋转矩阵定义为${\bar{\boldsymbol{R}}}_{i}$，由图1所示坐标参考系从${\boldsymbol{E}}_{i}$转换到${\boldsymbol{e}}_{i}^{1}$和${\boldsymbol{e}}_{i}^{2}$可以表达为：

由于${\boldsymbol{R}}_{r}^{T}{\boldsymbol{R}}_{r}=\boldsymbol{I}$，对式(37)转化可得：

从而得到局部的旋转角度为：

2.2   局部坐标系与整体坐标系之间位移向量的转化

定义梁单元整体位移向量为${\boldsymbol{P}}_{g}^{g}$，去除刚体变形后局部坐标系下位移向量为${\boldsymbol{P}}_{l}$。通过2.1节中介绍的旋转框架，从总位移${\boldsymbol{P}}_{g}^{g}$中剔除刚体位移来计算局部位移${\boldsymbol{P}}_{l}$。通过两者的转换关系计算局部坐标系下的内力向量${f}_{l}$和切线刚度矩阵${K}_{l}$，而内力向量在整体坐标系${F}_{g}$中的表达式，可以通过平衡整体与局部系统中的内部虚功来得到：

${\boldsymbol{P}}_{g}^{g}\mathrm{和}{\boldsymbol{P}}_{l}$位移向量变分为：

式中：$\delta {\bar{\boldsymbol{\vartheta }}}_{i},i=\mathrm{1,2}$为刚体变形后的局部坐标系下空间旋转角度的变化；$\delta {\boldsymbol{\theta }}_{i}^{g},i=\mathrm{1,2}$为整体坐标系下空间旋转角度的变化。

转换矩阵的变分会涉及一个新的旋转角度构成的矩阵：

上标波浪线表示向量对应的斜对称矩阵。

定义一个新的局部坐标系${P}_{a}$：

用${\boldsymbol{f}}_{\boldsymbol{a}}$表示与$\delta {\boldsymbol{P}}_{a}$对应的内力矢量，${\boldsymbol{K}}_{l}$为第一节中求得的局部坐标系下的单元刚度矩阵${\boldsymbol{K}}_{e}$转换为7个自由度的结果。向量${\boldsymbol{P}}_{a}$与${\boldsymbol{P}}_{l}$之间的转换矩阵可以通过两者对应的刚度矩阵的转换关系得到，${\boldsymbol{K}}_{l}$和${\boldsymbol{K}}_{a}$的转化最终可得：

${B}_{l}$可直接通过旋转向量求得。${\boldsymbol{K}}_{h1}$和${\boldsymbol{K}}_{h2}$的表达式由下式求得：

其中：

式中：$\boldsymbol{v}$为局部坐标系下内力矢量中的两端弯矩作用；$\boldsymbol{e}$为角度向量对应的单位向量。进而可以得到局部坐标系下的旋转向量与整体坐标系下位移向量之间的微分关系为：

式中，$\boldsymbol{G}=\dfrac{\partial {\boldsymbol{\theta }}_{r}^{e}}{\partial {\boldsymbol{P}}_{g}^{g}}$，$\boldsymbol{E}={\rm diag}[{\boldsymbol{R}}_{r}\;\; {\boldsymbol{R}}_{r}\;\; {\boldsymbol{R}}_{r}\;\; {\boldsymbol{R}}_{r}]$。

从而可以得到$\delta {\boldsymbol{P}}_{a}$与$\delta {\boldsymbol{P}}_{g}^{g}$的关系：

式中，$\boldsymbol{r}=[-{\boldsymbol{r}}_{1}^{\rm T}\;\; {0}_{1\times 3}\;\; {\boldsymbol{r}}_{1}^{\rm T}\;\; {0}_{1\times 3}]$。

式(48)中的G矩阵与$\delta {\boldsymbol{\theta }}_{r}^{e}$有关，由式(33)可得：

式中，${\boldsymbol{r}}_{1}$、${\boldsymbol{r}}_{2}$、${\boldsymbol{r}}_{3}$和$\delta {\boldsymbol{r}}_{1}$都容易求得，对于$\delta {\boldsymbol{r}}_{3}$，由式(36)可知与$\delta \boldsymbol{q}$有关。对于共旋法，其辅助向量的定义假设了小的纯变形及其变化且认为辅助向量和${\boldsymbol{r}}_{1}$、${\boldsymbol{r}}_{2}$在同一个平面内，但在求解过程中使用了简单的线性插值函数来求得$\boldsymbol{q}$。在使用逆向运动求解辅助向量后，辅助向量和${\boldsymbol{r}}_{1}$、${\boldsymbol{r}}_{2}$在同一个平面，求得的刚体转换矩阵更加精确，并且这里不假设小的纯变形，仅仅假设纯变形的增量较小，从而可以求得辅助向量的变化：

通过式(51)以及$\boldsymbol{G}=\dfrac{\partial {\theta }_{r}^{e}}{\partial {P}_{g}^{g}}，$即可求得G矩阵的表达式，详细推导见参考文献[19]。

由式(49)可得整体坐标的力向量与局部坐标下内力矢量的关系：

同样的，对式(49)求整体坐标的力向量的变化，可得：

式中，${\boldsymbol{f}}_{ai},i=1,2,\cdots ,7$是力向量${\boldsymbol{f}}_{a}$的分量。综上，可得整体坐标系下的切线刚度矩阵：

式中：

利用求得的切线刚度矩阵计算整体力向量的差值，通过迭代使结果逐渐收敛于精确解，计算流程图如图3所示。

图  3  利用改进共旋法进行静位移计算流程图

Figure  3.  Flow chart of static displacement calculation using improved co-rotational formulation

下载: 全尺寸图片 幻灯片

3   数值算例

为检验本文所提方法的合理性，本文使用MATLAB软件，编制相应的有限元程序。通过算例1验证该方法计算平面梁单元所得结果与解析解相比足够接近；算例2验证该方法可以用于计算不考虑耦合效应的空间梁单元非线性分析；算例3验证该方法可以用于计算空间耦合梁单元非线性分析；算例4验证该方法可以用于空间预弯梁单元非线性分析。

3.1   算例1

如图4所示，悬臂梁在自由端受到横向集中力P的作用，将梁划分成10个单元，迭代容许误差设定为${10}^{-6}$，表1给出了本文的计算竖直位移$w$、水平位移$u$及转角${\theta }_{0}$的结果与文献[21]的解析解对比。

图  4  集中荷载作用下的大挠度悬臂梁

Figure  4.  Cantilever of large deflection under concentrated load

下载: 全尺寸图片 幻灯片

表  1  悬臂梁承受集中荷载时的大挠度变形

Table  1.  Cantilever's large deformation under concentrated load

$P{L}^{2}/EI$	$w/L$				$u/L$				${\theta }_{0}/{\rm rad}$
	解析解	本文	误差/(%)		解析解	本文	误差/(%)		解析解	本文	误差/(%)
0.2	0.0664	0.0665	0.1506		0.0027	0.0026	2.1852		0.0996	0.0996	0.0000
0.8	0.2495	0.2499	0.1603		0.0382	0.0381	0.2618		0.3791	0.3791	0.0000
1.6	0.4294	0.4305	0.2562		0.1186	0.1185	0.0843		0.6707	0.6711	0.0596
3.0	0.6033	0.6054	0.3481		0.2544	0.2544	0.0000		0.9860	0.9871	0.1116
4.0	0.6700	0.6728	0.4179		0.3289	0.3290	0.0304		1.1212	1.1227	0.1338

下载: 导出CSV 

| 显示表格

从表1结果对比可知，采用改进共旋坐标法计算所得结果与解析解的结果相比，误差基本都小于0.5%，能较为精确的计算悬臂梁在集中荷载作用下的大挠度变形。验证了该方法用于计算平面梁单元非线性分析的正确性。

3.2   算例2

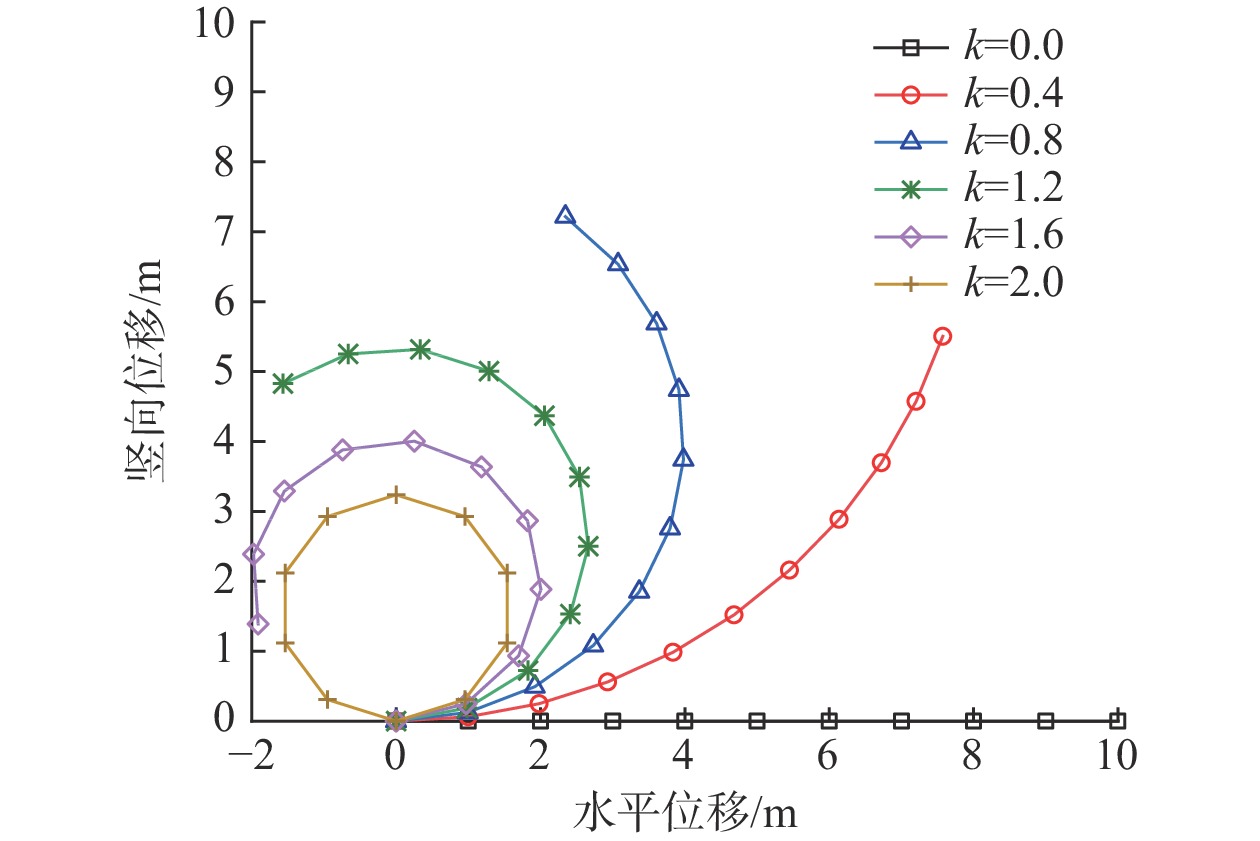
如图5所示的空间悬臂梁，弯矩${M}_{2}$作用在自由端，大小为：

式中：参数$k$在0到2之间取值。将悬臂梁划分为10个单元，梁端水平位移为$u$，竖向位移为$v$。所得不同弯矩大小作用下图5所示悬臂梁的变形结果示于图6；表2给出了本文算法计算的梁端水平位移和竖向位移结果，与解析解^[22-24]和文献[25]中HAWC2方法计算结果进行对比。

图  5  悬臂梁杆端受集中弯矩

Figure  5.  Cantilever beam with an end moment

下载: 全尺寸图片 幻灯片

图  6  悬臂梁的大转动变形

Figure  6.  Large rotation deformation of a cantilever

下载: 全尺寸图片 幻灯片

从表2可知，对于悬臂梁承受弯矩作用发生大变形，当$k$取值从0.4变化到2.0(即弯矩逐渐变大)，改进共旋坐标法的水平位移计算误差均在0.20%之内，竖直位移计算误差均在1.10%之内，而HAWC2-30水平位移计算误差多数超过了1.0%，竖直位移计算误差最大达到了22.7%，HAWC2-50水平位移计算误差多数超过0.4%，竖直位移计算误差最大达到了9.7%，说明本文方法与HAWC2软件计算结果相比，尤其是大变形情况的位移转角计算，本文方法要更加精确，验证了该方法适用于计算不考虑耦合效应的空间梁单元大转动变形。

表  2  悬臂梁承受弯矩作用的大变形

Table  2.  Cantilever’s large deformation under bending moment

$k$	水平位移 $u$解析 解/m	本文 解/m	HAWC2- 30解/m	HAWC2- 50解/m	本文误 差/(%)	HAWC2- 30误差/(%)	HAWC2- 50误差/(%)	竖直位移 $v$解析 解/m	本文 解/m	HAWC2- 30解/m	HAWC2- 50解/m	本文误 差/(%)	HAWC2- 30误差/(%)	HAWC2- 50误差/(%)
0.4	−2.4317	−2.4268	−2.4439	−2.4366	0.20	0.50	0.20	5.4987	5.5023	5.5042	5.4987	0.07	0.10	0.00
0.8	−7.6613	−7.6551	−7.7609	−7.6996	0.08	1.30	0.50	7.1978	7.2168	7.2194	7.2050	0.26	0.30	0.10
1.2	−11.5591	−11.5684	−11.6978	−11.6053	0.08	1.20	0.40	4.7986	4.8271	5.0145	4.8802	0.59	4.50	1.70
1.6	−11.8921	−11.9121	−12.0467	−11.9516	0.17	1.30	0.50	1.3747	1.3893	1.6868	1.5080	1.06	22.70	9.70
2.0	−10.0000	−10.0000	−10.5100	−10.2000	0.00	5.10	2.00	0.0000	0.0000	−0.0080	−0.0100	0.0000	−0.0080	−0.0100

下载: 导出CSV 

| 显示表格

3.3   算例3

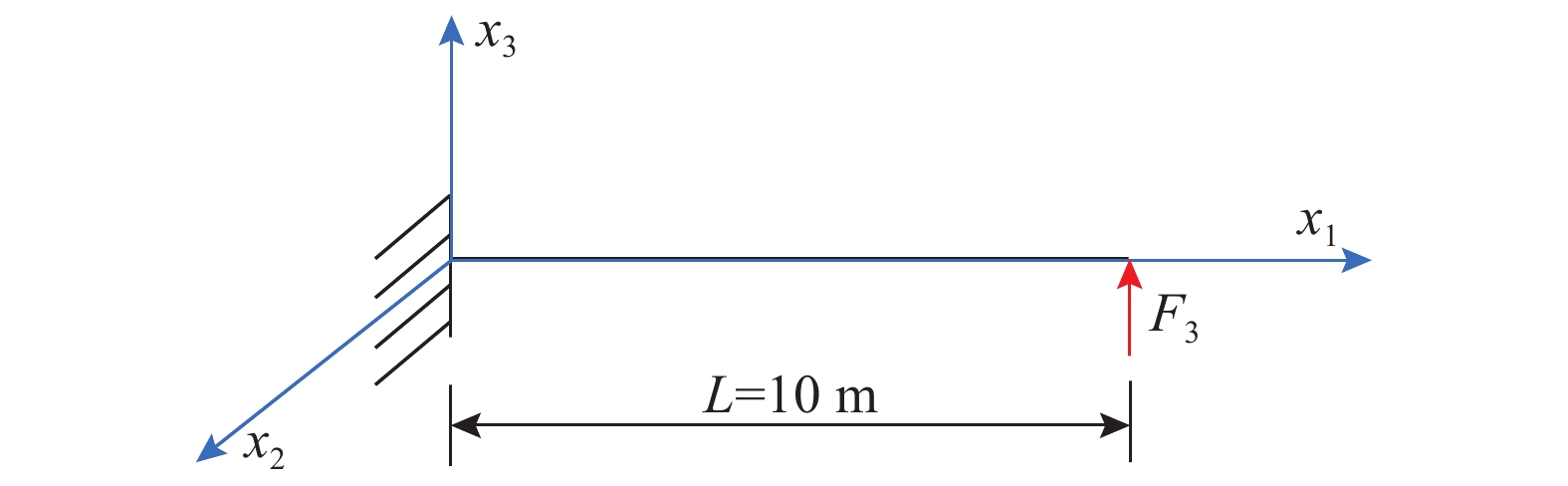
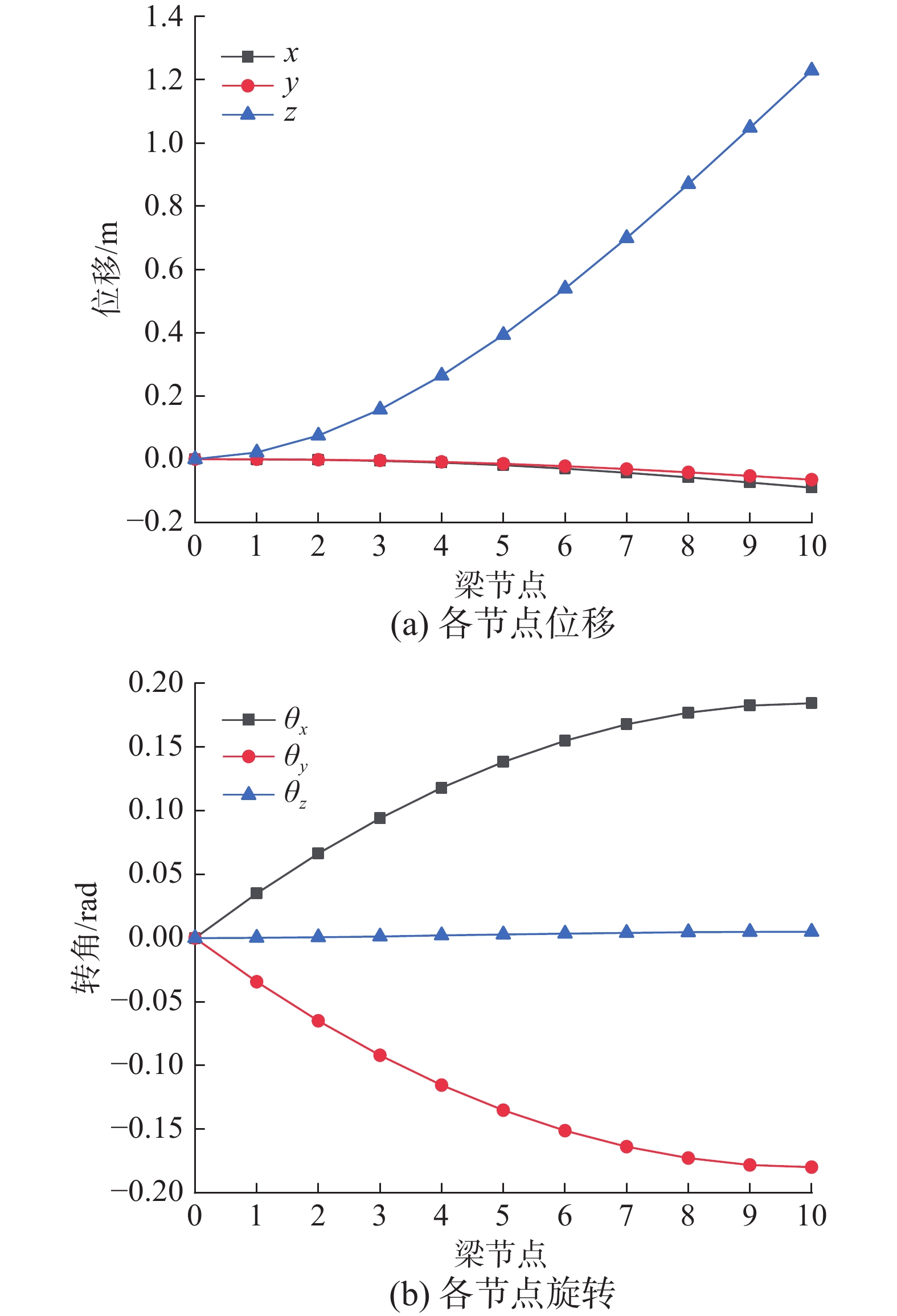
考虑耦合效应的悬臂梁结构如图7所示，在自由端作用一集中荷载${F}_{3}=150\; {\rm N}$，其耦合的截面刚度矩阵参数详见文献[23]。同样将梁划分为10个单元，图8给出了沿梁轴的每个节点的位移和转角所得计算结果。表3列出了自由端3个方向的位移和转角与参考文献[7]经典共旋坐标法和HAWC2^[25]方法计算结果的对比。

图  7  集中荷载作用下的耦合悬臂梁

Figure  7.  Coupled cantilever under concentrated load

下载: 全尺寸图片 幻灯片

图  8  沿梁轴向的位移和旋转参数

Figure  8.  Displacements and rotation parameters along beam axis

下载: 全尺寸图片 幻灯片

从图8可知，当耦合梁单元作用一面内荷载时，本文方法能计算出其他方向因耦合作用产生的位移和旋转。从表3可知，对于考虑耦合效应的空间Timoshenko梁单元，改进共旋坐标法的计算结果与经典共旋坐标法和HAWC2软件计算结果相比，误差均有所减小。尤其是对于经典共旋坐标法在计算时因虚假刚体转动产生的较大误差(如本算例中的y方向位移和z方向转角)，使用改进共旋坐标法后这一部分的误差分别减小了2.4%和4.5%，与HAWC2计算结果相比除z轴误差扩大了0.36%外，其他位移和转角结果均较好，尤其是HAWC2方法计算误差较大的y方向位移和x方向转角，误差分别减小了约3.6%和2.3%，验证了该方法适用于计算考虑耦合效应的空间Timoshenko梁单元的变形。

表  3  自由端位移和转角参数比较

Table  3.  Comparison of tip displacements and rotations

方法对比及误差分析	解析解/m	经典共旋法解/m	HAWC2解/m	本文解/m	共旋法误差/(%)	本文误差/(%)	HAWC2误差/(%)
x方向位移	−0.090 64	−0.090 13	−0.091 64	−0.090 09	0.56	0.61	1.10
y方向位移	−0.064 84	−0.063 20	−0.067 24	−0.064 76	2.53	0.12	3.70
z方向位移	1.229 98	1.229 50	1.229 98	1.229 18	0.04	0.06	0.00
x方向扭转角度	0.184 45	0.184 47	0.188 88	0.184 40	0.01	0.03	2.40
y方向旋转角度	−0.179 85	−0.179 87	−0.179 87	−0.179 84	0.01	0.01	0.01
z方向旋转角度	0.004 88	0.005 23	0.004 99	0.005 01	7.17	2.66	2.30

下载: 导出CSV 

| 显示表格

3.4   算例4

如图9所示，一个$45^{\circ }$的悬臂圆弧梁，圆弧半径R=100 m，在自由端受到竖向集中荷载F=600 N的作用，截面刚度矩阵详细参数见文献[26]所示，表4列出了本文计算的梁自由端三个方向位移x、y、z计算结果与解析解^[26] 、经典共旋坐标法的计算结果^[7]以及商用软件HAWC2^[25]的计算结果的对比分析。

从表4可知，对于预弯的空间Timoshenko梁，改进共旋坐标法的计算结果与经典共旋坐标法相比，三个方向位移的误差分别减小了0.2%、0.9%、0.1%，与HAWC2计算误差较小的结果相比本文方法也能较为精确的求得，而HAWC2计算误差较大的x和y方向位移，本文方法误差分别减小了1.9%和1.8%，验证了该方法适用于计算预弯式悬臂梁的大变形，也为后续研究预弯风力机叶片结构提供了研究基础。

图  9  预弯曲式悬臂梁

Figure  9.  Prebend cantilever

下载: 全尺寸图片 幻灯片

表  4  自由端受力下曲梁端部位移比较

Table  4.  Comparison of the curved beam tip displacements under a force applied at the free end

方法对比及 误差分析	解析 解	本文方 法解	经典共 旋法解	HAWC2 解	本文 误差/(%)	共旋法 误差/(%)	HAWC2/ (%)
$x/{\rm m}$	−23.7	−23.7	−23.8	−24.2	0.2	0.4	2.1
$y/{\rm m}$	−13.4	−13.6	−13.7	−13.8	1.3	2.2	3.1
${\textit{z} }/{\rm m}$	53.4	53.6	53.7	53.4	0.4	0.5	0.0

下载: 导出CSV 

| 显示表格

4   结论

本文基于共旋坐标法和Timoshenko梁理论，使用新型空间Timoshenko梁单元计算单元线刚度，使用逆向运动方法得到局部坐标系下的刚体转换矩阵，进而求得整体坐标系下的单元切线刚度。通过四个典型算例的比较，得到如下结论：

本文提出的改进共旋坐标法适用于不考虑耦合效应、考虑耦合效应及预弯等多种情况下的Timoshenko梁单元非线性分析，且计算精度与经典共旋理论和HAWC2方法相比均有所提高。