SHAPE-SENSING ARRAY BASED ON INVERSE FINITE ELEMENT METHOD AND EXPERIMENT OF BRIDGE DEFLECTION MONITORING
-
摘要: 桥梁挠度是桥梁工程从设计阶段到运维阶段的重要控制指标,对其进行实时监测对桥梁工程的性能评估至关重要。该文提出一种形状还原传感阵列,该传感阵列基于逆有限元方法,仅通过有限点的实测应变数据即可实时、准确地还原出桥梁挠曲线。详细阐述了逆有限元法基本原理与形状还原传感阵列装置,将该项技术应用于混凝土自锚式悬索桥梁模型进行挠度监测试验研究,分别对桥梁模型进行静态加载与动态加载,通过水准仪与激光位移计对还原得到的挠曲线形状与精度进行验证。结果表明:形状还原传感阵列对于桥梁挠度的监测具有易于安装、数据准确、实时性好的优点,不仅可以准确还原出桥梁挠度,而且可以实时反演出桥梁挠曲线形状,能够有效地评估桥梁工程性能质量。Abstract: Bridge deflection is an important indicator for the bridges from their design to their operation and maintenance stage. Real-time monitoring is crucial for the performance evaluation of bridges. A shape-sensing array based on the inverse finite element method (iFEM) is proposed. The deflection curve of a bridge can accurately be obtained by the strain data measured at limited points in real-time. Thusly, the basic principle of inverse finite element method and shape inversion sensing array device are described in detail. The technology is applied to the experimental study of deflection monitoring of a concrete self-anchored suspension bridge model. Static loading and dynamic loading were carried out on the bridge model, and the shape and the accuracy of the inverted deflection curve were verified by level gauge and laser displacement sensor. The results show that the shape-sensing array has the advantages of easy installation, good data accuracy and, excellent real-time performance for bridge deflection monitoring. This technology can accurately obtain bridge deflections and invert the curvature of deflection in real-time, which can effectively evaluate the performance and quality of a bridge.
-
Keywords:
- bridge deflection /
- iFEM /
- shape-sensing array /
- structural monitoring /
- Bernoulli-Euler beam
-
桥梁工程是交通互通互联的关键节点和枢纽工程,同时是国民经济发展和社会生活安全的重要保障。在桥梁工程保有量方面,我国已经是世界第一的桥梁大国,公路桥梁数量达80余万座,全国桥梁总数达100余万座,且在世界排名前十位的各类桥梁中,我国均占1/2以上[1-3]。随着桥梁建设的高速发展,桥梁坍塌事故时有发生,且事故发生频率总体上呈上升趋势[4]。桥梁结构在车辆等荷载作用、雨雪等自然因素的影响下,在长期服役期间不可避免地发生损伤与破坏[5-7]。而由上述原因引起的挠度直接反映了桥梁结构的刚度,桥梁挠度是从设计阶段到运维阶段的重要控制指标,当变形量超过其自身挠度容许范围,桥梁必然发生倒塌事故,故对桥梁工程进行挠度监测是必要的。
目前常见的桥梁结构挠度监测方法主要分为人工测量与自动测量。人工测量法主要包括水准测量法、全站仪三角高程法与连通管挠度监测法。人工测量法虽然能节省费用,但存在费时费力、使用不便、实时测量比较困难等不足之处,其中连通管法还存在液体响应速度慢,变形监测滞后的问题。自动测量主要包括倾角仪法、加速度计法、近景摄影测量技术、GPS技术、激光准直感光法、挠度仪法等。倾角仪法易造成测量误差积累,需对误差做合理分配与处理,加速度积分法受到积分初值与误差的制约。近景摄影测量技术虽然精度较高,但价格比较昂贵,监测过程较为复杂,而GPS技术精度较低,激光准直感光法又容易受到气流影响,挠度仪法则不能得到各点挠度变化曲线。综上,常用测量方法均存在不足之处:或是不能实现实时监测;或是成本过高,精度低;或是维护困难、不适合长期使用,安装条件苛刻、实用性存在问题;或是易受环境影响稳定性能差[8-15]。
“形状传感”是利用离散应变数据对变形形状进行实时重构,依赖于应变数据,可以连续测量静态和动态响应,根据静态和运动方程提出各种算法,以获得更高的精度和更快的运行效率[16]。JINEESH等[17]利用振型推导出应变-位移转换矩阵,由实测的离散应变数据重构结构的整体位移。KIM等[18]将基于模态方法的位移-应变关系应用于梁模型,实现叶片结构的动态变形监测。张合生[19]通过优化布局的FBG传感网络获取结构形态变化信息,然后,基于结构形态拟合重构方法实现板状结构的形态实时感知与重构。上述方法对静态、动态荷载作用下复杂结构的全域形状重构中不具有优势,且需要一定的材料或荷载信息还原结构变形。TESSLER和SPANGLER[20]提出一种用于工程结构位移监测的逆有限元法(iFEM),通过最小化加权最小二乘函数,应用实测表面应变重建结构变形,并基于Mindlin理论开发了一种新的三节点逆壳单元。随后,逆有限元法主要因为如下优势:① 可以仅通过有限点的应变快速、实时进行全域应变场重构,从而得到结构位移;② 仅基于应变-位移关系,不涉及力学平衡;③ 不需要材料信息,近些年来逐渐被应用于结构变形监测中[21-23]。
逆有限元法在桥梁变形监测的应用中存在一些问题:桥梁结构所用材料属性一般难以满足连续、均匀、各向同性;桥梁结构几何尺寸的改变难以实时准确地反应在逆有限元模型中。本文基于逆有限元方法提出了可以实时、高效地利用实测应变数据还原待测结构位移的形状还原传感阵列,解决了上述应用问题,并实现了将其应用于土木工程领域中的桥梁挠度监测,具有广阔的工程应用前景。
1 形状还原传感阵列
1.1 形状还原传感阵列概述
形状还原传感阵列由钢梁、固定支座、固定铰支座构成,将钢梁一端固接,每隔一定距离(一跨)布设固定铰支座,实现对钢梁垂直约束的同时不限制其产生转角。将钢梁每一跨视作一个传感单元,在每个传感单元上布设一定数量传感器,用以实测应变数据。将固定铰支座与待测结构固接,待测结构产生的变形即可视为与形状还原传感阵列发生的变形一致,通过还原传感阵列变形即可进而达到还原待测结构变形目的。在实际桥梁工程中,可将固定支座固接于桥墩或盖梁位置,将固定铰支座每隔一定距离固接于桥梁梁板,达到监测桥梁挠度目的。
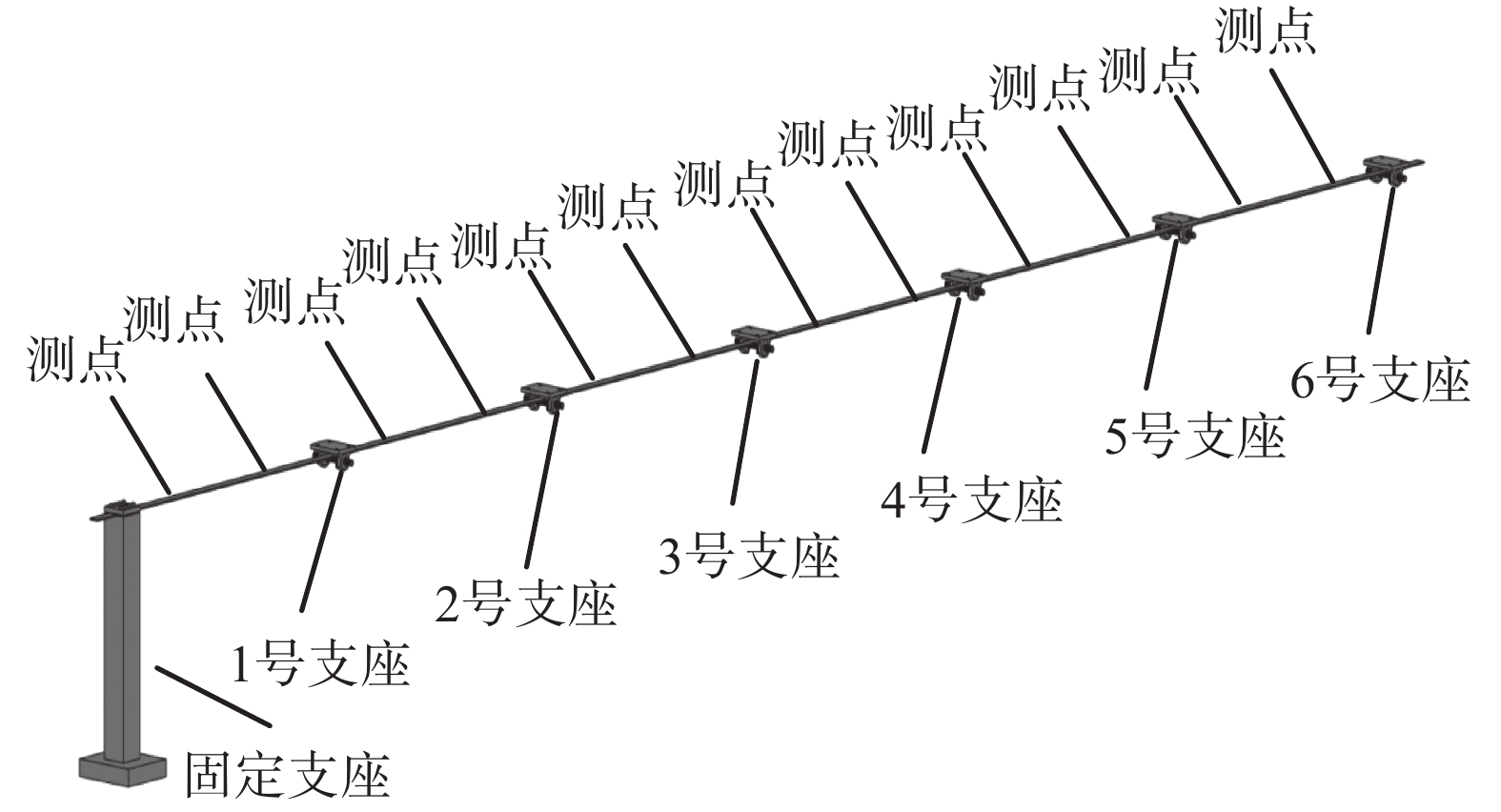
单元长度的选取和每个单元中应变传感器的数量是影响逆有限元方法准确性和鲁棒性的重要因素。跨长(即单元长度)L越小,且每个跨长L上安装传感器数量越多(即获得更多应变数据)的情况下,算法还原精度越高;而且,当L长度增加时,可以通过增加传感器数量,来保证还原精度,但监测成本也会随之增加。本文综合考虑精度需求、监测条件和测量环境,试验采用的形状还原传感阵列设计为6跨,跨长L为1 m,每个单元配置2个传感器,每跨上分别距离支座两侧L/6处为应变测点,采用应变片作为应变传感器。将靠近固定支座处的固定铰支座命名为1号支座,由近及远命名为2号~6号支座。设计图如图1所示。
1.2 逆有限元法基本原理
形状还原传感阵列的每个传感单元采用简单有效的用于梁式结构二维变形监测的新型二节点逆梁单元iBeam3[24]。该单元的逆有限元公式推导基于Euler-Bernoulli梁拉弯理论中考虑截面应变的最小二乘变分原理,由于公式中只使用了应变-位移关系,iBeam3单元能够在没有任何材料或荷载信息的情况下重建结构变形形状。此外,由于经典梁理论的平截面假设,该单元只需两端节点即可实现横向位移的3次插值。
如图2所示,各向同性直梁单元每个节点有3个位移自由度,厚度均匀2h,表面至中性层厚度为h,单元长度为L。(x,y,z)为局部坐标系,(X,Y,Z)为整体坐标系。局部坐标系的原点位于单元端点。
基于经典梁理论和有限元理论,iBeam3单元的位移场定义为:
u(x)=N1u1+N4u2 (1) v(x)=N2v1+N3φ1+N5v2+N6φ2 (2) φ(x)=∂v∂x=N2,xv1+N3,xφ1+N5,xv2+N6,xφ2 (3) 节点自由度包括
ui 、vi 、φi ,ui 和vi 为沿x轴与y轴的平动自由度,φi 为绕z轴的转动自由度,Ni 为经典梁单元形函数。由小变形假设,轴向应变ε 与曲率k 如下:\varepsilon = \frac{{\partial u}}{{\partial x}} = {{\boldsymbol{B}}_{\rm b}}{{\boldsymbol{u}}_e} (4) k = \frac{{{\partial ^2}v}}{{\partial {x^2}}} = {{\boldsymbol{B}}_{\rm m}}{{\boldsymbol{u}}_e} (5) 其中:
{{\boldsymbol{u}}_e} = {[ {\begin{array}{*{20}{c}} {{u_1}}&{{v_1}}&{{\varphi _1}}&{{u_2}}&{{v_2}}&{{\varphi _2}} \end{array}}]^{\rm T}} (6) 矩阵
{{\boldsymbol{B}}_{\rm b}} 和{{\boldsymbol{B}}_{\rm m}} 为形函数的导数,定义加权最小二乘函数{{\boldsymbol{\varPhi }}_e}({{\boldsymbol{u}}_e}) 与轴向拉伸和弯曲变形有关,则有:{{\boldsymbol{\varPhi }}_e}({{\boldsymbol{u}}_e}) = {w_{\rm b}}||{{\boldsymbol{B}}_{\rm b}}{{\boldsymbol{u}}_e} - \varepsilon |{|^2} + {w_{\rm m}}||{{\boldsymbol{B}}_{\rm m}}{{\boldsymbol{u}}_e} - k|{|^2} (7) 等式中所示的平方范数基于欧几里德范数定义为:
{w_{\rm b}}||{{\boldsymbol{B}}_{\rm b}}{{\boldsymbol{u}}_e} - \varepsilon |{|^2} = \sum\limits_{i = 1}^n {\int_{\frac{{(i - 1)L}}{n}}^{\frac{{iL}}{n}} {{w_{{\rm b}i}}} } {({({{\boldsymbol{B}}_{\rm b}}{{\boldsymbol{u}}_e})_i} - {\varepsilon _i})^2}{\rm d}x (8) \begin{split} & {w_{\rm m}}||{{\boldsymbol{B}}_{\rm m}}{{\boldsymbol{u}}_e} - k|{|^2} =\\&\qquad {(2h)^2}\sum\limits_{i = 1}^n {\int_{\frac{{(i - 1)L}}{n}}^{\frac{{iL}}{n}} {{w_{{\rm m}i}}} } {({({{\boldsymbol{B}}_{\rm m}}{{\boldsymbol{u}}_e})_i} - {k_i})^2}{\rm d}x \end{split} (9) 加权常数
{w_{{\rm b}i}} 和{w_{{\rm m}i}} 与每个单独的截面应变有关。当每个分析截面应变都有一个相近的试验值时,{w_{{\rm b}i}} ={w_{{\rm m}i}} =1。将式(8)和式(9)代入式(7),得:\frac{{\partial {{\boldsymbol{\varPhi }}_e}({{\boldsymbol{u}}_e})}}{{\partial {{\boldsymbol{u}}_e}}} = {{\boldsymbol{K}}_e}{{\boldsymbol{u}}_e} - {{\boldsymbol{f}}_e} = {\boldsymbol{0}} (10) 其中:
{{\boldsymbol{K}}_e} = \sum\limits_{i = 1}^n {\int_{\frac{{(i - 1)L}}{n}}^{\frac{{iL}}{n}} {({w_{{\rm b}i}}} } {\boldsymbol{B}}_{\rm b}^{\rm T}{{\boldsymbol{B}}_{\rm b}} + {(2h)^2}{w_{{\rm m}i}}{\boldsymbol{B}}_{\rm m}^{\rm T}{{\boldsymbol{B}}_{\rm m}}){\rm d}x (11) {{\boldsymbol{f}}_e} = \sum\limits_{i = 1}^n {\int_{\frac{{(i - 1)L}}{n}}^{\frac{{iL}}{n}} {({w_{{\rm b}i}}} } {{\boldsymbol{B}}_{\rm b}^{\rm T}}{\varepsilon _i} + {(2h)^2}{w_{{\rm m}i}}{{\boldsymbol{B}}_{\rm m}^{\rm T}}{k_i}){\rm d}x (12) 式中:
{{\boldsymbol{K}}_e} 为一个常数矩阵,只依赖于元素的长度和厚度;{{\boldsymbol{f}}_e} 为一个列向量,取决于测得的应变数据;{{\boldsymbol{u}}_e} 为节点位移向量。矩阵{{\boldsymbol{K}}_e} 和{{\boldsymbol{f}}_e} 为在局部坐标系中建立,使用坐标变换矩阵,即可将单元矩阵组装成整体方程组。带有边界条件的整体方程组如下:{{\boldsymbol{K}}_R}{{\boldsymbol{U}}_R} = {{\boldsymbol{F}}_R} (13) 将式(13)中等式两边乘以矩阵
{{\boldsymbol{K}}_R} 的逆矩阵,即可得到位移向量:{{\boldsymbol{U}}_R} = {\boldsymbol{K}}_R^{{{ - 1}}}{{\boldsymbol{F}}_R} (14) 综上,采用逆有限元法进行形状还原时,首先将结构求解域离散化为若干个逆单元,在单元内部建立求解矩阵方程,最后经过总体系统集成,实现结构变形求解。
1.3 有限元模拟验证
以图1所示形状还原传感阵列为算例,在有限元分析软件ANSYS中对其进行模拟分析,将每一跨划分为3个单元(逆有限元分析中每一跨划分为1个单元),建模采用Beam188单元,一端固接,将固接端位置记为0,在2号和4号支座位置(即形状还原传感阵列2000 mm和4000 mm处)进行5 mm位移控制加载,如图3所示。
加载后通过有限元模拟得到的图1中的各传感单元两个测点(分别距离支座两侧L/6处)的应变值如表1所示,将其代入上述算法,得到还原结果,验证形状还原传感阵列有效性。
表 1 各个测点应变值Table 1. Strain of measuring point测点 应变/(×10−5) 测点 应变/(×10−5) 1 −0.74 7 3.09 2 1.98 8 −2.67 3 1.51 9 −3.05 4 −3.07 10 1.19 5 −2.76 11 1.87 6 3.07 12 0.37 固定支座与1号~6号固定铰支座处还原得到的位移结果与ANSYS的数值模拟结果如表2所示。
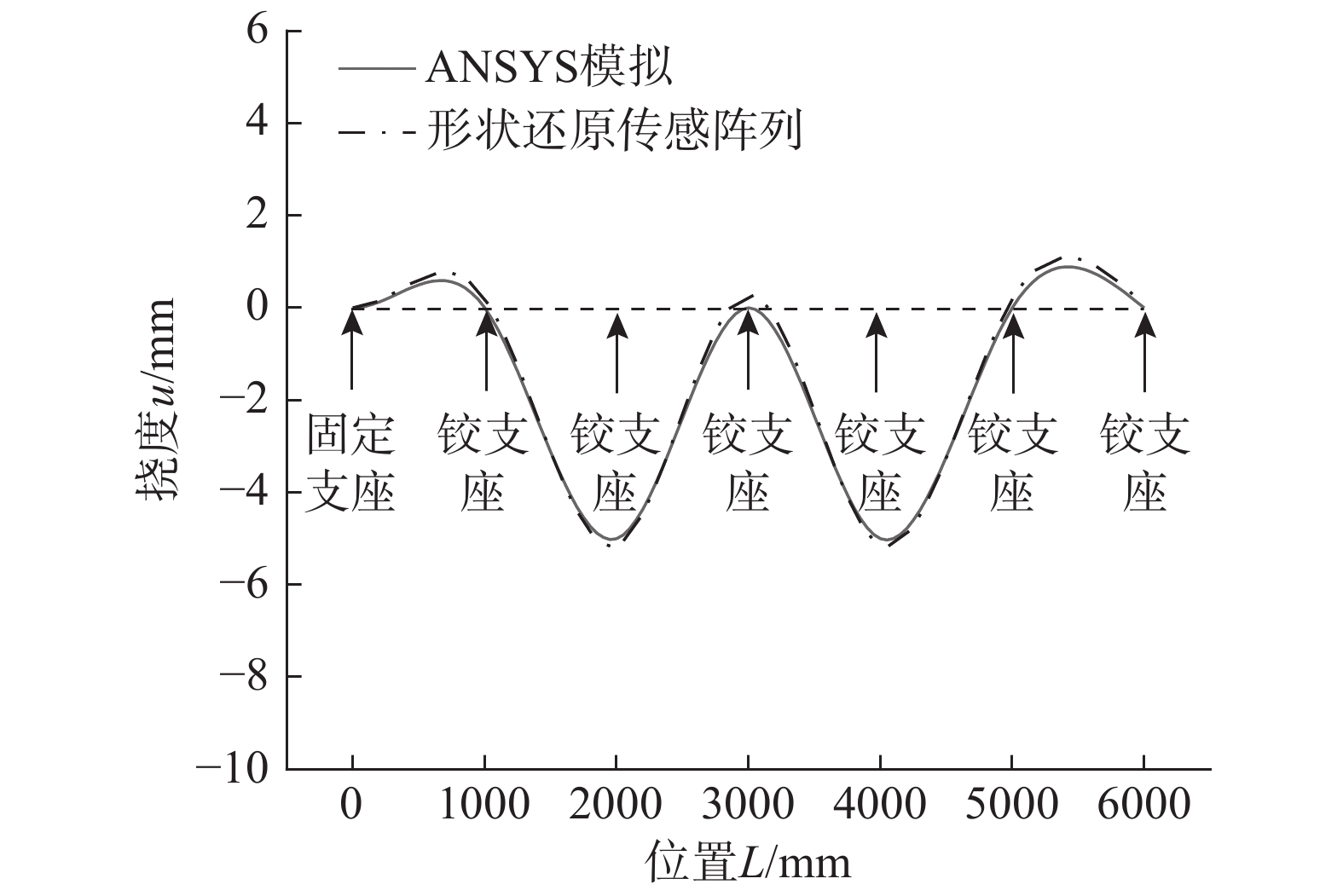
表 2 结果对比Table 2. Comparison of results支座 还原位移/mm ANSYS结果/mm 固定支座 0.000 0 1号支座 0.203 0 2号支座 −5.139 −5 3号支座 0.296 0 4号支座 −5.133 −5 5号支座 0.183 0 6号支座 0.072 0 对比还原结果与模拟结果可知,在发生位移节点处相对误差最大为2.78%,形状还原传感阵列能够准确获得节点位移向量。经过插值计算后还原结果如图4所示,仅通过有限测点的应变值即可还原得到其全域位移值,还原得到的全域位移值与ANSYS模拟结果最大相差0.296 mm,形状还原传感阵列能够有效还原被测结构位移场。
2 桥梁模型试验研究
2.1 桥梁基本情况
本次试验采用的桥梁模型原桥为大连市庄河建设大街东桥,该桥为混凝土自锚式悬索桥,跨径布置为70 m+200 m+70 m=340 m,桥面宽27 m,主梁为钢筋混凝土箱梁。
桥梁模型为混凝土自锚式悬索桥,模型图如图5所示,主梁采用实体断面,梁宽764 mm、高89 mm,沿桥梁模型横向方向,两侧设悬臂梁。桥塔为门式结构,设上、下横梁。桥梁两端为桥台。主缆和吊索采用钢丝绳制作。桥塔及桥台处支座采用5 mm厚橡胶板。
实拍图如图6所示,由近及远分别为桥梁模型主梁第一跨、第二跨、第三跨,设计为跨径组合2.5 m+7.14 m+2.5 m=12.14 m,本文所开展的试验研究均在桥梁模型小变形范围内进行。
2.2 装置布设
形状还原传感阵列设计如图1所示,共布设6 m,钢梁选用截面尺寸为30 mm×3 mm矩形弹簧钢板,沿桥梁模型主梁纵向方向布设于主梁第二跨底部,固定支座通过建筑结构胶与地面连接,固定铰支座通过建筑结构胶附着于桥梁模型主梁第二跨底部。6号支座位于桥塔侧,此处挠度值为0,但转角值不为0°。
装置具体布设位置如下:在桥梁模型主梁横向方向上,装置中的钢梁外边缘距离主梁第二跨外边缘80 mm。在桥梁模型主梁纵向方向上,3号支座位于桥梁模型主梁第二跨跨中,即1号~6号支座分别距离桥塔底部基础内侧边缘1336 mm、2336 mm、3336 mm、4336 mm、5336 mm、6336 mm。装置布设图如图7所示,实拍图如图8所示。
2.3 静态试验
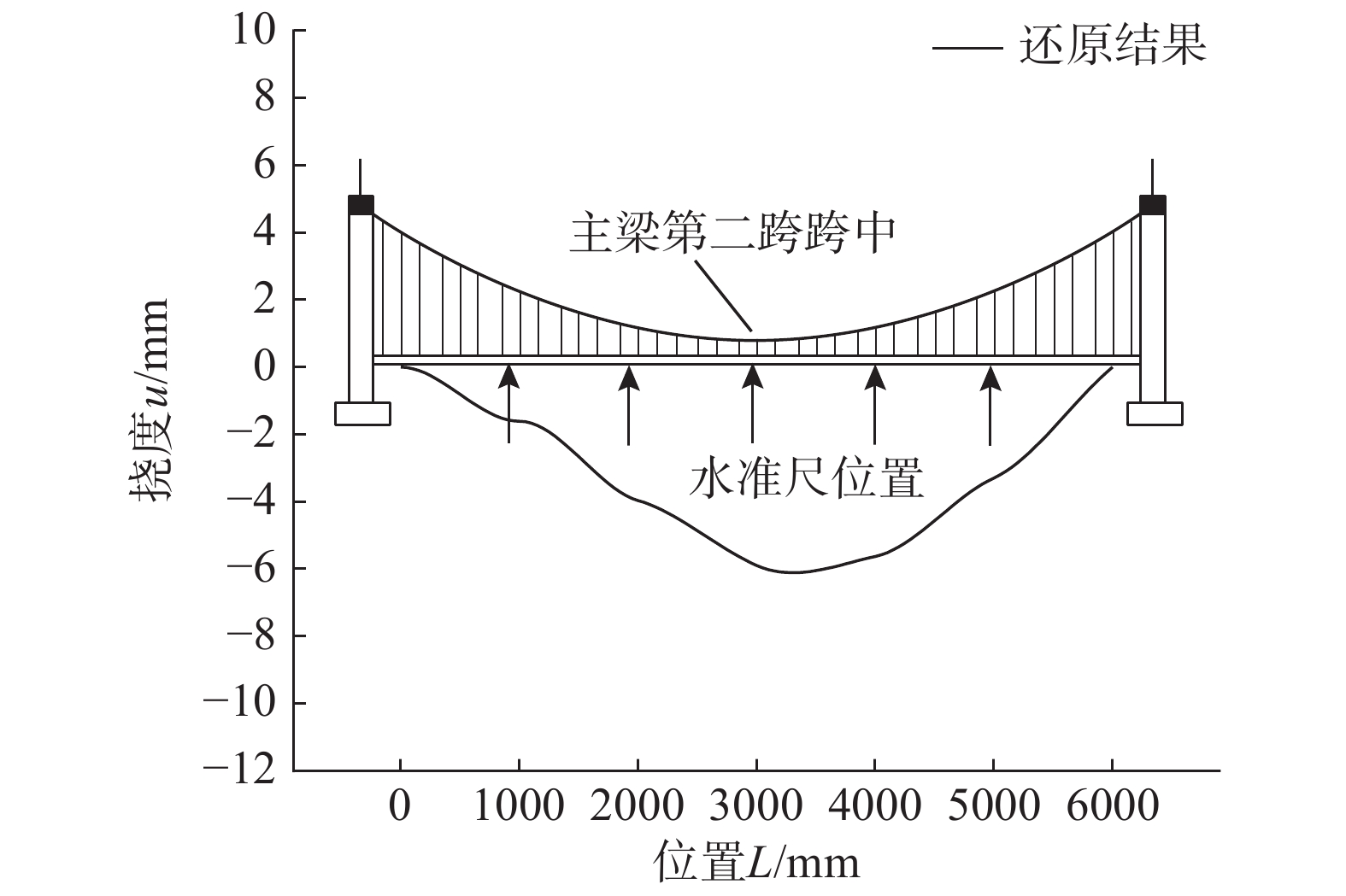
在2号~4号支座处桥梁模型主梁上部放置钢板实现加载,如图9所示。采用水准仪对桥梁挠度进行测量,如图10所示,加载前后分别在1号~5号支座处的桥梁模型主梁上部垂直放置水准尺,实测桥梁挠度变化。将形状还原传感阵列还原得到的桥梁挠曲线与水准仪实测结果进行对比分析。
形状还原传感阵列还原得到的桥梁挠曲线如图11所示,其中负号代表向下方向。由图中可以看出,在加载过后,桥梁模型主梁呈现跨中挠度大、两侧挠度小的趋势,与实际相符,说明挠曲线还原准确,形状还原传感阵列可以在静态加载条件下还原出桥梁挠曲线,在实际使用中效果良好。
各工况还原结果与实测挠度相比,最大相差0.82 mm,最小相差仅为0.012 mm,平均相差0.261 mm,吻合程度较好。
为验证还原结果准确性与精度,在桥梁模型主梁上部跨中位置放置钢板实现加载,分别在1号~5号支座下方设立激光位移计,如图12所示。形状还原传感阵列还原挠度与激光位移计测得数据结果如图13所示。
由形状还原传感阵列还原挠度与激光位移计测量所得挠度对比分析可知,两者相差均在0.8 mm以内,且最小仅相差0.115 mm。
2.4 动态试验
动态加载采用如图14所示的小车上放置钢板方式。首先将载有钢板的小车放于桥梁模型主梁第二跨的1号支座上方附近,而后在桥旁控制小车从起点由固定支座向固定铰支座方向运动,运动到桥梁模型主梁第三跨,最后小车由第三跨返回到桥梁模型主梁第二跨的运动起点。挠度测量方式为在桥梁模型主梁第二跨跨中支座下部布设激光位移计,并将还原结果与其进行对比分析。
动态加载后,形状还原传感阵列挠度还原如图15所示,由激光位移计测量跨中挠度与形状还原传感阵列还原得到的挠度吻合程度较好,由图中可以清晰看出小车静止后从起点出发,由远及近驶向测量点过程中,挠度逐渐增大,小车远离测量点过程中,挠度逐渐减小。当小车运动到桥梁模型主梁第三跨时,桥梁模型主梁第二跨出现向上位移。随后小车在返回起点过程中,桥梁模型主梁第二跨跨中挠度变化趋势与上述过程大致相同,最后当小车运动回起点时桥梁模型主梁第二跨跨中挠度基本稳定为0,与实际情况相符。
3 结论
本文提出一种形状还原传感阵列用以监测桥梁挠度,该传感阵列基于逆有限元法,比起常用的桥梁挠度监测方法,其易于安装,可以实时还原出桥梁挠曲线,且准确性良好。本文将形状还原传感阵列应用于混凝土自锚式悬索桥梁模型,并对桥梁模型进行静态试验与动态试验。还原得到挠曲线结果与水准仪读数最大相差0.82 mm,最小仅相差0.012 mm,平均相差0.261 mm,还原得到的挠曲线符合桥梁模型主梁挠度变化规律。采用激光位移计验证还原挠度准确性,两者相差0.8 mm以内,且最小仅相差0.115 mm。动态试验还原得到结果与激光位移计测得结果吻合程度良好,该传感阵列可以准确、及时地还原出桥梁模型结构挠度变化。
综上,本文所提出的形状还原传感阵列对于桥梁挠度的监测具有易于安装、数据准确、实时性好的优点,仅通过有限点的实测应变数据,即可实时、准确地还原出桥梁挠曲线,从而有效评估桥梁性能,对桥梁挠度监测具有重要意义。
-
表 1 各个测点应变值
Table 1 Strain of measuring point
测点 应变/(×10−5) 测点 应变/(×10−5) 1 −0.74 7 3.09 2 1.98 8 −2.67 3 1.51 9 −3.05 4 −3.07 10 1.19 5 −2.76 11 1.87 6 3.07 12 0.37 表 2 结果对比
Table 2 Comparison of results
支座 还原位移/mm ANSYS结果/mm 固定支座 0.000 0 1号支座 0.203 0 2号支座 −5.139 −5 3号支座 0.296 0 4号支座 −5.133 −5 5号支座 0.183 0 6号支座 0.072 0 -
[1] 中国公路学报编辑部. 中国桥梁工程学术研究综述·2021[J]. 中国公路学报, 2021, 34(2): 1 − 97. doi: 10.3969/j.issn.1001-7372.2021.02.002 Editorial Department of China Journal of Highway and Transport. Review on China's bridge engineering research: 2021 [J]. China Journal of Highway and Transport, 2021, 34(2): 1 − 97. (in Chinese) doi: 10.3969/j.issn.1001-7372.2021.02.002
[2] 李文杰, 赵君黎. 发展中的中国桥梁——张喜刚谈中国桥梁的现状与展望[J]. 中国公路, 2018(13): 64 − 68. doi: 10.3969/j.issn.1006-3897.2018.13.024 LI Wenjie, ZHAO Junli. Chinese bridges in development——Zhang Xigang's status quo and prospect of Chinese bridges [J]. China Highway, 2018(13): 64 − 68. (in Chinese) doi: 10.3969/j.issn.1006-3897.2018.13.024
[3] 陈炳聪, 黄海云, 刘嘉玲, 等. 亚健康简支T梁桥限载指标评估及验证[J]. 工程力学, 2020, 37(增刊): 68 − 74. doi: 10.6052/j.issn.1000-4750.2019.04.S009 CHEN Bingcong, HUANG Haiyun, LIU Jialing, et al. Evaluation and verification of limited load index of sub-health simply supported T beam bridge [J]. Engineering Mechanics, 2020, 37(Suppl): 68 − 74. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.04.S009
[4] 郑元勋, 郭慧吉, 谢宁. 基于统计分析的桥梁坍塌事故原因剖析及预防措施研究[J]. 中外公路, 2017, 37(6): 125 − 132. ZHENG Yuanxun, GUO Huiji, XIE Ning. Cause analysis and preventive measures of bridge collapse based on statistical analysis [J]. Journal of China & Foreign Highway, 2017, 37(6): 125 − 132. (in Chinese)
[5] 李宏男, 田亮, 伊廷华, 等. 大跨斜拱桥结构健康监测系统的设计与开发[J]. 振动工程学报, 2015, 28(4): 574 − 584. LI Hongnan, TIAN Liang, YI Tinghua, et al. Design and development of structural health monitoring system for long span skew arch bridge [J]. Journal of Vibration Engineering, 2015, 28(4): 574 − 584. (in Chinese)
[6] 牛艳伟, 石雪飞, 欣阮. 大跨径混凝土梁桥的长期挠度实测分析[J]. 工程力学, 2008, 25(增刊 Ⅰ): 116 − 119. NIU Yanwei, SHI Xuefei, RUAN Xin. Measured sustained deflection analysis of long-span prestressed concrete beam bridges [J]. Engineering Mechanics, 2008, 25(Suppl Ⅰ): 116 − 119. (in Chinese)
[7] 周毅, 孙利民, 符振慧, 等. 斜拉桥跨中竖向位移的温度灵敏度系数研究[J]. 工程力学, 2020, 37(6): 148 − 154. doi: 10.6052/j.issn.1000-4750.2019.08.0437 ZHOU Yi, SUN Limin, FU Zhenhui, et al. Study on temperature sensitivity coefficients of mid-span vertical displacement of cable-stayed bridges [J]. Engineering Mechanics, 2020, 37(6): 148 − 154. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.08.0437
[8] 孙丰春. 大跨径桥梁挠度变形监测技术应用实践[J]. 海洋测绘, 2020, 40(4): 77 − 82. doi: 10.3969/j.issn.1671-3044.2020.04.017 SUN Fengchun. Technical application and practice in deflection of long-span bridges [J]. Hydrographic Surveying and Charting, 2020, 40(4): 77 − 82. (in Chinese) doi: 10.3969/j.issn.1671-3044.2020.04.017
[9] 张文基, 刘喜元, 岳建平. 大跨径桥梁挠度观测方法评述[J]. 测绘通报, 2002(8): 41 − 42. doi: 10.3969/j.issn.0494-0911.2002.08.014 ZHANG Wenji, LIU Xiyuan, YUE Jianping. A review of surveying methods for flexibility of large span bridge [J]. Bulletin of Surveying and Mapping, 2002(8): 41 − 42. (in Chinese) doi: 10.3969/j.issn.0494-0911.2002.08.014
[10] 杨建春, 陈伟民. 桥梁结构挠度自动监测技术的现状与发展[J]. 传感器与微系统, 2006, 25(9): 1 − 3. doi: 10.3969/j.issn.1000-9787.2006.09.001 YANG Jianchun, CHEN Weimin. Status and development of auto-monitoring technology for bridge deflection [J]. Transducer and Microsystem Technologies, 2006, 25(9): 1 − 3. (in Chinese) doi: 10.3969/j.issn.1000-9787.2006.09.001
[11] 文雪中. 大型桥梁挠度监测的方法比较及实践[J]. 测绘地理信息, 2016, 41(5): 70 − 73. WEN Xuezhong. Comparison and practice of deflection monitoring methods in the long-span bridge [J]. Journal of Geomatics, 2016, 41(5): 70 − 73. (in Chinese)
[12] 李宏男, 伊廷华, 伊晓东, 等. 采用GPS与全站仪对大跨斜拉桥进行变形监测[J]. 防灾减灾工程学报, 2005, 25(1): 8 − 13. LI Hongnan, YI Tinghua, YI Xiaodong, et al. Integration of GPS and total station technology for deformation monitoring of long-span bridge [J]. Journal of Disaster Prevention and Mitigation Engineering, 2005, 25(1): 8 − 13. (in Chinese)
[13] XU Y, BROWNJOHN J M W. Vision-based systems for structural deformation measurement: Case studies [J]. Proceedings of the Institution of Civil Engineers - Structures and Buildings, 2018, 171(12): 917 − 930. doi: 10.1680/jstbu.17.00134
[14] 熊伟, 赵敏, 吴迪军. 港珠澳大桥首级GPS控制网建立与复测研究[J]. 导航定位学报, 2019, 7(1): 117 − 120. XIONG Wei, ZHAO Min, WU Dijun. Study on establishment and repetition survey of the first order GPS control network of Hong Kong-Zhuhai-Macao Bridge [J]. Journal of Navigation and Positioning, 2019, 7(1): 117 − 120. (in Chinese)
[15] 朱前坤, 陈建邦, 张琼, 等. 基于计算机视觉人行桥挠度影响线非接触式识别[J]. 工程力学, 2021, 38(8): 145 − 153. doi: 10.6052/j.issn.1000-4750.2020.08.0557 ZHU Qiankun, CHEN Jianbang, ZHANG Qiong, et al. A non-contact recognition for deflection influence line of footbridge based on computer vision [J]. Engineering Mechanics, 2021, 38(8): 145 − 153. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.08.0557
[16] AMANZADEH M, AMINOSSADATI S M, KIZIL M S, et al. Recent developments in fibre optic shape sensing [J]. Measurement, 2018, 128: 119 − 137.
[17] THOMAS J, GURUSAMY S, RAJANNA T R, et al. Structural shape estimation by mode shapes using fiber Bragg grating sensors: A genetic algorithm approach [J]. IEEE Sensors Journal, 2020, 20(6): 2945 − 2952. doi: 10.1109/JSEN.2019.2934366
[18] KIM H I, KANG L H, HAN J H. Shape estimation with distributed fiber Bragg grating sensors for rotating structures [J]. Smart Materials and Structures, 2011, 20(3): 35011. doi: 10.1088/0964-1726/20/3/035011
[19] 张合生. 基于正交离散FBG网络的柔板结构形态感知与重构研究[D]. 上海: 上海大学, 2015. ZHANG Hesheng. Shape perception and reconstruction for flexible plate structure based on discrete orthogonal FBG network [D]. Shanghai: Shanghai University, 2015. (in Chinese)
[20] TESSLER A, SPANGLER J L. A least-squares variational method for full-field reconstruction of elastic deformations in shear-deformable plates and shells [J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(2/3/4/5): 327 − 339. doi: 10.1016/j.cma.2004.03.015
[21] CERRACCHIO P, GHERLONE M, DI SCIUVA M, et al. Shape and stress sensing of multilayered composite and sandwich structures using an inverse finite element method [C]. Barcelona Spain: V International Conference on Computational Methods for Coupled Problems in Science and Engineering, 2013: 311 − 322.
[22] GHERLONE M, CERRACCHIO P, MATTONE M, et al. Shape sensing of 3D frame structures using an inverse finite element method [J]. International Journal of Solids and Structures, 2012, 49(22): 3100 − 3112. doi: 10.1016/j.ijsolstr.2012.06.009
[23] 蔡鹏越. 用于结构位移场重构的逆有限元法研究[D]. 南京: 南京航空航天大学, 2016. CAI Pengyue. Investigation on the inverse FEM for structural displacement reconstruction [D]. Nanjing: Nanjing University of Aeronautics And Astronautics, 2016. (in Chinese)
[24] YOU R Z, REN L, YUAN C L, et al. Two-dimensional deformation estimation of beam-like structures using inverse finite-element method: Theoretical study and experimental validation [J]. Journal of Engineering Mechanics, 2021, 147(5): 4021019. doi: 10.1061/(ASCE)EM.1943-7889.0001917



 下载:
下载: