A PREDICTION METHOD FOR THE CHLORIDE DIFFUSIVITY IN PRESTRESSED CONCRETE CONTAINMENT VESSELS IN NUCLEAR POWER PLANTS
-
摘要: 氯离子扩散系数是评价沿海环境中核电厂预应力混凝土安全壳耐久性的重要参数。该文基于两尺度方法,通过分析双轴等压下水泥浆基体、界面和混凝土细观结构,建立了水泥浆基体和界面毛细孔隙率与预应力之间的定量关系。为了量化预应力对微裂纹闭合、产生和扩展的影响,提出了临界毛细孔隙率与预应力之间的经验公式。将混凝土模拟成由骨料、界面和水泥浆基体组成的三相复合材料,获得预应力混凝土氯离子扩散系数比。通过与试验结果比较,校正了经验公式中的两个参数。用三组试验数据初步验证了该预测方法的有效性。Abstract: Chloride diffusivity is an important parameter for assessing the durability of prestressed concrete containment vessels in nuclear power plants located in a marine environment. Based on a two-scale method, a quantitative relationship between the capillary porosities of cement paste matrix and interfacial transition zone (ITZ), and the prestress is established by analyzing the mesostructures of cement paste matrix, ITZ and concrete under an equi-biaxial compression. To quantify the effect of prestress on the closure, initiation and extension of microcracks, an empirical formula between the critical capillary porosity and the prestress is proposed. Concrete is then modeled as a three-phase composite material, composed of aggregate, ITZ and cement paste matrix, and the chloride diffusivity ratio of concrete is obtained. Through comparison with experimental results, two parameters in the empirical formula are calibrated. The validity of the prediction method is preliminarily verified with three sets of experimental data.
-
安全壳作为核电厂最重要的构筑物,是安全纵深防御的最后一道实体屏障,在极端荷载作用下维持其功能是有效防止放射性物质泄漏的重要保证。目前我国所有的商用核电站均建在沿海地区,氯离子侵蚀是影响安全壳使用寿命的最关键因素。环境中的氯离子侵蚀到混凝土内部,造成钢筋锈蚀、保护层开裂[1-2],降低安全壳的使用功能和使用寿命。安全壳自身结构特殊、设计工况复杂(地震和失水事故等)、使用条件严苛(高温、高压和高腐蚀),这些因素对氯离子侵蚀机制均具有耦合效应[3-5]。同时,由于安全壳具有抵抗事故内压作用的包容性功能要求,设计时设置了双向大应力比预应力体系来增强安全壳抵抗内压爆破作用效应。预应力荷载的长期作用也会改变混凝土孔隙结构,进而影响氯离子的侵蚀速率。因此,通过试验和理论分析确定预应力混凝土氯离子扩散系数成为安全壳耐久性设计和评估的关键。
一般混凝土结构通常经受各种应力作用,由于混凝土抗压强度远高于抗拉强度,在拉应力作用下混凝土易产生微裂纹甚至宏观裂缝,混凝土氯离子扩散系数一般随着拉应力的增大而单调增大[6]。但如前所述,安全壳不同于一般结构,在双向预应力作用下混凝土基本处于双向受压状态,很少出现拉应力,即使局部出现拉应力,其应力水平也很低,不会产生拉伸开裂。例如,东南沿海某核电站的两座安全壳,混凝土强度等级为C60,在所计算的18个关键点中,只有4个关键点出现拉应力,其最大值仅为0.69 MPa,远小于混凝土抗拉强度,正是由于这个原因,本文仅讨论压应力对混凝土安全壳氯离子扩散的影响。同时,这两座安全壳的最大压应力为混凝土抗压强度的0.7倍,根据现有的试验结果,当压应力为混凝土抗压强度的0.3倍时,其氯离子扩散系数比普通混凝土低30%[6],而当压应力为混凝土抗压强度的0.7倍时,其氯离子扩散系数则比普通混凝土高30%[7]。因此,压应力不仅影响混凝土氯离子扩散系数,而且影响规律比拉应力更加复杂。
目前,国内外学者围绕混凝土中氯离子的扩散行为开展了大量试验分析和数值模拟研究[8-13],但针对预应力混凝土氯离子扩散系数的研究工作较少。孙继成等[6]通过螺纹杆对混凝土试件施加压力,应用NEL法[14]测定混凝土氯离子扩散系数,他们把压力与混凝土抗压强度之比定义为压力比,发现当压力比小于0.3时,混凝土氯离子扩散系数随压应力的增大而减小,而当压力比大于0.3时,由于混凝土内部微裂纹的产生和扩展,混凝土氯离子扩散系数随着压力比的增大而增大。袁承斌等[15]通过后张法给混凝土试件施加预压应力,采用盐雾箱测定暴露两个月后混凝土中的氯离子浓度分布,评价压力比对混凝土氯离子扩散的影响。熊建波等[16]通过一套自己设计的加载系统给混凝土试件施加压力,采用人工海水浸泡法模拟氯离子侵蚀,发现混凝土氯离子扩散系数随应力比的变化规律与孙继成等[6]的结论类似。张伟平等[17]通过试验机加压和拧紧螺栓的方式给混凝土试件施加预压应力,盐雾箱加速氯离子侵蚀试验表明:混凝土表观氯离子扩散系数随着压力的增大而减小。Tran等[7]采用圆柱形混凝土试件测定预应力混凝土氯离子扩散系数,试验结果与孙继成等[6]的结论十分类似,随后他们应用格构离散模型分析混凝土中的氯离子扩散,但混凝土氯离子扩散系数的模拟值随着应力比的增大而不断增大,与试验结果不完全一致。在解析预测方面,大多基于弹性力学理论,适合应力比小于0.3的预应力混凝土。金浏等[18]和Du等[19]应用三相复合球模型分析了混凝土氯离子扩散系数随压应力的变化,但理论预测明显高于试验结果。Xu和Li[20]也应用类似的理论方法评价压应力对混凝土氯离子扩散系数的影响,发现随着应力比的增大,理论预测偏离试验结果。Wang等[21]应用多相复合球模型预测预应力混凝土氯离子扩散系数,当应力比小于0.3时,理论预测与试验结果基本一致,但当应力比大于0.3时,他们采用回归方法,将混凝土氯离子扩散系数表示成压力比的二次函数。表1总结了这些方法所采用的模型和适用范围。
从上述文献综述可以看出,与实验室试验相比,理论预测尚待完善,预测结果还不能完全与试验结果吻合。为此,在前人工作的基础上,本文通过引入临界毛细孔隙率来考虑混凝土中微裂纹的闭合、产生和扩展对预应力混凝土氯离子扩散的影响,提出经验模型,通过与试验结果比较,初步验证了该预测方法的有效性。
1 基本假设和三相复合圆模型
在压应力作用下,混凝土氯离子扩散系数的计算非常复杂。为简化分析,现作下列假设。1) 混凝土完全饱和,表明混凝土中的氯离子以扩散为主,不考虑迁移和对流效应。2) 混凝土毛细孔体积变形主要由弹性变形引起,不考虑塑性效应,这与塑性力学中的经典假设类似,毛细孔体积变形体现了混凝土的弹性性质,压应力减小毛细孔隙率,减缓氯离子扩散速率,混凝土氯离子扩散系数随着压应力的增大而减小。3) 混凝土内部微裂纹的闭合、产生和扩展通过临界毛细孔隙率来描述,即初始微裂纹闭合,毛细孔连通性降低,临界毛细孔隙率增大,新微裂纹产生和扩展,毛细孔连通性增加,临界毛细孔隙率减小。临界毛细孔隙率的概念源自渗流理论[22],已应用于水泥基材料传输性能分析[23-24],它定义为纯水泥浆试件两个平行面的毛细孔相互连通的最小孔隙率,一般与水灰比无关,可以通过计算机模拟获得[25]。混凝土加载前,由于水泥硬化过程中的干燥收缩,在水泥浆基体和界面上存在初始微裂纹[26],这些不连续的微裂纹能加速氯离子传输速率,由于目前通过试验还很难准确地表征这些微裂纹,如单位体积的裂纹密度和裂纹长度分布等,不能直接应用微观力学方法分析微裂纹对混凝土氯离子扩散系数的影响。为此,本文采用临界毛细孔隙率来量化微裂缝对氯离子扩散的影响。这些不连续的微裂纹可以连接相邻毛细孔,提高毛细孔的连通性,减小临界毛细孔隙率,增大混凝土氯离子扩散系数。当压应力较小时,与压应力方向垂直的部分微裂纹闭合,降低毛细孔的连通性,提高临界毛细孔隙率,减小混凝土氯离子扩散系数。当压应力较大时,尽管与压应力方向垂直的微裂纹大多闭合,但与压应力方向平行的微裂纹开始延伸,并且相邻微裂纹相互相通,总体上提高毛细孔的连通性,减小临界毛细孔隙率,增大混凝土氯离子扩散系数。尽管目前还无法直接通过试验或理论分析来确定压应力与临界毛细孔隙率之间的关系,但是可以通过所测得的混凝土氯离子扩散系数来间接地建立临界毛细孔隙率与压应力之间的现象学模型。综合假设2)和假设3)可以看出,当压应力较小时,毛细孔隙率降低和临界毛细孔隙率提高都使得混凝土氯离子扩散系数随着压力的增大而减小。随着压应力的增大,毛细孔隙率和临界毛细孔隙率均降低,当前者效应大于后者效应时,混凝土氯离子扩散系数继续减小;当前者效应等于后者效应时,混凝土氯离子扩散系数达到最小值;当前者效应小于后者效应时,混凝土氯离子扩散系数随着压力的增大而增大,这与孙继成等[6]、熊建波等[16]和Tran等[7]的试验结果一致。因此,临界毛细孔隙率可以用来表征混凝土的非线性性质。4)骨料按球形颗粒处理,在细观水平上把混凝土模拟成由骨料、界面和水泥浆基体所组成的三相复合材料[27-30]。
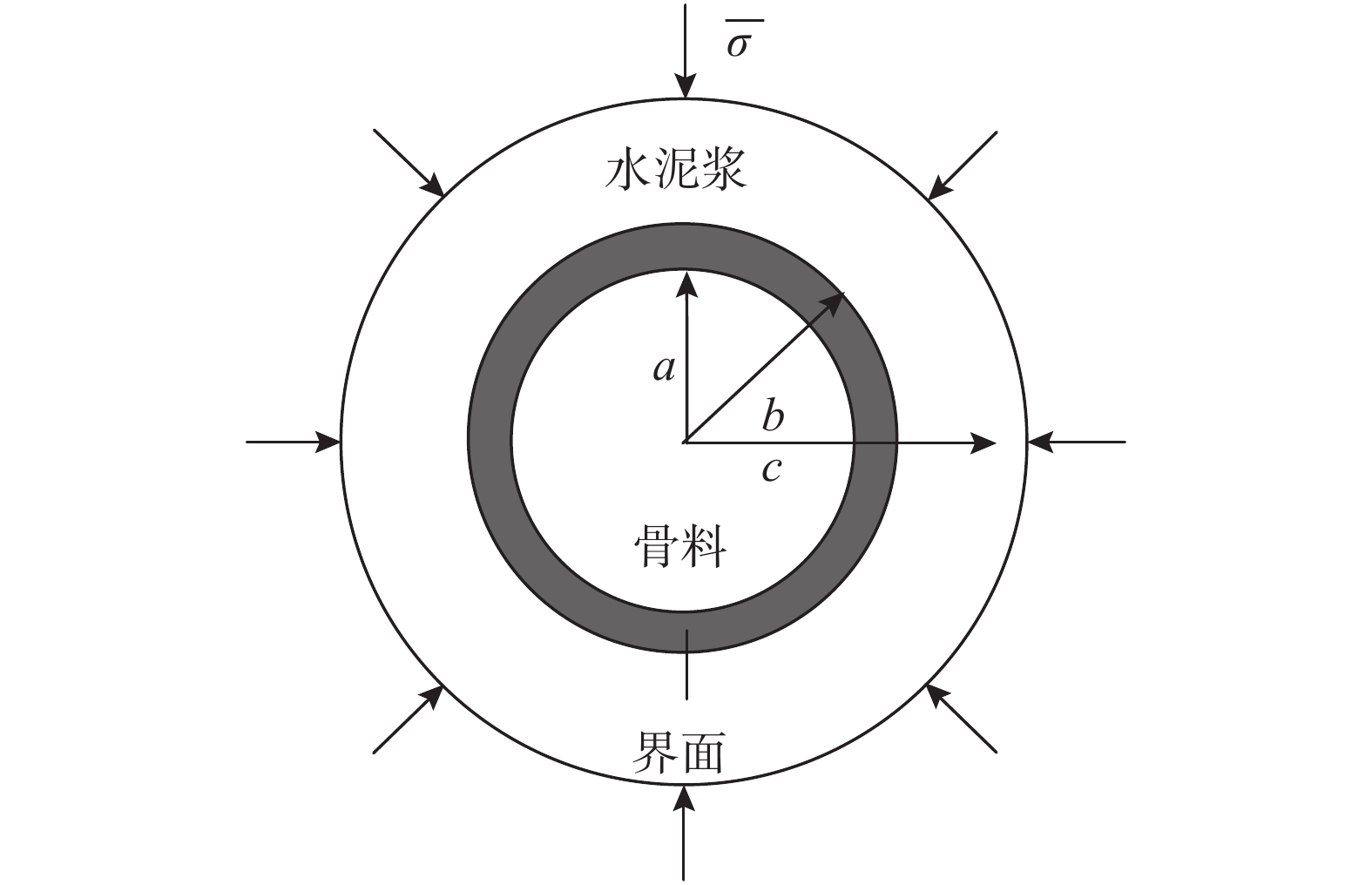
根据假设4),三相混凝土可用图1所示的复合圆表示。球形骨料关于骨料个数的概率密度函数
p1(D) 为[31]:p1(D)=nDmin (1) 式中:D为球形骨料直径;Dmin和Dmax分别为最小和最大骨料直径;n=3.0和n=2.5分别对应等体积级配和富勒级配骨料,它们代表骨料级配的上限、下限。
当用一个随机平面截取混凝土试件时,截面上的骨料呈圆形,根据体视学理论,圆形骨料的平均直径
\langle d\rangle 和直径平方的均值\langle {d^2}\rangle 为[31]:\langle d\rangle = \dfrac{{\pi (n - 1)({D_{\min }}D_{\max }^{n - 1} - D_{\min }^{n - 1}{D_{\max }})}}{{4(n - 2)(D_{\max }^{n - 1} - D_{\min }^{n - 1})}} (2) \langle {d^2}\rangle = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{2(D_{\min }^{n - 1}D_{\max }^2 - D_{\min }^2D_{\max }^{n - 1})}}{{D_{\max }^{n - 1} - D_{\min }^{n - 1}}},n = 2.5} \\ {\dfrac{{4D_{\min }^2D_{\max }^2(\ln {D_{\max }} - \ln {D_{\min }})}}{{3(D_{\max }^2 - D_{\min }^2)}},n = 3} \end{array}} \right. (3) 如果混凝土在施加预应力前骨料面积百分数为
{f^{\rm{agg}}} ,则界面面积百分数为[31]:{f^{\rm{itz}}} = (1 - {f^{\rm{agg}}})\{ 1 - \exp [ - 4{f^{\rm{agg}}}({t_1}h + {t_2}{h^2})/\langle {d^2}\rangle ]\} (4) 式中:h为界面厚度;t1和t2定义为:
{t_1} = \frac{{\langle d\rangle }}{{1 - {f^{\rm{agg}}}}} (5) {t_2} = \frac{1}{{1 - {f^{\rm{agg}}}}} + \frac{{{f^{\rm{agg}}}{{\langle d\rangle }^2}}}{{{{(1 - {f^{\rm{agg}}})}^2}\langle {d^2}\rangle }} (6) 水泥浆基体的面积百分数为:
{f^{\rm{cp}}} = 1 - {f^{\rm{agg}}} - {f^{\rm{itz}}} (7) 由图1可知:
{a^2}/{c^2} = {f^{\rm{agg}}} (8) {b^2}/{c^2} = {f^{\rm{agg}}} + {f^{\rm{itz}}} (9) 这样完全确定了三相复合圆模型的相对几何尺寸。
由于水泥颗粒在骨料表面附近分布的边壁效应,界面层上的初始水泥颗粒分布呈非均匀状态,设水化初期水泥面积率分布为[32]:
{f_{\rm c}}(r) = \left\{ \begin{aligned} & f_{\rm c}^{\rm{cp}}\sum\limits_{j = 1}^4 {\frac{{{q_j}{{(r - a)}^j}}}{{{q_0}{{(b - a)}^j}}},\;\;a \leqslant r < b} \\& f_{\rm c}^{\rm{cp}},\;\;\qquad\qquad\qquad b \leqslant r \leqslant c \end{aligned}\right. (10) 式中:
f_{\rm c}^{\rm{cp}} 为水泥浆基体的水泥面积率;r 为离骨料中心的距离;{q_0} 为{q_j} (j = 1,{\text{ }}2,{\text{ }}3,{\text{ }}4) 之和。根据Crumbie[33]的试验结果,通过拟合得到{q_j} 与混凝土水灰比w/c 的关系为:\begin{split} &{q_1} = 4.670 - 5.228(w/c) ,\\ & {q_2} = - 10.569 + 12.700(w/c) ,\\ & {q_3} = 9.950 - 12.195(w/c) ,\\ & {q_4} = - 3.397 + 4.195(w/c) \end{split} (11) 对图1的复合圆模型,由实际水泥含量等于界面水泥含量和水泥浆基体水泥含量之和可得:
f_{\rm c}^{\rm{cp}} = \frac{{({c^2} - {a^2})/[1 + {\rho _{\rm c}}(w/c)]}}{{({c^2} - {b^2}) + 2(b - a)\displaystyle\sum\limits_{j = 1}^4 {\frac{{{q_j}[a + (j + 1)b]}}{{{q_0}(j + 1)(j + 2)}}} }} (12) 这样,界面的平均水泥面积率为:
\begin{split} \bar f_{\rm c}^{\rm{itz}} =& \dfrac{1}{{\pi ({b^2} - {a^2})}}\int_a^b {2\pi r{f_{\rm c}}(r){\rm d}r} = \\ & \dfrac{{2f_{\rm c}^{\rm{cp}}}}{{a + b}} \cdot \displaystyle\sum\limits_{j = 1}^4 {\frac{{{q_j}[(j + 1)b + a]}}{{{q_0}(j + 1)(j + 2)}}} \end{split} (13) 水泥浆基体的水灰比
{(w/c)^{\rm{cp}}} 和界面的平均水灰比{(w/c)^{\rm{itz}}} 为:{(w/c)^{\rm{cp}}} = \frac{{1 - f_{\rm c}^{\rm{cp}}}}{{{\rho _{\rm c}}f_{\rm c}^{\rm{cp}}}} (14) {(w/c)^{\rm{itz}}} = \frac{{1 - \bar f_{\rm c}^{\rm{itz}}}}{{{\rho _{\rm c}}\bar f_{\rm c}^{\rm{itz}}}} (15) 有了水灰比,就可以根据Lam等[34]的水化度模型计算任一时刻水泥浆基体和界面的水化度,进而获得它们的毛细孔隙率[35]。
2 骨料、界面和水泥浆基体体积应变
混凝土安全壳施加双向预应力后,混凝土在两个方向上的压应力分别为
{\sigma _1} 和{\sigma _2} ,如图2(a)所示,将{\sigma _1} 和{\sigma _2} 分解为双向等压和纯剪两种情况,分别如图2(b)和图2(c)所示,其中\bar \sigma = ({\sigma _1} + {\sigma _2})/2 ,\tilde \sigma = ({\sigma _1} - {\sigma _2})/2 ,由于混凝土在纯剪作用下,其弹性体积应变为零,只需考虑图2(b)的双向等压情况。对于图1所示的三相轴对称混凝土,设外边界
r = c 处的径向位移和径向应力分别为u(c) 和\sigma (c) (=- \bar \sigma ),如果混凝土体积应变为\varepsilon _{\rm{v}}^{\rm con} ,当把混凝土看成均匀材料时,u(c) 和\sigma (c) 可以用\varepsilon _{\rm{v}}^{\rm con} 表示为:u(c)/c = \sqrt {1 + \varepsilon _{\rm{v}}^{\rm con}} - 1 (16) \sigma (c) = {K^{\rm con}}\varepsilon _{\rm{v}}^{\rm con} (17) 式中,
{K^{\rm con}} 为混凝土平面应力体积模量,它与混凝土弹性模量{E^{\rm con}} 和泊松比{\mu ^{\rm con}} 的关系为:{K^{\rm con}} = \frac{{{E^{\rm con}}}}{{2(1 - {\mu ^{\rm con}})}} (18) 在下面的分析中,
{K^{\rm{cp}}} 和{G^{\rm{cp}}} 分别为水泥浆基体的平面应力体积模量和剪切模量,{K^{\rm{itz}}} 和{G^{\rm{itz}}} 分别为界面的平面应力体积模量和剪切模量,并定义矩阵{{\boldsymbol{T}}^\alpha }(x,y) 为:{{\boldsymbol{T}}^\alpha }(x,y) = \left[ {\begin{matrix} {\dfrac{{{G^\alpha } + {K^\alpha }{{(y/x)}^2}}}{{{K^\alpha } + {G^\alpha }}}}&{\dfrac{{1 - {{(y/x)}^2}}}{{2({K^\alpha } + {G^\alpha })}}} \\ {\dfrac{{2{K^\alpha }{G^\alpha }[1 - {{(y/x)}^2}]}}{{{K^{\rm{cp}}} + {G^{\rm{cp}}}}}}&{\dfrac{{{K^\alpha } + {G^\alpha }{{(y/x)}^2}}}{{{K^\alpha } + {G^\alpha }}}} \end{matrix}} \right] (19) 当把混凝土看成三相复合材料时,由图1问题的轴对称性,水泥浆基体中的径向位移和径向应力分别为:
{u^{\rm{cp}}}(r) = {c_1}r + {c_2}{r^{ - 1}} (20) \sigma _r^{\rm{cp}}(r) = 2{c_1}{K^{\rm{cp}}} - 2{c_2}{G^{\rm{cp}}}{r^{ - 2}} (21) 式中,
{c_1} 和{c_2} 为待定系数。由条件式(16)和式(17)可得:\left\{ {\begin{aligned} {{c_1}} \\ {{c_2}} \end{aligned}} \right\} = \frac{1}{{2({K^{\rm{cp}}} + {G^{\rm{cp}}})}}\left[ {\begin{aligned} &\;\;\;\;{2{G^{\rm{cp}}}}\;\;\;\;1 \\ &{2{c^2}{K^{\rm{cp}}}}\;\;\;{ - {c^2}} \end{aligned}} \right]\left\{ {\begin{aligned} {u(c)/c} \\ {\sigma (c)} \end{aligned}} \right\} (22) 则
r = b 处的径向位移u(b) 和径向应力\sigma (b) 为:\begin{split} \left\{ {\begin{array}{*{20}{c}} {u(b)/b} \\ {\sigma (b)} \end{array}} \right\} = & \left[ {\begin{array}{*{20}{c}} 1&{{b^{ - 2}}} \\ {2{K^{\rm{cp}}}}&{ - 2{b^{ - 2}}{G^{\rm{cp}}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{c_1}} \\ {{c_2}} \end{array}} \right\}= \\ & {{\boldsymbol{T}}^{\rm{cp}}}(b,c)\left\{ {\begin{array}{*{20}{c}} {u(c)/c} \\ {\sigma (c)} \end{array}} \right\} \end{split} (23) 如果
r = a 处的径向位移和径向应力分别为u(a) 和\sigma (a) ,对图1的界面层进行类似分析有:\left\{ {\begin{array}{*{20}{c}} {u(a)/a} \\ {\sigma (a)} \end{array}} \right\} = {{\boldsymbol{T}}^{\rm{itz}}}(a,b)\left\{ {\begin{array}{*{20}{c}} {u(b)/b} \\ {\sigma (b)} \end{array}} \right\} (24) 结合式(23)和式(24)有:
\left\{ {\begin{array}{*{20}{c}} {u(a)/a} \\ {\sigma (a)} \end{array}} \right\} = {{\boldsymbol{T}}^{\rm{itz}}}(a,b){{\boldsymbol{T}}^{\rm{cp}}}(b,c)\left\{ {\begin{array}{*{20}{c}} {u(c)/c} \\ {\sigma (c)} \end{array}} \right\} (25) 骨料的体积应变为:
\begin{aligned} \varepsilon _{\rm{v}}^{\rm{agg}} =& \frac{{\pi {{[a + u(a)]}^2} - \pi {a^2}}}{{\pi {a^2}}}= {[1 + u(a)/a]^2} - 1 \end{aligned} (26) 类似地,界面和水泥浆基体的体积应变为:
\begin{split} \varepsilon _{\rm{v}}^{\rm{itz}} =& (1 + {f^{\rm{agg}}}/{f^{\rm{itz}}})\{ {[1 + u(b)/b]^2} - 1\} - \\ & {f^{\rm{agg}}}/{f^{\rm{itz}}}\{ {[1 + u(a)/a]^2} - 1\} \end{split} (27) \begin{split} \varepsilon _{\rm{v}}^{\rm{cp}} =& [1 + ({f^{\rm{agg}}} + {f^{\rm{itz}}})/{f^{\rm{cp}}}]\{ {[1 + u(c)/c]^2} - 1\} - \\ &({f^{\rm{agg}}} + {f^{\rm{itz}}})/{f^{\rm{cp}}}\{ {[1 + u(b)/b]^2} - 1\} \end{split} (28) 这样,由式(8)、式(9)、式(16)、式(17)、式(23)、式(25)~式(28)可获得骨料、界面和水泥浆基体的体积应变。
3 水泥浆基体和界面的毛细孔隙率
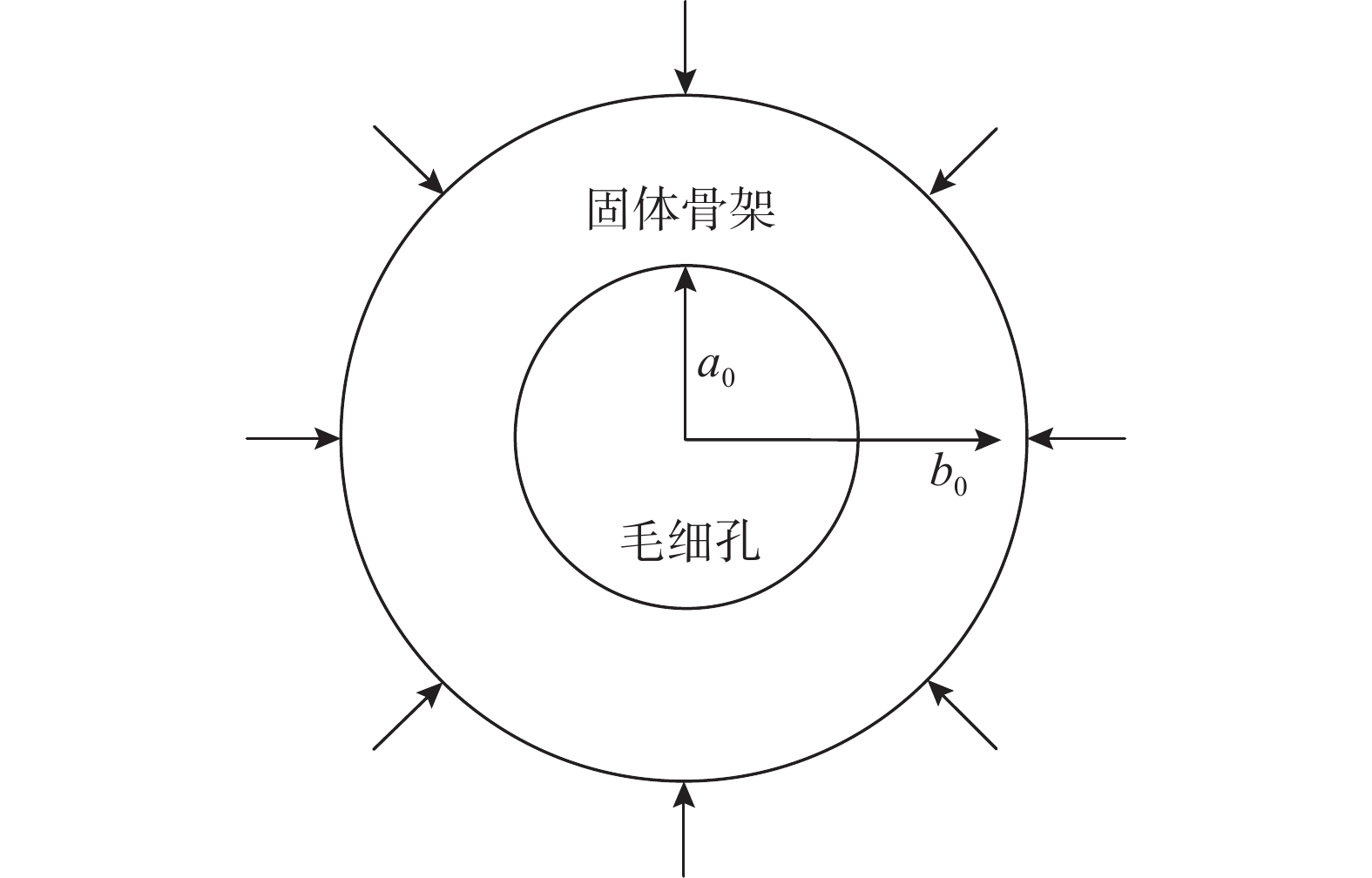
水泥浆基体和界面都是由水化产物和未水化水泥所形成的固体骨架和毛细孔两部分组成,在预应力作用下,毛细孔隙率减小,减缓了氯离子的扩散速率。水泥浆基体用两相复合圆模型来表示,如图3所示,半径为
{a_0} 的中心圆为饱和毛细孔,内半径为{a_0} 、外半径为{b_0} 的圆环为水泥浆固体骨架。如果受压前水泥浆基体的毛细孔隙率为f_0^{\rm{cp}} ,则{a_0} 和{b_0} 之间具有以下关系:\frac{{a_0^2}}{{b_0^2}} = f_0^{\rm{cp}} (29) 根据式(28)给出的水泥浆基体的体积应变,可以求得两相水泥浆基体复合圆外边界的径向位移
u({b_0}) 和径向应力\sigma ({b_0}) :u({b_0})/{b_0} = \sqrt {1 + \varepsilon _{\rm{v}}^{\rm{cp}}} - 1 (30) \sigma ({b_0}) = {K^{\rm{cp}}}\varepsilon _{\rm{v}}^{\rm{cp}} (31) 设水泥浆固体骨架的平面应力体积模量和剪切模量分别为
{K^{\rm{ss}}} 和{G^{\rm{ss}}} ,类似于式(23)的推导,r = {a_0} 处的径向位移u({a_0}) 和径向应力\sigma ({a_0}) 为:\left\{ {\begin{array}{*{20}{c}} {u({a_0})/{a_0}} \\ {\sigma ({a_0})} \end{array}} \right\} = {{\boldsymbol{T}}^{\rm{ss}}}({a_0},{b_0})\left\{ {\begin{array}{*{20}{c}} {u({b_0})/{b_0}} \\ {\sigma ({b_0})} \end{array}} \right\} (32) 这样,水泥浆基体受力后的毛细孔隙率
f_\sigma ^{\rm{cp}} 为:\begin{split} f_\sigma ^{\rm{cp}} =& \frac{{{{[{a_0} + u({a_0})]}^2}}}{{{{[{b_0} + u({b_0})]}^2}}} = \\ &\frac{{f_0^{\rm{cp}}}}{{1 + \varepsilon _{\rm{v}}^{\rm{cp}}}} \cdot \Bigg[1 + {\boldsymbol{T}}_{11}^{\rm{ss}}({a_0},{b_0})\left( {\sqrt {1 + \varepsilon _{\rm{v}}^{\rm{cp}}} - 1} \right) +\Bigg.\\ &\Bigg.{\boldsymbol{T}}_{12}^{\rm{ss}}({a_0},{b_0}){K^{\rm{cp}}}\varepsilon _{\rm{v}}^{\rm{cp}}\Bigg]^2 \end{split} (33) 对界面也可构造出类似于图3的两相模型,内半径为
{a_1} ,外半径为{b_1} ,且与受压前界面的毛细孔隙率为f_0^{\rm{itz}} 具有以下关系:\frac{{a_1^2}}{{b_1^2}} = f_0^{\rm{itz}} (34) 类似于水泥浆基体的分析,可得到界面受力后的毛细孔隙率
f_\sigma ^{\rm{itz}} 为:\begin{split} f_\sigma ^{\rm{itz}} =& \frac{{f_0^{\rm{itz}}}}{{1 + \varepsilon _{\rm{v}}^{\rm{itz}}}} \cdot \Bigg[1 + {\boldsymbol{T}}_{11}^{\rm{ss}}({a_1},{b_1})\left(\sqrt {1 + \varepsilon _{\rm{v}}^{\rm{itz}}} - 1\right) +\Bigg.\\ &\Bigg. {\boldsymbol{T}}_{12}^{\rm{ss}}({a_1},{b_1}){K^{\rm{itz}}}\varepsilon _{\rm{v}}^{\rm{itz}}\Bigg]^2 \end{split} (35) 4 混凝土氯离子扩散系数
基于计算机模拟,Garboczi和Bentz[23]在重构的水泥浆微观结构上模拟氯离子扩散,根据模拟结果提出水泥浆基体氯离子扩散系数公式:
\begin{split} D_0^{\rm{cp}} =& {D^{\rm{ps}}}[0.001 + 0.07f_0^{\rm{cp}} +\\ & 1.8H(f_0^{\rm{cp}} - {f_{0,{\rm c}}}) \times {(f_0^{\rm{cp}} - {f_{0,{\rm c}}})^2}] \end{split} (36) 式中:
{D^{\rm{ps}}} 为毛细孔溶液氯离子扩散系数;{f_{0,{\rm c}}} 为临界毛细孔隙率;H(f_0^{\rm{cp}} - {f_{0,{\rm c}}}) 为阶跃函数,定义为:H(f_0^{\rm{cp}} - {f_{0,{\rm c}}}) = \left\{ \begin{aligned} & {1,{\text{ }}f_0^{\rm{cp}} > {f_{0,{\rm c}}}} \\& {0.5,{\text{ }}f_0^{\rm{cp}} = {f_{0,{\rm c}}}} \\& {0,{\text{ }}f_0^{\rm{cp}} < {f_{0,{\rm c}}}} \end{aligned}\right. (37) 同时,他们给出临界毛细孔隙率为0.18。后来,随着计算机模拟精度的提高,Garboczi和Bentz[25]将临界毛细孔隙率修正为0.12。对于预应力混凝土,当预应力较小时,混凝土中与预应力方向垂直的部分初始微裂纹闭合,孔隙连通性降低,临界毛细孔隙率增大,而当预应力较大时,混凝土中与预应力平行的微裂纹延伸,并产生新的微裂纹,毛细孔的连通性提高,临界毛细孔隙率减小,因此,临界毛细孔隙率是预应力的函数。这样,预应力水泥浆基体氯离子扩散系数可以写成:
\begin{split} D_\sigma ^{\rm{cp}} =& {D^{\rm{ps}}}[0.001 + 0.07f_\sigma ^{\rm{cp}} +\\ & 1.8H(f_\sigma ^{\rm{cp}} - {f_{\sigma ,{\rm c}}}) \times {(f_\sigma ^{\rm{cp}} - {f_{\sigma ,{\rm c}}})^2}] \end{split} (38) 式中,fσ,c为预应力作用下临界毛细孔隙率。对界面进行类似分析,分别得到无应力作用界面氯离子扩散系数
D_0^{\rm{itz}} 和预应力作用界面氯离子扩散系数D_\sigma ^{\rm{itz}} :\begin{split} D_0^{\rm{itz}} = &{D^{\rm{ps}}}[0.001 + 0.07f_0^{\rm{itz}} +\\ & 1.8H(f_0^{\rm{itz}} - {f_{0,{\rm c}}}) \times {(f_0^{\rm{itz}} - {f_{0,{\rm c}}})^2}] \end{split} (39) \begin{split} D_\sigma ^{\rm{itz}} =& {D^{\rm{ps}}}[0.001 + 0.07f_\sigma ^{\rm{itz}} +\\ &1.8H(f_\sigma ^{\rm{itz}} - {f_{\sigma ,{\rm c}}}) \times {(f_\sigma ^{\rm{itz}} - {f_{\sigma ,{\rm c}}})^2}] \end{split} (40) 对于三相复合圆模型,Zheng和Zhou[31]获得了普通混凝土氯离子扩散系数的解析解,对他们的结果稍作简化有:
D_0^{\rm con} = D_0^{\rm{cp}} - \frac{{2[2{f^{\rm{agg}}} + (1 - {q_0}){f^{\rm{itz}}}]D_0^{\rm{cp}}}}{{2(1 + {f^{\rm{agg}}}) - (1 - {q_0}){f^{\rm{itz}}}{f^{\rm{cp}}}/(1 - {f^{\rm{cp}}})}} (41) 式中,
{q_0} 定义为:{q_0} = D_0^{\rm{itz}}/D_0^{\rm{cp}} (42) 当混凝土受预应力作用时,骨料、界面和水泥浆基体的面积百分数分别为
f_\sigma ^{\rm{agg}} 、f_\sigma ^{\rm{itz}} 和f_\sigma ^{\rm{cp}} ,根据上面所求得的各相体积应变有:f_\sigma ^{\rm{agg}} = {f^{\rm{agg}}}(1 + \varepsilon _{\rm{v}}^{\rm{agg}})/(1 + \varepsilon _{\rm{v}}^{\rm con}) (43) f_\sigma ^{\rm{itz}} = {f^{\rm{itz}}}(1 + \varepsilon _{\rm{v}}^{\rm{itz}})/(1 + \varepsilon _{\rm{v}}^{\rm con}) (44) f_\sigma ^{\rm{cp}} = {f^{\rm{cp}}}(1 + \varepsilon _{\rm{v}}^{\rm{cp}})/(1 + \varepsilon _{\rm{v}}^{\rm con}) (45) 则预应力混凝土氯离子扩散系数为:
D_\sigma ^{\rm con} = D_\sigma ^{\rm{cp}} - \frac{{2[2f_\sigma ^{\rm{agg}} + (1 - {q_\sigma })f_\sigma ^{\rm{itz}}]D_\sigma ^{\rm{cp}}}}{{2(1 + f_\sigma ^{\rm{agg}}) - (1 - {q_\sigma })f_\sigma ^{\rm{itz}}f_\sigma ^{\rm{cp}}/(1 - f_\sigma ^{\rm{cp}})}} (46) 式中,
{q_\sigma } 定义为:{q_\sigma } = D_\sigma ^{\rm{itz}}/D_\sigma ^{\rm{cp}} (47) 定义氯离子扩散系数比
\eta 为:\eta = \frac{{D_\sigma ^{\rm con}}}{{D_0^{\rm con}}} (48) \eta 表示预应力对混凝土氯离子扩散系数的影响,且从式(36)、式(38)~式(42)、式(46)~式(48)可以看出,该比值与毛细孔溶液氯离子扩散系数{D^{\rm{ps}}} 无关。5 预应力作用下临界毛细孔隙率
由式(38)、 式(40)、式(46)和式(48)可见:计算比值
\eta 的关键是确定预应力作用下临界毛细孔隙率与预应力的关系。考虑到目前应用理论方法确定这一关系还非常困难,本文采用试验校正方法。为了确定fσ,c的形式,主要考虑如下几点:1)所包含的参数尽可能少,便于试验校正;2)当预压应力\bar \sigma 为零时,fσ,c等于f0,c;3)现有的试验结果表明[6, 16],对于单向受压混凝土,由于混凝土中存在初始微裂纹,当应力比小于0.3时,即\bar \sigma /{f_{\rm c}} 小于0.15时,混凝土基本处于弹性状态,预应力不仅减小毛细孔隙率,而且使得与预应力方向垂直的部分初始微裂纹闭合,毛细孔隙率的连通性降低,fσ,c随\bar \sigma /{f_{\rm c}} 的增大而增大;4)当应力比大于0.3时,即\bar \sigma /{f_{\rm c}} 大于0.15时,混凝土开始呈现一定的非线性,平行于预应力方向的微裂纹延伸,并产生新的微裂纹,毛细孔的连通性增加,fσ,c随\bar \sigma /{f_{\rm c}} 增大而减小;5)在\bar \sigma /{f_c} = 0.15 处,fσ,c及其他的一阶导数保持连续。经过不断的尝试,设fσ,c具有以下形式:{f_{\sigma ,{\rm c}}} = \left\{ {\begin{aligned} &{{f_{0,{\rm c}}}{{\{ A}} - ({{A}} - 1){{[g(\bar \sigma )]}^{{A}}}\} ,{\text{ }}\bar \sigma \leqslant 0.15{f_{\rm c}}} \\ & {{f_{0,{\rm c}}}\{ {{A}} - {{B}}({f_{\rm c}} - 30){{[ - g(\bar \sigma )]}^{{A}}}\} ,{\text{ }}\bar \sigma \geqslant 0.15{f_{\rm c}}} \end{aligned}} \right. (49) 式中:
{f_{\rm c}} /MPa为混凝土抗压强度;A和B为系数;函数g(\bar \sigma ) 定义为:g(\bar \sigma ) = 1 - \bar \sigma /(0.15{f_{\rm c}}) (50) 在以下的计算中,由于界面厚度一般在0.01 mm和0.05 mm之间,取其均值,即
h =0.03 mm[31,32]。水泥浆固体骨架、水泥浆基体和界面的弹性常数按文[36]方法进行计算。为了确定A和B值,选择孙继成等[6]的试验结果进行校正。在他们的试验中,第一组混凝土水灰比为0.42,每立方米混凝土中粗骨料和砂子质量分别1075 kg和810 kg,28 d的抗压强度为35.6 MPa;第二组混凝土水灰比为0.40,每立方米混凝土中粗骨料和砂子质量分别1069 kg和826 kg,28 d的抗压强度为44.3 MPa。用螺纹杆对混凝土试件施加压力,当应力比为0.1、0.3、0.5和0.7时,通过NEL法测得混凝土氯离子扩散系数,可算得氯离子扩散系数比,如图4所示。通过与试验数据拟合可得: A=1.14,B=0.00864。这样,应用上面所提出的预测方法获得预应力混凝土氯离子扩散系数比,如图4所示,当水灰比为0.42和0.40时,理论预测与试验结果之间的相关系数分别为0.993和0.977。
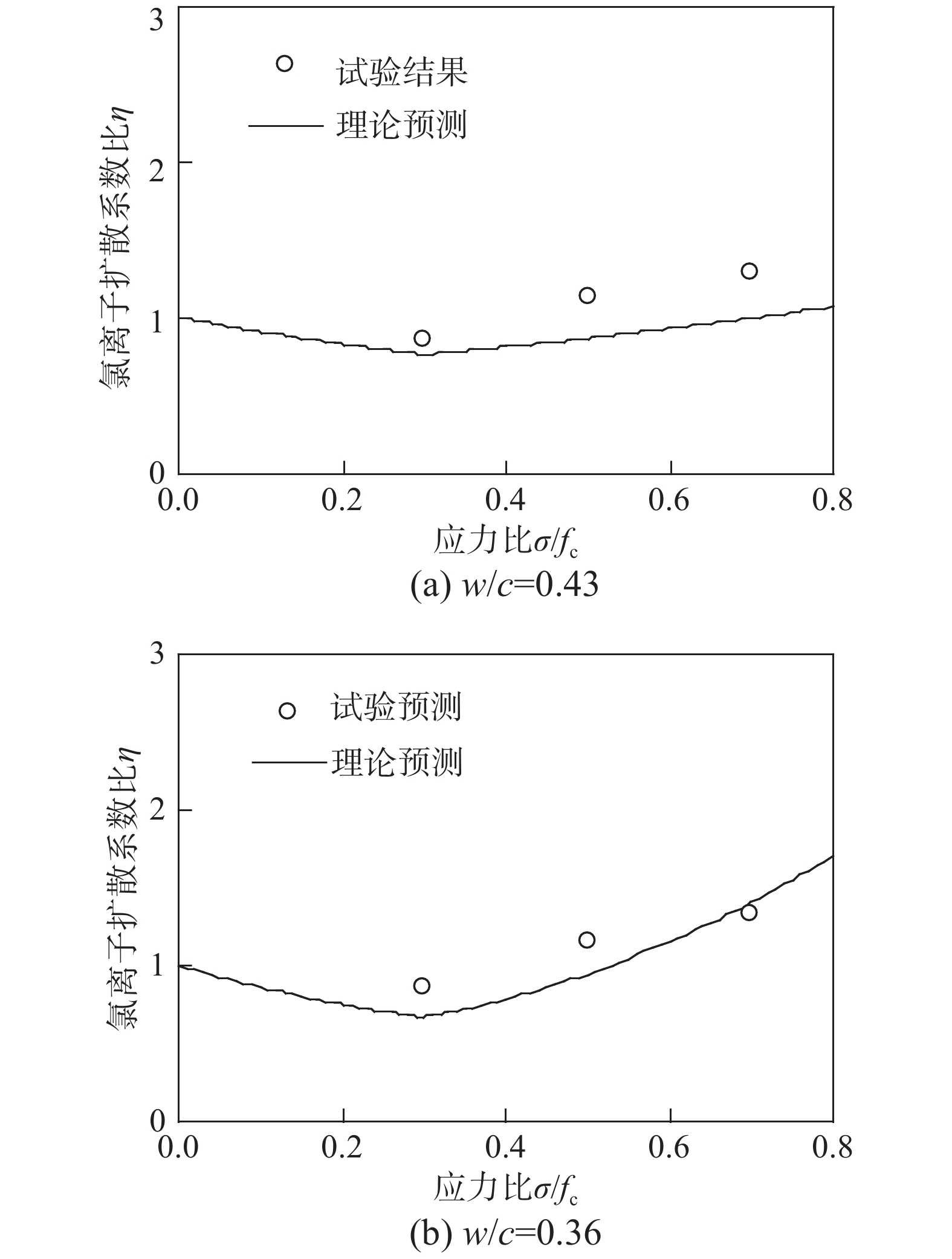
为验证上述预测方法的有效性,先考虑Tran等[7]试验结果。在他们的试验中,第一组混凝土的水灰比为0.43,每立方米混凝土中粗骨料和砂子质量分别1231 kg和695 kg,28 d的抗压强度为41.7 MPa,第二组混凝土的水灰比为0.36,每立方米混凝土中粗骨料和砂子质量分别1197 kg和626 kg,28 d的抗压强度为52.4 MPa。当压力比为0.3、0.5和0.7时,预应力混凝土氯离子扩散系数比的试验结果与理论预测如图5所示,从该图可以看出,理论预测与试验结果基本吻合,当水灰比为0.43和0.36时,它们之间的相关系数分别为0.972和0.962。
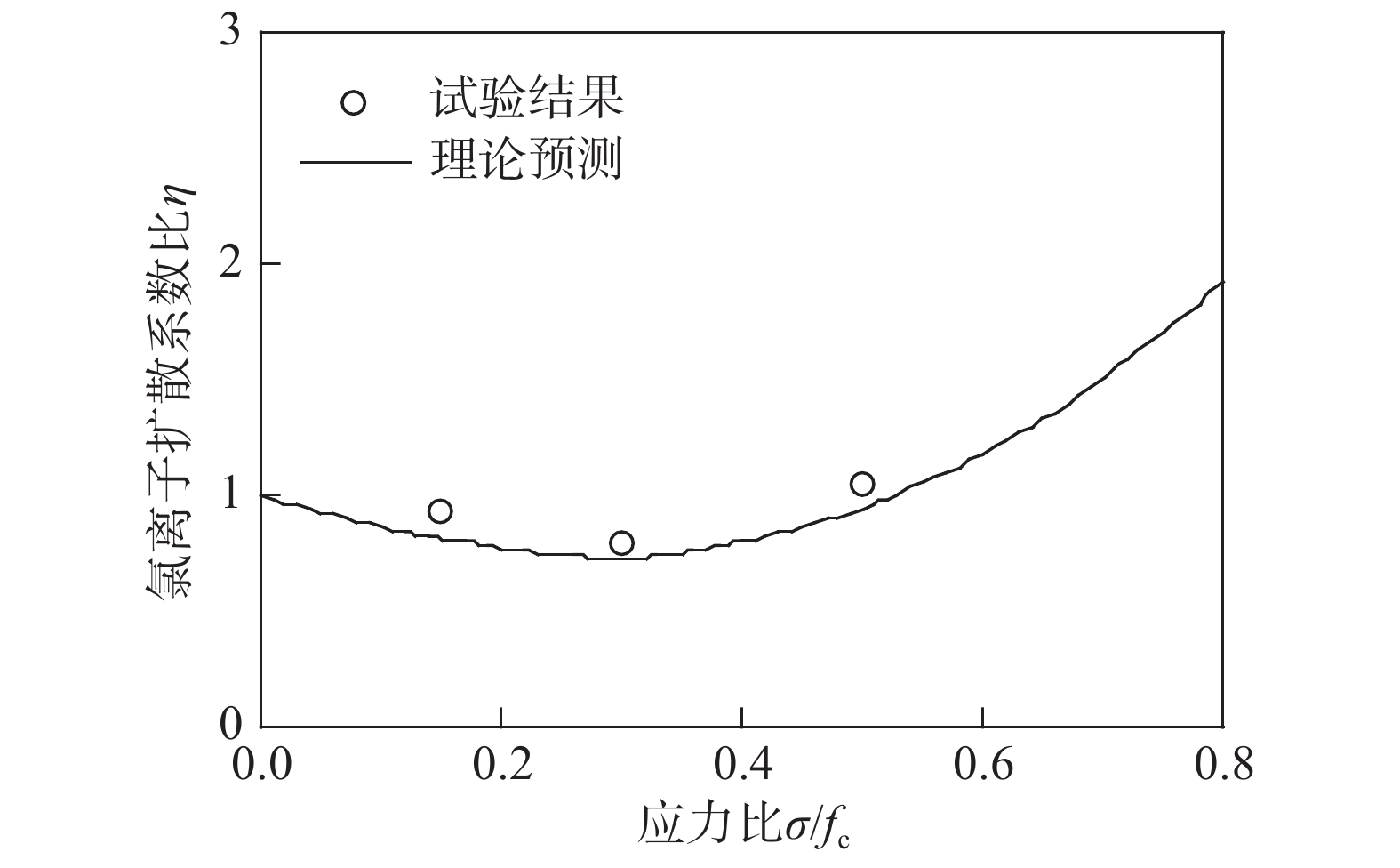
再考虑熊建波等[16]的试验结果。在他们的试验中,水胶比为0.35,粉煤灰掺量为20%,矿粉掺量为40%,每立方米混凝土中粗骨料和砂子质量分别为1084 kg和723 kg。当压力比为0.15、0.30和0.50时,预应力混凝土氯离子扩散系数比的试验结果和理论预测如图6所示,从该图可以看出,理论预测与试验结果良好吻合,它们之间的相关系数为0.981。从上述两个比较算例可以看出,本文预测方法的有效性得到试验的初步验证。
6 结论
本文基于弹性力学理论,建立了混凝土预应力与毛细孔隙率之间的关系,再通过分析试验数据,提出了临界毛细孔隙率的经验公式,最后给出了预应力混凝土氯离子扩散系数比的计算方法。理论分析和数值比较得到以下主要结论:
(1)以压力为主要变量,将三相复合材料理论分析与试验校正相结合,提出了预应力混凝土氯离子扩散系数的预测方法,在这个方法中,不仅考虑了毛细孔的弹性体积变形,而且还通过临界毛细孔隙率考虑了内部微裂纹的影响,适合于压力比小于0.7的混凝土。
(2)基于试验结果和三相复合圆模型,获得了水泥浆基体水灰比和界面平均水灰比。
(3)通过试验现象分析和试验数据校正,提出了临界毛细孔隙率的经验公式。
-
[1] 邢国华, 武名阳, 常召群, 等. 锈蚀预应力混凝土梁承载力及破坏模式研究[J]. 工程力学, 2020, 37(7): 177 − 188. doi: 10.6052/j.issn.1000-4750.2019.08.0503 Xing Guohua, Wu Mingyang, Chang Zhaoqun, et al. Load bearing capacity and failure mode of corroded prestressed concrete beams [J]. Engineering Mechanics, 2020, 37(7): 177 − 188. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.08.0503
[2] 金浏, 杜修力, 李悦. 氯离子在饱和混凝土裂缝中的扩散系数分析[J]. 工程力学, 2016, 33(5): 50 − 56, 73. doi: 10.6052/j.issn.1000-4750.2014.12.1008 Jin Liu, Du Xiuli, Li Yue. Study on chloride diffusivity coefficient in cracks within saturated concrete [J]. Engineering Mechanics, 2016, 33(5): 50 − 56, 73. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.12.1008
[3] 林刚, 向志海, 刘应华, 等. 置于氯盐环境中混凝土结构钢筋起锈时间预测[J]. 工程力学, 2010, 27(9): 147 − 153. Lin Gang, Xiang Zhihai, Liu Yinghua, et al. Initiation time prediction of reinforcement corrosion in concrete structures exposed to chloride environment [J]. Engineering Mechanics, 2010, 27(9): 147 − 153. (in Chinese)
[4] 罗大明, 牛荻涛, 苏丽. 荷载与环境共同作用下混凝土耐久性研究进展[J]. 工程力学, 2019, 36(1): 1 − 14, 43. doi: 10.6052/j.issn.1000-4750.2018.08.ST11 Luo Daming, Niu Ditao, Su Li. Research progress on durability of stressed concrete under environmental actions [J]. Engineering Mechanics, 2019, 36(1): 1 − 14, 43. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.08.ST11
[5] 金松, 李鑫波, 贡金鑫. 严重事故下核电厂安全壳结构概率性能评价[J]. 工程力学, 2021, 38(6): 103 − 112. doi: 10.6052/j.issn.1000-4750.2020.07.0437 Jin Song, Li Xinbo, Gong Jinxin. Probabilistic performance evaluation of nuclear containment structure subjected to severe accidents [J]. Engineering Mechanics, 2021, 38(6): 103 − 112. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.07.0437
[6] 孙继成, 姚燕, 王玲, 等. 应力作用下混凝土的氯离子渗透性[J]. 低温建筑技术, 2015, 33(3): 1 − 3. Sun Jicheng, Yao Yan, Wang Ling, et al. Permeability of chloride ions in concrete under stress [J]. Low Temperature Building Technology, 2015, 33(3): 1 − 3. (in Chinese)
[7] Tran T T, Pham D T, Vu M N, et al. Relation between water permeability and chloride diffusivity of concrete under compressive stress: experimental investigation and mesoscale lattice modelling [J]. Construction and Building Materials, 2021, 267: 121164. doi: 10.1016/j.conbuildmat.2020.121164
[8] Wang H L, Chen Z W, Zhang J, et al. Numerical scheme for predicting chloride diffusivity of concrete [J]. Journal of Materials in Civil Engineering, 2021, 33(9): 04021237-1 − 04021237-9.
[9] Zheng J J, Zhang J, Zhou X Z, et al. Numerical method for predicting Chloride diffusivity of mature cement paste [J]. Journal of Materials in Civil Engineering, 2019, 31(6): 04019080-1 − 04019080-12.
[10] 周新刚, 李克非, 陈肇元. 氯离子在混凝土中扩散传输的有限体积法模拟分析[J]. 工程力学, 2013, 30(7): 34 − 39. doi: 10.6052/j.issn.1000-4750.2012.03.0153 Zhou Xingang, Li Kefei, Chen Zhaoyuan. Simulation analysis of chloride penetration in concrete with finite volume method [J]. Engineering Mechanics, 2013, 30(7): 34 − 39. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.03.0153
[11] 余波, 凌干展, 范志宏, 等. 基于集中浓度矩阵和精细积分法的氯离子时变扩散模型[J]. 工程力学, 2021, 38(1): 174 − 182, 204. doi: 10.6052/j.issn.1000-4750.2020.03.0153 Yu Bo, Ling Ganzhan, Fan Zhihong, et al. Time- dependent chloride diffusion model based on lumped concentration matrix and precise time-integration method [J]. Engineering Mechanics, 2021, 38(1): 174 − 182, 204. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.03.0153
[12] 蔡健, 魏沐杨, 罗赤宇, 等. 弯曲荷载与氯盐侵蚀共同作用下的预应力混凝土梁耐久性能研究[J]. 工程力学, 2018, 35(7): 208 − 218, 242. doi: 10.6052/j.issn.1000-4750.2017.03.0256 Cai Jian, Wei Muyang, Luo Chiyu, et al. Durability of prestressed concrete beams under simultaneous flexural load and chloride erosion [J]. Engineering Mechanics, 2018, 35(7): 208 − 218, 242. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.03.0256
[13] 金浏, 杜修力, 张仁波. 荷载作用下饱和水泥浆体中氯离子扩散性能研究[J]. 工程力学, 2015, 32(6): 33 − 40. doi: 10.6052/j.issn.1000-4750.2013.12.1163 Jin Liu, Du Xiuli, Zhang Renbo. Chloride diffusivity in saturated cement paste subjected to external loadings [J]. Engineering Mechanics, 2015, 32(6): 33 − 40. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.12.1163
[14] Lu X Y. Application of the Nernst-Einstein equation to concrete [J]. Cement and Concrete Research, 1997, 27(2): 293 − 302. doi: 10.1016/S0008-8846(96)00200-1
[15] 袁承斌, 张德峰, 刘荣桂, 等. 不同应力状态下混凝土抗氯离子侵蚀的研究[J]. 河海大学学报(自然科学版), 2003, 31(1): 50 − 54. Yuan Chengbin, Zhang Defeng, Liu Ronggui, et al. Diffusivity of chloride in concrete in different stress states [J]. Journal of Hohai University (Natural Sciences), 2003, 31(1): 50 − 54. (in Chinese)
[16] 熊建波, 王胜年, 黎鹏平. 荷载与氯盐共同作用下海港工程混凝土耐久性研究[J]. 混凝土, 2016(4): 4 − 8. doi: 10.3969/j.issn.1002-3550.2016.04.002 Xiong Jianbo, Wang Shengnian, Li Pengping. Study on the durability of concrete structures under the combined action of load and chloride salts of harbor engineering [J]. Concrete, 2016(4): 4 − 8. (in Chinese) doi: 10.3969/j.issn.1002-3550.2016.04.002
[17] 张伟平, 张庆章, 顾祥林, 等. 环境条件和应力水平对混凝土中氯离子传输的影响[J]. 江苏大学学报(自然科学版), 2013, 34(1): 101 − 106. Zhang Weiping, Zhang Qingzhang, Gu Xianglin, et al. Effects of environmental conditions and stress level on chloride ion transport in concrete [J]. Journal of Jiangsu University (Natural Science Edition), 2013, 34(1): 101 − 106. (in Chinese)
[18] 金浏, 张仁波, 杜修力. 低应力水平下混凝土中氯离子扩散行为多尺度分析方法[J]. 工程力学, 2017, 34(3): 84 − 92. doi: 10.6052/j.issn.1000-4750.2015.08.0694 Jin Liu, Zhang Renbo, Du Xiuli. Multi-scale analysis for the chloride diffusivity in concrete subjected to low-level stress [J]. Engineering Mechanics, 2017, 34(3): 84 − 92. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.08.0694
[19] Du X L, Jin L, Zhang R B. Chloride diffusivity in saturated cement paste subjected to external mechanical loadings [J]. Ocean Engineering, 2015, 95: 1 − 10. doi: 10.1016/j.oceaneng.2014.11.028
[20] Xu J, Li F M. A meso-scale model for analyzing the chloride diffusion of concrete subjected to external stress [J]. Construction and Building Materials, 2017, 130: 11 − 21. doi: 10.1016/j.conbuildmat.2016.11.054
[21] Wang J, Ng P L, Su H, et al. Meso-scale modelling of stress effect on chloride diffusion in concrete using three-phase composite sphere model [J]. Materials and Structures, 2019, 52(3): 55. doi: 10.1617/s11527-019-1355-8
[22] Sahimi M. Applications of percolation theory [M]. London: Taylor & Francis, 1994.
[23] Garboczi E J, Bentz D P. Computer simulation of the diffusivity of cement-based materials [J]. Journal of Materials Science, 1992, 27(8): 2083 − 2092. doi: 10.1007/BF01117921
[24] Zheng J J, Zhou X Z. Analytical solution for the chloride diffusivity of hardened cement paste [J]. Journal of Materials in Civil Engineering, 2008, 20(5): 384 − 391. doi: 10.1061/(ASCE)0899-1561(2008)20:5(384)
[25] Garboczi E J, Bentz D P. The effect of statistical fluctuation, finite size error, and digital resolution on the phase percolation and transport properties of the NIST cement hydration model [J]. Cement and Concrete Research, 2001, 31(10): 1501 − 1514. doi: 10.1016/S0008-8846(01)00593-2
[26] 沈聚敏, 王传志, 江见鲸. 钢筋混凝土有限元与板壳极限分析 [M]. 北京: 清华大学出版社, 1993. Shen Jumin, Wang Chuanzhi, Jiang Jianjing. Finite element method of reinforced concrete and limit analysis of plates and shells [M]. Beijing: Tsinghua University Press, 1993. (in Chinese)
[27] 王志良, 张跃, 申林方, 等. 考虑微观结构影响的混凝土界面过渡区裂隙渗流-溶蚀耦合模型[J]. 工程力学, 2021, 38(6): 133 − 142. doi: 10.6052/j.issn.1000-4750.2020.07.0444 Wang Zhiliang, Zhang Yue, Shen Linfang, et al. Coupled model of fracture seepage and dissolution in concrete interface transition zone considering the influence of microstructure [J]. Engineering Mechanics, 2021, 38(6): 133 − 142. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.07.0444
[28] Wu L J, Ju X L, Liu M W, et al. Influences of multiple factors on the chloride diffusivity of the interfacial transition zone in concrete composites [J]. Composites Part B, 2020, 199: 108236-1 − 108236-13.
[29] Wu K, Long J F, Xu L L, et al. A study on the chloride diffusion behavior of blended cement concrete in relation to aggregate and ITZ [J]. Construction and Building Materials, 2019, 223: 1063 − 1073. doi: 10.1016/j.conbuildmat.2019.07.068
[30] Pollmann N, Larsson F, Runesson K, et al. Modeling and computational homogenization of chloride diffusion in three-phase meso-scale concrete [J]. Construction and Building Materials, 2021, 271: 121558-1 − 121558-11.
[31] Zheng J J, Zhou X Z. Prediction of the chloride diffusion coefficient of concrete [J]. Materials and Structures, 2007, 40(7): 693 − 701. doi: 10.1617/s11527-006-9182-0
[32] Zheng J J, Wong H S, Buenfeld N R. Assessing the influence of ITZ on the steady-state chloride diffusivity of concrete using a numerical model [J]. Cement and Concrete Research, 2009, 39(9): 805 − 813. doi: 10.1016/j.cemconres.2009.06.002
[33] Crumbie A K. Characterisation of the microstructure of concrete [D]. London: Imperial College London, 1994.
[34] Lam L, Wong Y L, Poon C S. Degree of hydration and gel/space ratio of high-volume fly ash/cement systems [J]. Cement and Concrete Research, 2000, 30(5): 747 − 756. doi: 10.1016/S0008-8846(00)00213-1
[35] Hansen T C. Physical structure of hardened cement paste: A classical approach [J]. Materials and Structures, 1986, 19(6): 423 − 436. doi: 10.1007/BF02472146
[36] Zheng J J, Zhou X Z, Shao L, et al. Simple three-step analytical scheme for prediction of elastic moduli of hardened cement paste [J]. Journal of Materials in Civil Engineering, 2010, 22(11): 1191 − 1194. doi: 10.1061/(ASCE)MT.1943-5533.0000103



 下载:
下载: