软土在我国东南沿海和内陆湖区广泛分布。软土除了具备弹塑性材料力学特性，还具有显著的变形随时间变化属性。在土力学中，软土变形时间属性可由固结和蠕变来描述。固结与蠕变从不同的角度反映土体变形的规律；前者反映的是孔隙水压力消散、有效应力逐渐变化引起的变形；后者是在保持应力不变的条件下，土体变形随时间增加的属性。软土固结与蠕变同时发挥作用，共同决定着软土地基及其构筑物的长期变形和稳定性。我国学者陈宗基和钱家欢^[1-2]最早将固结与蠕变结合起来研究土体变形。陈晓平和白世伟^[3]将Duncan非线弹性模型与 Kelvin模型相串联，将其引入到 Biot固结理论中，以此建立了固结蠕变耦合模型。陈昌富等^[4]同时考虑固结和蠕变影响，建立了红黏土受力变形时间效应的固结蠕变耦合模型。常温下软土的固结蠕变耦合模型研究已有大量报道，此处不再赘述。

近些年来，在节能环保、绿色可持续发展理念下，越来越多的涉热岩土工程，如地热能利用(能源桩)、海洋资源开发、核废料处治、垃圾填埋、高温输油管路、城市供热管网和热相关的软基处理等，在沿海和内陆湖区兴起或发展^[5-9]。上述能源结构或涉热技术应用时，在软土场地形成不可忽视的温度场；在热场和力场耦合作用下，软土固结蠕变是一个长期且较为显著的过程，它不仅影响主体结构设计和正常运营，还影响场地的稳定性及周边环境。由此，有必要研究考虑温度效应的软土固结蠕变特性及其力学模型。

一些学者用弹簧、黏壶和塑性体等元件串、并联组合来模拟土体的弹性、塑性和黏性，据此建立土体有效应力-应变-时间-温度关系。例如，郭华等^[10]在广义Merchant三元件模型基础上引入温度膨胀系数和温度黏滞系数，建立饱和土体三元件热流变模型。另一种思路是基于临界状态模型建立土体热本构模型。该研究最早可追溯到20世纪90年代，Hueckel与Borsetto^[11]通过引入热塑性理论扩展了修正剑桥模型。其后Modaressi考虑温度对孔隙比、屈服面以及蠕变参数影响，建立了热黏塑性本构模型^[11]。Cui等^[12]提出应力屈服面LY和温度屈服面TY，得到考虑土体超固结的热本构模型。Laloui团队^[13-14]结合Leroueil速率势模型和竖向屈服应力随温度变化经验式，建立了考虑温度效应的环境岩土本构模型。Di Donna 和 Laloui^[15]通过引入循环塑性半径，将该模型进一步扩展到考虑循环变温情况。Zhang 等^[16]将温度变化与应力等效由此建立了新的热弹黏塑性模型。Yao 和 Zhou^[17]引入热弹塑性压缩参数和热弹性压缩参数建立了考虑温度变量的UH模型。王立忠等^[18]采用Moritz提出的温度与先期固结压力双对数关系，得到考虑土体各向异性和温度效应的临界状态模型。第三种思路是基于热力学理论来建立土体的固结压缩模型。例如，程晓辉团队^[19-20]基于颗粒流体动力学理论和“熵”概念，建立了考虑饱和土体多相性和复杂应力条件的清华大学热力学模型；白冰团队^[21]基于多孔介质材料中的颗粒重排列，引入相变、粒子熵和能量耗散原理，建立了热水力耦合的新型本构模型。

另一种相对简单且便于推广的方法是在经典土力学基础之上，基于土体的热固结压缩试验结果，拟合土体有效应力-应变-时间-温度的关系并建立力学模型。例如：Leroueil^[22]基于多年研究成果，将Suklje速率势模型扩展到考虑温度效应情况；笔者围绕软土热固结问题开展了一系列研究^[23-25]，探讨了热力耦合下的有效应力和超静孔压发展，定义了热力耦合下的固结度，开展了软土地基热固结理论与试验研究。但要指出的是，涉热工程软土场地长期变形除了与热固结有关，还与土体的蠕变或次固结密切相关。因此，有必要在热固结分析中进一步考虑蠕变或次固结影响，建立考虑温度效应的固结蠕变统一分析模型。

基于此，拟针对典型滨海软土开展热固结蠕变试验，获得其热固结蠕变特性和相关的拟合公式及参数；结合已有热固结研究成果，推导建立考虑温度效应的固结蠕变耦合力学模型，并基于实测数据进行验证；最后开展算例分析，相关研究成果可为软土地区涉热岩土工程的设计、施工和安全运营提供参考。

1   软土热固结蠕变试验

1.1   试验土样、仪器及方案

1)试验土样

试验土样(埋深3 m~4 m)为滨海地区典型的淤泥质粉质黏土，呈灰色、软塑状，土质较均匀，因开挖卸荷作用受轻微扰动；其基本物理指标如表1所示。

表  1  试验土样基本物理指标

Table  1.  Basic physical properties of test soil

比重	密度 /(g/cm3)	含水率 /(%)	塑限 /(%)	液限 /(%)	孔隙比
2.71	1.785	38.4	24.0	39.5	1.10

下载: 导出CSV 

| 显示表格

2)试验仪器

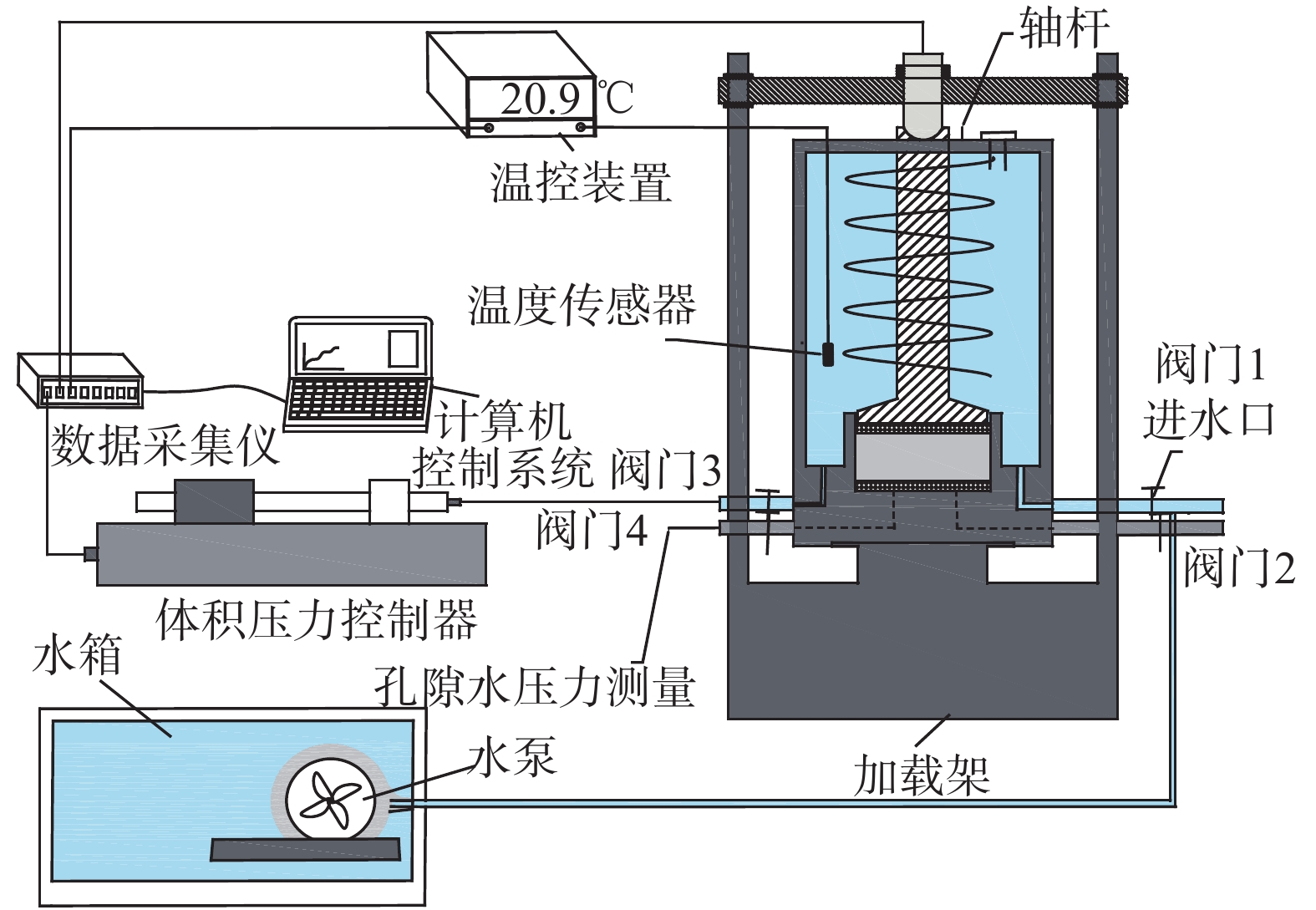
试验仪器如图1所示。试验系统硬件部分包括标准静态加载架(加载量程10 kN)、固结压力室(带高精度孔压传感器)、标准体积压力控制器、温度控制系统(温控范围为室温~ 65 ℃)、多通道数据采集装置。其中，温控系统又包括循环管、保温装置、管路接头、流体循环对流泵以及温度控制器。温控系统利用进出水口对固结压力室腔体内补排水，然后，通过升温装置对腔体内的水进行加热控制，由此实现对土样加热。孔压传感器具有内部压力补偿系统，还具有精确的温度补偿功能。试验软件系统为GeoSmartLab软件，能开展多种固结蠕变试验。试验仪器完全由计算机控制并采集数据，可测量轴向应力、反压、孔压、轴向位移、温度变量，具有土体饱和、B值检测、分级加载、等应变速率加载、等加载速率固结压缩功能。

图  1  高级温控固结仪试验系统

Figure  1.  Advanced temperature control consolidation test instrument

下载: 全尺寸图片 幻灯片

3)试验步骤和方案

试验步骤分三阶段：土样制备及安装、管路排气与土样饱和、不同温度-应力路径下固结压缩试验，首先，按土工标准制备土样，再依次将下透水板、滤纸、护环放置于固结容器底座上，然后，试样装入护环，再放滤纸和上透水板，套上上盖并拧紧密封。其后，将固结容器底部孔隙压阀门打开，充入脱气水，排除底部及管路中滞留的气泡。通过软件系统设置轴压和反压(压差5 kPa)使试样饱和；检测B值，设定B值达到0.95即可开始不同温度-应力路径的试验。

测试方案如表2所示。在前期已有相关研究基础之上开展两方面测试。系列1：不同温度下固结蠕变试验(单面排水)，旨在确定系数C_αT并研究竖向压力和温度对C_αT影响。温度范围26 ℃(室温)~56 ℃，竖向压力为25 kPa、0 kPa、100 kPa、200 kPa；每级荷载作用3 d。

表  2  土样试验方案

Table  2.  Soil sample test program

系列号	土样号	OCR	温度/(℃)	荷载 /kPa
系列1	1-1	1	26(室温)	25~200
	1-2	1	36	25~200
	1-3	1	46	25~200
	1-4	1	56	25~200
系列2	2-1	1	26~56	25~400
	2-2	2	26~56	25~400
	2-3	4	26~56	25~400
	2-4	10	26~56	25~400

下载: 导出CSV 

| 显示表格

系列2：开展不同OCR、不同荷载等级下的变温试验，旨在确定土样OCR和压力水平对土体热膨胀系数的影响(单面排水)。四组土样OCR分别为1、2、4和10，先期固结压力分别为25 kPa、50 kPa、100 kPa和250 kPa；竖向加载压力分别为25 kPa、50 kPa、100 kPa、200 kPa、400 kPa，每级荷载作用1 d；温度变化为室温26 ℃、36 ℃、46 ℃、56 ℃、室温，单级温度维持1 h。

1.2   试验成果及分析

1)热力耦合下的次固结系数

系列1试验得到不同温度下的e−lgt成果，结果表明主固结完成后土样变形在e−lgt曲线上表现为直线。据此得到不同温度下的次固结系数C_αT。图2(a)和图2(b)分别为温度和竖向压力对软土次固结系数影响图。由图可知：C_αT主要集中在0.003~0.005；随着温度升高，次固结系数增大；该趋势在前期发展快，后期渐缓；次固结系数随竖向压力增大而变小，但规律性不明显。

目前，关于加热对土体次固结系数C_αT影响研究有少量报道^[26-27]，但还没有公认的经验式来反映各因素对C_αT的影响。结合图2所示宁波典型软土热固结压缩测试结果，提出如下经验公式：

式中：Α、B为土性经验参数；参数B与竖向压力p有关。在e−lnt关系曲线上蠕变参数φ_T=C_αT/(ln10)。按式(1)拟合典型软土测试结果，得到相关参数：A= 0.0021、B=0.003~0.004。

图  2  温度和应力水平对次固结系数的影响

Figure  2.  The effects of temperature and vertical pressure on the coefficient of secondary compression

下载: 全尺寸图片 幻灯片

2)热膨胀系数

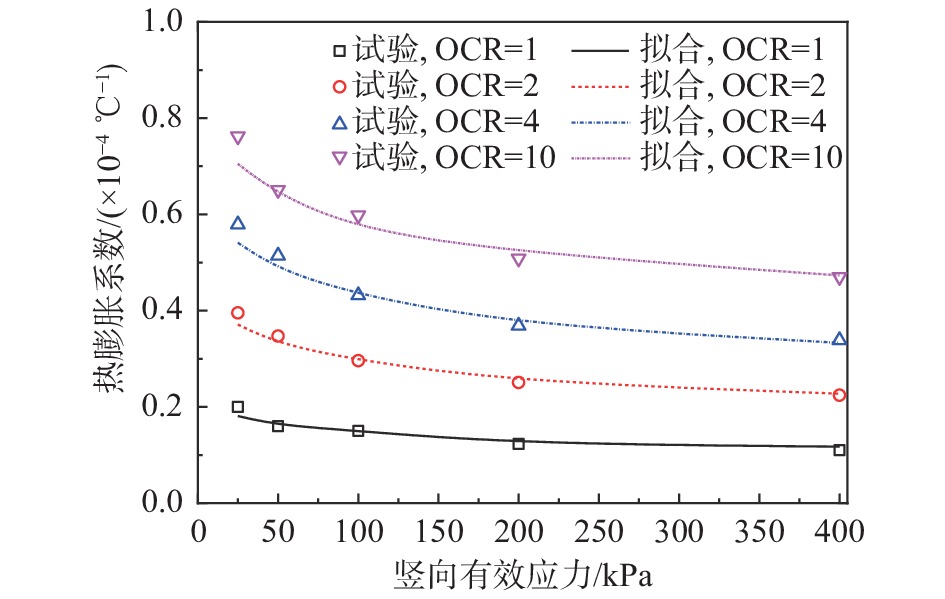
材料的热胀冷缩也引起土体的应变^[28]。热胀冷缩属性的大小可以用热膨胀系数α_T(℃⁻¹)来衡量。系数α_T与土体所处的状态有关(OCR)，此外还可能与固结压力有关。针对宁波典型软土开展的系列2热固结试验，得到不同OCR条件下不同加载等级土体热膨胀系数变化；如图3所示。由图可知：随着应力水平增大，土体热膨胀系数有减小趋势；OCR越大，土体热膨胀系数越大；相对来说，OCR对土体热膨胀系数的影响较为明显。

图  3  不同OCR情况下热膨胀系数随应力水平变化

Figure  3.  Variation of thermal expansion coefficient with stress level under different OCR

下载: 全尺寸图片 幻灯片

根据测试结果，提出下式来描述土体热膨胀系数α_T与竖向压力p及OCR的关系：

式中：α_T100为正常固结土(OCR=1)在100 kPa竖向压力下的热膨胀系数；a、b和c为经验系数，与土的类别及其微观结构等有关。采用式(2)对测试结果进行拟合(如图3)，可得试验土样热膨胀系数相关参数取值，即：α_T100=1.5×10⁻⁵；a=0.105；b=1.5；c=1.0。

2   热固结蠕变耦合模型

2.1   热弹黏塑性模型

殷建华^[1]基于Bjerrum时间线模型和等效时间概念，建立了一维弹粘塑性模型，并在此基础之上提出考虑蠕变的固结沉降简化计算方法，极大的推动了蠕变或次固结理论在工程中的应用。下文在该模型基础之上建立考虑温度效应的固结蠕变耦合模型。

1)瞬时压缩

首先，在瞬时压缩线上的应变可表示为：

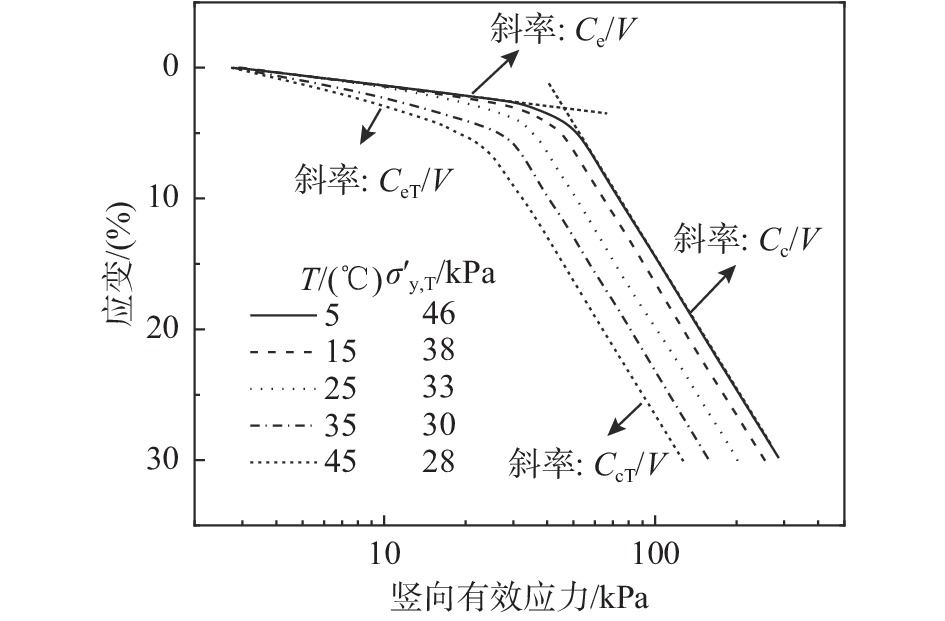
式中：${{\sigma }_0'}$为对应于竖向应变$\varepsilon _0^{\text{e}}$的参考竖向应力(可以是天然土体初始应力状态)；σ′为土体当前有效应力；V=1+e₀，e₀为土体初始孔隙比；κ_Τ为与温度有关的土体参数(常温下为κ_Τ0)。该式可以用来描述不同温度下超固结或卸载再加载阶段的应力应变发展。

已有研究表明^[28]，土体加热升温后，e−lgσ'曲线上的初始段斜率增大，即回弹指数C_eT(或κ_Τ)随温度T升高而增加。C_eT−T经验关系可以通过试验来获得；Eriksson研究了不同温度下的软土固结压缩过程，得到如图4所示不同温度下的应力-应变曲线^[28]。

图  4  加热温度对软土固结压缩的影响^[24]

Figure  4.  The influence of heating temperature on the consolidation of soft soil

下载: 全尺寸图片 幻灯片

基于该试验成果，提出下式来描述：

式中：${{\sigma }_{{\rm{y,T0}}}'}$为土体在常温下的屈服应力，对应于一维固结条件下的先期固结压力p_c；${\sigma }_{{\rm{y,T}}}'$为土体在升温下的屈服应力，对应于升温情况下土体表观先期固结压力p_cT。${\sigma }_0'$为土体当前竖向压力；对于正常固结土，${\sigma }_0'$= ${{\sigma }_{{\rm{y,T0}}}'}$。C_e为常温下土体回弹指数(超固结段或回弹再压缩指数)；C_eT为T温度下土体回弹指数。根据e−lgσ′与e−lnσ′曲线关系^[1]：κ_T=C_eT/(ln10)。

2)塑性压缩

在完全侧限压缩条件下，加热对主固结的影响包括三个方面：加热对屈服极限的影响(或热强度影响)；加热对压缩指数的影响(或热塑性影响)；加热对主固结过程的影响(热固结影响)。

① 加热对土体屈服极限影响，表现为对土体表观先期固结压力的影响。已有研究已经得到较为一致的认识^[26-28]，即：随着温度升高，土骨架结构受到冲击，其弹性变形范围缩小，土体更容易屈服。一些学者基于固结压缩试验建立了相应的经验式。其中，Laloui和Cekerevac的研究成果最具代表性^[29]，即：

式中，γ为土性参数，通常γ=0.3~0.4。

② 加热对土体压缩指数C_cT或λ_Τ的影响。国内外学者围绕土体压缩指数的温度效应进行了探讨^[27]：有少量文献认为加热影响压缩指数；但一般认为，加热对土体压缩指数C_cT或λ_Τ的影响很小(有机质土除外)，可以忽略不计。此处要指出的是，虽然压缩指数是土体主固结阶段的变形指标，但是在认同固结蠕变同时进行的观念(假设B)下，该指标还反映了蠕变变形对主固结压缩的贡献。

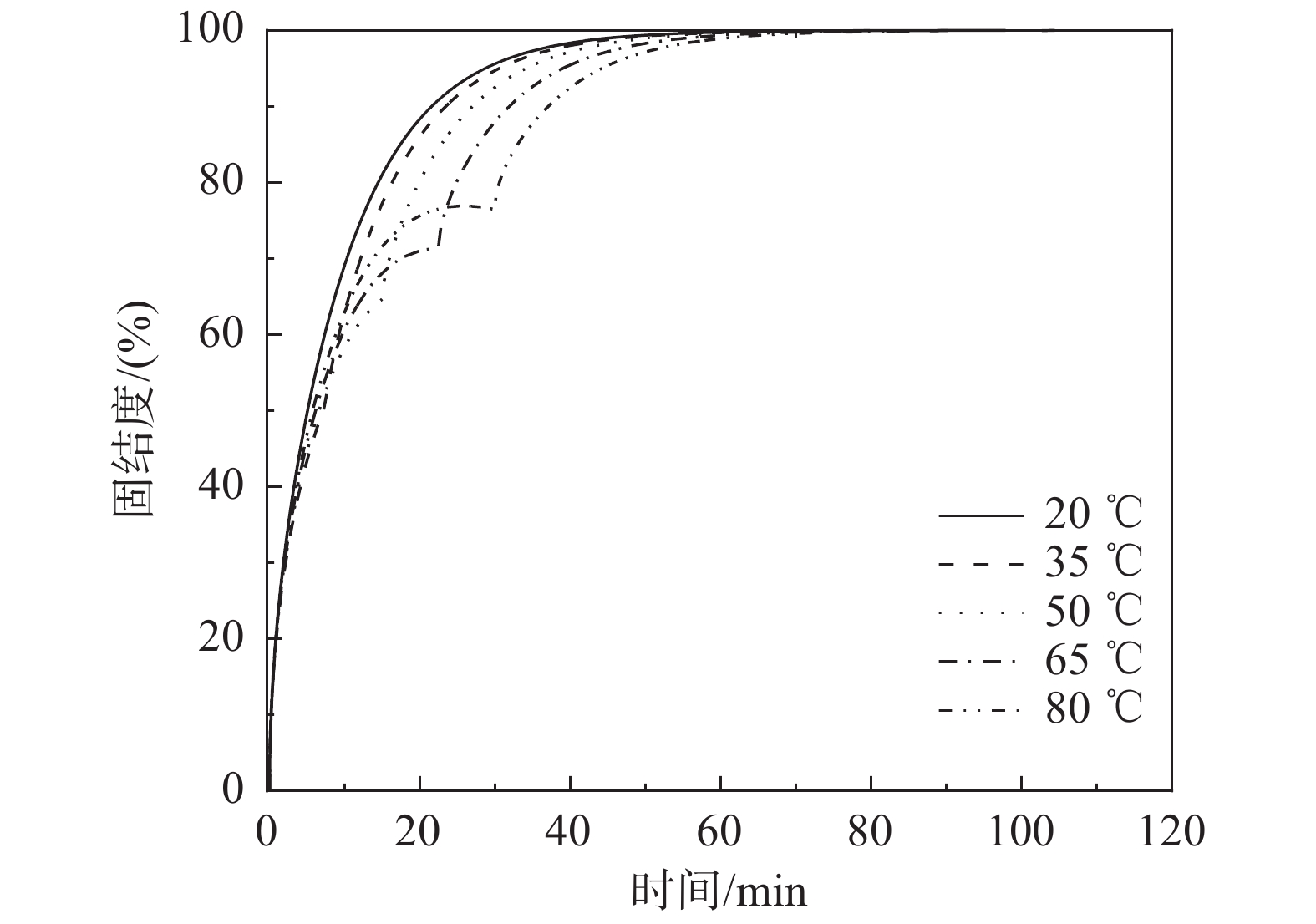
③ 加热对土体主固结过程的影响。在Passwell于1967年首次提出热固结概念之后，国内外学者开展了大量相应研究^[24]。普遍的共识是：加热提升土体固结性状，土体固结过程加快；热固结过程和经典的荷载作用下的固结过程有类似。

热力耦合作用下的固结度可采用下式计算^[24]：

式中：m=1,3,5,···；H为排水距离，对于单面排水H为土层厚度；c_vT为升温后土体的固结系数。固结系数c_vT与不同温度下水的粘滞系数有关，有：

式中：η_T0和η_T分别为常温和T温度下水的粘滞系数；T₀通常指20 ℃；c_v为常温下的固结系数。根据已有研究^[30]，在标准大气压下水的粘滞性系数与温度间的经验表达式为：η_T= −0.454 × 10⁻³ lnT+ 2.349×10⁻³。

热力耦合作用下的超静孔压计算式如下：

式中：u₀为初始超静孔压；初始超静孔压包括荷载引起的超静孔压u_q0和加热引起的超静孔压u_T0；且有u₀=u_q0+u_T0。根据饱和土理论，瞬时施加的外荷载全部转换为土中超静孔压，即：u_p0=q₀。对饱和土加热将产生超静孔隙水压力，且与外荷载、围压、排水边界和土类等有关。对于软黏土可采用下式来确定加热引起的初始超静孔隙水压力^[24]：

式中：α_f和α_s分别为水和土骨架膨胀系数；α_st为由于土的结构在温度作用下产生物理化学变化而产生的体积改变系数；n_v为孔隙率；m_v为土的体积压缩系数。

由此，在塑性压缩线上(${\sigma }'\geqslant {\sigma }_{{\rm{y,T}}}'$；${\sigma }_{{\rm{y,T}}}'$为不同温度下的土体屈服应力，在一维固结压缩时为表观先期固结压力)应变可以表示为：

式中：$\varepsilon _{\text{T}}^{\text{p}}$对应于竖向应力${\sigma }_{{\rm{y,T}}}'$时的竖向应变；竖向应力${\sigma }_{{\rm{y,T}}}'$可以表示为随温度变化的表观先期固结压力；λ_T为土体压缩指数(忽略温度对λ_T的影响)。该式可描述不同温度下正常固结压缩阶段的应力应变数据。

3)蠕变变形

加热对蠕变(次固结沉降)的影响，包括两方面。

① 加热对主固结结束时间t_p的影响。t_p为土体固结压缩e−lgt曲线上主次固结分界点。根据式(6)计算固结度，并选取固结度达到99%的时间为t_p，即：

关于式(12)说明如下：在很多情况下，超静孔压消散逐渐变缓，土体固结度很难达到100%^[31]；其次，由主固结阶段转为次固结阶段时，变形时间曲线逐渐变化，主次固结分界点是主固结基本结束时刻(并非完全结束时刻)，此时蠕变成为压缩变形的主要部分。另外，不同温度下土体的固结系数不同，根据式(6)不难得出不同温度下t_p不同。

另外，对于随时间变化的变形，有效应力保持不变，软土变形只随时间变化。用蠕变应变来描述土体的黏性。蠕变应变定义为：

式中：φ_T为e−lnt关系曲线上蠕变参数，通过固结蠕变试验得到；t_p为主固结结束时间；t_c为次固结时间。此处要说明的是：蠕变从固结压缩开始时就存在，主固结阶段的压缩指标包含了蠕变变形的贡献。

另外，热胀冷缩引起的应变。土体热胀冷缩属性也引起土体的应变变化，可采用下式来描述温度变化引起的土体变形(膨胀回弹为负变形)：

4)弹黏塑性变形

结合式(14)并引入变量β₁和β₂，可得综合计算式：

式中：${\sigma }_0'$为加荷之前的有效应力；$\Delta{\sigma }'$为增量有效应力；对于单级加载情况，$\Delta{\sigma }'$=q₀；${\sigma }'$为当前有效应力，是${\sigma }_0'$与$\Delta{\sigma }'$之和，即${\sigma }'={\sigma }_0'+\Delta{\sigma }'$。变量β₁和β₂为：

式(15)计算的是增量荷载Δσ′作用t_p+t_c时间土体一维压缩总的变形。该模型参数可在一维固结压缩试验或三轴各向等压固结试验基础之上获得。此外，关于lg曲线和ln曲线参数转换可参考已有研究^[1]。

2.2   热固结蠕变耦合模型

实际上，在荷载作用下，超静孔压和有效应力是逐渐变化的。因此，求软土或地基变形随时间发展，需要考虑超静孔压的变化。在单级加载情况下，超静孔压逐渐消散，有效应力逐渐增大，应变随时间发展。根据有效应力原理可得σ′=${\sigma }_0'$+q₀−u(t)；q₀为瞬时施加的荷载；u(t)为土体在t时刻的超静孔隙水压力，则：

式中，u(t)的计算见前文式(5)。

关于式(17)，说明如下：

1)固结蠕变耦合变形包括了固结与蠕变；蠕变在固结压缩就存在，C_cT中反映了主固结阶段的蠕变；C_αT为次固结阶段的蠕变。

2)该式反映了土体固结压缩的弹性(第一项)、塑性(第二项)、黏性(第三项)和热胀冷缩(第四项)。

3)弹性变形参数C_eT；塑性变形参数C_cT和p_cT；黏性变形参数为A和B；热胀冷缩属性参数为α_T100和a、b、c。可通过热固结蠕变试验获得上述各参数。

4)式(15)和式(17)是在完全侧限压缩条件下得到力学模型，可仿效殷建华的研究思路将其推广到三维力学模型^[1]。

2.3   计算流程

① 明确参数：e₀、σ′₀、σ′_y,T0、γ、T₀、ΔT、C_e(κ_Τ0)、c_v、C_cT(=C_c)、A、B、α_T100、a、b、c、OCR、q₀。

② 根据式(2)计算${\sigma }_{{\rm{y,T}}}'$；根据式(1)计算C_eT和κ_T；

③ 根据式(4)计算c_vT，再结合式(3)和式(7)计算t_p。

④ 根据外荷载q₀和变温T，结合式(6)和式(5)计算初始超静孔压u₀和超静孔压u(t)的发展变化。

⑤ 根据式(8)计算C_αT；进一步确定φ_T。

⑥ 计算有效应力原理计算σ′(t)，判断土体所处的弹塑性压缩阶段，由此确定β₁；

⑦ 比较t与t_p的大小关系，判断土体所处的主次固结阶段，由此确定β₂；

⑧ 根据式(9)计算α_T；进一步根据式(14)得到膨胀应变；

⑨ 根据式(15)计算总应变(沉降)；

⑩ 根据式(17)计算应变(沉降)随时间发展。

3   计算与分析

3.1   模型验证

为验证热固结蠕变耦合力学模型的合理性，以前文试验成果进行验证分析；计算参数如表3所示。图5和图6所示为理论与实测结果对比曲线。其中，图5为不同温度下软土固结压缩的e−p曲线；图6为恒定荷载(200 kPa)不同温度条件下土体变形随时间发展曲线。

表  3  计算参数及其取值

Table  3.  Parameters and their values

参数	取值		参数	取值
T0/(℃)	26		αT100/(℃−1)	1.5×10−5
OCR	1		a	0.105
e0	1.10		b	0.15
pc/kPa	95		c	1.0
cv/(×10−4 cm2/s)	6.58		αf/(℃−1)	4.5×10−4
Cc	0.345		αs/(℃−1)	3.0×10−5
Ce	0.045		αst/(℃−1)	3.0×10−5
γ	0.382		nv	0.55
Α	0.0021		mv/MPa−1	0.50
Β	0.0032		ΔT/(℃)	0~30

下载: 导出CSV 

| 显示表格

图  5  不同温度下软土的e−p曲线试验值和计算值

Figure  5.  Test and calculated e−p curves under different T conditions

下载: 全尺寸图片 幻灯片

图  6  不同温度下的Δe−t曲线试验值和计算值(p=200 kPa)

Figure  6.  Test and calculated Δe – t curve under different temperature conditions (p=200 kPa)

下载: 全尺寸图片 幻灯片

由图5可知：热力耦合作用下在固结压缩初始阶段土体发生回弹，温度越高回弹量越大；表观先期固结压力(或屈服应力)随温度升高而降低；土体弹性变形范围随温度升高而减小，弹性变形的斜率和弹性应变总量随温度升高而增大；各温度下正常固结压缩阶段压缩曲线平行。由图6可知：在主固结阶段，试样孔隙比变化Δe在高温时较低温时大，说明加热提高了软土的主固结速率；在次固结阶段，变形时间曲线斜率更大，表明加热提高了软土试样的次固结系数。图5和图6所示的计算值与实测值吻合度较高，由此较好的检验了本文力学模型的合理性。

3.2   算例分析

1)瞬时加温情况

以热力耦合作用下的标准固结压缩土样作为计算对象，土样高度20 mm，双面透水。荷载和温度均瞬时施加，加热温度变化范围为常温20 ℃~65 ℃。土性参数如表3；荷载范围为10 kPa~800 kPa。首先得到不同温度和不同固结时长下软土一维固结压缩的应力-应变曲线。结果发现：相同的热力耦合条件下，固结时间越长，土体蠕变量越大，土体总的压缩量越大；相同的荷载与相同的固结压缩时长条件下，温度越大，土体压缩量越大。

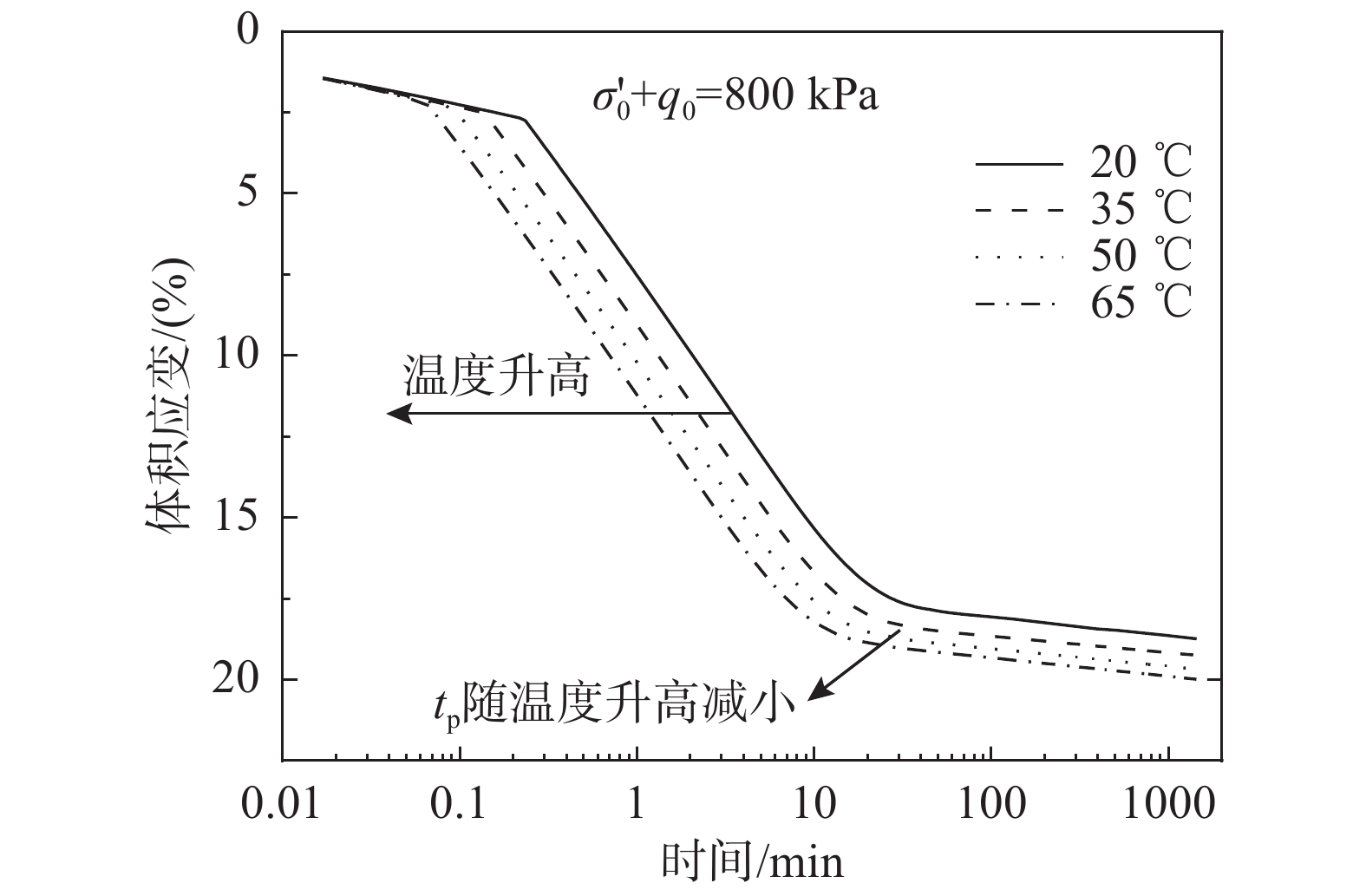
图7为不同温度条件土体应变随时间发展曲线对比情况。由图可知：① 应变随时间发展曲线有两个转折点，第一转折点之前为弹性变形为主，然后为黏弹塑性变形阶段(主固结)，第二转折点之后为蠕变变形为主；② 第一转折点可视为弹性变形转为塑性变形的临界时间点，随着温度升高该时间点提前，第二转折点为主固结结束时间t_p，随着温度升高t_p值减小；③ 升高温度条件下的应变-时间曲线位于低温度应变-时间曲线的下方，表明升高温度会增大土体的总应变。

图  7  不同温度下的应变-时间曲线

Figure  7.  Strain-time curves under different temperature conditions

下载: 全尺寸图片 幻灯片

2)线性变温情况

在很多情况下，土体温度是逐渐上升，然后保持恒定。对此，分别将初始温度20 ℃以2 ℃/min的升温速率，升温至35 ℃、50 ℃、65 ℃、80 ℃；如图8所示。外荷载q₀= 190 kPa瞬时施加(初始有效应力10 kPa)；其余参数同表3。

图  8  温度变化曲线

Figure  8.  Variation of temperature with time

下载: 全尺寸图片 幻灯片

图9所示为热力耦合下超静孔压计算结果。图9(a)为加热引起的超静孔压u_T及其发展过程曲线。由图可知：在固结初期，随着温度升高，超静孔压逐渐增大；由于热孔压的产生与热孔压的消散同时进行，热超静孔压并非温度越高越大；当升温停止后，热超静孔压逐渐消散，消散速率呈先快速后平缓的规律。图9(b)为总的超静孔压u_t发展曲线(包括加载引起的超静孔压和热超静孔压)。由图可知：随着时间发展，超静孔压逐渐消散，固结初期消散快，后期逐渐减缓；温度升高时，由于热超静孔压的产生，总的超静孔压相比于常温组要大；当加热停止后，加热组超静孔压以更快的速率消散。

图  9  孔压变化曲线

Figure  9.  Variation of excess pore water pressure

下载: 全尺寸图片 幻灯片

图10所示为热力耦合下土体固结度发展曲线。由图可知：随着时间的发展，固结度逐渐增大；热孔压的产生对固结度有一定影响；在固结前期，由于加温引起超静孔压，使得加热条件下固结度相对较小；随着时间发展，加热组固结度发展加快。

图  10  固结度曲线

Figure  10.  Curves of degree of consolidation

下载: 全尺寸图片 幻灯片

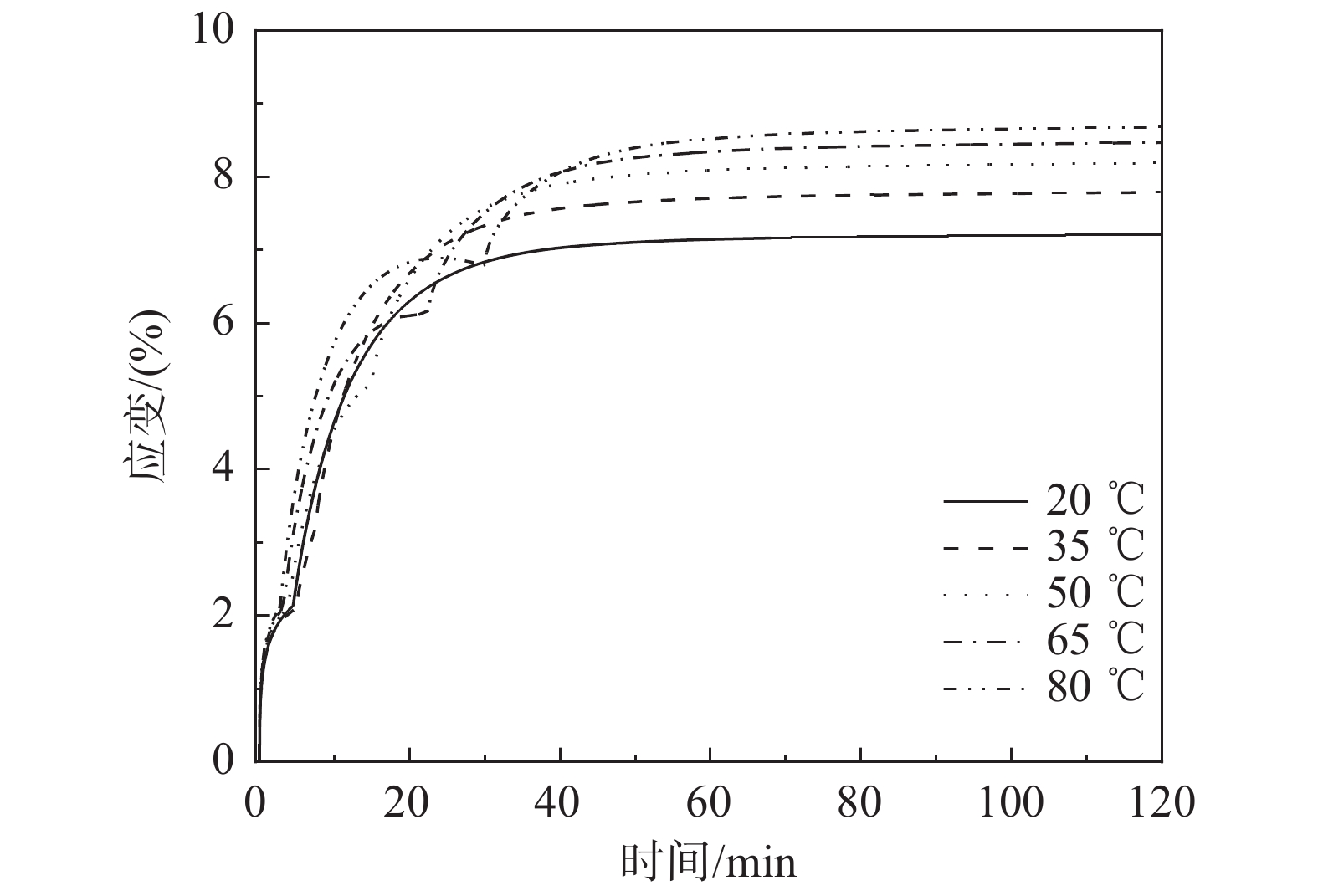
图11所示为热力耦合下土体变形随时间发展曲线。随着时间的发展，固结压缩变形逐渐增大；热孔压的产生对变形发展有一定影响；在固结前期，由于加温引起膨胀，使得加热条件下压缩变形相对较小；随着时间发展，加热组固结度发展加快；温度越高，软土最终应变量(沉降)越大。值得说明的是，上述计算得到的规律与已有研究实测成果近似一致^{[26, 28]}。

图  11  线性变温下应变变化曲线

Figure  11.  Stress-strain curves under linear variation of temperature

下载: 全尺寸图片 幻灯片

4   结论

基于温控固结仪对典型滨海软土开展热固结蠕变试验，得到软土次固结系数和热膨胀系数拟合公式及其参数取值。进一步结合弹黏塑性理论和热固结理论，考虑加热对软土固结和蠕变特性的影响，建立了考虑温度效应的固结蠕变耦合力学模型。主要认识如下：

(1)在侧限压缩条件下，加热对软土固结蠕变影响包括：土体加热升温后，回弹指数随温度升高而增加，弹性压缩变形增加；加热对压缩指数影响不明显，但加热使土体屈服极限减小；加热能加快主固结过程，并使次固结提前发生；次固结系数(或蠕变系数)与温度和应力水平有关，次固结系数随温度升高而增大，次压缩量由此增加；软土热膨胀系数随竖向压力增大略有减小，随超固结比OCR增大而增大。

(2)软土次固结系数与温度和应力水平有关；且C_αT−T关系和α_T−OCR关系可用自然对数函数描述。

(3)新型热固结蠕变模型综合反映了土体固结压缩的热弹性、热塑性、热黏性和热胀冷缩属性，较好的实现了温度效应与软土固结蠕变的结合。该模型参数简单，可在一维固结压缩试验或三轴各向等压固结试验基础之上获得。

(4)新型热固结蠕变模型能描述土体的热孔压、热回弹和热沉降现象。在固结初期，随着温度升高，热孔压逐渐增大；加热停止后，加热组超静孔压以更快的速率消散。在固结前期，加热条件下的固结度相对较小；随着时间发展，加热组固结度发展加快。在固结前期，由于土体加温膨胀使得加热条件下压缩变形相对较小；随着时间发展，加热组固结压缩速率加快；温度越高，软土最终应变量(沉降)越大。