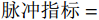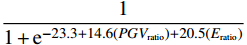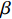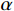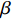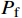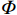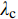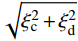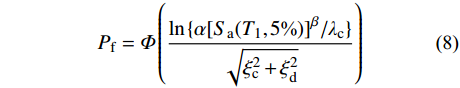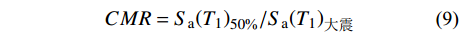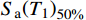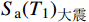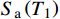EXPERIMENTAL STUDY ON SEISMIC PERFORMANCE OF ENERGY DISSIPATION AND POSITION LIMITATION STEEL BRACE AND STRUCTURE SEISMIC VULNERABILITY ANALYSIS
-
摘要: 该文提出一种消能限位型钢支撑以期改善建筑结构抗震性能,设计了5个钢支撑,设计参数为限位位移、限位块数量、钢芯截面尺寸及长度。通过低周往复加载试验对5个钢支撑的破坏特征、滞回特性、骨架曲线和刚度等抗震性能进行了研究。基于IDA分析评估了含钢支撑框架结构模型的抗地震倒塌性能。结果表明:该钢支撑构造合理,滞回性能稳定;增设限位块后可发挥限位作用,并可提供较大的附加刚度;限位块数量和截面尺寸以及其与支撑工作段连接面焊缝的刚度影响附加刚度的提升程度;该文提出的钢支撑各阶段刚度计算公式所得结果与试验值符合较好,可为钢支撑设计提供参考;设置含有限位块的消能限位型钢支撑结构的倒塌储备系数提高,有利于改善底层柔性结构的抗倒塌能力。Abstract: A kind of energy dissipation and position limitation type steel brace is proposed to improve the seismic performance of a building structure. Five steel braces are designed, and the limitation displacement, limitation block number, steel core section size and length are chosen as the design parameters. Based on the test study, the characteristics including the failure mode, hysteresis loops behavior, skeleton curves, and stiffness are demonstrated. The seismic collapse resistance of steel braced frame structures is evaluated through IDA analysis. The results show that: the steel brace structure is reasonable with stable hysteretic performance, and the position limitation block could play a limiting role and provide greater additional stiffness. The number and section size of the position limitation block and the weld stiffness of the joint surface with the steel core affect the lifting degree of the additional stiffness. The calculation results of the stiffness formulas presented are in a good agreement with the experimental values, which can provide a reference for the practical design of steel braces. The collapse reserve coefficient of this type of steel braces with position limitation blocks is increased, beneficial to improve the collapse resistance of soft first storey building.
-
近年,底部为商业用房或车库,上部作为住宅、写字楼使用的底层柔性建筑越来越多。台湾地区统帅饭店和云翠大楼即为此类建筑。2018年台湾花莲地震时,该建筑底部楼层柱端混凝土破坏严重并产生较大变形,导致结构受损严重进而发生倒塌破坏。究其原因:一方面,该类建筑虽然具有优越的使用功能,但由于建筑底层处很少设置墙体,导致结构沿竖向发生刚度突变而形成软弱层,地震作用下底部楼层易产生过大变形;另一方面,该建筑位于米仑断层带附近,近断层地震动中存在速度脉冲效应,速度峰值大且包含较高能量,地震发生时脆弱的底层支撑不住上方楼层的重量而导致较为严重的倒塌破坏[1-2]。
为了改善底层柔性结构的抗震性能,国内外学者进行了相关研究。马华等[3]通过振动台试验探讨了粗合成纤维混凝土耗能器对底层柔性结构抗震性能的影响。结果表明,该耗能器在大震时先于主体结构发生破坏并能够有效耗散地震能量,从而保护了主体结构的安全。李振宝等[4]采用RC耗能器—限位斜撑体系对底部大空间结构进行加固,并通过振动台试验表明了该体系的优越性。曹万林等[5]对底层柔性结构增设支撑及支撑合理设置问题进行了研究。结果表明,合理布置支撑使得结构底层位移及顶点位移得到有效控制。Rahai等[6]以3层和9层的支撑-框架结构为例,通过Pushover分析得到支撑-框架结构能减小结构的整体位移,提高结构的承载力。武娜等[7]使用带BRB的内嵌式钢框架对现有混凝土框架结构进行加固,并通过低周反复荷载试验探究了其减震效果。陆伟东等[8]进行了阻尼支撑控制结构薄弱层的设计方法研究,提出了控制薄弱层层间位移的阻尼支撑简化设计方法。以上研究表明,在结构柔性底层中增设耗能支撑,可有效降低结构地震响应,减轻主体结构破坏,从而改善结构整体抗震性能。消能减震结构因其减震效果好、构造简单、维护方便等特点受到学者们的重视,各种不同形式的防屈曲支撑已被研制出来并应用于实际工程。欧进萍等[9]进行了一字形内芯全钢防屈曲支撑性能试验研究,并针对一字形内芯全钢防屈曲支撑的失效模式,建立了其设计方法。郭彦林等[10-11]进行了双矩管装配式防屈曲支撑设计理论及其约束刚度取值的研究,在理论推导中考虑了刚度、强度及初始缺陷等一系列参数的影响,提出了一整套适用于双矩管装配式防屈曲支撑的设计方法,并通过数值分析验证了其可靠性。杨璐等[12]提出一种内核材料为LY315软钢的装配式屈曲约束支撑,该支撑耗能段采用对称十字形截面,支撑外约束单元由四块角钢通过高强螺栓连接而成。Iwata等[13]进行了多组不同截面形式的防屈曲支撑试验研究。结果表明,一字形内核防屈曲支撑的低周疲劳性能最好。Nip等[14]以冷弯型碳钢、热轧型碳钢和冷弯型不锈钢三种材料制作了16根方形钢管防屈曲支撑,通过循环往复试验和数值模拟对支撑抗压强度、滞回性能、侧向挠度及低周疲劳性能进行了对比研究。Oda等[15]对H型钢组装式屈曲约束支撑进行了试验研究,由槽钢和钢板装配形成的约束单元其约束能力较弱,试验过程中H型钢内核易发生局部失稳破坏。邓雪松、周云等[16-17]依据“核心单元局部削弱相当于其他部位加强”的原则设计制作了核心单元为开孔一字形钢板的全钢屈曲约束支撑,并对其进行了低周反复加载试验及理论设计方法研究。结果表明:支撑构造设计合理,能够保证支撑正常工作;建议的开孔参数设计取值范围,面积比为0.3~0.6、长宽比为0~10、间距比宜在1~1.5。万金国等[18]提出一种双屈服点免断裂屈曲约束支撑,并对其进行了试验研究与数值模拟分析。结果表明,该支撑具有良好的耗能能力和变形能力,第一耗能段和第二耗能段能够分时分段进行屈服,从而能够适应不同水平地震作用。闫维明等[19]通过拟静力试验,对比研究了全钢、摩擦、钢铅组合和销钉式防屈曲支撑。结果表明,销钉式防屈曲支撑初始刚度高,在大变形时销钉才会断裂使防屈曲支撑进入屈服耗能状态。周云等[20]研发了内核截面形式为一字形的钢板装配式屈曲约束支撑,以约束比、加载制度、耗能段截面面积、黏结材料为设计参数,对该支撑进行了试验研究。徐龙河等[21]提出一种装配式自复位耗能支撑,基于经典的Bouc-Wen模型建立了该支撑的恢复力模型,并通过试验对其进行了验证。严红等[22]针对支撑长度、内核芯材的不同,对一字形内核的全钢防屈曲支撑进行了轴向往复循环加载试验研究。结果表明,试件长度增加后,支撑的耗能能力、疲劳性能和变形能力均有所削弱。
底层柔性建筑因下部楼层刚度较弱,地震中易产生过大变形,在利用减震装置对其进行加固改造时,要求阻尼器应提供较大的抗侧刚度。上述研究中的防屈曲支撑只具有屈服后的一阶刚度,对于能够提供附加二阶刚度的防屈曲支撑的相关研究较少。为此,本文提出一种消能限位型钢支撑,该支撑可在耗散地震能量的同时还可为结构提供附加二阶刚度,有利于减小结构侧向变形和提高整体抗震性能。文中通过低周反复加载试验,明确该支撑工作机理及其力学性能变化规律,并基于IDA分析评估设置该支撑的底层柔性结构的地震易损性能,以期为提高该类建筑的抗地震倒塌能力提供参考。
1 消能限位型钢支撑试验设计
1.1 支撑构造及工作机理
消能限位型钢支撑主要由:1—端板、2—工字形连接段、3—十字形过渡段、4—一字形钢芯、5—焊接在钢芯上的限位块、附加在连接段上的8—侧向加劲肋和9—水平加劲板、带有11—限位槽的10—约束钢板、12—槽钢、13—垫板以及14—螺栓组成,支撑组成示意图如图1所示。图1(a)中在工字形连接段腹板两侧栓焊连接8—侧向加劲肋及9—水平加劲板以加强其刚度避免局部失稳;为避免约束钢板屈曲变形,在10—约束钢板表面焊接12—槽钢形成约束钢管体系,如图1(c)所示;支撑组装时将约束钢管分置在4—钢芯两侧,并通过13—垫板及14—螺栓装配成一体;为防止钢芯与约束钢管过大的相对滑动,在钢芯中部设置7—凸起并在相对应垫板下方设置凹槽;为保证钢芯受压过程中由于泊松效应产生的横向变形所需的空间,在钢芯与约束钢管之间设置2 mm的间隙。
消能限位型钢支撑的独特之处在于沿钢芯长度方向多个截面处交替焊接有若干个限位块,约束钢板上开设有若干个限位槽并与钢芯上的限位块配合使用。如图1(e)限位块局部实物图所示,支撑工作时:5—限位块会随4—钢芯变形而移动,当限位块随钢芯变形而移动达到预定限位位移d时,5—限位块与11—限位槽的边缘接触,通过限位装置的荷载传递从而使10—约束钢板与4—钢芯形成并联工作机制共同承担轴力,发挥限位功能的同时还可为结构提供附加二阶刚度。
1.2 试件设计
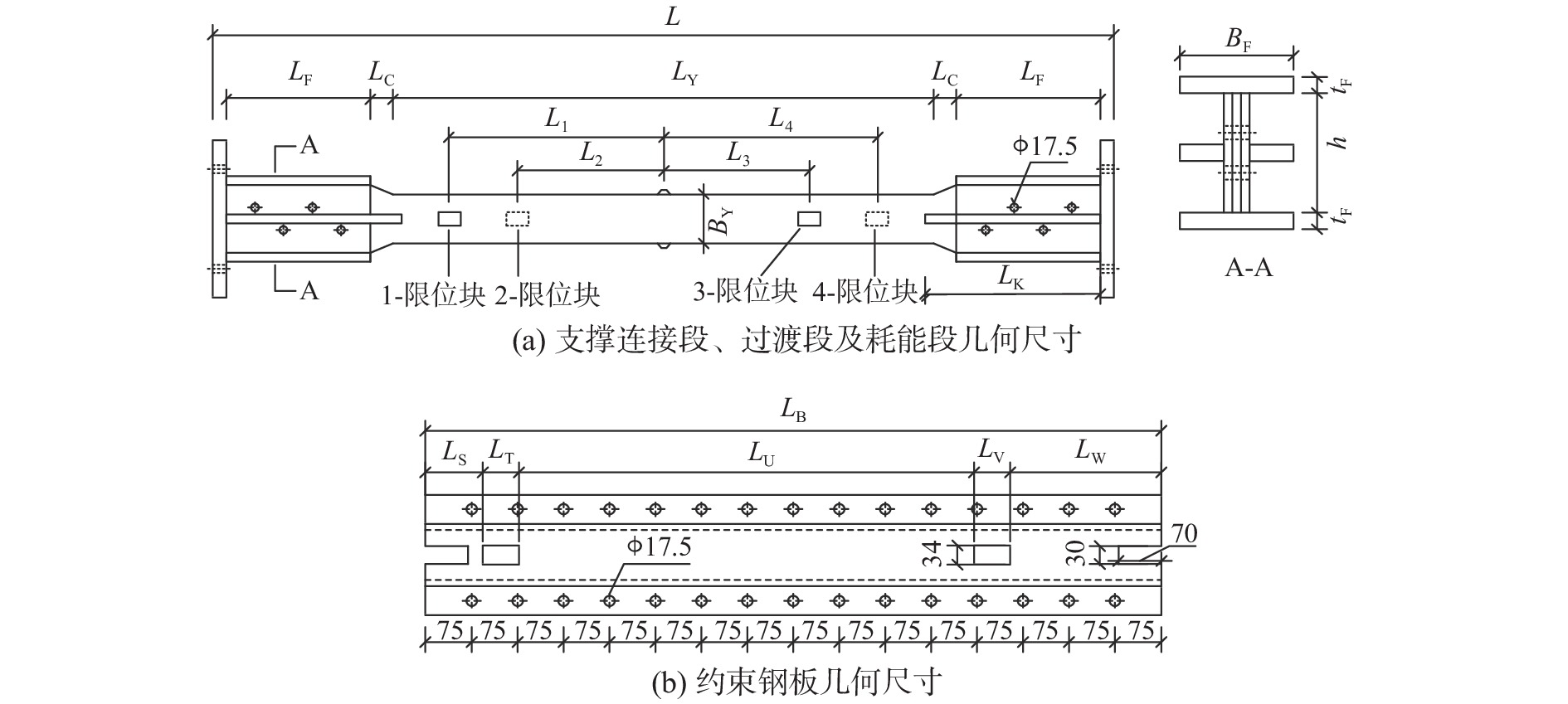
本次试验共设计5个消能限位型钢支撑试件。试件构造如图1所示,试件设计时主要考虑了支撑钢芯截面尺寸及长度、限位块数量以及限位应变等参数。各试件编号及设计参数见表1,表中试件ZC-1为对比试件未设置限位块;试件ZC-2的限位应变为1.0%约为屈服应变的5倍,钢芯截面对应的设计屈服荷载为425 kN;试件ZC-3同其他试件相比减小了钢芯截面尺寸以探究其对支撑附加刚度的影响,钢芯截面对应的屈服荷载为309 kN;试件ZC-4同其他试件相比减小了钢芯长度以探究其对支撑抗震性能的影响,钢芯截面对应的屈服荷载为425 kN;试件ZC5的限位应变为2.0%,主要探究较大限位应变对支撑抗震性能的影响。如图2所示,试件ZC-2~ZC-5沿钢芯工作段长度方向设置4个限位块,为满足图1(e)中限位位移的加工精度同时最大限度的发挥限位功能,于钢芯端部150 mm处设置限位块1、4,并于距限位块1、4约1倍截面高度处设置限位块2、3。各限位块理论限位位移(d1~d4)见表1,其中理论限位位移(di)为限位块中心到钢芯中间截面距离与限位应变的乘积,文献[23]中指出钢板屈服后应变平台段设计参考范围宜在0.15%~2.0%,为此本文选择1.0%、2.0%的限位应变对支撑进行对照设计,以探究不同限位应变对支撑抗震性能的影响。所有部件均采用Q235钢材,槽钢规格为[10,螺栓采用直径为16 mm的M8.8级高强螺栓,螺栓孔距为75 mm。限位块长50 mm×宽40 mm×厚20 mm;钢芯厚10 mm、水平加劲板厚10 mm、垫板厚14 mm、端板厚30 mm;约束钢板厚20 mm×宽200 mm;侧向加劲肋厚20 mm×宽52.5 mm;其余部件尺寸见表2~表3。钢材的主要力学性能见表4。
表 1 试件设计参数Table 1. Design parameters of specimen试件
编号钢芯截面
尺寸/mm2钢芯
长度/mm限位
应变/(%)限位
位移
d1/mm限位
位移
d2/mm限位
位移
d3/mm限位
位移
d4/mmZC-1 110×10 1200 0.0 − − − − ZC-2 110×10 1200 1.0 4.5 3 3 4.5 ZC-3 80×10 1200 1.0 4.5 3 3 4.5 ZC-4 110×10 800 1.0 3.0 2 2 3.0 ZC-5 110×10 1200 2.0 9.0 6 6 9.0 表 2 支撑连接段、过渡段及耗能段几何尺寸Table 2. Geometric dimension of support core unit试件编号 连接段 耗能段 过渡段长
LC/mm支撑总长
L/mmL1/mm L2/mm L3/mm L4/mm 长度
LF/mm翼缘宽
BF/mm翼缘厚
tF/mm侧向加劲
肋长LK/mm水平加劲
板高h/mm长度
LY/mm宽度
BY/mmZC-1 320 135 20 390 190 1200 110 50 2000 − − − − ZC-2 320 135 20 390 190 1200 110 50 2000 450 300 300 450 ZC-3 320 135 20 390 160 1200 80 50 2000 450 300 300 450 ZC-4 270 135 20 320 190 800 110 50 1500 300 200 200 300 ZC-5 320 135 20 390 190 1200 110 50 2000 450 300 300 450 注:L1~L4分别为相应限位块中心到钢芯中间截面的距离。 表 3 约束钢板几何尺寸Table 3. Geometric dimension of restrained steel plate试件编号 LB/mm LS/mm LT/mm LU/mm LV/mm LW/mm ZC-1 1200 − − − − − ZC-2 1200 120.5 59 692.5 56 272 ZC-3 1200 120.5 59 692.5 56 272 ZC-4 800 72 56 445 54 173 ZC-5 1200 116 68 685 62 269 表 4 钢材的主要力学性能Table 4. Mechanical properties of steel用途 钢号 板厚/
mm屈服
强度/MPa极限
强度/MPa断后
伸长率/(%)强屈比 钢芯 Q235 10 386 531 39 1.38 约束钢板 Q235 20 337 450 33 1.34 1.3 试验装置及加载制度
本实验在中国地震局地震工程与工程振动部门重点实验室进行。加载装置由MTS液压伺服作动器、地梁、滑动支座、转接工件及反力架等组成。加载装置示意图及实物图如图3所示。
试验加载采用位移控制方式进行,位移增量为2 mm,每级加载位移循环2次,当试件出现拉断或失稳时终止试验,加载制度如图4所示。加载时,规定MTS液压伺服作动器施加推力时对应的位移及荷载为正,施加拉力时对应的位移及荷载为负。通过在试件耗能段上下对称布置的两个拉线位移计获得支撑轴向位移。利用数据采集系统采集轴向力与轴向位移数据,并以其为依据绘制滞回曲线。
2 试验结果及分析
2.1 破坏特征
各试件最终破坏形态如图5所示。试件ZC-1在进行22 mm第一圈受压时,支撑右端的钢芯沿截面弱轴方向发生局部弯曲失稳破坏,支撑右端约束钢板上第一排的两根螺栓失效,约束钢板右端内表面出现多道摩擦划痕。试件ZC-2在进行18 mm第二圈受拉时,钢芯于支撑右端侧向加劲肋端部截面处被拉断,断面出现颈缩特征,钢芯截面高度由110 mm缩减至104 mm。试件ZC-3在进行18 mm第二圈受拉时,钢芯于靠近支撑左端第一块限位块截面处被拉断,钢芯截面高度由80 mm缩减至70 mm。试件ZC4在进行14 mm第一圈受拉时,钢芯于靠近支撑左端加劲肋端部截面处被拉断,钢芯截面高度由110 mm缩减至105 mm。对支撑拆解后发现,靠近断面处的限位块其焊缝出现裂口。试件ZC-5在进行18 mm第二圈受拉时,钢芯于靠近支撑右端第二块限位块截面处被拉断,断面也出现明显收缩特征,钢芯截面高度由110 mm缩减至102 mm。对支撑拆解后发现,在靠近支撑右端的第一块限位块发生脱落。
试验结束将支撑拆解后发现,钢芯呈现多波屈曲,约束钢板均无屈曲变形处于弹性状态,对钢芯具有较好的侧向约束效果。
2.2 滞回曲线
各试件滞回曲线试验结果如图6所示。由图可见,试验测得的各试件滞回曲线饱满,形状基本对称,规律性强。文中规定施加推力时为滞回曲线的正向加载过程,施加拉力时为滞回曲线的负向加载过程。试件ZC-1与ZC-4滞回曲线的对称性较差,这是由于钢芯与约束钢板之间的间隙较小,正向加载时钢芯变形挤压约束钢板产生法向应力,从而在钢芯与约束钢板之间产生一定的摩擦力,导致正向加载值较大;而在负向加载过程中钢芯变形可在一定程度上得到恢复,钢芯与约束钢板之间的摩擦力逐渐减小直至消失,使得负向加载值小于正向加载值,出现了滞回曲线不对称的现象。试件ZC-1加载位移达到22 mm时达到试验记录的峰值荷载481.4 kN。试件ZC-1正向加载时滞回曲线存在上翘趋势,承载力高于负向加载时的承载力。这主要是正向加载过程中支撑右端的钢芯沿弱轴方向发生局部屈曲,破坏先于此处发生,导致负向加载时的承载力偏低。试件ZC-2加载位移达到12 mm时限位块与限位槽接触开始发挥限位作用,加载位移达到18 mm时达到试验记录的峰值荷载477.2 kN。试件ZC-3加载位移达到12 mm时限位块与限位槽接触开始发挥限位作用,加载位移达到18 mm时达到试验记录的峰值荷载367.4 kN。试件ZC-4加载位移达到8 mm时限位块与限位槽接触开始发挥限位作用,加载位移达到14 mm时达到试验记录的峰值荷载575.8 kN。试件ZC-5加载位移达到受拉14 mm时两块限位块与限位槽接触开始发挥限位作用,加载位移达到受拉18 mm时所有限位块与限位槽接触,并达到试验记录的峰值荷载458.3 kN。相比于试件ZC-1,试件ZC-2~试件ZC-5在正负向加载过程中支撑限位块与约束钢板上的限位槽因接触而发挥限位作用,钢芯与约束钢板共同抵抗轴向荷载,支撑刚度增加,滞回曲线呈现出明显的上升强化特征。钢芯设计长度相同的试件极限位移接近,表明支撑具备发挥限位作用但并不显著降低其变形能力的特征,有利于结构抗震。试件ZC-2~ZC-5发挥限位作用后,钢芯工作耗能段长度减小的同时产生内力重分布,使得钢芯中部其他截面先于限位块处截面发生断裂破坏,钢支撑承载力无法继续提升,变形能力无法继续发挥。试件ZC-3因截面尺寸较小,承载力和滞回曲线所包含面积均小于其他试件。
2.3 骨架曲线及支撑刚度分析
各试件骨架曲线如图7所示。由图可见,各试件的承载力随轴向位移的增大而增大,无明显下降段。与试件ZC-1相比,试件ZC-2~ZC-5的骨架曲线都出现了屈服后上扬趋势,表明支撑可发挥限位作用。试件ZC-2、ZC-3、ZC-4达到限位距离时骨架曲线出现拐点,限位后骨架曲线的斜率大于支撑屈服后的骨架曲线斜率,但小于屈服前骨架曲线斜率。这主要是由于每块限位块与约束钢板的接触面积较小,限位块与钢芯连接焊缝提供的抗弯刚度较小,使得支撑附加刚度有限。实际使用时应考虑增大限位块截面尺寸和数量以及保证焊缝连接质量来进一步提高支撑限位后整体刚度。试件ZC-5限位应变和限位距离较大,限位块发挥限位作用时支撑接近破坏状态,导致其附加二阶刚度的提升作用有限。试件ZC-3因截面尺寸较小,各阶段刚度明显小于其他试件刚度。
消能限位型钢支撑的刚度会随钢芯与约束钢板的受力状态而改变,当钢芯处于弹性状态时,将钢芯与连接段、过渡段串联计算整个支撑的刚度,支撑刚度由式(1)计算。当钢芯进入塑性状态,约束钢板发挥限位作用之前,应对式(1)中的钢芯刚度乘以屈服系数,支撑刚度由式(2)计算。支撑发挥限位作用后,钢芯与约束钢板形成并联工作机制,将约束钢板提供的附加刚度与屈服后钢芯刚度并联考虑,支撑刚度由式(3)计算。
K1=1LyEAy+2LcEAc+2LtEAt (1) K2=11αLyEAy+2LcEAc+2LtEAt (2) K3=11α(EAyLy)+β(EnAfLf)+2LcEAc+2LtEAt (3) 式中:
Ly 、Lc 、Lt 和Lf 分别为钢芯、连接段、过渡段和约束钢板的长度;Ay 、Ac 、At 分别为钢芯、连接段和过渡段的截面面积;Af 为单块限位块与约束钢板的接触面积;n 为限位块数量;E 为钢材弹性模量;α 为屈服后刚度比,取值为0.03;β 为约束钢板弹性刚度利用率,根据试验结果分析建议数值为0.02。支撑各阶段刚度的理论计算值以及试验值见表5。由表可知,试件ZC-1~ZC-5各阶段刚度的理论计算值与试验值相差较小,相对误差均在10%以内,验证了文中计算公式的正确性。试件ZC-2~ZC-5的K3试验结果比K2提升大约37%~140%,约为屈服刚度K2的1.37倍~2.4倍。由于支撑在发挥限位作用时产生内力重分布,约束钢板与钢芯共同工作使得附加刚度K3明显提升,但因限位板尺寸较小以及数量有限,加之限位板焊接于钢芯侧面抗弯刚度较小,在与限位槽接触后的传力过程中弱化了约束钢板和钢芯之间的协同工作能力,导致附加刚度K3小于初始刚度K1。
表 5 支撑各阶段刚度值Table 5. Stiffness values of the brace试件编号 试验值 理论计算值 相对误差/(%) K1/(kN/mm) K2/(kN/mm) K3/(kN/mm) K1/(kN/mm) K2/(kN/mm) K3/(kN/mm) K1 K2 K3 ZC1 182.6 6.2 − 176.0 5.7 − 3.8 8.7 − ZC2 160.8 6.1 14.4 176.0 5.7 13.8 −8.6 7.0 4.3 ZC3 118.4 4.5 11.3 129.9 4.1 12.2 −8.9 9.8 −7.4 ZC4 164.8 5.9 15.0 176.0 5.7 13.8 −6.3 3.5 8.7 ZC5 159.2 6.0 9.3 176.0 5.7 9.7 −9.5 5.2 −4.1 3 近断层地震作用下含消能限位型钢支撑的结构地震易损性分析
3.1 结构模型与地震动选择
本文设计一个RC框架结构作为分析模型1。模型1设计时,结构平面尺寸为42 m×15.9 m,第1层层高4.8 m,第2层~第10层层高3.3 m,总高度34.5 m。抗震设防烈度为7度,抗震等级为二级,设计地震加速度为0.15 g,场地类别为II类,设计地震分组为第二组。梁截面为350 mm×700 mm,柱截面为700 mm×700 mm。混凝土强度等级均为C30,弹性模量为3×104 MPa,梁、柱主筋采用HRB400 级钢筋,箍筋采用HRB335级钢筋。填充墙采用加气混凝土砌块,墙厚200 mm,弹性模量为2000 MPa。考虑底层作为商业用途使用而不布置填充墙,上部楼层均设置填充墙。为了探究消能限位型钢支撑对底层柔性RC框架填充墙结构地震易损性的影响,在模型1的基础上增设消能限位型钢支撑进行加固。模型2采用无限位块的钢支撑进行加固;模型3采用带有限位块的钢支撑进行加固。结构平面和支撑平面布置如图8所示。支撑布置时,按照均匀对称的原则选择在结构首层Y向的第1、3、4、5、6、8轴线的两个边跨,并在结构首层X向的第A、D轴线的两个边跨设置支撑。支撑竖向布置如图9所示,仅在结构首层布置。采用SAP2000有限元程序对上述三种结构进行建模,梁、柱采用框架单元模拟,楼板采用膜单元模拟。有限元模型中钢支撑的几何参数如表6所示。无限位块的钢支撑采用Plastic-Wen模型模拟,屈服力为4136 kN,屈服前刚度为736.6 kN/mm,屈服后刚度为24.3 kN/mm;有限位块的钢支撑采用Plastic-Wen和Takeda模型模拟,其中Takeda模型用于模拟拉压限位功能,支撑的屈服力为4136 kN,屈服前刚度为736.6 kN/mm,屈服后一阶刚度24.3 kN/mm,屈服后二阶刚度50.7 kN/mm。填充墙按照等效斜撑模型进行简化,其有效宽度
a 按式(4)、式(5)计算[24]。由式(4)、式(5)可得,跨度6 m、3.9 m填充墙的有效宽度a 分别为1005 mm、783 mm。a=0.175(λhcol)−0.4rinf (4) λ=[(Emtsin2θ)/(4EfeIhinf)]0.25 (5) 式中:
hcol 为框架柱的高度;rinf 为填充墙的对角线长度;t 为填充墙的厚度;Em 为填充墙的弹性模量;θ 为填充墙对角线与水平方向的夹角;Efe 为框架柱的弹性模量;hinf 为填充墙的高度。表 6 钢支撑几何参数Table 6. Geometric parameters of steel bracing钢芯 约束钢板 限位块 连接段长度/mm 过渡段长度/mm 支撑总长度/mm 长度/mm 宽度/mm 厚度/mm 长度/mm 宽度/mm 厚度/mm 长度/mm 宽度/mm 厚度/mm 4460 440 40 4460 720 60 200 120 60 400 200 5660 已有的研究资料表明,选取10条~20条地震动记录进行IDA分析即可较为准确的评估结构地震需求[25]。因此本文从美国太平洋地震工程研究中心强震数据库中,选取了12条符合结构场地类型的近断层脉冲型地震动,地震动记录详细信息见表7。对于速度脉冲的判别,按照
脉冲指标= 11+e−23.3+14.6(PGVratio)+20.5(Eratio) 大于0.85,且原始记录的速度峰值大于30 cm/s进行筛选[26]。选取的12条近断层脉冲型地震动的加速度反应谱如图10所示。本文使用结构基本周期对应的谱加速度Sa(T1,5%)作为IM指标,楼层最大层间位移角θmax为DM指标。模型一至模型三的基本周期分别为0.79 s、0.72 s、0.70 s。不同性态水平的最大层间位移角限值见表8。表 7 近断层地震动记录Table 7. Near fault ground motion records序号 RSN 台站 震级 断层距/km PGA/g 脉冲周期/s 1 1476 TCU029 7.62 28.04 0.16 5.285 2 1176 YPT150 7.51 1.38 0.32 4.949 3 1510 TCU075 7.62 0.89 0.33 4.998 4 983 JGB022 6.69 5.43 0.57 3.535 5 147 G02140 6.53 8.47 0.26 0.35 6 767 G03090 6.93 12.23 0.37 2.639 7 802 STG090 6.93 7.58 0.33 4.571 8 1052 PKC360 6.69 5.26 0.43 0.728 9 3746 CBF360 7.01 16.44 0.48 1.967 10 568 GIC090 5.80 2.14 0.71 0.805 11 1086 SYL360 6.69 1.74 0.84 2.436 12 180 E05230 6.53 1.76 0.38 4.130 表 8 不同性态水平的最大层间位移角限值[27]Table 8. Maximum interlaminar displacement angle limits at different performance levels结构性能水平 性能状态描述 楼层最大层间位移角/(%) 立即使用(IO) 结构轻度破坏 1 生命安全(LS) 结构遭受一定的破坏 2 防止倒塌(CP) 结构遭受严重破坏 4 3.2 IDA曲线分析
对3.1中选取的12条近断层脉冲型地震动进行调幅处理,调幅后的Sa(T1, 5%)从0.10g开始,按照0.2增量步依次递增,直到IDA曲线斜率小于20%初始斜率时或结构最大层间位移角达到0.1时认为结构遭受严重破坏终止分析。IDA分析曲线如图11所示,其横轴为最大层间位移角,纵轴为地震动强度。由图11可见,初始阶段IDA曲线离散性较小且呈直线上升趋势,表明此时结构处于弹性阶段;随地震动强度的增加,IDA曲线离散性增大,曲线斜率逐渐减小,表明结构进入到弹塑性阶段;随地震动强度的进一步增强,部分曲线的最大层间位移角呈现出不增反减的现象,随后曲线斜率大幅度降低,这是由于结构经历了短暂的强化之后迅速进入倒塌状态。
3.3 地震概率需求模型
文献[28]指出楼层最大层间位移角θmax与地震动强度参数Sa
(T1, 5%)之间满足式(6): θmax (6) 对式(6)两边取对数得式(7):
\ln \left( {\theta _{\max} } \right) = \ln \alpha + \beta \ln \left[ {S_{\rm a}\left( {T_1,5\text{%} } \right)} \right] (7) 式(7)中的
\ln \alpha 、\beta 通过对IDA分析数据进行统计回归得到。将计算出的\alpha 、\beta 代入式(8)即可得到结构在各个性态水平下的失效概率公式P_{\rm f} 。式(8)中\varPhi 为标准正态分布函数;不同性态水平所对应的地震动强度平均值\lambda _{\rm c} 可由IDA数据得到;根据HAZUS99[29],当以Sa(T1,5%)为地震动强度指标时,\sqrt {\xi _{\rm c}^2 + \xi _{\rm d}^2} 取0.4。P_{\rm f} = \varPhi \left( {\frac{{\ln {{{\{ {\alpha [ {S_{\rm a}( {T_1,5\text{%} } )} ]} }^\beta }/\lambda _{\rm c}} \}}}{{\sqrt {\xi _{\rm c}^2 + \xi _{\rm d}^2} }}} \right) (8) 将图11中的数据取对数,再进行线性回归,可得各模型ln[Sa(T1,5%)]−ln(θmax)的回归曲线,回归分析结果如图12所示。
3.4 地震易损性分析
将不同的地震动强度代入式(8)中,并查询正态分布表,即可得到结构在不同地震动强度下的超越概率。不同性态水平下结构的地震易损性曲线如图13所示。由图13可得,在IO、LS和CP三种状态下,当地震动强度达到相同水平时各个结构模型的超越概率呈现出以下特点,即模型3的超越概率最小,其次为模型2,模型1的超越概率最高,这说明在底层柔性框架填充墙结构中增设消能限位型钢支撑,可有效提升其抗震性能,但相比无限位块的钢支撑,设置含有限位块的钢支撑结构的抗倒塌性能更优。
美国应用技术委员会提出了结构倒塌储备系数CMR[30],是评估结构整体抗震倒塌能力的重要指标,其计算公式如下。
CMR=S_{\rm a}{\left(T_1\right)}_{50\text{%}}/S_{\rm a}{\left(T_1\right)}_{{\text{大震}}} (9) 其中:
S_{\rm a}{\left( {T_1} \right)_{50\text{%} }} 为结构在CP状态下,超越概率达到50%时对应的S_{\rm a}\left( {T_1} \right) 值;S_{\rm a}{\left(T_1\right)}_{{\text{大震}}} 为对应设防烈度的罕遇地震作用下结构的S_{\rm a}\left( {T_1} \right) 值。各模型的倒塌储备系数见表9。表 9 结构倒塌储备系数CMRTable 9. Structural collapse reserve factor CMR模型编号 Sa(T1)50%/g Sa(T1) / g CMR 模型1 0.60 0.39 1.54 模型2 1.0 0.42 2.38 模型3 1.25 0.44 2.84 由表9可知,模型1的倒塌储备系数为1.54,设置不同类型的支撑后,模型2与模型3的CMR分别上升至2.38和2.84,上升幅度分别为55%和84%,表明增设消能限位型钢支撑使底层柔性框架填充墙结构的倒塌储备系数得到增强,减小了结构在大震作用下的倒塌概率。相比于无限位块的钢支撑,设置含有限位块的钢支撑结构的倒塌储备系数更高,更有利于提升结构的抗倒塌能力。
4 结论
通过对消能限位型钢支撑进行抗震性能试验,主要得到以下结论:
(1) 限位应变为由1%增为2%时限位距离增大,在限位块发挥限位作用时支撑接近破坏状态,导致其附加刚度发挥作用有限。工作段长度小的支撑变形能力最差,钢芯截面减小后支撑的承载力明显减小且滞回曲线饱满程度弱于其他支撑。
(2) 增设限位块可使支撑发挥限位作用并提供附加刚度,其值约为屈服刚度试验结果的1.37倍~2.4倍。实际使用时,需考虑增大限位块的刚度以增加钢芯与约束钢板的共同工作能力,保证附加刚度作用的充分发挥。
(3) 支撑刚度的计算结果与试验值吻合较好,说明文中刚度分析方法是可行的。增设消能限位型钢支撑和普通钢支撑可使结构的倒塌储备系数分别增加84%和55%,有利于提升底层柔性结构的抗倒塌能力。
-
表 1 试件设计参数
Table 1 Design parameters of specimen
试件
编号钢芯截面
尺寸/mm2钢芯
长度/mm限位
应变/(%)限位
位移
d1/mm限位
位移
d2/mm限位
位移
d3/mm限位
位移
d4/mmZC-1 110×10 1200 0.0 − − − − ZC-2 110×10 1200 1.0 4.5 3 3 4.5 ZC-3 80×10 1200 1.0 4.5 3 3 4.5 ZC-4 110×10 800 1.0 3.0 2 2 3.0 ZC-5 110×10 1200 2.0 9.0 6 6 9.0 表 2 支撑连接段、过渡段及耗能段几何尺寸
Table 2 Geometric dimension of support core unit
试件编号 连接段 耗能段 过渡段长
LC/mm支撑总长
L/mmL1/mm L2/mm L3/mm L4/mm 长度
LF/mm翼缘宽
BF/mm翼缘厚
tF/mm侧向加劲
肋长LK/mm水平加劲
板高h/mm长度
LY/mm宽度
BY/mmZC-1 320 135 20 390 190 1200 110 50 2000 − − − − ZC-2 320 135 20 390 190 1200 110 50 2000 450 300 300 450 ZC-3 320 135 20 390 160 1200 80 50 2000 450 300 300 450 ZC-4 270 135 20 320 190 800 110 50 1500 300 200 200 300 ZC-5 320 135 20 390 190 1200 110 50 2000 450 300 300 450 注:L1~L4分别为相应限位块中心到钢芯中间截面的距离。 表 3 约束钢板几何尺寸
Table 3 Geometric dimension of restrained steel plate
试件编号 LB/mm LS/mm LT/mm LU/mm LV/mm LW/mm ZC-1 1200 − − − − − ZC-2 1200 120.5 59 692.5 56 272 ZC-3 1200 120.5 59 692.5 56 272 ZC-4 800 72 56 445 54 173 ZC-5 1200 116 68 685 62 269 表 4 钢材的主要力学性能
Table 4 Mechanical properties of steel
用途 钢号 板厚/
mm屈服
强度/MPa极限
强度/MPa断后
伸长率/(%)强屈比 钢芯 Q235 10 386 531 39 1.38 约束钢板 Q235 20 337 450 33 1.34 表 5 支撑各阶段刚度值
Table 5 Stiffness values of the brace
试件编号 试验值 理论计算值 相对误差/(%) K1/(kN/mm) K2/(kN/mm) K3/(kN/mm) K1/(kN/mm) K2/(kN/mm) K3/(kN/mm) K1 K2 K3 ZC1 182.6 6.2 − 176.0 5.7 − 3.8 8.7 − ZC2 160.8 6.1 14.4 176.0 5.7 13.8 −8.6 7.0 4.3 ZC3 118.4 4.5 11.3 129.9 4.1 12.2 −8.9 9.8 −7.4 ZC4 164.8 5.9 15.0 176.0 5.7 13.8 −6.3 3.5 8.7 ZC5 159.2 6.0 9.3 176.0 5.7 9.7 −9.5 5.2 −4.1 表 6 钢支撑几何参数
Table 6 Geometric parameters of steel bracing
钢芯 约束钢板 限位块 连接段长度/mm 过渡段长度/mm 支撑总长度/mm 长度/mm 宽度/mm 厚度/mm 长度/mm 宽度/mm 厚度/mm 长度/mm 宽度/mm 厚度/mm 4460 440 40 4460 720 60 200 120 60 400 200 5660 表 7 近断层地震动记录
Table 7 Near fault ground motion records
序号 RSN 台站 震级 断层距/km PGA/g 脉冲周期/s 1 1476 TCU029 7.62 28.04 0.16 5.285 2 1176 YPT150 7.51 1.38 0.32 4.949 3 1510 TCU075 7.62 0.89 0.33 4.998 4 983 JGB022 6.69 5.43 0.57 3.535 5 147 G02140 6.53 8.47 0.26 0.35 6 767 G03090 6.93 12.23 0.37 2.639 7 802 STG090 6.93 7.58 0.33 4.571 8 1052 PKC360 6.69 5.26 0.43 0.728 9 3746 CBF360 7.01 16.44 0.48 1.967 10 568 GIC090 5.80 2.14 0.71 0.805 11 1086 SYL360 6.69 1.74 0.84 2.436 12 180 E05230 6.53 1.76 0.38 4.130 表 8 不同性态水平的最大层间位移角限值[27]
Table 8 Maximum interlaminar displacement angle limits at different performance levels
结构性能水平 性能状态描述 楼层最大层间位移角/(%) 立即使用(IO) 结构轻度破坏 1 生命安全(LS) 结构遭受一定的破坏 2 防止倒塌(CP) 结构遭受严重破坏 4 表 9 结构倒塌储备系数CMR
Table 9 Structural collapse reserve factor CMR
模型编号 Sa(T1)50%/g Sa(T1) / g CMR 模型1 0.60 0.39 1.54 模型2 1.0 0.42 2.38 模型3 1.25 0.44 2.84 -
[1] 李宗超, 陈学良, 吴健, 等. 台湾地区花莲地震(Ms6.5)工程地震动参数特征分析[J]. 建筑结构, 2018, 48(增刊 2): 308 − 313. Li Zongchao, Chen Xuelang, Wu Jian, et al. Engineering seismic parameters characteristic analysis of Hualian earthquake (Ms6.5) inTaiwan region [J]. Building Structure, 2018, 48(Suppl 2): 308 − 313. (in Chinese)
[2] Kun Ji, Ruizhi Wen, Yefei Ren, et al. Nonlinear seismic site response classification using K-means clustering algorithm: Case study of the September 6, 2018 Mw6.6 Hokkaido Iburi-Tobu earthquake, Japan [J]. Soil Dynamics and Earthquake Engineering, 2020, 128: 105907.1 − 105907.14.
[3] 葛庆子, 马华. 带纤维混凝土耗能器底层柔性结构的抗震研究[J]. 工程抗震与加固改造, 2012, 34(5): 20 − 26. doi: 10.3969/j.issn.1002-8412.2012.05.004 Ge Qingzi, Ma Hua. Aseismic study of flexible structures with fiber reinforced concrete dampers [J]. Earthquake Resistant Engineering and Retrofitting, 2012, 34(5): 20 − 26. (in Chinese) doi: 10.3969/j.issn.1002-8412.2012.05.004
[4] 李振宝, 马华, 闫维波, 等. 带RC耗能器-限位斜撑框架抗震性能研[J]. 建筑结构, 2008(11): 65 − 67. Li Zhenbao, Ma Hua, Yan Weibo, et al. Seismic behavior of frame with RC dampers and lock-up braces [J]. Building Structure, 2008(11): 65 − 67. (in Chinese)
[5] 曹万林, 刘建民, 王东增, 等. 异型柱框架结构底层支撑合理设置研究[J]. 地震工程与工程振动, 1997(1): 77 − 82. Cao Wanlin, Liu Jianmin, Wang Dongzeng, et al. Research on the reasonable setting of bottom support of special-shaped column frame structure [J]. Earthquake Engineering and Engineering Vibration, 1997(1): 77 − 82. (in Chinese)
[6] Rahai A R, Alinia M M. Performance evaluation and strengthening of concrete structures with composite bracing members [J]. Construction and Building Materials, 2008, 10(22): 2100 − 2110.
[7] 武娜, 高向宇, 李自强, 等. 用带防屈曲支撑的内嵌式钢框架加固混凝土框架的试验研究[J]. 工程力学, 2013, 30(12): 189 − 198. doi: 10.6052/j.issn.1000-4750.2012.08.0618 Wu Na, Gao Xiangyu, Li Ziqiang, et al. Experimental study on reinforced concrete frames retrofitted with in-filled steel frames and connected brbs [J]. Eengineering Mechanics, 2013, 30(12): 189 − 198. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.08.0618
[8] 陆伟东, 蓝宗建, 刘伟庆. 阻尼支撑控制结构薄弱层的设计方法研究[J]. 工程抗震与加固改造, 2011, 33(2): 57 − 62. doi: 10.3969/j.issn.1002-8412.2011.02.010 Lu Weidong, Lan Zhongjian, Liu Weiqing. Design method of damped bracings to control the structure with weak story [J]. Earthquake Resistant Engineering and Retrofitting, 2011, 33(2): 57 − 62. (in Chinese) doi: 10.3969/j.issn.1002-8412.2011.02.010
[9] 欧进萍, 马宁, 吴斌. 一字形内芯全钢防屈曲支撑设计方法[J]. 工程力学, 2012, 29(10): 137 − 141, 148. doi: 10.6052/j.issn.1000-4750.2011.01.0017 Ou Jinping, Ma Ning, Wu Bin. Design of all-stell buckling restrained brace with a flat plate core [J]. Eengineering Mechanics, 2012, 29(10): 137 − 141, 148. (in Chinese) doi: 10.6052/j.issn.1000-4750.2011.01.0017
[10] 郭彦林, 姜子钦, 王小安, 等. 双矩管装配式防屈曲支撑约束刚度取值研究[J]. 工程力学, 2015, 32(4): 22 − 32. doi: 10.6052/j.issn.1000-4750.2014.04.0322 Guo Yanlin, Jiang Ziqin, Wang Xiaoan, et al. Study on restraing stiffness of double rectaangular tube assembled buckling-restrained beace [J]. Eengineering Mechanics, 2015, 32(4): 22 − 32. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.04.0322
[11] 姜子钦, 郭彦林, 张博浩, 等. 双矩管装配式防屈曲支撑设计理论研究[J]. 工程力学, 2015, 32(6): 41 − 51, 61. doi: 10.6052/j.issn.1000-4750.2014.06.0502 Jiang Ziqin, Guo Yanlin, Zhang Bohao, et al. Theretical study on design methods for double rectangular tube assembled buckling-restrained beaces [J]. Eengineering Mechanics, 2015, 32(6): 41 − 51, 61. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.06.0502
[12] 杨璐, 卫璇, 施刚, 等. LY315钢屈曲约束支撑耗能性能试验研究[J]. 工程力学, 2019, 36(1): 200 − 206. doi: 10.6052/j.issn.1000-4750.2017.11.0879 Yang Lu, Wei Xuan, Shi Gang, et al. Experiment on energy dissipation performance of LY315 steel buckling-restrained braces [J]. Eengineering Mechanics, 2019, 36(1): 200 − 206. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.11.0879
[13] Iwata M, Kato T, Wada A. Buckling-restrained braces as hysteretic dampers [C]// Proceedings of Third International Conference on Behavior of Steel Structures in Seismic Areas. Montreal, Canada: Rotterdam and Brookfield, 2000: 3338.
[14] Nip K H , Gardner L, Elghazouli A Y. Cyclic testing and numerical modelling of carbon steel and stainless steel tubular bracing members [J]. Engineering Structures, 2010, 32(2): 424 − 441. doi: 10.1016/j.engstruct.2009.10.005
[15] Oda H, Usami T. Fabricating buckling-restrained braces from existing Hsectionbracing members: Experimental study [J]. Journal of Structural Engineering, JSCE, 2010, 56(A): 499 − 510.
[16] 邓雪松, 纪宏恩, 周云, 等. 开孔板式屈曲约束支撑拟静力滞回性能试验研究[J]. 土木工程学报, 2015, 48(1): 49 − 55. Deng Xuesong, Ji Hongen, Zhou Yun, et al. Quasi-static cyclic tests on hysteretic behavior of a perforating plate buckling restrained brace [J]. China Civil Engineering Journal, 2015, 48(1): 49 − 55. (in Chinese)
[17] 周云, 龚晨, 钟根全, 等. 开孔参数对装配式开孔钢板屈曲约束支撑性能影响研究[J]. 建筑结构学报, 2018, 39(增刊 2): 328 − 335. Zhou Yun, Gong Chen, Zhong Genquan, et al. Performance of perforated steel-plate assembled buckling-restrained brace with different perforated parameters [J]. Journal of Building Structures, 2018, 39(Suppl 2): 328 − 335. (in Chinese)
[18] 万金国, 杨凡, 李文峰, 等. 双屈服点免断裂屈曲约束支撑性能试验与数值模拟[J]. 建筑结构, 2013, 43(17): 105 − 108. Wan Jinguo, Yang Fan, Li Wenfeng, et al. Experiment research and mechanical simulation of BRB with double yield points and non-fracture [J]. Building Structure, 2013, 43(17): 105 − 108. (in Chinese)
[19] 赵堃宇, 闫维明, 贾洪, 等. 销钉式防屈曲支撑性能试验研究[J]. 工程抗震与加固改造, 2013, 35(5): 120 − 126. doi: 10.3969/j.issn.1002-8412.2013.05.020 Zhao Kunyu, Yan Weiming, Jia Hong, et al. Experimental research on performance of pin type BRB [J]. Earthquake Resistant Engineering and Retrofitting, 2013, 35(5): 120 − 126. (in Chinese) doi: 10.3969/j.issn.1002-8412.2013.05.020
[20] 周云, 钟根全, 陈清祥, 等. 不同构造钢板装配式屈曲约束支撑性能试验研究[J]. 土木工程学报, 2017, 50(12): 9 − 17. Zhou Yun, Zhong Genquan, Chen Qingquan, et al. Experimental study on hysteretic performance of steel-plate assembled buckling-restrained braces with different constructional details [J]. China Civil Engineering Journal, 2017, 50(12): 9 − 17. (in Chinese)
[21] 徐龙河, 孙雨生, 要世乾, 等. 装配式自复位耗能支撑恢复力模型与试验验证[J]. 工程力学, 2019, 36(6): 119 − 127. doi: 10.6052/j.issn.1000-4750.2018.04.0249 Xu Longhe, Sun Yusheng, Yao Shiqian, et al. Restoring force model and experimental verification of an assembled self-centering energy dissipation brace [J]. Eengineering Mechanics, 2019, 36(6): 119 − 127. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.04.0249
[22] 严红, 潘鹏, 王元清, 等. 一字形全钢防屈曲支撑耗能性能试验研究[J]. 建筑结构学报, 2012, 33(11): 142 − 149. Yan Hong, Pan Peng, Wang Yuanqing, et al. Experimental study of buckling-restrained braces with in-line steel core plate encased in double web wide flange steel outer unit [J]. Journal of Building Structures, 2012, 33(11): 142 − 149. (in Chinese)
[23] 陈奎. 可置换低屈服点金属钢节点的构造及特点 [D]. 北京: 北京工业大学, 2016: 37 − 39. Chen Kui. Seismic behavior and structure damage analysis of the replaceable beam-column connection with low yield point steel [D]. Beijing: Beijing University of Technology, 2016: 37 − 39. (in Chinese)
[24] Hashemi S A. Seismic evaluation of reinforced concrete buildings including effects of masonry infill walls [D]. Berkeley: University of California, 2007.
[25] Shome N. Probabilistic seismic demand analysis of nonlinear structures [D]. Stanford: Stanford University, 1999.
[26] Baker J W. Quantitative classification of near-fault ground motions using wavelet analysis [J]. Bulletin of Seismological Society of America, 2007, 97(5): 1486 − 1501. doi: 10.1785/0120060255
[27] FEMA. Prestandard and commentary for the seismic rehabilitation of buildings [M]. Washington, D.C.: Federal Emergency Management Agency, 2000.
[28] 任浩, 田勤虎, 张炜超, 等. 基于IDA方法的钢筋混凝土框架结构地震易损性分析[J]. 建筑结构, 2019, 49(增刊 2): 350 − 355. Ren Hao, Tian Qinhu, Zhang Weichao, et al. Seismic vulnerability analysis of reinforced concrete frame structure based on IDA method [J]. Building Structure, 2019, 49(Suppl 2): 350 − 355. (in Chinese)
[29] FEMA. HAZUS-MH technical manual [M]. Washington, D.C.: Federal Emergency Management Agency, 2003.
[30] Deierlein G G, Liel A B. ATC63 methodology for evaluating seismic collapse safety of archetype buildings [C]// Proceedings of ASCE-SEI Structures Congress, Vancouver, 2008.
-
期刊类型引用(3)
1. 吴山,何浩祥,兰炳稷. 面向均匀损伤的RC框架结构抗震优化设计方法. 工程力学. 2024(04): 210-221 .  本站查看
本站查看
2. 马传普. 焊接H型不锈钢梁柱抗震性能试验研究. 四川水泥. 2024(10): 37-39 .  百度学术
百度学术
3. 周洲,于晓辉,吕大刚,韩淼. 钢筋锈蚀与余震对RC框架结构地震损伤与易损性的影响分析. 工程力学. 2023(09): 203-213+256 .  本站查看
本站查看
其他类型引用(4)




 下载:
下载: