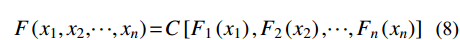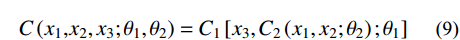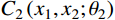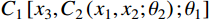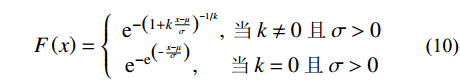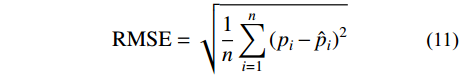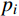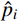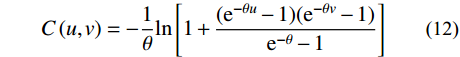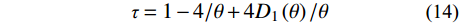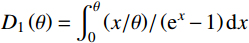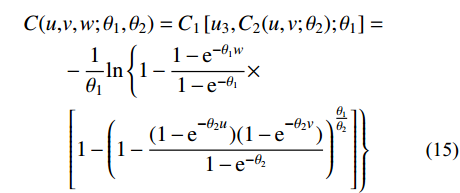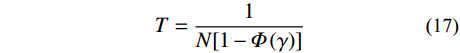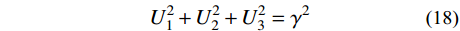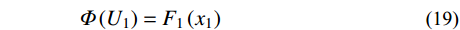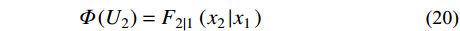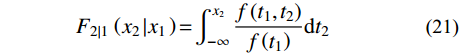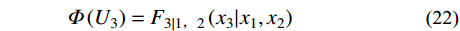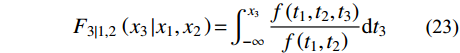ENVIRONMENTAL CONTOUR OF WIND-WAVE-STORM SURGES INDUCED BY TYPHOONS
-
摘要: 台风登陆时常伴随强风、巨浪和风暴潮,如何获取台风下的风、浪、潮数据并确定给定重现期下的环境参数成为制约跨海桥梁设计的关键科学问题。以跨海桥梁众多的舟山海域为例,采用SWAN+ADCIRC耦合模型,对过去32年间影响该海域的49次台风过程依次开展数值模拟,利用模拟出的台风作用下风、浪、潮参数建立100年重现期下的环境等值面,讨论了环境参数选取方法对环境等值面模型的影响。研究表明:该文建立的数值模型能为后期构建联合概率及环境等值面模型提供可靠的数据来源;三维嵌套Frank Copula能较好拟合风-浪-潮三维联合概率分布;给定重现期的环境等值面形状受数据选取时刻影响较大,其中风暴潮增水最大值对选取方法最为敏感。
-
关键词:
- 台风 /
- 波浪 /
- 风暴潮 /
- SWAN+ADCIRC 模式 /
- 三维嵌套Copula /
- 一阶逆可靠度方法
Abstract: Typhoons usually induce strong winds, huge waves and storm surges when they make landfall. The acquisition of data of the typhoon-generated winds, waves, and storm surges and the determination of the corresponding environmental design parameters with a given return period are two critical issues that restrict the design of sea-crossing bridges. Taking Zhoushan sea area where many sea-crossing bridges are located as an example, a SWAN+ADCIRC coupling model was employed to simulate the metocean conditions under typhoons. Hindcast simulations of 49 typhoons that affected the example site in the past 32 years were conducted. The environmental contours with a 100-year return period were calculated using the simulated winds, waves and storm surges. The influence of the data selection on the environmental contours was investigated. The results show that: The numerical model employed in this study can provide reliable data for developing joint probability and environmental contour models; The nested three-dimensional Copula well fits the trivariate joint probability distribution of typhoon-induced winds, waves and storm surges. The environmental contours with a given return period depend on the data selection method, and the maximum storm surge is the most sensitive parameter to this factor. -
台风是我国东南沿海常见的灾害性天气[1],登陆时常伴随着强风、巨浪、风暴潮,给近海工程,特别是跨海大桥的设计、建造和安全运营带来了严峻挑战[2]。近年来,桥梁风致振动[3-7]、波浪对桥梁的动力作用[8-11]、风-浪作用下的桥梁动力响应得到了较多关注[12-13]。风暴潮作为台风造成的海面异常升高现象,会加剧波浪对桥梁基础等结构的冲击作用[14]。随着跨海大桥跨径增大,风-浪-风暴潮增水(以下简称“潮”)共同作用下桥梁结构动力响应愈发明显,如何获取台风下的风、浪、潮数据并且确定给定重现期下的荷载参数成为制约跨海桥梁设计的关键科学问题。
我国过去在确定给定重现期下桥梁的风、浪、潮荷载参数时,常忽略变量间的相关性[2]。然而,台风下的风、浪、潮参数并非相互独立。现场实测是获取长期风、浪、潮数据以开展后续研究的有效途径,但由于布点有限、数据保密以及仪器损坏等原因,获取台风下的风、浪、潮数据非常困难。常根据有限的资料计算给定重现期下环境变量,陈子煜等[15]使用1984年−2005年间中国南海海域的观测资料推测了100年一遇的风暴增水和波高。近年来,随着数值模拟技术的快速发展,台风作用下海洋环境参数数值模拟得到了广泛应用。Chen等[16]基于FVCOM耦合模型模拟了中国沿海9个站点35年波高与风暴潮参数,并将其用于计算联合概率密度。魏凯等[17]则利用SWAN+ADCIRC开展了台风下近岸海域波浪-风暴潮耦合数值模拟,并通过实测数据验证了方法的有效性。
获取台风期间风、浪、潮数据之后,下一步就是如何考虑三者的相关性并确定不同重现期下的环境荷载参数。API RP 2A-WSD设计规范[18]和DNV-OS-J101设计规范[19]指出,在建立多个随机环境参数与重现期的关系时,可先建立多维联合概率分布,然后构造环境等值面模型。Copula函数可将多个一维边缘分布连接起来,描述多变量间相关结构[20],近年来被广泛应用于海洋环境下的多参数联合概率分析。环境等值面是由环境变量构成的面,可根据概率分布由一阶逆可靠度理论(IFORM)得到,其提供了给定重现期下多个环境荷载参数的组合[21]。上述研究为构建台风作用下的风-浪-潮三维联合概率和环境等值面模型提供了重要思路。
因此,本文以在建的西堠门公铁两用大桥所处的舟山海域为例,采用SWAN+ADCIRC建立台风作用下海洋环境参数数值模型,通过对1987年−2018年49条历史台风下的风、浪、潮进行数值模拟,获得台风下的风、浪、潮数据;采用嵌套Copula函数拟合上述数据,构造风-浪-潮三维联合概率分布;根据IFORM建立并得到了100年重现期下的环境等值面;重点讨论了4种环境参数选取方法对环境等值面模型的影响。
1 台风下风-浪-潮参数数值模拟
1.1 台风风场模型
本文的台风风场模型由参数风场(包含移行风场和梯度风场)及背景风场叠加组合而成。其中,移行风场采用宫崎正卫模型[22],移行风速vm根据台风中心的位置变化进行计算,其表达式为:
vm=vmcexp(−r500000) (1) 式中:vmc为台风中心移行风速;r为计算点到台风中心的距离。
梯度风场采用Holland气压模型[23],梯度风速vg通过求解环流空气质点的离心力、科氏力和压力梯度力构成的梯度方程得到(忽略地面摩擦力的影响),其表达式为:
vg=√v2maxe[1−(R/r)B](R/r)B+(rf2)2−rf2 (2) 式中:f为科氏力参数,
f=2ωsinφ ,ω为地球自转的角速度,φ是纬度;B为气压剖面参数,可利用最大梯度风速vmax进行求解,如式(3),其中,vmax 近似取从中国台风网获得的最大持续风速[17]。R为最大风速半径,采用Zhou等[24]提出的式(4)进行计算: B≈vmax (3) R = 29.178\exp \left[ {0.0158\left( {{P_{\rm{0}}} - 900} \right)} \right] (4) 式中:P0为台风中心气压;ρa为空气密度;ΔP为外围气压(取1010 hPa)与中心气压P0之差。
梯度风vg通过0.9的高度系数从大气边界层转换到海面高度[25],海面高度处的梯度风vgs与根据台风中心位置变化计算得到的海面高度处的移行风矢量叠加合成经验台风场ve,如式(5)。
{v_{\rm{e}}} = {v_{{\rm{gs}}}} + {v_{\rm{m}}} (5) 背景风场较参数风场能更精确地模拟距台风中心较远的风场,可利用其对参数风场进行改善[26]。本文选用Cross-Calibrated Multi-Platform(CCMP)再分析数据库提供的全球尺度的背景风场与上述参数风场按照距离加权叠加,如式(6)[27],得到改进的台风风场。在台风中心处为经验台风场,离台风中心较远处为CCMP背景风,过渡区为经验台风场ve
与CCMP背景风vb的结合,通过与到台风中心处距离相关的系数α进行叠加,α的计算公式如式(7)。 {v_{\sup }} = \left\{ {\begin{array}{*{20}{l}} {{v_{\rm{e}}}} ,\\ {\left( {1 - \alpha } \right)}{v_{\rm{e}}} + \alpha {v_{{\rm{b}}{\rm{ }}}},\\ {{v_{\rm{b}}}} , \end{array}} \right.\;\;\begin{array}{*{20}{l}} {r < {R_1}} \\ {{R_1} \leqslant r \leqslant {R_2}} \\ {r > {R_2}} \end{array} (6) \alpha = \frac{{r - {R_1}}}{{{R_2} - {R_1}}}\qquad\qquad\qquad\qquad\qquad\qquad (7) 式中:R1取300 km;R2取400 km。
1.2 边界水位模型
边界水位采用TPXO9_atlas模式中8个主要分潮(M2、S2、N2、K2、K1、O1、P1、Q1)进行模拟。
1.3 台风下波浪-风暴潮耦合模拟方法
台风作用下波浪-风暴潮的模拟利用SWAN+ADCIRC耦合模式进行。SWAN基于波作用量守恒方程进行计算,其考虑了风能输入,白帽耗散、底部摩擦,深度诱导破碎及非线性波-波相互作用等物理过程[2]。ADCIRC模式基于广义波动连续性方程和动量方程求解流速、水位。SWAN与ADCIRC共用一套网格,在台风风场和边界水位的共同驱动下,ADCIRC将计算出的流速、水位传递给SWAN,SWAN再将其计算出的波浪辐射应力传递给ADCIRC以实现耦合[25],如图1所示。风速(Vw)、有效波高(Hs)可由耦合模式直接输出,风暴潮(S)可利用数值模拟出的水位减去天文潮获得。其中,天文潮位利用无风场输入、仅由边界水位驱动的ADCIRC模式进行模拟,这里的边界水位同样由TPXO9_atlas模式进行计算。上述数值模拟方法的有效性已在作者之前的研究[25]中进行过验证。
2 数值模型验证及风、浪、潮选取
2.1 算例海域数值模型
常年受台风影响的舟山海域位于浙江省东北部,该地区周边经济发达,人口稠密,海域内建有多座跨海大桥。以舟山西堠门公铁两用大桥所在海域为中心,建立范围大致为115°E~127°E,25°N~41°N(网格边界为曲线,非矩形),包含了渤海、黄海以及东海部分海域的数值模型,如图2所示。工程海域附近网格尺寸最小为150 m,外海最大网格尺寸约60 km。采用非结构化三角形网格,网格数为70144,节点数为37064。
2.2 数值模型验证
合成风场的准确性通过对9711号台风“温妮”及1509号台风“灿鸿”期间的风速模拟进行验证。台风“温妮”路径如图3中带矩形标记的线所示。利用合成风场模拟了1997年8月17日0时−1997年8月20日0时的风场,以定海站的实测风速[28]进行对比验证,如图4(a)所示。台风“灿鸿”路径如图3中带圆形标记的线所示。同时利用合成风场模拟了2015年7月8日12 时−2015年7月12日0时的风场,以南麂岛站实测风速[29]进行对比验证,如图4(b)所示。合成风场对台风期间的风速变化趋势及极值均吻合较好。
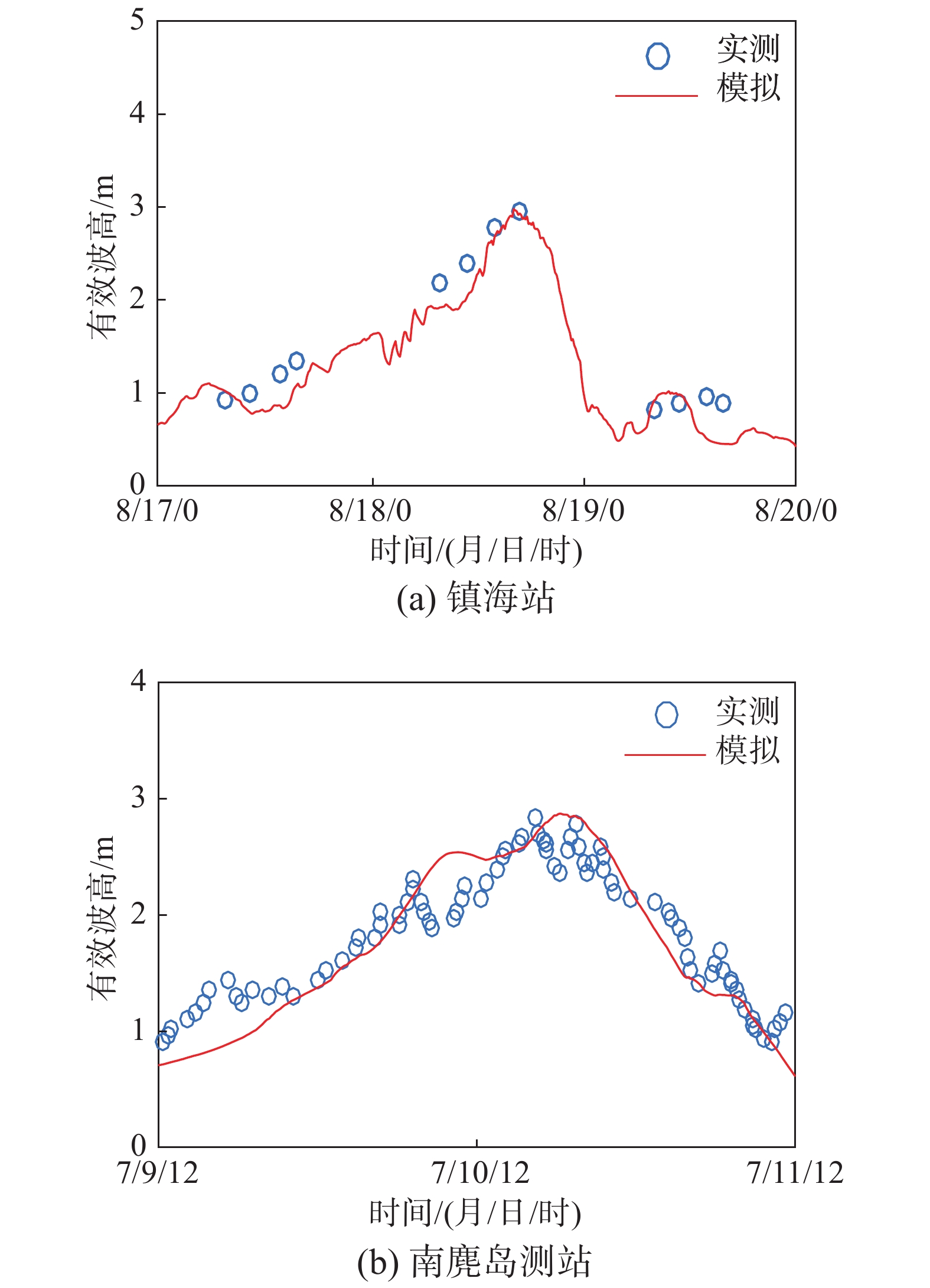
为验证数值模型模拟波高的有效性,模拟了1997年8月17日0时−1997年8月20日0时9711号台风“温妮”期间的环境参数。以镇海站的实测波高[28]进行对比验证,如图5(a)所示,实测最大波高为2.97 m,模拟最大波高为2.98 m,相对误差为0.3%。还模拟了2015年7月9日12时−2015年7月11日12时1509号台风“灿鸿”。图5(b)给出了在南麂岛测站的数值模拟与实测有效波高[29]的对比图。由图5(b)知,实测最大有效波高为5.69 m,模拟最大有效波高为5.74 m,相对误差为0.9%。数值模拟具有较高精度。
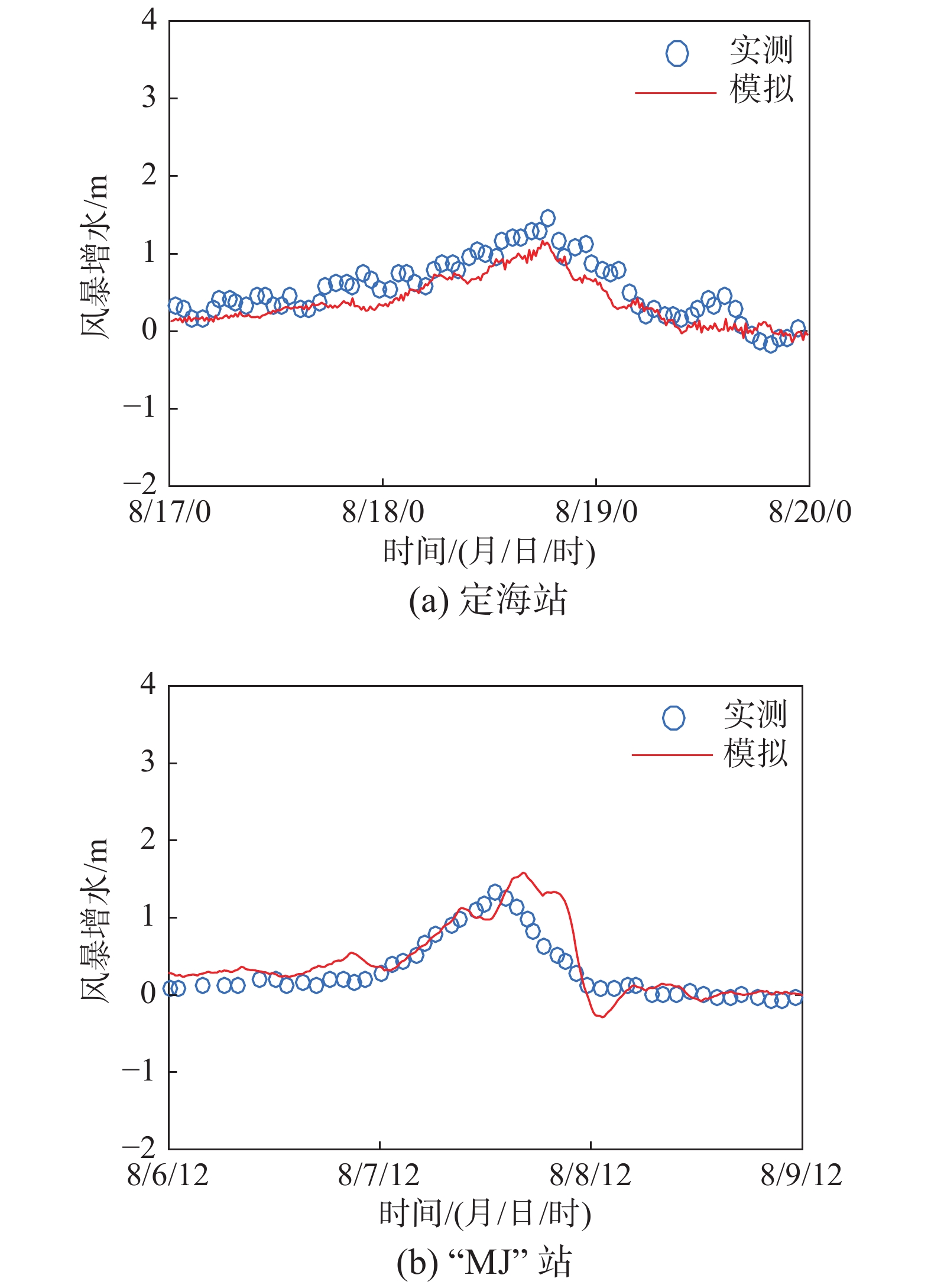
为验证数值模型模拟风暴潮的有效性,同样利用台风“温妮”期间定海站的实测风暴潮增水[28]进行对比验证,如图6(a)所示,实测最大增水为1.44 m,模拟最大增水为1.17 m。还模拟了2012年8月6日0时−2012年8月9日0时1211号台风“海葵”期间的环境参数。以“MJ”站的实测风暴增水[24]进行对比验证,如图6(b)所示,实测最大增水为1.31 m,模拟最大增水为1.58 m。数值模拟增水与实测增水吻合良好。
2.3 台风作用下风、浪、潮参数选取
仅关注某区域的环境变量时,为了节约计算资源,常忽略强度较低、距离较远的台风,只对经过指定范围的台风进行研究。Li和Hong[30]选择 200 km、250 km、300 km作为台风的选取半径,以研究台风选择范围对估计诱发灾害的影响,结果表明三种情况相差很小。基于验证的数值模型,根据中国台风网历史台风库数据,选取1987年−2018共32年间,对途经以金塘水道中点为圆心、250 km为半径范围内的49条台风(如图6所示)进行数值模拟,获得了各台风过程中风速Vw、波高Hs、风暴潮增水S的时程数据。这里的风速Vw指的是海平面以上10 m高度处10 min平均风速;波高Hs指的是有效波高;风暴潮S指的是台风引起的风暴潮增水。这里的风、浪、潮数据利用第1.3节中描述的方法获取。
需要注意的是,一次台风过程中的风、浪、潮往往不会同时达到最大,风、浪、潮参数选取会影响后续联合概率分析的结果。刘德辅等[31]指出,当结构最敏感荷载类型不明确时,可分别取不同时刻环境参数构建复合极值分布。因此,本文分别以风、浪、潮最大时刻以及假设三者同时取最大这四种情况选取每个台风的风、浪、潮参数,根据49个台风的选取结果建立四个数据集,如表1所示。4个数据集中风、浪、潮数据均值与标准差如表2。
表 1 4个数据集风、浪、潮的选取方式Table 1. Four ways of selecting wind, wave and storm surge data数据选取 波高选取 风速选取 风暴潮选取 数据集一 最大波高 相应时刻风速 相应时刻风暴潮 数据集二 相应时刻波高 最大风速 相应时刻风暴潮 数据集三 相应时刻波高 相应时刻风速 最大风暴潮 数据集四 最大波高 最大风速 最大风暴潮 表 2 4个数据集中环境参数均值与标准差Table 2. Means and standard deviations of environmental parameters of four data sets环境参数 波高/m 风速/(m/s) 风暴潮/m 均值 标准差 均值 标准差 均值 标准差 数据集一 1.82 1.15 16.6 6.4 0.19 0.31 数据集二 1.57 1.03 17.6 6.3 0.24 0.40 数据集三 1.22 0.93 14.4 7.1 0.46 0.40 数据集四 1.82 1.15 17.6 6.3 0.46 0.40 数据集一的最大风、浪、潮分别为31.48 m/s、5.02 m、1.17 m;数据集二的最大风、浪,潮分别为31.49 m/s、4.97 m、1.86 m;数据集三的最大风、浪,潮分别为31.00 m/s、3.36 m、1.86 m。这三个数据集49条台风过程中的最大风速基本一致,最大波高数据集三较小,最大风暴潮数据集一较小。数据集一、数据集三与数据集四风速差值的方差分别为1.4 m/s、4.5 m/s;数据集一、数据集二与数据集四的风暴潮差值的方差分别为0.38 m、0.33 m;数据集二、数据集三与数据集四的波高差值的方差分别为0.38 m、0.77 m。数据集三反映的每条台风期间风、浪的值偏小。
3 风-浪-潮参数联合概率Copula模型
3.1 多维联合概率模型
Copula函数可用于多维联合概率的建立。由Sklar定理,对于具有一元边缘分布函数F1, F2, ···, Fn的联合分布函数F,一定存在Copula函数C,满足式(8)[2],若边缘分布函数F1, F2, ···, Fn连续,则C唯一确定。采用嵌套Copula函数建立风-浪-潮联合概率分布,如式(9)。
F\left( {{x_1}, {x_2}, \cdots ,{x_n}} \right) = C\left[ {{F_1}\left( {{x_1}} \right),{F_2}\left( {{x_2}} \right), \cdots ,{F_n}\left( {{x_n}} \right)} \right] (8) C\left( {{x_1}{\rm{,}}{x_2},{x_3};{\theta _1},{\theta _2}} \right) = {C_1}\left[ {{x_3},{C_2}\left( {{x_1},{x_2};{\theta _2}} \right);{\theta _1}} \right]\;\; (9) 式中,θ1、θ2为相关性系数。其建立步骤如下:
1) 对风、浪、潮的边缘分布进行拟合。
2) 利用二维Copula函数将其中两个变量的边缘分布连接起来,形成第二层二维联合概率分布
{C_2}\left( {{x_1},{x_2};{\theta _2}} \right) 。3) 获得二维联合分布C2后,再次利用Copula函数将其与第三个变量X3的边缘分布连接,形成第一层风-浪-潮联合分布
{C_1}\left[ {{x_3},{C_2}\left( {{x_1},{x_2};{\theta _2}} \right);{\theta _1}} \right] 。3.2 风、浪、潮参数边缘分布
采用广义极值分布(GEV)对风速、波高、风暴潮的边缘分布进行拟合,GEV表达式如下:
F\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {{{\rm{e}}^{ - {{\left( {1 + k\frac{{x - \mu }}{\sigma }} \right)}^{ - 1/k}}}},\;{\text{当}}\;k \ne 0\;{\text{且}}\;\sigma > 0} \\ {{{\rm{e}}^{ - {{\rm{e}}^{\left( { - {\rm{ }}\frac{{x - \mu }}{\sigma }} \right)}}}},\;\;\;\;\;\;{\text{当}}\;k = 0\;{\text{且}}\;\sigma > 0} \end{array}} \right. (10) 式中,μ、σ、k分别为位置参数、尺度参数、形状参数。
利用最大似然法拟合边缘分布相关参数,并用RMSE及5%显著水平的K-S检验进行拟合程度判断。其中RMSE计算如下:
{\rm{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{p_i} - {{\hat p}_i}} \right)}^2}} } (11) 式中:n为观测值个数;
{p_i} 为根据数据直接计算出的经验频率;{\hat p_i} 为按照拟合的边缘分布得出的理论频率。四个数据集边缘分布拟合参数及检验结果如表3。利用GEV能较好拟合风、浪、潮的边缘分布。
表 3 广义极值分布参数Table 3. Fitted parameters of GEV参数 k σ μ RMSE K-S 数据集一 Hs 0.0962 0.8210 1.2644 0.0217 通过 Vw −0.0957 5.4349 13.8481 0.0255 S −0.0387 0.2447 0.0583 0.0337 数据集二 Hs 0.0608 0.7663 1.0731 0.0340 通过 Vw −0.0495 5.1981 14.7718 0.0286 S 0.0709 0.2695 0.0620 0.0322 数据集三 Hs 0.2066 0.5987 0.7394 0.0235 通过 Vw −0.0640 5.8555 11.3217 0.0339 S 0.2533 0.2338 0.2621 0.0287 数据集四 Hs 0.0962 0.8210 1.2644 0.0217 通过 Vw −0.0495 5.1981 14.7718 0.0286 S 0.2533 0.2338 0.2621 0.0287 3.3 风-浪-潮三维联合概率分布
获得边缘分布后用Copula函数将两个边缘分布连接起来。选取水文分析中常用的Frank Copula拟合风-浪、浪-潮、风-潮三个组合的二维联合分布,拟合结果如表4所示,其联合概率分布表达式如式(12)。
表 4 二维Frank Copula联合分布相关参数Table 4. Fitted parameters of Frank Copula参数 组合 θ τ RMSE 数据集一 Hs 和Vw 10.0401 0.6669 0.0298 Hs 和S 4.0794 0.3940 0.0297 S和Vw 3.8790 0.3790 0.0288 数据集二 Hs和Vw 10.1395 0.6695 0.0265 Hs 和S 3.4340 0.3439 0.0344 S和Vw 3.2888 0.3319 0.0405 数据集三 Hs和Vw 18.6043 0.8040 0.0199 H s和S9.1466 0.6413 0.0349 S和Vw 9.6429 0.6559 0.0381 数据集四 H s和Vw9.5989 0.6547 0.0262 Hs 和S 8.8959 0.6334 0.0327 S和Vw 6.3428 0.5316 0.0324 1) Frank Copula:
C\left( {u,v} \right) = {\rm{ - }}\frac{1}{\theta }{\rm{ln}}\left[{1 + \frac{{( {{{\rm{e}}^{ - \theta u}} - 1} )( {{{\rm{e}}^{ - \theta v}} - 1} )}}{{{{\rm{e}}^{ - \theta }} - 1}}} \right] (12) 式中:u、v为边缘分布;θ为Copula参数。
联合分布函数和概率密度函数的关系为:
f\left( {{x_1},{x_2}} \right) = \frac{{\partial C\left( {u,v} \right)}}{{\partial u\partial v}} \cdot f\left( {{x_1}} \right) \cdot f\left( {{x_2}} \right) (13) 式中:f (x1, x2)为二维联合概率密度;f (·)为概率密度函数。
利用Frank Copula函数拟合后以RMSE进行评判,由表4可知,Frank Copula函数对三个组合的联合分布拟合优度均较好,其能反映各变量间的相关性,故三维Copula的第一层函数选择Frank Copula。
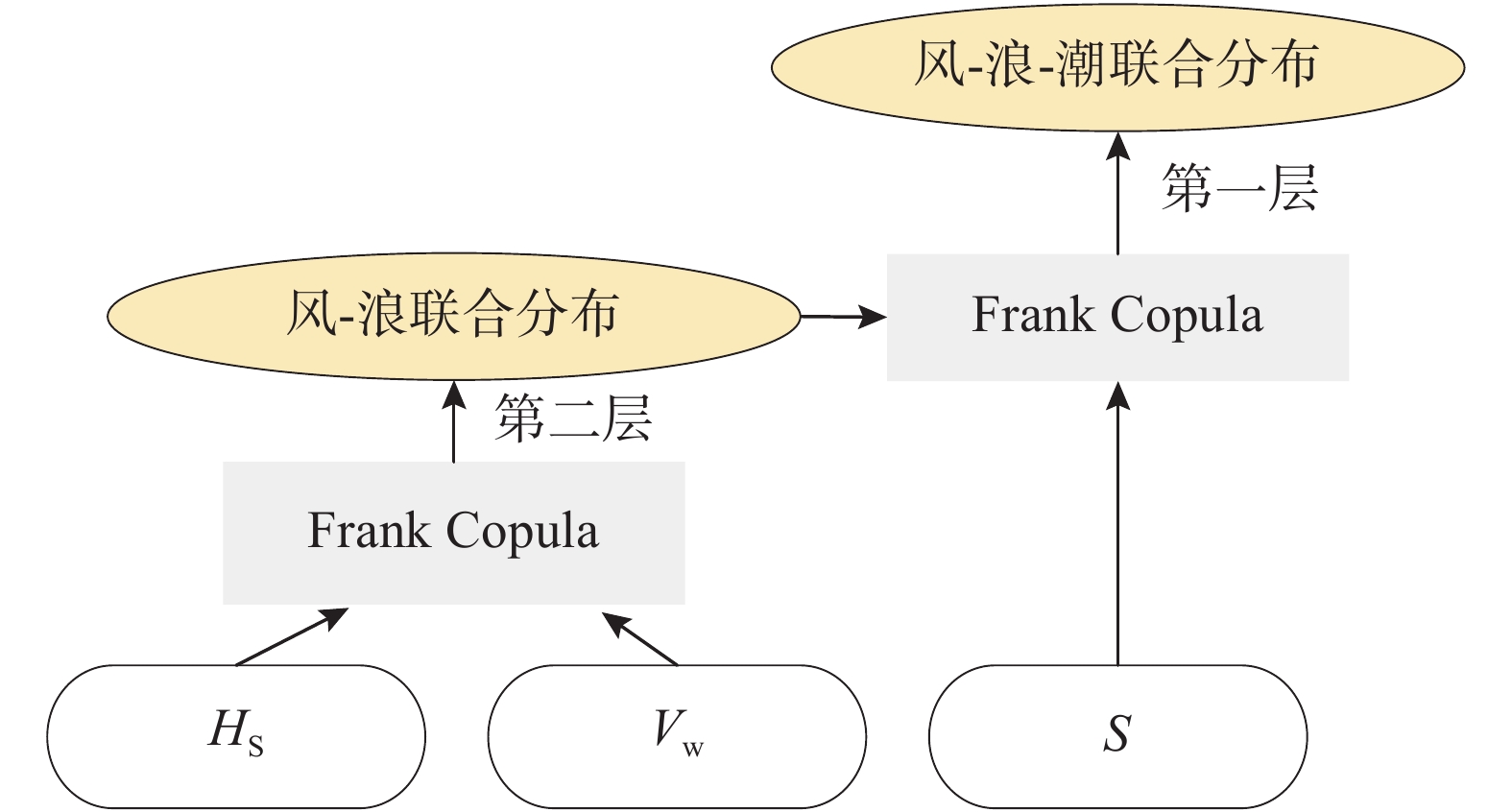
三维Copula的第二层函数一般取相关性较强的组合[2]。Kendall相关系数τ可利用Frank Copula函数中的θ相关性系数进行估计,如式(14)[32],利用其计算得到“波高和风速”、“波高和潮位”、“潮位和风速”的τ如表4。τ越大变量间相关性越强,由表3可知,三种二维变量组合中风-浪相关性最强,且拟合程度较好,故将风-浪联合分布作为三维Copula的第二层函数。综上,风-浪-潮联合概率构建过程如图7所示,其概率分布及概率密度表达式如式(15)~式(16)。
\tau = 1 - 4/\theta + 4{D_1}\left( \theta \right)/\theta (14) 式中,
{D_1}\left( \theta \right) =\displaystyle \int_0^\theta {\left( {x/\theta } \right)} /\left( {{{\rm{e}}^x} - 1} \right){\rm{d}}x 。\begin{split} & C( {{{u,}}v,w;{\theta _1},{\theta _2}} ) = {C_1}\left[ {{u_3},{C_2}( {u,v;{\theta _2}} );{\theta _1}} \right] = \\&\qquad - \frac{1}{{{\theta _1}}}{\rm{ln}}\left\{ 1 - \frac{{1 - {{\rm{e}}^{ - {\theta _{\rm{1}}}w}}}}{{1 - {{\rm{e}}^{ - {\theta _{\rm{1}}}}}}} \times \right. \\& \qquad\left. \left[ {1 - {{\left( {1 - \frac{{( {1 - {{\rm{e}}^{^{{{\rm{ - }}{\theta _2}u}}}}} )( {1 - {{\rm{e}}^{^{{{\rm{ - }}{\theta _2}v}}}} })}}{{1 - {{\rm{e}}^{{\rm{ - }}{\theta _2}}}}}} \right)}^{{\frac{{{\theta _1}}}{{{\theta _2}}}}}}} \right] \right\} \end{split} \;\;\;\; (15) f\left( {{x_1},{x_2},{x_3}} \right) = \frac{{\partial C\left( {u,v,w} \right)}}{{\partial u\partial v\partial w}} \cdot f\left( {{x_1}} \right) \cdot f\left( {{x_2}} \right) \cdot f\left( {{x_3}} \right) (16) 式中:f (x1, x2, x3)为三维联合概率密度;w为变量X3的边缘分布函数。
RMSE值越小,说明函数拟合越好,4个数据集风-浪-潮联合分布RMSE分别为0.0313、0.0438、0.0381、0.0363,三维嵌套Frank Copula能较好拟合4个数据集的风-浪-潮三维联合概率分布。
4 风-浪-潮三维环境等值面模型
4.1 环境等值面模型的确定方法
给定重现期的风-浪-潮参数可以通过联合超越概率或IFORM确定。后者能提供给定重现期下的环境等值面,为分析结构响应带来便利。基于Rosenblatt变换的IFORM可将三个不相关标准正态分布变量U1、U2、U3构造的半径为γ的球面转换到由风、浪、潮构成的联合随机变量空间[33]。球面半径γ与重现期T及随机事件平均年发生次数N(本文为1.53)的关系如下:
T = \frac{1}{{N[ {1 - \varPhi \left( \gamma \right)} ]}} (17) 式中,γ与U1、U2、U3关系如下:
U_1^2 + U_2^2 + U_3^2 = {\gamma ^2} (18) 利用求得的联合概率进行Rosenblatt变换。U1与随机变量X1的边缘分布F1关系如式(19);F1可利用GEV的拟合结果,U2与X2的条件概率分布F2|1的关系如式(20);可利用二维联合概率密度f (x1, x2)与X1的概率密度f (x1)积分求解,如式(21);U3与X3的条件概率分布F3|1,2的关系如式(22);F3|1,2可利用三维联合概率密度f (x1, x2, x3)与二维联合概率密度f (x1, x2)积分求解,如式(23)。
\varPhi \left( {{U_{\rm{1}}}} \right) = {F_{\rm{1}}}\left( {{x_{\rm{1}}}} \right)\qquad\qquad\qquad\qquad (19) \varPhi \left( {{U_2}} \right) = {F_{2\left| 1 \right.}}\left( {{x_2}\left| {{x_1}} \right.} \right)\qquad\qquad\qquad (20) {F_{2\left| 1 \right.}}\left( {{x_2}\left| {{x_1}} \right.} \right){\rm{ = }}\int_{{\rm{ - }}\infty }^{{x_2}} {\frac{{f\left( {{t_1},{t_2}} \right)}}{{f\left( {{t_1}} \right)}}} {\rm{d}}{t_2}\qquad\;\;\; (21) \varPhi \left({U}_{3}\right)={F}_{3|1,2}\left({x}_{3}|{x}_{1},{x}_{2}\right)\qquad\qquad\quad (22) {F_{3\left| {1,2} \right.}}\left( {{x_3}\left| {{x_1},{x_2}} \right.} \right){\rm{ = }}\int_{{\rm{ - }}\infty }^{{x_3}} {\frac{{f\left( {{t_1},{t_2},{t_3}} \right)}}{{f\left( {{t_1},{t_2}} \right)}}} {\rm{d}}{t_3} (23) 4.2 环境参数选取对环境等值面模型的影响
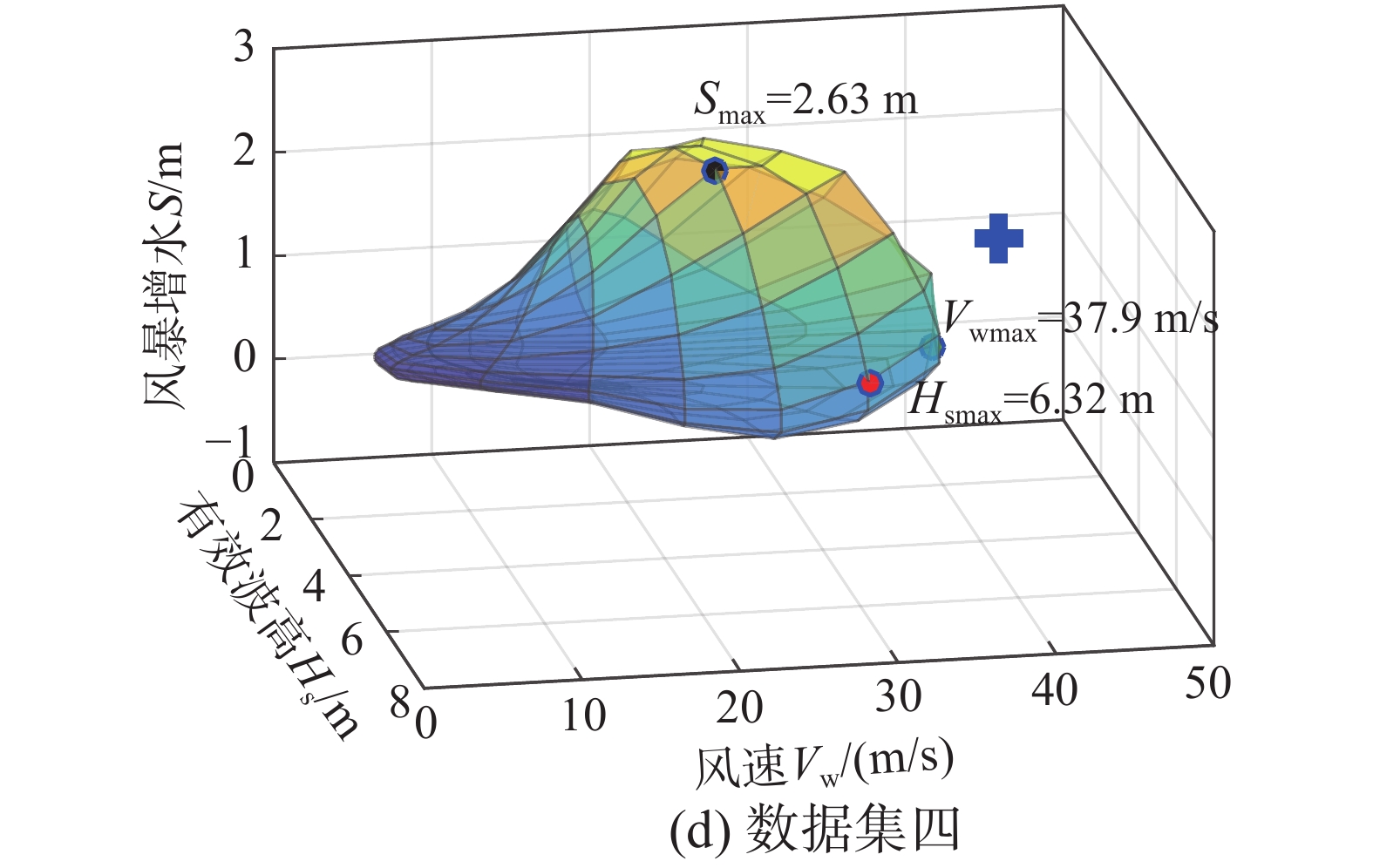
基于四个数据集,根据上述方法构建了舟山海域100年重现期下的环境等值面,对比图8中4种数据选取方法构造的环境等值面:a)在波高方向上取值较大,形状较扁平;b)在风速方向上取值较大;c)在风暴潮增水方向上取值较大,在风、浪、潮处在较低水平时,环境等值面出现“尖角”;d)在风、浪、潮处于较高水平时较a)、b)、c)更加“饱满”。风-浪-潮环境等值面形状受数据选取方式影响较大。
4个环境等值面的最大波高、风速、潮位见表5。数据集一、数据集二、数据集三求到的最大波高与数据集四的相对差异分别为0%、17%、14%;最大风速与数据集四的相对差异分别为6%、0%、4%;最大风暴潮与数据集四的相对差异分别为56%、36%、0%。风暴潮最大值受参数选取时刻影响最大。若结构响应对风暴潮较敏感,而选取风、浪最大时刻参数构建环境等值面模型可能导致结构不安全。
表 5 100年重现期下4个数据集的最大环境参数Table 5. Maximum environmental parameters with 100-year return period constructed by four data sets最大环境参数 最大波高/m 最大风速/(m/s) 最大风暴潮/m 数据集一 6.32 35.5 1.17 数据集二 5.58 37.9 1.68 数据集三 5.72 36.4 2.63 数据集四 6.32 37.9 2.63 不考虑变量间相关性,利用边缘分布计算得到100年重现期的浪、风、潮值分别为6.57 m、38 m/s、2.64 m,其直接组合结果如图8(d)中“+”点所示。该点位于100年环境等值面外,重现期大于100年,说明不考虑相关性直接组合估计的方式偏保守。
5 结论
利用SWAN+ADCIRC耦合模式对32年间影响舟山海域的49次台风进行模拟,建立了4个风、浪、潮数据集。在拟合边缘分布和二维联合分布的基础上利用嵌套Frank Copula函数建立风-浪-潮三维联合概率分布,并利用IFORM方法计算了100年重现期下风-浪-潮的环境等值面。主要结论如下:
(1) 本文建立的数值模型能较好地模拟台风作用下舟山海域风、浪、潮环境的发展历程,为后期构建联合概率分布模型及环境等值面模型提供了可靠的数据来源。
(2) 用GEV拟合台风期间风、浪、潮的边缘分布,Frank Copula拟合风-浪、风-潮、浪-潮的二维联合分布,由此建立的三维嵌套Frank Copula能较好反映4个数据集的风-浪-潮特征。
(3) 舟山海域给定重现期的环境等值面形状受数据选取时刻影响较大,其中风暴潮增水对选取方法最为敏感。不考虑风、浪、潮相关性,会高估给定重现期下的参数。
本文研究了基于台风数值模拟构建风-浪-潮联合概率及环境等值面模型的方法。碍于篇幅,本文未能结合实际工程,给出波-潮等作用的最不利叠加方法。未来应利用环境等值面上风-浪-潮变量的不同组合,从工程角度出发,分析结构受力和响应,通过研究结构响应与环境变量间的关系,为不同结构风、浪、潮设计参数的组合方法提供理论依据。
-
表 1 4个数据集风、浪、潮的选取方式
Table 1 Four ways of selecting wind, wave and storm surge data
数据选取 波高选取 风速选取 风暴潮选取 数据集一 最大波高 相应时刻风速 相应时刻风暴潮 数据集二 相应时刻波高 最大风速 相应时刻风暴潮 数据集三 相应时刻波高 相应时刻风速 最大风暴潮 数据集四 最大波高 最大风速 最大风暴潮 表 2 4个数据集中环境参数均值与标准差
Table 2 Means and standard deviations of environmental parameters of four data sets
环境参数 波高/m 风速/(m/s) 风暴潮/m 均值 标准差 均值 标准差 均值 标准差 数据集一 1.82 1.15 16.6 6.4 0.19 0.31 数据集二 1.57 1.03 17.6 6.3 0.24 0.40 数据集三 1.22 0.93 14.4 7.1 0.46 0.40 数据集四 1.82 1.15 17.6 6.3 0.46 0.40 表 3 广义极值分布参数
Table 3 Fitted parameters of GEV
参数 k σ μ RMSE K-S 数据集一 Hs 0.0962 0.8210 1.2644 0.0217 通过 Vw −0.0957 5.4349 13.8481 0.0255 S −0.0387 0.2447 0.0583 0.0337 数据集二 Hs 0.0608 0.7663 1.0731 0.0340 通过 Vw −0.0495 5.1981 14.7718 0.0286 S 0.0709 0.2695 0.0620 0.0322 数据集三 Hs 0.2066 0.5987 0.7394 0.0235 通过 Vw −0.0640 5.8555 11.3217 0.0339 S 0.2533 0.2338 0.2621 0.0287 数据集四 Hs 0.0962 0.8210 1.2644 0.0217 通过 Vw −0.0495 5.1981 14.7718 0.0286 S 0.2533 0.2338 0.2621 0.0287 表 4 二维Frank Copula联合分布相关参数
Table 4 Fitted parameters of Frank Copula
参数 组合 θ τ RMSE 数据集一 Hs 和Vw 10.0401 0.6669 0.0298 Hs 和S 4.0794 0.3940 0.0297 S和Vw 3.8790 0.3790 0.0288 数据集二 Hs和Vw 10.1395 0.6695 0.0265 Hs 和S 3.4340 0.3439 0.0344 S和Vw 3.2888 0.3319 0.0405 数据集三 Hs和Vw 18.6043 0.8040 0.0199 H s和S9.1466 0.6413 0.0349 S和Vw 9.6429 0.6559 0.0381 数据集四 H s和Vw9.5989 0.6547 0.0262 Hs 和S 8.8959 0.6334 0.0327 S和Vw 6.3428 0.5316 0.0324 表 5 100年重现期下4个数据集的最大环境参数
Table 5 Maximum environmental parameters with 100-year return period constructed by four data sets
最大环境参数 最大波高/m 最大风速/(m/s) 最大风暴潮/m 数据集一 6.32 35.5 1.17 数据集二 5.58 37.9 1.68 数据集三 5.72 36.4 2.63 数据集四 6.32 37.9 2.63 -
[1] Zhao Lin, Lu Anping, Zhu Ledong , et al. Radial pressure profile of typhoon field near ground surface observed by distributed meteorologic stations [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 122: 105 − 112. doi: 10.1016/j.jweia.2013.07.009
[2] 刘高, 张喜刚, 陈上有, 等. 特大型桥梁风-浪-流耦合作用设计[M]. 北京: 人民交通出版社, 2019. Liu Gao, Zhang Xigang, Chen Shangyou, et al. Wind-wave-current coupling action of super–large bridge [M]. Beijing: China Communications Press, 2019. (in Chinese)
[3] 刘黎阳, 张志田. 低扭转刚度悬索桥扭转发散特征及抗风对策[J]. 工程力学, 2020, 37(11): 146 − 155. doi: 10.6052/j.issn.1000-4750.2020.01.0002 Liu Liyang, Zhang Zhitian. Aerostatic divergence properties of suspension bridges with low torsional stiffness and anti-wind countermeasures [J]. Engineering Mechanics, 2020, 37(11): 146 − 155. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.01.0002
[4] 李海飞, 梁新华, 孙一飞, 等. 流线型桥梁断面表面脉动风荷载特性研究[J]. 工程力学, 2020, 37(增刊 1): 242 − 248, 260. doi: 10.6052/j.issn.1000-4750.2019.04.S045 LI Haifei, Liang Xinhua, Sun Yifei, et al. The characteristics of fluctuating wind load on the surface of a streamlined bridge section [J]. Engineering Mechanics, 2020, 37(Suppl 1): 242 − 248, 260. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.04.S045
[5] Ge Y J, Zhao L. Wind-excited stochastic vibration of long-span bridge considering wind field parameters during typhoon landfall [J]. Wind and Structures, 2014, 19(4): 421 − 441. doi: 10.12989/was.2014.19.4.421
[6] 葛耀君. 大跨度桥梁抗风的技术挑战与精细化研究[J]. 工程力学, 2011, 28(增刊 2): 11 − 23. Ge Yaojun. Technical challenges and refinement research on wind resistance of long-span bridges [J]. Engineering Mechanics, 2011, 28(Suppl 2): 11 − 23. (in Chinese)
[7] 王浩, 徐梓栋, 陶天友, 等. 基于小波变换的苏通大桥非平稳抖振响应演变谱实测研究[J]. 工程力学, 2016, 33(9): 164 − 170. doi: 10.6052/j.issn.1000-4750.2015.02.0116 Wang Hao, Xu Zidong, Tao Tianyou, et al. Field measurement study on the EPSD of non-stationary buffeting response of sutong bridge based on WT [J]. Engineering Mechanics, 2016, 33(9): 164 − 170. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.02.0116
[8] Ti Zilong, Li Yongle, Qin Shunquan. Numerical approach of interaction between wave and flexible bridge pier with arbitrary cross section based on boundary element method [J]. Journal of Bridge Engineering, 2020, 25(11): 04020095-1 − 04020095-16.
[9] Yang Zhiying, Huang Bo, Zhu Bing, et al. Comparative study of tsunami-like wave-induced forces on medium-scale models of box girder and T-girder bridges [J]. Journal of Bridge Engineering, 2021, 26(2): 04020125-1 − 04020125-19.
[10] 张家瑞, 魏凯, 秦顺全. 基于贝叶斯更新的深水桥墩波浪动力响应概率模型[J]. 工程力学, 2018, 35(8): 138 − 143, 171. doi: 10.6052/j.issn.1000-4750.2017.04.0299 Zhang Jiarui, Wei Kai, Qin Shunquan. An Bayesian updating based probabilistic model for the dynamic response of deep-water bridge piers under wave loading [J]. Engineering Mechanics, 2018, 35(8): 138 − 143, 171. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.04.0299
[11] 魏凯, 周聪, 徐博. 跨海桥梁高桩承台波浪冲击荷载概率模型[J]. 工程力学, 2020, 37(6): 216 − 224. doi: 10.6052/j.issn.1000-4750.2019.08.0500 Wei Kai, Zhou Cong, Xu Bo. Probability model of wave impact load on the elevated pile cap for sea-crossing bridges [J]. Engineering Mechanics, 2020, 37(6): 216 − 224. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.08.0500
[12] Fang Chen, Tang Haojun, Li Yongle, et al. Stochastic response of a cable-stayed bridge under non-stationary winds and waves using different surrogate models [J]. Ocean Engineering, 2020, 199: 106967-1 − 106967-15.
[13] Guo Auxin, Liu Jiabin, Chen Wenli, et al. Experimental study on the dynamic responses of a freestanding bridge tower subjected to coupled actions of wind and wave loads [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 159: 36 − 47. doi: 10.1016/j.jweia.2016.10.003
[14] Navid A, Jamie E P. Limit state capacities for global performance assessment of bridges exposed to hurricane surge and wave [J]. Structural Safety, 2013, 41: 73 − 81. doi: 10.1016/j.strusafe.2012.10.005
[15] 陈子煜, 刘德辅, 王风清. 中国南海极端海况概率预测及海洋工程防灾标准研究[J]. 中国海洋大学学报(自然科学版), 2019, 49(1): 115 − 120. Chen Ziyu, Liu Defu, Wang Fengqing. Study of probability prediction of extreme sea hazards and disaster prevention design criteria at South China Sea [J]. Periodical of Ocean University of China, 2019, 49(1): 115 − 120. (in Chinese)
[16] Chen Yongping, Li Jiangxia, Pan Shunqi, et al. Joint probability analysis of extreme wave heights and surges along China's coasts [J]. Ocean Engineering, 2019, 177: 97 − 107. doi: 10.1016/j.oceaneng.2018.12.010
[17] 魏凯, 沈忠辉, 吴联活, 等. 强台风作用下近岸海域波浪-风暴潮耦合数值模拟[J]. 工程力学, 2019, 36(11): 139 − 146. doi: 10.6052/j.issn.1000-4750.2018.12.0646 Wei Kai, Shen Zhonghui, Wu Lianhuo, et al. Coupled numerical simulation on wave and storm surge in coastal areas under strong typhoons [J]. Engineering mechanics, 2019, 36(11): 139 − 146. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.12.0646
[18] API RP 2A-WSD, Recommended practice for planning, designing and constructing fixed offshore platforms−working stress design [S]. America: API, 2007.
[19] DNV-OS-J101, Design of offshore wind turbine structures [S]. Norway: DNV, 2007.
[20] 秦振江, 孙广华, 闫同新, 等. 基于Copula函数的联合概率法在海洋工程中的应用[J]. 海洋预报, 2007(2): 83 − 90. Qin Zhenjiang, Sun Guanghua, Yan Tongxin, et al. Application of multivariate probability analysis using copulas to ocean engineering [J]. Marine Forecasts, 2007(2): 83 − 90. (in Chinese)
[21] Valamanesh V, Myers A T, Arwade S R. Multivariate analysis of extreme metocean conditions for offshore wind turbines [J]. Structural Safety, 2015, 55: 60 − 69. doi: 10.1016/j.strusafe.2015.03.002
[22] Miyazaki M, Ueno T, Unoki S. Theoretical investigations of typhoon surges along the Japanese coast [J]. Oceanographic Magazine, 1962, 13(2): 103 − 117.
[23] Holland G J. An analytic model of the wind and pressureprofiles in hurricanes [J]. Monthly Weather Review, 1980, 108(8): 1212 − 1218. doi: 10.1175/1520-0493(1980)108<1212:AAMOTW>2.0.CO;2
[24] Zhou Tianyi, Ya Tan, Ao Chu, et al. Integrated model for astronomic tide and storm surge induced by typhoon for Ningbo Coast [R]. Japan: International Society of Offshore and Polar Engineers, 2018.
[25] Wei Kai, Shen Zhonghui, Ti Zilong, et al. Trivariate joint probability model of typhoon-induced wind, wave and their time lag based on the numerical simulation of historical typhoons [J]. Stochastic Environmental Research and Risk Assessment, 2020, 35(2): 325 − 344.
[26] Murty P L N, Srinivas K S, Rao E P R, et al. Improved cyclonic wind fields over the Bay of Bengal and their application in storm surge and wave computations [J]. Applied Ocean Research, 2020, 95: 102048-1 − 102048-12.
[27] Pan Yi, Chen Yongping, Li Jiangxia, et al. Improvement of wind field hindcasts for tropical cyclones [J]. Water Science and Engineering, 2016, 9(1): 58 − 66. doi: 10.1016/j.wse.2016.02.002
[28] 孙志林, 王辰, 钟汕虹, 等. 浪潮耦合的舟山渔港台风暴潮数值模拟[J]. 海洋通报, 2019, 38(2): 150 − 158. Sun Zhilin, Wang Chen, Zhong Shanhong, et al. Numerical simulation of storm surge coupled with wave in Zhoushan fishing port [J]. Marine Science Bulletin, 2019, 38(2): 150 − 158. (in Chinese)
[29] 应王敏, 郑桥, 朱陈陈, 等. 基于SWAN模式的“灿鸿”台风浪数值模拟[J]. 海洋科学, 2017, 41(4): 108 − 117. Ying Wangmin, Zheng Qiao, Zhu Chenchen, et al. Numerical simulation of “CHAN-HOM” typhoon waves using SWAN model [J]. Marine Sciences, 2017, 41(4): 108 − 117. (in Chinese)
[30] Li S H, Hong S H P. Use of historical best track data to estimate typhoon wind hazard at selected sites in China [J]. Natural Hazards, 2015, 76(2): 1395 − 1414. doi: 10.1007/s11069-014-1555-z
[31] 刘德辅, 温书勤, 王利萍. 泊松-混合冈贝尔复合极值分布及其应用[J]. 科学通报, 2002, 47(17): 1356 − 1360. doi: 10.1360/csb2002-47-17-1356 Liu Defu, Wen Shuqin, Wang Liping, et al. Poisson-Gumbel mixed distribution and its application [J]. Chinese Science Bulletin, 2002, 47(17): 1356 − 1360. (in Chinese) doi: 10.1360/csb2002-47-17-1356
[32] Genest C, Favre A C. Everything you always wanted to know about copula modeling but were afraid to ask [J]. Journal of Hydrologic Engineering, 2007, 12(4): 347 − 368. doi: 10.1061/(ASCE)1084-0699(2007)12:4(347)
[33] Rosenblatt M. Remarks on a multivariate transformation [J]. Annals of Mathematical Statistics, 1952, 23(3): 470 − 472. doi: 10.1214/aoms/1177729394
-
期刊类型引用(10)
1. 魏凯,钟茜,沈忠辉. 台风登陆期间跨海大桥风-浪-流作用结构振动分析. 铁道标准设计. 2024(03): 113-123 .  百度学术
百度学术
2. 赵欣旺,遆子龙,周远洲. 基于台风期实测风浪联合分布的跨海桥梁动力响应研究. 交通科学与工程. 2024(06): 82-92 .  百度学术
百度学术
3. 徐青云,周嬴涛,冯卫兵,林祥. 瓜达尔港东湾快速路工程近岸波浪要素推算及断面稳定性试验研究. 中国港湾建设. 2024(12): 36-42+56 .  百度学术
百度学术
4. 徐青云,周嬴涛,冯卫兵,林祥. 瓜达尔港东湾快速路工程近岸波浪要素推算及断面稳定性试验研究. 中国港湾建设. 2024(12): 36-42+56 .  百度学术
百度学术
5. 《中国公路学报》编辑部. 中国桥梁工程学术研究综述·2024. 中国公路学报. 2024(12): 1-160 .  百度学术
百度学术
6. 刘章军,张文远,彭辉. 多向不规则波浪模拟的降维方法. 工程力学. 2023(04): 12-20 .  本站查看
本站查看
7. 王晓磊,吕大刚,阎卫东. 双变量与条件地震重现期理论及应用. 工程力学. 2023(08): 47-58 .  本站查看
本站查看
8. 魏凯,徐洪权,钟茜. 台风作用下杭州湾跨海铁路大桥嘉甬通道海域风浪流特性分析. 铁道标准设计. 2023(08): 97-102+146 .  百度学术
百度学术
9. 尚黛梦,魏凯,钟茜,秦顺全. 台风浪-潮-流相关性对桥梁群桩基础波流力的影响. 工程力学. 2022(S1): 187-194 .  本站查看
本站查看
10. 钟茜,魏凯,沈忠辉,遆子龙. 台风“玛莉亚”风场WRF模拟及最大风速半径的非对称特性. 工程力学. 2022(S1): 389-396 .  本站查看
本站查看
其他类型引用(5)




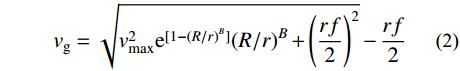



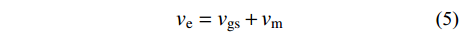
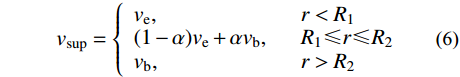


 下载:
下载: