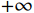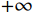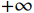UNCERTAINTY ANALYSIS ON PROGRESSIVE COLLAPSE RESISTANCE OF RC BEAM-COLUMN SUBSTRUCTURES
-
摘要: 近年来,结构的抗连续倒塌问题在国内外引起了广泛关注。RC框架作为实际工程中最常见的结构形式被广泛研究。然而,已有RC框架梁柱子结构的连续倒塌性能相关研究多基于确定性分析且主要针对静力拆除构件工况。该文基于OpenSees分别建立了典型RC框架梁柱子结构的静力和动力连续倒塌分析有限元模型,通过试验对比验证了模型的准确性。在此基础上,考虑结构截面几何属性、材料特性等不确定性因素,基于拉丁超立方抽样生成不同模型并分析了结构不确定性对RC框架梁柱子结构静力和动力抗连续倒塌性能的影响。参数不确定性分析结果表明:悬链线机制对RC框架梁柱子结构的抗连续倒塌性能十分重要;而以梁端转角达到0.20 rad作为RC框架梁柱子结构动力失效指标在一定程度上偏于保守。参数敏感性分析结果表明:纵筋屈服强度、极限强度为影响RC框架梁柱子结构抗连续倒塌能力的主要因素。Abstract: In recent years, the problem of progressive collapse of building structures has aroused widespread concern at home and abroad. As one of the most commonly used structure systems in engineering practice, the reinforced concrete (RC) frame structures have been widely involved in many existing progressive collapse studies. However, most of the studies were mainly based on deterministic and static analyses of column removal scenarios. In this study, the finite element (FE) model of a typical RC frame beam-column substructure is built based on OpenSees. Both static and dynamic progressive collapse analyses of the beam-column substructure are performed and validated against the experimental results. Furthermore, several structural models were generated for the uncertainty analyses by the Latin hypercube sampling method. The influences of various uncertainty factors are discussed, including the sectional geometries, material properties and so on. The results indicate that the catenary action plays a crucial role in RC frame beam-column substructures against progressive collapse. However, the use of 0.2 rad chord rotation as the failure index in the dynamic progressive collapse analyses is to a certain extent conservative. Moreover, according to the sensitivity analyses, the yield strength and ultimate strength of the longitudinal reinforcement are the major factors that affect the progressive collapse resistance of RC frame beam-column substructures.
-
在美国土木工程协会的ASEC/SEI 7-10[1]中,结构的连续倒塌定义为:“由于初始的局部破坏在构件间扩散,最终导致结构整体倒塌或大面积的不成比例倒塌”。因此,初始的局部破坏是连续倒塌发生的关键。在实际工程中,有许多原因都能导致结构出现初始局部破坏,如地震、爆炸、风荷载、撞击以及地基不均匀沉降等。20世纪以来,在全球范围内发生了许多连续倒塌事件,例如1968年伦敦Ronan Point公寓爆炸事件、1995年韩国三丰百货店倒塌事件、2001年纽约世贸中心9•11恐怖袭击事件以及1995年美国Alfred P. Murrah联邦政府大楼炸弹袭击事件[2]等。结构的连续倒塌会造成极大的人员伤亡和经济损失,近年来引起了国内外学者的广泛关注,开展了许多针对性的研究。
目前抗连续倒塌相关的研究主要基于拆除构件法。国内外诸多学者均基于该方法开展了RC框架结构抗连续倒塌试验和数值模拟相关研究[3-10]。Ren等[3]基于静力拆除构件方法测试了7个不同截面尺寸、缩尺为1/3的试件的RC框架试件连续倒塌响应,其中2个为无板梁试件,其余为板梁试件。肖哲宇等[4]在Ren等[3]的试验基础上,制作了4个尺寸、材料全部相同的RC框架梁柱子结构试件,开展了考虑拆除中柱工况的连续倒塌动力试验研究。王少杰等[5]、钱凯等[6]和Feng等[7]则分别研究了RC框架结构在移除中柱、边柱、边柱与内部柱工况下的静力抗连续倒塌性能。易伟建等[8]通过分级加载模拟了缩尺为1/3的3层4跨RC框架结构底层柱的失效过程,并对RC框架结构在倒塌过程中受力机制转换过程进行了讨论。程小卫等[9]分别建立了全精细模型和多尺度模型并进行了基于拆除构件法以及模拟撞击全过程的连续倒塌分析。Fascetti等[10]利用开源有限元软件OpenSees建立宏观模型并提出了一种评估RC框架结构局部鲁棒性的方法。
随着对结构连续倒塌研究的逐渐深入,国内外许多学者开始关注结构参数不确定性对其抗连续倒塌可靠度的影响。结构的可靠度计算应确定荷载和抗力的不确定性[11],已有许多研究讨论了RC框架梁柱子结构设计参数对于其连续倒塌性能的影响。例如,Yu等[12]和Feng等[7, 13]考虑了结构尺寸、材料强度以及荷载等因素,开展了RC框架结构静力抗连续倒塌不确定性分析和敏感性分析,结果表明荷载、钢筋屈服强度是影响结构抗连续倒塌能力的重要因素;He等[14]则提出了可用于评估结构抗连续倒塌能力鲁棒性的公式,并开展了相应的不确定性分析和参数敏感性分析。贾明明等[15]以活荷载、混凝土抗压强度、钢筋屈服强度和钢筋弹性模量为不确定性因素,通过改进的拉丁超立方抽样对RC框架填充墙结构分别进行了基于静力移除柱和动力移除柱工况的易损性分析。
然而,目前的研究工作多基于确定性分析且主要针对静力拆除构件工况,而结构连续倒塌往往是由于偶然荷载导致的局部构件破坏造成,因此结构参数的不确定性对其抗连续倒塌性能可能起到关键影响。本文在已有研究的基础上,基于文献中的试验试件[3-4],建立了典型RC框架梁柱子结构静力和动力连续倒塌有限元模型。在此基础上,考虑纵筋屈服强度、纵筋极限强度、截面几何特性等10个不确定性参数,通过拉丁超立方抽样,开展了考虑参数不确定性的RC框架梁柱子结构静力和动力拆除构件分析,研究了参数不确定性对RC框架梁柱子结构的静力和动力抗连续倒塌性能的影响规律。进一步研究了基于能量原理的简化动力分析方法在开展RC框架梁柱子结构连续倒塌参数不确定性分析的可行性和准确性。
1 模型验证
虽然考虑楼板的作用可以提高RC框架梁柱子结构的连续倒塌承载力[3, 6, 16-17],但是,已有研究表明梁-板耦合作用对于结构抗力的影响十分复杂,因此,目前的RC框架连续倒塌抗力不确定性相关研究[12-13]也首先基于梁柱子结构开展,为了明确研究对象以及简化分析,本文暂未考虑楼板对于结构抗力的影响。本文首先参考Ren等[3]和肖宇哲等[4]开展的RC框架梁柱子结构连续倒塌系列试验研究,选取了Ren等[3]试验中的B3试件以及肖宇哲等[4]试验中的DT试件验证所使用的有限元模型。Ren等[3]的试验通过拟静力试验法对试件进行按位移控制的加载;肖宇哲等[4]进行的动力试验则是通过瞬间释放脱钩模拟中柱的动力失效,加载装置如图1所示。本文首先基于众多文献[18-20]中常用的开源有限元软件OpenSees分别建立了上述试验中典型RC框架梁柱子结构试件的连续倒塌静力和动力分析模型。
1.1 有限元模型
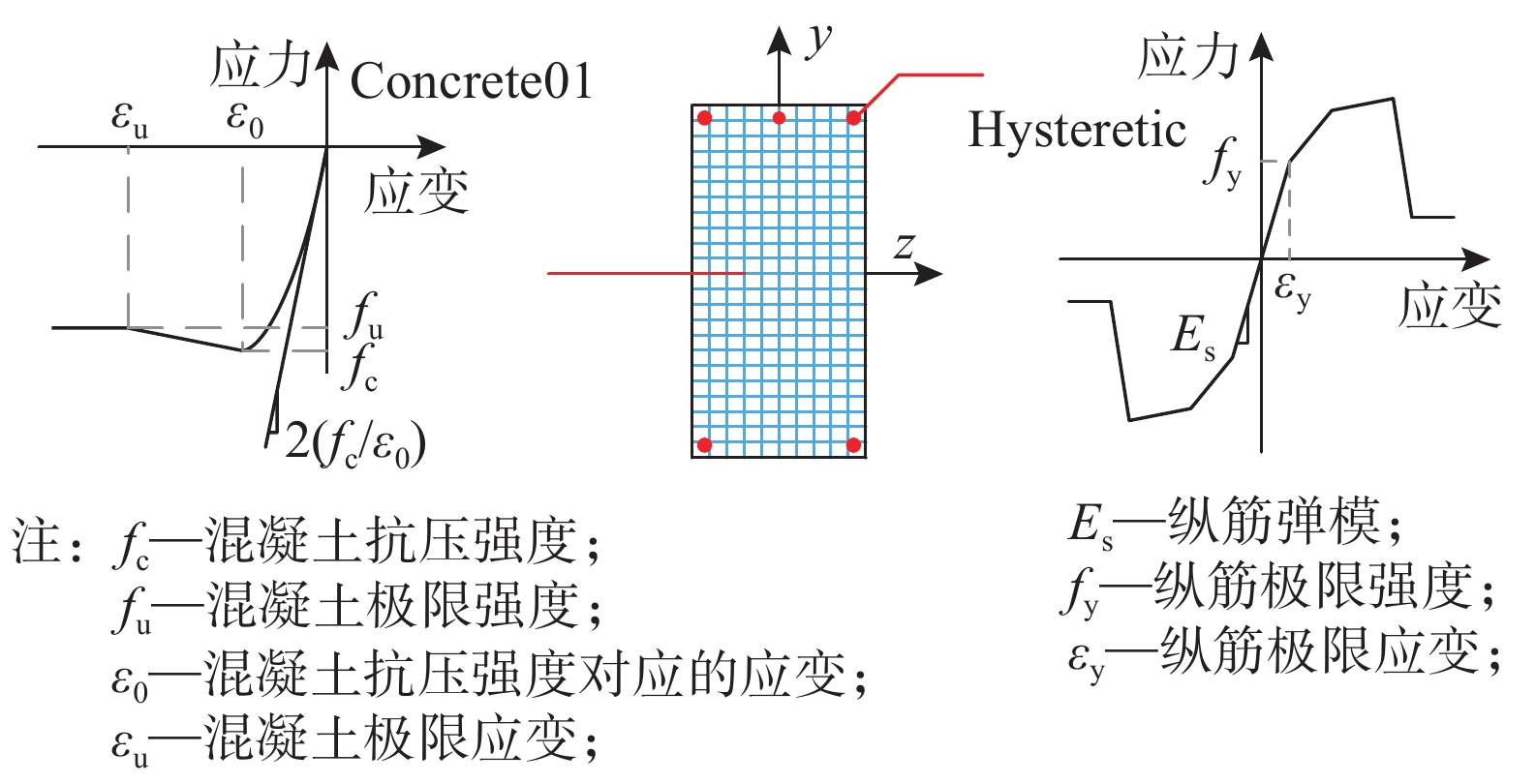
试件B3和DT的截面尺寸、配筋、材料强度等信息可以参见相应原文[3-4]。在数值模型中,框架梁柱构件采用基于位移的纤维梁柱单元模拟,混凝土使用Concrete01材料模拟,梁内纵筋则采用OpenSees中的滞回材料(Hysteretic Material),通过设置滞回材料在特征点处的应力、应变数值来模拟钢筋在试验过程中的断裂,如图2所示。静力分析模型中,通过将外荷载单调施加在移除柱头处来模拟试验中的静力加载工况,动力移除柱工况则是通过“生死单元”方法模拟脱钩释放的过程,以施加试验中的动力荷载。
1.2 模型验证
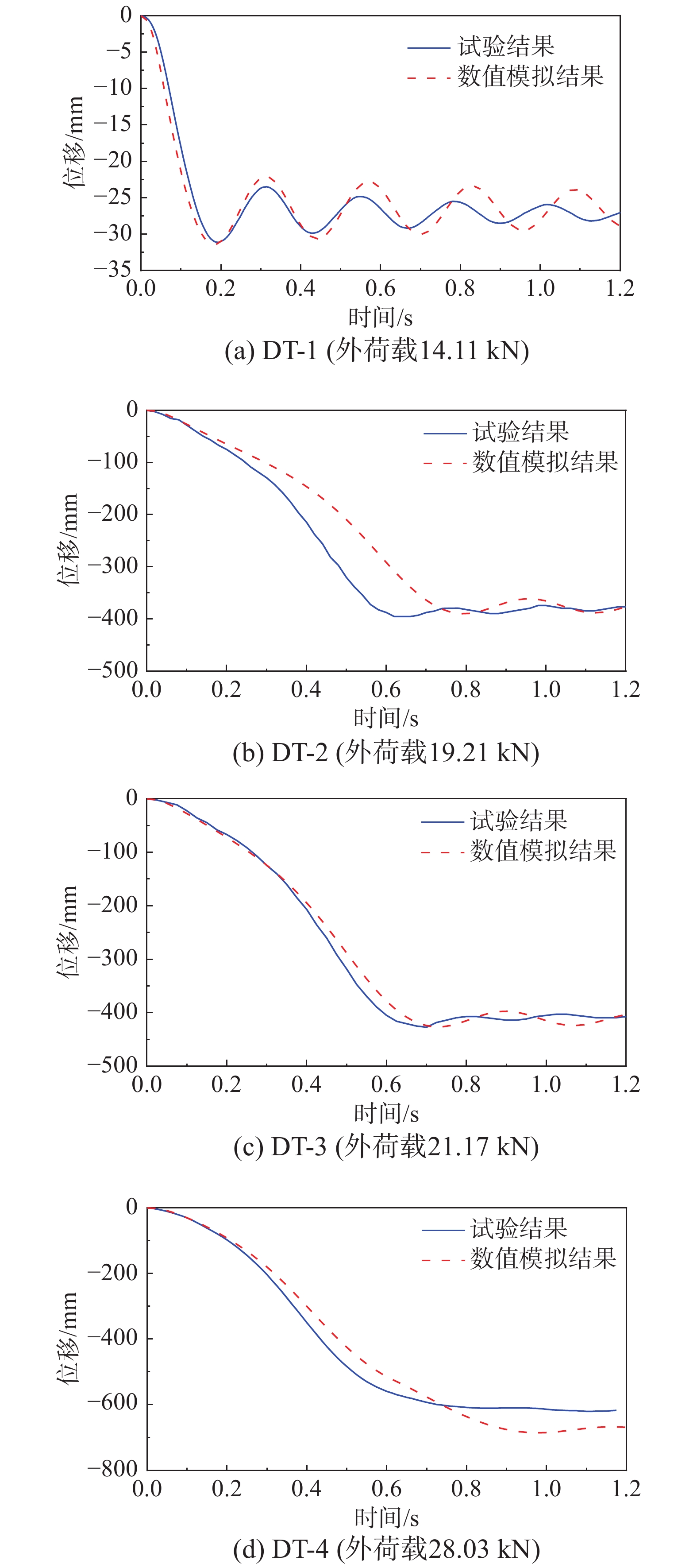
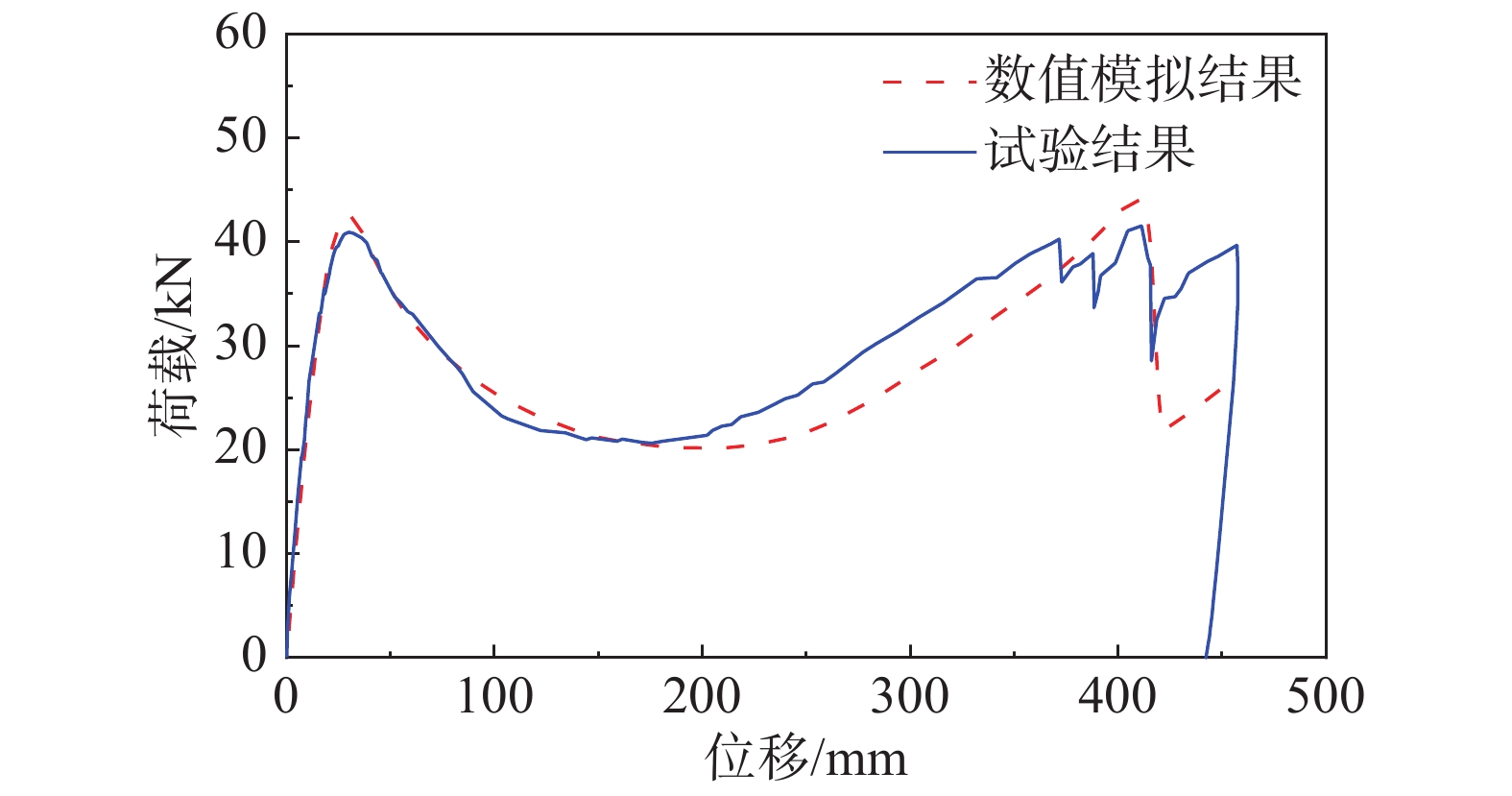
基于上述有限元模型,将计算结果与Ren等[3]和肖宇哲等[4]相应试件的试验结果对比,如图3、图4所示。其中图3的DT试件包括4个不同的工况,DT1-DT4分别对应施加的动力荷载分别为14.11 kN、19.21 kN、21.17 kN、28.03 kN对应的工况。结果表明,试验结果与数值模拟结果吻合度较高,因此本文采用的建模方法能够准确地模拟出RC框架梁柱子结构在静力拆除构件工况和动力拆除构件工况下的连续倒塌响应,可以用于后续的不确定性分析。
2 参数选取与抽样
为了分析参数不确定性对于RC框架梁柱子结构抗连续倒塌性能的影响,通常需要对所考虑的参数进行抽样分析,已有RC框架结构抗连续倒塌相关研究中广泛使用了蒙特卡洛模拟(Monte Carlo Simulation)[21],但其计算消耗量过大,因此本文采用更加有效率的拉丁超立方抽样方法(Latin Hypercube Sampling)抽样生成分析所需的有限元模型。拉丁超立方抽样属于蒙特卡洛法的一种,通过将累积分布函数的取值空间进行分层,得到n个概率相同的子层,并在每个子层中选取样本点,以大大提高抽样的效率和精度,该方法也被广泛运用到考虑参数不确定性的结构性能研究中[12, 22]。
由于结构荷载的不确定性往往需要更详细的讨论研究,因此本文主要考虑参数不确定性对于结构连续倒塌抗力的影响。国内外已有研究表明,影响RC框架梁柱子结构连续倒塌抗力的主要因素主要包括配筋、混凝土强度、构件及截面尺寸等[3, 7, 12-13, 16, 23-24]。为了充分研究结构参数不确定性对基于静力拆除构件工况和动力拆除构件工况下的RC框架梁柱子结构抗连续倒塌性能的影响,本文以肖宇哲等[4]试验中的DT试件为基础,考虑了包括材料属性、截面尺寸等的10个随机变量,假设各随机变量之间相互独立[7, 25],开展拉丁超立方抽样和对应的数值模拟工作。抽样过程中,各变量的均值取为DT试件设计值或材性试验数值,变量的变异系数取值及各随机变量服从的分布函数参考相关的经典研究[12-13, 26, 27],假设如下:1) 跨度、截面尺寸等服从正态分布;2) 混凝土抗压强度服从对数正态分布;3) 纵筋屈服强度和极限强度服从β分布,其中,β分布的形状系数α和β分别为3.2和4.28[25],详细信息如表1所示。
表 1 随机变量分布Table 1. Distributions of the random variables随机变量 均值 变异系数/(%) 分布函数 跨度L 2000 mm 0.23 正态分布 梁高h 170 mm 0.54 正态分布 梁宽b 85 mm 0.75 正态分布 混凝土保护层厚度t 6 mm 5.00 正态分布 纵筋弹性模量Es 200 GPa 3.30 正态分布 纵筋断裂应变εf 0.25 15.00 正态分布 纵筋直径d 6 mm/8 mm 4.00 正态分布 混凝土抗压强度fc 26.6 MPa 18.00 对数正态分布 纵筋屈服强度fy 336/292 MPa* 9.30 β分布 纵筋极限强度fu 512/459 MPa* 8.00 β分布 注:336 MPa、512 MPa为直径6 mm纵筋的屈服强度和极限强度;292 MPa、459 MPa为直径8 mm纵筋的屈服强度和极限强度。 3 参数不确定性分析
在DT试件的基础上,基于表1中的各随机变量信息,采用拉丁超立方抽样方法抽样并建立1000个不同RC框架梁柱子结构有限元模型,分别开展模型的动力和静力连续倒塌分析,统计并分析结构参数不确定性对RC框架梁柱子结构连续倒塌响应的影响。
3.1 静力工况
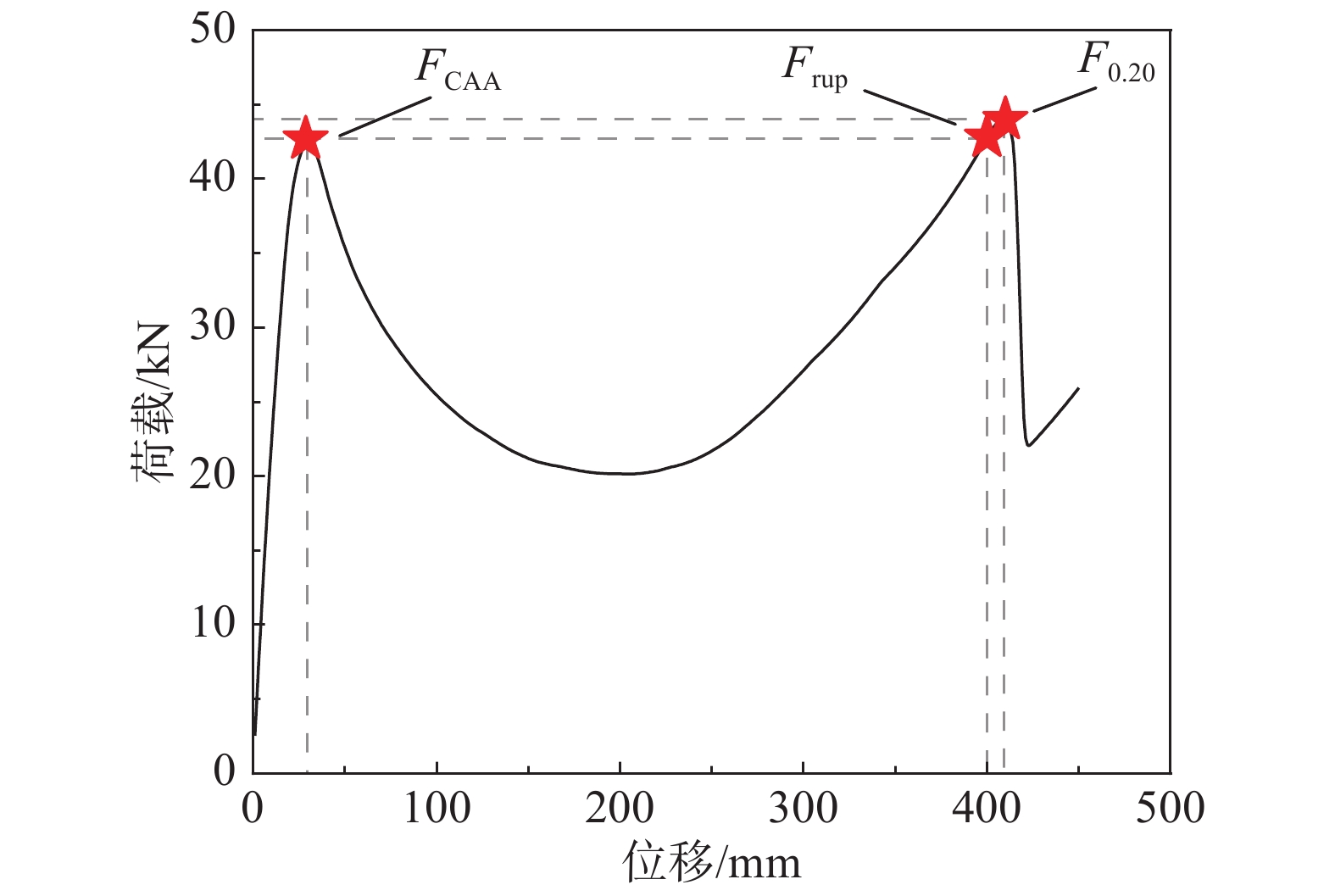
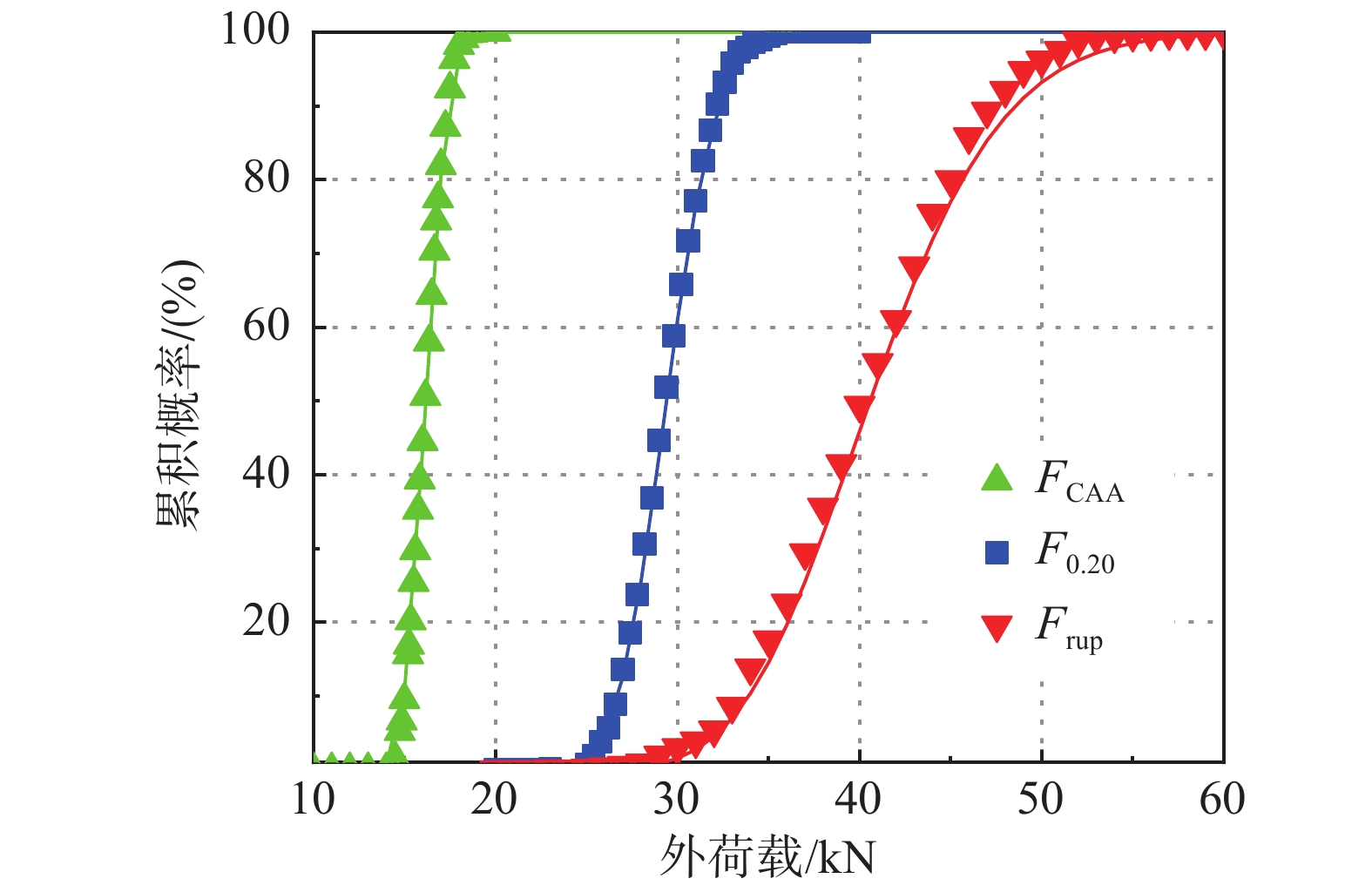
对于静力拆除构件工况,本文主要考虑结构参数不确定性对于已有研究中常用的3种RC框架结构静力抗连续倒塌承载力特征值的影响[3],即:1) 压拱作用阶段峰值承载力(FCAA);2) 梁端转角达到0.20 rad时对应的承载力(F0.20)[28];3) 框架梁首根纵筋断裂时对应的承载力(Frup),如图5所示。
对于上述3个承载力特征值,统计抽样产生的1000个RC框架梁柱子结构模型的静力分析结果如图6所示。其中,图6中的数据点表示,外荷载取某值时,抽样生成的模型中,静力拆除构件分析得到的对应承载力特征值小于等于该值的模型数量占模型总数的百分比。不同类型的数据点分别代表不同承载力特征值指标的统计结果。统计数据可得,考虑结构参数不确定性后,1000个RC框架梁柱子结构模型的FCAA、F0.20和Frup的均值分别为16.16 kN、29.37 kN和40.23 kN。F0.20和Frup的均值相比FCAA增加分别为81.74%和148.95%,因此,悬链线机制对于RC框架梁柱子结构在极端情况下的抗连续倒塌起到至关重要的作用。此外,计算得到的FCAA、F0.20和Frup的标准差分别为0.89 kN、2.09 kN和5.45 kN。因此,参数不确定性对RC框架梁柱子结构压拱作用阶段峰值承载力(FCAA)影响较小,对RC框架梁柱子结构首根纵筋断裂时对应的悬链线承载力(Frup)的影响最大。
3.2 动力工况
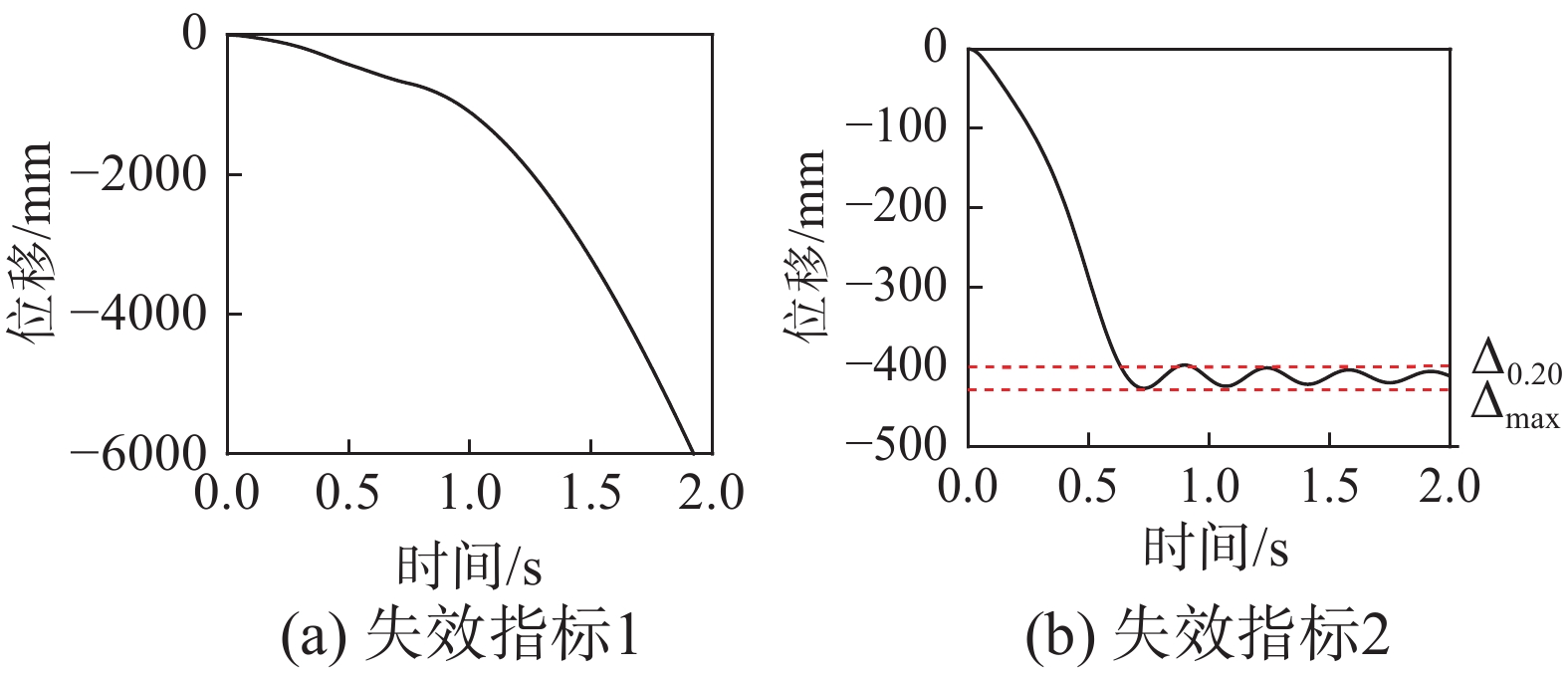
对于动力工况,本文主要考虑了两种常用的失效判别指标,即:1)失效指标1,结构无法恢复受力平衡状态,失效处竖向位移持续增长;2)失效指标2,结构未达到平衡条件或最大竖向位移Δmax大于梁端转角达到0.20 rad时对应的竖向位移Δ0.20[28],如图7所示。
基于以上两种失效指标,对统计抽样产生的1000个模型开展动力分析,统计结果如图8所示。结果表明,两种指标计算得到的动力失效荷载均值分别为:Fi1=27.98 kN,Fi2=19.93 kN;标准差分别为:σi1=2.74 kN,σi2=1.43 kN(其中,i1和i2分别代表失效指标1和失效指标2);失效指标1和失效指标2连续倒塌率为50%时对应的失效荷载分别为27.97 kN和19.93 kN,前者约为后者的1.4倍。此外,当采用失效指标2判定所有构件均发生连续倒塌时,按照失效指标1在对应荷载下计算得到的构件倒塌破坏率仅为8.73%,因此对于本文所研究的RC框架梁柱子结构,采用目前国际条文中常用的梁端转角达到0.20 rad作为判别指标是偏于保守的[28]。
3.3 基于能量原理的简化动力分析
由于非线性动力分析过程通常较为复杂,多需要借助数值模拟开展,不适用于结构抗连续倒塌设计。因此,在非线性动力分析的基础上,本文进一步采用基于能量原理的简化动力分析方法开展了RC框架梁柱子结构抗连续倒塌性能不确定性分析,并讨论了其可行性和准确性。
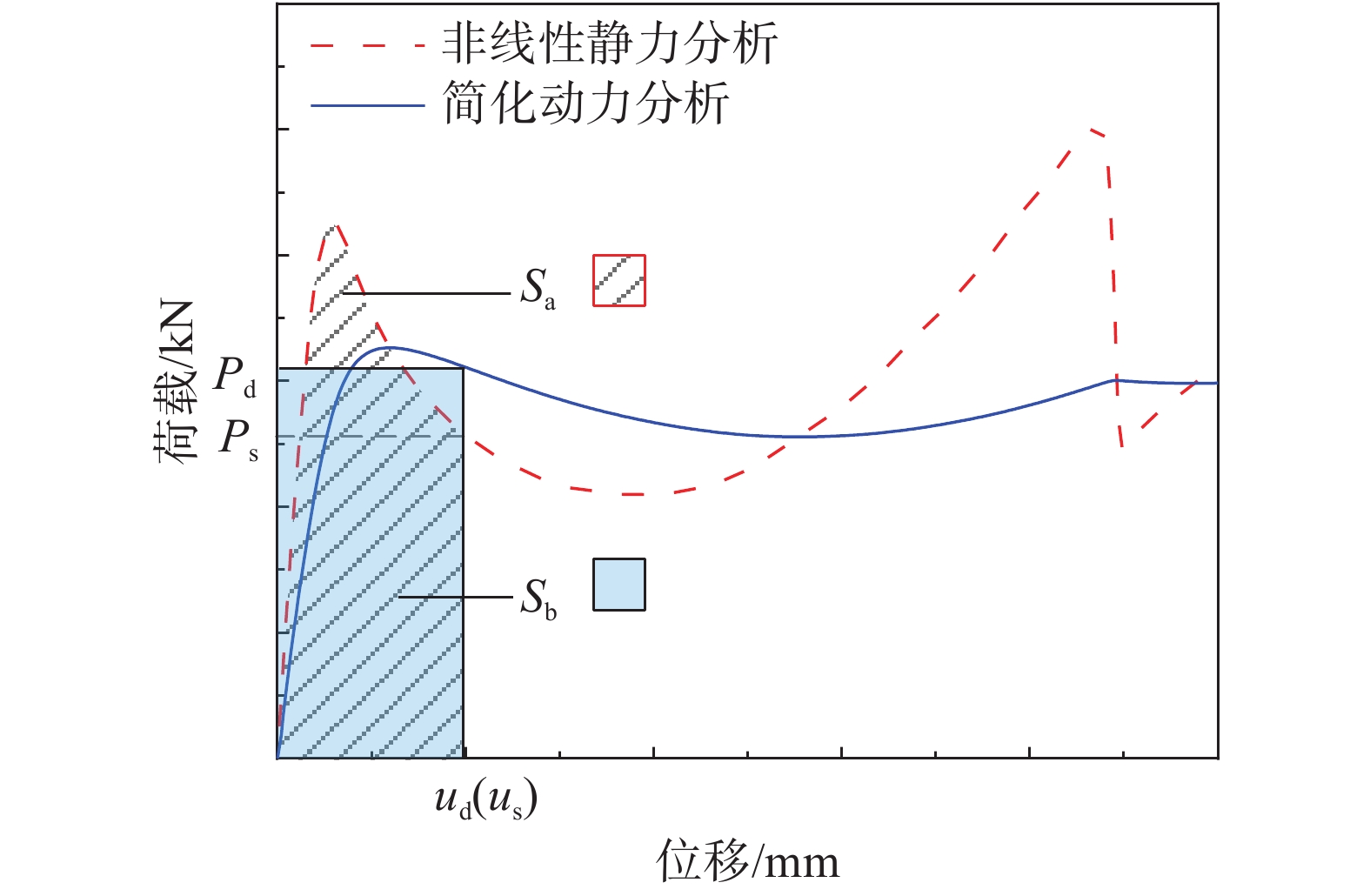
基于能量原理的简化动力分析方法如图9所示,在结构抵抗连续倒塌过程中,结构有效地耗散了重力做功W,当重力做功W与结构内力虚功U相等时(即图9中阴影面积Sa=Sb时),对应的荷载即为结构在动力分析中达到位移ud时对应的临界动力荷载Pd[29],即:
Pd=1ud∫Ps(us)dus (1) 式中:Ps为静力荷载;us为静力位移。采用上述简化动力分析方法将1000个样本的静力荷载-位移曲线转换为简化动力分析曲线,其中典型试件的简化动力分析曲线与其静力荷载-位移曲线对比如图9所示,统计分析参数不确定性对RC框架梁柱子结构连续倒塌率的影响,如图8所示。
结果表明,采用简化动力分析方法计算所得的动力失效荷载均值为Fi3=26.33 kN,标准差为σi3=2.39 kN (其中,i3代表简化动力分析),与失效指标1(结构无法恢复平衡状态)对应的失效荷载均值误差为−5.90%;且简化方法得到的倒塌率为50%时对应的失效荷载为26.39 kN,与非线性动力分析误差为−5.65%。同时,简化动力分析得到倒塌易损性曲线与非线性动力分析结果大致相同。因此,在开展RC框架梁柱子结构抗连续倒塌性能参数不确定性分析中使用简化动力分析方法不仅能够保证结果的准确性,同时还可以很大程度上减少计算消耗,将该方法用于作为结构动力失效判定也可以得到优于传统规范中以梁端转角达到0.20 rad(失效指标2)的判定结果。
4 参数敏感性分析
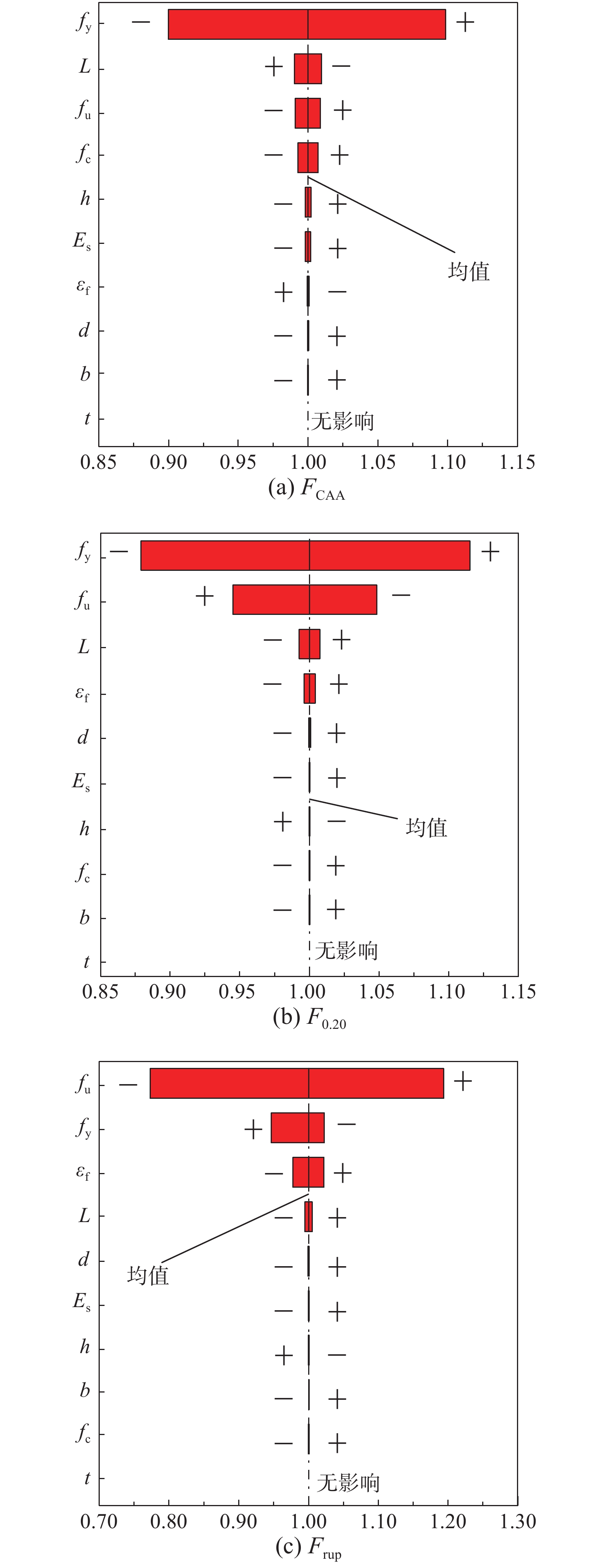
本文基于参数不确定性分析进一步研究了各参数对RC框架梁柱子结构抗连续倒塌能力的影响。参数敏感性分析研究了各随机变量分别取均值(Mean)、均值减1倍标准差(Mean-Std)和均值加1倍标准差(Mean+Std)时RC框架梁柱子结构连续倒塌的结构响应。为更加清晰地展示各参数的敏感性,将结果归一化并绘制表征不同随机变量敏感性的龙卷风图,如图10与图11所示。各变量含义如表1所示,图中“+”为Mean+Std计算结果,“−”为Mean-Std计算结果。
4.1 静力工况
在基于静力拆除构件工况的参数敏感性分析中,选定的判别指标与参数不确定性分析中相同,同样为FCAA、F0.20和Frup三个承载力特征值指标。
由图10可知,纵筋屈服强度对FCAA和F0.20的影响最大,纵筋极限强度对Frup的影响最大。纵筋屈服强度对F0.20和FCAA的影响大于对Frup的影响,前者约为后者的2倍。除此之外,纵筋极限强度对F0.20也有较大影响,这是由于:若钢筋梁端转角达到0.20 rad前发生断裂,则F0.20的值取为纵筋断裂时对应的Frup。表2列出了各判别指标的最大影响参数及相应的影响程度。其余不确定性参数包括截面几何属性和纵筋弹性模量等对于基于静力工况下的RC框架梁柱子结构承载力影响较小。
表 2 静力工况参数敏感性分析结果Table 2. Sensitivity analysis results for static scenario判别指标 Mean-Std/(%) Mean+Std/(%) 主要指标 FCAA −10.1 +9.8 fy F0.20 −12.1 +11.5 fy Frup −22.7 +19.3 fu 4.2 动力工况
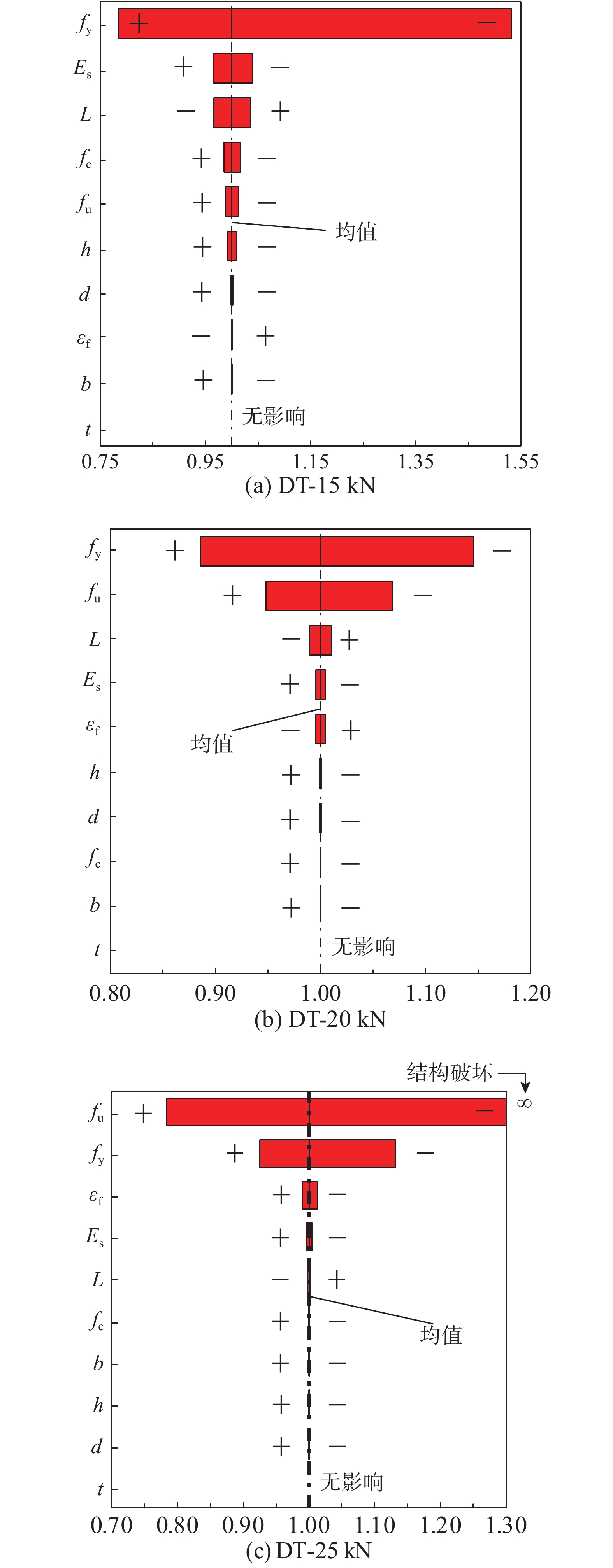
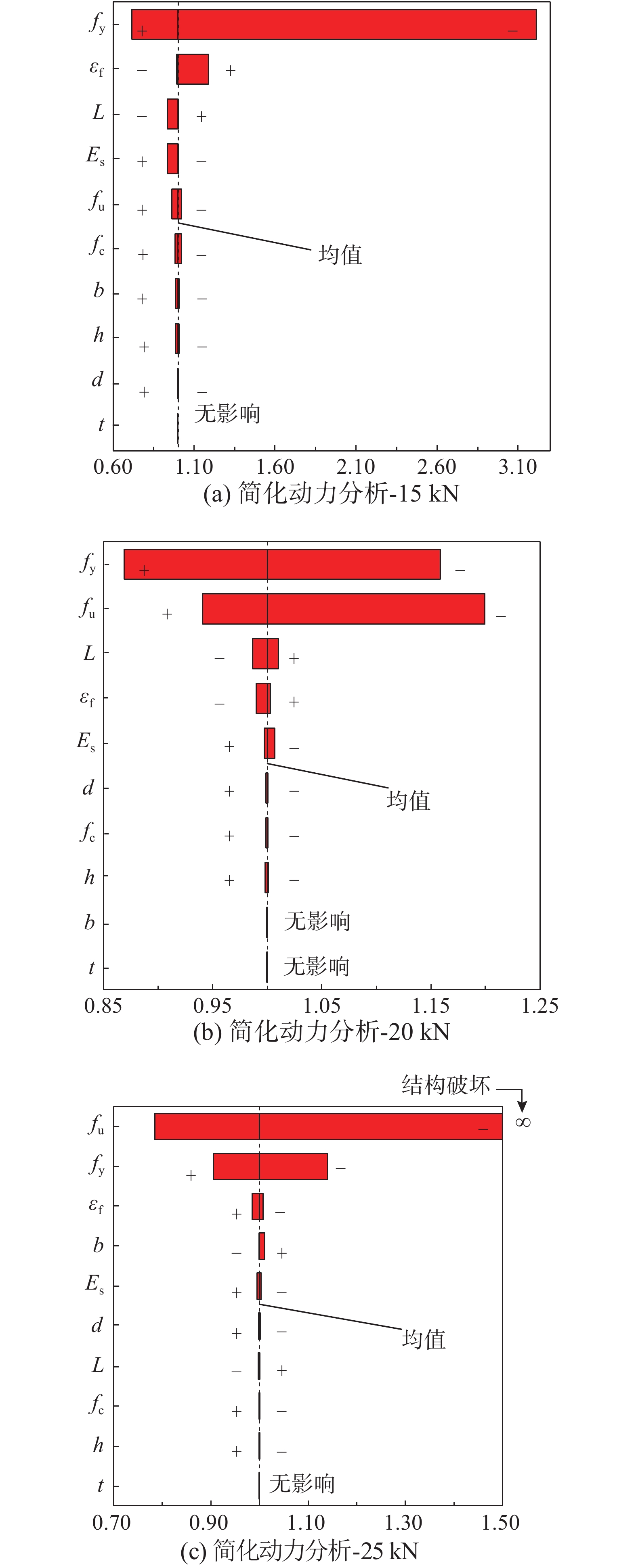
在本文基于动力拆除工况的敏感性分析中,研究了各随机变量对外荷载分别为15 kN、20 kN和25 kN时DT模型的连续倒塌动力位移响应的影响,如图11所示。
结果表明,纵筋屈服强度和极限强度为影响基于动力工况的RC框架梁柱子结构连续倒塌峰值位移响应的最主要因素。表3列出了各外荷载作用在基于动力工况的RC框架梁柱子结构时,对应的最大影响参数及相应的影响程度。值得注意的是,纵筋屈服强度对基于动力工况的RC框架梁柱子结构峰值位移的影响随着外荷载的增加而降低,随着外荷载从15 kN增加到25 kN,纵筋极限强度对基于动力工况的RC框架梁柱子结构峰值位移的影响程度由[−1.2%,1.3%]增加到[−21.17%,
+∞ ],其中+∞ 表示结构破坏,即失效柱头处竖向位移无法稳定在某个值处上下波动,如图7(a)。除此之外,梁长和纵筋弹性模量对基于动力工况的RC框架梁柱子结构峰值位移也有一定影响。其余不确定性参数对基于动力工况的RC框架梁柱子结构峰值位移影响较小。表 3 动力工况参数敏感性分析结果Table 3. Sensitivity analysis results for dynamic scenario外荷载 Mean-Std/(%) Mean+Std/(%) 主要指标 15 kN −21.59 +53.15 fy 20 kN −11.39 +14.62 fy 25 kN −21.65 +∞ fu 4.3 基于能量原理的简化动力分析
与动力工况相同,在简化动力分析中外荷载同样选择了15 kN、20 kN和25 kN,相应敏感性分析结果如图12所示。
与非线性动力分析结果大致相同,纵筋屈服强度及极限强度为影响基于简化动力分析工况的RC框架梁柱子结构抗连续倒塌性能的重要因素,且随着外荷载由15 kN增加至25 kN时,纵筋极限强度对基于简化动力分析工况的RC框架梁柱子结构动力峰值位移的影响程度由[−3.82%,2.33%]增加到[−21.53%,
+∞ ]。其余不确定性参数对基于简化动力分析工况的RC框架梁柱子结构动力峰值位移影响较小。5 结论
近年来,结构的抗连续倒塌问题在国内外已经引起了大量学者的注意。本研究基于开源有限元软件OpenSees,考虑结构几何属性、材料特性和外荷载等多种参数,分析了结构参数不确定性对RC框架梁柱子结构静力和动力抗连续倒塌性能的影响,主要结论如下:
(1) 静力工况下,RC框架梁柱子结构的悬链线阶段的F0.20和Frup均值相比梁机制阶段的FCAA分别增加为81.74%和148.95%,因此悬链线机制抗力对RC框架梁柱子结构抗连续倒塌性能起至关重要。同时,Frup的标准差大于F0.20和FCAA,说明参数不确定性对子结构的悬链线阶段承载力影响最明显,实际结构设计中应予以充分考虑。
(2) 动力工况下,分别以结构是否达到平衡状态和规范中常用的梁端转角达到0.20 rad为失效判别指标时,前者计算得到的50%倒塌概率对应的失效荷载约为后者的1.4倍,就本文试件而言,将梁端转角达到0.20 rad作为失效判别指标的结果偏保守。
(3) 根据敏感性分析结果,静力工况下,纵筋屈服强度fy为FCAA和F0.20的主要影响因素,纵筋极限强度fu为Frup的主要影响因素。动力工况下,外荷载较小时,fy对动力峰值位移的影响最大;外荷载较大时,fu则成为影响连续倒塌动力失效的主要因素。
(4) 基于能量原理的简化动力分析方法计算所得的连续倒塌易损性曲线与非线性动力分析结果的误差仅为−5.90%,表明相比0.20 rad梁端转角而言,该方法更适用于RC框架梁柱子结构是否发生动力失效的简化判定。
-
表 1 随机变量分布
Table 1 Distributions of the random variables
随机变量 均值 变异系数/(%) 分布函数 跨度L 2000 mm 0.23 正态分布 梁高h 170 mm 0.54 正态分布 梁宽b 85 mm 0.75 正态分布 混凝土保护层厚度t 6 mm 5.00 正态分布 纵筋弹性模量Es 200 GPa 3.30 正态分布 纵筋断裂应变εf 0.25 15.00 正态分布 纵筋直径d 6 mm/8 mm 4.00 正态分布 混凝土抗压强度fc 26.6 MPa 18.00 对数正态分布 纵筋屈服强度fy 336/292 MPa* 9.30 β分布 纵筋极限强度fu 512/459 MPa* 8.00 β分布 注:336 MPa、512 MPa为直径6 mm纵筋的屈服强度和极限强度;292 MPa、459 MPa为直径8 mm纵筋的屈服强度和极限强度。 表 2 静力工况参数敏感性分析结果
Table 2 Sensitivity analysis results for static scenario
判别指标 Mean-Std/(%) Mean+Std/(%) 主要指标 FCAA −10.1 +9.8 fy F0.20 −12.1 +11.5 fy Frup −22.7 +19.3 fu 表 3 动力工况参数敏感性分析结果
Table 3 Sensitivity analysis results for dynamic scenario
外荷载 Mean-Std/(%) Mean+Std/(%) 主要指标 15 kN −21.59 +53.15 fy 20 kN −11.39 +14.62 fy 25 kN −21.65 +∞ fu -
[1] ASCE/SEI 7-10, Minimum design loads for buildings and other structures [S]. Reston, Virginia: American Society of Civil Engineers, 2010.
[2] Osteraas J D. Murrah building bombing revisited: A qualitative assessment of blast damage and collapse patterns [J]. Journal of Performance of Constructed Facilities, 2006, 20(4): 330 − 335. doi: 10.1061/(ASCE)0887-3828(2006)20:4(330)
[3] Ren P Q, Li Y, Lu X Z, et al. Experimental investigation of progressive collapse resistance of one-way reinforced concrete beam-slab substructures under a middle-column-removal scenario [J]. Engineering Structures, 2016, 118: 28 − 40. doi: 10.1016/j.engstruct.2016.03.051
[4] 肖宇哲, 李易, 陆新征, 等. 混凝土梁柱子结构连续倒塌动力效应的试验研究[J]. 工程力学, 2016, 36(5): 44 − 52. doi: 10.6052/j.issn.1000-4750.2015.07.ST08 Xiao Yuzhe, Li Yi, Lu Xinzheng, et al. Experimental study on the dynamic effects in progressive collapse of beam-column concrete substructures [J]. Engineering Mechanics, 2016, 36(5): 44 − 52. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.07.ST08
[5] 王少杰, 刘福胜, 徐赵东. RC空间框架结构竖向倒塌全过程试验研究与理论分析[J]. 工程力学, 2015, 32(5): 162 − 167. doi: 10.6052/j.issn.1000-4750.2013.11.1094 Wang Shaojie, Liu Fusheng, Xu Zhaodong. Experimental and theoretical analyses on entire course of vertical progressive collapse of spatial frame structures [J]. Engineering Mechanics, 2015, 32(5): 162 − 167. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.11.1094
[6] 钱凯, 李治, 翁运昊, 等. 钢筋混凝土梁-板子结构抗连续性倒塌性能研究[J]. 工程力学, 2019, 36(6): 237 − 247. doi: 10.6052/j.issn.1000-4750.2018.05.0297 Qian Kai, Li Zhi, Weng Yunhao, et al. Behavior of beam-slab substructures to resist progressive collapse [J]. Engineering Mechanics, 2019, 36(6): 237 − 247. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.05.0297
[7] Feng D C, Xie S C, Xu J, et al. Robustness quantification of reinforced concrete structures subjected to progressive collapse via the probability density evolution method [J]. Engineering Structures, 2020, 202: 109877. doi: 10.1016/j.engstruct.2019.109877
[8] 易伟建, 何庆峰, 肖岩. 钢筋混凝土框架结构抗倒塌性能的试验研究[J]. 建筑结构学报, 2007, 28(5): 101 − 109. Yi Weijian, He Qingfeng, Xiao Yan. Collapse performance of RC frame structure [J]. Journal of Building Structures, 2007, 28(5): 101 − 109. (in Chinese)
[9] 程小卫, 李易, 陆新征, 等. 基于多尺度模型的RC框架撞击倒塌响应数值分析[J]. 振动与冲击, 2016, 35(5): 82 − 88. Cheng Xiaowei, Li Yi, Lu Xinzheng, et al. Numerical analysis for collapse response of a RC frame subjected to impact loading based on multi-scale model [J]. Journal of Vibration and Shock, 2016, 35(5): 82 − 88. (in Chinese)
[10] Fascetti A, Kunnath S K, Nisticò N. Robustness evaluation of RC frame buildings to progressive collapse [J]. Engineering Structures, 2015, 86: 242 − 249. doi: 10.1016/j.engstruct.2015.01.008
[11] Melchers R E, Beck A T. Structural reliability analysis and prediction [M]. Hoboken, NJ: Wiley, 2018.
[12] Yu X H, Lu D G, Qian K, et al. Uncertainty and sensitivity analysis of reinforced concrete frame structures subjected to column loss [J]. Journal of Performance of Constructed Facilities, 2017, 31(1): 1 − 14.
[13] Feng D C, Xie S C, Deng W N, et al. Probabilistic failure analysis of reinforced concrete beam-column sub-assemblage under column removal scenario [J]. Engineering Failure Analysis, 2019, 100: 381 − 392. doi: 10.1016/j.engfailanal.2019.02.004
[14] He X H C, Yuan X X, Yi W J. Irregularity index for quick identification of worst column removal scenarios of RC frame structures [J]. Engineering Structures, 2019, 178: 191 − 205. doi: 10.1016/j.engstruct.2018.10.026
[15] 贾明明, 杨先霖, 吕大刚, 等. 基于易损性的RC空间框架填充墙结构连续倒塌能力分析[J]. 建筑结构学报, 2018, A1: 230 − 236. Jia Mingming, Yang Xianlin, Lü Dagang, et al. Fragility-based progressive collapse capacity analysis of RC frame structures with infilling walls [J]. Journal of Building Structures, 2018, A1: 230 − 236. (in Chinese)
[16] 初明进, 周育泷, 陆新征, 等. 钢筋混凝土单向梁板子结构抗连续倒塌试验研究[J]. 土木工程学报, 2016, 49(2): 31 − 40. Chu Mingjin, Zhou Yulong, Lu Xinzheng, et al. An experimental study on one-way reinforced concrete beam-slab substructures for resisting progressive collapse [J]. China Civil Engineering Journal, 2016, 49(2): 31 − 40. (in Chinese)
[17] 杜轲, 滕楠, 燕登, 等. 楼板对RC空间框架结构抗连续倒塌性能影响试验研究[J]. 土木工程学报, 2019, 52(6): 14 − 23. Du Ke, Teng Nan, Yan Deng, et al. Experimental study on the effect of floor slab on the progressive collapse resistance of RC spatial frame structure [J]. China Civil Engineering Journal, 2019, 52(6): 14 − 23. (in Chinese)
[18] 喻君, 甘艺平, 李爽. 考虑全填充墙作用的钢筋混凝土框架抗连续倒塌性能分析[J]. 建筑结构学报, 2019, 40(11): 112 − 121. doi: 10.14006/j.jzjgxb.2018.0412 Yu Jun, Gan Yiping, Li Shuang. Analysis of progressive collapse performance of reinforced concrete frames with full-height infill walls [J]. Journal of Building Structures, 2019, 40(11): 112 − 121. (in Chinese) doi: 10.14006/j.jzjgxb.2018.0412
[19] 杜轲, 滕楠, 孙景江, 等. 基于共旋坐标和力插值纤维单元的RC框架结构连续倒塌构造方法[J]. 工程力学, 2019, 36(3): 95 − 104. doi: 10.6052/j.issn.1000-4750.2018.01.0055 Du Ke, Teng Nan, Sun Jingjiang, et al. A progressive collapse analytical model of RC frame structures based on corotational formulation for force-based fiber elements [J]. Engineering Mechanics, 2019, 36(3): 95 − 104. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.01.0055
[20] 周云, 张琴, 胡翔, 等. 基于拆除构件法的全装配式框架结构连续倒塌分析[J]. 湖南大学学报(自然科学版), 2020, 47(5): 1 − 13. doi: 10.16339/j.cnki.hdxbzkb.2020.05.001 Zhou Yun, Zhang Qin, Hu Xiang, et al. Progressive collapse analysis of fully assembled precast concrete frame structures based on column removal method [J]. Journal of Hunan University (Natural Sciences), 2020, 47(5): 1 − 13. (in Chinese) doi: 10.16339/j.cnki.hdxbzkb.2020.05.001
[21] Brunesi E, Nascimbene R, Parisi F, et al. Progressive collapse fragility of reinforced concrete framed structures through incremental dynamic analysis [J]. Engineering Structures, 2015, 104: 65 − 79. doi: 10.1016/j.engstruct.2015.09.024
[22] Le J L, Xue B. Probabilistic analysis of reinforced concrete frame structures against progressive collapse [J]. Engineering Structures, 2014, 76: 313 − 323. doi: 10.1016/j.engstruct.2014.07.016
[23] Qian K, Li B, Ma J X. Load-carrying mechanism to resist progressive collapse of RC buildings [J]. Journal of Structural Engineering, 2015, 141(2): 04014107. doi: 10.1061/(ASCE)ST.1943-541X.0001046
[24] 张沛洲, 孙宝印, 古泉, 等. 基于数值子结构方法的低延性RC框架结构抗震性能精细化分析[J]. 工程力学, 2017, 34(A1): 38 − 48. doi: 10.6052/j.issn.1000-4750.2016.04.S018 Zhang Peizhou, Sun Baoyin, Gu Quan, et al. Refined aseismic analysis of low-ductility RC frame building based on numerical substructure method [J]. Engineering Mechanics, 2017, 34(A1): 38 − 48. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.04.S018
[25] Barbato M, Gu Q, Conte J P. Probabilistic push-over analysis of structural and soil-structure systems [J]. Journal of Structural Engineering, 2010, 136(11): 1330 − 1341. doi: 10.1061/(ASCE)ST.1943-541X.0000231
[26] Mirza S A, MacGregor J G. Variations in dimensions of reinforced concrete members [J]. Journal of the Structural Division, 1979, 105(4): 751 − 766. doi: 10.1061/JSDEAG.0005132
[27] Mirza S A, MacGregor J G. Variability of mechanical properties of reinforcing bars [J]. Journal of the Structural Division, 1979, 105(5): 921 − 937. doi: 10.1061/JSDEAG.0005146
[28] DoD 2016, Design of structures to resist progressive collapse [S]. Washington D. C.: Department of Defense, 2016.
[29] Izzuddin B A, Vlassis A G, Elghazouli A Y, et al. Progressive collapse of multi-storey buildings due to sudden column loss-Part I: Simplified assessment framework [J]. Engineering Structures, 2008, 30(5): 1308 − 1318. doi: 10.1016/j.engstruct.2007.07.011
-
期刊类型引用(13)
1. 何羽,钱凯,于晓辉. 钢筋混凝土结构抗连续倒塌研究进展. 河北工业大学学报. 2025(01): 16-31+63 .  百度学术
百度学术
2. 李治,原小兰,薛天琦,钱凯. 不同去柱工况下多层钢框架结构抗连续倒塌机理研究. 工程力学. 2024(04): 140-150 .  本站查看
本站查看
3. 姚颖康,章强,侯永恒,贾永胜. RC框架楼房中心立柱爆破失效条件下结构动力响应特性分析. 爆破. 2024(03): 121-129 .  百度学术
百度学术
4. 李治,薛天琦,原小兰,张毅,钱凯. 角柱失效下不等跨RC空间梁-柱子结构抗连续倒塌机理研究. 振动与冲击. 2023(06): 115-125+179 .  百度学术
百度学术
5. 黄咏政,梁子晗,王森钠,薛晓光,李易. 主要设计参数对规则RC框架结构抗连续倒塌性能的影响. 工程力学. 2023(S1): 184-190 .  本站查看
本站查看
6. 黄咏政,王森钠,梁子晗,尹续峰,李易. 常规混凝土框剪结构连续倒塌动力响应分析. 工程力学. 2023(S1): 227-233 .  本站查看
本站查看
7. 王景玄,王文琦,周侃. 钢管混凝土柱-波纹腹板H形钢梁栓焊混合加腋节点抗倒塌能力研究. 工程力学. 2023(09): 190-202 .  本站查看
本站查看
8. 兰冬璆,邓小芳,金浏,钱凯. 次边缘柱失效下预应力混凝土框架抗连续倒塌性能研究. 工程力学. 2023(10): 58-70 .  本站查看
本站查看
9. 郄禄文,李猛,宋鹏彦,刘静,王岳. 考虑参数不确定性的RC框架柱滞回性能分析. 河北大学学报(自然科学版). 2022(01): 1-7 .  百度学术
百度学术
10. 熊学玉,谢一凡,姚刚峰. 基于修正的软化拉压杆模型的RC框架边节点受剪性能研究. 工程力学. 2022(06): 55-71 .  本站查看
本站查看
11. 甘艺平,喻君,陈隽,申家旭. 不等跨RC框架的抗连续倒塌理论分析及鲁棒性评判指标研究. 工程力学. 2022(08): 210-222 .  本站查看
本站查看
12. 李正良,王成,王涛,方智远. 下击暴流作用下直立锁缝屋面系统抗风揭可靠度评估. 湖南大学学报(自然科学版). 2022(09): 90-99 .  百度学术
百度学术
13. 祖庆芝. RC框架结构在不同类型地震作用下的破坏分析. 长春工程学院学报(自然科学版). 2022(02): 43-50 .  百度学术
百度学术
其他类型引用(8)




 下载:
下载: