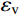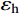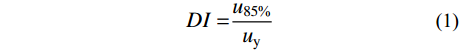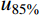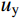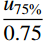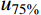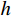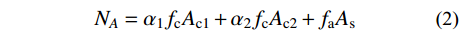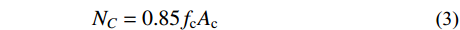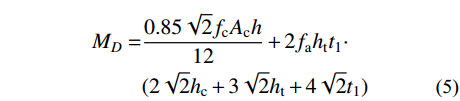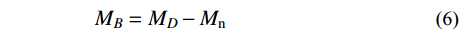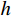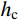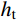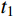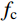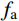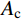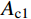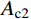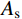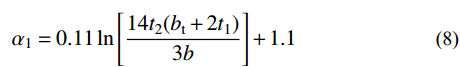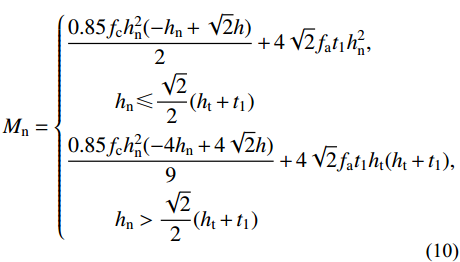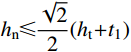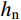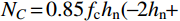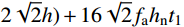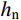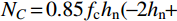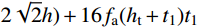BEHAVIOUR AND BEARING CAPACITY OF CONCRETE-FILLED HORIZONTAL CORRUGATED STEEL PLATE-TUBULAR COMPOSITE COLUMNS UNDER BI-AXIAL ECCENTRIC COMPRESSION
-
摘要: 为研究横肋波纹钢板-方钢管混凝土组合柱的双向偏压力学性能，对两根横肋波纹钢板-方钢管混凝土组合柱试件展开了双向偏压加载试验，探究了不同偏心距对试件在双向偏压荷载下的荷载-变形曲线、破坏模态和截面应变发展状况的影响，分析了波纹板与钢管、混凝土之间的相互作用机理。在试验基础上运用有限元模拟，分析了偏心距、加载角度、钢管厚度、波纹板厚度等多种参数对横肋波纹钢板-方钢管混凝土组合柱双向偏压荷载下承载力、延性、刚度等力学性能的影响规律，得出钢管厚度增大柱的极限承载力显著提高，加载角度对极限承载力影响不大等主要结论。最后，参考欧洲《EC4》规范钢混组合柱承载力的计算方法，提出了横肋波纹钢板-方钢管混凝土组合柱双向偏压承载力实用计算公式，以期为工程实践提供参考。Abstract: In order to investigate the mechanical performance of concrete-filled horizontal corrugated steel plate-tubular composite columns under bi-axial eccentric compression, two specimens were prepared for bi-axial eccentric loading test. Load versus deformation curves, failure mode and longitudinal strain were analyzed. A reasonable explanation of interaction between corrugated plate and steel tubes and concrete were proposed. Furthermore, a finite element analysis model was established. The influence of loading, the ductility and stiffness under different eccentricities, loading angles, thickness of the steel tubes and thickness of the corrugated plates were also analyzed. It is found that with the increase of the thickness of steel tubes, the bearing capacity of columns are improved evidently. And loading angles have barely influence on the bearing capacity. Finally, based on the bearing capacity calculation formula of steel-concrete composite columns in Eurocode 4, a calculation formula of the bearing capacity under bi-axial eccentric loading is proposed, which agrees well with the finite element results and is practical in actual engineering.
-
与钢筋混凝土柱相比，钢管混凝土柱有延性好、承载力高等受力特点[1]。其原因为钢管对混凝土产生了一定的约束效应，使组合柱各部分的材性可以得到更为充分的利用[2-3]。但钢管混凝土柱存在钢管纵向应变大、局部屈曲风险高等问题。而钢管约束混凝土柱中钢管不直接承担纵向荷载，改善了钢管混凝土柱的缺陷，可以让钢管起到更好的约束作用[4]。
在钢管约束混凝土柱的研究基础上，方勇和王玉银等[5-6]自2015年起对波纹钢管混凝土柱开展了一系列研究。研究表明，波纹钢管混凝土柱中波纹钢管的受力性质与钢管约束混凝土柱类似，波纹钢管可对混凝土产生有效的约束、不易屈曲，且相较于钢管约束混凝土柱具有更好的承载力与延性。
2020年，邹昀课题组康金鑫等[7]提出了一种新型横肋波纹钢板-方钢管混凝土组合柱，这种柱由四角方钢管和侧壁波纹钢板焊接形成的多腔体与混凝土组合而成，钢管部分可有效承担拉、压荷载，波纹板则能对混凝土起到有效约束作用。康金鑫等通过试验与有限元模拟探究了此种组合柱的轴压性能，研究表明，横肋波纹钢板-方钢管混凝土组合柱具有较好的延性与较高的承载力。随后课题组对此种柱的偏压、抗弯、抗剪性能做出了进一步研究，其研究成果已应用于实际工程中(如图1所示)。
在实际工程中，由于风荷载、水平地震作用等因素，结构往往处于双向偏压受力状态，因此深入研究柱在双向偏压荷载下的力学性能是十分有必要的。王连广等[8]、Li等[9]、Li等[10]已对钢管混凝土柱、钢管-钢骨混凝土柱的双向偏压受力性能进行了一系列试验、有限元模拟研究，验证了运用有限元模拟进行组合柱双向偏压受力性能研究的可行性。基于此，本文探究了横肋波纹钢板-方钢管混凝土组合柱的双向偏压性能，结合试验与有限元分析，得出了横肋波纹钢板-方钢管混凝土组合柱在双向偏压荷载下的受力特征及实用承载力计算公式，以期为工程设计提供参考。
1 试验设计
1.1 试件参数
为研究横肋波纹钢板-方钢管混凝土组合柱(concrete-filled horizontal corrugated steel plate-tubular composite columns，简称CFHCSPTC柱)在双向偏压荷载下的力学性能，共设计制作了C1、C2两根试件，试件截面如图2所示，截面尺寸参数如表1所示，两试件除加载偏心距不同之外其他各参数均相同。参照《混凝土结构试验方法标准》(GB 50152−92)[11]进行混凝土材性试验，测得混凝土实测立方体强度为35 MPa；参照《金属材料室温拉伸试验方法》(GB 228−2002)[12]，测得钢管、波纹板实测强度分别为400.6 MPa与403.1 MPa。
表 1 试件参数Table 1. Parameters of specimens试件编号 柱高/mm 偏心距/mm 边长h/mm 钢管尺寸 边长ht/mm 厚度t1/mm C1 1400 49.5 350 69 3 C2 1400 99.0 350 69 3 试件编号 波纹板尺寸 宽度hc/mm 厚度t2/mm 波高hr/mm 峰谷长度l1/mm 波腹长度l2/mm C1 200 1 20 31.5 15.5 C2 200 1 20 31.5 15.5 1.2 试验过程
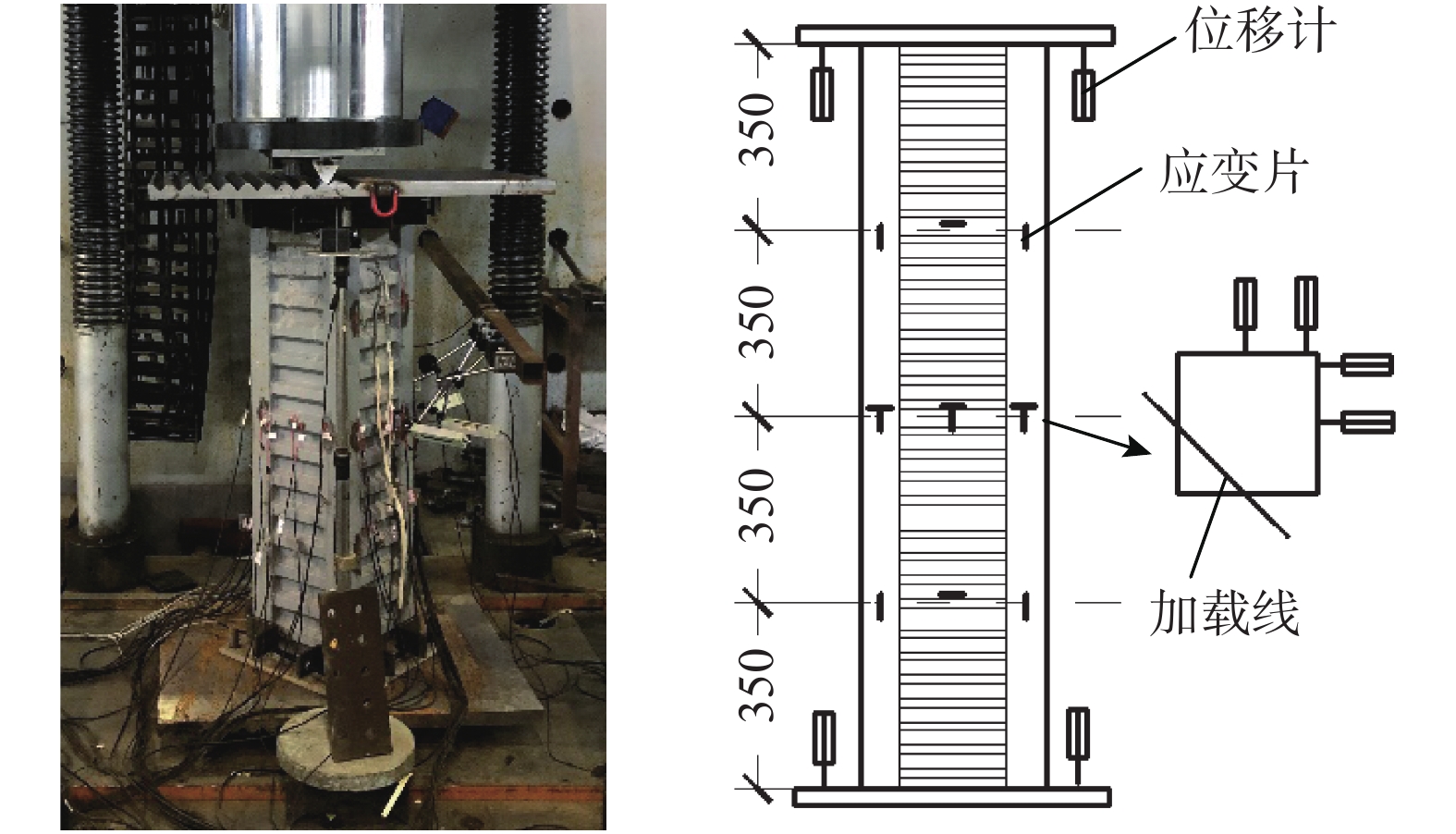
试验在1000 t压力机上进行。在试件两侧设置端板，通过端板与加载板的栓接实现双向偏压加载。加载板相对于端板成45°角放置，以达到双向偏压加载的效果。试件两端采用双向刀铰加载来模拟两端铰接的边界条件，如图3所示。双向偏心加载中，偏心距为双向刀铰加载线到试件形心的距离。刀铰通过螺栓固定在压力机的上、下承压板上。同时，为防止试件端部出现局部破坏，加载时在柱的两端设置钢套，达到保护试件端部的目的。
位移计与应变片布置如图4所示。分别在试件柱顶、柱底、柱中位置布置位移计以量测加载过程中柱的纵向位移与柱中挠度；在试件各个侧面分别布置12片钢材电阻应变片，测量钢管与波纹侧板的纵向、横向应变。
采用一次性压溃加载方式，开始阶段采用荷载控制加载，每级荷载增量为50 kN，持续时间约为2 min；当柱发生屈服变形后，改用位移控制加载，每级位移增量为1 mm，持续时间约为2 min；当试件钢管的鼓曲变形剧烈时改为缓慢连续加载。在试验过程中，连续记录加载过程的位移、应变情况，直至荷载下降至峰值的50%或出现严重破坏时，停止试验。
2 试验结果与分析
为方便说明，参照试件各部分的受力特征，按图5所示对试件钢管、混凝土及波纹侧板各部分进行命名。将试件中四根钢管分为Ⅰ管、Ⅱ管、Ⅲ管、Ⅳ管，并对各钢管、波纹板外露的面分别进行了命名。其中，钢管上a1、a2，b1、d1，b2、d2，c1、c2等面互为等效加载面，使用相关应变数据时均取两等效面的平均值以减少数据随机性。根据波纹板内侧混凝土的受力方式，将其分为核心混凝土与外凸混凝土两部分。在加载时，核心混凝土可以正常承受压力与拉力，且受到波纹板的保护，其受力方式类似于钢管约束混凝土；而外凸混凝土则因无法传递纵向荷载，在加载前期对结构承载力贡献较小。
2.1 试验现象
试件荷载-纵向位移(N-Δ)曲线与荷载-柱中挠度(N-um)曲线如图6所示。其中Δ为柱顶与柱底端板截面形心的相对纵向位移，um为试件柱中垂直于加载线方向的横向位移。
对于C1试件，在加载初期，试件处于弹性阶段，没有明显变形现象。当加载至2400 kN左右时，Ⅰ管纵向应变的绝对值超过钢材屈服应变，N-Δ曲线斜率开始下降，试件进入弹塑性阶段。当加载至位移5.4 mm时，试件达到其峰值荷载3047 kN。当位移加载至7.5 mm时，Ⅰ管上出现明显鼓曲，鼓曲附近波纹板也出现明显变形。继续加载至试件破坏，最终破坏形态如图7所示，破坏集中于a1面与a2面接近柱顶处；波纹板也出现明显鼓曲，AB面波纹板与Ⅱ管间的焊缝被拉裂。加载试验结束后，切开试件破坏严重处钢管及波纹板，来观察试件内部混凝土破坏情况。Ⅰ管混凝土为压碎破坏，共有3处混凝土明显压碎胀出，与钢管的3处鼓曲相对应；Ⅱ管也在钢管鼓曲处出现了两处混凝土压碎；Ⅲ管转角最大处混凝土被拉裂，出现多处横向裂纹。
对于C2试件，当加载至1800 kN时，Ⅲ管纵向应变超过钢材屈服应变，试件进入弹塑性阶段。当加载至2027 kN(位移3.1 mm)时，试件承载力达到峰值。位移加载至9.8 mm时，Ⅰ管靠近柱脚处严重鼓曲，鼓曲处附近的波纹板也出现明显鼓曲。当位移加载至13.9 mm时，Ⅰ管因鼓曲严重而开裂，混凝土压碎；同时，Ⅲ管在靠近柱脚处发生拉裂，管内混凝土出现数道横向裂缝(如图8所示)。其余两根方钢管虽有明显转角变形，但并未产生屈曲。
2.2 应变分析
加载过程中各试件钢管纵向应变与横向应变均呈一拉一压的状态，且纵向应变(
εv )绝对值均远大于横向应变(εh )，各钢管力学性质均由纵向应变主导。取试件各钢管柱中纵向应变研究钢管受力情况，并绘出如图9所示的沿截面高度柱中纵向应变对比图，图9中各纵向截面高度依次对应钢管a1(a2)面、b1(b2)面、c1(c2)面、d1(d2)面。由图9可得，两试件在加载前期，钢管纵向应变情况均基本符合平截面假定，且均呈Ⅰ、Ⅱ、Ⅳ管受压，Ⅲ管受拉的受力状态。而当加载至荷载接近试件极限承载力时，Ⅲ管纵向拉应变发展明显快于其余3根钢管。其原因为受拉区混凝土在加载至接近极限荷载时开始开裂，不再承担拉应力。此时截面受压区的力由钢管和混凝土共同承担，而受拉区的力绝大部分由钢管独自承担，已不符合平截面假定，且出现截面受拉区增大、中性轴向受压区移动等现象。对比图9(a)、图9(b)可知，当加载偏心距由49.5 mm增大到99 mm时，极限承载力时中性轴由BC、CD面移动至b2(d2)面附近。
![]()
图 9 柱中沿截面高度钢管纵向应变对比Figure 9. Vertical strain comparison of steel tube at midspan on different height of section2.3 混凝土破坏机理分析
根据图9柱中钢管的纵向应变情况可知，波纹板内侧混凝土因其两侧钢管受力状态不同，破坏形态也可分为两侧钢管受压破坏形态(如图10(a)所示)、两侧钢管受拉破坏形态(如图10(c)所示)、一侧受压一侧受拉破坏形态(如图10(b)所示)3种。
在加载前期，钢管、钢管内混凝土、核心混凝土协同受力，外凸混凝土基本不承受纵向荷载，只随整体协同变形。两侧钢管受压的波纹板，波腹相对于外凸混凝土有纵向缩短的趋势，即波腹有“夹紧”外凸混凝土的趋势，形成了波纹板向外凸混凝土施加较为均匀的压应力的局部受力状况(如图11所示)。加载至钢管开始出现屈曲现象以后，波纹板在钢管的拉动下产生了较大的形变，从而让外凸混凝土的受力状态发生了改变。受压钢管屈曲后，屈曲处钢管及其邻接波纹板产生局部纵向位移，使波纹板施加在外凸混凝土上的均匀压应力转变为不均匀压应力。外凸混凝土因不均匀压应力而受到纵向剪切作用，产生了一道道纵向裂纹，较为接近的纵向裂纹贯通后便出现混凝土破碎剥离的现象。两侧钢管受拉的波纹板，则与两侧钢管受压的波纹板相反，波腹有脱离外凸混凝土的趋势，因而波纹板对外凸混凝土作用力较小，不会使外凸混凝土产生破坏。所以两侧钢管受拉的波纹板内混凝土破坏情况为：核心混凝土纵向受拉出现横向开裂，而外凸混凝土基本不破坏。一侧钢管受压、一侧钢管受拉的区域，则呈现出上述两种破坏现象混合的情况，靠近受压钢管处为外凸混凝土纵向开裂，靠近受拉钢管处则以核心混凝土横向开裂为主。
3 有限元分析
3.1 有限元模型建立
采用有限元分析软件ABAQUS进行CFHCSPTC柱双向偏压加载的模拟。使用实体单元C3D8R进行混凝土的构建[13]，使用壳单元S4R构建波纹板、钢管。由试验现象可知，钢管、波纹板与混凝土共同受力情况较好，因此，通过Tie接触定义钢管与混凝土、波纹板与混凝土、钢管与波纹板、柱顶与端板之间的相互作用关系。通过与端板耦合的参考点，在模型上施加双向偏压荷载。有限元模型如图12所示。
在模型中，钢管与波纹板的本构模型采用理想弹塑性模型，钢材的屈服强度、弹性模量取实测值，钢材泊松比取0.3。混凝土采用混凝土塑性损伤模型进行模拟，采用规范[14]中推荐的本构关系，混凝土弹性模量与抗压强度按材性试验结果取值，泊松比取0.2。
C1与C2试验荷载-位移曲线、荷载-柱中挠度曲线与有限元曲线对比如图6所示，有限元结果与试验结果拟合良好，试验与有限元的极限承载力误差分别为5%与2%。忽略试验中端部虚位移造成试件初始刚度较小的问题，则有限元与试验各阶段刚度对应情况良好。
两根试件的钢材破坏模态、混凝土破坏模态模拟结果如图13所示，C1中Ⅰ管率先受压破坏，C2中Ⅲ管与Ⅰ管相继破坏，而两根试件的混凝土破坏区域均集中于Ⅰ管柱中偏上的位置，与试验破坏现象基本一致。
对比试验与有限元中钢管柱中横纵向应变，典型结果如图14所示，可以发现有限元对钢管应变拟合较好，可以较为准确模拟加载前期钢管应变增长情况及极限荷载对应应变，通过有限元对CFHCSPTC柱进行参数分析较为可靠。
![]()
图 14 试验、有限元钢管应变对比Figure 14. Comparison of test and calculated load-strain curves of steel tubes3.2 参数分析
为进一步研究CFHCSPTC柱的受力性能，通过有限元模拟探究了偏心距、加载角度、钢管厚度、波纹板厚度等参数对柱双向偏压受力性能的影响。同时，为探究各参数对CFHCSPTC柱延性的影响，参照Tao和Han[15]对偏压柱延性系数(DI)的定义，使用以下公式计算双偏压柱模型延性系数：
DI=u85%uy (1) 式中：
u85% 为极限承载力后，荷载降至承载力85%时对应的柱中挠度；uy 为u75%0.75 ，u75% 为弹塑性阶段荷载达到极限荷载75%时对应的柱中挠度。设置多种参数变量，共进行了67个有限元模型分析。取其中混凝土强度为C40、钢材强度为Q345的模型，展开参数分析，相应的有限元计算结果如表2所示。
表 2 有限元计算结果Table 2. Results of finite element analysis变化参量 模型编号 极限承载力Nu/kN 延性系数DI 钢管厚度 spy-1-3-1 3293.67 3.57 spy-1-4-1 3838.76 4.26 spy-1-6-1 4552.23 5.40 spy-1-8-1 5217.41 7.27 spy-1-10-1 5869.24 8.74 spy-1-12-1 6500.20 10.50 波纹板厚度 spy-1-3-2 3416.11 3.87 spy-1-3-3 3495.62 4.31 spy-1-3-4 3577.88 4.60 偏心距 spy-2-3-1 2287.73 3.44 spy-3-3-1 1637.05 3.93 spy-4-3-1 971.42 5.98 加载角度 spy-1-3-1-15 3253.08 2.81 spy-1-3-1-30 3264.42 3.13 spy-1-6-1-15 4295.27 3.64 spy-1-6-1-30 4333.10 4.38 注：前3个字母SPY代表双偏压，其后各组数字分别代表偏心距(1~4依次对应49.5 mm、99 mm、148.5 mm、247.5 mm)、钢板厚度、波纹板厚度、加载角度(未标注时默认为45°)。 3.2.1 偏心距对模型受力性能的影响
保持加载角度为45°不变，取单轴偏心率分别为0.2、0.4、0.6、1.0这4种情况进行研究，其对应的偏心距分别为49.5 mm、99.0 mm、148.5 mm、247.5 mm。模型荷载-柱中挠度曲线随偏心距的变化情况如图15(a)所示，随着偏心距的增大，CFHCSPTC柱极限承载力显著下降，延性系数则不断增大。偏心距由49.5 mm提升至148.5 mm时，极限承载力下降了一半；由148.5 mm提升至247.5 mm时，极限承载力又下降了一半。随着偏心距的增大，N-um曲线承载力下降段趋于平缓，延性随之增强。
3.2.2 加载角度对模型受力性能的影响
图15(b)为在相同偏心距下，不同加载角度模型的荷载-柱中挠度曲线。可知双向偏压荷载加载角度的变化对柱承载力的影响基本可以忽略。而柱的延性则呈现出加载角度越接近45°，延性越好的现象。其原因为，当加载角度不为45°时，弯矩会使柱受扭，从而处于压弯扭的三相受力状态，影响到柱的延性。
3.2.3 钢管厚度对模型受力性能的影响
钢管的厚度是影响CFHCSPTC柱承截力的重要因素之一。如图15(c)所示，随着钢管厚度的增大，柱的极限承载力与残余承载力不断提升。在偏心距为49.5 mm时，钢管每增厚1 mm承载力平均上升375 kN。钢管厚度增大对初始刚度影响不明显，但可明显提升柱的延性。
3.2.4 波纹板厚度对模型受力性能的影响
提升波纹板厚度对柱的初始刚度没有影响(如图15(d)所示)，但会提升柱的极限承载力及残余承载力。在偏心距为49.5 mm时，波纹板厚度每提升1 mm，承载力提升2.7%左右。
4 实用计算公式
现有规范中尚无CFHCSPTC柱的双向偏压承载力计算公式，本文参照欧洲规范《EC4》[16]中对钢混组合柱承载力的计算方法及康金鑫等[7]提出的CFHCSPTC柱轴压承载力计算方法，提出CFHCSPTC柱双向偏压承载力实用计算公式。
《EC4》中将钢混组合柱N-M曲线通过3条直线表示，3条直线的端点为A、B、C、D这4点(如图16(a)所示)，各点所代表的CFHCSPTC柱截面受力状态如图16(b)所示。其中，受压混凝土纵向应力按0.85fc考虑，忽略混凝土受拉强度；受拉钢管与受压钢管应力均按钢管屈服强度考虑。点A代表柱受轴压荷载，点B代表柱受纯弯荷载，点C代表截面受压且受到与B点相同弯矩的时刻，点D代表截面弯矩最大的时刻(《EC4》中将此点荷载取为C点的一半)。在柱的各参数已知的情况下，依据弯矩平衡可依次求出NA、NC、ND、MD，依据式(10)及其后注解经过试算得出B点对应中性轴位置后即可得出MB、MC，完成对N-M曲线的计算。
本文中提出的CFHCSPTC柱双向偏压承载力计算公式，参考《EC4》中钢混组合柱N-M曲线进行柱的压弯、纯弯状态下的承载力计算；参考康金鑫等[7]提出的公式进行柱轴压承载力的计算。在公式中，考虑波纹板、钢管对混凝土的约束效应，且为减小计算的复杂性，将混凝土截面视为一个边长为
h 的完整正方形；同时，忽略波纹板对承载力的直接贡献。![]()
图 16 EC4钢混组合柱N-M曲线图Figure 16. N-M curve of steel-concrete composed columns on Eurocode 4本文建议公式如下：
NA=α1fcAc1+α2fcAc2+faAs (2) NC=0.85fcAc (3) ND=0.5NC (4) MD=0.85√2fcAch12+2fahtt1⋅(2√2hc+3√2ht+4√2t1) (5) MB=MD−Mn (6) MC=MB (7) 式中：
h 、hc 、ht 、t1 为构件几何参数，如图1所示；fc /MPa为混凝土棱柱体强度；fa /MPa为钢管强度；Ac /mm2为混凝土总面积 ；Ac1 /mm2为钢管内混凝土面积；Ac2 /mm2为核心及外凸混凝土面积；As /mm2为钢管面积。式中相关系数按下列公式计算：
α1=0.11ln[14t2(bt+2t1)3b]+1.1 (8) α2=1.15 (9) Mn={0.85fch2n(−hn+√2h)2+4√2fat1h2n,hn⩽ (10) 当
{h_{\rm{n}}} \!\leqslant\! \dfrac{{\sqrt 2 }}{2}({h_{\rm{t}}} \!+\! {t_1}) 时，{h_{\rm{n}}} 按{N_{{C}}} \!=\! 0.85{f_{\rm{c}}}{h_{\rm{n}}} ( \!-\! 2{h_{\rm{n}}} \!+ 2\sqrt 2 h) + 16\sqrt 2 {f_{\rm{a}}}{h_{\rm{n}}}{t_1} 计算；当
{h_{\rm{n}}} \! > \! \dfrac{{\sqrt 2 }}{2}({h_{\rm{t}}} \!+\! {t_1}) 时，{h_{\rm{n}}} 按{N_{{C}}} \!=\! 0.85{f_{\rm{c}}}{h_{\rm{n}}} (\! -\! 2{h_{\rm{n}}} \!+\! 2\sqrt 2 h) + 16f_{\rm{a}}({h_{\rm{t}}}+{t_1} ) {t_1} 计算。以spy-x-3-1(x为多个不同偏心距)系列有限元模型为例，将有限元结果与公式计算结果进行对比(如图16(a)所示)。为检验在不同材料强度条件下公式的实用性，改变有限元模型钢材、混凝土强度，再次进行对比，其结果如图17所示。图17中也对试验值与公式值进行了对比。可以看出，在不同材料强度下，本文中的公式可以对CFHCSPTC柱双向偏压加载各阶段极限承载力及极限弯矩情况做出较为准确的预测，且公式大偏压部分计算结果稍偏保守，作为实用计算公式安全性较高。由3.2.2节结论可知，此公式也可计算加载角度不等于45°的CFHCSPTC柱双向偏压极限承载力，具有较好的实用性。
5 结论
通过对不同偏心距横肋波纹钢板-方钢管混凝土组合柱双向偏压加载试验的力学分析，以及4种参数的有限元参数分析，得出以下结论：
(1) 横肋波纹钢板-方钢管混凝土组合柱在受双向偏压荷载时具有较高的承载力与较好的延性。
(2) 横肋波纹钢板-方钢管混凝土组合柱中波纹板在受压钢管焊缝与受拉钢管焊缝的带动下分别有夹紧外凸混凝土与脱离外凸混凝土的趋势，波纹板内侧混凝土的破坏情况主要受其两侧钢管受力状况影响。
(3)有限元参数分析表明，随着偏心距的增大，组合柱的承载力与延性显著降低，增厚钢管厚度可有效提高柱的双向偏压承载力，加载角度对承载力基本无影响但对延性有一定影响，提升波纹板厚度也可在一定程度上提高柱的极限承载力。
(4)通过《EC4》规范推导出横肋波纹钢板-方钢管混凝土组合柱双向偏压N-M曲线，与有限元结果拟合良好，公式安全性高，可以在实际工程中采用。
-
![]()
图 9 柱中沿截面高度钢管纵向应变对比
Figure 9. Vertical strain comparison of steel tube at midspan on different height of section
![]()
图 14 试验、有限元钢管应变对比
Figure 14. Comparison of test and calculated load-strain curves of steel tubes
![]()
图 16 EC4钢混组合柱N-M曲线图
Figure 16. N-M curve of steel-concrete composed columns on Eurocode 4
表 1 试件参数
Table 1 Parameters of specimens
试件编号 柱高/mm 偏心距/mm 边长 h /mm 钢管尺寸 边长 {h_{\rm{t}}} /mm 厚度 {t_1} /mm C1 1400 49.5 350 69 3 C2 1400 99.0 350 69 3 试件编号 波纹板尺寸 宽度 {h_{\rm{c}}} /mm 厚度 {t_2} /mm 波高 {h_{\rm{r}}} /mm 峰谷长度 {l_1} /mm 波腹长度 {l_2} /mm C1 200 1 20 31.5 15.5 C2 200 1 20 31.5 15.5 
下载: 导出CSV
表 2 有限元计算结果
Table 2 Results of finite element analysis
变化参量 模型编号 极限承载力Nu/kN 延性系数DI 钢管厚度 spy-1-3-1 3293.67 3.57 spy-1-4-1 3838.76 4.26 spy-1-6-1 4552.23 5.40 spy-1-8-1 5217.41 7.27 spy-1-10-1 5869.24 8.74 spy-1-12-1 6500.20 10.50 波纹板厚度 spy-1-3-2 3416.11 3.87 spy-1-3-3 3495.62 4.31 spy-1-3-4 3577.88 4.60 偏心距 spy-2-3-1 2287.73 3.44 spy-3-3-1 1637.05 3.93 spy-4-3-1 971.42 5.98 加载角度 spy-1-3-1-15 3253.08 2.81 spy-1-3-1-30 3264.42 3.13 spy-1-6-1-15 4295.27 3.64 spy-1-6-1-30 4333.10 4.38 注：前3个字母SPY代表双偏压，其后各组数字分别代表偏心距(1~4依次对应49.5 mm、99 mm、148.5 mm、247.5 mm)、钢板厚度、波纹板厚度、加载角度(未标注时默认为45°)。
下载: 导出CSV
-
[1] 韩林海. 钢管混凝土结构: 理论与实践[M]. 北京: 科学出版社, 2007. Han Linhai. Concrete filled steel tubular structures theory and practice [M]. Beijing: Science Press, 2007. (in Chinese)
[2] 蔡绍怀. 现代钢管混凝土结构(修订版)[M]. 北京: 人民交通出版社, 2007. Cai Shaohuai. Modern steel tube confined concrete structures [M]. Beijing: China Communications Press, 2007. (in Chinese)
[3] 关少钰, 白涌滔, 刘卫辉, 等. 基于统一强度理论的高强钢管混凝土柱压弯屈服准则[J]. 工程力学, 2019, 36(增刊 1): 170 − 174, 183. doi: 10.6052/j.issn.1000-4750.2018.05.S035 Guan Shaoyu, Bai Yongtao, Liu Weihui, et al. Unified strength theory for concrete filled steel tube columns [J]. Engineering Mechanics, 2019, 36(Suppl 1): 170 − 174, 183. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.05.S035
[4] Wang X D, Liu J P, Zhou X H. Behaviour and design method of short square tubed-steel-reinforced-concrete columns under eccentric loading [J]. Journal of Constructional Steel Research, 2016, 116: 193 − 203. doi: 10.1016/j.jcsr.2015.09.018
[5] 方勇. 波纹钢管型钢混凝土短柱轴压力学性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2018. Fang Yong. Axial behavior of corrugated steel tubular steel reinforced concrete short columns [D]. Harbin: Harbin Institute of Technology University, 2018. (in Chinese)
[6] Wang Y Y, Yang L G, Yang H, et al. Behavior of concrete-filled corrugated steel tubes under axial compression [J]. Engineering Structures, 2019, 183: 475 − 495. doi: 10.1016/j.engstruct.2018.12.093
[7] 康金鑫, 邹昀, 王城泉, 等. 新型波纹侧板-方钢管混凝土柱轴压性能研究[J]. 建筑结构学报, 2020, 41(7): 146 − 153. Kang Jinxing, Zou Yun, Wang Chengquan, et al. Study on the behavior of new corrugated plate-square concrete filled steel tubular columns under axial compression [J]. Journal of Building Structures, 2020, 41(7): 146 − 153. (in Chinese)
[8] 王连广, 赵同峰, 安山河. 方钢管-钢骨混凝土双向偏压试件试验研究与理论分析[J]. 工程力学, 2009, 26(5): 137 − 141, 147. Wang Lianguang, Zhao Tongfeng, An Shanhe. Experimental research and theoretical analysis of square tube filled with reinforced concrete subjected to axial compression and bi-axial bending moment [J]. Engineering Mechanics, 2009, 26(5): 137 − 141, 147. (in Chinese)
[9] Li Y J, Liu W H, Han H. Analytical behaviour of rectangular concrete filled stainless steel tubular columns under bi-axial eccentric compression [J]. IOP Conference Series: Materials Science and Engineering, 2019, 490: 1 − 6.
[10] Li G C, Zhan Z C, Yang Z J, et al. Behavior of concrete-filled square steel tubular stub columns stiffened with encased I-section CFRP profile under biaxial bending [J]. Journal of Constructional Steel Research, 2020, 169: 1 − 16.
[11] GB 50152−92, 混凝土结构试验方法标准[S]. 北京: 中国建筑工业出版社, 2010. GB 50152−92, Standard for test method of concrete structures [S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
[12] GB/T 228−2002, 金属材料室温拉伸试验方法[S]. 北京: 中国标准出版社, 2002. GB/T 228−2002, Metallic materials tensile testing at ambient temperature [S]. Beijing: Standards Press of China, 2002. (in Chinese)
[13] 刘晓, 徐建烨, 王兵. 高温后中空夹层钢管混凝土柱压弯机理分析[J]. 工程力学, 2018, 35(增刊 1): 40 − 45. doi: 10.6052/j.issn.1000-4750.2017.06.S001 Liu Xiao, Xu Jianye, Wang Bing. Mechanical behavior analysis of concrete filled double skin steel tubular columns after high temperature [J]. Engineering Mechanics, 2018, 35(Suppl 1): 40 − 45. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.06.S001
[14] GB 50010−2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010. GB 50010−2010, Code for design concrete structures [S]. Beijing: China Architecture&Building Press, 2010. (in Chinese)
[15] Tao Z, Han L H. Behaviour of fire-exposed concrete-filled steel tubular beam columns repaired with CFRP wraps [J]. Thin-Walled Structures, 2007, 45: 63 − 76. doi: 10.1016/j.tws.2006.11.004
[16] European Committee for Standardization. Eurocode 4: Design of composite steel and concrete structures [S]. British: British Standards Institution, 2004.
-
期刊类型引用(5)
1. 朱卫华. 钢-混凝土组合短柱偏压性能有限元分析. 四川水泥. 2025(02): 35-37+40 . 
百度学术
2. 蔡哲罕，卓卫东，王志坚，黄新艺，刘秋江. 钢管混凝土柱-软钢板组合高墩的受压承载力. 工程力学. 2024(03): 150-162 . 本站查看
3. 舒赣平，姚震，张萌，刘忠华. 中空波纹夹层钢管混凝土柱抗震性能拟静力试验研究. 东南大学学报(自然科学版). 2024(03): 539-548 . 百度学术
4. 甘丹，张鑫泽，周绪红，李泽湘. 斜拉肋加劲方钢管混凝土柱偏压承载力简化计算方法. 建筑结构学报. 2023(S1): 256-265 . 百度学术
5. 蒋俊玲，张祥，柯长仁. 波纹侧板-方钢管混凝土框架子结构抗连续倒塌性能模拟. 工程抗震与加固改造. 2023(06): 105-114 . 百度学术
其他类型引用(8)
计量
- 文章访问数: 473
- HTML全文浏览量: 167
- PDF下载量: 76
- 被引次数: 13
