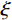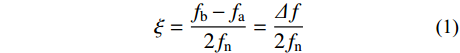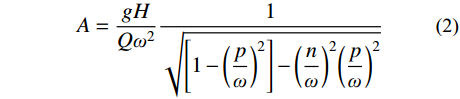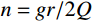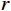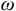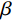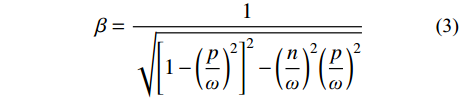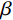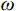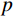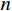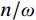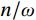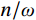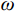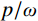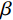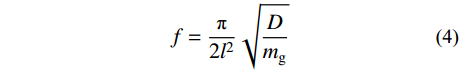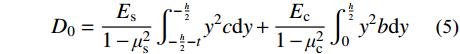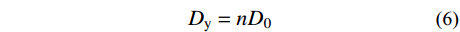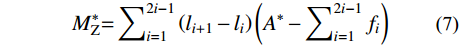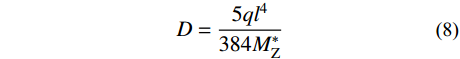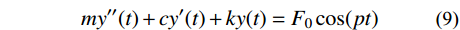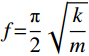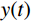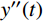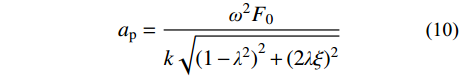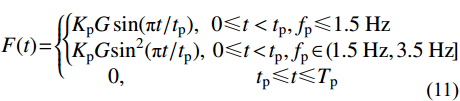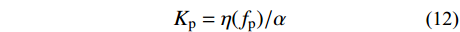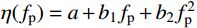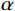踮脚和跳跃荷载下全装配式RC楼盖振动特性试验研究

庞瑞; 王文康; 张天鹏; 徐科

doi:10.6052/j.issn.1000-4750.2020.03.0192

踮脚和跳跃荷载下全装配式RC楼盖振动特性试验研究

河南工业大学土木工程学院，郑州 450001

基金项目: 国家自然科学基金项目(51778214)；中原青年拔尖人才支持项目(ZYQR201912170)；河南省属高校基本科研业务专项基金项目(2017RCJH04)

详细信息

作者简介:
王文康(1993−)，男，河南禹州人，硕士生，从事装配式混凝土结构研究(E-mail: 1143557931@qq.com)

张天鹏(1994−)，男，河南南阳人，硕士生，从事装配式混凝土结构研究(E-mail: 1351863198@qq.com)

徐　科(1997−)，男，河南开封人，硕士生，从事装配式混凝土结构研究(E-mail: 836528868@qq.com)

通讯作者:
庞　瑞(1981−)，男，河南信阳人，副教授，工学博士，硕导，从事装配式混凝土结构研究(E-mail: seupangrui@163.com)

中图分类号: TU375.2
计量
- 文章访问数: 565
- HTML全文浏览量: 121
- PDF下载量: 75
出版历程
- 收稿日期: 2020-03-26
- 修回日期: 2020-06-27
- 网络出版日期: 2020-07-08
- 刊出日期: 2020-11-24

EXPERIMENTAL STUDY ON THE VIBRATION CHARACTERISTICS OF UNTOPPED PRECAST RC FLOORS UNDER BOUNCEAND JUMPING LOADS

College of Civil Engineering, Henan University of Technology, Zhengzhou 450001, China

摘要

摘要: 为研究分布式连接全装配RC楼盖(DCPCD)在人致激励下的动力特性和振动响应，进行了6个足尺DCPCD试件和1个现浇对比试件的锤击法试验和在踮脚、单人跳跃荷载下的人致激励试验，研究了板缝和连接件布置对DCPCD振动特性的影响。结果表明：DCPCD与现浇楼盖的低阶振型基本相同，但自振频率略低；DCPCD与现浇楼盖有相同的振动传递机制；相同激励下DCPCD的振动响应略大于现浇楼盖，现浇楼盖的加速度峰值出现在跨中的边缘，DCPCD的加速度峰值出现在近跨中板缝的边缘；DCPCD的自振频率随连接件的增加而提高，随板缝的增加降低，连接件对频率的影响大于板缝的影响；提出了两对边简支条件下DCPCD横板向竖向自振频率与加速度计算方法，并以试验验证了所提方法的准确性。
- 全装配式RC楼盖 /
- 分布式板缝连接节点 /
- 振动特性 /
- 人致激励试验 /
- 竖向振动加速度
Abstract: To study the dynamic characteristics and vibration responses of discretely connected precast RC diaphragms (DCPCD) under human-induced excitation, six full-scale DCPCD specimens and one cast-in-place specimen were tested by hammer modal test and human-induced excitation test under bounce and jumping loads. The effects of plate seam and connector layout on DCPCD vibration characteristics were examined. The results show that the low-order vibration mode of DCPCD and cast-in-situ floor was basically the same, but the natural frequency of DCPCD was slightly lower. The DCPCD had the same vibration transmission mechanism as the cast-in-situ floor. The vibration response of DCPCD was slightly larger than that of the cast-in-situ floor under the same excitation. The peak acceleration value of the cast-in-situ floor appeared at the edge of the mid-span, and the peak acceleration of DCPCD appeared at the edge of the slab joint near the mid-span. The natural frequency of DCPCD increased with the increase of the slab joint connectors and with the decrease of the slab joint connections, where the effect of the connector on the frequency was greater than that of the slab joint connection. Methods for calculating the vertical natural frequency and acceleration of the DCPCD in the orthogonal slab laying directions with two pairs of sides simply supported were proposed. The accuracy of the proposed methods was verified by the experimental results.
- untopped precast RC floor /
- discrete slab joint connection /
- vibration characteristic /
- human-induced excitation test /
- vertical vibration acceleration

HTML全文

随着计算机技术、施工技术和新型高强材料的快速发展，建筑结构向着“自重轻、楼层高、跨度大、体系柔、阻尼低”的方向发展，因此在人致激励作用下大跨度桥梁、楼盖、柔性楼梯等的竖向振动问题日益凸显^[1-2]。现实生活中，人体对于建筑物施加的荷载通常为正常行走、奔跑和跳跃等。除此之外，还有踮脚，即bounce运动^[3]。踮脚是指双脚尖不离开地面，只有脚后跟抬起和落下的人体上下往复的运动，通常出现在球赛、演唱会等的舞台和观众台上，并常伴随着一定的节拍。当人致激励频率与结构的自振频率接近时就会导致共振，引起结构过大的振幅和强烈的振动响应，使人体感到不适^[4]，甚至导致结构破坏，因此人行荷载下楼盖的振动问题引起国内外学者广泛关注^[5-8]。

当前，我国主要采用叠合式楼盖^[9]。研究表明叠合式楼盖拼缝处的混凝土在温度和体积收缩作用下常产生裂缝^[10]，对于同时采用机械连接和后浇层的楼盖，混凝土开裂后板缝平面内承载力和刚度迅速降低到仅有连接件时的水平。叠合层可提高楼盖的初始刚度，但对极限承载力提高作用有限^[11]。叠合层的存在增加了楼盖自重，增大了地震作用和基础压力，并且不利于预制混凝土、高强与高性能材料、预应力等高技术的充分利用。因此，全装配楼盖在北美和欧洲等国家和地区得到了广泛应用。

目前应用最多的全装配式楼盖是双T板楼盖体系。双T板楼盖翼缘板缝连接件已有超过50年的使用历史，通过对双T板楼盖在板缝连接节点和板缝的抗剪与抗拉(压)性能^[12]、楼盖的平面内受力性能^[13]和采用双T板楼盖的多层建筑(多为停车场建筑)地震响应机理 ^[14]等 4个层面的系统研究，提出了楼盖敏感类多层建筑结构的抗震设计方法^[15]，解决了全装配式双T板楼盖在高烈度区应用的瓶颈。双T板楼盖可满足大跨、重载等设计要求，但存在楼盖板底不平整、结构高度较大等问题，应用范围存在一定的局限性。

为了拓宽干式楼盖的应用形式，发挥全装配式楼盖的性能优势，庞瑞等^[16]根据国内外规范对装配式楼盖受力和抗震性能的要求，研发了基于分布式连接全装配RC楼盖体系(discretely connected precast RC diaphragm (DCPCD))。该体系采用全干式连接件来代替现浇层里的钢筋传递预制板之间的内力，在连接方便的同时保证楼盖具有较好的整体性、承载能力与抗震性能。

DCPCD以预制企口平板(夹层板或多孔板)和挑耳梁(墙)为基本构件，梁(墙)-板之间和板-板之间采用上下企口两两匹配的分布式连接件连接的全干式楼盖体系，其构造如图1所示。

图 1 DCPCD体系示意图

Figure 1. Schematic diagram of DCPCD

下载: 全尺寸图片幻灯片

DCPCD的横板向以分布式连接件连接，使得内力和振动传递规律发生了较大改变，进而影响楼盖的竖向承载能力与振动特性。庞瑞、朱筱俊等^[17-18]进行了DCPCD平面内刚度试验和竖向承载力试验，验证了楼盖具有较大的平面内刚度和竖向承载能力。在此基础上，孙崇芳等^[19]进行了DCPCD在人行荷载下的竖向振动试验，结果表明，试件符合我国规范^[20]规定的自振频率和加速度双控条件下楼盖舒适度的评价标准。

为进一步揭示DCPCD横板缝方向竖向振动特性与人致激励响应规律，本文进行了6个DCPCD试件和1个现浇板对比试件在两端简支条件下的动力特性试验和单人踮脚、跳跃激励下的竖向振动性能试验研究。以期为四边约束条件下DCPCD的竖向振动特性与人致激励响应研究提供基础数据和参考依据。

1 试验概况

1.1 试件设计

现浇板(CISS)试件与DCPCD试件均为3700 mm×1800 mm×100 mm的两短边简支单向板(支座间距为3.5 m)，其中DCPCD由若干块预制板通过发卡-盖板混合式板缝连接件(HP-CPC)连接，发卡式连接件(HPC)中间通过嵌条与发卡锚板焊接连接；盖板连接件(CPC)通过开孔板从底部覆盖于锚板上焊接连接，焊接时两侧采用U形焊缝，预留自由变形段。

制作了6个DCPCD试件和1个现浇对比试件，试件设计见表1。楼板配筋根据钢筋混凝土单向板理论进行设计，为双层双向8@170布置。试件的平面布置图见图2(各试件除板缝数量和连接件数量不同外，其余参数均相同，以S5C3为例)，预制板配筋图详见图3，连接件大样图详见图4。

表 1 试件设计

Table 1. Specimen design

试件编号	板缝构造	每条板缝连接件数/个
CISS	−	−
S3C2	3块预制板2条板缝	2
S3C3	3块预制板2条板缝	3
S4C2	4块预制板3条板缝	2
S4C3	4块预制板3条板缝	3
S5C2	5块预制板4条板缝	2
S5C3	5块预制板4条板缝	3
注：试件编号采用“S-C-”格式，其中，S代表预制板个数，C代表每条板缝连接件个数。

下载: 导出CSV

| 显示表格

图 2 试件S5C3结构平面布置图　/mm

Figure 2. Plane of specimen S5C3

下载: 全尺寸图片幻灯片

图 3 预制板配筋详图　/mm

Figure 3. Details of PC slab reinforcement

下载: 全尺寸图片幻灯片

图 4 连接件详图　/mm

Figure 4. Details of slab joint connectors

下载: 全尺寸图片幻灯片

1.2 材料属性

混凝土等级为35，混凝土保护层厚度为10 mm，纵向受力钢筋为8，连接件锚筋为10。钢筋(板)与混凝土实测材料特性见表2和表3。

表 2 钢筋(板)实测力学性能

Table 2. Mechanical properties of steel bars (plate)

钢筋(板)规格	屈服强度f_y/MPa	抗拉强度f_u/MPa
8	443.33	633.74
10	380.34	668.61
Q345钢板	463.11	518.33

下载: 导出CSV

| 显示表格

表 3 混凝土实测力学性能

Table 3. Mechanical properties of concrete

试块编号	立方体抗压强度f_cu/MPa	抗压强度实测值f_cb/MPa	弹性模量E_c/MPa
S1	33.29	22.26	3.09×10⁴
S2	31.31	20.94	3.01×10⁴
S3	31.14	20.83	3.03×10⁴
均值	31.91	21.34	3.04×10⁴

下载: 导出CSV

| 显示表格

1.3 加载装置

加载装置图详见图5。试验装置由钢柱、支承钢梁、滚轴、牛腿和防护钢梁等组成。采用两端简支条件，一端为固定刚滚轴，另一端为活动刚滚轴。将楼盖平放在钢支架上，在楼盖上进行锤击、踮脚和跳跃等试验。

图 5 试验装置

Figure 5. Test setup

下载: 全尺寸图片幻灯片

2 模态参数分析

本试验采用锤击法^[21-22]进行楼盖的模态参数分析，采用东华动态采集仪DH-5922D和量程为2 kN的模态力锤LC-2进行模态试验，加速度传感器为ICP压电型加速度传感器，选择单点激励的试验方法，采样频率为500 Hz，模态试验的流程图如图6所示。

图 6 锤击法模态试验流程图

Figure 6. Flow chart of hammer modal test

下载: 全尺寸图片幻灯片

测点的布置：布置在所关心的点，避免布在振型节点上；测点数要大于测试的模态阶数；测点数要足够多，以保证测试数据的精确性和问题测点的可替代性。试件加速度传感器布置方案如图7所示，DCPCD试件以S3C3和S5C3为例。

图 7 加速度传感器布置图　/mm

Figure 7. Layout of acceleration sensors

下载: 全尺寸图片幻灯片

2.1 模态振型

锤击法得到的各试件前3阶振型如表4所示。由表4可知DCPCD与现浇楼盖的前3阶振型是基本一致的，区别在于现浇楼盖构件材质均匀连续，各阶振型更平滑，而DCPCD试件由于板缝的存在使得板缝连接处出现变形集中和弯折现象。

表 4 各试件前3阶振型

Table 4. First three mode shapes of each component

试件	CISS(现浇试件)	S3C2(3板2连接件试件)	S4C2(4板2连接件试件)	S5C2(5板2连接件试件)
一阶振型
二阶振型
三阶振型

下载: 导出CSV

| 显示表格

2.2 一阶自振频率与阻尼比

人体产生的荷载频率主要分布在1 Hz~3 Hz^[23]，且结构的振动主要为低阶振动形式，而结构安全的自振频率的评价也是最小频率，即一阶频率，限于篇幅仅分析试件的一阶频率。通过锤击法得到频响函数，并用半功率带宽法求得一阶特征频率对应的阻尼比。如图8所示为频响函数其中一个特征频率f_n处的幅频曲线，在峰值y_n附近搜索 ${{\sqrt 2 {y_{\rm n}}} / 2}$ 的两个点a和b称为半功率点，对应的频率分别为f_a和f_b，则阻尼比 $\xi$ 为

图 8 幅频曲线

Figure 8. Amplitude-frequency curve

下载: 全尺寸图片幻灯片

$\xi = \frac{{{f_{\rm b}} - {f_{\rm a}}}}{{2{f_{\rm n}}}} = \frac{{\varDelta f}}{{2{f_{\rm n}}}}$

(1)

DCPCD试件与现浇板试件的第1阶振动频率及其比值和阻尼比如表5所示。

表 5 实测一阶频率对比

Table 5. First-order frequency comparison

试件编号	一阶频率f/Hz	DCPCD试件/CISS试件	锤击法实测阻尼比ξ/(%)
CISS	13.63	1.00	1.16
S3C2	8.69	0.64	3.19
S3C3	10.04	0.74	1.20
S4C2	8.19	0.60	3.66
S4C3	9.03	0.66	2.15
S5C2	7.57	0.56	5.32
S5C3	9.13	0.67	2.08

下载: 导出CSV

| 显示表格

由表5可知：

1) DCPCD试件的一阶自振频率较现浇板的有所降低，其大小顺序为：f_CISS>f_S3C3> f_S5C3> f_S4C3> f_S3C2 > f_S4C2> f_S5C2。

2) 预制板数量相同时，连接件数量越多，一阶频率越大，其中奇数装配板每增加一个连接件，一阶频率增加15%(3个预制板为15.54%，5个预制板为20.61%)以上，4个预制板每增加一个连接件，频率增加10.26%。可知，当预制板的数量越多，连接件的对楼板基频的贡献越大。

3) 连接件数量相同时，预制板的数量越少，一阶频率越大，即刚度越大。但偶数块板试件(S4C2、S4C3)时板缝位于跨中(一阶振型中心)，楼盖刚度受板缝影响较大，使得与同条件下奇数板方案(S5C2、S5C3)相比无明显提高。

4) 通过对比有3个连接件的试件，发现S4C3较S3C3下降10.06%，S4C3较S5C3下降1.10%。说明当板缝位于楼盖跨中时，楼盖的基频下降的较多，是不利的布置形式。

5) 阻尼比随着楼盖自振频率的减小而增大，与楼盖刚度呈反比关系，阻尼比随板缝个数和连接件个数的变化规律可参照一阶频率变化规律。现浇试件和3个连接件试件的阻尼比在1%~3%，2个连接件试件的抗弯刚度较小，阻尼比在3%~5.5%，整体符合楼盖阻尼比取值范围^[24]。

3 人致激励响应

单人定点试验包括1 Hz踮脚、2 Hz踮脚、3 Hz踮脚、1 Hz跳跃、2 Hz跳跃、3 Hz跳跃等6种工况，每种工况进行3次试验。按照AISC规范，人的体重服从均值为700 N，标准差为145 N的正态分布，本次试验人员体重为80 kg，试验实景图详见图9。

图 9 人致激励试验现场照片

Figure 9. Photos of human incentive test

下载: 全尺寸图片幻灯片

3.1 加速度响应

3.1.1 加速度时程曲线

为了探究DCPCD试件是否因板缝的存在和由于连接节点的特殊形式而使得振动传递与现浇试件间存在差异，对同一试件沿跨度方向的不同测点进行了对比。图10所示为1Hz跳跃荷载下试件CISS和试件S3C3、S4C3、S5C3中测点2、测点5、测点8的加速度响应时程曲线。

图 10 1 Hz跳跃荷载下的加速度响应

Figure 10. Acceleration response under 1 Hz jump load

下载: 全尺寸图片幻灯片

由图10可知，同一试件的不同测点处有相同的响应规律，即在同一激励下，试件各点处的振动趋势相同，同时达到波峰(波谷)。各测点振动加速度时程曲线相似，而峰值不同，表现为越靠近低阶振型中心加速度峰值越大。由此可知分布式连接件可有效传递振动，使得DCPCD与现浇楼盖有相同的振动传递机制，不会因为板缝的存在而产生相位差。

图11所示为1 Hz跳跃荷载下CISS、S3C3、S4C3、S5C3中8点(中心点)的加速度时程曲线。由图11可知，相同激励下，DCPCD试件的加速度普遍较CISS试件大，随着板缝数的增加楼盖刚度减小，振动加速度时程曲线包络线的纵坐标相应增大，各个峰值均也有所增大，S4C3由于板缝位于跨中，振动更加明显，因此出现与S5C5相近的峰值加速度。

图 11 1 Hz跳跃荷载下各试件8点响应

Figure 11. Response of eight measurement points of each component under 1 Hz jump load

下载: 全尺寸图片幻灯片

3.1.2 各测点响应

由于连接件的存在，使得DCPCD试件与现浇楼试件的传力方式不同，加速度最大的点所在位置也有差异，限于篇幅，以试件CISS、S3C3和S5C3中各个测点各工况下的最大振动加速度为例加以说明，如图12所示。

图 12 各测点加速度

Figure 12. Acceleration of each measuring point

下载: 全尺寸图片幻灯片

通过观察可总结如下规律：

1) 试件CISS的加速度响应最大的点一般出现在跨中的边缘，因为此处既是试件一阶振型的中心也是二阶振型的中心，与文献[25]的结论一致。

2) DCPCD试件的加速度响应最大点一般出现在最靠近跨中的连接缝处的边缘，即使接缝不在跨中，不在一阶振型的中心，也只是处在靠近二阶振型中心的区域，但是因为远离连接件，缺少足够的约束，这些点也都是振动响应的最大点。

3) 不同于现浇试件各点处加速度大小较连续的特性，在DCPCD的接缝处的两侧加速度会出现跳跃式的变化，靠近跨中的那一侧加速度更大。

3.2 各工况下的加速度响应

各工况下7个试件的峰值加速度实测值如图13所示。

图 13 各工况下的加速度响应

Figure 13. Acceleration response under various operating conditions

下载: 全尺寸图片幻灯片

图中横坐标B和J分别代表踮脚Bounce和跳跃Jumping，数字代表频率(Hz)，观察可知：

1) DCPCD试件与CISS试件随工况变化的走势基本相同，相同的激励下有相似的振动响应。

2) 不同试件在相同荷载下，严格按照一阶自振频率由大到小，即刚度由大到小的顺序(f_CISS>f_S3C3> f_S5C3> f_S4C3> f_S3C2 > f_S4C2> f_S5C2)，加速度响应越来越大。

3)相同频率下，通常情况，跳跃时的加速度响应要大于踮脚时的加速度响应，首先因为跳跃时脚底给楼板的附加反力要大于踮脚的情况，其次因为踮脚时人不离开楼板，可把人视为楼盖的附属构件，具有增大楼盖阻尼的效果。

4) 对于同一试件来说，相同的激励类型下，频率越高，结构加速度响应就越大。因为选定激励的频率分别为1 Hz、2 Hz和 3 Hz，均小于结构的一阶频率。根据强迫振动的振幅公式^[26]，可知：

$A = \frac{{gH}}{{Q{\omega ^2}}}\frac{1}{{\sqrt {\left[ {1 - {{\left( {\dfrac{p}{\omega }} \right)}^2}} \right] - {{\left( {\dfrac{n}{\omega }} \right)}^2}{{\left( {\dfrac{p}{\omega }} \right)}^2}} }}$

(2)

式中：A为振幅； $n = {{gr}/ {2Q}}$ ，为振动衰减系数； $r$ 为阻尼常数；g为重力加速度；Q为结构自重；H为干扰力； $\omega$ 为结构自振圆频率；p为干扰力圆频率。

引入振动放大系数 $\beta$ ，令：

$\beta = \frac{1}{{\sqrt {{{\left[ {1 - {{\left( {\dfrac{p}{\omega }} \right)}^2}} \right]}^2} - {{\left( {\dfrac{n}{\omega }} \right)}^2}{{\left( {\dfrac{p}{\omega }} \right)}^2}} }}$

(3)

可得 $\beta$ 与 $\omega$ 、 $p$ 和 $n$ 的关系，如图14所示。

图 14 强迫振动的放大系数

Figure 14. Amplification factor of forced vibration

下载: 全尺寸图片幻灯片

图14中的曲线由下至上依次对应为 $n/\omega$ = 0.20， $n/\omega$ =0.10， $n/\omega$ =0的情况。由式(2)可知，在强迫振动中，结构的振幅与干扰力的大小H、频率p和结构自身的自重Q、自振频率 $\omega$ 有关。在人行荷载中，人的自重为干扰力，人行走的步频为干扰力频率，结构的一阶频率为最低的自振频率。由图14可知，干扰力的频率与结构自振频率的比值 $p/\omega$ 越接近于1，则放大系数 $\beta$ 就越大，那么此时振幅也就越大，这就是共振现象。而在结构振动的波形图中，是振幅关于时间的曲线，将振幅对于时间求二阶导数便得到加速度。因此，在同一采样频率的波形图中，振幅越大的地方加速度也就越大，这很好的解释了频率逐渐增大的荷载工况中加速度呈逐渐增大的现象。

4 DCPCD的理论计算

4.1 自振频率的计算方法

对于对边简支单向板自振频率的计算通常采用欧洲规范EN 1995−1-1^[27]中的计算方法，公式为：

$f = \frac{\pi }{{2{l^2}}}\sqrt {\frac{D}{{{m_{\rm g}}}}}$

(4)

式中：f为楼盖自振频率；D为楼盖抗弯刚度；m_g为楼盖单位面积质量；l为楼盖跨度。

对于DCPCD试件来说，计算自振频率的难点在于它为非均质连续构件，如何计算横板缝方向上的抗弯刚度是关键。文献[17]提出了DCPCD板缝所在截面楼盖的横板向抗弯刚度的计算方法，该方法中单个连接件区域的抗弯刚度为：

${D_0} = \frac{{{E_{\rm{s}} }}}{{1 - \mu _{\rm{s}} ^2}}\int_{ - \frac{h}{2} - t}^{ - \frac{h}{2}} {{y^2}c{\rm d}y + \frac{{{E_{\rm{c}}}}}{{1 - \mu _{\rm{c}} ^2}}\int_0^{\frac{h}{2}} {{y^2}b{\rm d}y} }$

(5)

式中：b/mm为横板向抗弯刚度计算宽度；t/mm为板底连接件开孔板厚度；c/mm为开孔板板缝截面宽度；E_s/MPa、E_c/MPa分别为开孔板钢材、混凝土的弹性模量；μ_s、μ_c分别为开孔板钢材、混凝土的泊松比。

则板缝处的横板向的抗弯刚度为：

$D_{\rm{y}} = n{D_0}$

(6)

式中，N为单条板缝处连接件的数量。

DCPCD楼盖横板向沿跨度方向的截面由板缝和预制板组成，板缝截面的抗弯刚度与预制板的抗弯刚度不同，属于变截面刚度受弯构件。共轭法可将实梁的挠度转角求解转化为其对应虚梁的弯矩剪力求解问题，虚梁中的弯矩即对应实梁中的挠度，课题组基于共轭法和等效梁法提出了DCPCD横板向抗弯刚度的计算方法。其基本思路为：实梁中的弯矩与梁截面抗弯刚度的比值代表虚梁中的分布荷载，为简化计算，按照一定原则将虚梁上的分布荷载转化为若干节点上的集中荷载，进而可求得虚梁的跨中弯矩，见式(7)，此弯矩代表实梁的跨中挠度，由简支梁在均布荷载下的挠度公式可反算出DCPCD横板向等效抗弯刚度，见式(8)。其主要表达式为：

共轭虚梁跨中弯矩为：

$M_{\rm Z}^*{\rm{ = }}\sum\nolimits_{i = 1}^{2i - 1} {\left( {{l_{i + 1}} - {l_i}} \right)} \left( {{A^*} - \sum\nolimits_{i = 1}^{2i - 1} {{f_i}} } \right)$

(7)

DCPCD横板向等效抗弯刚度为：

$D = \frac{{5q{l^4}}}{{384M_{\rm Z}^*}}$

(8)

式中：I表示将梁划分为I个单元段；f_i为虚梁第i个节点的集中荷载；l_i为与f_i对应的节点距梁端的距离；A^*为虚梁支座反力；q为梁的自重荷载；l为梁的跨度。

由于连接件数量和板缝数量的不同导致各试件的抗弯刚度发生变化，详见表6。

表 6 各试件抗弯刚度对比

Table 6. Comparison of bending stiffness of specimens

试件编号	CISS	S3C2	S3C3	S5C2	S5C3
D/MPa	4.65	1.47	2.03	1.20	1.68
D/D′	1.00	0.32	0.44	0.26	0.36
注：D为DCPCD试件的抗弯刚度；D′为现浇试件的抗弯刚度。

下载: 导出CSV

| 显示表格

由表6可知，DCPCD横板向抗弯刚度小于现浇楼盖，且抗弯刚度与板缝数量负相关，与连接件数量正相关。连接件数量相等条件下，S5C2较S3C2的抗弯刚度减少18.37%，S5C3较S3C3的抗弯刚度减少17.24%；而板缝数量相等条件下，S3C3较S3C2的抗弯刚度增加38.10%，S5C3较S5C2的抗弯刚度增加40.00%，可知板缝和连接件数量对楼盖横板向抗弯刚度有较大影响，在连接件规格相同的情况下，板缝的影响更为显著。

各试件自振频率计算结果与试验结果对比情况详见表7，由表可知，自振频率理论计算值与实测值吻合较好，表明该方法适用于DCPCD自振频率的计算，且有一定的精度保证。

表 7 计算值与试验值对比

Table 7. Comparison of calculated and test results

试件编号	实测自振频率f₁/Hz	理论计算自振频率f₂/Hz	修正后自振频率f₃/Hz	修正值/ 实测值f₃/f₁
CISS	13.63	16.52	14.87	1.09
S3C2	8.69	9.83	8.84	1.02
S3C3	10.04	11.53	10.38	1.03
S5C2	7.57	8.88	7.99	1.06
S5C3	9.13	10.52	9.46	1.04

下载: 导出CSV

| 显示表格

4.2 单人踮脚和跳跃荷载下峰值加速度的计算

计算DCPCD楼盖在跳跃和踮脚荷载下的峰值加速时，可以把DCPCD楼盖视为单自由度体系，人致荷载采用简谐荷载模型，则DCPCD楼盖在跳跃和踮脚荷载下的动力方程^[28]为：

$my''(t) + cy'(t) + ky(t) = {F_0}\cos (p t)$

(9)

式中：m为楼盖体系等效质量，两端简直条件下取0.5倍自重；c为楼盖阻尼；k为刚度，可按 $f{\rm{ = }}\dfrac{\pi }{{\rm{2}}}\sqrt {\dfrac{k}{m}}$ 计算； $y(t)$ 、 $y'(t)$ 和 $y''(t)$ 分别为楼盖位移、速度和加速度；F₀为荷载幅值；p为荷载圆频率。

通过化简计算可得DCPCD楼盖峰值加速度的计算表达式为：

${a_{\rm{p}} } = \frac{{{\omega ^2}{F_0}}}{{k\sqrt {{{(1 - {\lambda^2})}^2} + {{(2\lambda\xi )}^2}} }}$

(10)

式中：a_p为楼盖峰值加速度；λ为施加荷载频率与楼盖一阶自振频率的比值。

单人跳跃和踮脚的数学模型采用陈隽等^[29]提出的修正半正弦平方模型：

$F(t) = \left\{ {\begin{array}{*{20}{l}} {\left\{ {\begin{array}{*{20}{l}} {{K_{\rm{p}} }G\sin ({{\pi t} / {{t_{\rm{p}} }}}),\;\;0 \leqslant t < {t_{\rm{p}} },{f_{\rm{p}} } \leqslant 1.5\;{\rm{Hz}} } \\ {{K_{\rm{p}} }G{{\sin }^2}({{\pi t} / {{t_{\rm{p}} }}}),\;\;0 \leqslant t < {t_{\rm{p}} },{f_{\rm{p}} } \in \left( {1.5\;{\rm{Hz}},3.5\;{\rm{Hz}} } \right]} \end{array}} \right.} \\ {\qquad0,\;\;\qquad\qquad\qquad{t_{\rm{p}} } \leqslant t \leqslant {T_{\rm{p}} }} \\[-5pt] \end{array}} \right.$

(11)

式中：G为人体质量力；t_p为脚掌与楼盖接触时间；T_p为荷载周期；f_p为荷载频率；K_p为脉冲系数，可按下式计算：

${K_{\rm{p}} } = \eta ({f_{\rm{p}} })/\alpha$

(12)

式中： $\eta ({f_{\rm{p}} }) = a + {b_1}{f_{\rm{p}} } + {b_2}f_{\rm{p}} ^2$ ，a=−0.592，b₁=1.908，b₂=−0.332； $\alpha$ 为接触率，取值范围为0.4~0.92，一般有氧跳跃取0.5，剧烈跳跃取0.4。

取各试件在1 Hz跳跃荷载下的振动响应为说明对象，单人1 Hz跳跃荷载下各楼盖峰值加速度理论计算结果与实测结果对比如表8所示。

表 8 理论计算值与实测值对比

Table 8. Comparison of theoretical and test results

试件编号	实测峰值加速度 a_p1/(m·s⁻²)	理论计算峰值加速度 a_p2/(m·s⁻²)	实测值/理论计算值 a_p1/a_p2
CISS	0.85	0.78	1.09
S3C2	1.23	1.10	1.12
S3C3	0.98	0.91	1.08
S5C2	1.42	1.32	1.08
S5C3	1.12	1.00	1.12

下载: 导出CSV

| 显示表格

由表8可知，现浇楼盖试件与DCPCD试件峰值加速度的理论计算值与试验实测值吻合良好，说明单自由度简支梁振动微分方程和跳跃荷载下的修正半正弦平方模型应用于预测DCPCD竖向振动峰值加速度的可行性。

5 结论

通过对比分析七个足尺试件在人致激励下的动力特性及振动响应规律，可得到如下结论：

(1) DCPCD试件与现浇试件的低阶振型高度一致，由于分布式连接件特殊的传力机制导致振型出现细微差别，二者的动力特性十分相似。

(2)分布式连接件可有效传递振动，DCPCD试件与现浇试件的振动传递相似，未因分布式连接件和拼接板缝的存在而使得位于不同的预制板上的测点产生相位差。

(3) DCPCD试件的自振频率较现浇试件有所降低，板缝越多频率越小，连接件越多频率越大，连接件对楼盖自振频率的影响大于板缝对自振频率的影响，可以适当增加连接件来抵消板缝带来的自振频率的折减量，以保证DCPCD有足够大的刚度和振动性能指标。

(4)在DCPCD中，阻尼比随着预制板数增加而增加，随着连接件数增加而减小，整体的阻尼比符合钢筋混凝土楼盖阻尼比正常范围。

(5)当板缝处于跨中时(偶数板)，自振频率折减较多，此时板缝处在弯矩和正应力最大处，是最不利的结构布置形式，应尽量避免。

(6)板缝越多会对竖向刚度折减越大，对楼盖竖向振动舒适度有不利影响，同时增加了较多的现场连接工作量，因此，在运输和安装等条件许可的情况下，建议采用宽板预制方案。

(7)常采用的欧洲规范中自振频率的计算公式适用于DCPCD体系，基于两短边简支的DCPCD横板向刚度计算方法和本文提出的自振频率计算方法能准确计算DCPCD的自振频率；单自由度简支梁振动微分方程和跳跃荷载下的修正半正弦平方模型能准确预测DCPCD竖向振动峰值加速度，可为DCPCD的舒适度设计与评价提供参考。

图 1 DCPCD体系示意图

Figure 1. Schematic diagram of DCPCD

下载: 全尺寸图片幻灯片

图 2 试件S5C3结构平面布置图　/mm

Figure 2. Plane of specimen S5C3

下载: 全尺寸图片幻灯片

图 3 预制板配筋详图　/mm

Figure 3. Details of PC slab reinforcement

下载: 全尺寸图片幻灯片

图 4 连接件详图　/mm

Figure 4. Details of slab joint connectors

下载: 全尺寸图片幻灯片

图 5 试验装置

Figure 5. Test setup

下载: 全尺寸图片幻灯片

图 6 锤击法模态试验流程图

Figure 6. Flow chart of hammer modal test

下载: 全尺寸图片幻灯片

图 7 加速度传感器布置图　/mm

Figure 7. Layout of acceleration sensors

下载: 全尺寸图片幻灯片

图 8 幅频曲线

Figure 8. Amplitude-frequency curve

下载: 全尺寸图片幻灯片

图 9 人致激励试验现场照片

Figure 9. Photos of human incentive test

下载: 全尺寸图片幻灯片

图 10 1 Hz跳跃荷载下的加速度响应

Figure 10. Acceleration response under 1 Hz jump load

下载: 全尺寸图片幻灯片

图 11 1 Hz跳跃荷载下各试件8点响应

Figure 11. Response of eight measurement points of each component under 1 Hz jump load

下载: 全尺寸图片幻灯片

图 12 各测点加速度

Figure 12. Acceleration of each measuring point

下载: 全尺寸图片幻灯片

图 13 各工况下的加速度响应

Figure 13. Acceleration response under various operating conditions

下载: 全尺寸图片幻灯片

图 14 强迫振动的放大系数

Figure 14. Amplification factor of forced vibration

下载: 全尺寸图片幻灯片

表 1 试件设计

Table 1 Specimen design

试件编号	板缝构造	每条板缝连接件数/个
CISS	−	−
S3C2	3块预制板2条板缝	2
S3C3	3块预制板2条板缝	3
S4C2	4块预制板3条板缝	2
S4C3	4块预制板3条板缝	3
S5C2	5块预制板4条板缝	2
S5C3	5块预制板4条板缝	3
注：试件编号采用“S-C-”格式，其中，S代表预制板个数，C代表每条板缝连接件个数。

下载: 导出CSV

表 2 钢筋(板)实测力学性能

Table 2 Mechanical properties of steel bars (plate)

钢筋(板)规格	屈服强度f_y/MPa	抗拉强度f_u/MPa
8	443.33	633.74
10	380.34	668.61
Q345钢板	463.11	518.33

下载: 导出CSV

表 3 混凝土实测力学性能

Table 3 Mechanical properties of concrete

试块编号	立方体抗压强度f_cu/MPa	抗压强度实测值f_cb/MPa	弹性模量E_c/MPa
S1	33.29	22.26	3.09×10⁴
S2	31.31	20.94	3.01×10⁴
S3	31.14	20.83	3.03×10⁴
均值	31.91	21.34	3.04×10⁴

下载: 导出CSV

表 4 各试件前3阶振型

Table 4 First three mode shapes of each component

试件	CISS(现浇试件)	S3C2(3板2连接件试件)	S4C2(4板2连接件试件)	S5C2(5板2连接件试件)
一阶振型
二阶振型
三阶振型

下载: 导出CSV

表 5 实测一阶频率对比

Table 5 First-order frequency comparison

试件编号	一阶频率f/Hz	DCPCD试件/CISS试件	锤击法实测阻尼比ξ/(%)
CISS	13.63	1.00	1.16
S3C2	8.69	0.64	3.19
S3C3	10.04	0.74	1.20
S4C2	8.19	0.60	3.66
S4C3	9.03	0.66	2.15
S5C2	7.57	0.56	5.32
S5C3	9.13	0.67	2.08

下载: 导出CSV

表 6 各试件抗弯刚度对比

Table 6 Comparison of bending stiffness of specimens

试件编号	CISS	S3C2	S3C3	S5C2	S5C3
D/MPa	4.65	1.47	2.03	1.20	1.68
D/D′	1.00	0.32	0.44	0.26	0.36
注：D为DCPCD试件的抗弯刚度；D′为现浇试件的抗弯刚度。

下载: 导出CSV

表 7 计算值与试验值对比

Table 7 Comparison of calculated and test results

试件编号	实测自振频率f₁/Hz	理论计算自振频率f₂/Hz	修正后自振频率f₃/Hz	修正值/ 实测值f₃/f₁
CISS	13.63	16.52	14.87	1.09
S3C2	8.69	9.83	8.84	1.02
S3C3	10.04	11.53	10.38	1.03
S5C2	7.57	8.88	7.99	1.06
S5C3	9.13	10.52	9.46	1.04

下载: 导出CSV

表 8 理论计算值与实测值对比

Table 8 Comparison of theoretical and test results

试件编号	实测峰值加速度 a_p1/(m·s⁻²)	理论计算峰值加速度 a_p2/(m·s⁻²)	实测值/理论计算值 a_p1/a_p2
CISS	0.85	0.78	1.09
S3C2	1.23	1.10	1.12
S3C3	0.98	0.91	1.08
S5C2	1.42	1.32	1.08
S5C3	1.12	1.00	1.12

下载: 导出CSV

参考文献(29)

[1]	Rijal R, Samali B, Shrestha R, et al. Experimental and analytical study on dynamic performance of timber floor modules (timber beams) [J]. Construction and Building Materials, 2016, 122: 391 − 399. doi: 10.1016/j.conbuildmat.2016.06.027
[2]	Ebadi M M, Doudak G, Smith I. Evaluation of floor vibration caused by human walking in a large glulam beam and deck floor [J]. Engineering Structures, 2019, 196: 109349.
[3]	陈隽, 王磊, 楼佳悦, 等. 单人Bounce荷载下楼盖结构加速度反应谱设计[J]. 振动与冲击, 2015, 34(5): 14 − 19, 38. Chen Jun, Wang Lei, Lou Jiayue, et al. Acceleration response spectrum for predicting floor vibration due to single human bounce load [J]. Journal of Vibration and Shock, 2015, 34(5): 14 − 19, 38. (in Chinese)
[4]	管宇, 周绪红, 卫世杰, 等. 冷弯薄壁型钢组合楼盖振动性能及静力挠度研究[J]. 工程力学, 2018, 35(5): 131 − 142. Guan Yu, Zhou Xuhong, Wei Shijie, et al. Study on vibration performance and static deflection of cold-formed thin-walled steel composite floors [J]. Engineering Mechanics, 2018, 35(5): 131 − 142. (in Chinese)
[5]	Chen Jun, Han Ziping, Xu Ruotian. Effects of human-induced load models on tuned mass damper in reducing floor vibration [J]. Advances in Structural Engineering, 2019, 22(11): 2449 − 2463.
[6]	朱前坤, 李宏男, 杜永峰, 等. 不同行走步速下人行桥振动舒适度定量化评估[J]. 工程力学, 2016, 33(10): 97 − 104. Zhu Qiankun, Li Hongnan, Du Yongfeng, et al. Quantitative evaluation of vibration serviceability of pedestrian bridge underdifferent walking speed [J]. Engineering Mechanics, 2016, 33(10): 97 − 104. (in Chinese)
[7]	朱前坤, 蒲兴龙, 惠晓丽, 等. 基于人群-结构耦合作用甘肃省体育馆悬挂结构振动舒适度评估及控制[J]. 工程力学, 2018, 35(增刊 1): 46 − 52. doi: 10.6052/j.issn.1000-4750.2017.06.S003 Zhu Qiankun, Pu Xinglong, Hui Xiaoli, et al. Serviceability evaluation and control of suspension structure of gansu gymnasium based on pedestrlan-structure coupled vibration [J]. Engineering Mechanics, 2018, 35(Suppl 1): 46 − 52. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.06.S003
[8]	陈隽, 熊杰程, 李果. 跑步荷载下大跨结构的竖向振动加速度反应谱研究[J]. 工程力学, 2017, 34(3): 173 − 181. Chen Jun, Xiong Jiecheng, Li Guo. Acceleration pesponse spectrum for predicting vibrations of long-span structures due to human running load [J]. Engineering Mechanics, 2017, 34(3): 173 − 181. (in Chinese)
[9]	吴方伯, 刘彪, 罗继丰. 预应力混凝土叠合空心楼板的受剪性能试验研究[J]. 工程力学, 2016, 33(3): 196 − 203. Wu Fangbo, Liu Biao, Luo Jifeng. Experimental study on shear resisting properties prestressed concrete composite hollow core slabs [J]. Engineering Mechanics, 2016, 33(3): 196 − 203. (in Chinese)
[10]	Davies G, Elliott K S, Omar W. Horizontal diaphragm action in precast concrete floors [J]. The Structural Engineer, 1990, 68(2): 25 − 32.
[11]	Baran E. Effects of cast-in-place concrete topping on flexural response of precast concrete hollow-core slabs [J]. Engineering Structures, 2015, 98(9): 109 − 117.
[12]	Ren R, Naito C J. Precast concrete diaphragm connector performance database [J]. ASCE, Journal of Structural Engineers, 2013, 139(1): 15 − 27. doi: 10.1061/(ASCE)ST.1943-541X.0000598
[13]	Wan G, Zhang D H, Fleischman R B. A coupled connector element for nonlinear static pushover analysis of precast concrete diaphragms [J]. Engineering Structures, 2015, 86: 58 − 71.
[14]	Zhang D, Fleischman R B, Schoettler, et al. Precast Diaphragm Response in Half-Scale Shake Table Test ASCE [J]. Journal of Structural Engineers, 2019, 145(5): 04019024-1 − 04019024-15.
[15]	Fleischman R B, Restrepo J, Naito C J. Integrated Analytical and Experimental Research to Develop a New Seismic Design Methodology for Precast Concrete Diaphragms [J]. ASCE, Journal of Structural Engineers, 2013, 139(7): 1192 − 1204. doi: 10.1061/(ASCE)ST.1943-541X.0000734
[16]	庞瑞, 陈桂香, 倪红梅, 等. 全干式连接预制混凝土板、楼盖及其抗震性能提升方法[P]. 中国: ZL 2015 1 0247926. 5, 2017-07-14. Pang Rui, Chen Guixiang, Ni Hongmei, et al. Untopped precast slab and floor diaphragm [P]. China patent: ZL 2015 1 0247926. 5, 2017-07-14. (in Chinese)
[17]	庞瑞, 许清风, 梁书亭, 等. 分布式连接全装配RC楼盖竖向承载力与变形分析[J]. 工程力学, 2019, 36(4): 147 − 157. Pang Rui, Xu Qingfeng, Liang Shuting, et al. Analysis of the vertical strength and deflection of discretely connected precast RC floor systems [J]. Engineering Machanics, 2019, 36(4): 147 − 157. (in Chinese)
[18]	朱筱俊, 庞瑞, 梁书亭. 全装配式钢筋混凝土楼盖竖向受力性能试验研究[J]. 建筑结构学报, 2013, 34(1): 123 − 130. Zhu Xiaojun, Pang Rui, Liang Shuting. Experimental study on vertical mechanical properties of fully assembled reinforced concrete floor [J]. Journal of Building Structures, 2013, 34(1): 123 − 130. (in Chinese)
[19]	Sun Chongfang, Liang Shuting, Zhu Xiaojun. Experimental study and comfort analysis of a new-type precast assembly floor under human-induced loads [J]. KSCE Journal of Civil Engineering, 2016, 20(7): 2868 − 2874. doi: 10.1007/s12205-016-0617-z
[20]	GB50010−2010, 混凝土结构设计规范 [S]. 北京: 中国建筑工业出版社, 2011. GB50010−2010, Concrete structure design specification [S]. Beijing: China Building Industry Press, 2011. (in Chinese)
[21]	Liu Fangzhou, Battin J M, Pacoste C, et al. Experimental and numerical dynamic analyses of hollow core concrete floors [J]. Structures, 2017(12): 286 − 297.
[22]	Casagrande D, Giongo I, Pederzolli F, et al. Analytical, numerical and experimental assessment of vibration performance in timber floors [J]. Engineering Structures, 2018, 168: 748 − 758. doi: 10.1016/j.engstruct.2018.05.020
[23]	陆春华, 金伟良, 宋志刚. 基于振动舒适度要求的混凝土楼板自振频率分析[J]. 建筑科学, 2010, 26(7): 43 − 46. doi: 10.3969/j.issn.1002-8528.2010.07.011 Lu Chunhua, Jin Weiliang, Song Zhigang. Study on natural frequency of concrete floor based on vibration serviceability [J]. Building Science, 2010, 26(7): 43 − 46. (in Chinese) doi: 10.3969/j.issn.1002-8528.2010.07.011
[24]	严世鑫, 陈隽, 叶艇. 大跨楼盖振动舒适度分析中阻尼比取值讨论[J]. 建筑结构, 2014, 9(增刊 44): 460 − 464. Yan Shixin, Chen Jun, Ye Ting. Values of damping ration in long-span floor vibration serviceability assessment [J]. Building structure, 2014, 9(Suppl 44): 460 − 464. (in Chinese)
[25]	逯静洲, Sim S H, Jr B F S. 基于随机减量法的分布式结构模态参数识别[J]. 振动与冲击, 2017, 36(17): 48 − 54. Lu Jingzhou, Sim S H, Jr B F S. Modal parametric identification of distribution type structures based on random decrement technique [J]. Journal of Vibration and Shock, 2017, 36(17): 48 − 54. (in Chinese)
[26]	金忠谋. 材料力学[M]. 北京: 机械工业出版社, 2005: 191 − 193. Jin Zhongmou. Material mechanics [M]. Beijing: Mechanical Industry Press, 2005: 191 − 193. (in Chinese)
[27]	European Committee for Standardization. General rules and rules for buildings: EN 1995−1-1: 2004 [S]. Brussels: European Committee for Standardization, 2004.
[28]	杜浩, 胡夏闽, 王汉成, 等. 胶合木-混凝土组合楼盖人行荷载激励下振动舒适度研究[J]. 建筑结构学报, 2020, 41(1): 140 − 148. Du Hao, Hu Xiamin, Wang Hancheng, et al. Vibration serviceability of glulam-concrete composite floor under pedestrian excitation [J]. Journal of Building Structures, 2020, 41(1): 140 − 148. (in Chinese)
[29]	陈隽, 王玲, 陈博, 等. 跳跃荷载动力特性与荷载模型实验研[J]. 振动工程学报, 2014, 27(1): 16 − 24. doi: 10.3969/j.issn.1004-4523.2014.01.003 Chen Jun, Wang Ling, Chen Bo, el al. Experimental study on dynamic characteristics and load model of jump loads [J]. Journal of Vibration Engineering, 2014, 27(1): 16 − 24. (in Chinese) doi: 10.3969/j.issn.1004-4523.2014.01.003

施引文献(50)

期刊类型引用(24)

1.	杨欣，张举兵，李小龙，何秋雨，李子欣，周毅. 基于监测数据的钢桁梁桥温度变形研究. 工程力学. 2024(S1): 310-316 . 本站查看
2.	张文东，胡君涛，马志亮，景伟，李龙花. 大跨度波形钢腹板箱梁桥的温度效应研究. 青海大学学报. 2024(06): 75-82 . 百度学术
3.	栾心国. 波形钢腹板PC连续箱梁桥支座偏移成因分析及更换技术. 铁道建筑技术. 2023(05): 138-142 . 百度学术
4.	王凤. 基于日照下波形钢腹板箱梁桥竖向温度的作用分布情况分析. 交通世界. 2023(24): 130-132 . 百度学术
5.	Leilei Chen，Xinyuan Zhao，Zhendong Qian，Jiaqi Li. A systematic review of steel bridge deck pavement in China. Journal of Road Engineering. 2023(01): 1-15 . 必应学术
6.	王雨权. 铁路实体墩墩顶温差位移及规范适应性研究. 铁道标准设计. 2022(03): 78-82 . 百度学术
7.	王力，刘世忠，李子奇，黄佼佼，丁万鹏. 组合桥面板–波形腹板钢箱简支组合梁温度效应. 工程科学与技术. 2022(02): 133-140 . 百度学术
8.	刘阳帆，钟扬，樊林杰，袁以鑫. 日照下波形钢腹板箱梁桥竖向温度分布研究. 公路与汽运. 2022(03): 86-89+103 . 百度学术
9.	王力，刘世忠，丁万鹏，牛思胜，武维宏. 干寒地区新型波形钢腹板组合箱梁温度效应分析. 工程科学与技术. 2021(01): 60-66 . 百度学术
10.	王力，刘世忠，路韡，牛思胜，施鑫磊. 新型波形钢腹板组合箱梁温度效应. 浙江大学学报(工学版). 2021(04): 675-683 . 百度学术
11.	王欲敏，杨未蓬，周丹，邬江红. 高温沥青混合料摊铺时正交异性钢桥面板温度响应分析. 公路交通科技. 2021(07): 60-68 . 百度学术
12.	姜竹昌，高华睿，曹洪亮，张峰. 大跨径波形钢腹板箱梁桥截面竖向温度梯度研究. 中外公路. 2021(04): 125-130 . 百度学术
13.	李小拥. 大桥桥塔温度及温度效应分析. 四川建筑. 2021(05): 177-182 . 百度学术
14.	王达，谭本坤，赵鹏鑫. 钢-混凝土组合桥面板温度梯度效应的试验研究与数值模拟. 建筑结构学报. 2021(S2): 74-82 . 百度学术
15.	曾文宋武，黄方林，申成庆，侯文崎. 长联大跨连续梁桥温度场实测与仿真分析. 铁道科学与工程学报. 2021(12): 3278-3285 . 百度学术
16.	张峰，刘佳琪，高磊，韩福洲，高华睿. 波形钢腹板PC组合箱梁内衬混凝土部位温度分布研究. 应用基础与工程科学学报. 2020(01): 123-133 . 百度学术
17.	刘永健，刘江. 钢-混凝土组合梁桥温度作用与效应综述. 交通运输工程学报. 2020(01): 42-59 . 百度学术
18.	孙增寿，夏云飞，韩培琰. 基于实测数据的混凝土曲线梁桥温差代表值研究. 铁道科学与工程学报. 2020(07): 1751-1759 . 百度学术
19.	张清华，马燕，王宝州. 高原环境新型组合桥塔温度场与温度应力特性分析. 桥梁建设. 2020(05): 30-36 . 百度学术
20.	曹洪亮，沈佳，张峰. 大跨径波形钢腹板箱梁内衬混凝土温度效应. 筑路机械与施工机械化. 2020(11): 30-34 . 百度学术
21.	蔡巍，林一宁，温芳. 大跨度板桁组合梁温差效应分析. 桥梁建设. 2019(02): 41-46 . 百度学术
22.	马虎迎，石明星，严娟，陈茜. 高海拔地区日照对箱式渡槽热力效应分布研究. 南水北调与水利科技. 2019(04): 156-164+171 . 百度学术
23.	盛兴旺，郑纬奇，朱志辉，杨鹰，李帅. 小半径曲线刚构箱梁桥日照时变温度场与温度效应. 交通运输工程学报. 2019(04): 24-34 . 百度学术
24.	郭峰. 拖吊结合式挂篮在波形钢腹板预应力连续梁中的设计及应用研究. 铁道建筑技术. 2018(07): 26-27+32 . 百度学术

其他类型引用(26)

资源附件(0)

图(14) / 表(8)

计量

文章访问数: 565
HTML全文浏览量: 121
PDF下载量: 75
被引次数: 50

1 试验概况
1.1 试件设计
1.2 材料属性
1.3 加载装置
2 模态参数分析
2.1 模态振型
2.2 一阶自振频率与阻尼比
3 人致激励响应
3.1 加速度响应
3.1.1 加速度时程曲线
3.1.2 各测点响应
3.2 各工况下的加速度响应
4 DCPCD的理论计算
4.1 自振频率的计算方法
4.2 单人踮脚和跳跃荷载下峰值加速度的计算
5 结论

1 试验概况
1.1 试件设计
1.2 材料属性
1.3 加载装置
2 模态参数分析
2.1 模态振型
2.2 一阶自振频率与阻尼比
3 人致激励响应
3.1 加速度响应
3.1.1 加速度时程曲线
3.1.2 各测点响应
3.2 各工况下的加速度响应
4 DCPCD的理论计算
4.1 自振频率的计算方法
4.2 单人踮脚和跳跃荷载下峰值加速度的计算
5 结论

参考文献(29)

施引文献(50)

资源附件(0)

踮脚和跳跃荷载下全装配式RC楼盖振动特性试验研究

通讯作者: 庞 瑞(1981−)，男，河南信阳人，副教授，工学博士，硕导，从事装配式混凝土结构研究(E-mail: seupangrui@163.com)

计量

出版历程

EXPERIMENTAL STUDY ON THE VIBRATION CHARACTERISTICS OF UNTOPPED PRECAST RC FLOORS UNDER BOUNCEAND JUMPING LOADS

1 试验概况

1.1 试件设计

1.2 材料属性

1.3 加载装置

2 模态参数分析

2.1 模态振型

2.2 一阶自振频率与阻尼比

3 人致激励响应

3.1 加速度响应

3.1.1 加速度时程曲线

3.1.2 各测点响应

3.2 各工况下的加速度响应

4 DCPCD的理论计算

4.1 自振频率的计算方法

4.2 单人踮脚和跳跃荷载下峰值加速度的计算

5 结论

期刊类型引用(24)

其他类型引用(26)

计量

出版历程

目录

1 试验概况

1.1 试件设计

1.2 材料属性

1.3 加载装置

2 模态参数分析

2.1 模态振型

2.2 一阶自振频率与阻尼比

3 人致激励响应

3.1 加速度响应

3.1.1 加速度时程曲线

3.1.2 各测点响应

3.2 各工况下的加速度响应

4 DCPCD的理论计算

4.1 自振频率的计算方法

4.2 单人踮脚和跳跃荷载下峰值加速度的计算

5 结论

通讯作者:
庞　瑞(1981−)，男，河南信阳人，副教授，工学博士，硕导，从事装配式混凝土结构研究(E-mail: seupangrui@163.com)