DISCRETE ELEMENT SIMULATION OF THE SHEAR BEHAVIOR OF CEMENTED METHANE HYDRATE-BEARING SANDS
-
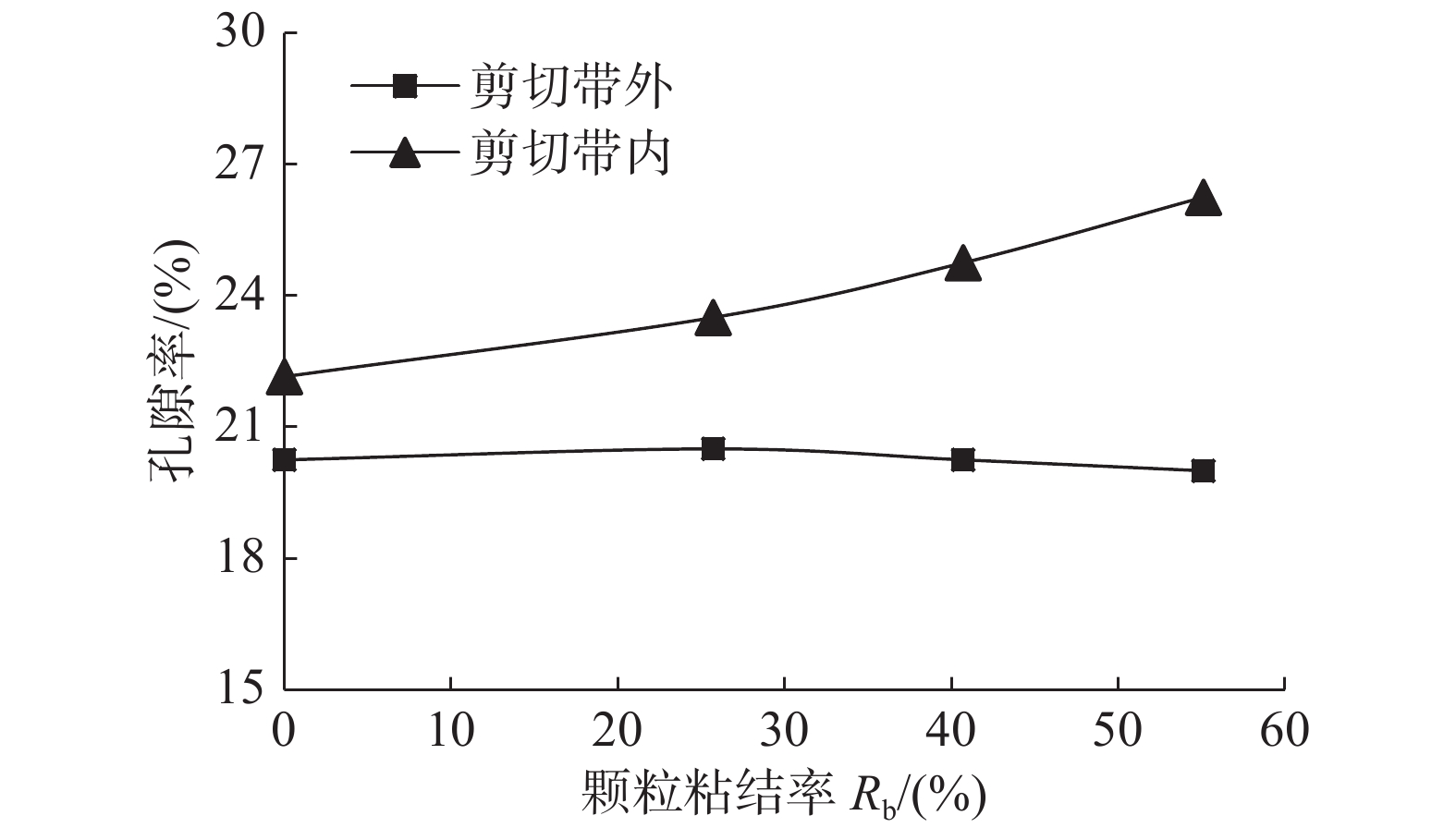
摘要: 可燃冰是一种新型清洁能源，广泛分布于深海土体和常年冻土中，对其开采需要深入认识含可燃冰土体的力学特性。该文提出了一种胶结型含可燃冰砂土离散元模型建立方法，并利用该模型完成了排水双轴剪切试验的模拟。通过与前人试验数据对比，验证了该离散元模型的准确性，结合该模型分析了剪切过程中含可燃冰砂土的宏细观变化规律。结果表明：砂土抗剪强度、应变软化特性及剪胀性均随可燃冰饱和度的增加而增加；可燃冰胶结断裂数量的演化与偏应力紧密相关，偏应力达到峰值时胶结断裂数量增长速率最快；剪切过程中剪切带内外土体的胶结断裂、颗粒运动、孔隙率变化均表现出明显的差异。通过对模型粘结断裂率、剪切带内外局部孔隙率等细观指标的分析，对土体的偏应力变化、体积变化等宏观现象的机理做出了更进一步的阐释。Abstract: The methane hydrate is a new type of clean energy, and is widely distributed in deep sea sediments and permafrost. It is necessary to study the mechanical properties of the methane hydrate-bearing sands. In this paper, a method of generating the discrete element model of cemented methane hydrate-bearing sands is proposed. The model is used to simulate a drained biaxial test. The accuracy of the discrete element model is verified by comparing it with previous experimental data. The macro and micro characteristics of the methane hydrate-bearing sands are then analyzed using the model. The results show that the shear strength, strain softening characteristics and dilatancy of the sand increase with the increase of methane saturation, that the evolution of the hydrate fracture number is closely related to the deviator stress, that the hydrate fracture number increases most rapidly when the deviator stress reaches the peak value, and that the hydrate fracture, particle movement and the porosity change inside and outside the shear band during the test are obviously different. Through the analysis of some micro indexes such as the bond breaking ratio and local porosity inside and outside the shear band, the mechanism of the macro behavior such as the deviator stress and volume change of the methane hydrate-bearing sand is further explained.
-
Keywords:
- methane hydrate /
- sand /
- discrete element method /
- dilatancy /
- shear band
-
雪灾被认为是当今世界面临的十大灾害之一[1]，在多雪大风的地区，建筑周边积雪对道路通行和行人行车安全形成了很大的挑战。例如：门窗布置位置、道路选择方位、室外花园选址，等等，都应考虑积雪堆积位置，如若规划合理，除雪和建筑周边设施毁坏成本将大大降低，大型场所的逃生避难安全性也会相应地提高。
风速较低时，跃移为风雪运动中雪颗粒传输的主要途径[2]，积雪在建筑周边的分布，就是雪颗粒在大风作用下重新分布，在建筑和雪堆的影响下形成特有的形状，以往对建筑周边积雪分布的研究主要可以分为理论分析、风洞试验、现场实测和数值模拟。Beyers等[3]和Tominaga等[4]的研究中表明积雪的累积过程是随时间变化的；李雪峰[5]以细硅砂作为雪颗粒的模拟物，对不同时刻的立方体周边积雪分布情况进行了风洞试验研究；Oikawa等[6]在日本札幌市郊区降雪条件持续一天的情况下，选取了七种不同风速的工况，测量了边长为1 m的立方体周围的积雪分布；Beyers等[3]在南极洲风速较高的情况下对一个2 m立方体周边积雪分布进行实测；张玉杰等[7]和孙晓颖等[8]采用数值方法模拟了立方体周边的积雪分布情况。
以上研究仅针对单个立方体周边积雪分布情况，为了明确长宽比对机构周边积雪分布的影响，本文针对不同长宽比建筑周边风致积雪分布进行了现场实测，并通过CFD(Computational Fluid Dynamic)数值模拟方法计算了不同工况下的风场并与实测结果对比，研究了长宽比对建筑周边风场及风致积雪分布的影响，为建筑周边积雪堆积预测方法提供了对比和验证数据。
1 试验概况
1.1 现场实测概况
实测场地选择在新疆北疆九大风区之一的玛依塔斯风区，该位置处于两座山脉之间狭长的山谷之中，两侧为盆地，由于狭管效应，风速风向较为稳定，并且在冬季会受到西伯利亚寒流的影响出现大范围的降雪，提供了充足的干雪颗粒，具体测试区域如图1中三角标识所示。
选取边长B=500 mm的立方体模型分别拼接成长宽比为1∶1、2∶1、1∶2三个模型工况进行，拼接后的模型尺寸定义长度方向为顺风向壁面与地面相交的模型边长，宽度方向为横风向壁面与地面相交的模型边长，模型如图2所示。
风速选取模型前侧来流方向1 m高度处，实测期间日平均风速7 m/s，将不同长宽比的模型按照主导风向顺风向置于实测场地24 h以上，使风雪流充分发展，在积雪堆积范围内以横纵5 cm为间隔剖分，用量雪尺测量积雪深度。由于来流风向的微小变化，积雪分布也具有一定的不对称性，对表征性较强的区域进行了加密处理，两侧无较大差异的只采集模型顺风向单侧数据，空缺处利用克里金插值法填补。
1.2 数值模拟
数值模拟工况与现场实测工况相同，计算域长×宽×高选为21B×11B×10B，如图3所示，为1∶1模型计算域示意图。
采用结构化网格剖分，边界层最小网格尺寸为0.005 m，网格总数为1 380 000左右，以控制方程残差降到10−7为收敛标准，双精度求解。
空气入流面采用速度入口边界(Velocity-Inlet)，指数型风剖面，即：
v(z)=v0(zz0)α (1) 式中：v(z)为离地高度z处平均风速；z0为参考高度，一般取10 m；v0为参考高度处平均风速，选取当日内平均风速7 m/s；α为地面粗糙系数，取0.15。
湍流入口均参考徐枫等[9]文献中所述，出流面：采用自由出流为边界条件(Outflow)；计算域顶面和侧面：采用对称边界条件(Symmetry)；地面和结构表面：均采用无滑移壁面为边界条件(Wall)。
2 研究结果
2.1 数值计算模型的选择
Richards等[10]测量了边长为6 m的立方体表面中线的压力以及风速值发现，建筑物表面风压分布和其周边风场存在一定关系，并且建筑物周边风场决定了风致积雪分布。
本文分别采用Realizable k-ε模型和k-kl-ω模型模拟立方体风压分布，将模拟结果与Richards等[10]的实测值结果对比，平均风压系数如图4所示，结果表明：数值模拟结果平均风压系数趋势与实测值大体相同，k-kl-ω模型在模型顶部拐角处相比实测的风压系数出现了较小值，是由于该模型的壁面函数处理近壁面流场时，减小了越过模型顶面产生的涡，相对于k-kl-ω模型，Realizable k-ε模型更接近实测值。
2.2 现场实测积雪分布
图5(a)为1∶1模型现场实测积雪分布，和以往已有结果吻合[6]，模型周边呈现出马蹄形，迎风区最大积雪深度堆积位置在1.75B，在距离模型中心约为1.5B范围内侵蚀，模型两侧在距离模型中心1.5B范围内侵蚀，背风区在距离模型中心0.65B的积雪堆积后侵蚀，在距离模型中心1.75B处有积雪二次堆积，其后侵蚀范围在2.85B，迎风区及背风区模型壁面处形成“V”型积雪堆积，尾侧区有长尾迹积雪。
图5(b)为2∶1模型现场实测积雪分布，模型迎风区积雪最大堆积位置在1.85B，在距离模型中心约为1.6B范围内侵蚀，与1∶1模型积雪分布相比侵蚀范围略有增大，模型两侧在距离模型中心3.15B范围内侵蚀，随着模型长度增大一倍，侵蚀范围也扩大了将近一倍，背风区在距离模型中心0.85B的积雪堆积后侵蚀，背风区壁面积雪范围增大，积雪在距离模型中心约为2.5B处产生明显的二次堆积，侵蚀范围也增大，为1∶1模型的两倍以上。尾侧区积雪影响范围更广。
图5(c)为1∶2模型现场实测积雪分布，模型迎风区积雪最大堆积位置在1.85B，在距离模型中心约为1.5B范围内侵蚀，相对于1∶1模型积雪堆积变化不大。
比较三种模型发现，迎风区积雪分布只与建筑高度有关，长宽比对其影响不大，模型两侧被完全侵蚀，背风区在积雪堆积距离模型中心0.75B后侵蚀，积雪在距离模型中心约2.25B处产生二次堆积，再后方无积雪，此时有可能是由于实测客观环境因素，风速降低，无法带动雪颗粒移动，在本文后续章节中有数值计算加以辅助。
2.3 顺风向中轴线风场
图6(a)为1∶1模型数值模拟顺风向中轴线风场分布，当气流流经模型时，受到模型干扰，风速值产生较大波动，迎风区壁面对气流产生阻挡，在模型壁面前侧形成驻涡，使风速值在迎风区壁面与地面交界处急剧降低，达到风速最小值，在模型前侧因驻涡造成的风速回流，使反向风速值骤然增大，在距离模型中心约为1.65B处消失。风速值在模型迎风面与顶面交界处达到最大，且气流在此处发生分离，气流流经模型顶面时，风速值略微减小但降幅不大，当气流流过模型顶面，在模型后方形成背风涡，风速值急剧降低，在背风区壁面与地面交界处达到最小值，背风涡在模型后侧产生风速回流，产生增大的反向风速，相比迎风侧风速回流风速值较小，在距离模型中心约为1.85B处产生风速最小值，气流在距离模型中心约为3B处趋于平缓，并逐渐恢复初始状态。风场风速减弱区和旋涡回流风速增大区分别与风雪流经过时的积雪堆积区域和风雪流经过时的侵蚀区域相对应，且效果较好，简化了数值计算模型。
图6(b)为2∶1模型数值模拟顺风向中轴线风场分布，气流在模型前侧因驻涡造成的风速回流相对于实测模型略微增大，在距离模型中心约为1.75B处消失。背风涡在模型后侧产生风速回流相比迎风侧风速回流风速值较小，在距离模型中心2.5B处风速值达到最小，气流在距离模型中心约为4.35B处趋于平缓，并逐渐恢复初始状态。与实测侵蚀范围变化规律一致。
图6(c)为1∶2模型数值模拟顺风向中轴线风场分布，气流在模型前侧因驻涡造成的风速回流在距离模型中心约为2.15B处消失，为单个立方体下的1.65B。迎风区风场变化规律与积雪分布一致，均不受长宽比影响，背风涡在模型后侧产生风速回流在距离模型中心约2.25B处风速值最小，为单个立方体下的1.75B，在距离模型中心约为3.5B处趋于平缓，为单个立方体下的3B，和1∶1模型相同，并逐渐恢复初始状态。和1∶1模型相同，由此可见，建筑宽度对其周边积雪分布影响较小。
2.4 横风向中轴线风场
图7(a)为1∶1模型数值模拟横风向中轴线风场分布，气流经过模型时被模型切割，分离产生马蹄涡，贴近两侧壁面处风速值减小，模型两侧风速值增大，在距离模型中心约为1.5B处逐渐恢复。与实测积雪堆积侵蚀范围相对应。
图7(b)为2∶1模型数值模拟横风向中轴线风场分布，由马蹄涡造成的风速值增大区域随着模型长度的增加而增大，在距离模型中心约为2.25B处。相对于实测值略小。
图7(c)为1∶2模型数值模拟横风向中轴线风场分布，由马蹄涡造成的风速值增大区域随着模型宽度的增加无太大变化，在距离模型中心约为1.6B处，相对于实测值略小。因宽度的增加，使气流在模型顶部减速范围加大，风速值略有减小，建筑宽度对其周边风场影响也不大。
3 结论
通过实测对不同长宽比模型周边风致积雪分布进行测量，采用数值模型方法对风场进行模拟，与实测数据进行对比，进而对周边的积雪分布情况进行分析，得到如下结论：
(1) 采用数值方法模拟建筑周边风场，气流受到模型的扰动，在其周边产生风速变化，以风速增大减速区域范围推测建筑周边积雪侵蚀堆积的范围与实测较为接近，且该方法简单有效，可以定性判断积雪分布的规律。
(2) 气流受到模型干扰，在迎风区形成驻涡，经过模型时在两侧产生分离，形成马蹄涡，绕过模型后在背风区形成回流，旋涡区域风速较大，积雪被风吹走发成侵蚀现象，相对周围的风速较小，对应位置积雪产生堆积。
(3) 在风雪流的作用下，迎风区只与建筑高度有关，长宽比对其影响不大，横风向侵蚀影响范围与建筑长度成正比，约为距离建筑中心1.65倍的模型长度，随着建筑长度的增大，背风区侵蚀影响范围增大，产生积雪的二次沉积，建筑宽度对其周边积雪分布影响较小。
-
![]()
图 2 不同颗粒粘结率Rb/可燃冰饱和度SMH下应力-应变关系
Figure 2. Stress-strain curves with different bonding ratios Rb/hydrate saturation SMH
![]()
图 3 不同颗粒粘结率Rb/可燃冰饱和度SMH下体应变关系
Figure 3. Volumetric curves with different bonding ratios Rb/hydrate saturation SMH
![]()
图 4 不同颗粒粘结率Rb/可燃冰饱和度SMH下内摩擦角φ及粘聚力c变化
Figure 4. Friction angle φ and cohesion c with different bonding ratios Rb/hydrate saturation SMH
![]()
图 5 不同颗粒粘结率Rb下粘结断裂率Rbk-轴应变变化关系
Figure 5. Relationship between bond breaking ratio Rbk and axial strain with different bonding ratios Rb
![]()
图 6 不同围压下粘结断裂率Rbk-轴应变变化关系
Figure 6. Relationship between bond breaking ratio Rbk and axial strain under different confining pressures
![]()
图 7 不同轴应变下砂土粘结断裂分布(Rb=55.1%)
Figure 7. Bond breaking distribution at different axial strains (Rb=55.1%)
![]()
图 8 不同轴应变下砂土颗粒转角(Rb=55.1%)
Figure 8. Rotation of particles at different axial strains (Rb=55.1%)
![]()
图 9 不同轴应变下砂土局部孔隙率(Rb=55.1%)
Figure 9. Local porosity of sand at different axial strains (Rb=55.1%)
![]()
图 10 剪切带内外颗粒位移对比(ε1=14%)
Figure 10. Particle displacement inside and outside shear band (ε1=14%)
![]()
图 11 ε1=14%时不同颗粒粘结率Rb砂土剪切带内外孔隙率
Figure 11. Porosity of sands inside and outside shear band with different bonding ratios Rb at ε1=14%
表 1 离散元模型参数取值
Table 1 Parameters of DEM model
参数 取值 模型尺寸/mm 160×80 圆盘单元总数 20 117 圆盘单元密度/(kg/m3) 2600 圆盘单元直径/mm 0.6~1.0 成样时圆盘单元摩擦系数 0.2 成样后圆盘单元摩擦系数 1.0 初始模型孔隙率/(%) 21 圆盘单元切向刚度/(N/m) 1.6×109 圆盘单元法向刚度/(N/m) 2.4×109 墙单元切向刚度/(N/m) 1.6×109 墙单元法向刚度/(N/m) 2.4×109 切向粘结强度/Pa 1.1×104 法向粘结强度/Pa 1.1×104 颗粒粘结率Rb/(%) 取值等于可燃冰饱和度SMH 
下载: 导出CSV
-
[1] Makogon Y F, Holditch S A, Makogon T Y. Natural gas-hydrates — A potential energy source for the 21st Century [J]. Journal of Petroleum Science & Engineering, 2007, 56(1/2/3): 14 − 31.
[2] 马小娟, 呼方涛, 王锦华. 浅析可燃冰的研究现状与发展前景[J]. 科技信息, 2011(7): 351 − 382. Ma X J, Hu F T, Wang J H. Research status and development prospect of combustible ice [J]. Science & Technology Information, 2011(7): 351 − 382. (in Chinese)
[3] Locat J, Lee H J. Submarine landslides: advances and challenges [J]. Canadian Geotechnical Journal, 2002, 39(1): 193 − 212. doi: 10.1139/t01-089
[4] Soga K, Klar A. Characterisation and engineering properties of methane hydrate soils [C]// The Second International Workshop on Characterisation and Engineering Properties of Natural Soils. Singapore: Taylor and Francis Group, 2007: 2591 − 2642.
[5] Masui A, Haneda H, Ogata Y. Effects of methane hydrate formation on shear strength of synthetic methane hydrate sediments [C]// Proceedings of the 15th International Offshore and Polar Engineering Conference. Seoul, Korea: The International Society of Offshore and Polar Engineers, 2005: 364 − 369.
[6] Li Y, Liu W. Experimental Research on the Mechanical Properties of Methane Hydrate-Ice Mixtures [J]. Energies, 2012, 5: 181 − 192.
[7] Miyazaki K, Masui A, Sakamoto Y, et al. Triaxial compressive properties of artificial methane-hydrate-bearing sediment [J]. Journal of Geophysical Research: Solid Earth, 2011, 116(B06102): 1 − 12. doi: 10.1029/2010JB008049
[8] Pinkert S, Grozic J L H. Failure Mechanisms in Cemented Hydrate-Bearing Sands [J]. Journal of Chemical & Engineering Data, 2015, 60(2): 376 − 382. doi: 10.1021/je500638c
[9] Hyodo M, Yoneda J, Yoshimoto N, et al. Mechanical and dissociation properties of methane hydrate-bearing sand in deep seabed [J]. Soils Found, 2013, 53(2): 299 − 314. doi: 10.1016/j.sandf.2013.02.010
[10] Song Y, Zhu Y, Liu W, et al. Experimental research on the mechanical properties of methane hydrate-bearing sediments during hydrate dissociation [J]. Marine & Petroleum Geology, 2014, 51(Complete): 70 − 78.
[11] Zhang X H, Luo D S, Lu X B, et al. Mechanical properties of gas hydrate-bearing sediments during hydrate dissociation [J]. Acta Mechanica Sinica, 2018, 34(2): 266 − 374. doi: 10.1007/s10409-017-0699-y
[12] Cundall P A, Strack O D L. A discrete numerical model for granular assemblies [J]. Géotechnique, 1979, 29(1): 47 − 65. doi: 10.1680/geot.1979.29.1.47
[13] 齐念, 叶继红. 弹性DEM方法在杆系结构中的应用研究[J]. 工程力学, 2017, 34(7): 11 − 20. Qi N, Ye J H. Application of elastic discrete element method in member structures [J]. Engineering Mechanics, 2017, 34(7): 11 − 20. (in Chinese)
[14] 王蕴嘉, 周梦佳, 宋二祥. 考虑颗粒破碎的堆石料湿化变形特性离散元模拟研究[J]. 工程力学, 2018, 35(增刊 1): 217 − 222. doi: 10.6052/j.issn.1000-4750.2017.05.S043 Wang Y J, Zhou M J, Song E X. DEM simulation of wetting deformation characteristics of rockfill considering particle breakage [J]. Engineering Mechanics, 2018, 35(Suppl 1): 217 − 222. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.05.S043
[15] 孟凡净, 刘焜, 吴华伟. 颗粒流润滑剪切膨胀的力学机制研究[J]. 工程力学, 2018, 35(8): 236 − 244. Meng F J, Liu K, Wu H W. Research on mechanical mechanism of shear dilatancy for granular flow lubrication [J]. Engineering Mechanics, 2018, 35(8): 236 − 244. (in Chinese)
[16] Brugada J, Cheng Y P, Soga K, et al. Discrete element modelling of geomechanical behaviour of methane hydrate soils with pore-filling hydrate distribution [J]. Granular Matter, 2010, 12(5): 517 − 525. doi: 10.1007/s10035-010-0210-y
[17] 蒋明镜, 肖俞, 朱方园. 深海能源土微观力学胶结模型及参数研究[J]. 岩土工程学报, 2012, 34(9): 1574 − 1583. Jiang M J, Xiao Y, Zhu F Y. Micro-bond contact model and its parameters for the deep-sea methane hydrate bearing soils [J]. Chinese Journal of Geotechnical Engineering, 2012, 34(9): 1574 − 1583. (in Chinese)
[18] 蒋明镜, 肖俞, 朱方园. 深海能源土宏观力学性质离散元数值模拟分析[J]. 岩土工程学报, 2013, 35(1): 157 − 163. Jiang M J, Xiao Y, Zhu F Y. Numerical simulation of macro-mechanical properties of deep-sea methane hydrate bearing soils by DEM [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(1): 157 − 163. (in Chinese)
[19] Jiang M, Zhu F, Liu F, et al. A bond contact model for methane hydrate-bearing sediments with interparticle cementation [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(17): 1823 − 1854. doi: 10.1002/nag.2283
[20] Xu M, Song E, Jiang H, et al. DEM simulation of the undrained shear behavior of sand containing dissociated gas hydrate [J]. Granular matter, 2016, 18(79): 1 − 13. doi: 10.1007/s10035-016-0675-4
[21] Hong J, Xu M. DEM study on the undrained mechanical behavior of gassy sand [J]. Acta Geotechnica, 2020, 15(8): 2179 − 2193. doi: 10.1007/s11440-019-00910-x
[22] Itasca Consulting Group Inc. User's Manual for PFC2D [M].Minnesota: Itasca Consulting Group Inc., 2005.
[23] 胡高伟, 李承峰, 业渝光, 等. 沉积物孔隙空间天然气水合物微观分布观测[J]. 地球物理学报, 2014, 57(5): 1675 − 1682. doi: 10.6038/cjg20140530 Hu G W, Li C F, Ye Y G, et al. Observation of gas hydrate distribution in sediment pore space [J]. Chinese Journal of Geophysics, 2014, 57(5): 1675 − 1682. (in Chinese) doi: 10.6038/cjg20140530
[24] Zhou W, Yang L, Ma G, et al. DEM modeling of shear bands in crushable and irregularly shaped granular materials [J]. Granular Matter, 2017, 19(25): 1 − 12. doi: 10.1007/s10035-017-0712-y
[25] 杨智勇, 曹子君, 李典庆, 等. 颗粒接触摩擦系数空间变异性对颗粒流双轴数值试验的影响[J]. 工程力学, 2017, 34(5): 235 − 246. Yang Z Y, Cao Z J, Li D Q, et al. Effect of spatially variable friction coefficient of granular materials on its macro-mechanical behaviors using biaxial compression numerical simulation [J]. Engineering Mechanics, 2017, 34(5): 235 − 246. (in Chinese)
计量
- 文章访问数: 802
- HTML全文浏览量: 145
- PDF下载量: 106
