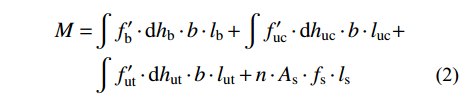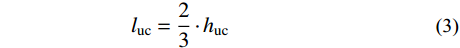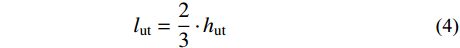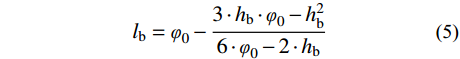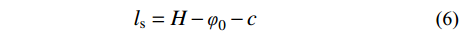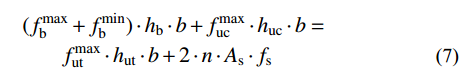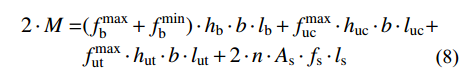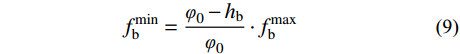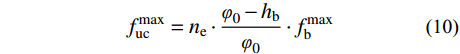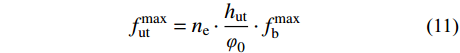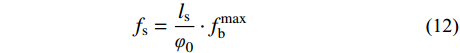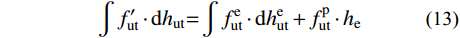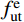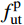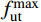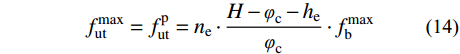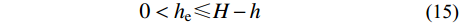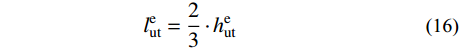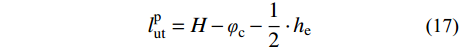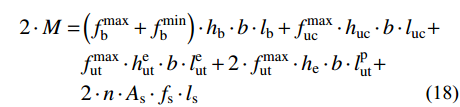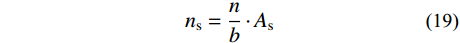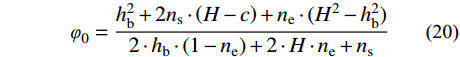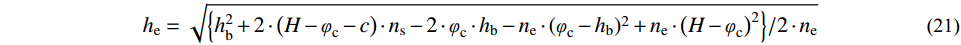CRACKING LOAD CALCULATION FOR STEEL-UHPC COMPOSITE SLABS BASED ON THE SECTION-STRESS METHOD
-
摘要: 负弯矩作用下钢-超高性能混凝土(ultra-high-performance concrete，UHPC)组合板结构层的局部受拉开裂问题，是该类新型组合桥面板结构体系应用和发展的基础性研究课题。基于平截面假定和双折线UHPC拉伸本构模型，提出了能够描述UHPC结构层实际应力分布的截面应力法，用于计算这种新型结构在纯弯曲作用下的开裂荷载。通过2组4个模型试验并结合相关文献试验结果对所提出的计算方法进行了验证，研究结果表明：利用截面应力法能够较为准确的描述钢-UHPC组合板在纯弯曲作用下的开裂行为，计算给出的开裂荷载与实测值比值平均为0.95；UHPC的开裂强度仅取决于其自身材料特性，钢-UHPC组合板开裂荷载的提高不会影响UHPC层的开裂强度；UHPC层在可视裂缝出现时的应变硬化高度是组合效应及配筋对其约束的直观体现；减小纵筋保护层厚度或提高配筋率能够提高UHPC应变硬化区域高度，提高钢-UHPC组合板抗弯性能。
-
关键词:
- 桥梁与隧道工程 /
- 钢-UHPC组合板 /
- 超高性能混凝土(UHPC) /
- 截面应力法 /
- 开裂强度
Abstract: The local cracking problem of steel-UHPC (ultra-high-performance concrete) composite structures under negative bending moments is the basis of the application and development. Based on the UHPC tensile bilinear constitutive model and plane cross-section assumption, a section stress method is set up to describe the stress distribution of the steel-UHPC composite slabs and calculate the cracking load under a pure bending condition. The proposed method is verified by 4 specimens of 2 groups and the test results in the literature. The results indicate that the section-stress method can accurately describe the cracking behavior of steel-UHPC composite plates under pure bending and the average ratio of calculated to measured values is 0.95. The UHPC cracking strength is an intrinsic property dependent on the nature of the material itself and is not influenced by the steel-UHPC composite slab. The height of the UHPC strain hardening zone represents the combination effect and reinforcement constraint when visible cracks appear. By reducing the cover thickness or increasing the reinforcement ratio, the UHPC strain hardening height can be increased and the flexural behavior of the steel-UHPC composite slab can be improved. -
钢桥面板疲劳开裂和桥面铺装易损是制约正交异性钢桥面板可持续发展应用的困难所在。国内外学者通过引入超高性能混凝土(Ultra-high-performance concrete，UHPC)结构层，通过栓钉剪力连接件与正交异性钢桥面板组成组合受力体系，提出了钢-UHPC组合桥面板结构体系[1-3]，并从多个方面对该类新型组合桥面板结构体系进行了试验和理论研究[4-6]，目前钢-UHPC组合桥面板结构体系已在国内多座大跨度桥梁中得到了成功应用[7]。研究结果表明：UHPC具有优异的力学性能和良好的承载力及耐久性[8-9]；超薄UHPC层强度能够满足组合桥的设计要求[7]；钢-UHPC组合桥面板结构是从结构体系层面解决钢桥面板疲劳问题的有效途径之一[10-15]。该新型结构形式在承受负弯矩时，存在局部开裂风险[16]，从而影响其耐久性。
针对第三体系负弯矩作用下钢-UHPC组合板存在的局部开裂风险问题，试验和工程实践中多以出现肉眼可观测裂缝作为开裂标准，并认为当UHPC表面最大裂缝宽度不超过0.05 mm时对其耐久性的影响可以忽略[17]。国内外学者通过模型试验研究了配筋钢-UHPC板的受弯性能，总结了配筋率及UHPC保护层厚度对钢-UHPC组合板受弯性能的影响[16, 18]。相关研究为深刻认识钢-UHPC组合桥面板结构体系的受力特性奠定了重要基础，并推动了其应用和发展。相关研究对于钢-UHPC组合板的开裂荷载及开裂强度的计算多基于线弹性的换算截面法[7]，这种方法难以体现UHPC自身应变硬化特性[19]，所得结果不能准确描述截面开裂状态的应力分布。目前国内外对于钢-UHPC组合板在正负弯矩作用下裂缝的发展已有较为完善的试验研究及理论分析[20-22]，但对负弯矩作用下UHPC受拉区的应力重分布现象以及组合板开裂荷载作用下的截面应力分布研究鲜见报道，尚没有结合UHPC材料自身本构关系特性及截面组合形式直接推算开裂荷载的计算方法。
本文通过引入UHPC双线性受拉本构模型，结合组合截面相关参数，提出了描述钢-UHPC组合板实际应力分布的截面应力法，通过设计2组4个试验试件并结合文献[7]与文献[18]试验结果对算法进行验证。结果显示，理论计算结果与试验值吻合良好；结合相关计算公式，讨论了影响钢-UHPC组合板负弯矩受力性能的影响因素。所提出的钢-UHPC组合板开裂弯矩计算公式，概念明确，计算简洁，所得应力分布能够反映UHPC双折线本构模型，可为钢-UHPC组合板抗裂性设计提供借鉴。
1 方法的提出
1.1 换算截面法
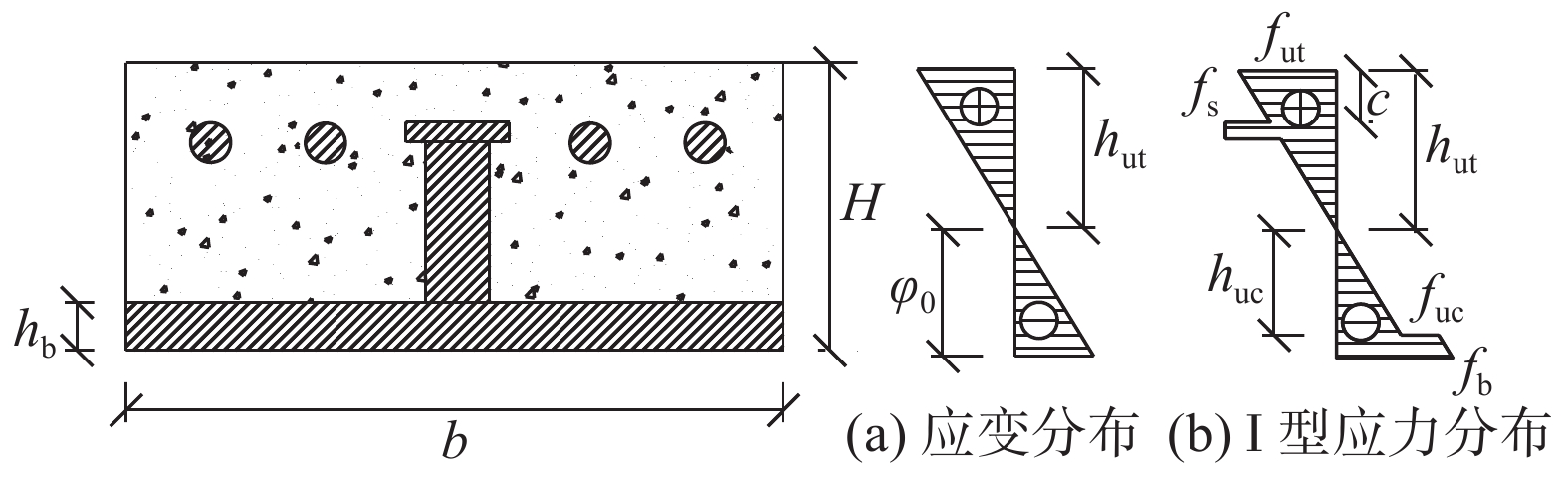
当前通常以第三体系(盖板体系)进行钢-UPHC组合桥面受力特性试验和理论研究，并据此确定UHPC层的开裂强度[7]，据此分析钢-UHPC组合板截面在纯弯曲作用下的开裂荷载。基于平截面假定，对开裂前截面工作状态进行分析，钢材与UHPC在开裂前均为理想材料，忽略钢底板与UHPC的层间滑移[16]，由平截面假定可知，钢-UHPC组合板截面应变分布见图1(a)。
![]()
图 1 组合板应变分布示意图(拉为+，压为−)Figure 1. Schematic drawing for theoretical analysis of strain (‘+’ tension, ‘−’ compression)图1中：H为截面总高度；b为板宽；φ0为中性轴距底边距离；c为纵筋(受拉钢筋)保护层厚度。平截面假定成立，在完全弹性阶段截面满足轴力平衡及弯矩平衡方程，将其工作状态定义为I型应力分布见图1(b)，即为一般的换算截面法[7]：
∫f′b⋅dhb⋅b+∫f′uc⋅dhuc⋅b=∫f′ut⋅dhut⋅b+nAsfs (1) M=∫f′b⋅dhb⋅b⋅lb+∫f′uc⋅dhuc⋅b⋅luc+∫f′ut⋅dhut⋅b⋅lut+n⋅As⋅fs⋅ls (2) 式中：
f′ 表示各区域应力分布函数；f表示应力值，带下标的h表示各受力部分高度；l表示各受力部分力臂；下标b、uc、ut及s分别表示钢板、UHPC受压区域、UHPC受拉区域及钢筋；As表示钢筋截面面积；n为钢筋数量。根据几何关系，用h表示l：
luc=23⋅huc (3) lut=23⋅hut (4) lb=φ0−3⋅hb⋅φ0−h2b6⋅φ0−2⋅hb (5) ls=H−φ0−c (6) 积分后式(1)及式(2)可表示为：
(fbmax (7) \begin{split} 2 \cdot M =& {\rm{ }}( {{f_{\rm{b}}^{\max }} + {f_{\rm{b}}^{\min }}} ) \cdot {h_{\rm{b}}} \cdot b \cdot {l_{\rm{b}}} + f_{{\rm{uc}}}^{{\rm{max}}} \cdot {h_{{\rm{uc}}}} \cdot b \cdot {l_{{\rm{uc}}}} + \\& f_{{\rm{ut}}}^{{\rm{max}}} \cdot {h_{{\rm{ut}}}} \cdot b \cdot {l_{{\rm{ut}}}} + 2 \cdot n \cdot {A_{\rm{s}}} \cdot {f_{\rm{s}}} \cdot {l_{\rm{s}}} \\[-15pt] \end{split} (8) 式中，上标max与min分别表示最大值与最小值。
由于钢底板应力远远低于其容许应力，为便于计算将各部分应力表示为钢底板应力最大值：
f_{\rm{b}}^{{\rm{min}}} = \frac{{{\varphi _0} - {h_{\rm{b}}}}}{{{\varphi _0}}} \cdot f_{\rm{b}}^{{\rm{max}}}\quad\quad (9) f_{{\rm{uc}}}^{{\rm{max}}} = {n_{\rm{e}}} \cdot \frac{{{\varphi _0} - {h_{\rm{b}}}}}{{{\varphi _0}}} \cdot f_{\rm{b}}^{{\rm{max}}} (10) f_{{\rm{ut}}}^{{\rm{max}}} = {n_{\rm{e}}} \cdot \frac{{{h_{{\rm{ut}}}}}}{{{\varphi _0}}} \cdot f_{\rm{b}}^{{\rm{max}}}\quad\;\; (11) {f_{\rm{s}}} = \frac{{{l_{\rm{s}}}}}{{{\varphi _0}}} \cdot f_{\rm{b}}^{{\rm{max}}}\quad\quad\quad\quad (12) 式中，ne为UHPC与钢材弹性模量比。
将相关参数代入式(7)及式(8)即可得到换算截面法计算结果。文献试验结果表明[7]，不同配筋率、保护层厚度的钢-UHPC组合板在纯弯曲作用下开裂荷载差异较大，由于UHPC本构拉伸模型包含应变硬化应力-应变关系及应力软化应力-裂缝宽度关系[16]，始终采用线弹性本构模型的换算截面法无法反映截面真实应力分布，计算结果不能反映UHPC的真实开裂强度。综上所述，换算截面法无法描述截面开裂前真实的应力历程，难以准确界定钢-UHPC组合板受弯开裂状态，不能总结出统一的开裂量化标准，需要进行修正。
1.2 截面应力法
在换算截面法的基础上引入双折线UHPC抗拉本构模型[16]，UHPC受拉进入应变硬化阶段后截面的应力分布模型如图2(b)所示。
图2(a)中εp为峰值应变，εe为极限应变，图2(b)中he表示应变硬化区域高度，φc为II型应力分布的中性轴距底边距离。UHPC层部分受拉区域进入应变硬化阶段时，截面应力分布转为II型，UHPC受拉应力分为弹性区域及高度为he的应变硬化区域。为保证式(7)成立，中性轴φc随he的增加而降低，该分布模型描述了一个动态平衡过程。
![]()
图 2 截面应力分布模式示意图(拉为+，压为−)Figure 2. Schematic drawing for theoretical analysis of stress (‘+’ tension, ‘−’ compression)当截面处于II型应力分布时，式(2)中UHPC受拉分量表示为：
\int {{{f}_{{\rm{ut}}}'} \cdot {\rm{d}}{h_{{\rm{ut}}}}} {\rm{ = }}\int {f_{{\rm{ut}}}^{\rm{e}} \cdot {\rm{d}}h_{{\rm{ut}}}^{\rm{e}}} + f_{{\rm{ut}}}^{\rm{p}} \cdot {h_{\rm{e}}} (13) 式中：
f_{\rm{ut}}^{\rm{e}} 为UHPC受拉线性区域应力分布，f_{\rm{ut}}^{\rm{p}} 为UHPC应变硬化区域应力值，UHPC受拉区应力最大值f_{\rm{ut}}^{\rm{max}} ：f_{{\rm{ut}}}^{{\rm{max}}} = f_{{\rm{ut}}}^{\rm{p}} = {n_{\rm{e}}} \cdot \frac{{H - {\varphi _{\rm{c}}} - {h_{\rm{e}}}}}{{{\varphi _{\rm{c}}}}} \cdot f_{\rm{b}}^{{\rm{max}}} (14) II型应力分布成立的条件及UHPC受拉区力臂为：
0 < {h_{\rm{e}}} \leqslant H - h\quad\quad\quad (15) l_{{\rm{ut}}}^{\rm{e}} = \frac{2}{3} \cdot h_{{\rm{ut}}}^{\rm{e}}\quad\quad\quad\quad (16) l_{{\rm{ut}}}^{\rm{p}} = H - {\varphi _{\rm{c}}} - \frac{1}{2} \cdot {h_{\rm{e}}} (17) 当II型应力分布成立时，弯矩平衡方程表示为：
\begin{split} 2 \cdot M = &{\rm{ }}\left( {f_{\rm{b}}^{\max } + {f_{\rm{b}}^{\min }}} \right) \cdot {h_{\rm{b}}} \cdot b \cdot {l_{\rm{b}}} + f_{{\rm{uc}}}^{{\rm{max}}} \cdot {h_{{\rm{uc}}}} \cdot b \cdot {l_{{\rm{uc}}}} + \\ & f_{{\rm{ut}}}^{{\rm{max}}} \cdot h_{{\rm{ut}}}^{\rm{e}} \cdot b \cdot l_{{\rm{ut}}}^{\rm{e}} + {\rm{ 2}} \cdot f_{{\rm{ut}}}^{{\rm{max}}} \cdot {h_{\rm{e}}} \cdot b \cdot l_{{\rm{ut}}}^{\rm{p}} + \\& 2 \cdot n \cdot {A_{\rm{s}}} \cdot {f_{\rm{s}}} \cdot {l_{\rm{s}}} \\[-16pt] \end{split} (18) 对轴力平衡方程进行整理可以得出，在钢筋形式相同情况下，配筋对截面的影响与截面宽度有关。为便于计算，定义配筋作用系数：
{n_{\rm{s}}} = \frac{n}{b} \cdot {A_{\rm{s}}} (19) 使用ns进行分析时，相关公式中除钢筋应力分量外，其余应力分量不再包含参数b。联立方程组式(3)~式(18)并代入相关参数进行迭代计算，即可得到开裂状态下钢-UHPC截面实际应力分布。设计试验模型对理论进行验证，并综合文献[7]及文献[18]试验数据进行参数分析，验证理论分析方法的正确性。
2 方法的试验验证
2.1 试验模型设计
试验采用免蒸汽养护的UHPC材料，钢纤维体积含量为2.5%，其基本力学性能如表1所示。试验模型共设计2组4个试件：第一组为1个UHPC无配筋板，简称S-1试件和1个UHPC配筋板，简称S-2试件，用于探索配筋对UHPC板承载能力和延性的影响；第二组模型针对钢-UHPC组合板开裂荷载等相关问题进行研究，即2个纵筋保护层厚度不同的钢-UHPC配筋组合板S-3试件与S-4试件，对比分析纵筋保护层厚度对组合结构在纯弯曲荷载下力学性能的影响，进而对理论分析所提出的截面应力法进行验证。试件的基本尺寸如表2所示。
表 1 UHPC基本力学性能Table 1. Basic mechanical properties of UHPC抗压强度/MPa 抗折初裂强度/MPa 弹性模量/GPa 容重/(kg/m3) 119.7 9.6 44.6 2450 表 2 试验汇总表Table 2. Parameters of specimens试验模型 试件参数 试件尺寸/m 试件样本 UHPC板 无配筋 1.40×0.40×0.06 S-1 配筋 1.40×0.40×0.06 S-2 钢-UHPC组合板 配筋 1.40×0.40×0.07 S-3 配筋 1.40×0.40×0.07 S-4 在S-2试件中布置等级为HRB400的钢筋网，钢筋直径为10 mm，如图3(a)所示。钢-UHPC配筋组合钢板底板厚12 mm，材质为Q345，钢底板上布置直径16 mm、高度40 mm的剪力钉，间距为200 mm，如图3(b)所示。钢-UHPC配筋组合板试件配筋如图3(c)所示，布置等级为HRB400，钢筋直径为10mm的钢筋网，纵筋保护层厚度为35 mm的S-3试件纵筋置于横筋下方，纵筋保护层厚度为25 mm的S-4试件纵筋置于横筋上方。
试验加载装置示意图如图4所示，实物照片如图5所示，试验加载方式为四点弯曲加载。试验过程中实测了纯弯区域的顶点位移、UHPC受拉表面裂缝宽度及钢-UHPC组合板UHPC层与钢底板的层间滑移。采集器布置如图4所示，使用LVDT(Linear Variable Differential Transformer)直线位移传感器测量跨中位移Dis-M、两侧钢-UHPC层滑移量Dis-L与Dis-R，在UPHC受拉表面连续布置Pi位移传感器测量裂缝宽度，其精度为0.01 mm。试验荷载由MTS内置传感器通过位移控制加载方法给定，便于采集试件屈服强化阶段的跨中位移、裂缝宽度及滑移量。
2.2 主要试验结果
各试件的荷载-跨中位移曲线如图6所示，以下简称P-δ曲线。由图6可知，各试件的P-δ曲线表现出3个阶段：I弹性阶段、II裂缝发展阶段和III屈服阶段。图6(a)为S-1试件和S-2试件的P-δ历程，两组曲线具有相似的弹性阶段及裂缝发展阶段：S-1试件表现出线性的弹性阶段I，P-δ曲线首次出现转折后进入非线性的裂缝发展阶段II，出现第二次明显转折后进入短暂的屈服阶段III；而S-2试件表现出略微优异于S-1试件的线性弹性阶段I及非线性裂缝发展阶段II，在出现第二次转折后的屈服阶段III表现出近似线性的位移增长阶段。由图6(b)可知S-3试件和S-4试件的P-δ曲线同样历经了两次明显转折，表现为线性的弹性阶段I，非线性的裂缝发展阶段II和非线性波动的屈服阶段III。由于配筋UHPC具有良好的延性[7]，试件在达到极限承载力后仍具有持久的下降破坏阶段，图6仅列出P-δ到达极限承载力前的变化曲线。
![]()
图 6 负弯矩作用下荷载-跨中位移曲线Figure 6. Load-deflection curves at mid-span of specimens under negative bending test结合试验过程中的观察可以得出：S-1试件与S-2试件在弹性阶段时未出现可视裂缝；在裂缝发展阶段，纯弯段UHPC层顶面出现可视裂缝，UHPC水泥基逐渐退出工作，拉力由内部钢纤维承担，截面发生应力重分布后P-δ曲线仍然上升。对于UHPC板件，是否配筋导致P-δ的曲线在屈服阶段III表现出截然不同的历程。S-1试件在开裂后随着裂缝发展，钢纤维拉力超过其水泥基的握裹力后拔出，截面迅速破坏，P-δ曲线经历短暂的上升后即丧失承载能力，其延性较差。而对于S-2试件，裂缝发展阶段初期UHPC受拉区进入应变硬化阶段后不会立即退出工作，截面应力重分布使P-δ曲线呈现非线性增长，荷载进一步提高后UHPC拉断退出工作使钢筋单独承受拉力，在钢筋尚未达到屈服强度前，P-δ曲线在第三阶段呈现近似线性增长。
S-3试件与S-4试件的P-δ曲线初期表现出线性增长的弹性阶段I，与UHPC板类似；进入裂缝发展阶段后II，UHPC受拉区受到配筋约束，带裂缝工作能力较强，进入强化阶段的UHPC导致截面不断地发生应力重分配，呈现出较为稳定的非线性增长阶段；与配筋UHPC板不同，图6(b)表明钢-UHPC组合板在屈服后，纵筋的约束能够限制UHPC受拉层裂缝的进一步发展，UHPC受拉区不会立即退出工作，而不断出现局部UHPC拉断退出工作导致整个受拉区域持续发生应力重分布的动态平衡状态，这就是图6(b)表现出P-δ曲线的屈服阶段III为波动的非线性增长的原因。对比图6(a)和图6(b)可知，配筋钢-UHPC组合板具有更好的延性，极限承载力远高于UHPC板，S-1试件与S-2试件极限荷载为6.6 kN与14.3 kN，而S-3试件与S-4试件的极限荷载为58.6 kN与70.7 kN。
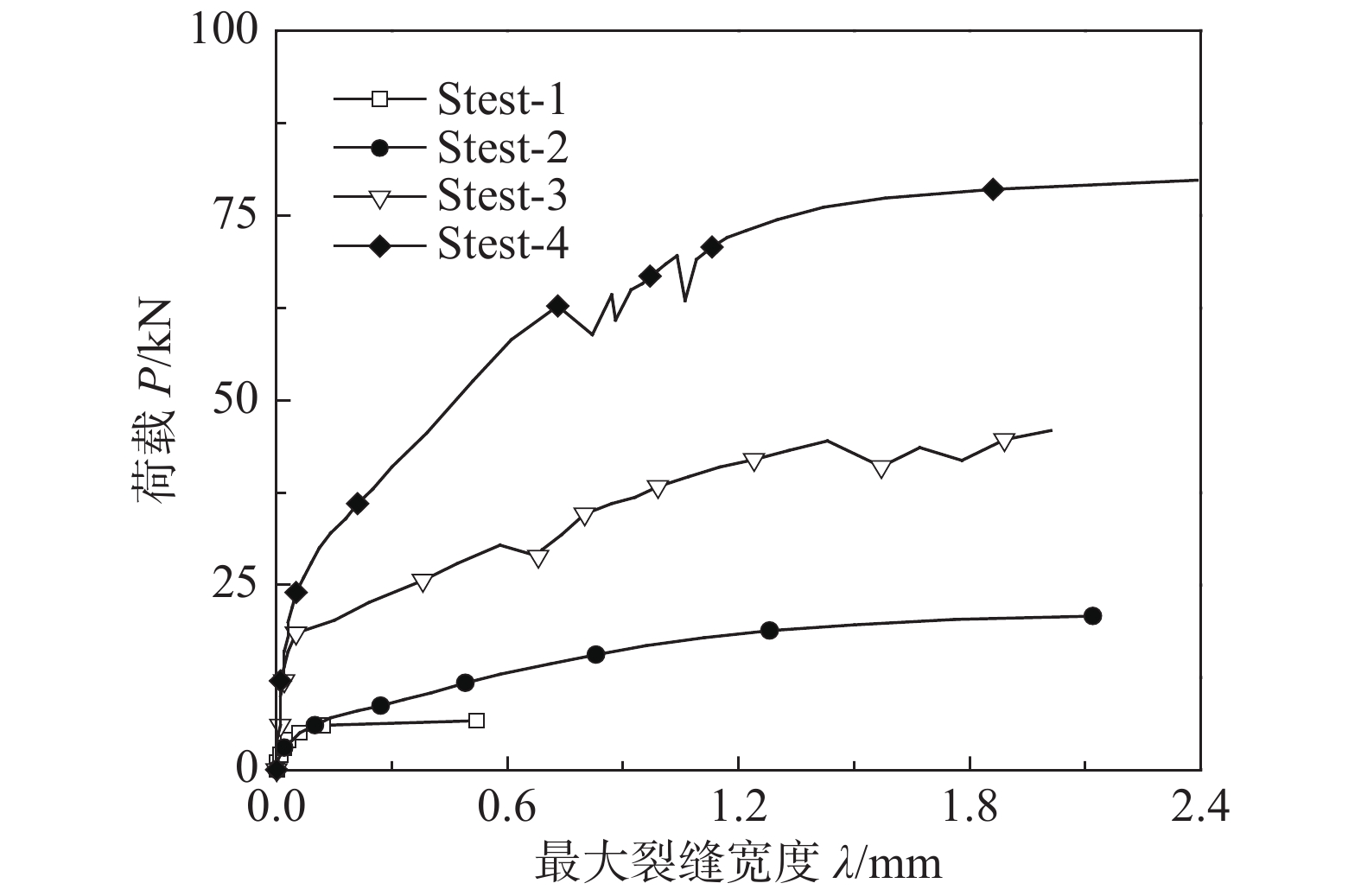
通过对试验过程的观察还可以得出，S-1试件及S-2试件在达到弹性极限后即能观察到肉眼可视裂缝，而S-3试件与S-4试件在达到线弹性极限后不会立即观测到肉眼可视裂缝，图7为各试件丧失承载力时的裂缝分布，图8给出了各试件的荷载-最大裂缝宽度P-λ曲线。
试验过程中UHPC板与组合板试件的裂缝萌生规律类似：加载过程中在弹性阶段结束后UHPC层受拉顶面最先观察到短小横向分布的可见裂缝，其宽度发展稳定且缓慢，P-λ曲线呈近似线性关系。S-1试件表面短小裂缝在裂缝发展阶段快速贯通形成1条主裂缝，其余短小裂缝自动愈合，屈服阶段主裂缝快速发展导致截面突然丧失承载能力，如图7(a)；S-2试件的P-λ曲线在裂缝发展阶段及屈服阶段均呈现出较为稳定的非线性增长关系，其表面短小裂缝在裂缝发展阶段随荷载增加逐渐发展，形成多条贯通裂缝，其中一条贯通裂缝进一步发展，在进入屈服时贯穿UHPC，如图7(b)，其余伴生贯通裂缝宽度基本保持不变。S-3试件及S-4试件的表面短小裂缝在发展阶段随着荷载的增加持续出现，其裂缝宽度在裂缝发展阶段中期仍能保持较低的发展速度，但在宽度约0.1 mm后增长加快，横向延伸贯通截面竖直向梁底发展，在纯弯区域形成6条~8条贯通裂缝，在屈服后出现一定的波动，裂缝发展贯穿截面形成若干条贯穿裂缝如图7(c)与图7(d)。
通过以上现象分析可以得出，配筋及组合效应能够有效限制UHPC层受拉裂缝的发展，提高试件承载能力，特别是配筋钢-UHPC组合板延性良好；纵筋保护层厚度对UHPC的开裂约束影响显著，由图8可知S-4试件的承载能力明显优于S-3试件，纵筋保护层厚度对试件力学性能影响明显，最大裂缝宽度达到约0.1 mm、0.15 mm及0.2 mm时S-4试件承载力较S-3试件分别提高了约49%，60%和63%。由此可见，充分发挥钢-UHPC组合构件受拉钢筋的工作效率，是提高其承载能力，延迟裂缝发展的有效途径，这对工程应用具有重要的理论指导意义。
2组试件的试验关键点数值汇总见表3，弹性极限指荷载-跨中位移关系偏离线性阶段的极值点；以出现肉眼可见裂缝作为开裂判别标准，对应荷载定义为试件的开裂荷载。
表 3 主要试验结果Table 3. Main test results试件
样本弹性极限 开裂
荷载/kN屈服
荷载/kN屈服层间
滑移/mm最大
位移/mm最大
荷载/kN层间
滑移/mmS-1 0.73 3.22 − 3.22 5.96 − S-2 0.67 4.07 − 4.07 7.76 − S-3 0.71 7.11 0/0 16.06 43.03 0.08/0.09 S-4 0.78 7.96 0/0 17.97 62.59 0.05/0.05 注：“a/b”表示LVDT采集的试件两端滑移分别为a和b。 试验同时得到了钢板与UHPC层之间的滑移量，表3分别列出弹性极限与屈服破坏时的实测滑移量。实时采集结果表明，组合试件至弹性极限前未发生滑移，为本文以开裂前状态建立的相关公式忽略钢-UPHC之间滑移提供了试验依据。
2.3 理论计算结果与试验的对比
文献[7]、文献[18]中采用将钢和UHPC两种材料组成的实际截面换算成拉压性能相同的假想材料组成的均质截面的换算截面法，进而采用材料力学公式进行中性轴位置及开裂强度的计算。使用换算截面法对本文试验及文献试验所得数据进行计算，其中文献[7]截面钢底板厚度为14 mm，UHPC层高度为39 mm，弹性模量为43.3 GPa，钢筋直径为10 mm，截面宽度为200 mm；文献[18]截面钢底板厚度为12 mm，UHPC层高度为50 mm，弹性模量为43.3 GPa，钢筋直径为10 mm，截面宽度为200 mm。换算截面法的开裂强度计算如表4。结果显示，截面配筋率、保护层厚度对计算开裂强度的影响规律与其对开裂荷载的影响规律一致[18]，文献[18]同时表明负弯矩计算开裂强度可提高至42.7 MPa。
表 4 换算截面法开裂强度计算Table 4. Calculation of cracking load based on transformed section method由表4可以得出，换算截面法将相关参数对截面工作性能的影响直接反映为计算开裂强度，其计算结果能够直观反映组合截面的工作性能。换算截面法将配筋率、保护层厚度等关键参数直观的反映为换算截面特性，这种计算方法的局限性表现为：1)钢底板及UHPC均采用线性本构关系，计算模型不能体现真实的开裂状态截面应力分布；2)难以反映UHPC受拉时的力学特性，不能体现其双折线抗拉本构关系；3)这种计算方法必然导致UHPC计算开裂强度随结构参数的改变而大幅度变化。显然，任何工程材料在相同受力模式下其开裂强度与其结构形式无关是学者们的普遍共识，而文献[7]结果显示采用换算截面法计算不同参数组合下的开裂强度差距可达1.77倍。
由表4可知，换算截面法计算所得S-4开裂强度较S-3相差3.61 MPa，而文献[18]试验样本计算结果开裂强度差距可达13.08 MPa。UHPC作为一种水泥基工程材料，在相同工作条件下不可能出现开裂强度差距如此之大的情况，这种计算结果与对UHPC材料的认知相悖，换算截面法仅能用于截面工作性能的初步判断。使用截面应力法进行计算，所得结果见表5。
由表5可知，试件开裂荷载计算值与实测值的比值在0.92~0.98，均值为0.95，采用截面应力法进行计算的开裂荷载与实测值吻合良好。截面应力法通过引入UHPC双折线本构模型，能够更为合理的描述截面应力分布，具有广泛的适用性。迭代计算结果显示钢-UHPC组合板抗弯开裂荷载与其截面参数联系紧密，截面的中性轴位置及UHPC的应变硬化区域变化能够显著影响截面的开裂荷载。
表 5 截面应力法开裂荷载分析Table 5. Calculation of cracking load based on section stress method3 开裂荷载关键影响因素
钢-UHPC组合板在纯弯曲荷载作用下的开裂荷载是其截面应力分布的宏观表现，其主要影响的相关参数为UHPC抗折强度、弹性模量、钢底板厚度、UHPC层厚度、组合板宽度、配筋率及受拉钢筋保护层厚度。试验结果与理论分析表明：UHPC受拉开裂强度仅取决于其自身的材料性能，不会因试件开裂荷载的提高而增大，配筋率与保护层厚度对UHPC受拉层的约束表现为肉眼可见裂缝出现时其应变硬化区域的高度变化。
利用截面应力法进行计算时，首先需要计算UHPC受拉层处于线弹性工作时的中性轴高度，将式(9)~式(12)代入式(7)，初始中性轴高度φ0表达式为：
{\varphi _0} = \frac{{h_{\rm{b}}^{\rm{2}} + 2{n_{\rm{s}}} \cdot \left( {H - c} \right) + {n_{\rm{e}}} \cdot ( {{H^2} - h_{\rm{b}}^{\rm{2}}} )}}{{2 \cdot {h_{\rm{b}}} \cdot \left( {1 - {n_{\rm{e}}}} \right) + 2 \cdot H \cdot {n_{\rm{e}}} + {n_{\rm{s}}}}} (20) 相关计算结果汇总如表6，降低保护层厚度或提高配筋作用系数均能调整中性轴高度。
将式(13)代入式(1)，即可得到截面应力法应力分布的平衡条件，将式(14)代入式(7)并展开，可以将应变硬化高度he表示为截面相关参数的函数表达式：
{h_{\rm{e}}} = \sqrt {{{\left\{ h_{\rm{b}}^{\rm{2}} + 2 \cdot \left( {H - {\varphi _{\rm{c}}} - c} \right) \cdot {n_{\rm{s}}} - 2 \cdot {\varphi _{\rm{c}}} \cdot {h_{\rm{b}}} - {n_{\rm{e}}} \cdot {({\varphi _{\rm{c}}} - {h_{\rm{b}}})^2} + {n_{\rm{e}}} \cdot {\left( {H - {\varphi _{\rm{c}}}} \right)^2} \right\}} / {2 \cdot {n_{\rm{e}}}}}} (21) 将相关数据代入，通过迭代计算可以得到开裂状态的实际中性轴高度φc及硬化高度，计算结果如表7。塑性化系数定义为UHPC受拉层进入应变硬化区域占整个受拉区域的比值，该项系数直接反应了UHPC受拉时进入塑性工作的能力，能够直观反映结构自身对UHPC受拉层的约束。迭代计算过程表明，组合板结构相关参数均会影响塑性化系数，而对于实际工程，如UHPC材料的选型、钢底板厚度与UHPC层厚度等参数的取值需与实际工程相结合，由表7可知，降低纵筋保护层厚度及提高配筋作用系数均能提高UHPC受拉硬化高度。
表 6 中性轴初始高度汇总Table 6. Initial neutral heights表 7 截面应力法参数汇总Table 7. Parameters of section-stress method配筋作用系数的主要影响因素为配筋率，而过高的配筋率会提高工程成本，且不利于施工。在相关规范容许范围内尽可能的降低纵筋保护层厚度，是增强塑性化系数，提高试件开裂荷载的有效手段。
4 结论
在换算截面法的基础上，引入UHPC双折线拉伸本构模型建立能够描述截面真实应力分布的截面应力法，通过2组4个试件进行负弯矩试验，并结合文献试验结果对截面应力法进行验证及参数分析，主要研究结论如下：
(1)通过引入UHPC双折线本构关系推导出了截面应力计算方法，其对试件开裂荷载的计算值与实测值的比值在0.92~0.98，均值为0.95，计算结果与试验值吻合良好，验证了方法的正确性；
(2)截面应力法能够较为准确的反映纯弯曲作用下钢-UHPC组合板截面开裂状态时的实际应力分布，UHPC开裂强度仅与其自身材料性能相关，而组合板的开裂荷载与其结构体系有关，UHPC开裂强度不会因组合板开裂荷载的提高而增大。
(3)组合效应及配筋对UHPC受拉区的约束表现为肉眼可视裂缝出现时UHPC层的应变硬化高度的变化，提高配筋率或降低保护层厚度均能提高该项指标；
(4)本文仅分析了钢-UHPC组合板在纯弯曲荷载作用下的力学行为，如何将其推广至复杂受力状态下的钢-UHPC组合桥面板体系是下一步工作的重点。
-
![]()
图 1 组合板应变分布示意图(拉为+，压为−)
Figure 1. Schematic drawing for theoretical analysis of strain (‘+’ tension, ‘−’ compression)
![]()
图 2 截面应力分布模式示意图(拉为+，压为−)
Figure 2. Schematic drawing for theoretical analysis of stress (‘+’ tension, ‘−’ compression)
![]()
图 6 负弯矩作用下荷载-跨中位移曲线
Figure 6. Load-deflection curves at mid-span of specimens under negative bending test
表 1 UHPC基本力学性能
Table 1 Basic mechanical properties of UHPC
抗压强度/MPa 抗折初裂强度/MPa 弹性模量/GPa 容重/(kg/m3) 119.7 9.6 44.6 2450 
下载: 导出CSV
表 2 试验汇总表
Table 2 Parameters of specimens
试验模型 试件参数 试件尺寸/m 试件样本 UHPC板 无配筋 1.40×0.40×0.06 S-1 配筋 1.40×0.40×0.06 S-2 钢-UHPC组合板 配筋 1.40×0.40×0.07 S-3 配筋 1.40×0.40×0.07 S-4
下载: 导出CSV
表 3 主要试验结果
Table 3 Main test results
试件
样本弹性极限 开裂
荷载/kN屈服
荷载/kN屈服层间
滑移/mm最大
位移/mm最大
荷载/kN层间
滑移/mmS-1 0.73 3.22 − 3.22 5.96 − S-2 0.67 4.07 − 4.07 7.76 − S-3 0.71 7.11 0/0 16.06 43.03 0.08/0.09 S-4 0.78 7.96 0/0 17.97 62.59 0.05/0.05 注：“a/b”表示LVDT采集的试件两端滑移分别为a和b。
下载: 导出CSV
-
[1] Sedran F. De Larrardt. Optimization of ultra-high-performance concrete by the use of a packing model [J]. Cement & Concrete Research, 1994, 24(6): 997 − 1009.
[2] 李召辉. 钢-UHPC轻型组合桥面板局部修补技术研究 [D]. 长沙: 湖南大学, 2016. Li Zhaohui. The study on partial repair technology of light-weighted composite bridge deck composed of steel and UHPC layer [D]. Changsha: Hunan University, 2016. (in Chinese)
[3] Graybeal B. Ultra-high performance concrete [J]. Technote, 2011, 19(10): 848 − 854.
[4] 刘君平, 徐帅, 陈宝春. 钢-UHPC组合梁与钢-普通混凝土组合梁抗弯性能对比试验研究[J]. 工程力学, 2018, 35(11): 92 − 98, 145. doi: 10.6052/j.issn.1000-4750.2017.06.0454 Liu Junping, Xu Shuai, Chen Baochun. Experimental study on flexural behaviors of steel-UHPC composite girder and steel-conventional concrete composite girder [J]. Engineering Mechanics, 2018, 35(11): 92 − 98, 145. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.06.0454
[5] 徐明雪, 梁兴文, 汪萍, 等. 超高性能混凝土梁正截面受弯承载力理论研究[J]. 工程力学, 2019, 36(8): 70 − 78. Xu Mingxue, Liang Xingwen, Wang Ping, et al. Theoretical investigation on normal section flexural capacity of UHPC beams [J]. Engineering Mechanics, 2019, 36(8): 70 − 78. (in Chinese)
[6] 梁兴文, 汪萍, 徐明雪, 等. 配筋超高性能混凝土梁受弯性能及承载力研究[J]. 工程力学, 2019, 36(5): 110 − 119. Liang Xingwen, Wang Ping, Xu Mingxue, et al. Investigation on flexural capacity of reinforced ultra high performance concrete beams [J]. Engineering Mechanics, 2019, 36(5): 110 − 119. (in Chinese)
[7] 邵旭东, 胡建华. 钢-超高性能混凝土轻型组合桥梁结构 [M]. 北京: 人民交通出版社, 2015. Shao Xudong, Hu Jianhua. The steel-UHPC lightweight comomposite bridge structures [M]. Beijing; China Communications Press, 2015. (in chinese)
[8] Sevil T , Baran M , Bilir T, et al. Use of steel fiber reinforced mortar for seismic strengthening [J]. Construction & Building Materials, 2011, 25(2): 892 − 899.
[9] 小野秀一, 平林泰明, 下里哲弘. 既設鋼床版の疲労性状と鋼繊維補強コンクリート敷設工法による疲労強度改善効果に関する研究[J]. 土木学会論文集A, 2009, 65(2): 335 − 347. Shuichi Ono, Yasuaki Hirabayashi, Tetsuhiro Shimozato, et al. Fatigue properties and retrofitting of existing orthotropic steel bridge decks[J]. Japan Society of Civil Engineering Symposium A, 2009, 65(2): 335 − 347. (in Japanese)
[10] 丁楠, 邵旭东. 轻型组合桥面板的疲劳性能研究[J]. 土木工程学报, 2015, 48(1): 74 − 81. Ding Nan, Shao Xudong. Study on fatigue performance of light-weighted composite bridge deck [J]. China Civil Engineering Journal, 2015, 48(1): 74 − 81. (in Chinese)
[11] 张清华, 张鹏, 刘益铭, 等. 新型大纵肋正交异性组合桥面板力学性能研究[J]. 桥梁建设, 2017, 47(3): 30 − 35. doi: 10.3969/j.issn.1003-4722.2017.03.006 Zhang Qinghua, Zhang Peng, Liu Yiming, et al. Study of mechanical behavior of new type of orthotropic composite bride deck with lame longitudinal U ribs [J]. Bridge Construction, 2017, 47(3): 30 − 35. (in Chinese) doi: 10.3969/j.issn.1003-4722.2017.03.006
[12] 张清华, 刘益铭, 卜一之, 等. 大纵肋正交异性组合桥面板疲劳性能研究[J]. 中国公路学报, 2017, 30(3): 226 − 235. doi: 10.3969/j.issn.1001-7372.2017.03.025 Zhang Qinghua, Liu Yiming, Bu Yizhi, et al. Study on fatigue performance of orthotropic composite bridge deck with large longitudinal ribs [J]. China Journal of Highway and Transport, 2017, 30(3): 226 − 235. (in Chinese) doi: 10.3969/j.issn.1001-7372.2017.03.025
[13] 黄细军. 超高性能混合梁钢-混结合段受力性能有限元分析 [D]. 长沙: 湖南大学, 2016. Huang Xijun, Multiscale finite element analysis of mechanical behavior of Steel-concrete joint section of ultra-high performance hybrid girder [D]. Changsha: Hunan University, 2016. (in Chinese)
[14] Hor Yin, Wee Teo, Kazutaka Shirai. Experimental investigation on the behavior of reinforced concrete slabs strengthened with ultra-high performance concrete [J]. Construction and Building Materials, 2017, 155: 463 − 474. doi: 10.1016/j.conbuildmat.2017.08.077
[15] 邵旭东, 方恒, 李文光. 钢-超薄UHPC组合桥面板界面抗剪性能研究[J]. 湖南大学学报(自然科学版), 2016, 43(5): 44 − 51. Shao Xudong, Fang Heng, Li Wenguang. Research on the interfacial shear resistant performance of the composite deck system composed of orthotropic deck and ultra-thin UHPC layer [J]. Journal of Hunan University (Natural Sciences), 2016, 43(5): 44 − 51. (in Chinese)
[16] 张哲. 钢-配筋UHPC组合桥面结构弯曲受拉性能研究 [D]. 长沙: 湖南大学, 2016. Zhang Zhe. Bending behaviors of composite bridge deck system composed of OSD and reinforced UHPC layer [D]. Changsha: Hunan University, 2016. (in Chinese)
[17] Rafiee A. Computer modeling and investigation on the steel corrosion in cracked ultra high performance concrete [D]. Kassel: University of Kassel, 2012.
[18] 李文光, 邵旭东, 方恒, 等. 钢-UHPC组合板受弯性能的试验研究[J]. 土木工程学报, 2015, 48(11): 93 − 102. Li Wenguang, Shao Xudong, Fang Heng, et al. Experimental study on flexural behavior of steel-UHPC composite slabs [J]. China Civil Engineering Journal, 2015, 48(11): 93 − 102. (in Chinese)
[19] Lappa E S. High strength fiber reinforced concrete: static and fatigue behaviour in bending [M]. Netherlands: Gildeprint, 2007.
[20] Jun Luo, Xudong Shao, Wei Fan, et al. Flexural cracking behavior and crack width predictions of composite (steel+UHPC) lightweight deck system [J]. Engineering Structures, 2019, 194: 120 − 137. doi: 10.1016/j.engstruct.2019.05.018
[21] Jun Luo, Xudong Shao, Junhui Cao, et al. Transverse bending behavior of the steel-UHPC lightweight composite deck: Orthogonal test and analysis [J]. Journal of Constructional Steel Research, 2019, 162: 105708. doi: 10.1016/j.jcsr.2019.105708
[22] 邵旭东, 罗军, 曹君辉, 等. 钢-UHPC轻型组合桥面结构试验及裂缝宽度计算研究[J]. 土木工程学报. 2019, 52(3): 61 − 75. Shao Xudong, Luo Jun, Cao Junhui, et al. Experimental study and crack width calculation of steel-UHPC lightweight composite deck structure [J]. 2019, 52(3): 61 − 75. (in Chinese)
计量
- 文章访问数: 660
- HTML全文浏览量: 159
- PDF下载量: 83
