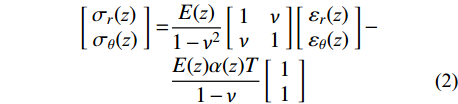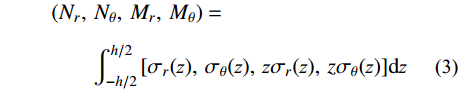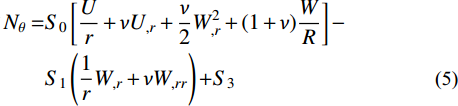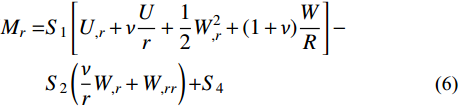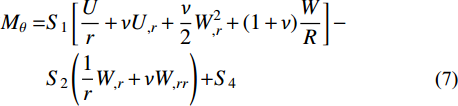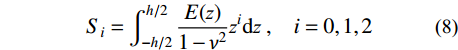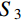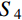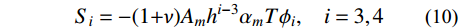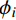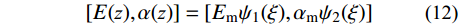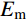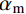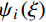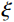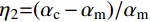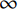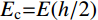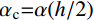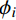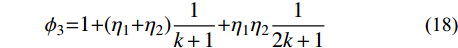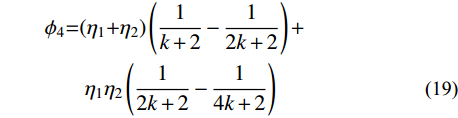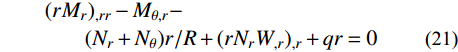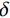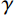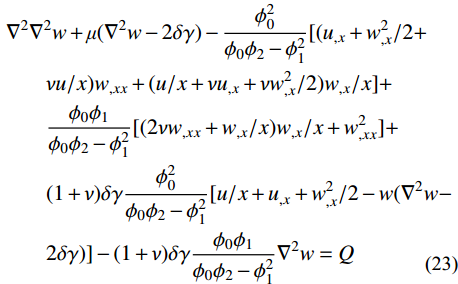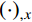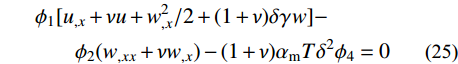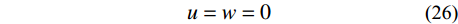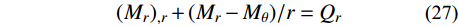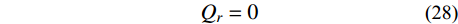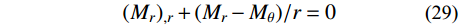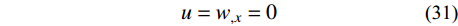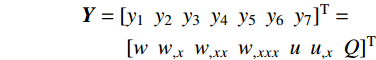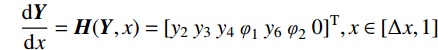NONLINEAR STABILITY ANALYSIS OF FUNCTIONALLY GRADED SHALLOW SPHERICAL SHELLS IN THERMAL ENVIRONMENTS
-
摘要: 基于经典壳理论和von Karman几何非线性理论,导出了功能梯度圆底扁球壳的位移型几何非线性控制方程及简支边界条件,推导过程考虑了均匀变温场及均布外侧压力。用打靶法计算了由控制方程和边界条件提出的两点边值问题,得到了壳体轴对称变形的数值结果。考察了壳体几何参数、材料横向梯度特性、组份材料体积分数指数和弹性模量以及均匀变温场对壳体屈曲平衡路径、上/下临界荷载和平衡构形的影响。数值结果表明:随组分材料体积分数指数的增加和弹性模量的减小,壳体上临界荷载均会显著减小;体积分数指数对壳体下临界荷载影响规律较复杂;均匀升温使壳体上/下临界荷载显著增加/减小。材料横向梯度特性对简支边功能梯度圆底扁球壳屈曲平衡路径和后屈曲稳态构形有显著影响。该文末给出了便于工程设计的两个数表和一些数值曲线。Abstract: Based on the classical shell theory and von Karman geometric nonlinear theory, the displacement-type geometric nonlinear governing equations and simply supported boundary conditions for functionally graded shallow circular spherical shells were derived. The uniform temperature field and the external uniform pressure were considered in the derivation. The two-point boundary value problem posed by this set of governing equations and the boundary conditions was solved with the shooting method. The numerical results of axisymmetric deformation of the shells were obtained. The effects of the geometric parameters of the shell, the transverse gradient properties of the shell’s materials, the volume fraction index and elasticity modulus of the constituent materials, and uniform temperature field on the buckling equilibrium paths, upper/lower critical loads and equilibrium configurations of the shell were investigated. The numerical results show that the upper critical load of the shells decreases significantly with the increase of the volume fraction index and the decrease of the elasticity modulus of the constituent materials. The effects of the volume fraction index on the lower critical load of the shells is complicated. The rise of the uniform temperature brings obvious increase/decrease of the upper/lower critical loads of the shells. The transverse gradient properties of the shell’s materials on the effects of the buckling equilibrium paths and post buckling stable configurations of functionally graded shallow circular spherical shells with simply supported edges are very significant. Two numerical tables and some numerical curves are given for the convenience of designers.
-
薄壁弹性扁球壳结构在核反应、石油工业、舰船、航空航天、精密仪器等领域有着广泛的应用。为使此类结构能够可靠的服役,需要对其屈曲行为进行精确分析。早在20世纪30年代,von Karman等[1]首次用非线性分析方法分析了扁球壳的屈曲行为。在此之后,用非线性分析方法分析薄壳的屈曲行为吸引了诸多学者的注意。Huang[2]研究了均质扁球壳在外压力作用下的非对称屈曲问题,并指出非对称变形可能是轴对称屈曲理论与试验临界压力不一致的原因。叶开源等[3]提出了修正迭代法,并用该方法成功地研究了均质扁球壳的非线性稳定问题。Uemura[4]采用两项挠度近似法处理了均布外压作用的周边夹紧带缺陷均质材料扁球壳的轴对称屈曲问题,并利用总势能的二次变分评估了球壳矢高对解的非唯一性的影响。Yan[5]采用分步加载法研究了均布外压作用下变厚度开顶扁球壳的非线性稳定性。Nie[6]提出了一种渐近迭代法,并用该方法分析了外侧压力作用的均匀材料扁球壳的非线性屈曲问题,分析过程考虑了缺陷、边界弹性约束和弹性地基的影响。Shahsiah等[7]运用解析方法,考虑热-机荷载联合作用,研究了均质扁球壳线性屈曲行为,并考察了缺陷对解的的影响。Li等[8]基于一阶剪切变形壳理论,运用修正迭代法研究了均匀外压下均质扁薄球壳的屈曲行为。考虑横向剪切变形效应,Zhu等[9]考察了对称层合圆柱正交各向异性扁球壳的热屈曲行为。Xu等[10]采用修正迭代法研究了双层网状圆形扁球壳在均布外压作用下的屈曲行为。运用有限元方法,张平等[11]对用于高速战斗机自适应进气道的均质扁球壳的双稳态特性进行了讨论。李忱等[12]针对均布外压与温度耦合作用的均质薄球壳的屈曲行为开展了研究。赵伟东等[13]基于数值打靶法分析了热环境中的周边简支均质扁球壳在外侧均布压力作用下的稳定性问题。
自从功能梯度材料[14]问世以来,对功能梯度材料板壳结构力学行为的研究吸引了很多研究人员的关注。Woo等[15]给出了在压力和温度场作用下的功能梯度材料板和浅圆柱壳的后屈曲行为的解析解。并指出热-机耦合效应和边界条件对功能梯度板/壳在边缘压力作用下的响应中起着重要作用。Shahsiah等[16]基于Sanders应力-应变关系和变分法研究了功能梯度扁球壳的热弹性失稳。Prakash等[17]和Ganapathi[18]基于一阶剪切变形理论,用有限元方法研究了固支边功能梯度扁球壳的非线性轴对称动力稳定性问题。Bich等[19]利用经典壳理论研究了功能梯度扁球壳在均匀外压(包括温度效应)作用下的非线性轴对称响应,研究过程考虑了球壳缺陷对其响应的影响。Boroujerdy等[20-21]研究了压电-功能梯度扁球壳的非线性轴对称热-机械响应和热屈曲。Mao等[22]考察了功能梯度扁球壳在低速冲击下的非线性动力响应和损伤行为。Fu等[23]对功能梯度扁球壳在随时间变化的热机械荷载作用下的非线性瞬态响应进行了分析。
用有限单元法分析功能梯度材料板壳结构,为了能够反映组分材料特性,通常需要沿厚度方向划分单元,这使求解过程变得复杂。另外,要想用有限单元法得到壳体屈曲过程的完整的荷载-挠度曲线,其计算工作量非常繁重。邵玉龙等[24]的工作表明:用二阶一致无网格法对功能梯度材料进行数值分析,有较高的计算效率。张鹏飞等[25]用有限质点法分析了薄壳屈曲问题,该方法有望成为分析复杂边界功能梯度扁球壳屈曲完整过程的有效数值方法。考虑到工程中较为常见的周边固支或简支功能梯度圆底扁球壳是轴对称结构,若荷载和温度场也是轴对称的(事实上这种情况较常见,如外侧均布压力和沿厚度均匀或一维热传导温度场),在这种情况下,对于满足一定几何条件的扁球壳,其弯曲乃至屈曲变形经常是轴对称的。基于此,如果利用球壳中曲面的横向和径向位移函数建立数学模型,则扁球壳轴对称弯曲/屈曲控制方程和边界条件为典型的常微分方程两点边值问题。赵伟东等[26]曾经运用变分原理推导了均匀温度场中的不可移夹紧边功能梯度圆底扁球壳在外侧均布压力作用下的轴对称弯曲/屈曲几何非线性常微分控制方程及其边界条件,并借助打靶法得到了一些对工程设计有帮助的数值结果。根据对文献的调阅可以发现,到目前为止,可以用来参考的简支边功能梯度圆底扁球壳弯曲/屈曲的研究数据还比较稀缺。因此,本文在文献[26]工作的基础上,基于经典壳理论和von Karman几何非线性理论,借用球壳平衡微分方程,导出了均匀外压与均匀温度场联合作用下的功能梯度圆底扁球壳轴对称变形的位移型几何非线性控制方程,推导了功能梯度圆底扁球壳位移型简支边界条件。借用数值打靶法求解了该两点边值问题,分析了简支边功能梯度圆底扁球壳的几何非线性力学行为。考虑到工程界更关注扁球壳的承载力(即上临界载荷),文中提供了此类结构承载力的两个数表和一些有益的数值曲线,供设计人员参考。
1 问题的基本方程
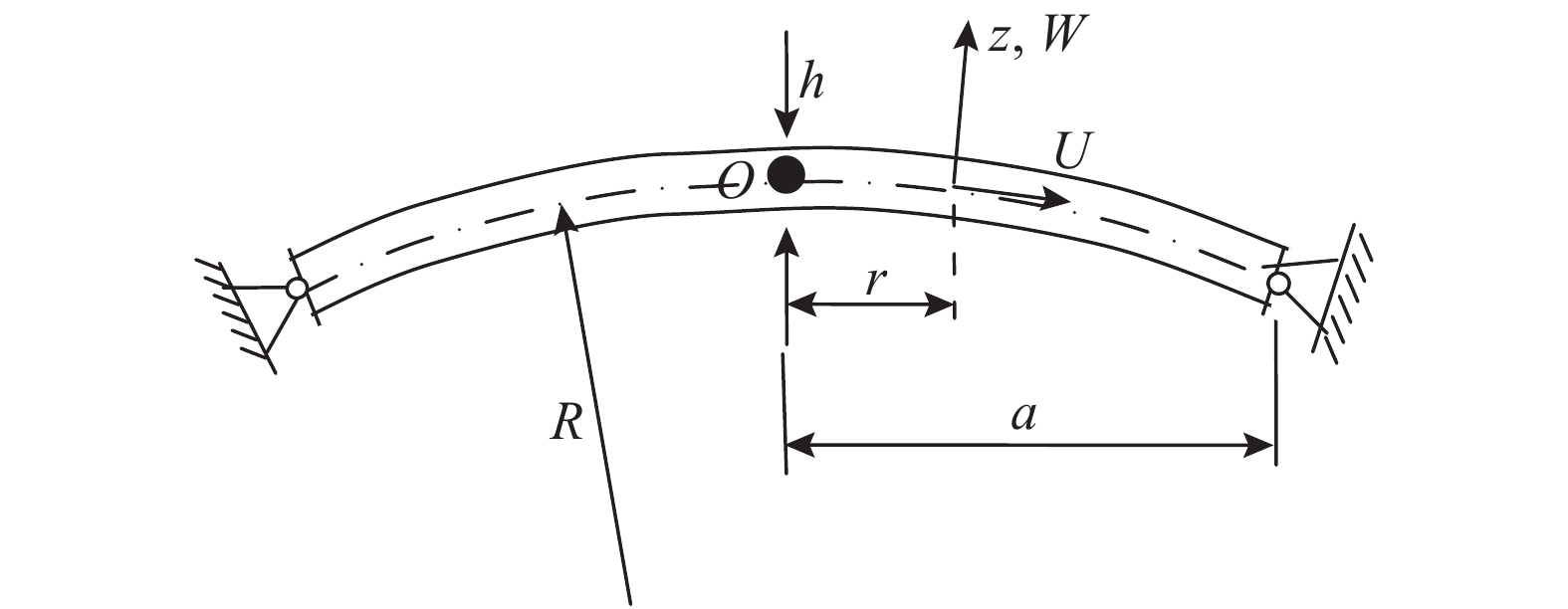
如图1所示简支边功能梯度圆底扁球壳,假设其材料性质沿厚度方向连续变化。其中曲面曲率半径、壳体厚度和底圆半径分别为R、h和a。球坐标系(φ,θ,z)分别为子午、圆周和厚度坐标,z(−h/2≤z≤h/2)坐标轴正向与球壳中曲面的外法线方向相同,坐标原点位于中曲面的中心。
1.1 几何方程
对于扁球壳,考虑球壳底圆径向坐标r(r=Rsinφ)及近似关系dr=Rdφ(cosφ≈1)会给方程的推导和求解带来方便。在轴对称变形和基于上述坐标系的情况下,扁球壳中曲面上任意点A(φ,θ,0)的横向和径向位移W和U仅是半径r的一元函数。根据经典壳理论与von Karman几何非线性理论,壳体上任意点A(φ,θ,z)处的应变分量与壳体中曲面位移分量和横向坐标z的关系为[20]:
[εr(z)εθ(z)]=(U,r+W/R+W2,r/2−zW,rrU/r+W/R−zW,r/r) (1) 式中,
(⋅),r 表示(⋅) 对r的一阶导数。1.2 物理方程
计及温度应力的球壳线弹性应力-应变关系为:
[σr(z)σθ(z)]=E(z)1−ν2[1νν1][εr(z)εθ(z)]−E(z)α(z)T1−ν[11] (2) 式中:T为球壳相对初始无应力状态的均匀变温场;弹性模量E、热膨胀系数α和泊松比ν为坐标z的连续函数。通常功能梯度板的泊松比变化不大,本文将其假设为常数。
球壳的内力分量与应力分量及横向坐标的关系为:
(Nr,Nθ,Mr,Mθ)=∫h/2−h/2[σr(z),σθ(z),zσr(z),zσθ(z)]dz (3) 式中:Nr和Nθ分别指壳体径向和环向截面内单位宽度上的薄膜力;Mr和Mθ分别指壳体径向和环向截面内单位宽度上的弯矩。将式(1)代入式(2),再将式(2)代入式(3),沿厚度方向积分可得用位移表示的壳体薄膜力和弯矩表达式:
Nr=S0[U,r+νUr+12W2,r+(1+ν)WR]−S1(νrW,r+W,rr)+S3 (4) Nθ=S0[Ur+νU,r+ν2W2,r+(1+ν)WR]−S1(1rW,r+νW,rr)+S3 (5) Mr=S1[U,r+νUr+12W2,r+(1+ν)WR]−S2(νrW,r+W,rr)+S4 (6) Mθ=S1[Ur+νU,r+ν2W2,r+(1+ν)WR]−S2(1rW,r+νW,rr)+S4 (7) 其中,刚度系数定义分别为:
Si=∫h/2−h/2E(z)1−ν2zidz,i=0,1,2 (8) 上述刚度系数可分别表示为:
Si=Amhiϕi,i=0,1,2 (9) 式(4)~式(7)中的热薄膜力
S3 和热弯矩S4 可分别表示为:Si=−(1+ν)Amhi−3αmTϕi,i=3,4 (10) 其中:
Am=Emh/(1−ν2) (11) 式中:Am为参考均匀金属球壳的拉伸刚度;
ϕi 为无量纲系数。球壳的弹性模量及热膨胀系数可表示为:
[E(z),α(z)]=[Emψ1(ξ),αmψ2(ξ)] (12) 式中:
ξ=z/h ;Em 、αm 分别为参考均匀金属球壳的弹性模量及热膨胀系数;ψi(ξ) 为坐标ξ 的连续函数。于是可给出无量纲系数ϕi 的计算公式:ϕi={∫1/2−1/2ψ1(ξ)ξidξ,i=0,1,2∫1/2−1/2ψ1(ξ)ψ2(ξ)ξi−3dξ,i=3,4 (13) 考虑材料性质在横向按幂率函数变化(需要指出,如果材料性质按其他函数形式变化,只要函数仅是厚度坐标z或ξ的一元函数,在轴对称热机荷载的情况下,本文的求解方法依然适用),则函数ψi (ξ)可表示为[27]:
ψi(ξ)=1+ηi(0.5+ξ)k,i=1,2 (14) 式中:
η1=(Ec−Em)/Em ;η2=(αc−αm)/αm ;0⩽ \infty ;{E_{\rm{c}}}{\rm{ = }}E(h/2) ;{\alpha _{\rm{c}}}{\rm{ = }}\alpha (h/2) 。将式(14)代入式(13),可得无量纲系数
{\phi _i} 的解析表达式如下:{\phi _0}{\rm{ = }}1{\rm{ + }}\frac{{{\eta _1}}}{{k + 1}} (15) {\phi _1}{\rm{ = }}{\eta _1}\left( {\frac{1}{{k + 2}} - \frac{1}{{2k + 2}}} \right) (16) {\phi _2}{\rm{ = }}\frac{1}{{12}}{\rm{ + }}{\eta _1}\left( {\frac{1}{{k + 3}} - \frac{1}{{k + 2}}{\rm{ + }}\frac{1}{{4k + 4}}} \right) (17) {\phi _3}{\rm{ = }}1{\rm{ + }}({\eta _1}{\rm{ + }}{\eta _2})\frac{1}{{k + 1}}{\rm{ + }}{\eta _1}{\eta _2}\frac{1}{{2k + 1}} (18) \begin{split}& {\phi _4}{\rm{ = }}({\eta _1}{\rm{ + }}{\eta _2})\left( {\frac{1}{{k + 2}} - \frac{1}{{2k + 2}}} \right){\rm{ + }}\\&\qquad{\eta _1}{\eta _2}\left( {\frac{1}{{2k + 2}} - \frac{1}{{4k + 2}}} \right) \end{split} (19) 1.3 平衡方程
在轴对称的情况下,壳体平衡微分方程可以由文献[20]给出的相应方程退化为如下形式:
{(r{N_r})_{,r}} - {N_\theta } = 0 (20) \begin{split} & {(r{M_r})_{,rr}} - {M_{\theta ,r}} -\\&\qquad ({N_r} + {N_\theta })r/R + {(r{N_r}{W_{,r}})_{,r}} + qr = 0 \end{split} (21) 式中,q为横向均匀分布荷载,沿z坐标轴方向为正。
2 两点边值问题
2.1 位移型控制方程
为便于讨论,采用如下无量纲变换:
\begin{split} & x = r/a,\;\;w = W/h,\;\;u = Ua/{h^2},\;\;\delta = a/h,\;\\ &\gamma = a/R,\;\;\mu = (1 + \nu ){\alpha _m}T{\delta ^2}{\phi _0}{\phi _3}{\rm{/}}({\phi _0}{\phi _2}{\rm{ - }}\phi _1^2),\\& Q = (1 - {\nu ^2})q{\delta ^4}{\phi _0}{\rm{/}}[{E_{\rm{m}}}({\phi _0}{\phi _2} - \phi _{1}^2)] \end{split}\,\, (22) 式中:x为无量纲的径向坐标;w和u分别为球壳中曲面无量纲的横向和径向位移;
\delta 为球壳底圆半径a与球壳厚度h的比;\gamma 为球壳底圆半径a与球壳中曲面曲率半径R的比;µ为球壳相对初始无应力状态的无量纲均匀变温场;Q为无量纲的法向均匀分布力集度。将式(9)~式(11)代入式(4)~式(7),再将结果代入式(20)~式(21),考虑无量纲变换式(22),得到一组无量纲形式的位移型几何非线性常微分控制方程:
\begin{split} &{\nabla ^2}{\nabla ^2}w + \mu ({\nabla ^2}w - 2\delta \gamma ) - \frac{{\phi_0^2}}{{{\phi_0}{\phi_2} - \phi_1^2}}[({u_{,x}} + w_{,x}^2/2 + \\&\qquad \nu u/x){w_{,xx}} + (u/x + \nu {u_{,x}} + \nu w_{,x}^2/2){w_{,x}}/x] + \\&\qquad \frac{{{\phi_0}{\phi_1}}}{{{\phi_0}{\phi_2} - \phi_1^2}}[(2\nu {w_{,xx}} + {w_{,x}}/x){w_{,x}}/x + w_{,xx}^2] + \\&\qquad (1 + \nu )\delta \gamma \frac{{\phi_0^2}}{{{\phi_0}{\phi_2} - \phi_1^2}}[u/x + {u_{,x}} + w_{,x}^2/2 - w({\nabla ^2}w - \\&\qquad 2\delta \gamma )] - (1 + \nu )\delta \gamma \frac{{{\phi_0}{\phi_1}}}{{{\phi_0}{\phi_2} - \phi_1^2}}{\nabla ^2}w = Q \\[-15pt]\end{split} (23) \begin{split}& {u_{,xx}} + {u_{,x}}{\rm{/}}x - u/{x^2} + {w_{,x}}{w_{,xx}} + (1 - \nu )w_{,x}^2/(2x) + \\&\qquad (1 + \nu )\delta \gamma \,{w_{,x}} - {\phi_1}/{\phi_0}{({\nabla ^2}w)_{,x}} = 0 \end{split} (24) 式中,
{\nabla ^2}( \cdot ) = {( \cdot )_{,x}}/x + {( \cdot )_{,xx}} ,{( \cdot )_{,x}} 为( \cdot ) 对x的一阶导数。2.2 位移型简支边界条件
在简单支撑边界面上,弯矩Mr为0。将Si(i=1,2,4)代入式(6),考虑无量纲变换式(22),得到x=1处的一个位移型边界条件如下:
\begin{split} &{\phi _1}[{u_{,x}} + \nu u + w_{,x}^2/2 + (1 + \nu )\delta \gamma {\mkern 1mu} w] -\\ & \qquad{\phi _2}({w_{,xx}} + \nu {w_{,x}}) - (1 + \nu ){\alpha _{\rm{m}}}T{\delta ^2}{\phi _4} = 0 \end{split} (25) 易知,在x=1处还有两个位移型边界条件如下:
u = w = 0 (26) 扁球壳在轴对称变形情况下有如下平衡微分方程:
{({M_r})_{,r}} + ({M_r} - {M_\theta })/r = {Q_r} (27) 式中,Qr为壳体单位宽度径向截面上的剪力。
在均布法向荷载作用下,据内力对称特性,在r=0处有:
{Q_r} = 0 (28) 联立式(27)~式(28),在r=0处有:
{({M_r})_{,r}} + ({M_r} - {M_\theta })/r = {\rm{0}} (29) 将式(6)~式(7)代入式(29),并考虑Si(i=1,2,4)的结果及无量纲变换式(22),得到在x=0处的一个位移型中心对称条件如下:
{w_{,xxx}} + {w_{,xx}}{\rm{/}}x - {w_{,x}}/{x^2} = 0 (30) 易知,在x=0处还有两个位移型中心对称条件如下:
u = {w_{,x}} = 0 (31) 3 打靶法求解说明
式(23)~式(24)、边界条件式(25)~式(26)及中心对称条件式(30)~式(31)为热环境中的简支边功能梯度圆底扁球壳在沿球面法向均布荷载作用下的轴对称弯曲变形的常微分控制方程及其边界条件,属于典型的位移型两点边值问题。可用打靶法容易地获得该两点边值问题的足够精确的数值解。
对上述两点边值问题用打靶法求解时,可设:
\begin{array}{l} {{Y}} = {[{y_1}\;\;{y_2}\;\;{y_3}\;\;{y_4}\;\;{y_5}\;\;{y_6}\;\;{y_7}]^{\rm{T}}} = \\ \qquad \;{[w\;\;{w_{,x}}\;\;{w_{,xx}}\;\;{w_{,xxx}}\;\;u\;\;{u_{,x}}\;\;Q]^{\rm{T}}} \end{array} 式(23)、式(24)及式(30)在x=0处存在奇异性,为使数值解收敛,需要将解域定义在区间[Δx ,1]上,其中,Δx为能够满足解的精度要求的足够小的正数。则原来的两点边值问题转化为如下初值问题:
\frac{{{\rm d}{{Y}}}}{{{\rm d}x}} = {{H}}({{Y}},x) = {[{y_2}\;{y_3}\;{y_4}\;{\varphi _1}\;{y_6}\;{\varphi _2}\;0]^{\rm{T}}},x \in [\Delta x,1] 式中,φ1和φ2分别由式(23)和式(24)得到。因为位移函数在x=0处连续可导,当Δx足够小时,可以用Δx处的值代替x=0处的边界条件:
{{Y}}(\Delta x) = {[\zeta \;\;0\;\;{V_1}\;\; - {V_1}/x\;\;0\;\;{V_2}\;\;{V_3}]^{\rm{T}}} 式中:ζ为x=Δx处的挠度初值(赋值);V1、V2和V3为待定参数,需要通过x=1处的边界条件确定。
4 数值结果分析
由于第1节定义的横向挠度函数W(r)及均布荷载q均以凸面侧外法线方向一致为正,而本文重点考察扁球壳在凸面侧压力作用下的屈曲行为,在这种情况下,挠度W(r)及荷载q的数值结果均为负值。为了方便描述和容易理解,下文给出的横向挠度W(r)和荷载集度q在数值计算时添加了负号(也即向球壳内凹的一侧为正)。
4.1 简化模型数值结果对比
由于功能梯度简支边圆底扁球壳屈曲数值解很难找到。考虑到当k=0或趋于+∞时,功能梯度材料扁球壳分别退化为弹性模量为Ec或Em的均匀材料扁球壳。需要指出的是,当k趋于+∞时,与Ec=Em,αc=αm及取任意的k是等效的。现在考虑泊松比ν=0.3、E=Ec=Em=70 GPa的均质扁球壳,取球壳中曲面曲率半径R=1600 mm、底圆半径a=160 mm和厚度h=5 mm,表1给出了该均质扁球壳在多个外侧压力集度q作用下的球壳中心有量纲挠度W(0)的打靶法解和有限元解(表中加粗的数据为壳体上临界荷载qu)。可以看出,当扁球壳接近临界失稳状态时,打靶法解与有限元解有一定程度偏离,其余情况下,两者一致性较好。需要指出的是,对于均匀材料扁球壳,用打靶法得到的球壳上临界荷载(指球壳S形荷载-挠度曲线上极大值点对应的荷载。当外侧压力从零逐渐增加并达到该值时,球壳的平衡形态会由整体外凸形态突然改变为整体或局部内凹形态,该过程是以“跳跃”的形式实现的,并伴随明显的声音信号)与三次样条函数法得到的相应解一致性很好(见文献[28])。据此可以判断,用打靶法求解扁球壳屈曲问题,解的精度是可以保证的。
表 1 均质扁球壳在外侧均布压力q作用下的中心挠度W(0)Table 1. Uniform external pressure q & central deflection W(0) for an homogeneous shallow spherical shell外侧均布压力q/MPa R=1600 mm, a=160 mm, h=5 mm, ν=0.3, E=70 GPa 中心挠度W(0)/mm 有限元解 打靶法解 0.011968 0.0499 0.0500 0.109892 0.4982 0.5000 0.360569 2.4720 2.5000 0.399206 3.3900 3.5000 0.403717(qu) 3.6541 4.0100 0.557400 17.5540 17.5000 0.754463 18.0586 18.0000 0.980981 18.5600 18.5000 4.2 功能梯度扁球壳屈曲平衡路径
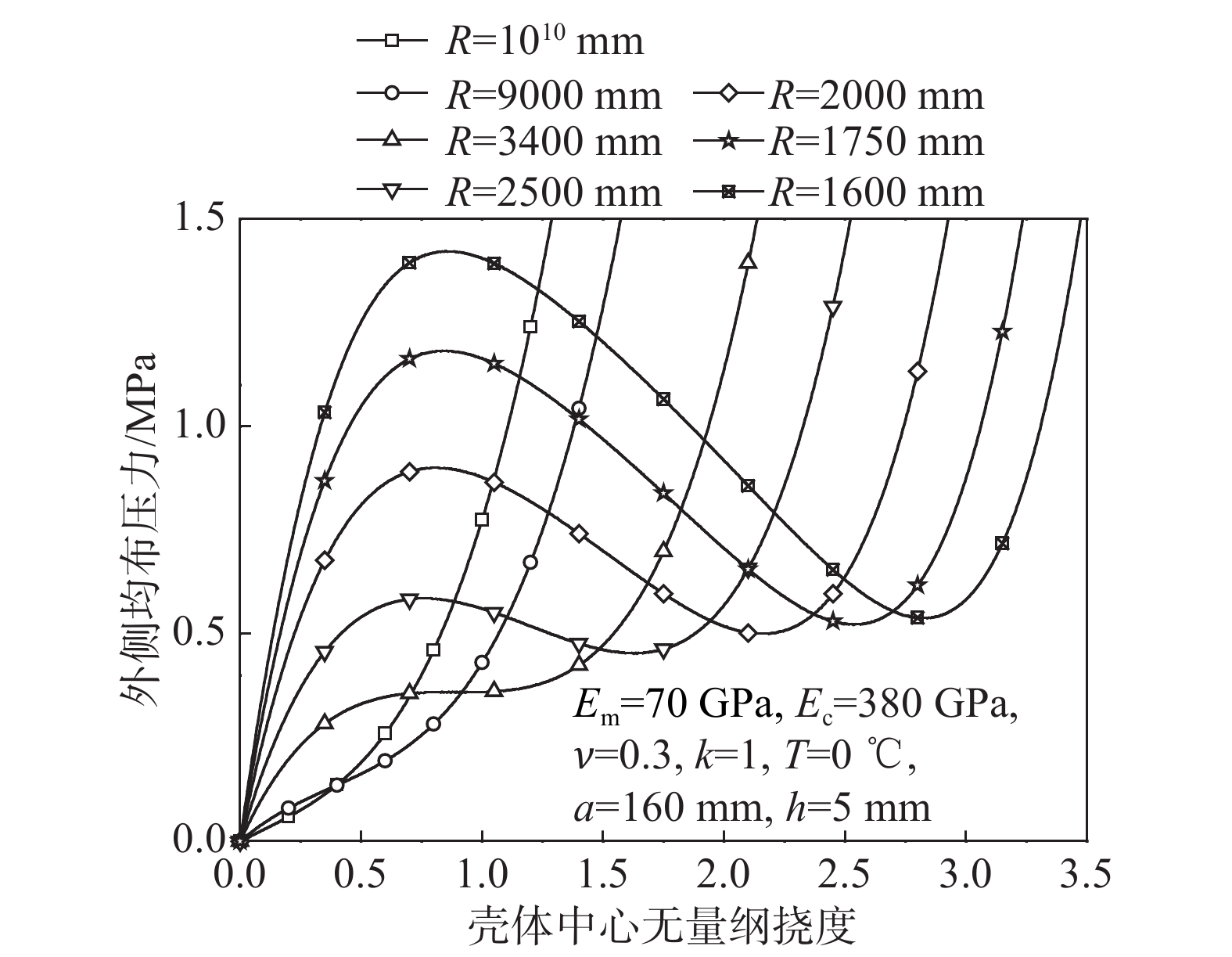
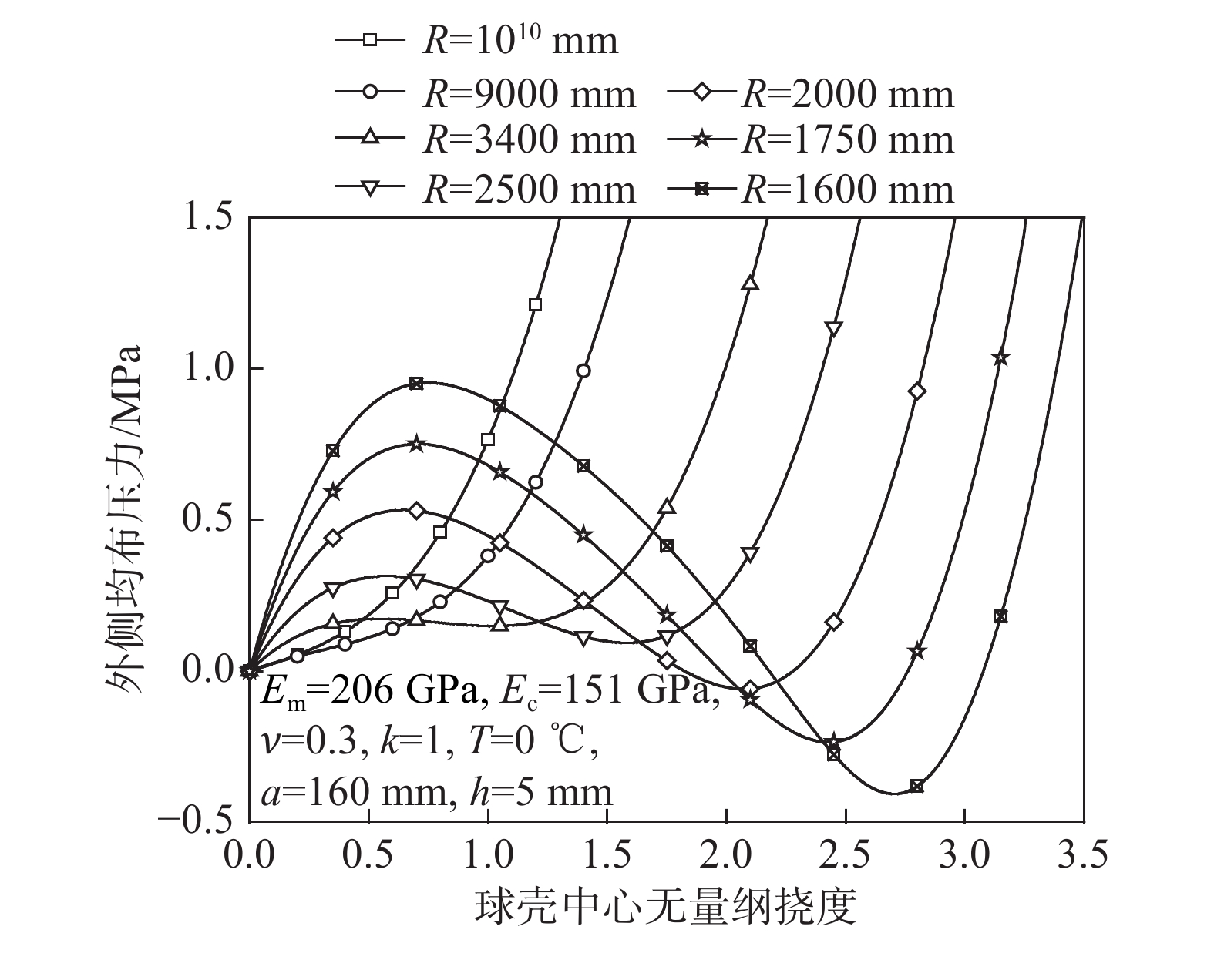
为了揭示不变温情况下简支边功能梯度圆底扁球壳屈曲平衡路径,针对陶瓷及金属组分材料分别为黏土(Ec=380 GPa)和铝(Em=70 GPa)、泊松比均为ν=0.3,在指定指数k=1、圆底半径a=160 mm和厚度h=5 mm的情况下,图2给出了中曲面曲率半径R=1600 mm、1750 mm、2000 mm、2500 mm、3400 mm、9000 mm和1010 mm分别对应的扁球壳型结构的屈曲平衡路径。计算表明:当R≥3400 mm时,挠度与荷载一一对应,球壳可视为具有一定初曲率的圆板。当R<3400 mm时,屈曲平衡路径出现了迂回。迂回特性是浅壳从凸面侧承受压力而屈曲的平衡路径的典型特征,此类曲线明确地示出了壳体的上临界荷载及下临界荷载(指球壳S形荷载-挠度曲线上极小值点对应的荷载。若规定凸面侧压力为正,当该值大于零时,其指要维持后屈曲状态的最小压力,换句话说,在后屈曲状态,如果凸面侧压力小于该值,球壳将会回跳到屈曲前状态;当该值小于零时,表示对于屈曲后的球壳,即使没有凸面侧压力作用,球壳也不能自动回跳到屈曲前状态,该值指使球壳能够回跳的最小反向压力)。从图2可以看出:随着R的减小,球壳上临界荷载单调增加,这是扁球壳承载力变化规律的普遍特征,不必赘述。计算表明:对于简支边功能梯度圆底扁球壳(不考虑变温),在指数k、圆底半径a、厚度h给定的情况下,随中曲面曲率半径R逐渐减小(球壳深度逐渐增加),其下临界荷载变化规律是复杂的。图2所涉及的功能梯度扁球壳,其材料弹性模量从外侧向内侧逐渐减小,从图2可以看出,随R逐渐减小,球壳下临界荷载略有增加。为了对比,在球壳几何参数、梯度指数以及材料泊松比与图2中的相应参数完全相同的情况下,图3给出了组分材料为氧化锆(Ec=151 GPa)和钢(Em=206 GPa)的球壳(其材料弹性模量从外侧向内侧逐渐增加)的屈曲平衡路径,从图3可以看出,随R逐渐减小,下临界荷载是逐渐减小的。上述结果表明:对于简支边功能梯度扁球壳,在梯度指数、球壳圆底半径以及厚度给定的情况下,随球壳深度增加(中曲面曲率半径R减小),球壳下临界荷载的变化规律与壳体横向材料弹性模量梯度特性有关。
在不变温的情况下,为了揭示材料体积分数指数k对FGM扁球壳屈曲平衡路径的影响,现在考虑几何参数a/R=0.1、R/h=320的球壳,图4给出了多个梯度指数k对应的球壳的屈曲平衡路径。从图4易见,当指数k增加时,球壳上临界荷载是单调减小的,k越大,影响程度越小。指数k对下临界荷载的影响规律比较复杂,从图4可以看出,当k=0时,下临界荷载最小(指代数量,而不是力的绝对大小,下同);对于图4中给定的一些离散的k值,当k从0逐渐增加到1时,下临界荷载逐渐增加并达到最大值,在此之后,随k增加,下临界荷载逐渐减小。当k趋于正无穷(球壳已过渡为均匀材料的金属壳)时,其下临界荷载仍大于均质陶瓷球壳(k=0)的下临界荷载。
为了考察组分材料弹性模量对功能梯度扁球壳屈曲平衡路径的的影响,在其他参数不变的情况下,将图4中的弹性模量为Ec =380 GPa的陶瓷材料(黏土)用弹性模量为Ec=151 GPa的陶瓷材料(氧化锆)替换,并由图5给出该功能梯度扁球壳的屈曲平衡路径。比较图4与图5不难发现,在金属组分材料弹性模量不变的情况下,当陶瓷组分材料弹性模量显著减小时,功能梯度扁球壳上临界荷载会明显降低。对于图5中给定的一些离散的k值,当k=2时,下临界荷载达到最大(其值与k=1对应的球壳下临界荷载相差很小),其他变化规律与图4相似。需要指出:虽然图4、图5竖坐标是有量纲荷载,但只要球壳几何参数(R,a,h)满足图中比例关系,其有量纲荷载不会改变,该性质对工程设计是有意义的。
为了揭示沿壳体厚度均匀温度改变对功能梯度扁球壳屈曲平衡路径的影响,在梯度指数k=1时,选取球壳几何参数a/R=0.1和R/h=320,图6给出了均匀变温T=60 ℃、40 ℃、20 ℃、0 ℃、−20 ℃和−40 ℃6个变温参数时的该功能梯度扁球壳的屈曲平衡路径。从图6易见,温度变化对球壳屈曲平衡路径有明显的影响,温度升高时,其上临界荷载明显增加,下临界荷载明显减小。据此推测,球壳试验环境温度相对初始无应力状态的壳体温度变化可能是屈曲理论解与试验临界压力不一致的一个重要原因。因此,对不涉及变温的球壳进行稳定性试验,建议在严格恒温环境中制作被试验球壳,并在相同环境温度下进行稳定性试验。若要测试变温对球壳临界压力的影响,则是一个比较困难的问题。因为球壳的超静定特性,在球壳温度相对初始无应力状态的壳体温度发生改变时,如何保证支座的温度不发生变化是困难的。另外易见,温度升高,屈曲过程跳跃幅度增加。
4.3 功能梯度扁球壳双稳态构形
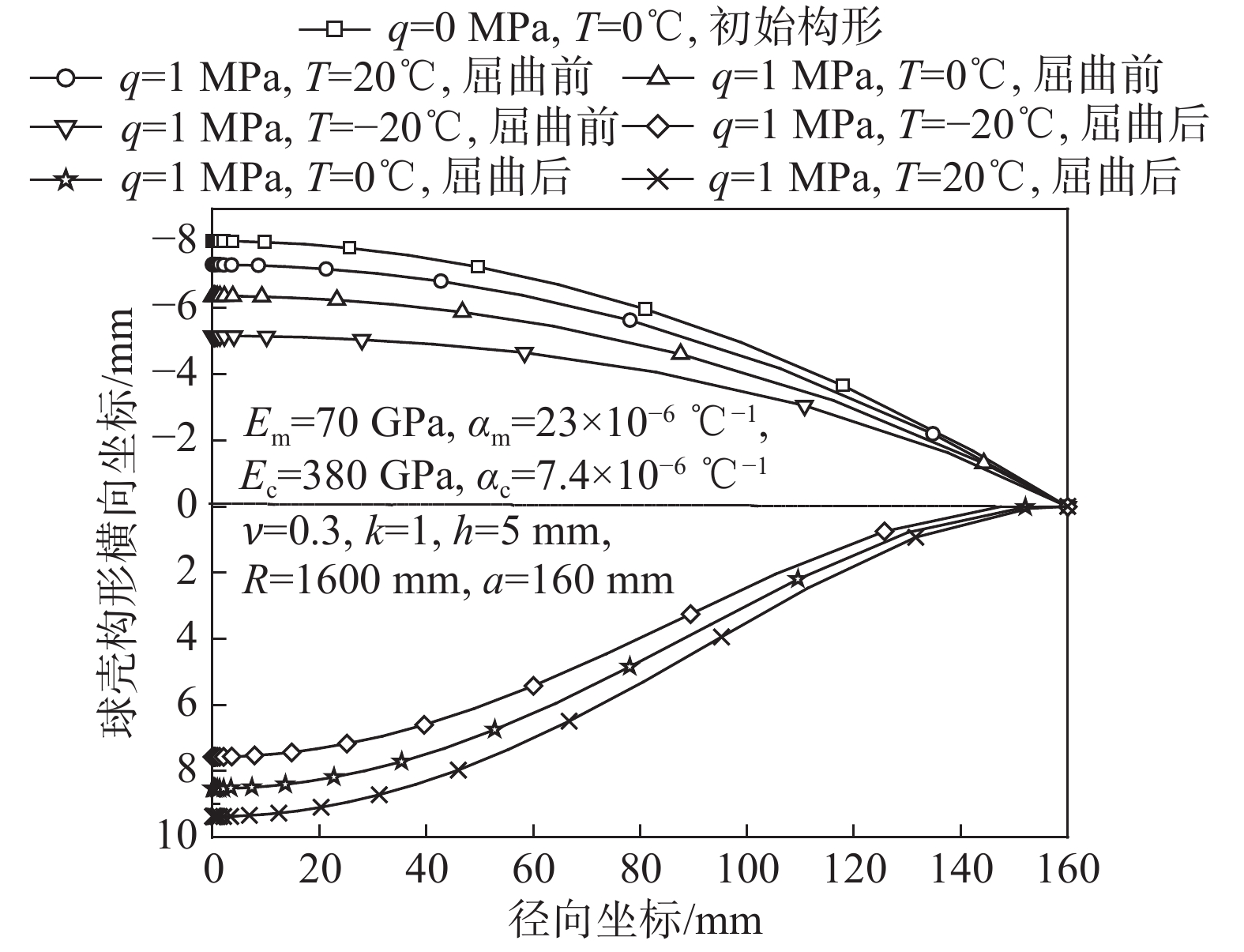
在球壳工作环境温度相对初始无应力状态温度不发生改变的情况下,取外侧均布压力q=1 MPa,图7给出了梯度指数k=0.2和1.0对应的扁球壳屈曲前和屈曲后的稳态构形。为了对比,还给出了扁球壳的初始构形(即扁球壳未发生变形的初始几何形状)。对于屈曲前的构形,从图7可以看出,k越大,其变形越大。这是因为随指数k增加,球壳弯曲刚度减小,进而引起壳体变形增加,与预期结果一致。对于屈曲后的情况,此类球壳(球壳材料弹性模量从外侧向内侧逐渐减小),屈曲后边界并未充分翻转,进而使屈曲后构形呈现了较复杂的特性。在外侧均布压力q=1 MPa和梯度指数k=1时,图8给出了三个变温值T=20 ℃、0 ℃和−20 ℃对应扁球壳屈曲前和屈曲后的稳态构形。为了对比,还给出了扁球壳的初始构形。对于屈曲前的构形,从图8可以看出,随温度升高,球壳变形显著减小,反之则显著增大。这是因为:球壳屈曲前,随温度升高,热膨胀引起的球壳横向变形沿凸面外法线方向,与荷载引起的向内侧的挠度相抵消;另外,热膨胀引起球壳深度增加,导致球壳承载力(即上临界荷载)显著增加,对应于给定荷载的变形(指屈曲前)会减小。还容易看出,温度升高会导致球壳屈曲过程的跳跃幅度明显增加。另外,球壳后屈曲构形在边界处的形状再次显示了此类球壳(其材料弹性模量从外侧向内侧逐渐减小)屈曲后其边界并不能充分翻转。图9给出了材料特性参数Em=206 GPa,Ec=151 GPa,ν=0.3,几何参数R=1600 mm,a=160 mm,h=5 mm的扁球壳在荷载q=0.6 MPa和未变温情况下的屈曲前和屈曲后稳态构形,同时给出了球壳的初始构形。从图9可以看出,此类功能梯度球壳(其材料弹性模量从外侧向内侧逐渐增加)后屈曲状态下边界发生了充分的翻转。
5 实用数表和曲线
分析本文无量纲两点边值问题可知:在球壳工作环境温度相对初始无应力状态的温度不发生改变的情况下,对给定几何参数a2/(Rh)、指数k和组分材料泊松比ν的扁球壳,其无量纲荷载与球壳中心无量纲挠度的关系与球壳组分材料弹性模量的绝对值无关,仅取决于其弹性模量比。考虑到工程界更关注壳体上临界荷载,即承载力。因此,在未变温的情况下,针对工程界常见的铝/黏土(Em/Ec=7/38,ν=0.3)和铝/氧化锆(Em/Ec=70/151,ν=0.3)两种组分材料组合,考虑一组几何参数a2/(Rh)和一组梯度指数k,通过表2和表3分别给出了对应的扁球壳的无量纲上临界荷载Qu。对表中的数据进行换算,能够方便的得到具有实际参数简支边功能梯度圆底扁球壳的有量纲上临界荷载。
表 2 不同几何参数a2/(Rh)与材料体积分数指数k对应的扁球壳无量纲上临界荷载QuTable 2. Dimensionless upper critical load Qu of shallow spherical shells for different geometric parameters a2/(Rh) and volume fraction index k几何参数a2/(Rh) 材料体积分数指数k 0.0 0.1 0.2 0.3 0.4 0.6 0.8 1.0 1.5 2.0 5.0 10.0 1.6 14.1192 15.6243 16.9932 18.2223 19.3158 21.1303 22.5181 23.5586 25.0928 25.6970 − − 1.8 17.4372 19.2112 20.8109 22.2368 23.4967 25.5664 27.1241 28.2708 29.8791 30.4043 28.3723 25.0629 2.0 21.5475 23.6330 25.4955 27.1412 28.5839 30.9266 32.6609 33.9137 35.5931 36.0453 33.2287 29.3255 2.2 26.4943 28.9243 31.0710 32.9497 34.5814 37.1979 39.1018 40.4506 42.1756 42.5378 38.9173 34.4238 2.4 32.3387 35.1389 37.5826 39.6973 41.5158 44.3917 46.4455 47.8705 49.6042 49.8519 45.3904 40.3028 2.6 39.1475 42.3348 45.0766 47.4195 49.4110 52.5143 54.6860 56.1612 57.8552 57.9633 52.6295 46.9552 2.8 46.9896 50.5668 53.5928 56.1414 58.2807 61.5605 63.8083 65.2979 66.8985 66.8395 60.6196 54.3814 3.0 55.9321 59.8838 63.1593 65.8729 68.1214 71.5088 73.7808 75.2483 76.6979 76.4460 69.3343 62.5757 3.2 66.0395 70.3209 73.7862 76.608 78.9120 82.3291 84.5691 85.9717 87.2155 86.7445 78.7473 71.5269 3.4 77.3713 81.8993 85.4691 88.3241 90.6259 93.9857 96.1370 97.4410 98.4236 97.7100 88.8267 81.2121 3.6 89.9795 94.6269 98.1906 100.9977 103.2360 106.4557 108.4685 109.6395 110.3121 109.3251 99.5474 91.6072 3.8 103.9154 108.5073 111.9430 114.6168 116.7321 119.7400 121.5666 122.5765 122.8866 121.5978 110.8828 102.6870 4.0 119.2528 123.5701 126.7431 129.2052 131.1364 133.8637 135.4602 136.2732 136.1792 134.5519 122.8326 114.4252 4.2 136.1466 139.8992 142.6586 44.8096 146.5040 148.8697 150.2036 150.7955 150.2392 148.2310 135.4039 126.8146 4.4 154.9787 157.6906 159.8243 161.5504 162.9364 164.8598 165.8811 166.2169 165.1355 162.6952 148.6207 139.8578 4.6 176.9418 177.3170 178.4684 179.6003 180.5737 181.9467 182.5896 182.6288 180.9483 178.0196 162.5219 153.5781 表 3 不同几何参数a2/(Rh)与材料体积分数指数k对应的扁球壳无量纲上临界荷载QuTable 3. Dimensionless upper critical load Qu of shallow spherical shells for different geometrical parameters a2/(Rh) and volume fraction index k几何参数a2/(Rh) 材料体积分数指数k 0.0 0.1 0.2 0.3 0.4 0.6 0.8 1.0 1.5 2.0 5.0 10.0 1.6 14.1192 15.0701 15.8697 16.5358 17.0862 17.9070 18.4462 18.7886 19.1349 19.1181 17.8700 16.5175 1.8 17.4372 18.5579 19.4910 20.2599 20.8884 21.8077 22.3918 22.7445 23.0396 22.9332 21.3089 19.8198 2.0 21.5475 22.8654 23.9521 24.8388 25.5560 26.5875 27.2231 27.5896 27.8373 27.6428 25.6311 23.9597 2.2 26.4943 28.0311 29.2854 30.2987 31.1095 32.2560 32.9416 33.3182 33.5064 33.2123 30.7787 28.9112 2.4 32.3387 34.1118 35.5431 36.6871 37.5925 38.8499 39.5779 39.9563 40.0663 39.6588 36.7702 34.7035 2.6 39.1475 41.1688 42.7807 44.0537 45.0494 46.4055 47.1635 47.5314 47.5407 47.0045 43.6349 41.3763 2.8 46.9896 49.2628 51.0504 52.4435 53.5187 54.9520 55.7204 56.0631 55.9458 55.2674 51.4007 48.9686 3.0 55.9321 58.4498 60.3972 61.8911 63.0261 64.5039 65.2578 65.5562 65.2847 64.4505 60.0860 57.5139 3.2 66.0395 68.7768 70.8514 72.4159 73.5837 75.0602 75.7679 76.0005 75.5448 74.5445 69.6990 67.0339 3.4 77.3713 80.2771 82.4294 84.0188 85.1820 86.6036 87.2295 87.3724 86.7018 85.5266 80.2319 77.5385 3.6 89.9795 92.9740 95.1321 96.6907 97.8054 99.1116 99.6158 99.6439 98.7295 97.3695 91.6679 88.9959 3.8 103.9154 106.8832 108.9605 110.4243 111.4428 112.5675 112.9111 112.7992 111.6052 110.0542 103.9810 101.4725 4.0 119.2528 122.0431 123.9377 125.2358 126.1079 126.9844 127.1230 126.8428 125.3300 123.5633 117.1580 114.8758 4.2 136.1466 138.5555 140.1426 141.1933 141.8600 142.4096 142.2970 141.8099 139.9310 137.9316 131.2014 129.2368 4.4 154.9787 156.6574 157.7490 158.4379 158.8210 158.9460 158.5170 157.7849 155.4713 153.2020 146.1419 144.5963 4.6 176.9418 176.8444 177.0816 177.2171 177.1971 176.7504 175.9218 174.8845 172.0509 169.4649 162.0491 161.0382 注:1) 表2、表3中的数据分别是在Em/Ec=7/38、70/151和ν=0.3的前提下计算得到的,对其他材料弹性模量比和泊松比不适用;
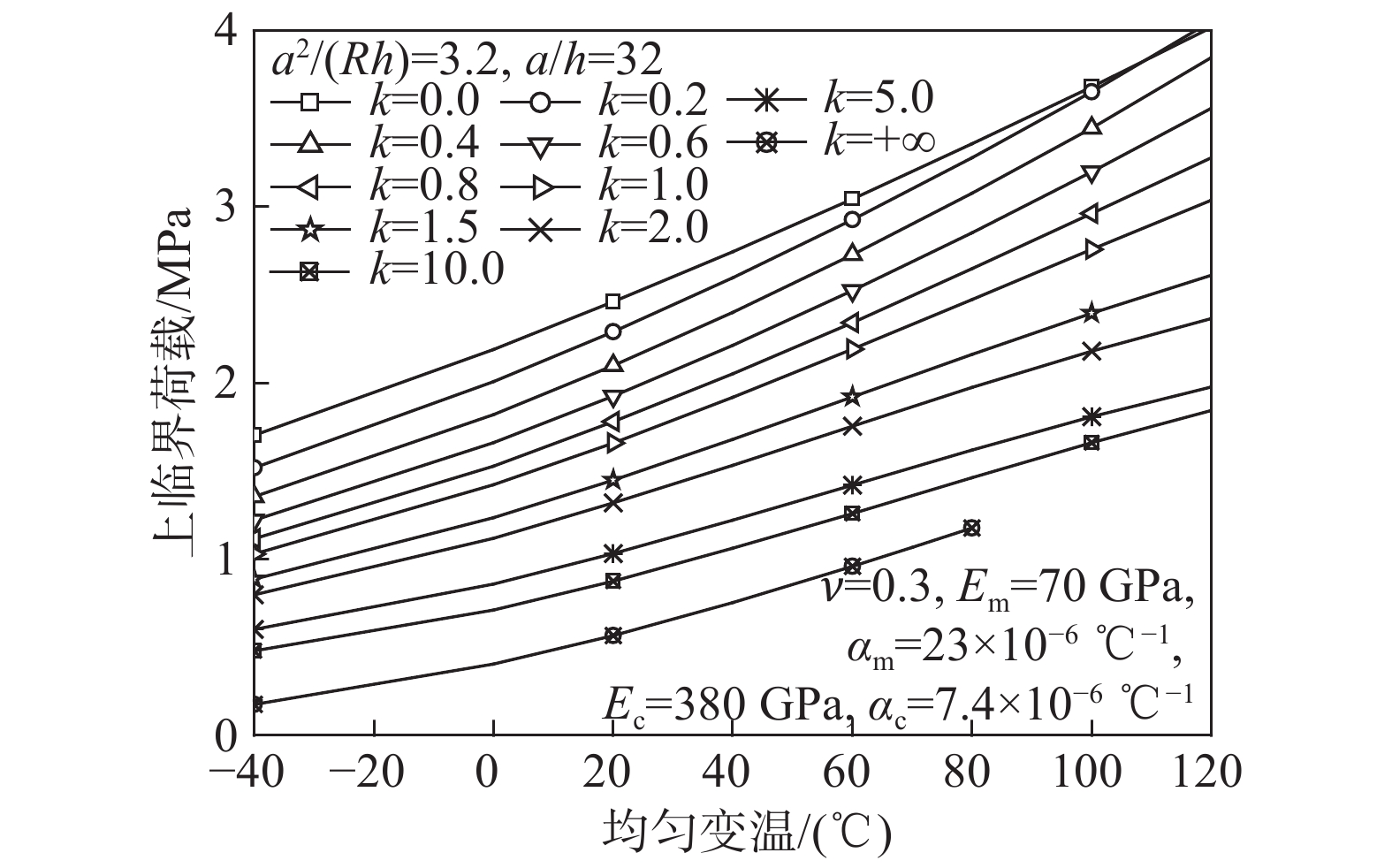
2) 使用表2、表3时,对于指定的材料体积分数指数k和几何参数a2/(Rh),首先查表得到球壳无量纲上临界荷载Qu,再依据设计要求选取参数R、a和h,最后根据公式{q_u} = {Q_u}{E_{\rm{m}}}({\varphi _0}{\varphi _2} - \varphi _{_1}^2)/[(1 - {\nu ^2}){\delta ^4}{\varphi _0}]换算出所设计的功能梯度球壳的有量纲上临界荷载qu/GPa。考虑到扁球壳工作环境温度会发生变化,因此,在计及变温的情况下,制作类似表2与表3的数表能够方便地指导结构设计工作。遗憾的是,计及变温时,即使在组分材料常数给定的情况下,球壳的几何参数、材料体积分数指数和无量纲变温的组合种类仍然很多,用数表无法表达。若用平面曲线来表达,也需要非常多的曲线图形。限于篇幅,在给定几何参数a2/(Rh)=3.2和a/h=32(球壳有量纲温度不但与a2/(Rh)的值有关,还与a/h的值有关)和一组体积分数指数k(见图10、图11)的情况下,针对组分材料组合铝/黏土和铝/氧化锆的简支边功能梯度圆底扁球壳,分别由图10和图11给出了球壳的有量纲上临界荷载qu随均匀变温T的变化曲线,供设计人员参考。
6 结论
本文基于经典壳理论和von Karman几何非线性理论,考虑材料性质沿厚度按幂率函数变化,建立了简支边功能梯度材料圆底扁球壳在热机械荷载作用下的弹性稳定性问题的位移型控制方程及其边界条件。采用数值打靶法求得了壳体的平衡路径和平衡构形。分析了简支边功能梯度圆底扁球壳在热机载荷共同作用下的跳跃屈曲行为。得出如下主要结论:
(1) 材料体积分数指数增加时,壳体上临界荷载显著减小,壳体下临界荷载变化规律比较复杂;
(2) 组分材料弹性模量减小时,壳体上临界荷载显著减小,壳体下临界荷载变化不明显;
(3) 温度均匀升高时,壳体上临界荷载显著增加,壳体下临界荷载显著减小;
(4) 横向梯度特性对球壳屈曲平衡路径和后屈曲稳态构形有显著影响。
-
表 1 均质扁球壳在外侧均布压力q作用下的中心挠度W(0)
Table 1 Uniform external pressure q & central deflection W(0) for an homogeneous shallow spherical shell
外侧均布压力q/MPa R=1600 mm, a=160 mm, h=5 mm, ν=0.3, E=70 GPa 中心挠度W(0)/mm 有限元解 打靶法解 0.011968 0.0499 0.0500 0.109892 0.4982 0.5000 0.360569 2.4720 2.5000 0.399206 3.3900 3.5000 0.403717(qu) 3.6541 4.0100 0.557400 17.5540 17.5000 0.754463 18.0586 18.0000 0.980981 18.5600 18.5000 表 2 不同几何参数a2/(Rh)与材料体积分数指数k对应的扁球壳无量纲上临界荷载Qu
Table 2 Dimensionless upper critical load Qu of shallow spherical shells for different geometric parameters a2/(Rh) and volume fraction index k
几何参数a2/(Rh) 材料体积分数指数k 0.0 0.1 0.2 0.3 0.4 0.6 0.8 1.0 1.5 2.0 5.0 10.0 1.6 14.1192 15.6243 16.9932 18.2223 19.3158 21.1303 22.5181 23.5586 25.0928 25.6970 − − 1.8 17.4372 19.2112 20.8109 22.2368 23.4967 25.5664 27.1241 28.2708 29.8791 30.4043 28.3723 25.0629 2.0 21.5475 23.6330 25.4955 27.1412 28.5839 30.9266 32.6609 33.9137 35.5931 36.0453 33.2287 29.3255 2.2 26.4943 28.9243 31.0710 32.9497 34.5814 37.1979 39.1018 40.4506 42.1756 42.5378 38.9173 34.4238 2.4 32.3387 35.1389 37.5826 39.6973 41.5158 44.3917 46.4455 47.8705 49.6042 49.8519 45.3904 40.3028 2.6 39.1475 42.3348 45.0766 47.4195 49.4110 52.5143 54.6860 56.1612 57.8552 57.9633 52.6295 46.9552 2.8 46.9896 50.5668 53.5928 56.1414 58.2807 61.5605 63.8083 65.2979 66.8985 66.8395 60.6196 54.3814 3.0 55.9321 59.8838 63.1593 65.8729 68.1214 71.5088 73.7808 75.2483 76.6979 76.4460 69.3343 62.5757 3.2 66.0395 70.3209 73.7862 76.608 78.9120 82.3291 84.5691 85.9717 87.2155 86.7445 78.7473 71.5269 3.4 77.3713 81.8993 85.4691 88.3241 90.6259 93.9857 96.1370 97.4410 98.4236 97.7100 88.8267 81.2121 3.6 89.9795 94.6269 98.1906 100.9977 103.2360 106.4557 108.4685 109.6395 110.3121 109.3251 99.5474 91.6072 3.8 103.9154 108.5073 111.9430 114.6168 116.7321 119.7400 121.5666 122.5765 122.8866 121.5978 110.8828 102.6870 4.0 119.2528 123.5701 126.7431 129.2052 131.1364 133.8637 135.4602 136.2732 136.1792 134.5519 122.8326 114.4252 4.2 136.1466 139.8992 142.6586 44.8096 146.5040 148.8697 150.2036 150.7955 150.2392 148.2310 135.4039 126.8146 4.4 154.9787 157.6906 159.8243 161.5504 162.9364 164.8598 165.8811 166.2169 165.1355 162.6952 148.6207 139.8578 4.6 176.9418 177.3170 178.4684 179.6003 180.5737 181.9467 182.5896 182.6288 180.9483 178.0196 162.5219 153.5781 表 3 不同几何参数a2/(Rh)与材料体积分数指数k对应的扁球壳无量纲上临界荷载Qu
Table 3 Dimensionless upper critical load Qu of shallow spherical shells for different geometrical parameters a2/(Rh) and volume fraction index k
几何参数a2/(Rh) 材料体积分数指数k 0.0 0.1 0.2 0.3 0.4 0.6 0.8 1.0 1.5 2.0 5.0 10.0 1.6 14.1192 15.0701 15.8697 16.5358 17.0862 17.9070 18.4462 18.7886 19.1349 19.1181 17.8700 16.5175 1.8 17.4372 18.5579 19.4910 20.2599 20.8884 21.8077 22.3918 22.7445 23.0396 22.9332 21.3089 19.8198 2.0 21.5475 22.8654 23.9521 24.8388 25.5560 26.5875 27.2231 27.5896 27.8373 27.6428 25.6311 23.9597 2.2 26.4943 28.0311 29.2854 30.2987 31.1095 32.2560 32.9416 33.3182 33.5064 33.2123 30.7787 28.9112 2.4 32.3387 34.1118 35.5431 36.6871 37.5925 38.8499 39.5779 39.9563 40.0663 39.6588 36.7702 34.7035 2.6 39.1475 41.1688 42.7807 44.0537 45.0494 46.4055 47.1635 47.5314 47.5407 47.0045 43.6349 41.3763 2.8 46.9896 49.2628 51.0504 52.4435 53.5187 54.9520 55.7204 56.0631 55.9458 55.2674 51.4007 48.9686 3.0 55.9321 58.4498 60.3972 61.8911 63.0261 64.5039 65.2578 65.5562 65.2847 64.4505 60.0860 57.5139 3.2 66.0395 68.7768 70.8514 72.4159 73.5837 75.0602 75.7679 76.0005 75.5448 74.5445 69.6990 67.0339 3.4 77.3713 80.2771 82.4294 84.0188 85.1820 86.6036 87.2295 87.3724 86.7018 85.5266 80.2319 77.5385 3.6 89.9795 92.9740 95.1321 96.6907 97.8054 99.1116 99.6158 99.6439 98.7295 97.3695 91.6679 88.9959 3.8 103.9154 106.8832 108.9605 110.4243 111.4428 112.5675 112.9111 112.7992 111.6052 110.0542 103.9810 101.4725 4.0 119.2528 122.0431 123.9377 125.2358 126.1079 126.9844 127.1230 126.8428 125.3300 123.5633 117.1580 114.8758 4.2 136.1466 138.5555 140.1426 141.1933 141.8600 142.4096 142.2970 141.8099 139.9310 137.9316 131.2014 129.2368 4.4 154.9787 156.6574 157.7490 158.4379 158.8210 158.9460 158.5170 157.7849 155.4713 153.2020 146.1419 144.5963 4.6 176.9418 176.8444 177.0816 177.2171 177.1971 176.7504 175.9218 174.8845 172.0509 169.4649 162.0491 161.0382 注:1) 表2、表3中的数据分别是在Em/Ec=7/38、70/151和ν=0.3的前提下计算得到的,对其他材料弹性模量比和泊松比不适用;
2) 使用表2、表3时,对于指定的材料体积分数指数k和几何参数a2/(Rh),首先查表得到球壳无量纲上临界荷载Qu,再依据设计要求选取参数R、a和h,最后根据公式{q_u} = {Q_u}{E_{\rm{m}}}({\varphi _0}{\varphi _2} - \varphi _{_1}^2)/[(1 - {\nu ^2}){\delta ^4}{\varphi _0}]换算出所设计的功能梯度球壳的有量纲上临界荷载qu/GPa。 -
[1] von Karman T, Tsien H S. The buckling of spherical shells by external pressure [J]. Journal of the Aeronautical Sciences, 1939, 7(2): 43 − 50. doi: 10.2514/8.1019
[2] Huang N C. Unsymmetrical buckling of thin shallow spherical shells [J]. Journal of Applied Mechanics, 1964, 31(3): 447 − 457. doi: 10.1115/1.3629662
[3] 叶开源, 刘人怀, 李思来, 等. 在对称线布载荷作用下的圆底扁薄球壳的非线性稳定问题[J]. 兰州大学学报, 1965, 18(2): 10 − 33. Ye Kaiyuan, Liu Renhuai, Li Silai, et al. Nonlinear stabilities of thin circular shallow shells under actions of axisymmetrical uniformly distributed line loads [J]. Journal of Lanzhou University, 1965, 18(2): 10 − 33. (in Chinese)
[4] Uemura M. Axisymmetrical buckling of an initially deformed shallow spherical shell under external pressure [J]. International Journal of Non-linear Mechanics, 1971, 6(2): 177 − 192. doi: 10.1016/0020-7462(71)90054-0
[5] Yan S P. Nonlinear stability of truncated shallow spherical shell with variable thickness under uniformly distributed load [J]. Applied Mathematics and Mechanics, 1997, 18(10): 1015 − 1020. doi: 10.1007/BF00189293
[6] Nie G H. Asymptotic buckling analysis of imperfect shallow spherical shells on non-linear elastic foundation [J]. International Journal of Mechanical Sciences, 2001, 43(2): 543 − 555. doi: 10.1016/S0020-7403(99)00118-6
[7] Shahsiah R, Eslami M R. Thermal and mechanical instability of an imperfect shallow spherical cap [J]. Journal of Thermal Stresses, 2003, 26(7): 723 − 737. doi: 10.1080/713855992
[8] Li Q S, Liu J, Tang J. Buckling of shallow spherical shells including the effects of transverse shear deformation [J]. International Journal of Mechanical Sciences, 2003, 45(9): 1519 − 1529. doi: 10.1016/j.ijmecsci.2003.09.020
[9] Zhu Y A, Wang F, Liu R H. Thermal buckling of axisymmetrically laminated cylindrically orthotropic shallow spherical shells including transverse shear [J]. Applied Mathematics and Mechanics, 2008, 29(3): 291 − 300. doi: 10.1007/s10483-008-0302-7
[10] Xu J C, Li Y, Wang F, Liu R H. Nonlinear stability of double-deck reticulated circular shallow spherical shell [J]. Applied Mathematics and Mechanics, 2010, 31(3): 279 − 290. doi: 10.1007/s10483-010-0302-7
[11] 张平, 周丽, 邱涛. 用于自适应进气道的扁薄球壳双稳态特性分析[J]. 工程力学, 2013, 30(10): 264 − 271. Zhang Ping, Zhou Li, Qiu Tao. Analysis of bi-stable behavior of shallow thin spherical shell applied in adaptive inlet [J]. Engineering Mechanics, 2013, 30(10): 264 − 271. (in Chinese)
[12] 李忱, 田雪坤, 王海任, 等. 薄球壳在均布外压与温度耦合作用下的热屈曲研究[J]. 应用数学和力学, 2015, 36(9): 924 − 935. doi: 10.3879/j.issn.1000-0887.2015.09.004 Li Chen, Tian Xuekun, Wang Hairen, et al. Thermal buckling of thin spherical shells under interaction of uniform external pressure and uniform temperature [J]. Applied Mathematics and Mechanics, 2015, 36(9): 924 − 935. (in Chinese) doi: 10.3879/j.issn.1000-0887.2015.09.004
[13] 赵伟东, 高士武, 马宏伟. 扁球壳在热-机械荷载作用下的稳定性分析[J]. 应用数学和力学, 2017, 38(10): 1146 − 1154. Zhao Weidong, Gao Shiwu, Ma Hongwei. Thermo- mechanical stability analysis of shallow spherical shells [J]. Applied Mathematics and Mechanics, 2017, 38(10): 1146 − 1154. (in Chinese)
[14] Koizumi M. The concept of FGM [J]. Ceramic Transaction, Functionally Gradient Materials, 1993, 34: 3 − 10.
[15] Woo J, Meguid S A, Liew K M. Thermomechanical postbuckling analysis of functionally graded plates and shallow cylindrical shells [J]. Acta Mechanica, 2003, 165(1/2): 99 − 115. doi: 10.1007/s00707-003-0035-4
[16] Shahsiah R, Eslami M R, Naj R. Thermal instability of functionally graded shallow spherical shell [J]. Journal of Thermal Stresses, 2006, 29(8): 771 − 790. doi: 10.1080/01495730600705406
[17] Prakash T, Sundararajan N, Ganapathi M. On the nonlinear axisymmetric dynamic buckling behavior of clamped functionally graded spherical caps [J]. Journal of Sound and Vibration, 2007, 299(1/2): 36 − 43. doi: 10.1016/j.jsv.2006.06.060
[18] Ganapathi M. Dynamic stability characteristics of functionally graded materials shallow spherical shells [J]. Composite Structures, 2007, 79(3): 338 − 343. doi: 10.1016/j.compstruct.2006.01.012
[19] Bich D H, Van Tung H. Non-linear axisymmetric response of functionally graded shallow spherical shells under uniform external pressure including temperature effects [J]. International Journal of Non-linear Mechanics, 2011, 46(9): 1195 − 1204. doi: 10.1016/j.ijnonlinmec.2011.05.015
[20] Boroujerdy M S, Eslami M R. Nonlinear axisymmetric thermomechanical response of piezo-FGM shallow spherical shells [J]. Archive of Applied Mechanics, 2013, 83(12): 1681 − 1693. doi: 10.1007/s00419-013-0769-y
[21] Boroujerdy M S, Eslami M R. Thermal buckling of piezo-FGM shallow spherical shells [J]. Meccanica, 2013, 48(4): 887 − 899. doi: 10.1007/s11012-012-9642-2
[22] Mao Y Q, Ai S G, Chen C P, et al. Nonlinear dynamic response and damage analysis for functionally graded metal shallow spherical shell under low-velocity impact [J]. Archive of Applied Mechanics, 2015, 85(11): 1627 − 1647. doi: 10.1007/s00419-015-1009-4
[23] Fu Y M, Hu S M, Mao Y Q. Nonlinear transient response of functionally graded shallow spherical shells subjected to mechanical load and unsteady temperature field [J]. Acta Mechanica Solida Sinica, 2014, 27(5): 496 − 508. doi: 10.1016/S0894-9166(14)60058-6
[24] 邵玉龙, 段庆林, 李锡夔, 等. 功能梯度材料的二阶一致无网格法[J]. 工程力学, 2017, 34(3): 15 − 21. Shao Yulong, Duan Qinglin, Li Xikui, et al. Quadratically consistent meshfree method for functionally graded materials [J]. Engineering Mechanics, 2017, 34(3): 15 − 21. (in Chinese)
[25] 张鹏飞, 罗尧治, 杨超. 薄壳屈曲问题的有限质点法求解[J]. 工程力学, 2017, 34(2): 12 − 20. Zhang Pengfei, Luo Yaozhi, Yang Chao. Buckling analysis of thin shell using the finite particle method [J]. Engineering Mechanics, 2017, 34(2): 12 − 20. (in Chinese)
[26] 赵伟东, 高士武, 马宏伟. 功能梯度扁球壳在热-机械荷载作用下的屈曲分析[J]. 工程力学, 2018, 35(12): 220 − 228. Zhao Weidong, Gao Shiwu, Ma Hongwei. Thermalmechnical buckling analysis of functionally graded shallow spherical shells [J]. Engineering Mechanics, 2018, 35(12): 220 − 228. (in Chinese)
[27] 万泽青, 李世荣, 李秋全. 功能梯度Levinson圆板弯曲解的均匀化和经典化表示[J]. 工程力学, 2015, 32(1): 10 − 16. Wan Zeqing, Li Shirong, Li Qiuquan. Homogenized and classical expressions for bending solutions of functionally graded Levinsion circular plates [J]. Engineering Mechanics, 2015, 32(1): 10 − 16. (in Chinese)
[28] 赵伟东, 杨亚平. 扁球壳在均布压力与均匀温度场联合作用下的屈曲[J]. 应用数学和力学, 2015, 36(3): 262 − 273. doi: 10.3879/j.issn.1000-0887.2015.03.004 Zhao Weidong, Yang Yaping. Buckling of shallow spherical shells under uniform pressure in uniform temperature field [J]. Applied Mathematics and Mechanics, 2015, 36(3): 262 − 273. (in Chinese) doi: 10.3879/j.issn.1000-0887.2015.03.004
-
期刊类型引用(8)
1. 杜建,钱文振,李云飞,李春奇. 车辆载荷作用下穿越公路管段动力响应仿真研究. 管道技术与设备. 2024(04): 6-11+62 .  百度学术
百度学术
2. 蒋宏业,陈霈夫,宋静晗,李又绿,徐涛龙. 车辆载荷下输油管道力学响应及影响因素分析. 中国安全生产科学技术. 2024(10): 160-167 .  百度学术
百度学术
3. 李乔楚,庄波,李联合. 岩溶塌陷区埋地管道的挠度和应力分析. 焊管. 2023(04): 23-30 .  百度学术
百度学术
4. 任建新,龙光辉,李蔚,杨栋. 智能高速铁路信号技术发展研究. 中国铁路. 2022(07): 76-83 .  百度学术
百度学术
5. 王伏妮. VR技术在交互式虚拟服装特征提取中的应用. 现代电子技术. 2022(17): 112-116 .  百度学术
百度学术
6. 张宇鹏. PE燃气管的应用与施工研究. 造纸装备及材料. 2022(10): 173-175 .  百度学术
百度学术
7. 李春奇,姚文彦,李强林,孙彩云,沈勋诚,廖健成. 车辆载荷下埋地管道应力应变测试系统. 管道技术与设备. 2022(06): 23-25+30 .  百度学术
百度学术
8. 李乔楚,何沙. 基于单元生死技术的岩溶区域PE管道应力分析. 应用力学学报. 2021(04): 1512-1522 .  百度学术
百度学术
其他类型引用(2)



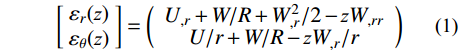

 下载:
下载: