近年来我国地震工程的研究呈现从抗震、减隔震走向可恢复功能的趋势[1]。自复位钢框架结构可有效降低甚至消除结构震后残余变形,减小建筑物震后拆除的经济损失及相关社会影响,因而成为目前的研究热点。自复位支撑具有与框架连接相对简单、易实现工厂化预制、可避免梁膨胀效应[2]等特点因而得到广泛的关注。
现阶段对于自复位支撑的研究主要集中在构造典型的旗帜形滞回曲线。目前自复位支撑的功能构造主要可分为两部分,即自复位部分和耗能部分。自复位功能多采用预应力筋和弹簧实现,多采用的预应力筋有芳纶纤维筋[2-4]、玻璃纤维筋[5-7]、形状记忆合金(SMA)筋[8-11]等,采用的弹簧主要有螺旋弹簧[12]、碟形弹簧[13-15]、环形弹簧[16-17]等。耗能功能多采用摩擦、金属软钢和SMA材料实现,如摩擦片、低屈服点钢、SMA筋等。其中,采用SMA材料和环形弹簧等可将自复位功能和耗能功能集于一体,可有效简化自复位支撑构造。目前对于自复位支撑的研究仍存在以下问题:1) 采用 PT筋(预应力筋)的自复位支撑在强震作用下的变形能力不足且存在断裂风险;2) SMA材料需要解决温度敏感性、性能稳定性和成本相对较高的问题;3)现有自复位支撑构造复杂、张拉施工繁琐;4) 支撑经历强震作用后性能退化,需要更换受损耗能元件;5) 采用高强钢环簧的自复位支撑尺寸较大,可能影响建筑使用功能。
本文在自复位支撑研究的基础上,结合对高强钢环簧的研究,提出了基于并联高强钢环簧组的自复位阻尼器,充分利用阻尼器内部空间,同等情况下有效提高了阻尼器的承载力。并通过滞回试验探究阻尼器在多次序列地震下的稳定性,探究了环簧接触表面摩擦对自复位阻尼器的影响。
1 并联高强钢环簧自复位阻尼器的设计及工作机理
1.1 高强钢环簧的工作机理简介
高强钢环簧由内圆柱面外锥面的内环及外圆柱面内锥面的外环沿其锥面拼叠而成,环簧受压时外环膨胀、内环收缩,外环或内环间的空隙减小,环簧组轴向被压缩。
图1中:D01和D02分别为内、外环形心直径;b1为内环最小壁厚;D1为内环内缘直径;D1′为内环最外缘直径;β为内外环的楔角;H为单环总高度;b2为外环最小壁厚;D2为外环外缘直径;D2′为外环最内缘直径;δ0为自由状态下相邻两外环的间距。
由于内环和外环接触面间摩擦的存在,环簧在工作过程中可耗能。环簧在加载和卸载过程中摩擦力方向相反,因此滞回曲线呈三角形,如图2所示。

图1 高强钢环簧构造示意图
Fig.1 Details and geometry of high-strength ring springs

图2 高强钢环簧受压滞回曲线
Fig.2 High-strength steel ring spring hysteresis curve under pressure
假设环形弹簧在轴向荷载作用下环向应变均匀变化,经计算可得环形弹簧在加载和卸载阶段的刚度公式。
环簧加载刚度KAB按式(1)计算:

其中:
式中:ρ为由接触面摩擦系数换算的摩擦角;A2为外环单边横截面面积;A1为内环单边横截面面积;n为内外环接触面对数。
环簧卸载刚度KCD按式(3)计算:

其中:
1.2 高强钢环簧自复位阻尼器概念及构造设计
由于高强钢环簧滞回曲线为三角形,若对环簧组提前施加预压力,则其三角形加卸载曲线将转变为四边形加卸载曲线,通过构造可保证拉压同性的旗帜形滞回行为。
如图3所示,采用活塞式的构造可保证自复位阻尼器形成旗帜形的滞回曲线。相较普通自复位支撑,采用高强钢环簧的自复位阻尼器变形能力只需根据设计要求调整内外环的个数或直径;环簧的内外环间隙完全闭合后也不会产生断裂,因此阻尼器无失效风险;另外,由于环簧兼具耗能能力和自复位能力,可有效简化自复位阻尼器的构造。但由于环簧壁厚较薄,直径较大,内部空间利用不充分,因此可在外部环簧内继续并联一组直径较小的环簧。如图4所示,相同尺寸下,在阻尼器内部并联一组环簧可有效提高自复位阻尼器的预紧力。

图3 自复位阻尼器概念设计
Fig. 3 Concept design of self-centering damper

图4 并联高强钢环簧组自复位阻尼器概念设计
Fig. 4 Concept design of self-centering damper with parallel high-strength steel ring spring groups
1.3 并联高强钢环簧自复位阻尼器构造设计
在概念设计的基础上,为保证并联高强钢环簧组自复位阻尼器拉压同性,特采用如图5所示的构造。并联高强钢环簧自复位阻尼器由内杆、上外筒、下外筒、垫片、螺母以及导向套筒组成。内部的导向套筒分为上、下两个部分,且分别与两个垫片相连,以保证阻尼器能够自由伸缩。

图5 并联高强钢环簧组自复位阻尼器构造设计
Fig. 5 Detailing design of self-centering damper with parallel high-strength steel ring spring groups
并联高强钢环簧组作为阻尼器的核心元件,通过内杆和垫片来约束经过预紧后的高强钢环簧并且外包套筒的设计,通过设置导向套筒,保证环簧组在安装及工作过程中不产生屈曲。消压之前内、外套筒之间无相对位移,消压之后,环簧被进一步压缩,内、外套筒之间产生相对位移。
1.4 并联高强钢环簧自复位阻尼器工作机理
如图6所示为并联高强钢环簧自复位阻尼器的不同工作状态。

图6 并联高强钢环簧组自复位阻尼器工作状态图示Fig.6 Working condition of self-centering damper with parallel high-strength steel ring spring groups
当阻尼器处于平衡态时或荷载未达到环簧中所加的预紧力时,两边的垫片与内杆和外筒均接触,当阻尼器受到的荷载大于环簧中的预紧力时,环簧产生压缩变形。
当阻尼器处于受压状态时,荷载通过上外筒传给与上外筒相连的垫片,然后传给高强钢环簧组,由高强钢环簧组再传递给与内杆耳板侧相连的垫片进而将荷载传递给内杆,然后传至支座。
当阻尼器处于受拉状态时,荷载通过下外筒传给与下外筒相连的垫片,然后传给高强钢环簧组,由高强钢环簧组再传递给与内杆螺母侧相连的垫片进而将荷载传递给内杆,然后传至支座。
由阻尼器工作状态受力可知其在各阶段的刚度,如图 3。当阻尼器处于未消压状态时其初始刚度由内杆和外筒共同提供,理想初始刚度KOA可按式(5)计算:
式中:KW为外套筒轴向刚度;KN为内杆轴向刚度。考虑到阻尼器在实际加工及安装过程中可能存在间隙,实际初始刚度的取值按式(6)计算:

式中:KR为实际初始刚度;Fy为阻尼器预紧力;Lg为加工安装间隙,一般取0.5 mm~1 mm。
当荷载大于消压荷载时,环簧开始工作,即图3中AB段和EF段,此时阻尼器的屈服后刚度为并联环簧组加载刚度;开始卸载时即BC段和FG段,摩擦力方向相反,刚度趋近于无穷;阻尼器复位过程中,其自复位刚度为并联环簧组卸载刚度。
自复位阻尼器的屈服后刚度为:
式中:KAB,I为内部环簧组加载刚度;KAB,O为外部环簧组加载刚度,二者均按照式(1)计算。
自复位阻尼器的自复位刚度为:
式中:KCD,I为内部环簧组加载刚度;KCD,O为外部环簧组加载刚度,二者均按照式(3)计算。
2 试验概况
2.1 试件设计
设计了3个高强钢环簧锥形接触面处理条件不同的并联高强钢环簧组自复位阻尼器试件,并增加了一组无内部环簧组的自复位阻尼器对比。由表1,以接触面经历1次约15 min喷丸且未加润滑的阻尼器 PSP1为基准试件。阻尼器的外套筒采用 Q235钢,内杆采用屈服强度为800 MPa的38CrMoAl钢,垫片采用 Q345钢,高强钢环簧采用屈服强度为1350 MPa的60Si2MnA。单个环簧尺寸见图7,内杆、外筒、垫片和螺母的尺寸见图8。
表1 自复位阻尼器试件一览表
Table 1 Overview of self-centering damper specimens

试件名称 环簧组描述 滞回加载次数PNP 未经喷丸加润滑并联环簧组 3 PSP1 经1次喷丸约15 min不加润滑并联环簧组 3 PSP2 经2次喷丸约25 min不加润滑并联环簧组 3 SP1 经1次喷丸约15 min不加润滑非并联环簧组 3
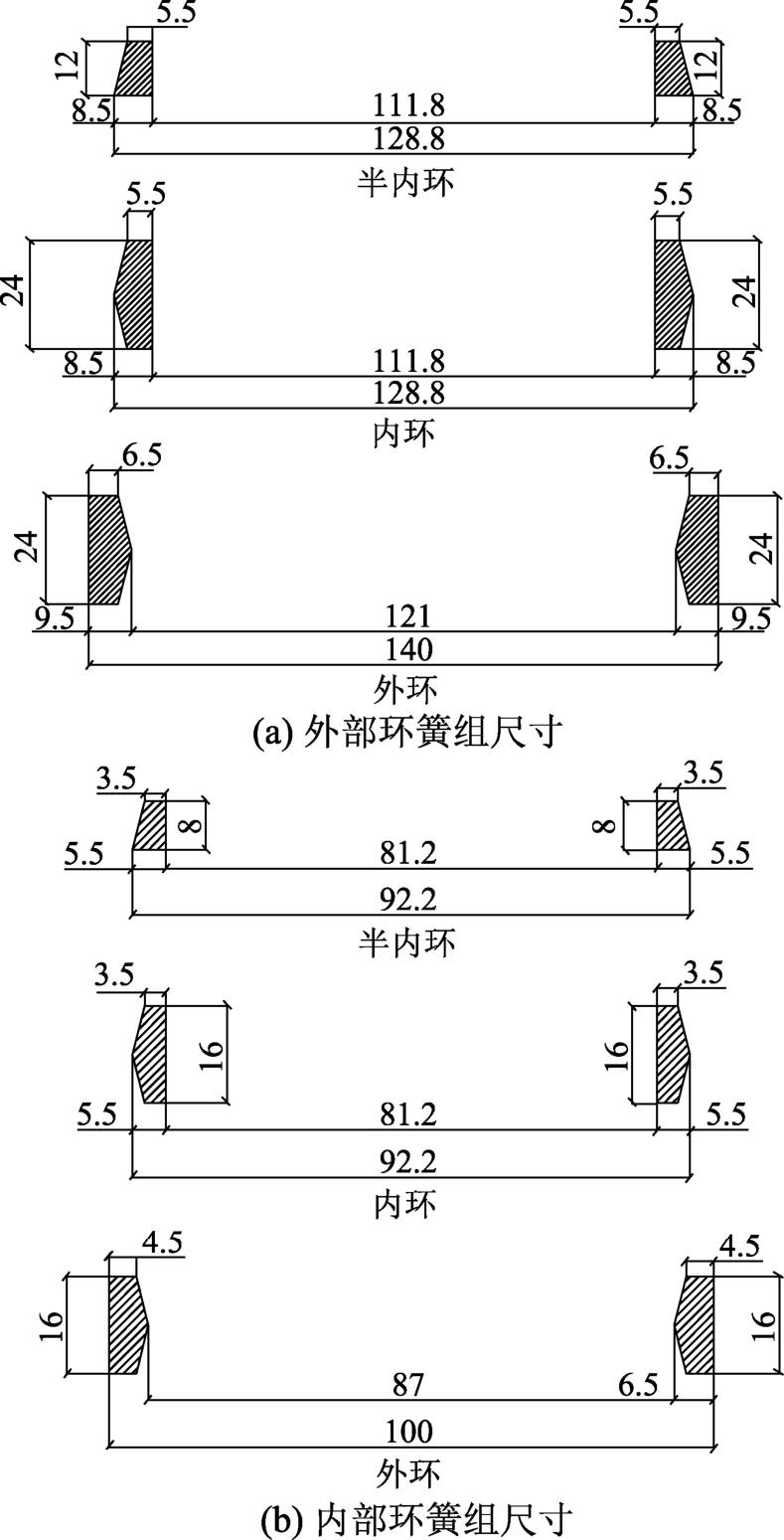
图7 摩擦环簧试件尺寸
Fig.7 Specimen size of friction spring
标准件PSP1试件的设计预紧力为150 kN,设计最大承载力为 300 kN,设计最大轴向位移为42.5 mm。其余试件的预紧位移和PSP1试件保持一致。每个并联环簧组阻尼器中外部环簧组含外环16个、内环15个、半内环2个,内部环簧组含外环24个、内环23个、半内环2个。
2.2 环簧预压缩试验
在进行自复位阻尼器滞回试验前,对高强钢环簧的性能进行了预压缩试验。图9(a)为试验装置,通过上、下加载头与 MTS试验机相连,加载头之间放置2个外环、2个半内环和1个完整内环。本试验试件对应环簧接触面经喷丸不加润滑对应阻尼器试件PSP1。为与并联环簧组形式对比,用一组只有外部环簧组的压缩试验作对照。
如图9(b)和图9(c)所示,从并联环簧组和非并联环簧组压缩试验的荷载-位移曲线来看,并联环簧组的承载力约为 253.65 kN,与预期相比较低,主要原因是加工精度未达预期,内部环簧组和外部环簧组未同时开始工作,环簧组加载过程中明显可见两段刚度。并联环簧组较未采用并联形式的环簧组承载力有约58 kN的提高。

图8 自复位阻尼器主要构件尺寸
Fig.8 Main components size of self-centering damper


图9 摩擦环簧压缩试验
Fig.9 Friction spring compression experiment
2.3 自复位阻尼器试验装置及加载方案
自复位阻尼器的试验装置如图 10所示。阻尼器垂直放置,其上、下耳板分别连接伺服作动器和基底梁。通过作动器施加循环拉压荷载。将一对位移计(LVDT)连接至上、下耳板以测量相对位移,其平均值即为阻尼器的轴向变形。同时还在外管表面设置应变计以监控其应力状况。加载制度如图 11所示。对每个阻尼器试件进行基于上述加载制度的3次连续拟静力循环拉压试验,以模拟多次连续地震作用,考察经历序列地震工况后阻尼器的响应和性能稳定性。

图10 自复位阻尼器试验装置
Fig.10 Self-centering damper test device

图11 自复位阻尼器加载制度
Fig.11 Loading protocol of self-centering damper
3 试验结果与分析
3.1 滞回性能
图12给出了每个自复位阻尼器试件在3次连续滞回试验中的荷载-位移曲线,其中横坐标为阻尼器轴向位移,T1、T2、T3分别表示第一次、第二次和第三次滞回加载。从图 12可以看出,所有阻尼器均能够完全自复位;每个试件3次试验的滞回曲线重合度很高,这表明高强钢环簧自复位阻尼器能够抵御多次地震而不出现性能退化,具有极好的稳定性。从试件滞回曲线的相互对比可以看出,PNP试件较PSP1和PSP2试件荷载水平和耗能能力均较低,但曲线重合性最高。PSP1试件各加载级的荷载水平较SP1试件明显提高。


图12 自复位阻尼器试验荷载-位移滞回曲线
Fig.12 Self-centering damper load-displacement hysteretic curve
3.2 刚度和承载力
自复位阻尼器试件的典型承载力和刚度特性总结在表2中。屈服荷载Fy由沿未消压段荷载-位移曲线的切线与屈服后荷载-位移曲线的交点确定,对应图3中阻尼器滞回曲线的A点或E点荷载。试件的屈服后刚度 KAB为消压后加载段荷载-位移曲线的斜率值,对应图3中阻尼器滞回曲线的AB段或EF段刚度。如图12所示,从阻尼器的荷载-位移曲线可以明显看出,高强钢环簧在施加相同的预压缩变形时,较高的摩擦系数导致较大的屈服荷载。此外,当阻尼器进行后续2次加载时,屈服荷载趋于减小。但是,对于试件PSP1和试件PSP2,一次和两次喷丸对二者的影响较小。3个并联环簧组自复位阻尼器试件轴向位移为±42.5 mm时的最大荷载Fmax从252.1 kN增大到308.9 kN,对应的屈强比Fmax/Fy最高达2.28。在保证梁柱构件不发生屈服的条件下,较大的屈强比可防止薄弱层的产生[18]。
在表2中,初始刚度 KR是基于从原点到屈服点的正割线的等效刚度,对应图3中OA段或OE段刚度。本实验中,并联环簧自复位阻尼器试件初始刚度范围为149.8 kN/mm~196.8 kN/mm。初始刚度值经历多次加载后略有降低,最大降幅为21%,但仍可表明阻尼器在经历序列地震后对侧向荷载作用(例如风)可提供较稳定的刚度。
3.3 自复位能力
试验表明,所有阻尼器试件均能够承受多次重复循环加载,而且几乎没有残余变形。自复位能力可以通过恢复力 Frst进行评估,试件的恢复力为荷载-位移曲线卸载段与未消压段的交点,对应图 3中阻尼器滞回曲线的D点或H点荷载。如图12所示并结合表2,PNP试件旗帜形滞回曲线中较大的恢复力表明其自复位能力较高,但代价是滞回曲线变窄继而减少了耗能。从表2可以看出,试件PNP的Frst值明显大于试件PSP1和PSP2的值。当试件PNP经历重复循环加载时,Frst略微减小,可能是由于润滑剂的消耗,锥面上的摩擦有所增加。对于试件PSP1和PSP2,Frst在重复循环加载循环期间几乎无变化。
表2 阻尼器试验结果
Table 2 Test result of damper specimens

试件 试验次数 屈服荷载Fy/kN 最大荷载Fmax/kN 初始刚度KR/(kN/mm)屈服后刚度KAB /(kN/mm) 恢复力Frst /kN 耗能WD/kJ EVD 1 121.5 254.5 173.4 3.15 73.30 6.30 9.28 PNP PSP1 PSP2 2 117.2 252.1 154.2 3.18 69.54 6.35 9.57 3 118.5 253.3 149.8 3.20 67.51 6.58 9.83 1 141.0 308.9 196.8 3.85 53.61 11.30 13.79 2 129.5 295.66 172.0 3.88 56.07 10.36 13.32 3 131.8 293.8 154.1 3.86 56.54 10.24 13.15 1 139.1 305.4 158.2 3.90 53.45 11.54 14.28 2 135.4 299.2 168.7 3.91 55.21 11.11 14.04 3 139.3 299.1 153.5 3.84 55.13 11.10 13.93 1 98.9 214.1 84.7 2.80 29.90 8.20 14.80 SP1 2 88.2 209.0 81.2 2.80 29.60 8.10 14.60 3 86.8 207.2 80.1 2.80 29.80 8.10 14.70
当采用具有恢复力较高的阻尼器时,会导致建筑物上部的高阶模态响应更明显[19]。当Frst/Fy大于0.5时会导致显著的高阶模态响应。本试验除 PNP试件的Frst/Fy大于0.5外,其余试件Frst/Fy均小于0.5。从峰值响应控制的角度看,宜采用Frst值相对较低的阻尼器,因此不建议采用环簧接触表面润滑程度较高的阻尼器。
3.4 耗能能力
在一个完整的加载循环期间自复位阻尼器试件的能量耗散可以通过每个循环的绝对耗能WD和等效粘滞阻尼比(EVD)来量化。WD是由滞回环包围的区域面积,EVD按照式(9)来进行计算:

式中,WE是由线弹性系统吸收的能量,该系统经受相同的最大位移,具有与阻尼器试件相同的最大荷载。无论响应幅度如何,EVD仅取决于滞回的形状。
图 13为各次加载过程中试件每圈的耗能以及等效阻尼比的曲线图。表2中耗能WD以及EVD为加载至最大荷载时的对应值。每级加载的能量损失随着加载位移的增加而增加。由于环簧接触面摩擦的增加会使滞回环变宽,环簧接触面的处理方式对WD有明显的影响。PSP1试件和 PSP2试件通过对环簧接触面喷丸和未添加润滑剂提高了摩擦系数,PSP2的WD约为PNP的1.8倍。PSP1试件和PSP2试件在同一次试验加载的相同加载级下,随加载圈数增加,WD略微降低,但是对于接触面经过润滑处理的试件 PNP,这种趋势不明显。PSP1试件的耗能面积较SP1试件明显提高。
由图12(b)可知,所有试件中,SP1试件的等效阻尼比最大,主要原因是SP1试件滞回圈形状更趋近于扁平。对于3个采用并联环簧组的自复位阻尼器,EVD同样受到接触面摩擦条件的影响,试件的最大EVD接近20%,而且EVD在整个加载过程中较为稳定。EVD峰值不一定在最大加载幅度处产生,因为 EVD仅取决于滞回曲线的形状。并且,在每次测试开始时 EVD值均较大,这意味着即使在非常小的层间位移中,自复位阻尼器也能提供耗能。小变形时的能量耗散归因于试验前对高强钢环簧组施加的预紧力,一旦阻尼器变形,高强钢环簧就会产生显著的摩擦耗能。
3.5 理论预测与试验结果的对比分析
选取标准件PSP1的试验结果和前文的理论公式预测进行对比,其中初始刚度按式(6)计算并引入实测的0.3 mm间隙值,“屈服”后刚度和自复位刚度计算所用的摩擦系数由环簧预压缩试验得出。理论预测曲线和试验曲线的对比,如图14所示。

图13 试件加载过程中耗能能力对比
Fig.13 Comparison of energy dissipation capacity of the test
整体来看,PSP1试验曲线和理论预测总体吻合较为理想,恢复力和理论预测的微小差别是由于外筒内壁和高强钢环簧外壁之间存在一定的摩擦。由于阻尼器试件加工和安装精度问题,“屈服”后刚度较理论计算得到的刚度大,因此试验加载至42.5 mm时最大荷载较理论预测略大。

图14 PSP1试件试验和理论预测
Fig.14 Specimen PSP1 comparison of test and theoretical prediction
4 结论
(1) 采用并联高强钢环簧组的自复位抗震阻尼器可有效利用阻尼器内部空间,同等外包尺寸下可提高阻尼器预紧力,可用于建筑空间受限的条件。
(2) 相同阻尼器外包尺寸下,采用并联高强钢环簧组的自复位阻尼器相对采用一组高强钢环簧的自复位阻尼器的等效阻尼比略低,但是耗能面积更大。
(3) 模拟多次序列地震作用的低周往复加载试验表明,并联高强钢环簧组自复位阻尼器滞回性能稳定,可实现经历多次地震后无须更换,具有良好的抗震可恢复性。
(4) 环簧锥形摩擦面处理工艺对阻尼器自复位性能与耗能能力会产生影响,当摩擦系数增大时,自复位性能有所降低,但耗能能力增大,本试验中喷丸时长对阻尼器性能影响不大。
(5) 本文提出的阻尼器理论刚度预测公式与试验结果吻合较好,可为工程设计提供参考。
[1] 周颖, 吴浩, 顾安琪. 地震工程: 从抗震、减隔震到可恢复性[J]. 工程力学, 2019, 36(6): 1-12.Zhou Ying, Wu Hao, Gu Anqi. Earthquake engineering:From earthquake resistance, energy dissipation, and isolation, to resilience [J]. Engineering Mechanics, 2019,36(6): 1-12. (in Chinese)
[2] Christopoulos C, Tremblay R, Kim H J, et al.Self-centering energy dissipative bracing system for the seismic resistance of structures: Development and validation [J]. Journal of Structural Engineering ASCE,2008, 134(1): 96-107.
[3] Erochko J, Christopoulos C, Tremblay R. Design, testing,and detailed component modelling of a high-capacity self-centering energy-dissipative damper [J]. Journal of Structural Engineering ASCE, 2015, 141(8): 04014193.
[4] Erochko J, Christopoulos C, Tremblay R. Design and testing of an enhanced-elongation telescoping selfcentering energy-dissipative damper [J]. Journal of Structural Engineering ASCE, 2015, 141(6): 04014163.
[5] Chou C C. Development and seismic tests of steel dual-core self-centering braces: Fibre-reinforced polymer composites as post-tensioning tendons [J]. China Civil Engineering Journal, 2012, 45: 202-206.
[6] Chou C C, Chen Y C, Pham D H, et al. Steel damped frames with dual-core SCBs and sandwiched BRBs:Mechanics, modelling and seismic demands [J].Engineering Structures. 2014, 72: 26-40.
[7] Chou C C, Wu T H, Beato A R O, et al. Seismic design and tests of a full-scale one-story one-bay steel frame with a dual-core self-centering damper [J]. Engineering Structures, 2016, 111: 435-450.
[8] Gao N, Jeon J S, Hodgson D E, et al. An innovative seismic bracing system based on a superelastic shape memory alloy ring [J]. Smart Materials and Structures,2016, 25(5): 055030.
[9] Massah S R, Dorvar H. Design and analysis of eccentrically braced steel frames with vertical links using shape memory alloys [J]. Smart Materials and Structures,2014, 23(11): 115015.
[10] Miller D J, Fahnestock L A, Eatherton M R. Development and experimental validation of a nickel-titanium shape memory alloy self-centering buckling-restrained damper[J]. Engineering Structures. 2012, 40: 288-298.
[11] Ahn J H , Hu J W . Performance-based optimal design of self-centering friction damping brace systems between recentering capability and energy dissipation [J]. Journal of Mechanical Science and Technology, 2014, 28(8):3129-3136.
[12] Yang C S W, Desroches R, Leon R T. Design and analysis of braced frames with shape memory alloy and energy-absorbing hybrid devices [J]. Engineering Structures, 2010, 32(2): 498-507.
[13] 徐龙河,樊晓伟,代长顺, 等.预压弹簧自恢复耗能支撑受力性能分析与试验研究[J]. 建筑结构学报, 2016,37(9): 142-148.Xu Longhe, Fan Xiaowei, Dai Changshun, et al.Mechanical behavior analysis and experimental study on pre-pressed spring self-centering energy dissipation damper [J]. Journal of Building Structures, 2016, 37(9):142-148. (in Chinese)
[14] Xu L, Fan X, Lu D, et al. Hysteretic behavior studies of self-centering energy dissipation bracing system [J]. Steel and Composite Structures, 2016, 20(6): 1205-1219.
[15] 韩强, 贾振雷, 王晓强, 等. 内嵌碟簧型自复位防屈曲支撑性能试验及其恢复力模型研究[J]. 工程力学,2018, 35(6): 144-150, 190.Han Qiang, Jia Zhenlei, Wang Xiaoqiang, et al. Restoring force model and experimental verification of an assembled self-centering energy dissipation brace [J].Engineering Mechanics, 2018, 35(6): 144-150, 190. (in Chinese)
[16] Filiatrault A, Tremblay R, Kar R. Performance evaluation of friction spring seismic damper [J]. Journal of Structural Engineering, 2000, 126(4): 491-499.
[17] Wang W, Fang C, Zhang A, et al. Manufacturing and performance of a novel self-centring damper with shape memory alloy ring springs for seismic resilience [J].Structural Control and Health Monitoring, 2019, 26(18):2337.
[18] Gupta A, Krawinkler H. Report No.132,Seismic demands for performance evaluation of steel moment resisting frame structures (SAC Task 5.4.3) [R]. Stanford University, CA: John A. Blume Earthquake Engineering Center, 1999.
[19] Qiu C X, Zhu S. High-mode effects on seismic performance of multi-story self-centering damped steel frames [J]. Journal of Constructional Steel Research,2016, 119: 133-143.