目前,国内外学者对混凝土板抗火性能开展了较多研究,但多集中在混凝土单个简支板或连续板整个空间受火工况,对不同跨升降温相互作用或火灾蔓延工况等研究较少。实际上,从空间上说,火灾可以发生在不同房间,且一房间燃料燃尽其会进入降温阶段,而相邻房间由于烟气或其他原因(防火墙失效)也引发火灾。因此,有必要研究火灾蔓延作用对多跨混凝土连续板力学行为和破坏特征等影响规律。
鉴于单一混凝土板火灾试验不能合理反映相邻结构或构件约束作用,国内外学者对普通混凝土连续板[1-2]、预应力混凝土连续板[3-4]和整体结构中楼板[5-7]开展了火灾试验研究,取得了大量研究成果。此外,近年来,文献[8-12]进行了转动约束和面内作用下混凝土双向板火灾试验,结果表明约束类型和配筋率等对混凝土双向板裂缝方向、爆裂、破坏模式(如完整性破坏)和变形趋势有重要影响。然而,上述研究主要针对整个空间均匀受火工况,而多未考虑火灾蔓延行为对混凝土板不同跨温度分布、爆裂、裂缝和变形趋势等影响。因此,文献[13]开展了不同跨依次受火作用下混凝土连续板力学行为研究,研究了配筋率和配筋方式(双层双向和负弯矩配筋)等对其火灾行为影响。结果表明,火灾蔓延工况和边界条件对连续板各跨跨中平面外变形有不同程度影响。对于边跨,其变形趋势取决于不同跨受火顺序和时间间隔。对于中跨,火灾蔓延工况、边界约束和拱效应等对其变形趋势有决定性影响。配筋率和配筋方式对混凝土连续板各跨板顶(底)裂缝分布(长度、宽度和裂缝间距)有重要影响。
除了试验方面,国内外学者采用自编软件或商用程序对混凝土双向板火灾行为进行大量数值分析。例如,Liao和Huang[14]基于扩展有限元方法,发展Vulcan软件对结构中混凝土楼板火灾行为进行分析(如变形、爆裂、裂缝发展和薄膜机理)。Wang等[15]建立忽略骨料类型影响的混凝土高温本构模型,提出应力-应变关系、峰值应变(与应力相对应部分的应变)、抗压强度、膨胀应变和瞬态热应变等,编程对混凝土双向板火灾行为进行分析。文献[16―19]采用SAFIR软件,发展高温下混凝土本构模型,对火灾下混凝土构件(板和柱)变形行为进行数值分析。Jiang和Li[20]采用ANSYS软件研究了荷载比、边界条件、板厚、配筋类型和长宽比等对火灾下混凝土双向板薄膜效应的影响,并提出火灾下混凝土双向板五种破坏模式。然而,上述数值分析主要针对空间均匀受火工况,有必要开展火灾蔓延工况下混凝土连续板力学机理分析。例如,文献[21]采用ANSYS研究了火灾蔓延工况(水平和竖向)和整体空间均匀受火工况下多层钢框架力学行为(各跨变形、轴力和弯矩等),研究表明两种火灾工况下结构力学行为完全不同,在结构抗火设计中应考虑火灾蔓延行为影响。
基于上述研究,本文开展4块不同跨升降温作用下(模拟火灾蔓延影响)的三跨混凝土连续双向板力学行为试验研究,获得试验板炉温、板温、板平面内(外)变形和破坏模式等变化规律,与相关试验结果进行对比。在此基础上,采用Vulcan软件对一块混凝土试验板进行数值模拟,重点分析了火灾蔓延工况对混凝土连续板弯矩分布和薄膜机理的影响规律。
1 试验方案
1.1 试验炉设计
如图1(a)和图1(b)所示,自制火灾试验炉平面尺寸为4.4 m×1.9 m,炉内净腔高为1.5 m,支座和加载装置见文献[13]。

图1 自制火灾试验炉 /mm
Fig.1 Self-designed furnace
1.2 试件设计
根据现行混凝土结构设计规范[22],设计4块钢筋混凝土三跨连续板(编号为B1、B2、B3和B4),尺寸均为4700 mm×2100 mm×50 mm,试验板尺寸与配筋如图2(a)和图2(b)所示。

图2 试验板尺寸与配筋 /mm
Fig.2 Dimension and reinforcement of concrete slabs
试件采用C30商品混凝土,配合比为水泥∶砂∶石子∶水∶掺合料=1∶2.32∶4.91∶0.77∶0.64。混凝土立方体抗压强度和含水率分别为37.4 MPa和3.1%。板内钢筋采用双层双向布置,钢筋采用HRB400,直径为4 mm,间距100 mm,钢筋实测屈服强度和抗拉强度平均值分别为439 MPa和521 MPa。混凝土保护层厚度为8 mm。
1.3 测量方案
温度测量采用K型热电偶,通过安捷伦数据采集仪(34980A)进行采集,采集时间间隔为15 s。
1) 炉温测量
每跨布置3个炉温热电偶,编号分别为F-1、F-2和F-3,如图3所示。

图3 每跨炉温热电偶布置图
Fig.3 Positions of thermocouples in each span
2) 混凝土和钢筋温度测量
对于每一试验板,三跨编号从左至右分别为A、B和C跨,其中A和C为边跨,B为中跨。每跨布置6组板截面温度测点(图4(a))。以A跨为例,截面测组为TA1~TA6,每组共有10个热电偶测点,如图4(b)所示。其中,编号1~编号6为混凝土温度测点,编号R-1和编号R-2(编号R-3和编号R-4)测量板底(顶)钢筋温度。

图4 连续板热电偶布置平面图 /mm
Fig.4 Layout of thermocouples in continuous slab
1.4 位移测量方案
采用差动式位移传感器(LVDT)测量试验板平面外(内)变形,如图5(a)所示。其中,测量试验板平面外跨中位移编号为VA、VB和VC;平面内位移计编号为H1、H2、H3和H4,其中编号H1和编号H3(编号H2和编号H4)测量长跨(短跨)方向平面内位移。
1.5 火灾工况
根据《建筑设计防火规范》防火墙或承重墙耐火极限(如3 h或1.5 h等)[23],确定火灾试验方案,采用单跨受火和三跨依次受火,如表1所示。其中:F表示受火时间;C表示点火时刻间隔。具体为:板B1仅边跨A受火;板B2仅中跨B受火;板B3:A、B和C三跨,依次受火90 min,随后停火;板B4:中跨受火90 min停火,随后两边跨同时受火90 min。

图5 试验板位移计和支座布置 /mm
Fig.5 Positions of LVDT and support in tested slabs
表1 试验板受火方案
Table 1 Fire scenarios of test slabs

板 荷载/kPa A跨 B跨 C跨 龄期/d 室温/(℃)相对湿度/(%)B1 1.0 F180 * * 92 21 87 B2 1.0 * F180 * 153 7 81 B3 3.0 F90 C90F90 C180F90 182 4 91 B4 3.0 C90F90 F90 C90F90 196 -6 39
1.6 加载和支座方案
板面放置配重块,模拟均布活荷载为1.0 kN/m2或3.0 kN/m2。如图5(b)所示,板外边支座采用钢滚轴(直径为50 mm)和角钢,炉内支座采用耐火球,直径为50 mm,间隔约为100 mm。试验板其他参数见表1。
2 试验结果及分析
2.1 试验现象
1) 板B1
受火5 min时,A跨出现爆裂,并发出巨大爆裂声,37 min时,爆裂停止。45 min~50 min时,板顶出现少量水蒸汽,180 min时停火。板顶(底)裂缝如图6(a)~图6(d)所示。

图6 板B1板顶和板底裂缝图 /mm
Fig.6 Crack pattern on top and bottom surfaces of Slab B1
由图6(a)可知,板顶裂缝集中在A跨板角和临近第2支座位置(图5)。由于负弯矩作用,非受火跨B出现少量南北向裂缝,且C跨板顶未出现裂缝。此外,由图6(b)可知,A跨爆裂较为严重,露出大量钢筋,且最大爆裂深度和总爆裂面积分别为45 mm和0.98 m2;主要原因在于板龄期较短(含水率较高)。可知A跨灾后剩余承载力严重降低,而非受火跨仍具有较强承载力。
2) 板B2
10 min时,B跨板底混凝土爆裂和板顶出现水蒸汽,直至47 min。值得指出的是,约在34 min,B跨板底发出一声巨大爆裂,试验板产生很大震动,且加载块被振起。180 min时,B跨停火,板顶(底)破坏模式如图7(a)~图7(d)所示。

图7 板B2板顶和板底裂缝分布图 /mm
Fig.7 Crack pattern on top and bottom surfaces of Slab B2
由图7(a)和图7(b)可知,一方面,板顶裂缝主要集中在受火跨B跨,且主要为南北向裂缝。另一方面,板底最大爆裂深度(42 mm)和面积(1.15 m2)基本与B1板A跨类似。
3) 板B3
27 min时,A跨板顶出现少量水蒸汽,沿裂缝处形成水膜;31 min时,A跨板顶水蒸汽逐渐增多,直至67 min。90 min时,A跨停火,B跨点火,109 min时,B跨出现水蒸汽且逐渐增多,117 min时,B跨水蒸汽达到顶峰,直至149 min;期间,B跨板底出现一声爆裂。180 min时,B跨停火,C跨点火,C跨水蒸汽集中出现在200 min~236 min。板顶(底)裂缝如图8(a)~图8(d)所示。
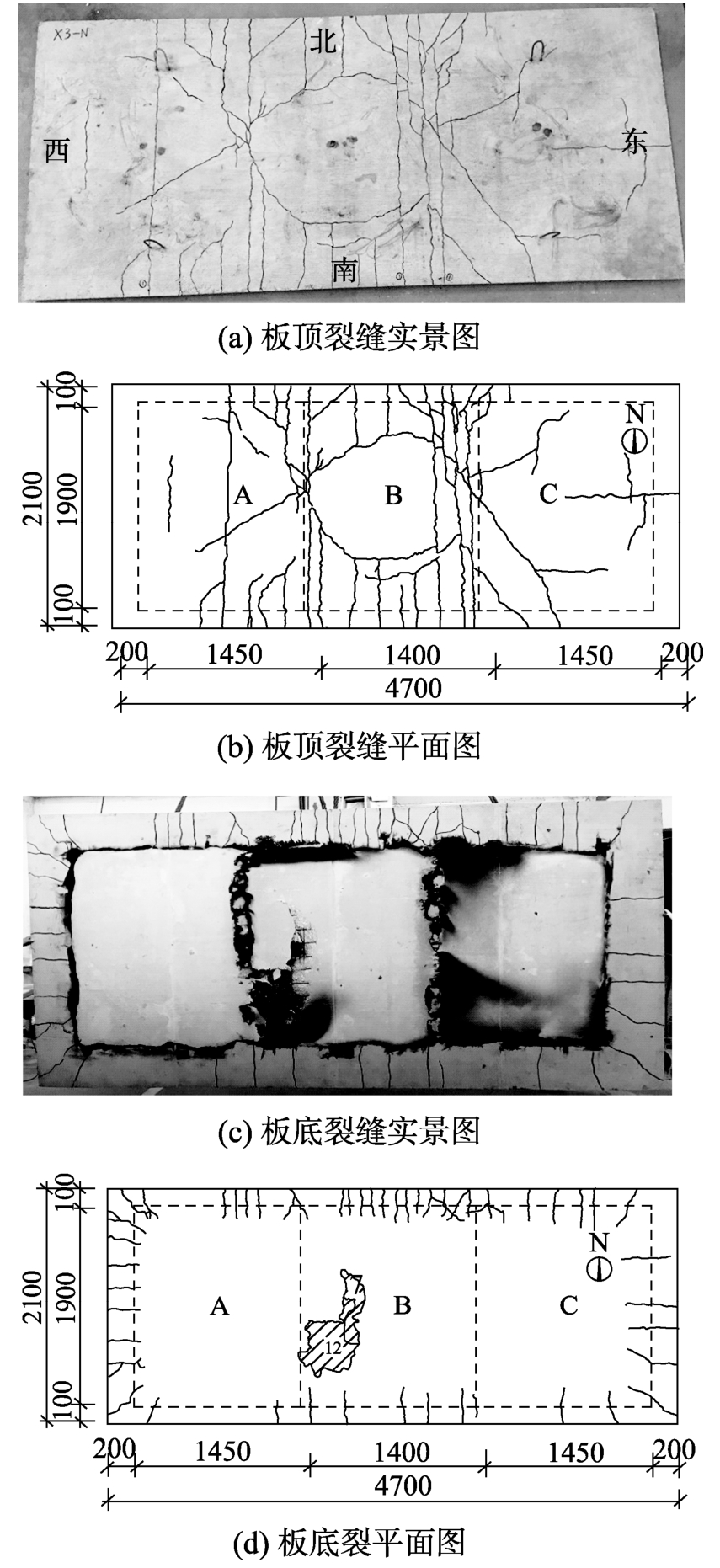
图8 板B3板顶和板底裂缝分布图 /mm
Fig.8 Crack pattern on top and bottom surfaces of Slab B3
由图8(a)和图8(b)可知,一方面,板顶裂缝大致基本呈现对称分布,裂缝主要集中在边界和两内部支座位置。相比两边跨,B跨裂缝相对较多。另一方面,板底短向裂缝主要集中在短边,B跨板底出现轻微爆裂,少量钢筋基本露出,最大爆裂深度和总面积分别为12 mm和0.15 m2。对比B1和B2板可知,混凝土板龄期对板底爆裂有决定性影响。
4) 板B4
0 min时,B跨点火,23 min~66 min该跨出现水蒸汽,且26 min~44 min板底爆裂。110 min~140 min,两边跨水蒸汽发展阶段,106 min~130 min为A跨板底爆裂阶段。试验后,板顶(底)裂缝如图9(a)~图9(d)所示。

图9 板B4板顶和板底裂缝分布图 /mm
Fig.9 Crack pattern on top and bottom surfaces of Slab B4
由图9(a)和图9(b)可知,一方面,由于荷载和火灾工况对称,板顶裂缝大致呈现对称分布。另一方面,相比A和C跨,B跨爆裂较为严重,B跨最大爆裂深度和总面积分别为36 mm和0.53 m2。原因在于,B跨先受火时,由于两边跨温度较低,B跨热膨胀作用受到限制,产生较强压力,致使爆裂较为严重。因此,火灾发生顺序对混凝土板板底爆裂行为有重要影响,特别是中跨。
5) 对比分析
通过对四块板破坏模式进行对比,可知火灾蔓延工况、龄期和荷载对混凝土板顶(底)裂缝和爆裂行为有重要影响。
一方面,对任一火灾工况,受火跨板顶裂缝数量较多,且随着受火跨增多,总体裂缝数量增多。相比两边跨,中跨及第二和第三支座处南北向裂缝相对较多,应加强该位置配筋。另一方面,相比火灾工况和荷载,龄期对混凝土板爆裂行为有决定性影响,特别是中跨,严重时整跨出现爆裂。
同时,本文结果与文献[13]试验板裂缝、爆裂行为进行定性对比分析,相同火灾工况下,增加板厚,延长龄期,可以降低混凝土板爆裂程度,但不能改变板顶(底)裂缝破坏样式,即板顶多为南北向裂缝,板底多为周边短裂缝。
2.2 试验结果
2.2.1 炉温
四板各跨炉温-时间曲线如图10(a)~图10(d)所示。可知,受火跨炉温-时间曲线与ISO-834标准升温曲线大体一致,满足试验要求。

图10 四板平均炉温-时间曲线
Fig.10 Average furnace temperature-time curves of four slabs
由图10可知,对于任一火灾工况,升温阶段受火跨炉温远远高于非受火跨。例如,停火时,受火跨炉温集中在900 ℃~1060 ℃,而非受火跨炉温约为低于200 ℃,如表2所示。此外,停火后,受火跨炉温逐渐降低,而非受跨炉温基本维持不变或略微升高。
表2 各试验板炉温情况
Table 2 Furnace temperature of slabs

板 跨 最高 停火时 结束时平均炉温/(℃)A 1137 1009 303 B1B 196 169 192 B2 C 83 37 83 A 181 131 175 B 1030 1029 285 B3 C 173 93 170 A 1004 943 175 B 1027 907 231 B4 C 1025 962 263 A 1060 1060 227 B 966 955 220 C 1013 968 241
2.2.2 混凝土温度
图11~图14为连续板每跨截面混凝土温度-时间曲线,其中B4-B跨混凝土温度未测到。由图可知,炉温对板截面温度分布起决定性作用。

图11 板B1三跨混凝土温度-时间曲线图
Fig.11 Concrete temperature-time curves of three spans in Slab B1

图12 板B2三跨混凝土温度-时间曲线图
Fig.12 Concrete temperature-time curves of three spans in Slab B2
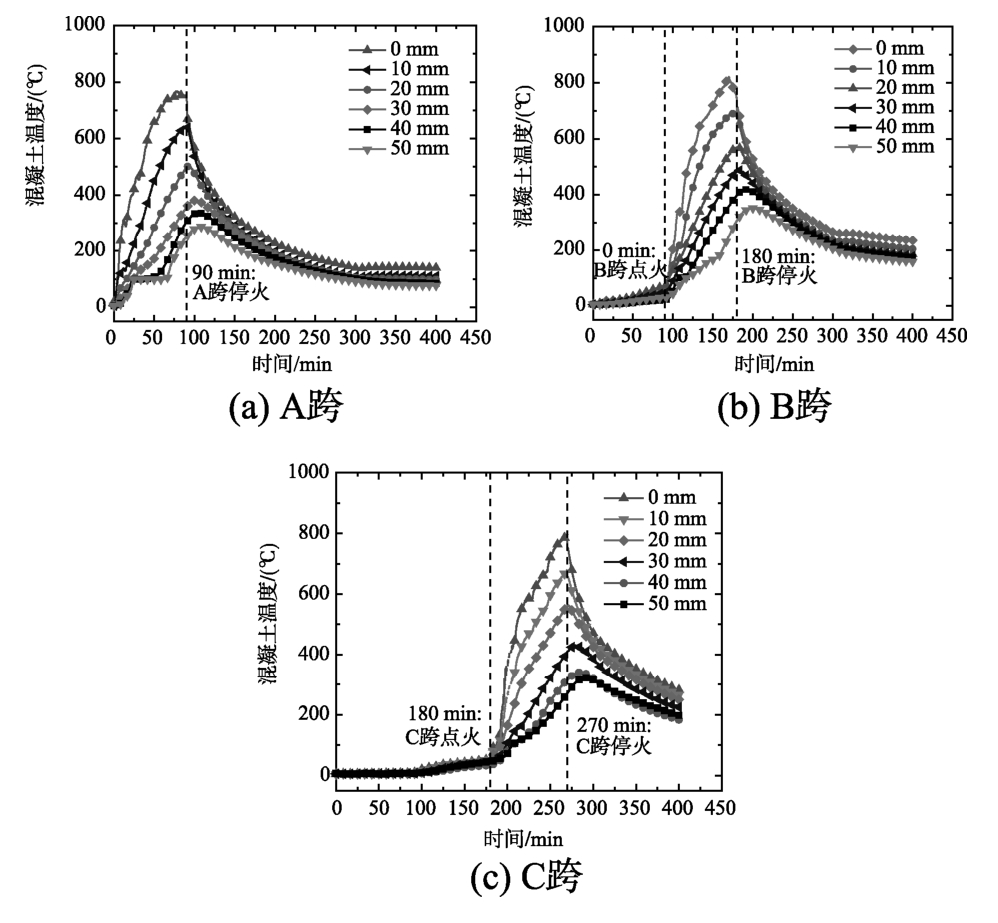
图13 板B3三跨混凝土温度-时间曲线图
Fig.13 Concrete temperature-time curves of three spans in Slab B3

图14 板B4三跨混凝土温度-时间曲线图
Fig.14 Concrete temperature-time curves of three spans in Slab B4
由图11~图14可知,由于厚板较小(基本没有温度平台),停火时,受火跨板顶混凝土温度较高,特别是爆裂较为严重的B1和B2板。例如,对于B1(B2)板,停火时,板底、顶温度值分别为1004.6 ℃(1085.3 ℃)和622.6 ℃(610.1 ℃),温度梯度为382 ℃(475.2 ℃)。对于B3和B4板,受火时长较短,温度较低,受火跨板底(顶)温度平均值分别为751 ℃和495 ℃。对于B1和B2非受火跨,其平均温度通常较低,约为250 ℃,可知其仍具有较强材料强度和结构性能。
2.2.3 钢筋温度
四板各跨板顶(底)钢筋平均温度-时间曲线如图15(a)~图15(d)所示。

图15 四板钢筋平均温度-时间曲线
Fig.15 Average reinforcement temperature-time curves in four slabs
由图15可知,与混凝土温度变化趋势一致,炉温和爆裂对钢筋温度起决定性作用。例如,B1-A跨和B2-B跨板底钢筋较高,停火时板底钢筋平均温度为795.6 ℃和916.2 ℃。对于B3和B4板,受火时长较短,钢筋温度偏低,停火时平均温度约为671.2 ℃和630.8 ℃。此外,对于非受火跨,钢筋平均温度均低于300 ℃。
2.2.4 竖向位移
四板各跨跨中竖向(平面外)位移-时间曲线,如图16(a)~图16(d)所示。其中,负值代表向下,正值代表向上。
1) 板B1
B1板三跨跨中竖向变形-时间曲线,如图16(a)所示。由图16可知,三跨变形趋势明显不同,且A和B跨变形较大,C跨变形基本维持不变。可知单一跨受火时,火灾对较远跨变形行为影响基本可以忽略。

图16 四板跨中竖向位移-时间曲线图
Fig.16 Mid-span vertical deflection-time curves of four slabs
对于受火A跨,前10 min,随着温度增加,变形增加,直至达到−10 mm。随后,A跨混凝土板底出现爆裂(较小温度梯度),且荷载较小(表1),变形出现反转,即变形持续向上发展,直至180 min,变形达到15 mm。这一行为明显与文献[13]边跨试验结果不同。对于文献[13]试验板或简支板[24],通常跨中变形随着温度增加,始终向下发展,原因在于材料性能退化、温度梯度和荷载共同作用。
对于未受火B跨,变形始终向上发展,早期阶段变形速率较大,随后变形速率降低,且180 min最大变形值为6 mm。可见,相比A跨,B跨竖向变形较大,而C跨变形基本可忽略。降温阶段,A和B跨变形逐渐恢复,400 min时残余变形分别为-1 mm和2 mm。
2) 板B2
板B2三跨跨中竖向变形-时间曲线,如图16(b)所示。由图16可知,由于边界条件对称,试验板两边跨变形趋势基本一致,变形值较小,明显与中跨变形趋势不同。
对于中跨B,随着温度升高,变形上拱(拱效应),总体表现为逐渐增加,180 min时,变形达到21.9 mm。降温阶段,中跨变形随后恢复,400 min残余变形为3.4 mm。对于两边跨,早期阶段变形向下发展,30 min左右达到最大值,随后变形开始向上发展直至180 min。总之,相比受火跨B,两边跨变形基本可以忽略。对比B1板,可知受火跨位置对非受火跨变形行为有一定影响。
此外,与文献[13]中跨受火试验板进行对比,表明各跨变形趋势基本一致。因此,相比板厚和活荷载,中跨炉温对其变形趋势影响更大。同时,与B1板对比分析,表明火灾发生位置对结构中各板跨中变形趋势有重要影响。
3) 板B3和B4
图16(c)为板B3三跨跨中竖向变形-时间曲线。明显地,板B3中三跨跨中变形趋势与B1和B2板不同,特别是B3板中B跨,原因可能在于较大活荷载(表1)。值得指出的是,B3板中B跨变形趋势与文献[13]中相同火灾蔓延工况三跨连续板B跨变形趋势不同,原因在于文献中板较厚(100 mm),有较大温度梯度。
一方面,对于A和C两边跨,各自升温阶段变形趋势基本一致,且受火90 min时变形分别为-29 mm和-32 mm,较为接近。可见边跨变形主要取决于炉温和受火时长。另一方面,对于该板B跨,受火前变形基本维持不变,90 min开始受火后变形快速增加,180 min变形达到-23 mm。对比B1和B2板,可知中跨变形取决于其临跨火灾工况。然而,与文献[13]连续板相比,相比临跨火灾工况,板厚(跨厚比)和荷载对火灾下连续板B跨跨中变形影响也有一定影响,即随着跨厚比增大和荷载增加,临跨火灾工况对连续板中跨变形行为的影响逐渐降低,此时中跨跨中变形趋近于单一简支板火灾行为,即自身火灾工况成为关键影响因素之一。
图16(d)为板B4三跨跨中竖向变形-时间曲线。由图可知,对比板B3,受火次序对板B4中跨变形有重要影响,对边跨影响相对较小。
一方面,对于中跨B,36 min前,B跨竖向变形达到最大-5 mm;随后,由于两临跨约束作用,变形向上发展,90 min停火时,变形为5.5 mm。可见,受压薄膜效应有助于降低板变形。然而,值得指出的是,对比B2、B3和B4板可知,较强受压薄膜效应,会致使中跨更易爆裂。因此,有必要加强连续板中跨抗爆裂设计,防止其过早出现完整性破坏。
另一方面,对于两边跨,变形规律与B3板两边跨一致,即随着温度增加变形持续增加,180 min停火时,两边跨变形值均为−27.6 mm,可见变形值基本与B3板中两边跨相同,即自身火灾工况对边跨位移最大值起决定性作用。这一点与文献[13]研究结果类似。
4) 对比分析
通过以上分析,火灾蔓延工况、板厚、荷载和龄期对混凝土连续板各跨火灾行为有重要影响,可得出以下结论:
① 龄期和保护层对混凝土连续板各跨爆裂有决定性影响。龄期较短时,各跨易发生爆裂。随着龄期增加,边跨爆裂可能性大大降低;然而,中跨爆裂可能性仍较大,特别是两边跨未受火时。由于板保护层较小,爆裂后通常露出板底钢筋。
② 连续板各跨板顶裂缝主要集中在受火跨及其内部支座附近,板底多为板边短裂缝。随着受火跨数量增多,裂缝数量逐渐增多。因此,相比其他因素,火灾蔓延工况对混凝土连续板整体裂缝分布和破坏模式有决定性影响,特别是板顶方面。
③ 火灾蔓延工况、荷载和爆裂情况对混凝土连续板各跨变形趋势有决定性影响,火灾时长对最大变形值有重要影响。对于边跨,未发生爆裂时,其跨中变形通常向下发展,且随着受火时间延长,变形增大。对于中跨,其变形趋势取决于各跨受火次序,最大变形值取决于受火时长。
④ 相比单向连续板[1-2]和预应力混凝土连续板[3-4],混凝土双向连续板具有较好的抗火性能,特别是完整性方面。例如,连续单向板易出现贯穿板厚裂缝和板块断裂,预应力连续板易出现爆裂和预应力筋断裂等。
总之,混凝土连续板各跨火灾行为取决于上述很多因素,即火灾下连续板每跨最不利工况不能仅仅通过一个或几个因素来确定,需要综合考虑各方面因素相互影响。这一点明显不同于常温工况。因此,对于相同板,不同火灾工况下,两者变形趋势可能较为一致,但力学机理可能完全不同。
2.2.5 平面内位移
四板平面内位移-时间曲线,如图17(a)~图17(d)所示。其中,正值代表膨胀,负值代表收缩。
由图17可知,对于任一火灾工况,升温阶段混凝土板趋向于向外膨胀,且火灾蔓延工况对各方向平面内位移发展趋势有重要影响。
一方面,测点距离受火跨越近,其膨胀越大,反之越小。例如,相比板B1-H1测点位移,其余三测点平面内位移基本可忽略。同时,可见平面内位移早期膨胀阶段速率较大,后期速率明显降低,原因在于裂缝开展和升温速率降低。另一方面,相比短跨(南北)方向,长跨(东西)方向平面内位移通常较大。这一点与文献[13]结果相同,但最大变形值较小。
对于降温阶段,平面内位移逐渐恢复。由于纵横向裂缝存在,平面内位移存在残余变形,各测点残余值存在一定差别。
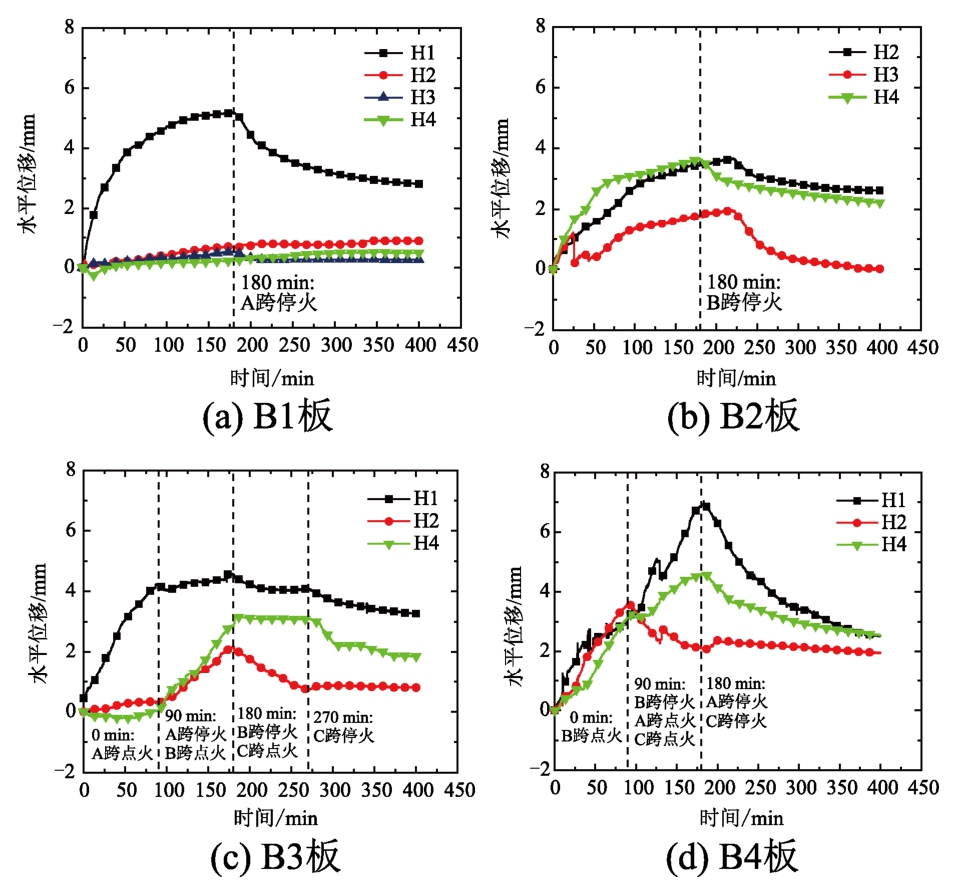
图17 四板平面内位移-时间曲线
Fig.17 In-plane deflection-time curves of four slabs
2.3 耐火极限
混凝土结构耐火极限准则包括温度(钢筋和混凝土)准则、完整性准则和承载力准则(变形准则)[25]。混凝土温度准则为板顶平均温度超过140 ℃或任一测点温度超过180 ℃;钢筋温度准则为板底钢筋温度超过593 ℃。变形破坏准则为跨中位移超过一定值,如l/50、l/30或l/20。因此,采用上述准则确定混凝土连续板各跨耐火极限,如表3所示。值得指出的是,耐火极限从板各跨直接受火开始进行计算,其中“*”代表未发生破坏,“-”未获得相应温度试验数据(B4-B跨)。
由表3可知,对于受火跨,由于板厚较小,混凝土和钢筋破坏准则通常被达到,相应耐火极限平均值分别为13.1 min(板厚和爆裂)和63.6 min。然而,对于变形破坏准则(l/50),其耐火极限值相对较大,且多数受火跨未出现破坏。总之,与试验结果相比,上述破坏准则所得耐火极限偏于保守。此外,对于非受火跨,可不考虑火灾工况对其耐火性能影响。
总之,对于传统温度和变形破坏准则,均基于单个因素确定板耐火极限。然而,试验表明,混凝土板破坏行为取决于火灾蔓延工况、龄期、板厚、荷载、爆裂和边界情况等,并非单一因素决定。可见,传统破坏准则可能不适用于火灾蔓延工况。
表3 基于不同破坏准则的混凝土板耐火极限
Table 3 Fire resistance of concrete slabs based on different failure criteria

板 钢筋温度准则 混凝土温度准则 变形准则(l/50)耐火极限/min A41.7 5.7 *B1B * 118.0 ** * *A* * *B58.3 14.2 *C B2* * *A74.5 18.8 89.7 B65.2 7.7 *C B3 B4 C52.3 12.3 70.2 A69.3 13.7 *B― ― *C83.7 19 *
3 数值分析
在试验基础上,采用Vulcan软件仅对试验板开展数值分析,由于模型限制(未考虑爆裂),仅对B3板进行温度场和变形计算,并开展机理分析(弯矩分布和薄膜机理)。
3.1 单元模型
温度场分析时,计算采用矩形单元模型,如图18(a)所示,即沿板厚划分25层,每层厚度2 mm。其中,混凝土表面辐射系数取值为 0.8,火焰辐射系数取值为0.6,表面吸收系数为 0.8。混凝土热工性能采用 EC2 模型[26],骨料类型采用钙质。
如图18(b)~图18(d)所示,结构分析时采用9节点厚板单元(9个高斯点G1~G9),平面单元网格为7×14,单元数为98,沿板厚划分11层(包括4层等效钢筋层和7层混凝土层)。分析时,板边界支座以及中间支座均采用简支边界。除特殊说明外,高温材料力学性能采用 EC2 模型[26]。
3.2 温度场分析
B3板三跨温度计算结果和试验结果对比,如图19(a)~图19(c)所示。由图19可知,计算结果与试验结果吻合较好,变化趋势较为一致,计算温度可用于混凝土连续双向板变形和力学机理分析。

图18 试验板温度和结构分析单元模型 /mm
Fig.18 Element models of temperature and structural analysis of tested slabs
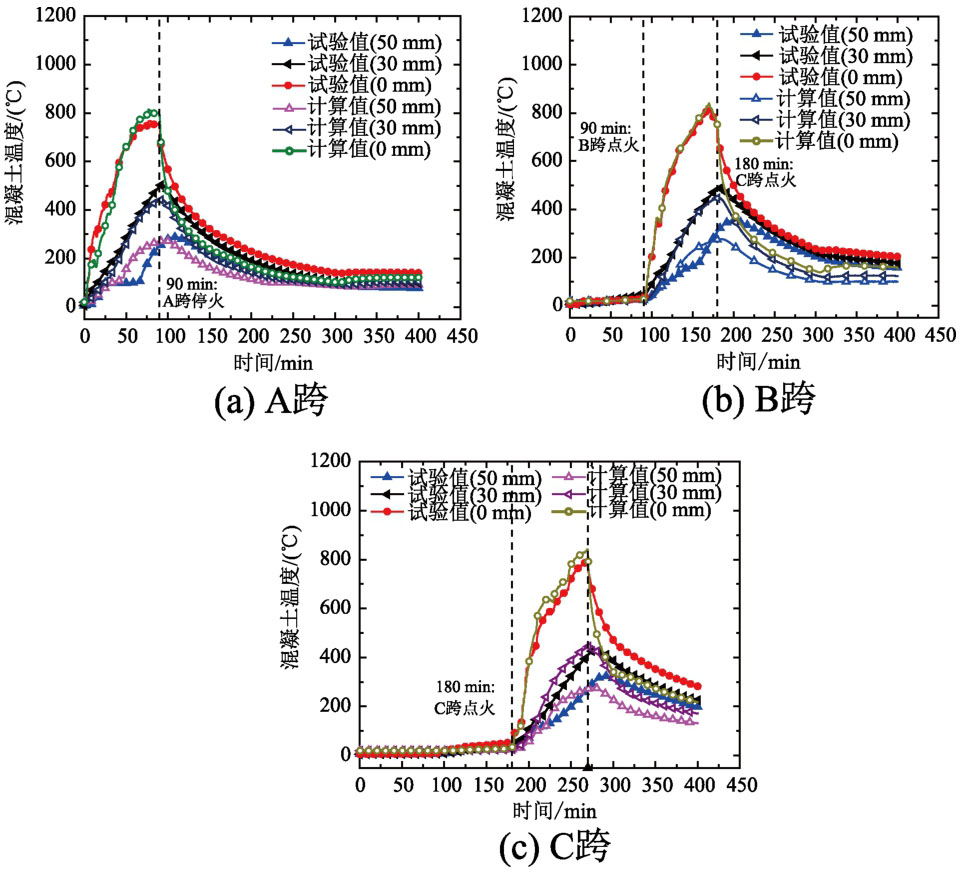
图19 板B3温度计算值和试验值对比
Fig.19 Comparison of predicted and tested temperatures of Slab B3
3.3 变形和机理分析
3.3.1 变形分析
采用几何(非)线性模型以及两混凝土膨胀应变模型(EC2模型[26]和Lie模型[27]),对混凝土连续板各跨变形进行分析,计算结果如图20(a)~图20(c)所示。
由图20可知,对于火灾初期,由于变形较小和温度较低,几何(非)线性和混凝土膨胀应变对混凝土板各跨火灾行为影响较小;然而,随着变形增加和温度升高,上述因素影响逐渐增大。与试验结果相比,基于EC2模型,并采用几何非线性方法所得计算结果较为合理。然而,Lie模型混凝土膨胀应变较小,倾向于低估混凝土板各跨跨中变形。同时,由于几何线性方法忽略薄膜效应影响,与试验结果相比,其计算变形偏小,特别是Lie模型。这一点与文献[28]结论类似。
对于降温阶段,几何(非)线性和混凝土膨胀应变对各跨跨中变形影响逐渐降低,相互差异逐渐减小,且计算残余变形绝对值通常小于试验值。主要原因在于降温阶段所用混凝土和钢筋力学模型未能反映该阶段实际材性。因此,降温阶段力学模型有待改进[29-30]。

图20 板B3跨中挠度-时间计算曲线与试验曲线对比
Fig.20 Comparison of predicted and tested mid-span deflection-time curves of Slab B3
3.3.2 机理分析
在变形分析基础上,对连续板各跨弯矩分布和薄膜机理进行分析。
1) 弯矩分布
图21(a)~图21(d)为采用几何(非)线性程序所得B3板不同时刻弯矩图(x方向),即为单元(43~56)中G5点弯矩值(图18(c)和图18(d))。对于任一膨胀应变模型,由于变形较小,几何(非)线性计算结果所得弯矩值和发展趋势较为接近。然而,相比几何(非)线性模型,混凝土热膨胀应变对连续板各跨弯矩影响较大,致使两模型所得变形值差别较大。
以EC2模型为例(图21(a)),板边弯矩较小,其变化幅度较小;相反,各跨跨中弯矩较大,且随温度变化幅度较大。0 min时,各跨跨中均为正弯矩,且较接近;随后,A跨升温,其负弯矩逐渐增加,变形逐渐增加。相比A跨,B和C两跨弯矩较小,进而变形较小。例如90 min时,A、B和C三跨跨中弯矩分别为-354.65 N·m、-63.47 N·m和46.93 N·m。待A跨停火,B跨升温,A跨负弯矩逐渐降低(变形恢复),B跨负弯矩增加(变形增加),此时C跨负弯矩开始发展。例如,180 min时,A、B和C三跨跨中弯矩分别为-151.25 N·m、-352.87 N·m和-56.74 N·m。同样,待A和B跨停火,C跨开始升温,各跨弯矩发展也存在类似规律。
总之,相比EC2模型,Lie模型倾向于低估各跨弯矩值,进而致使其计算变形值偏小。同时,当变形较小时,火灾蔓延行为对各跨弯矩发展情况有决定性影响。

图21 不同混凝土膨胀模型和几何特性所得板B3弯矩对比
Fig.21 Comparison of bending moments of Slab B3 predicted by different thermal models and geometrical properties
2) 薄膜机理分析
在弯矩分析基础上,对B3板薄膜发展规律(EC2模型和Lie模型)进行对比分析,如图22和图23所示。值得指出的是,对于薄膜效应(单位:N/mm),灰色代表受拉薄膜效应,黑色为受压薄膜效应,线长度表示薄膜大小。清晰可见,图22(a)和图23(a)数据均放大100倍,其余图中数据均缩小20倍。
图22(a)~图22(d)为EC2模型所得连续板B3在不同时刻薄膜效应图。由图22可知,0 min,连续板各跨薄膜力较小,且各跨跨中区域为受拉薄膜效应,周边为受压薄膜效应。以A跨为例,中心区域(单元31、32、45、46、59和60)受拉薄膜效应均值为0.018,周边区域(单元16~19)受压薄膜效应均值为0.021。

图22 板B3不同时刻薄膜效应分布 (EC2 model)
Fig.22 Membrane action distributions of Slab B3 at different time instances (EC2 model)
随着温度升高,A跨跨中区域受压薄膜效应逐渐增加,而该跨外周边为受拉薄膜效应,致使沿外周边出现垂直板边短裂缝(见图8(d));同时,相邻B跨以受拉薄膜效应为主,且C跨拉压薄膜力均较小,如图22(b)所示。可见各跨拉压薄膜效应分布和大小发生较大变化。例如,90 min时,A跨支座区域受压薄膜效应较大(如33、47和61三单元均值约为179.2),其跨中区域受压薄膜效应较小。B跨跨中区域(如35、36、49、50、63和64单元)受拉薄膜效应均值约为35.83,C跨整垮所有单元压(拉)薄膜效应均值约为15.02(9.14)。
90 min后,A跨跨中区域受压薄膜效应逐渐降低,且第2支座附近区域逐渐出现受拉薄膜效应,进而出现较多裂缝(见图8(a))。同时,B跨跨中受压薄膜效应和第3支座附近受拉薄膜效应逐渐增加,如图22(c)所示。对于C跨,也存在类似薄膜效应发展规律。因此,对比可知,火灾蔓延行为对各跨跨中区域受压薄膜效应及其支座区域受拉薄膜效应的发展有决定性影响。
此外,图23(a)~图23(d)为Lie模型所得连续板B3薄膜效应图。与弯矩值类似,相比EC2模型,Lie模型所得受(压)薄膜效应区域形状基本类似,但相应值较小。

图23 板B3不同时刻薄膜效应分布 (Lie 模型)
Fig.23 Membrane action distributions of Slab B3 at different time instances (Lie model)
4 结论
本文开展火灾蔓延工况下混凝土连续板力学行为试验研究,获得了受火跨位置和数量、火灾蔓延时间间隔、龄期和荷载等对试验板各跨温度、变形、裂缝、爆裂和破坏模式等影响规律;在此基础上,采用Vulcan程序,对一试验板火灾行为进行数值分析,具体得出以下结论:
(1) 混凝土龄期、受火跨位置和数量对混凝土连续板整体裂缝模式和爆裂有重要影响;对于短龄期混凝土连续板,任一火灾工况,受火跨均易发生严重爆裂;对于长龄期混凝土连续板,相比边跨,受火中跨爆裂可能较大。随着受火跨增多,板顶裂缝数量总体增加,且多集中在受火跨内部支座附近。
(2) 初始受火跨位置和火灾蔓延方向对连续板各跨跨中竖向变形趋势有决定性影响,特别是中跨。具体地,除非严重爆裂,边跨通常出现向下变形;对于中跨,其可能出现向上或向下变形。
相比受火跨及其临跨,远端非受火跨跨中变形基本可以忽略。此外,对于各跨最大变形值,取决于火灾蔓延时间间隔和受火时长。
(3) 混凝土膨胀应变对连续板各跨弯矩值有重要影响;火灾蔓延行为对各跨薄膜机理发展有决定性影响,进而建立相应耐火极限准则时应考虑火灾蔓延行为影响。
[1]陈礼刚, 董毓利, 李晓东.钢筋混凝土三跨连续板中跨受火试验研究[J].建筑结构, 2004, 34(4): 39―41, 53.Chen Ligang, Dong Yuli, Li Xiaodong.Experimental study on mid-span fire of reinforced concrete three-span continuous slab[J].Building Structure, 2004, 34(4): 39―41, 53.(in Chinese)
[2]陈礼刚, 高立堂, 李晓东, 等.两邻跨受火RC三跨连续板抗火性能试验研究[J].西安建筑科技大学学报:自然科学版, 2006, 38(1): 100―104.Chen Ligang, Gao Litang, Li Xiaodong, et al.Study on the fire resistance of the 3-span RC continuous slabs when the two adjacent spans are on fire[J].Journal of Xi’an University: Science and Technology Edition, 2006,38(1): 100―104.(in Chinese)
[3]袁爱民, 董毓利, 戴航, 等.无粘结预应力混凝土三跨连续板火灾试验研究[J].建筑结构学报, 2006, 27(6):60―66.Yuan Aimin, Dong Yuli, Dai Hang, et al.Experimental investigation of unbonded prestressed concrete continuous slab subjected to fire[J].Journal of Building Structures, 2006, 27(6): 60―66.(in Chinese)
[4]郑文忠, 侯晓萌, 许名鑫.两跨无粘结预应力混凝土连续板抗火性能试验与分析[J].建筑结构学报, 2007,28(5): 1―13.Zheng Wenzhong, Hou Xiaomeng, Xu Mingxin.Experimentand analysis on fire resistance of two-span unbonded prestressed concrete continuous slabs[J].Journal of Building Structures, 2007, 28(5): 1―13.(in Chinese)
[5]杨志年, 董毓利, 吕俊利, 等.整体结构中钢筋混凝土双向板火灾试验研究[J].建筑结构学报, 2012, 33(9):96―103.Yang Zhinian, Dong Yuli, Lü Junli, et al.Experimental study of two-way reinforced concrete slab subjected to fire in a whole structure[J].Journal of Building Structures, 2012, 33(9): 96―103.(in Chinese)
[6]Wang Y, Dong Y L, Li B.A fire test on continuous reinforced concrete slabs in a full-scale multi-story steel-framed building[J].Fire Safety Journal, 2013, 61:38―48.
[7]李兵, 董毓利, 娄永杰, 等.足尺钢框架中连续板格火灾试验研究[J].工程力学, 2015, 32(1): 145―153.Li Bing, Dong Yuli, Lou Yongjie, et al.A fire test of continuous panels in a full-scale steel-framed structure[J].Engineering Mechanics, 2015, 32(1): 145―153.(in Chinese)
[8]Dong Y L, Zhu C J.Limit load carrying capacity of two-way slabs with two edges clamped and two edges simply supported in fire[J].Journal of Structural Engineering, 2011, 137(10): 1182―1192.
[9]Wang Y, Yuan G L, Huang Z H, et al.Experimental study on the fire behavior of reinforced concrete slabs under combined uni-axial in-plane and out-of-plane loads[J].Engineering Structures, 2016, 128: 316―332.
[10]Wang Y, Bisby L A, Wang T Y, et al.Fire behaviour of reinforced concrete slabs under combined biaxial in-plane and out-of-plane loads[J].Fire Safety Journal, 2018, 96:27―45.
[11]王勇, 段亚昆, 张亚军, 等.单向面内约束混凝土双向板抗火性能试验研究及数值分析[J].工程力学, 2018,35(3): 65―78.Wang Yong, Duan Yakun, Zhang Yajun, et al.Experiment and numerical analysis on the fire-resistant performance of two-way concrete slabs with unilateral in-plane restraints[J].Engineering Mechanics, 2018, 35(3):65―78.(in Chinese)
[12]王勇, 史伟男, 王腾焱, 等.单向面内约束混凝土双向板火灾试验及承载力分析[J].工程力学, 2017, 34(11):145―157.Wang Yong, Shi Weinan, Wang Tengyan, et al.Fire test and limit carrying capacity analysis of two-way concrete slabs with unilateral in-plane restraints[J].Engineering Mechanics, 2017, 34(11): 145―157.(in Chinese)
[13]王勇, 段亚昆, 张亚军, 等.不同跨依次受火混凝土连续板试验研究及理论分析[J].土木工程学报, 2019,52(9): 23―40.Wang Yong, Duan Yakun, Zhang Yajun, et al.Experimental study and theoretical analysis of concrete continuous slabs with different spans subject to fire in order[J].China Civil Engineering Journal, 2019, 52(9):23―40.(in Chinese)
[14]Liao F Y, Huang Z H.Modelling localised fracture of reinforced concrete structures[J].Engineering and Computational Mechanics, 2016, 169(2): 53―69.
[15]Wang Y, Yuan G L, Huang Z H, et al.Modelling of reinforced concrete slabs in fire[J].Fire Safety Journal,2018, 100: 171―185.
[16]Linus L, Andrew B, Peter M, et al.Numerical modelling of two-way reinforced concrete slabs in fire[J].Engineering Structures, 2004, 26: 1081―1091.
[17]Tom M, Ruber V C, Thomas G.Assessment of damage and residual load bearing capacity of a concrete slab after fire: Applied reliability-based methodology[J].Engineering Structures, 2017, 150: 969―985.
[18]Thomas G, Jean-Marc F.A plastic-damage model for concrete in fire: Applications in structural fire engineering[J].Fire Safety Journal, 2015, 71: 268―278.
[19]Gernay T, Franssen J M.A formulation of the Eurocode 2 concrete model at elevated temperature that includes an explicit term for transient creep[J].Fire Safety Journal,2012, 51: 1―9.
[20]Jiang J, Li G Q.Parameters affecting tensile membrane action of reinforced concrete floors subjected to elevated temperatures[J].Fire Safety Journal, 2018, 96: 59―73.
[21]Egle R, Panagiotis K, Ann J, et al.Structural analysis of multi-storey steel frames exposed to travelling fires and traditional design fires[J].Engineering Structures, 2017,150: 271―287.
[22]GB 50010―2010, 混凝土结构设计规范[S].北京: 中国建筑工业出版社, 2010.GB 50010―2010, Code for design of concrete structures[S].Beijing: China Architecture and Building Press,2010.(in Chinese)
[23]GB 50016―2014, 建筑设计防火规范[S].北京: 中国计划出版社, 2014.GB 50016―2014, Code for fire protection design of buildings[S].Beijing: China Planning Press, 2014.(in Chinese)
[24]王滨, 董毓利.四边简支钢筋混凝土双向板火灾试验研究[J].建筑结构学报, 2009, 30(6): 23―33.Wang Bin, Dong Yuli.Experimental research of four-edge simple support two-way reinforced concrete slab under fire[J].Journal of Building Structures, 2009,30(6): 23―33.(in Chinese)
[25]GB/T 9978―2008, 建筑构件耐火试验方法[S].北京:中国标准出版社, 2008.GB/T 9978―2008, Fire-resistance tests-elements of building[S].Beijing: China Standard Press, 2008.(in Chinese)
[26]Eurocode 2: design of concrete structures, ENV 1992:Part 1-2: General rules-structural fire design[S].Brussels: Belgian Application Document, 1999.
[27]ASCE: Structural fire protection, Manual No.78, ASCE committee on fire protection, structural division[S].New York: American Society of Civil Engineers, 1992.
[28]王勇, 袁广林, 王腾焱, 等.双向面内约束混凝土板火灾试验及数值分析[J].土木工程学报, 2018, 51(5):48―59.Wang Yong, Yuan Guanglin, Wang Tengyan, et al.Fire test and numerical analysis on concrete slabs with bi-axial in-plane restraints[J].China Civil Engineering Journal, 2018, 51(5): 48―59.(in Chinese)
[29]Guo S, Bailey C G.Experimental behaviour of composite slabs during the heating and cooling fire stages[J].Engineering Structures, 2011, 33: 563―571.
[30]Akanshu S, Josipa B, Saskia B.Experimental investigations on residual bond performance in concrete subjected to elevated temperature[J].Engineering Structures, 2019, 187: 384―395.