我国中西部地区地形和地貌复杂，交通线路常需桥梁结构跨越深谷与沟壑。矮塔斜拉桥因同时具有连续梁桥整体刚度大、经济性好以及斜拉桥跨越能力强等优点而成为该地区常用的桥梁形式[1]。但因缺乏相关抗震性能研究成果，国内外抗震设计规范并未提出此类桥梁的简化设计方法，而一般采用时程分析法得到地震响应。此外，桥梁因地形原因而采用较大跨径时，地震动的行波效应则不应忽视。李小珍等[2]发现相比于一致激励，矮塔斜拉桥墩柱在非一致激励下的弹塑性响应会增大，因此不考虑行波效应易造成墩柱延性设计的误判。但项海帆[3]利用影响矩阵概念发现对于大跨度斜拉桥，非同步激励能起到抵消位移的有利作用。可见行波效应对大跨度桥梁地震响应的影响存在两面性，常因地震动视波速或结构形式等条件而改变[4－5]。此观点已通过振动台试验得到证实[6－7]。因此，在对大跨度矮塔斜拉桥进行地震分析时需采用非一致激励以捕捉行波效应带来的双面影响。但非一致激励的引入极易引起桥梁上部结构发生碰撞破坏。这一碰撞现象已引起许多学者的关注[8－11]，Zheng等[9]以考虑主梁与桥台间碰撞的连续桥梁为对象，对比了一致激励和非一致激励输入时的动力响应，发现非一致激励会增大碰撞带来的不利影响。但Won等[10]通过时程分析却得出碰撞的出现能减小墩柱内力和位移的结论。此外，闫聚考等[11]在振动台试验中发现考虑行波效应时，大跨度悬索桥与引桥间的碰撞力大小和发生次数因地震动不同而存在差异。由此可见地震下的碰撞对桥梁结构响应的影响未取得统一定论，其同样与结构形式和地震动特性有关。因此，为更为准确地模拟大跨度桥梁在地震作用下的碰撞响应，为抗震设计提供数据支持，较为合理的方法是使用多条地震动进行非一致激励输入时程分析。但此作法需要消耗大量时间和运算成本，效率较低。
为高效获取复杂结构在不同地震动强度下的动力响应，伊朗学者Estekanchi提出了耐震时程法(ETM)的理念[12]，且被证实可用于多种结构体系的抗震分析，如钢筋混凝土框架[13－14]、钢框架[15－16]、钢储液罐[17]和拱形大坝等[18]。此方法通过输入幅值随时间增大的地震动进行结构抗震设计和性能评估，综合了时程分析的动力效应和Pushover分析的简便性。此外，对于桩土相互作用或碰撞接触等复杂的边界约束条件，耐震时程法也可捕捉到其对结构响应的影响[19－20]。然而这种方法还未被用于考虑行波效应时的大跨度矮塔斜拉桥抗震分析中。
本文首先依据《城市桥梁抗震设计规范》中的反应谱合成了三条适用于我国桥梁结构的耐震时程曲线；并以一座跨越山谷地带的典型大跨度矮塔斜拉桥为研究对象，对比耐震时程分析(ETA)与增量动力分析(IDA)结果，验证了考虑行波效应时，耐震时程分析快速得到大跨度桥梁碰撞响应的可行性；最后，采用此方法进行了不同地震动视波速下，矮塔斜拉桥与桥台间碰撞力、主梁和塔顶位移以及墩柱曲率变化趋势的分析。
1 耐震时程法
1.1 耐震时程法基本原理
作为一种新的动力评估方法，耐震时程分析的基本理念是将幅值随时间不断增长的人工地震动作用于结构上进行动力分析评估。与传统IDA分析需要对地震动调幅进行大量运算不同，耐震时程法所施加地震动的幅值是随时间不断增大的，因此只需一次时程分析便可使结构完成从弹性到屈服、损伤以至倒塌的全过程。在ETA分析中，耐震时间成为表征地震动强度的指标，因此结构达到目标性能时所经历的耐震时间越长，表明此结构抗震性能越优。
得到合适的耐震加速度时程曲线是保证耐震分析准确的关键，在第二代耐震时程曲线的合成中，需满足从0开始至任意时刻t的地震时程曲线，其所得加速度反应谱值与该持时t成线性关系，即如式(1)所示[21]：
式中：T为结构的自振周期；SaC(T)为规范反应谱；t为任意耐震时刻；tT为用于缩放耐震时程的目标时间；SaT(T,t)为t时刻的目标加速度反应谱。
从式(1)可以看出：在tT和SaC(T)给定的前提下，当t取为tT/2时得到的反应谱为规范反应谱的一半，而取t=tT时的加速度反应谱与规范反应谱吻合，以此类推。为满足式(1)中任意时刻时间t都与反应谱保持线性关系，采用无约束变量优化法进行优化，得到式(2)：
式中：ag为合成的耐震加速度时程曲线；F(ag)为目标耐震方程；Sa(T,t)为0～t时段内的耐震加速度反应谱；Tmax和tmax分别为优化时的反应谱最大周期和耐震加速度最大持时。此优化方程通过不断迭代得到一条最优地震动ag，使该地震动在任意时刻的反应谱和目标谱能最大程度吻合。
1.2 基于我国桥梁抗震规范的耐震曲线
本文以我国《城市桥梁抗震设计规范》(CJJ 166 －2011)的加速度反应谱为目标谱，采用MATLAB软件合成了三条适用于桥梁抗震分析的耐震时程曲线，其中规范谱的平台段谱值取为0.5 g，对应的场地类别、分区和特征周期分别为Ⅰ类、3区和0.35 s。在求解式(2)的非线性最小二乘问题时需大量的运算迭代，周期Tmax和耐震持时tmax分别取为6 s和30 s，优化间隔分别取为0.01 s和0.05 s，因此，周期和耐震持时优化点均为600个；目标时间tT的取值与结构自振周期和耐震曲线最大持时有关，在本研究中取为10 s，即合成的耐震曲线在0 s～10 s的反应谱曲线与规范反应谱曲线保持一致。此外，因优化效率与初始输入地震动有关，为平衡优化时间与精度，以三条SIMQK软件生成的人工地震动为初始输入进行优化迭代。SIMQK软件是一种依据目标反应谱合成人工地震动的程序，其机理是从目标谱中计算出功率谱密度函数，并采用此密度函数推导出0～2π相位角的不同幅值正弦波，进行组合得到地震时程[22]。使用者可依据需求合成不同总持续时间、加速度平稳段开始时间和平稳段持续时间等参数的地震动。本文初始输入生成准则为：地震动只存在上升段，且同样以《城市桥梁抗震设计规范》中反应谱为目标谱。
图1给出其中一条耐震时程曲线图以及此耐震曲线在0 s～10 s、0 s ～20 s和0 s ～30 s三个时间段的耐震反应谱，并与三个时间段内的规范反应谱(将目标规范谱谱值分别扩大1倍、2倍和3倍)进行对比。从图1(a)中可以看到耐震时程曲线的峰值随着时间不断增长，在三个时间段内的最大值分别为0.25 g、0.54 g和0.72 g，与耐震时程法的理念一致。此外，如图1(b)所示，合成的耐震时程曲线在三个时间段内的加速度反应谱与规范反应谱均能较好的吻合，表明此条耐震时程曲线满足合成准则。由式(2)可知合成耐震时程曲线是以加速度反应谱为基础，因此上述与规范加速度谱的吻合是基本条件。而本文需采用大刚度法对基础进行位移输入以考虑行波效应[23]，因此需进一步观察位移谱的吻合性。图1(c)给出了耐震位移反应谱在三个时间段内与规范位移谱的对比。其中规范位移谱可通过式(3)得到：
图1 一条耐震时程曲线及其不同耐震时间下反应谱
Fig.1 An ET accelerogram and the corresponding response spectra with different endurance time
式中，Sa(T,)ξ和Sd(T,)ξ分别为规范加速度和位移反应谱。图1(c)中可以看出虽加速度谱保持一致是合成耐震时程曲线的基本条件，但耐震位移谱与规范位移谱在不同时间段内也能很好的吻合，为行波效应耐震分析提供可能。
2 桥梁计算模型
2.1 桥梁原型概况
本文以我国山谷地带某一实际大跨度三塔双索面矮塔斜拉桥为原型，如图2所示，跨径布置为120 m+2×235 m+120 m，左、右侧通过球形钢支座支撑于桥台处，伸缩缝宽0.5 m。主梁为宽10.3 m的单箱单室混凝土变截面，如截面A-A所示，梁高由跨中6.5 m按圆曲线变化至支点根部12.5 m，顶板和底板厚则分别由0.6 m和0.5 m变化至1.0 m和1.7 m。主梁上部索塔为双柱式，中塔和边塔桥面以上塔高分别为45.0 m和35.5 m，塔身采用矩形实体截面(截面B-B和C-C)，具体尺寸详见图2中表格。上部拉索为平行双索面体系，单侧布置8+9+8=25对斜拉索，拉索在梁上和塔上间距分别为9.0 m和1.1 m，全桥共计100根斜拉索。因山谷地势高差，从左至右墩柱高度分别为80.5 m、164.5 m和53.5 m，其中左、右墩为混凝土矩形双肢薄壁式墩柱(截面D-D)，纵横向长度分别为12.0 m和11.5 m，双肢中心距详见图2中表格；中墩柱采用混凝土空心矩形变截面(截面E-E)，纵向长度为16.0 m，横向宽度由11.5 m渐变至30.0 m。基础均采用承台桩基础，左、右承台截面为17.4 m×26.6 m矩形，由24根直径2.2 m钻孔灌注桩支撑于地基上，其中左侧承台桩长29.0 m，右侧承台桩长20.0 m；中承台截面是31.5 m×37.5 m的矩形，由30根直径2.8 m钻孔灌注桩支撑，桩长为25.0 m。
2.2 桥梁有限元模型
基于Sap2000分析软件建立了考虑主梁与桥台碰撞和桩-土相互作用影响的三维非线性有限元模型，如图3所示，其中桥梁纵向为x轴方向。主梁在地震时假设仍保持为弹性[20]，因此采用弹性模量3.55×104 MPa的三维弹性梁单元进行模拟，除承受自重外，主梁上还需考虑横隔板质量和二期恒载。依据文献[24]的多塔矮塔斜拉桥振动台试验结果可发现，主梁上部塔柱在地震下并未出现裂纹和破坏，因此同样采用弹性梁单元模拟，弹性模量取为3.60×104 MPa。考虑到墩柱在地震作用下易遭受损伤，因此对有限元模型的墩柱采用集中塑性单元用于考虑非线性的影响[25－26]；图3左下部给出塑性区域的典型弯矩-转角示意图，其中屈服点和极限点性能指标依据各截面尺寸和配筋而定，超过极限发生破坏后，截面承载能力降至极限能力的20%[25]。斜拉索采用桁架单元模拟，弹性模量为1.95×105 MPa，同时采用Ernst[27]提出的弹性模型修正公式考虑拉索的垂度效应。此外，通过在单元中以P-Δ力的形式施加恒载轴力用于考虑桥塔、墩柱和斜拉索的几何非线性。为真实模拟出原桥结构的边界条件，如图3中下部所示，采用承台底施加六个方向的弹簧来模拟土与桩基的相互作用，弹簧的平动和转动刚度依据土层状况和桩的布置形式按静力等效原则确定。因重力式桥台埋置于坚硬岩层中，所以采用与场地固结约束模拟。桥台与主梁间的球形钢支座纵横向均采用双线性理想弹塑性弹簧单元模拟，其中初始滑动位移dy取2 mm；为确保支座在地震下不出现脱空现象，竖向刚度取值为无穷大。当主梁和桥台间伸缩缝间隙无法满足主梁位移响应时会发生碰撞，本研究采用考虑碰撞过程中能量损失的Kelvin碰撞单元模拟此现象[28]，其示意图见图3右上部分，碰撞过程中的碰撞力Fp可由式(4)表示：
图2 大跨度矮塔斜拉桥示意图 /m
Fig.2 Schematic diagram of the long-span extradosed cable-stayed bridge
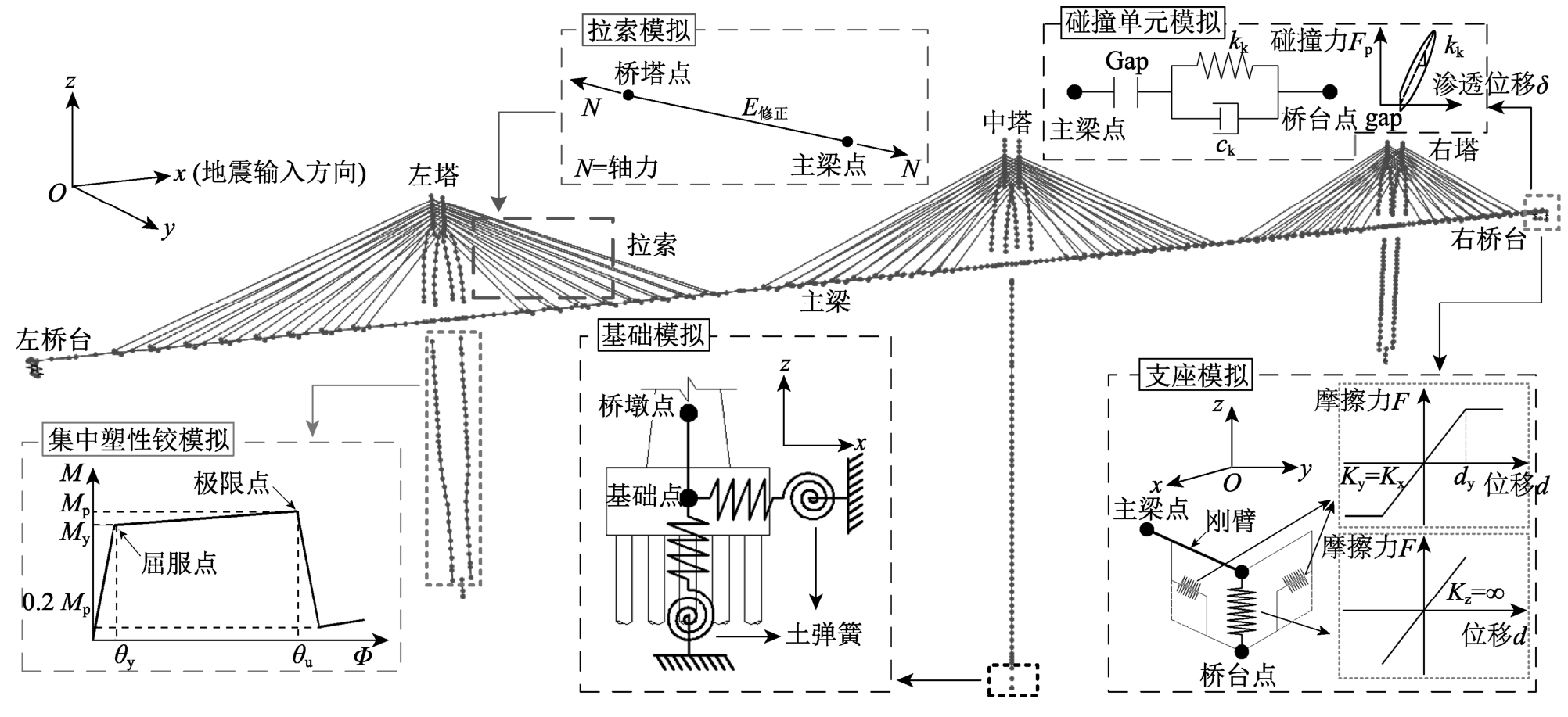
图3 桥梁三维有限元模型图
Fig.3 The 3D finite element model of the bridge structure
式中：kk和ck分别为接触刚度和阻尼系数，具体取值参见文献[29]；δ和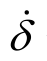
分别为碰撞渗透位移和速度；gap为伸缩缝间隙，本文取0.5 m。
对建立的三维有限元模型进行模态分析，得到桥梁前两阶周期分别为纵向振动(4.56 s)和横向振动(3.27 s)。由于本研究仅考虑结构纵向碰撞响应，因此地震输入沿纵向施加。
3 耐震时程法结果与讨论
3.1 耐震时程曲线输入下的响应分析
图4是三条耐震时程曲线输入下中塔顶位移和中墩顶弯矩时程图，从图4可以看出随着耐震时间的增长，中塔顶位移和中墩顶弯矩的最大值是在不断增大的，这与耐震时程法的理念相同。为更好地表征耐震时程的响应随时间不断增大的特征，同时能与IDA均值结果保持统一，采用最大绝对值曲线的形式给出耐震时程法结果，见图4中实线。后续分析中，耐震分析结果均以最大绝对值曲线的平均值形式给出[20]。
图4 耐震曲线输入下中塔顶位移和中墩顶弯矩
Fig.4 Top displacement of the middle tower and top bending moment of the middle pier under ET accelerograms
3.2 地震动选取和处理
考虑到IDA分析同样表征不同地震动强度与结构响应的关系，且理论成熟，得到广泛运用[30]。因此，本文以该方法结果为对照组，进行考虑地震动视波速为600 m/s时，耐震时程法能否捕捉到大跨度矮塔斜拉桥碰撞响应的研究。
对于IDA方法，首先以合成耐震时程曲线的规范反应谱为目标谱，在PEER-NGA强震数据库中挑选16条天然地震动。挑选原则是调幅后的16条地震动加速度反应谱均值与规范反应谱具有较小的离散性。图5给出16条调幅后的地震动加速度反应谱均值和规范谱的对比。从图5可以看出天然地震动反应谱均值和规范反应谱曲线能较好地吻合。对调幅后的天然加速度时程和合成的三条耐震时程进行两次积分得到位移时程，并做基线修正处理以消除零位漂移误差。此外，因碰撞的瞬时性，需将位移输入的时间间隔线性插值为0.001 s。
图5 天然地震动反应谱及其均值与规范反应谱对比
Fig.5 Response spectra of natural earthquake records and the comparison between their mean spectrum and code spectrum
3.3 适用性结果分析
考虑到等步长调幅方法的简便性且利于软件程序化[31]，本文IDA分析采用此调幅方式。通过多次非线性时程分析得到响应最大值的离散点，并运用三次Hermite插值获取完整的IDA曲线。需注意，常用IDA分析表征的是地震响应与谱加速度值的关系，而ETA表征是响应与耐震持时的关系，因此在进行两种方法对比验证时需通过式(5)建立起谱加速度值与耐震持时t的关系：
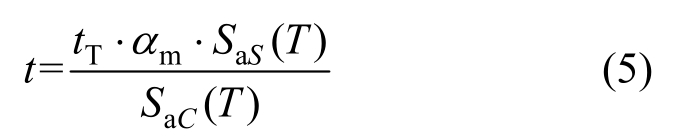
式中：αm为单条地震动调幅系数；SaS(T)为单条地震动反应谱值。
图6给出了视波速600 m/s时，三座索塔在两种方法下的塔顶位移和塔底弯矩图，可以看出两种响应的耐震和IDA曲线都随着时间不断增大，但与平滑的IDA曲线不同，ETA分析结果因统计的离散性而呈现锯齿状。此外，因行波效应的存在，耐震分析下三桥塔第一次出现响应值的时间存在差异，如图6(a)左上角详图所示，左、中、右塔顶位移分别在0.200 s、0.592 s和0.983 s后才出现明显的增长趋势，但IDA曲线因插值拟合的原因而规避了此现象。
图6 IDA和ETA方法下桥塔响应对比
Fig.6 Comparison of responses of the bridge towers between IDA and ETA
对比图6中的IDA和ETA曲线，发现不论是塔顶位移还是塔底弯矩，两者分析结果均较好地吻合。在图6(a)中，虽耐震时间20 s附近，两方法得到的位移值存在一定误差，左、中、右塔最大误差值分别为9.32%、2.86%和16.26%，但考虑到ETA只进行了三次分析，相比IDA分析减少95%以上的运算量，且耐震曲线存在“锯齿”平台段，因此这些误差可接受。从图6(b)可以看出两方法对于塔底弯矩捕捉与位移类似，即中小震时(小于15 s)弯矩几乎重合；随着耐震时间的增长，两方法的误差有所增大，但处于可接受范围内。此外，因外型尺寸和索力引起三座桥塔间位移或弯矩的差异，即任何地震动强度下左塔顶位移最大，但弯矩最大却出现在中塔底的现象，耐震时程法也能很好地捕捉到。表明耐震时程法可有效预测考虑行波效应时上部索塔的位移和内力响应。
基于软件分析数据结果，图7给出了考虑行波效应时，主梁中点位移在IDA和ETA两种方法下的对比结果，可以看出16条天然地震动IDA均值与三条ETA的均值一致性较好。虽在耐震时间12 s后出现了ETA方法低估主梁位移的现象，最大低估为12.22%，但考虑到大震下碰撞的出现以及支座和桥墩进入非线性等因素使主梁位移响应复杂化，而耐震时程法作为一种预测主梁碰撞响应的快捷方法，此误差可接受。此外，图7中同样可看出ETA曲线因地震动视波速而出现了响应滞后现象。
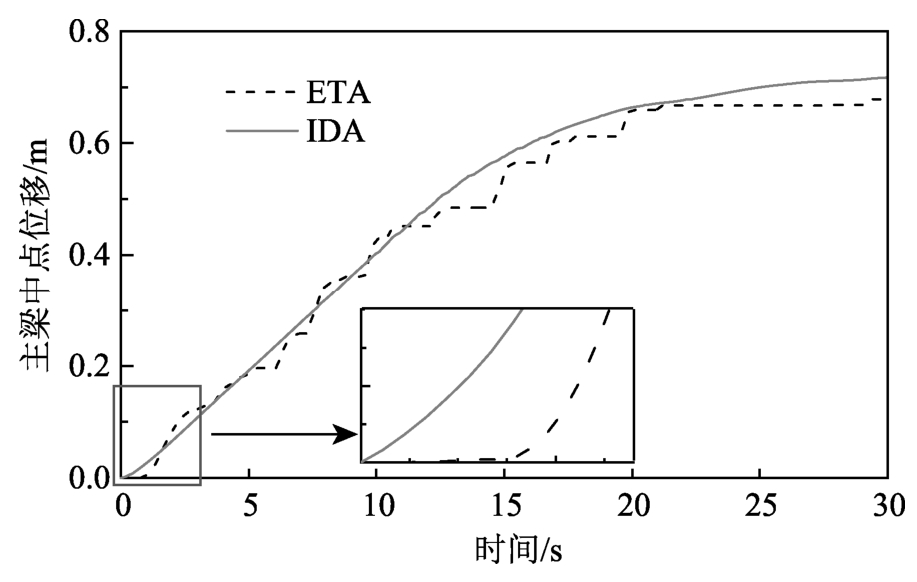
图7 IDA和ETA方法下主梁位移对比
Fig.7 Comparison of displacement of the bridge deck between IDA and ETA
图8给出左墩顶部和底部弯矩以及对应曲率延性系数的IDA和ETA对比曲线。可以发现墩底截面在30 s耐震时间内一直保持线性；而墩顶部截面在16 s附近进入非线性，此时随着地震动增大，仅曲率增大而弯矩并未明显变化。从图8(a)两种方法捕捉桥墩弯矩可发现桥墩顶响应曲线基本重合，IDA和ETA几乎同一时刻捕捉到截面进入塑性，分别是16.192 s和16.765 s；对于墩底弯矩的预测，ETA虽有高估其响应的趋势，20 s时的误差达到19.31%，但差距随着时间增长趋于缓和。此外，对于桥墩顶和墩底截面的延性系数，耐震时程曲线也能很好地反映出16条天然地震动下的IDA结果，如图8(b)所示，最大误差分别为10.08%和16.86%。从图8还可以看出，在耐震时间较小时，两种方法存在明显误差，这是因为对于耐震时间较小的情况，两方法捕捉碰撞力出现的时间存在差异，ETA首次出现碰撞的时间较IDA分析首次出现碰撞的时间提前(见图9)。
图8 IDA和ETA方法下左桥墩响应对比
Fig.8 Comparison of responses of the left bridge pier between IDA and ETA
表1列出了耐震时程法在大震时(大于20 s)预测左、中、右三墩响应与IDA分析的最大误差。从表1可以发现中墩顶和墩底在30 s耐震时间内均保持为弹性，因此，两种方法的误差相比于边墩更小；此外，表1中两种方法预测桥墩响应的相对误差在20%以内，但考虑到分析时因引入非线性碰撞单元和行波效应，动力响应更加复杂，以及墩身结构在大震下经历强非线性和耐震时程曲线的持时和变化趋势与真实地震动存在差异(耐震曲线幅值一直增长，而天然地震动具有平台段和衰减段)，此误差是可接受的。因此，耐震时程法可用于考虑行波效应时大跨度矮塔斜拉桥墩柱碰撞性能评估。
图9给出了IDA和ETA两方法下主梁与桥台间的碰撞力曲线，可以发现两方法下碰撞力值以相同的趋势不断地随耐震时间增长，且左侧伸缩缝因较早受地震影响而产生比右侧大的碰撞力。对于左、右侧伸缩缝处碰撞发生时间，IDA分析结果得到分别位于9.1 s和11.2 s附近；但ETA分析时，两侧伸缩缝在5 s前均已发生碰撞，这是因为行波效应使耐震方法下的主梁位移出现滞后现象(图7)，导致伸缩缝间隙在较小的地震强度下便满足不了桥台与主梁间的相对位移，因此碰撞现象更早地发生。但随着耐震持时增加到10 s后，ETA分析的碰撞力逐渐与IDA结果相近。考虑到ETA分析是结构抗震分析的一种简化方法，此误差在可接受范围内。因此，耐震时程法可用于预测大震下大跨度矮塔斜拉桥与两侧桥台间的碰撞力大小。
图9 IDA和ETA方法下碰撞力对比
Fig.9 Comparison of the pounding force between IDA and ETA
表1 大震时IDA和ETA两方法桥墩响应误差最大值
Table 1 The maximum errors of responses of the piers between IDA and ETA under large earthquakes
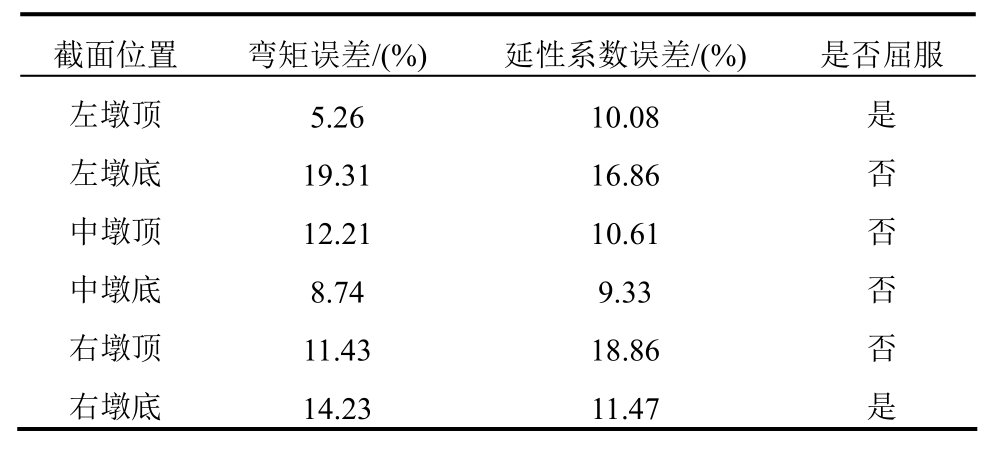
截面位置 弯矩误差/(%) 延性系数误差/(%) 是否屈服左墩顶 5.26 10.08 是左墩底 19.31 16.86 否中墩顶 12.21 10.61 否中墩底 8.74 9.33 否右墩顶 11.43 18.86 否右墩底 14.23 11.47 是
4 行波效应影响的耐震时程分析
基于3.3节耐震时程法适用性验证可知，其是一种仅需少量分析便可解决地震动视波速对大跨度桥梁碰撞影响问题的潜在方法。因此，使用此方法进行不同地震动视波速对大跨度矮塔斜拉桥碰撞响应影响的分析。
图10列出了左、右侧碰撞力在视波速为200 m/s、400 m/s、600 m/s、1000 m/s、1500 m/s和一致激励下的耐震曲线。由图10可以看出，当视波速为200 m/s或400 m/s时，左、右侧桥台与主梁发生第一次碰撞的时间分别约为2.5 s和3.0 s，而一致激励时，碰撞出现的时间则推迟至10 s后，可见随着地震动视波速的增大，两侧伸缩缝第一次出现碰撞力的时间在延后。对于图10中不同视波速下的碰撞力耐震曲线，可以发现存在显著差异性，表明碰撞力大小受地震动视波速的影响。此外，碰撞力值还依赖于地震动强度，如图10(b)所示，对于右侧伸缩缝处碰撞力，当耐震时间处于[10, 22]s时，除视波速为200 m/s外，其他波速下的行波效应使碰撞力值有减小趋势，而其他耐震时间下，视波速有增大碰撞力的效果；同样的现象也可在图10(a)的左侧碰撞力曲线中发现。
图10 不同视波速下ETA碰撞力
Fig.10 The pounding force with various apparent wave velocities by ETA
图11给出了不同地震视波速下主梁位移的耐震时程曲线。可以发现当波速大于1000 m/s时，行波效应对主梁位移的影响可忽略；而当波速小于1000 m/s时，主梁位移明显小于一致激励下的响应，这是因主梁两侧的碰撞力对主梁运动起约束作用。但在视波速为200 m/s时的大震下(大于25 s)，因巨大碰撞力且多数桥墩进入塑性，主梁位移从0.73 m迅速增大到1.11 m。由此可见，即使碰撞单元和行波效应等复杂边界和输入条件能减小大跨度矮塔斜拉桥主梁地震响应，但因结构自身进入非线性，可能使上述有利作用转变为不利影响。
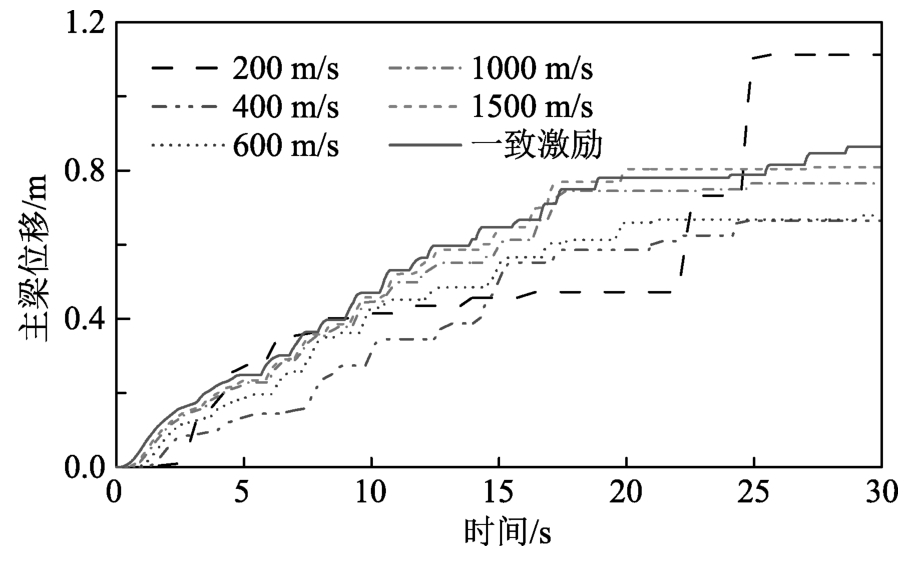
图11 不同视波速下ETA主梁位移
Fig.11 The deck displacement with various apparent wave velocities by ETA
图12给出了主梁上部三座索塔顶部位移在不同地震动视波速下的ETA分析图，可以发现视波速对三座索塔顶位移的影响存在差异。从图12(a)表达的左塔顶位移耐震图看出15 s前(200 m/s视波速为5 s前)，行波效应对于塔顶位移的影响很小，曲线几乎重合；但随着地震动强度的增大，视波速增大左塔顶位移的现象逐渐明显，且增大幅度与视波速大小无关，但需注意的是当视波速继续增大到一定程度时，大震下增大左塔顶位移现象会逐渐减弱，最后与一致激励下的左塔顶位移保持一致。而视波速对于中塔顶位移的影响与主梁位移相似，如图12(b)所示，即总体上行波效应起抑制位移作用，但大震时的200 m/s视波速下出现位移增大现象。此外，由图12(c)可知，波速大于200 m/s时的行波效应对右塔顶位移影响很小，但波速为200 m/s时需要考虑行波效应增大位移响应的不利影响。结合塔顶和上述主梁位移在不同视波速下的ETA分析可知，对于软土地质(视波速一般小于200 m/s)，需考虑地震动行波效应带来的位移增大现象，且右索塔受其影响最大。
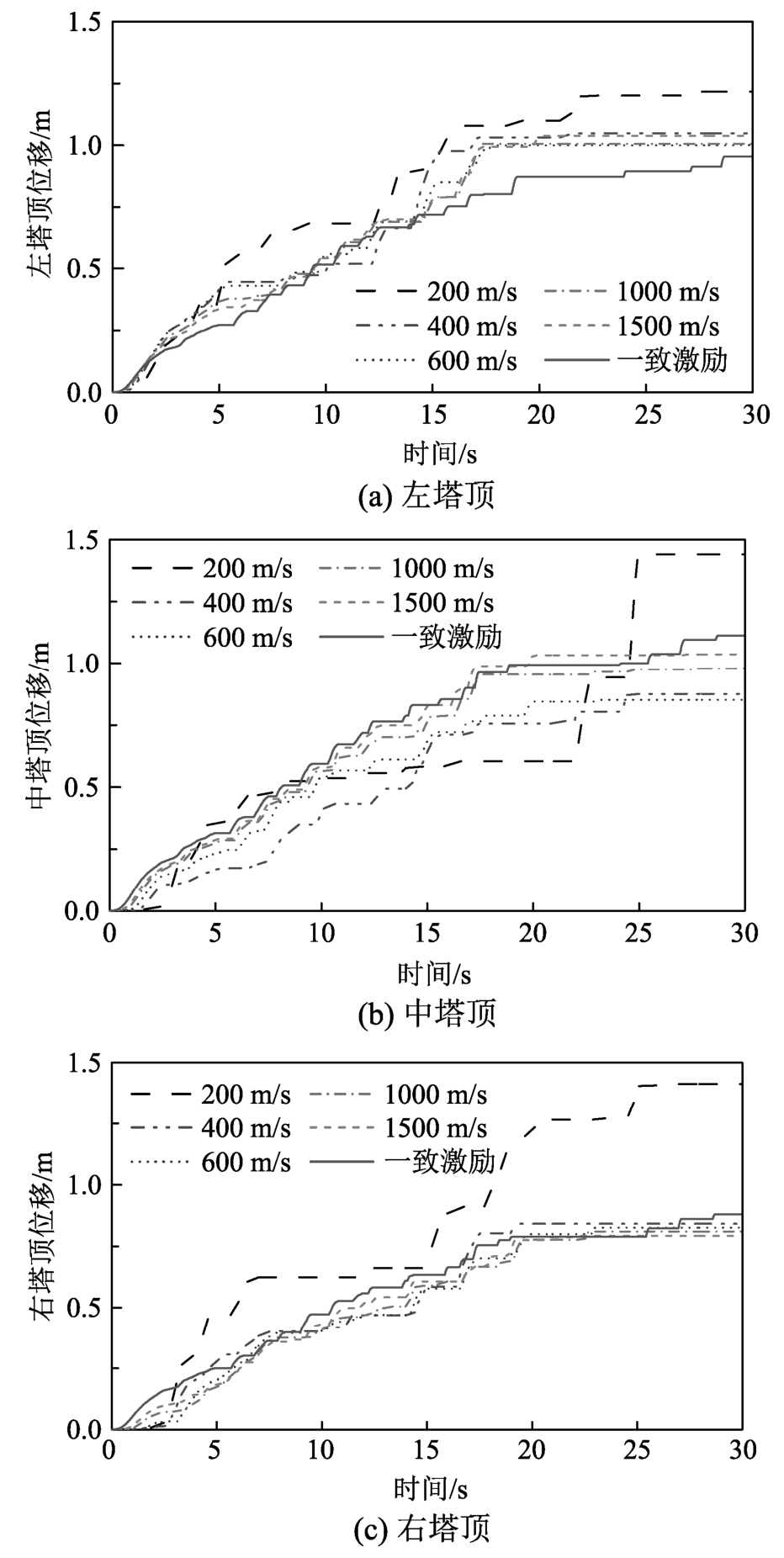
图12 不同视波速下ETA塔顶位移
Fig.12 The displacement of tower top with various apparent wave velocities by ETA
为研究不同视波速对大跨度矮塔斜拉桥墩柱响应的影响，图13给出了桥墩顶部和底部两处关键截面处的曲率延性系数耐震图。由图13可知，当视波速大于200 m/s时，除左墩顶外，其他墩柱关键截面的延性系数受行波效应影响小。与图13(b)～图13(f)对比后发现，对于图13(a)左墩顶延性系数，当截面屈服后(大于1)，不同波速下的ETA曲线出现离散，表明桥墩截面进入塑性易激发起不同波速对截面曲率的影响。观察图13中波速为200 m/s时的曲线发现，六个墩柱关键截面的延性系数明显大于其他视波速下的对应值，可见软土下左、右侧碰撞力的增大，易加剧墩柱截面进入塑性；此外，当墩柱进入塑性后，截面的延性系数会急剧增大，再一次表明了桥墩截面屈服状态与行波效应的影响存在相关性。
图13 不同视波速下ETA墩柱关键截面曲率延性系数
Fig.13 The curvature ductility coefficients of the bridge pier with various apparent wave velocities by ETA
5 结论
基于耐震时程法可高效评估结构地震响应的优势，本文以考虑碰撞影响的典型大跨度矮塔斜拉桥为例，验证了此方法预测行波效应下大跨度桥梁碰撞响应的有效性。并在可行性验证基础上进行了不同地震动视波速对大跨度桥碰撞响应影响的研究。得到主要研究结论如下：
(1) 考虑行波效应时，耐震时程法预测大跨度桥梁碰撞响应与IDA分析结果存在一定误差，这是因为耐震时程曲线在持时和变化趋势与真实地震动存在差异，但ETA作为一种简化的抗震分析方法，此误差在可接受范围内。
(2) 耐震时程分析只需少量运算便可表达出多种视波速与地震动强度组合的矮塔斜拉桥碰撞响应。
(3) 行波效应对大跨度矮塔斜拉桥碰撞响应的影响存在复杂性和不确定性，与地震动视波速、地震动强度和结构是否进入非线性相关。总体而言，位于软土地质条件(视波速小)的强非线性结构，在大震时应考虑行波效应的不利影响。
(4) 耐震时程法可用于预测考虑行波效应时大跨度矮塔斜拉桥的碰撞响应。但桥梁地震碰撞响应易受到各种复杂条件的影响，如伸缩缝宽度、桥台动力特性以及局部场地效应等[32]。因此，此方法在考虑这些影响因素下的适用性还需进一步研究。
[1]陈从春, 周海智, 肖汝诚.矮塔斜拉桥研究的新进展[J].世界桥梁, 2006(1): 70―73.Chen Congchun, Zhou Haizhi, Xiao Rucheng.Recent research advancement of extradosed cable-stayed bridge[J].World Bridges, 2006(1): 70―73.(in Chinese)
[2]李小珍, 刘桢杰, 雷虎军, 等.行波效应对矮塔斜拉桥弹塑性地震响应的影响[J].铁道工程学报, 2015,32(11): 49―54.Li Xiaozhen, Liu Zhenjie, Lei Hujun, et al.Effect of travelling wave on elastic-plastic seismic response of low-pylon cable-stayed bridge[J].Journal of Railway Engineering Society, 2015, 32(11): 49―54.(in Chinese)
[3]项海帆.斜张桥在行波作用下的地震反应分析[J].同济大学学报, 1983(2): 4―12.Xiang Haifan.Earthquake response analysis of cablestayed bridges under the action of travelling waves[J].Journal of Tongji University, 1983(2): 4―12.(in Chinese)
[4]黄学漾, 宗周红, 夏坚, 等.强震作用下独塔斜拉桥模型的非线性动力响应分析[J].东南大学学报: 自然科学版, 2015, 45(2): 354―359.Huang Xueyang, Zong Zhouhong, Xia Jian, et al.Nonlinear dynamic response analysis of cable-stayed bridge with single tower under strong earthquake excitations[J].Journal of Southeast University (Natural Science Edition), 2015, 45(2): 354―359.(in Chinese)
[5]布占宇, 谢旭, 郑荣跃.索-桥动态相互作用及行波效应对斜拉桥地震反应的影响[J].地震工程与工程振动,2011, 31(2): 82―90.Bu Zhanyu, Xie Xu, Zheng Rongyue.Study on effects of travelling waves on the seismic responses of cablestayed bridges in consideration of dynamic cable-deck interaction[J].Journal of Earthquake Engineering and Engineering Vibration, 2011, 31(2): 82―90.(in Chinese)
[6]闫聚考, 李建中, 彭天波, 等.三塔两跨悬索桥行波效应振动台试验及数值研究[J].振动与冲击, 2016, 35(7):44―48.Yan Jukao, Li Jianzhong, Peng Tianbo, et al.Shake table tests and numerical analysis for traveling wave effect of a three-tower two-span suspension bridge[J].Journal of Vibration and Shock, 2016, 35(7): 44―48.(in Chinese)
[7]孙利民, 谢文, 楼梦麟, 等.行波激励下桩-土-斜拉桥多点振动台试验[J].中国公路学报, 2017, 30(12):221―233.Sun Limin, Xie Wen, Lou Menglin, et al.Multiple shaking table tests on pile-soil-cable-stayed bridge under travelling wave excitations[J].China Journal of Highway and Transport, 2017, 30(12): 221―233.(in Chinese)
[8]吴巧云, 王涛, 魏敏, 等.基于地震碰撞易损性的相邻结构临界间距研究[J].工程力学, 2019, 36(7): 89―98.Wu Qiaoyun, Wang Tao, Wei Min, et al.Study on the critical separation distance of adjacent structures based on seismic pounding fragility[J].Engineering Mechanics,2019, 36(7): 89―98.(in Chinese)
[9]Zheng Y, Xiao X, Zhi L, et al.Evaluation on impact interaction between abutment and steel girder subjected to nonuniform seismic excitation[J].Shock and Vibration 2015: 981804.
[10]Won J H, Mha H S, Kim S H.Effects of the earthquake-induced pounding upon pier motions in the multi-span simply supported steel girder bridge[J].Engineering Structures, 2015, 93: 1―12.
[11]闫聚考, 李建中, 彭天波, 等.大跨度悬索桥主引桥碰撞效应振动台试验及数值研究[J].振动与冲击, 2017,36(7): 234―240.Yan Jukao, Li Jianzhong, Peng Tianbo, et al.Shaking table tests and numerical analysis for pounding analysis between main span and approach span of long-span suspension bridge[J].Journal of Vibration and Shock, 2017, 36(7): 234―240.(in Chinese)
[12]Estekanchi H E, Valamanesh V, Vafai A.Application of endurance time method in linear seismic analysis[J].Engineering Structures, 2007, 29(10): 2551―2562.
[13]白久林, 欧进萍.基于耐震时程法的钢筋混凝土框架结构抗震性能评估[J].工程力学, 2016, 33(10): 86―96.Bai Jiulin, Ou Jinping.Seismic performance evaluation of reinforced concrete frame structure using the endurance time method[J].Engineering Mechanics, 2016, 33(10):86―96.(in Chinese)
[14]白久林.钢筋混凝土框架结构地震失效模式分析与优化[D].哈尔滨: 哈尔滨工业大学, 2015.Bai Jiulin.Main seismic failure mode analyses and optimization of reinforced concrete frame structures[D].Harbin: Harbin Institute of Technology, 2015.(in Chinese)
[15]Rahimi E, Estekanchi H E.Collapse assessment of steel moment frames using endurance time method[J].Earthquake Engineering and Engineering Vibration,2015, 14(2): 347―360.
[16]Mirzaee A, Estekanchi H E.Performance-based seismic retrofitting of steel frames by the endurance time method[J].Earthquake spectra, 2015, 31(1): 383―402.
[17]Estekanchi H E, Alembagheri M.Seismic analysis of steel liquid storage tanks by endurance time method[J].Thin-Walled Structures, 2012, 50(1): 14―23.
[18]Hariri-Ardebili M A, Furgani L, Meghella M, et al.A new class of seismic damage and performance indices for arch dams via ETA method[J].Engineering Structures, 2016,110: 145―160.
[19]Bai J, Jin S, Zhao J, et al.Seismic performance evaluation of soil-foundation-reinforced concrete frame systems by endurance time method[J].Soil Dynamics and Earthquake Engineering, 2019, 118: 47―51.
[20]Guo A, Shen Y, Bai J, et al.Application of the endurance time method to the seismic analysis and evaluation of highway bridges considering pounding effects[J].Engineering Structures, 2017, 131: 220―230.
[21]Valamanesh V, Estekanchi H E, Vafai A.Characteristics of second generation endurance time acceleration functions[J].Scientia Iranica, 2010, 17(1): 53―61.
[22]Gasparini D, Vanmarcke E H.SIMQKE: Gram for artificial motion generation[D].Cambridge:Massachusetts Institute of Technology, 1976.
[23]田玉基, 杨庆山.地震地面运动作用下结构反应的分析模型[J].工程力学, 2005, 22(6): 170―174.Tian Yuji, Yang Qingshan.Analysis models and methods for structural seismic responses[J].Engineering Mechanics, 2005, 22(6): 170―174.(in Chinese)
[24]王琦.多塔矮塔斜拉桥振动台模型试验与分析[D].上海: 同济大学, 2019.Wang Qi.Shaking table model test and analysis of multi-tower extra-dosed cable-stayed bridge[D].Shanghai: Tongji University, 2019.(in Chinese)
[25]Aviram A, Mackie K R, Stojadinović B.Guidelines for nonlinear analysis of bridge structures in California[R].Berkeley: University of California, Pacific Earthquake Engineering Research Center, 2008.
[26]艾庆华, 王东升, 李宏男, 等.基于塑性铰模型的钢筋混凝土桥墩地震损伤评价[J].工程力学, 2009, 26(4):158―166.Ai Qinghua, Wang Dongsheng, Li Hongnan, et al.Seismic damage evaluation of RC bridge columns based on plastic hinge model[J].Engineering Mechanics, 2009,26(4): 158―166.(in Chinese)
[27]Ernst J H.Der E-Modul von Seilen unter berucksichtigung des Durchhanges[J].Der Bauingenieur, 1965, 40(2):52―55.
[28]Shakya K, Wijeyewickrema A C.Mid-column pounding of multi-story reinforced concrete buildings considering soil effects[J].Advances in Structural Engineering, 2009,12(1): 71―85.
[29]Jankowski R, Wilde K, Fujino Y.Pounding of superstructure segments in isolated elevated bridge during earthquakes[J].Earthquake Engineering and Structural Dynamics, 1998, 27(5): 487―502.
[30]Vamvatsikos D, Cornell C A.Applied incremental dynamic analysis[J].Earthquake Spectra, 2004, 20(2):523―553.
[31]吕大刚, 于晓辉, 王光远.基于单地震动记录 IDA 方法的结构倒塌分析[J].地震工程与工程振动, 2009,29(6): 33―39.Lü Dagang, Yu Xiaohui, Wang Guangyuan.Structural collapse analysis based on single-record IDA method[J].Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(6): 33―39.(in Chinese)
[32]沙奔, 王浩, 陶天友, 等.考虑混凝土损伤的隔震连续梁桥碰撞响应分析[J].工程力学, 2018, 35(3): 193―199.Sha Ben, Wang Hao, Tao Tianyou, et al.Analysis on pounding response of isolated continuous girder bridge considering concrete damage[J].Engineering Mechanics,2018, 35(3): 193―199.(in Chinese)