基于性能抗震评价方法已经被广泛应用于各种结构体系的抗震设计之中，该评价方法中很重要的一方面是计算在给定的地震动强度指标(IM)下，结构超过某个需求指标(DM)的平均年超越概率。选择合理的地震动强度指标将有效地降低由于地震动差异带来的结构响应的离散性，对于基于性能的抗震评价体系具有重要意义[1]。
烟囱、广播电视塔、导航塔、石油化工塔、排气塔和水塔等高耸混凝土结构属于高柔的悬臂结构，由于不具备多道抗震防线，且对竖向地震比较敏感[2]，这类结构在强震作用下很容易发生破坏。然而，现有的地震动参数研究多集中于建筑结构，对于高耸混凝土结构的地震动强度指标适用性研究较少。
现有的研究表明，地震动强度指标可分为向量型参数指标和标量型参数指标。由于缺少相应地震动衰减关系，向量型强度指标在我国并没有得到广泛应用[3]。此外，考虑地面运动参数信息的地震动参数指标如地面峰值加速度(PGA)，地面峰值速度(PGV)和地面峰值位移(PGD)由于形式简单，使用方便，目前仍得到大量的使用。但是这些指标没有考虑结构的动力特征。基本周期对应的谱加速度Sa(T1)既有地震动信息也包括结构的弹性动力特性，但该指标对于高阶振型显著的高层结构充分性不足并且没有考虑结构刚度退化而引起的周期延长现象。因此很多学者提出了基于谱加速度的多种修正指标模型。Cordova等[4]提出了一种考虑周期延长效应的地震动强度指标S*，延长的周期表示为cT1。Vamvatsikos等[5]提出了一对指数型地震动参数指标IM12和IM123，分别考虑结构进入塑性阶段的周期延长效应和前三阶振型的参与。在此基础上，Lin等[6]基于框架结构提出了二种指标SN1和SN2。其中：SN1考虑了周期延长效应，并建议对于框架结构，延长的周期取1.5T1；SN2考虑了前二阶振型在高层混凝土框架结构动力响应的参与情况。周颖等[7]提出了适用于超高层建筑结构的指数型地震动参数指标S12和S123，这二者分别考虑了前两阶振型和前三阶振型的参与。卢啸等[8]提出了考虑高阶模态的谱加速度平均指标
，并利用简化的超高层结构开展实例验证。Shome[9]提出了基于谱加速度的线性组合地震动指标
在此基础上，Zhang等[10]引入结构模态质量参与系数作为加权因子，提出了一种新的线性组合的地震动强度指标
。表1总结了上述地震动指标的详细信息，并从形式上将这些指标分为基本强度指标，基于谱加速度的指数型指标以及基于谱加速度的线性指标。
综上所述，现有的部分地震动强度指标多单独考虑高阶振型效应或结构周期延长效应，而事实上这2种效应在高耸混凝土结构的动力响应中同时存在[11]：一方面，在地震荷载的作用下高阶振型对于高耸混凝土结构的动力响应贡献较大；另一方面当地震动强度超过一定数值后结构将不可避免地进入塑性阶段。因此有必要在现有的研究基础上提出一种同时考虑这2种效应的地震动强度指标。此外，现有的地震动参数多考虑一维地震动或者二维地震动输入的情况。而高耸结构的震害是大多是由水平和竖向地面运动共同作用引起的[12]，因此有必要在三维地震动作用下检验地震动强度指标在此类结构的适用性。鉴于此，本文提出了一种新的地震动强度指标，并基于一座高耸烟囱结构和一座混凝土水塔结构，在三维地震动输入的条件下研究了该指标的充分性和有效性。
表1 地震动强度指标信息
Table 1 Information of earthquake intensity measures
基本强度指标 指数型地震动强度指标 线性组合地震动强度指标SSTST (Shome[9])a12a1a2*=+0.8()0.2()PGA a SSTRSTST (Cordova等[4])*=a1a1af()()()α α1-α S=SSTSTST (Shome[9])a123a1a2a3*=++0.8()0.15()0.05()IM(,5%)(,5%)12aaab=SτSτβ 1-β PGV SST (Zhang等[10])(Vamvatsikos等[5])1 123aaabac a*ii i1--=Sβγβγ τ τ τ(Vamvatsikos等[5])=Σnαa ()IM(,5%)(,5%)(,5%)S S=PGD SSTST (Lin等[6])SSTST (Lin等[6])0.750.25 N2a1a2 0.50.5 N1a1a1=()(1.5)=()()―ST 12a1a2(,)(,)SSTST (周颖等[7])=ζζ α β a(1)SSTSTST (周颖等[7]) ―123a1a2a3=(,)(,)(,)ζζζ α β γ SST (卢啸等[8])a =∏n ni i1()=a―
1 一种新的地震动强度指标
本文提出的地震动强度指标(IM)同时考虑了周期延长效应和高阶振型效应，并结合了指数型强度指标和线性组合型强度指标的形式特点。其具体表达式如下：
式中：Sa(Ti)是第i阶周期对应谱加速度值；αi表示第i阶模态的模态质量参与系数；常数C为周期延长系数；β为周期延长效应权重系数，根据Cordova等[4]、Vamvatsikos等[5]和Lin等[6]的建议，本文取0.5。从组成内容上看，本文提出的
指标同时涵盖了地震动信息，结构自身动力特征，结构进入非线性阶段的软化效应以及结构动力响应中高阶模态参与情况。从形式上，
具有很强的适应性。具体而言，如果不考虑周期延长效应(C=1)，则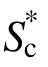
“退化”成强度指标
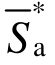；另一方面，如果不考虑高阶振型效应，则
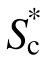将具备S*，IM12以及SN1等考虑周期延长效应指标相同的性质。因此，
是一种复合形式的地震动强度指标，其在地震动强度指标的层面上考虑了高阶模态和结构非线性软化效应的共同作用。
2 三维地震动输入下的IM和DM复合形式
目前建筑结构的最大层间位移角(θmax)是应用最为广泛的结构需求指标(DM)，但是高耸混凝土结构高细比很大，在地震作用下以弯曲破坏为主且不存在楼层构造，因此本文选取结构最大弯曲曲率作为DM。本文利用差分法，基于Python语言编制了ABAQUS后处理程序来计算和提取结构的最大曲率。
在三维地震动输入下，每条地震动记录分量的IM一般不同，而在x、y方向的结构响应也会不同。为了能定量描述地震动指标的性质，有必要在三维地震动输入下对复合的IM和DM值进行定义。周颖等[13]在二维输入条件下定义了IM和DM值。本文在其结论的基础上，将该结论拓展到三维输入情况下。本文定义三维输入下的DM值如下：
对应的IM值定义如下：
式(2)和式(3)中：φx，max 和φy，max分别是结构在三维地震动激励下x和y方向的最大曲率；IMx、IMy和IMz分别是x、y和z方向的地震动分量对应的IM值。
3 高耸结构分析模型的建立与验证
本文选取的结构研究对象为一座混凝土单筒式烟囱以及一座混凝土倒锥壳式水塔。该烟囱建于20世纪90年代，结构总高度240 m，顶部出口内壁直径为7.34 m，底部内壁直径为22.94 m，结构底部设置了2个对称的矩形烟道洞口。混凝土水塔结构总高43 m，水箱为倒锥壳形式，有效容量为200 m3，筒身主体结构外径3.2 m，壁厚为0.18 m，支筒结构两侧交叉分布7扇窗口，底部设置了一道洞口。
基于大型通用有限元软件ABAQUS，本文分别建立了烟囱结构和水塔结构的三维弹塑性模型。烟囱和水塔结构筒体采用分层壳模型，壳体单元利用适用性较强的四节点四边形有限薄膜线性减缩积分单元S4R。通过ABAQUS提供的质量单元将烟囱每节筒壁上的内衬和隔热层作用于环形悬臂梁上来模拟其对结构的动力响应的影响。图1为烟囱结构和水塔结构的有限元模型。
图1 2种结构的有限元模型
Fig.1 FEM model of two structures
本文混凝土材料模型选取ABAQUS\Standard提供的混凝土塑性损伤模型，该模型可以模拟混凝土材料的开裂和压碎等力学现象。如图2(a)和图2(b)所示：σc0、σcu和σt0分别为混凝土单轴受压屈服应力，受压峰值应力以及混凝土单轴受拉峰值应力；
分别是混凝土等效塑性压应变和等效塑性拉应变；E0为初始弹性模量；dc和dt分别为混凝土受压和受拉损伤因子。本文的钢筋采用随动硬化的Plastic塑性模型，该模型为考虑包辛格效应的双折线强化模型，其包括线弹性段、强化阶段以及卸载后再加载段。如图2(c)所示：E0为钢筋初始弹性模量；E为钢筋强化阶段弹性模量；fy是钢筋的屈服应力；εy是钢筋的屈服应变。本文结构阻尼比取0.05，并考虑了重力二阶效应。
图2 混凝土和钢筋材料本构模型
Fig.2 Material models of steel and concrete
为了验证有限元模型的合理性，表2列出了模型的各阶自振周期值与实际测量值[14-15]。可以看出，结构的各阶自振周期值与实测值吻合较好，误差大部分都在10%以内，由此认为利用该模型分析地震作用下的动力响应是可靠。
表2 结构模型动力信息
Table 2 Dynamic properties of models
结构振型模型自振周期/s实测自振周期/s误差/(%)模态质量参与系数1 3.325 3.413 2.57 0.290烟囱2 0.980 1.025 4.39 0.200 3 0.450 0.502 10.35 0.120 4 0.360 — — 0.075 1 1.760 1.890 5.37 0.748水塔2 0.205 0.201 1.95 0.117 3 0.087 0.093 6.45 0.040
4 地震动强度指标有效性
为了保证基于性能的抗震评价方法的可靠性，一个理想的地震动强度指标应同时具备有效性和充分性[16]。地震动强度指标的有效性描述了在给定地震动强度水平下结构响应的离散程度。提高地震动强度的有效性能降低由于地震动之间的差异而带来的离散性，即通过较少的地震波获得相同置信度的结果。
地震动强度指标的有效性可以通过地震动强度指标(IM)和结构需求指标(DM)之间的相关程度量化衡量。二者的相关程度越高，则该地震动强度指标的有效性就越高。Shome[9]指出DM和IM之间满足如下关系：
式中，(ε|IM)为残差。将式(4)两边同时取对数，则可建立二者之间的对数线性关系，具体的表达式如下：
在式(5)的基础上，可通过线性回归手段，利用相关系数ρ值来计算线性相关程度，从而定量地衡量地震动强度指标的有效性。
有证据表明，近断层脉冲地震将使结构产生更大的变形、位移等其它结构动力响应[17]。为了充分考虑地震动类型以及竖向地震对高耸结构地震动强度指标的影响，本文选取FEMA[18]推荐的28条远场地震波(56条分量记录)以及14条近场脉冲地震波(28条分量记录)，在三维方向输入的情况下验证IM有效性。在此之前，首先要确定结构的振型参与情况与结构周期延长系数。
4.1 高耸结构高阶振型参与情况
对于考虑高阶模态的地震动强度指标而言，虽然目前对建筑结构的振型参与情况已有一些结论[8,10]，但是这些结论并不能完全适用于高耸混凝土结构，原因在于高耸结构的振型以弯曲振型为主，且分布离散，高阶振型频率和基本振型自振频率相差较大。因此，有必要对高耸混凝土结构的振型参与情况进行研究。
如图3所示，地震动强度参数的有效性随着参与振型数量的增加而发生变化，然而引入尽可能多的振型数量并不能保证强度指标有效性的递增。如图3(a)所示，高耸烟囱结构在三维远场地震和近场脉冲地震作用下的最佳阵型参与数量为2。而对于水塔结构而言，在2种地震动作用下最佳的参与振型为一阶。总体来看，在地震动强度指标的层面上近场地震动的脉冲效应并没有激起结构更高振型的参与。为了研究三维地震动输入对于振型参与情况的影响，本文列举了一维地震动条件下的结果作为对比。如图3(c)和图3(d)所示，在一维地震动作用下，烟囱结构最佳的振型参与数量没有发生变化。而对于水塔结构，在一维地震动输入下应用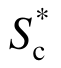
指标时也只需考虑第一阶振型的参与。因此，对于本文的高耸混凝土结构而言，考虑竖向地震作用并没有在地震动强度指标的有效性层面上激发出更高阶阵型的参与。
4.2 高耸结构周期延长效应情况
周期延长现象刻画了结构进入非线性阶段的刚度退化效应。为了合理地应用地震动强度指标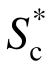
，在获得最佳的模态数量后，另一个关键就在于确定周期延长系数C。Cordova等[4]、Lin等[6]及Vamvatsikos等[5]根据框架结构的动力响应分别建议周期延长系数取2.0、1.5和2.0。为了研究三维地震动输入下高耸结构的周期延长现象，本文将C值分别取1(无延长效应)、1.2、1.5、1.8、2.0及2.2，通过指标有效性的变化来确定
指标中的合理的周期延长系数。
图4表示了结构周期延长系数与结构DM和IM的相关性系数之间的关系。地震动强度指标的有效性随着烟囱结构周期延长系数的增大而呈现先增后降的变化趋势。如图4(a)所示，在三维输入的远场地震动作用下，烟囱结构的周期延长系数为1.2，在三维输入的近断层脉冲地震动作用下，该烟囱结构周期延长系数为1.5，较远场地震动情况有所增长。这表明近断层地震的脉冲效性加剧了烟囱结构进入非线性状态的程度。但是由于保守设计，该烟囱的周期延长系数仍然比其他学者[4-5]建议的框架结构系数值小。
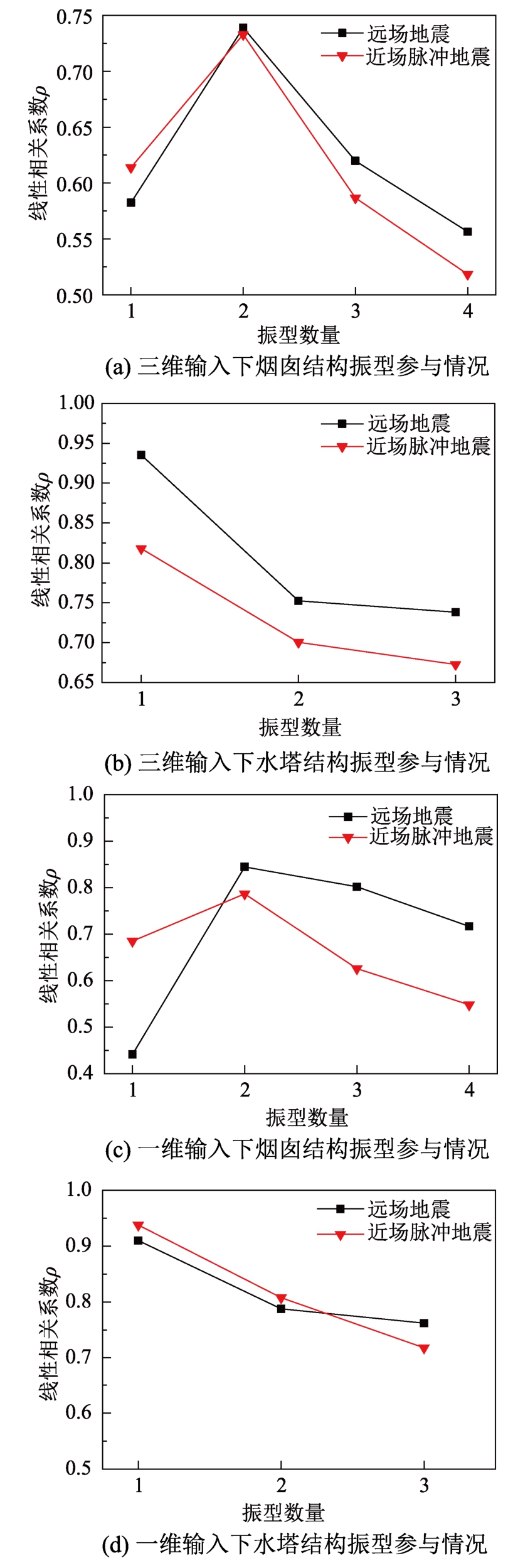
图3 烟囱和水塔结构在远场地震和近场脉冲地震作用下的振型参与情况
Fig.3 Optimal number of modes involved in chimney and water tower structures under far-field earthquake ground motions and near-fault earthquake groundmotions with pulse-like effect
图4 烟囱和水塔结构在远场地震和近场脉冲地震作用下的周期延长系数情况
Fig.4 Period elongation coefficients in chimney and water tower structures under far-field earthquake ground motions and near-fault earthquake ground motions with pulse-like effect
如图4(b)，在三维远场地震动以及近断层脉冲地震动激励下，水塔结构的周期延长系数分别为1.5和2.0，这一结论与建筑结构相近。与烟囱结构相比，低矮的水塔结构周期延长现象更加明显。为了研究竖向地震动对于结构周期延长系数的影响，图4(c)和图4(d)引入了在一维地震动输入下的情况作为对比。
表3总结了一维和三维输入地震动作用下的周期延长系数情况。考虑竖向地震动后，烟囱结构的周期延长系数在远场地震动和近场脉冲地震动作用下均有增加，而水塔结构周期延长系数并没有明显的改变。这说明从地震动强度有效性角度上，随着高耸结构的高度的增加，结构越容易受到竖向地震动分量的影响。此外，不论是一维地震动还是三维地震动输入，近场地震动的脉冲效应会使高耸结构进入塑性阶段的程度更深，产生了更多不可恢复的弯曲变形，因此，烟囱结构和水塔结构的周期延长系数均得到了提高。
表3 周期延长系数对比
Table 3 Comparison of period elongation coefficients
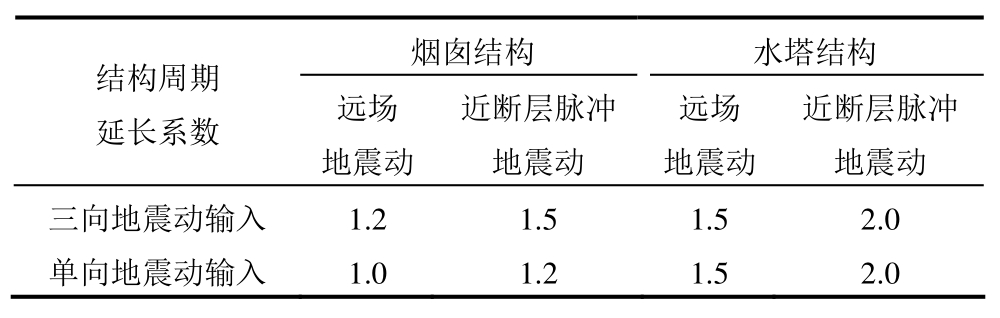
结构周期延长系数 远场地震动烟囱结构 水塔结构近断层脉冲地震动远场地震动近断层脉冲地震动三向地震动输入 1.2 1.5 1.5 2.0单向地震动输入 1.0 1.2 1.5 2.0
4.3 三维地震动输入下IM有效性对比
图5列举了上文总结的16种常见的IM与烟囱结构的DM(φmax)的线性相关系数情况。这16种地震动指标排列顺序依次是指数型指标、基本地震动强度指标以及线性叠加指标，最右侧列举的是本文提出的复合型IM。
图5(a)表示在三维方向输入的远场地震动作用下的各IM的有效性对比。在指数型强度指标中，考虑前三阶模态参与的指数型强度指标S123具有最高的有效性。在基本地震动强度指标(Sa(T1)，PGA，PGV，PGD)中，PGV具有较高的有效性。研究表明[19－20]，对于高层建筑结构，PGV具有较好的有效性，本文的计算结果也验证了这个结论。在线性组合指标中，
有效性最高。从整体上看，无论是指数型强度指标还是线性叠加型指标，考虑高阶振型参与的指标的有效性要好于仅考虑周期延长现象的指标。考虑周期延长的地震动指标S*、SN1以及IM12的相关系数分别是0.444、0.494和0.444，而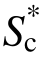
达到0.733，这表明在三维远场地震动作用下引入高阶振型效应能显著提高高耸烟囱结构地震动强度参数有效性。在所有的强度指标中，本文提出的
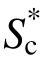具备最高的有效性。这说明为提高高耸结构地震动强度指标的有效性，有必要同时考虑周期延长效应和高阶振型效应的影响。
图5(b)是三维近断层脉冲地震动输入下各强度指标与烟囱结构最大曲率线性相关情况。在三维近断层脉冲地震动激励下，
以相关系数0.739在所有强度指标中位列首位。在基本指标方面，和图5(a)所示的情况相同，PGV具备最高有效性。此外，S*、SN1及IM12等仅考虑周期延长效应指标的有效性较远场地震动作用情况下有所增长，且与考虑高阶振型的指标表现差距较远场地震动作用相比有很大程度上的减小。这说明了脉冲地震动作用会提高结构进入塑性阶段的程度，在脉冲地震动下考虑周期延长的强度指标有较强的适用性。而和其它仅考虑高阶振型的指标相比，由于竖向地震动分量使得该烟囱的周期延长现象更加明显，所以综合而言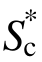
的有效性就比单独考虑某种效应的指标高。因此，对于高耸烟囱结构在三维地震动作用下抗震评价，本文建议的指标有一定优势，可以作为一种合理选择。
图5 烟囱结构的各地震动强度指标有效性对比
Fig.5 Comparison of efficiency in different earthquake intensity measures for chimney
图6是倒锥壳水塔结构的最大曲率与地震动强度指标(IM)的相关性情况。根据上文的结论，本文的水塔结构无需考虑二阶及以上振型的参与。因此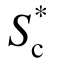
的有效性与仅考虑周期延长效应的指数型指标相近。图6(a)表示水塔结构在三维远场地震动作用下各指标的有效性情况，不论是指数型指标还是线性叠加型指标，考虑周期延长指标的总体表型强于高阶振型强度指标。将考虑高阶振型效应的指标
与第一周期的谱加速度Sa(T1)相比，发现对于高度较低的水塔结构，考虑高阶振型反而会降低IM的有效性。
和SN1的有效性并列位于所有地震动强度指标首位。在基本指标中，基本周期谱加速度Sa(T1)的有效性最好，而PGV以微弱的差异位居第二。
图6 水塔结构的各地震动强度指标有效性对比
Fig.6 Comparison of efficiency in different earthquake intensity measures for water tower
图6(b)表示水塔结构在三维近断层脉冲地震动作用下各指标的有效性情况，和图6(a)的情况类似，考虑周期延长效应的指标有效性要高于考虑高阶振型的指标。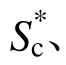
S* 及IM12的有效性并列位于所有地震动强度指标首位。在基本地震动指标中，PGV有效性最高。此外，在图6(b)中，将Sa(T1)与
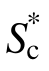对比可发现在引入周期延长效应后，指标有效性进一步提高，这表明在低矮的水塔结构中，考虑周期延长效应是非常必要的。
5 三维地震动输入下IM的充分性
除了有效性之外，一个合理的地震动强度指标还应该具有充分性。结构的动力响应会随着地震动记录的不同而存在差异，而一个具备充分性的IM能确保不同地震动条件下获得大致相近的平均年超越概率计算结果。评估IM的充分性需要检验在某一地震动指标下结构DM与震级M、震中距R的相关性。具体而言可检验式(5)中的残差(ε|IM)与M和R的线性关系的显著性水平。本文选择显著性水平为5%的F检测法进行线性关系的检验，当显著性水平p值大于5%时，二者线性关系不显著，则表明被检验的地震动强度指标具备充分性。
图7表示在三维地震动激励下DM，IM拟合残差和震级及震中距的关系。图7(a)和图7(b)显示对于烟囱结构，结构最大曲率与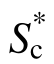
的拟合残差与震级和震中距的p值分别是0.223和0.783，均大于5%。按照显著性水平检验标准，此时
的充分性满足条件。同理对于水塔结构，如图7(c)和图7(d)，结构最大曲率与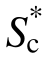
的拟合残差与震级和震中距的p值分别是0.306和0.539，p值亦大于5%，此时，
的充分性满足条件。综上所述，对于本文的高耸混凝土结构，在三维地震动作用下
的充分性是满足要求的。
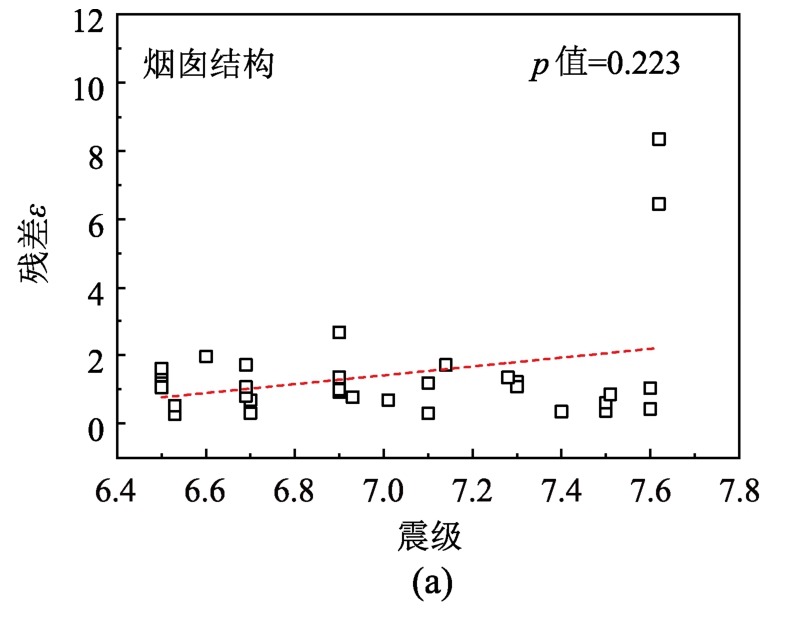
图7 本文地震动强度指标的充分性
Fig.7 Sufficiency of proposed earthquake intensity measure
6 结论
(1) 本文针对高耸混凝土结构，在三维地震动作用下提出了一种同时考虑高阶振型和周期延长效应的地震动强度指标。该指标的有效性受到地震动种类的影响，并随着参与振型数量及周期延长系数的变化而变化。
(2) 对于高耸烟囱结构，有必要同时考虑周期延长现象和高阶振型效应。在三维地震动输入下，周期延长现象开始显现，近断层地震动的脉冲效应会加剧结构进入塑性阶段的程度，结构的周期延长系数较远场地震动有所增加，周期延长现象更加明显。而对于水塔结构，考虑周期延长效应的指标有效性比考虑高阶振型效应的指标更高，对于这类结构使用周期延长效应的指标更合适。
(3) 对于高耸混凝土结构，在三维地震动输入条件下指标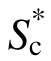
的充分性满足要求。与既有的地震动强度指标的有效性相比，
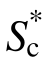具有一定优势。因此，
可作为分析和评价高耸混凝土结构抗震性能的合理选择。
[1]张锐, 李宏男, 王东升, 等.结构时程分析中强震记录选取研究综述[J].工程力学, 2019, 36(2): 1―16.Zhang Rui, Li Hongnan, Wang Dongsheng, et al.Selection and scaling of real accelerograms as input to time-history analysis of structures: a state-of-the art review.[J].Engineering Mechanics, 2019, 36(2): 1―16.(in Chinese)
[2]陈健云, 周晶, 马恒春, 等.高耸烟囱结构竖向地震响应的模型试验研究及分析[J].建筑结构学报, 2005,26(2): 87―93.Chen Jianyun, Zhou Jing, Ma Hengchun, et al.Study on model test of highrise chimney subjected to vertical seismic action[J].Journal of Building Structures, 2005,26(2): 1―16.(in Chinese)
[3]韩建平, 陈继强, 闫青, 等.考虑谱形影响的地震动强度指标研究进展[J].工程力学, 2015, 32(10): 9―17.Han Jiangping, Chen Jiqiang, Yan Qing, et al.State of the art of ground motion intensity measures accounting for the influence of spectral shape[J].Engineering Mechanics, 2015, 32(10): 9―17.(in Chinese)
[4]Cordova P P, Deierlein G G, Mehanny S S, et al.Development of a two-parameter seismic intensity measure and probabilistic assessment procedure[C].Sapporo, Hokkaido: Proceedings of the 2nd U.S.-Japan Workshop on Performance-based Earthquake Engineering Methodology for Reinforced Concrete Building Structures, 2000: 187―206.
[5]Vamvatsikos D, Cornell C A.Developing efficient scalar and vector intensity measures for IDA capacity estimation by incorporating elastic spectral shape information[J].Earthquake Engineering ＆ Structural Dynamics, 2005, 34(13): 1573―1600.
[6]Lin L, Naumoski N, Saatcioglu M, et al.Improved intensity measures for probabilistic seismic demand analysis.Part 1: development of improved intensity measures[J].Canadian Journal of Civil Engineering,2010, 38(1): 79―88.
[7]周颖, 苏宁粉, 吕西林.高层建筑结构增量动力分析的地震动强度参数研究[J].建筑结构学报, 2013, 34(2):53―60.Zhou Ying, Su Ningfen, Lu Xilin.Study on intensity measure of incremental dynamic analysis for high-rise structures[J].Journal of Building Structures, 2013, 34(2):53―60.(in Chinese)
[8]卢啸, 陆新征, 叶列平, 等.适用于超高层建筑的改进地震动强度指标[J].建筑结构学报, 2014, 35(2): 15―21.Lu Xiao, Lu Xinzheng, Ye Lieping, et al.Development of an improved ground motion intensity measure for super high-rise buildings[J].Journal of Building Structures,2014, 35(2): 15―21.(in Chinese)
[9]Shome N.Probabilistic seismic demand analysis of nonlinear structures[D].Stanford, USA: Stanford University, 1999: 320.
[10]Zhang Y T, He Z, Lu W G, et al.A spectralacceleration based linear combination-type earthquake intensity measure for high-rise buildings[J].Journal of Earthquake Engineering, 2018, 22(8): 1479―1508.
[11]谈臻.高耸烟囱结构在竖向和水平地震作用下的抗震性能分析[D].上海: 同济大学, 2007.Tan Zhen, Study on seismic behavior of stack-like structure under vertical and horizonal earthquake action[D].Shanghai: Tongji University, 2007.(in Chinese)
[12]Zhou C, Tian M, Guo K.Seismic partitioned fragility analysis for high-rise RC chimney considering multidimensional ground motion[J].Structural Design of Tall and Special Buildings, 2019, 28: e1568.
[13]Zhou Y, Ge P, Li M, et al.An area-based intensity measure for incremental dynamic analysis under two-dimensional ground motion input[J].The Structural Design of Tall and Special Buildings, 2017, 26(12): e1374.
[14]曾绪朗.高耸钢筋混凝土烟囱结构抗震性能研究[D].北京: 北京交通大学, 2014.Zeng Xulang, Study on seismic performance of high-rise reinforcd concrete chimney structure[D].Beijing:Beijing Jiaotong University, 2014.(in Chinese)
[15]张晓阳.倒锥壳式水塔抗震性能及地震易损性分析[D].北京: 北京交通大学, 2016.Zhang Xiaoyang, Seismic behavior and fragility analysis of inverted cone water tower[D].Beijing: Beijing Jiaotong University, 2016.(in Chinese)
[16]Tothong P, Luco N.Probabilistic seismic demand analysis using advanced ground motion intensity measures[J].Earthquake Engineering ＆ Structural Dynamics, 2007,36(13): 1837―1860.
[17]Gunes N, Ulucan Z C.Nonlinear dynamic response of a tall building to near-fault pulse-like ground motions[J].Bulletin of Earthquake Engineering, 2019, 17: 2989―3013.
[18]Federal Emergency Management Agency, Quantification of building seismic performance factors: FEMA P695[R].Washington DC: Federal Emergency ManagementAgency, 2009: A14―A21.
[19]Lu X, Lu X Z, Guan H, et al.Comparison and selection of ground motion intensity measures for seismic design of super high-rise buildings[J].Advances in Structural Engineering, 2013, 16(7): 1249―1262.
[20]杨参天, 解琳琳, 李爱群, 等.适用于高层隔震结构的地震动强度指标研究[J].工程力学, 2018, 35(8): 21―29.Yang Cantian, Xie Linlin, Li Aiqun, et al.Intensity measures for seismically isolated tall buildings[J].Engineering Mechanics, 2018, 35(8): 21―29.(in Chinese)