钢筋混凝土(RC)结构遭遇水平荷载时，其梁柱节点和柱脚处的受拉钢筋易产生应变累积，当混凝土受拉开裂后，受拉钢筋产生相对混凝土的滑移，进而产生由钢筋滑移变形所引起的柱顶附加水平位移。Saatcioglu和Ozcebe[1]、Sezen和Moehle[2]、Lynn等[3]均进行了RC框架柱的低周往复加载试验，结果表明由钢筋滑移变形引起的柱顶附加水平位移可占总位移的30%以上，极端情况下这种钢筋滑移变形与柱弯曲变形引起的位移占总位移的比重相当。试验[4－6]表明柱脚处受拉钢筋的滑移会降低柱的刚度、延性和耗能等力学性能，甚至会改变RC框架结构的薄弱层机制。研究[6－8]表明，与采用中高强材料的新建结构相比，许多既有RC结构由于混凝土强度较低和箍筋约束效应较弱，钢筋滑移现象会尤为突出。此外，研究[9－10]指出RC结构在遭受强震作用时，在柱脚的塑性铰区域内，钢筋滑移会逐渐增加，其抗震性能会进一步下降。因此，为更为准确地模拟RC结构的抗震性能，在有限元模型中应当考虑此钢筋滑移效应。
模拟此钢筋滑移效应的有限元模型基本可分为两类。在细观模型方面，常采用黏结应力-滑移本构模型[11]来模拟钢筋的滑移效应。细观尺度有限元模型虽可取得较为满意的精度，但也有些许不足之处：单元的数量过多，大量的网格划分，时间成本较高等，这与整体结构的抗震性能模拟往往不相兼容。而基于纤维截面的宏观尺度有限元模型[12－14]可以兼具高效和精度，被广泛用于工程结构的抗震分析中。Monti和Spacone[15]、Pan等[16]分别提出了可考虑钢筋滑移的宏观梁柱单元，但其单元截面和钢筋纤维的受力状态需重新进行修正，需要大量复杂的计算过程，时间成本较高。Zhao和Sritharan[17]、成虎等[18]和朱绩超等[19]采用零长度纤维模型，即通过在构件端部附加一个零长度截面单元来模拟钢筋滑移所造成构件端部的转角效应。但由于零长度截面单元与平截面假定存在一定的矛盾，会造成混凝土的最外侧受压纤维产生过大的变形。此外，抗震分析方法的多样性(动力推覆、时程分析和增量动力分析等)也决定了需要提出更为高效的模拟方法。
综上，本文拟提出一种简化的可考虑钢筋滑移效应的双线性应力-应变本构关系，即假设通过增加钢筋在受拉状态的应变来体现钢筋滑移效应。随后将该钢筋本构模型应用于纤维截面的宏观单元模型中以模拟既有14根RC柱的荷载-位移反应，并与试验结果、不考虑钢筋滑移效应的纤维模型和零长度纤维模型进行对比，以校准该模型的可靠性并讨论其适用范围，最终为RC结构的抗震性能模拟提供更多的选择。
1 钢筋滑移模型
首先基于黏结应力分布简化模型，推导钢筋的应力-滑移关系，通过已有拉拔试验数据对该钢筋滑移关系进行验证，为下一步提出考虑滑移效应的钢筋应力-应变理论关系建立基础。
1.1 钢筋滑移计算
图1所示为钢筋滑移计算模型。图1(b) 所示为两段式黏结应力分布简化模型[5, 20]，在钢筋屈服前后的黏结应力分别为τe和τp。图1(a) 所示为钢筋锚固在混凝土中的受力图，其中A为钢筋截面面积；fs为钢筋应力。在长度lb内任取一微小长度dx的微元体，通过力的平衡方程可得该微元体中黏结应力τ(x)表达式为：
式中：d为钢筋截面直径；dfs为钢筋应力增量。由式(1)可知，对图1(b) 的黏结应力τe和τp进行积分，可得钢筋应力沿长度lb为双线性分布，如图1(c) 所示。再假定钢筋应力-应变关系为双线性本构：
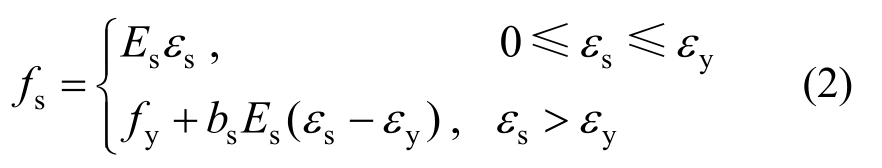
式中：Es为钢筋弹性模量；εs为钢筋应变；bs为钢筋硬化率；fy和εy分别为钢筋屈服强度和屈服应变。由式(2)可得钢筋应变沿长度lb也为双线性分布，如图1(d)所示。
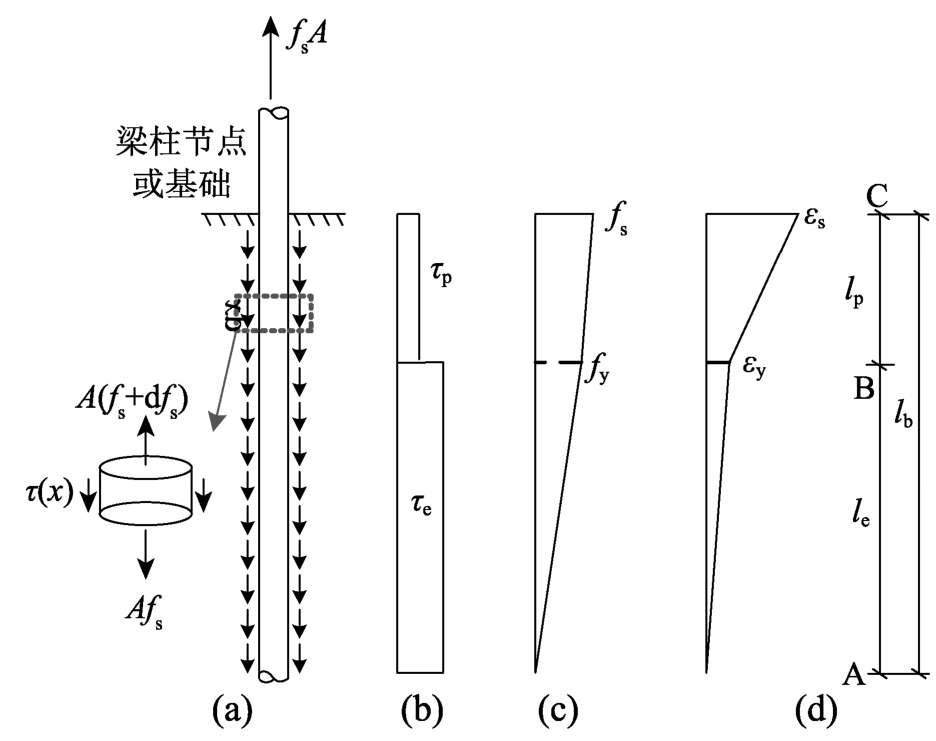
图1 钢筋滑移计算模型
Fig.1 Calculation model of rebar slip
将图1(b)的黏结应力τe和τp代入钢筋加载端力的平衡方程
并结合式(2)可得长度le和lp的表达式分别为：
对图1(d)长度lb内的钢筋应变进行积分，可得钢筋加载端处的滑移S为：
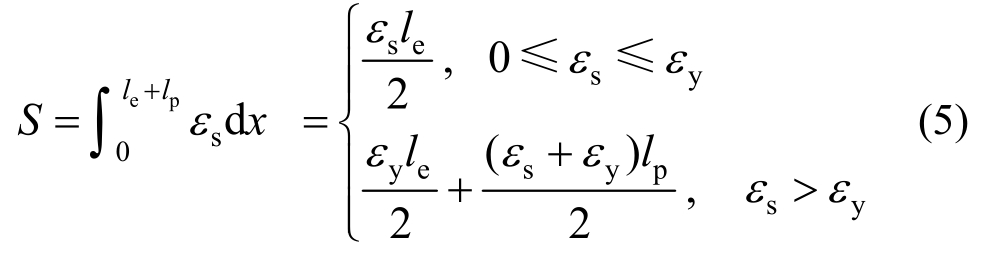
将式(2)～式(4)代入式(5)，可得钢筋的应力-滑移关系为：
1.2 黏结应力计算
确定本文黏结应力τe和τp的计算模型时采用黏结应力除以混凝土轴心抗压强度的开方根使其标准化的方法[5, 20－21]。虽然国内外关于黏结滑移的试验资料较为丰富，然而本文仅选择钢筋屈服时未发生黏结劈裂破坏的试验进行统计分析。筛选文献[3, 20－25]中相关的试验数据，回归得到黏结应力与混凝土轴心抗压强度fc的关系如图2所示，虚线为试验数据的平均值。其中黏结应力τe和τp分别由试验所测加载端的钢筋滑移和钢筋应力代入式(6)求得。由此，可得黏结应力τe和τp的表达式分别为：
图2 黏结应力
Fig.2 Bond stress
1.3 钢筋应力滑移关系验证
来自文献[24]和文献[25]的拉拔试验数据将与式(6)的钢筋应力-滑移关系进行对比，以验证该钢筋滑移关系的可靠性，试验数据取钢筋加载端的应力和滑移。表1所示为拉拔试验构件的设计参数，图3所示为拉拔试验结果与式(6)的对比。
表1 拉拔构件设计参数
Table 1 Design parameters of pull-out specimen
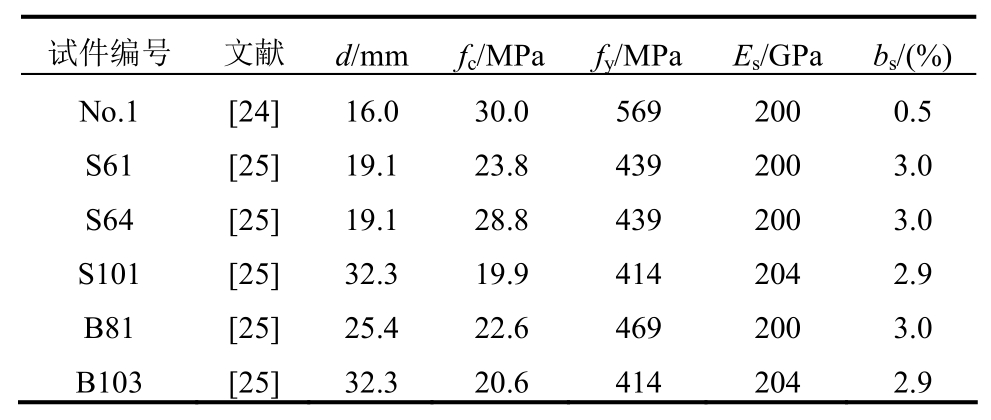
试件编号文献d/mmfc/MPa fy/MPa Es/GPabs/(%)No.1[24]16.0 30.0 569 200 0.5 S61[25]19.1 23.8 439 200 3.0 S64[25]19.1 28.8 439 200 3.0 S101[25]32.3 19.9 414 204 2.9 B81[25]25.4 22.6 469 200 3.0 B103[25]32.3 20.6 414 204 2.9
如图3所示，式(5)在弹性阶段的应力-滑移曲线与拉拔试验数据吻合精度较好，在非弹性阶段，式(5)预计的钢筋滑移量稍大。总体而言，式(5)可反映钢筋弹性和非弹性变形下的滑移特征。
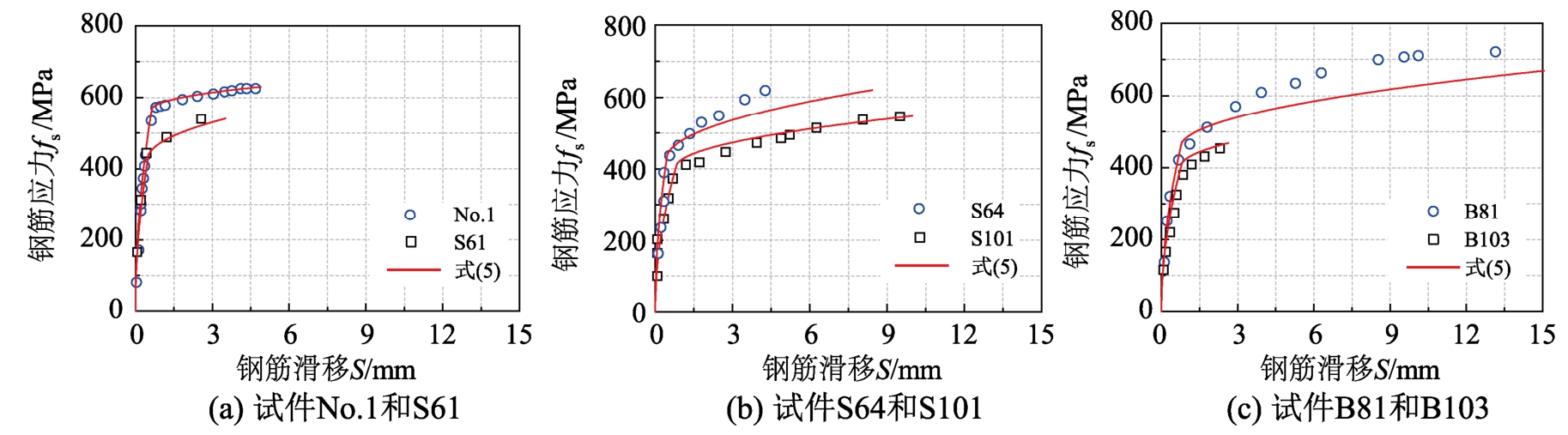
图3 拉拔试验结果与式(6)的对比
Fig.3 Comparison of pull-out test results and Eq.(6)
2 考虑滑移效应的钢筋本构模型
通过分析RC构件受拉开裂处钢筋的总滑移量，并结合式(6)的钢筋滑移关系和塑性铰长度模型将钢筋滑移效应进一步考虑到钢筋的应力-应变关系中，在此基础上通过参数分析，可对该理论关系进一步简化，最终提出考虑滑移效应的双线性钢筋本构模型。
2.1 RC梁柱中的钢筋滑移
在水平荷载P作用下，RC框架柱在与梁或与基础相交的节点处会产生裂缝，在该裂缝处受拉钢筋会发生相对于混凝土的滑移Stot，如图4(a)所示。受拉钢筋在RC框架柱(A部分)中产生的相对滑移为SA，在梁或基础(B部分)中产生的相对滑移为SB，因此有：
在充分锚固的情况下，同一构件中SA和SB的大小由该截面的钢筋应力水平决定，即SA和SB分别由fs(SA)和fs(SB)决定，如图4(b)所示。而对于同一截面处有fs(SA)=fs(SB)，因此有：
图4 RC梁柱中的钢筋滑移
Fig.4 Rebar slip in RC beams and columns
2.2 考虑滑移效应的钢筋应力-应变理论关系
RC结构在水平荷载作用下构件的非弹性变形主要集中在塑性铰区域，由此假设考虑滑移效应后的钢筋应变为：
式中，ls为构件塑性铰长度。
将式(6)和式(10)代入式(11)，可得考虑滑移效应的钢筋应力-应变理论关系为：
塑性铰长度采用Bae和Bavrak[26]模型，该模型较为有效地描述了构件的非线性变形，其表示为：
式中，h为构件截面高度。
2.3 参数分析
由式(12)可知，考虑滑移效应的钢筋应力-应变理论关系，除了与钢筋的材料参数有关，还与混凝土轴心抗压强度fc和构件塑性铰长度ls有关。采用一组控制模型来分析以上各个参数对该理论关系的影响，控制模型的基本参数如表2所示，其中一个参数变化时，其他参数均保持不变。不同材料参数下考虑滑移效应的钢筋应力-应变理论关系如图5所示，其中曲线的特征点参数如表3所示。
表2 控制模型参数
Table 2 Properties of control model
注：fu为钢筋极限强度。
参数 fc/MPad/mmfy/MPa Es/GPa bs/(%) fu/MPals/mm数值 30 16360 200 1 520100
由图5和表3分析可知，在图5(a)的混凝土轴心抗压强度组，考虑滑移效应的钢筋弹性模量
随着混凝土强度的提高而增大，即混凝土强度越高，钢筋滑移效应越不明显。在图5(b)的钢筋直径组，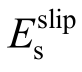
随钢筋直径的增大而减小，即采用较细的钢筋有利于减小钢筋滑移。在图5(c)～图5(d)的屈服强度和弹性模量组，
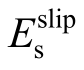随屈服强度的提高而减小，随弹性模量的提高而增大。而在图5(e)的硬化率组，
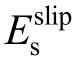不随硬化率的增减而发生改变。在图5(g)的塑性铰长度组，
随塑性铰长度的增大而增大。
此外，如表3所示，考虑滑移效应的钢筋硬化率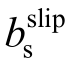
不随混凝土强度、钢筋直径、钢筋弹性模量和塑性铰长度的增大或减小而发生改变。且在钢筋硬化率bs组，
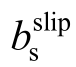与bs相差不大。
2.4 简化关系
基于以上分析，为便于应用，可假设考虑滑移效应的钢筋硬化率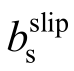
与bs相同，并将式(12)简化为双线性关系。且假设钢筋在受压状态下与混凝土界面不会产生滑移，其受压本构与不考虑滑移效应的钢筋模型一致，以上简化模型如图6所示。
综上，本文所提考虑滑移效应的双线性钢筋本构模型可表示为：
图5 参数分析
Fig.5 Parameter analysis
表3 特征点参数
Table 3 Characteristic point parameters
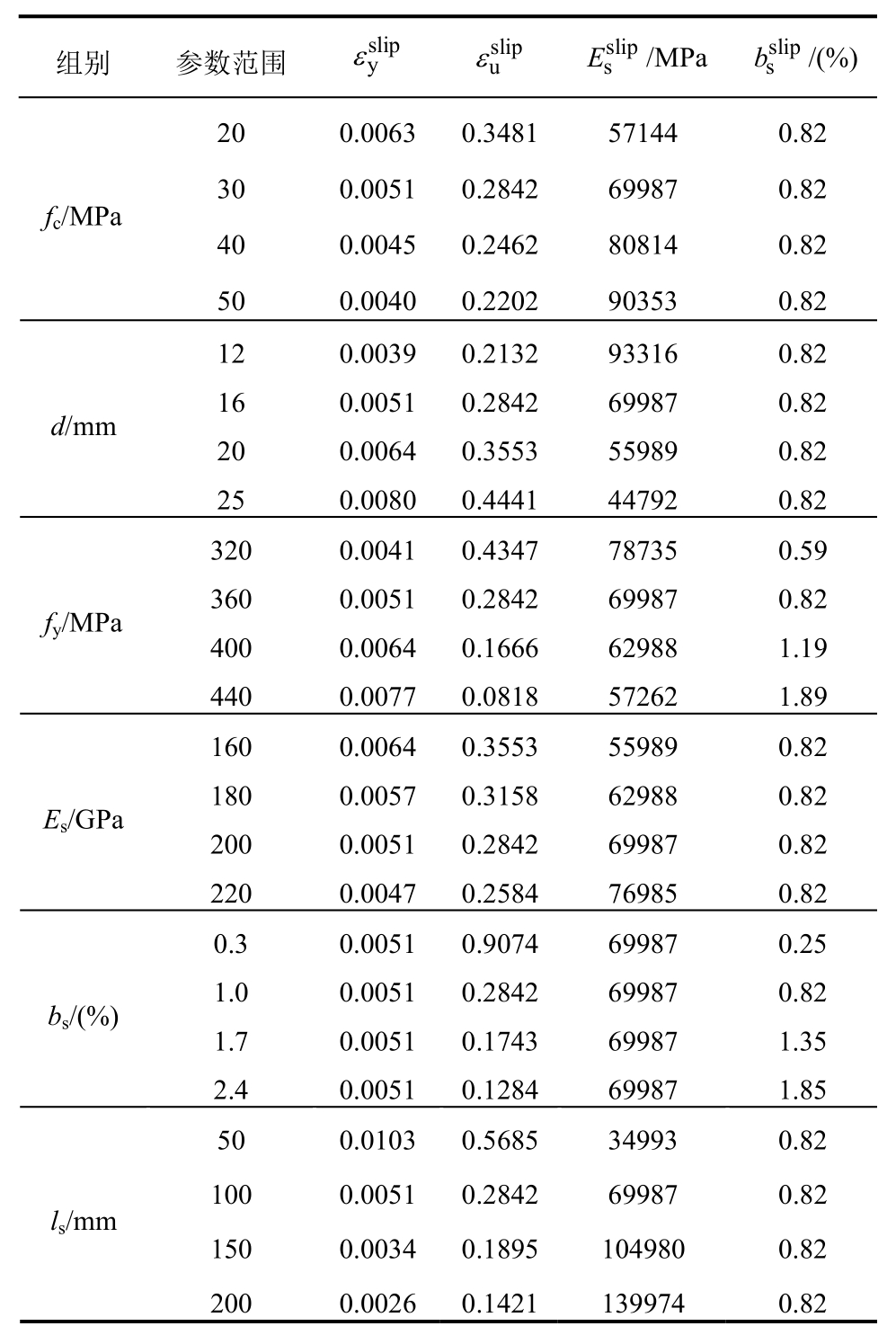
注：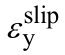
和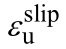
分别为考虑滑移效应的钢筋屈服应变和极限应变；
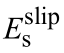和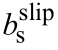
分别为考虑滑移效应的钢筋弹性模量和硬化率。
组别 参数范围 slipyε slipuε Eslips/MPa bslips/(%)20 0.0063 0.3481 57144 0.82 fc/MPa 30 0.0051 0.2842 69987 0.82 40 0.0045 0.2462 80814 0.82 50 0.0040 0.2202 90353 0.82 12 0.0039 0.2132 93316 0.82 d/mm 16 0.0051 0.2842 69987 0.82 20 0.0064 0.3553 55989 0.82 25 0.0080 0.4441 44792 0.82 320 0.0041 0.4347 78735 0.59 fy/MPa 360 0.0051 0.2842 69987 0.82 400 0.0064 0.1666 62988 1.19 440 0.0077 0.0818 57262 1.89 160 0.0064 0.3553 55989 0.82 Es/GPa 180 0.0057 0.3158 62988 0.82 200 0.0051 0.2842 69987 0.82 220 0.0047 0.2584 76985 0.82 0.3 0.0051 0.9074 69987 0.25 1.0 0.0051 0.2842 69987 0.82 1.7 0.0051 0.1743 69987 1.35 bs/(%)2.4 0.0051 0.1284 69987 1.85 50 0.0103 0.5685 34993 0.82 ls/mm 100 0.0051 0.2842 69987 0.82 150 0.0034 0.1895 104980 0.82 200 0.0026 0.1421 139974 0.82
图6 考虑滑移效应前后的双线性钢筋本构模型
Fig.6 Bilinear steel constitutive model before and after considering slippage effect
模型参数计算如下：
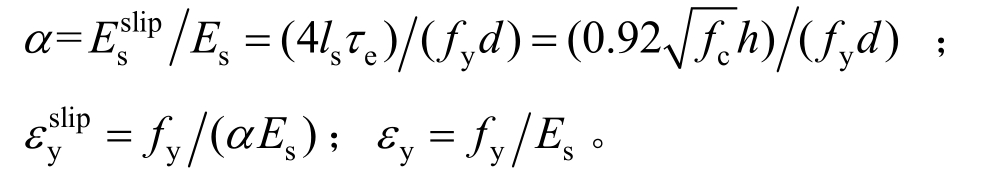
式中，α 定义为钢筋弹性模量折减率。
3 模型验证及对比分析
OpenSEES有限元平台[27]丰富的单元和材料模型足以用来模拟各类工程结构的性能且实现效率和精度的统一，使其成为地震工程领域研究最为常用的宏观有限元平台之一。为了更好地与国内外研究成果形成互动，同时便于其他学者重复本文的研究工作。本文基于OpenSEES平台，采集已有试验结果对本文模型进行验证。
目前国内外在基于纤维截面的宏观尺度有限元模型模拟钢筋滑移效应时，采用较多的是Zhao和Sritharan[17]提出的零长度纤维模型，即通过在柱与基础交界处附加零长度截面单元来模拟钢筋滑移变形引起的柱底截面转动效应，本文采用零长度纤维模型进行辅助验证。
3.1 试验概况
本文所述的钢筋滑移效应在以延性破坏为主的RC框架结构中更加突出，为避免尺寸效应，本文尽量选择缩尺比较大，截面尺寸较大，且破坏形态以延性破坏为主的试验资料进行验证。文献[1-5]分别对大比例尺RC框架柱和桥墩进行了拟静力试验研究，试验框架柱和桥墩的设计参数如表4所示，截面及配筋如图7所示。
表4 试验框架柱和桥墩设计参数
Table 4 Design parameters of test frame columns and bridge columns
注：n为纵筋数量；c为混凝土保护层厚度；fyv为箍筋屈服强度；dv和sv分别为箍筋直径和间距；N为轴向压力。
试件编号 文献 截面 fc/MPafy/MPa Es/GPa d/mmn bs/(%)c/mmfyv/MPadv/mmsv/mm N/kN ls/mmα U1[1]1-1 43.6 430 200 25.0 6 1.50 23 470 10.0 150 0 88 0.198 U2[1]1-1 30.2 453 200 25.0 6 1.50 23 470 10.0 150 600 88 0.156 U3[1]1-1 34.8 430 200 25.0 6 1.50 23 470 10.0 75 600 88 0.177 U4[1]1-1 32.0 438 200 25.0 6 1.50 23 470 10.0 50 600 88 0.166 S1[2]2-2 21.2 438 189 28.7 8 2.00 20 476 9.5 305 667 114 0.154 S2[2]2-2 21.2 438 189 28.7 8 2.00 20 476 9.5 305 2670 114 0.154 3CLH18[3]3-3 25.6 331 199 31.8 8 0.43 50 399 9.5 457 481 114 0.202 2CLH18[3]3-3 33.1 331 199 25.4 8 0.43 50 399 9.5 457 484 114 0.288 3CMH18[3]3-3 27.6 331 199 31.8 8 0.43 50 399 9.5 457 1498 114 0.210 3CMD12[3]4-4 27.6 331 199 31.8 8 0.43 50 399 9.5 305 1498 114 0.210 P1[4]5-5 28.6 354 200 13.0 161.50 28 354 6.0 50 160 100 0.428 407[5]6-6 29.7 483 193 16.0 111.00 19 668 6.4 32 654 153 0.395 415[5]7-7 30.3 483 193 16.0 221.00 19 668 6.4 32 654 153 0.400 430[5]8-8 31.7 483 193 16.0 441.00 19 668 6.4 32 654 153 0.409
图7 试验框架柱和桥墩构造 /mm
Fig.7 Details of test frame column and bridge column
3.2 宏观有限元模型
宏观尺度有限元模型如图8所示，图8(a)的模型A为采用本文钢筋模型的纤维宏观单元模型，图8(b)的模型B为采用不考虑滑移的钢筋模型的纤维宏观单元模型，图8(c)的模型C为零长度纤维宏观单元模型。其中模拟Saatcioglu试验、Kawashima试验和Lehman试验时，模型悬臂长度ln取水平荷载到基础的距离，分别为1000 mm、1350 mm和2440 mm；而模拟Sezen和Lynn试验时模型悬臂长度ln取构件的反弯点至基础的距离，为1473 mm。构件的塑性铰长度ls和钢筋弹性模量折减率α见表4。
除模型C中Node 1～Node 2的构件单元采用零长度截面单元外，其他构件单元均采用基于位移法的非线性梁柱单元，以上3个模型均采用纤维截面。模型A的钢筋纤维本构关系为本文所提出的双线性钢筋模型，采用OpenSEES的Hysteretic材料模拟，如图8(d)所示；模型B的钢筋纤维本构关系为不考虑滑移效应的双线性钢筋模型，采用OpenSEES的Steel01材料模拟，如图8(e)所示。
如图8(f)所示，保护层混凝土纤维本构关系为非约束混凝土模型，分为2部分：第1部分为Kent-Scott-Park混凝土模型[28]；第2部分为Roy和Sozen模型[29]；即采用OpenSEES的Concrete 01材料模拟。箍筋内混凝土纤维本构关系为约束混凝土模型，分为3部分：第1部分为Mander混凝土模型[30]，采用OpenSEES的Concrete 04材料模拟；第2部分采用OpenSEES的MinMax材料来给定应变阀值，当混凝土应变超过εccu时，Mander混凝土模型失效；第3部分对于约束混凝土压碎后的行为采用OpenSEES的Hysteretic材料模拟，斜率根据Roy和Sozen模型[29]计算。
3.3 荷载-位移反应
图9所示为模拟结果与Saatcioglu试验结果的对比。由图9(a)可看到模型A的刚度与试验结果较为相符，模型B明显高估柱的刚度，模型C轻微高估柱的刚度。正负加载时的试验结果差别较大，可能是试验加载时柱脚产生了偏移。从图9(b)～图9(d)可以看到当轴压比为0.14～0.16，模型B的刚度明显大于试验结果，而模型A和模型C则轻微高估柱的刚度，可能是由于未考虑柱剪切变形。但由于在延性破坏的构件中剪切变形占比较小且并不是本文关注的主要内容，因此以上3个模型中均未考虑柱剪切变形的影响。
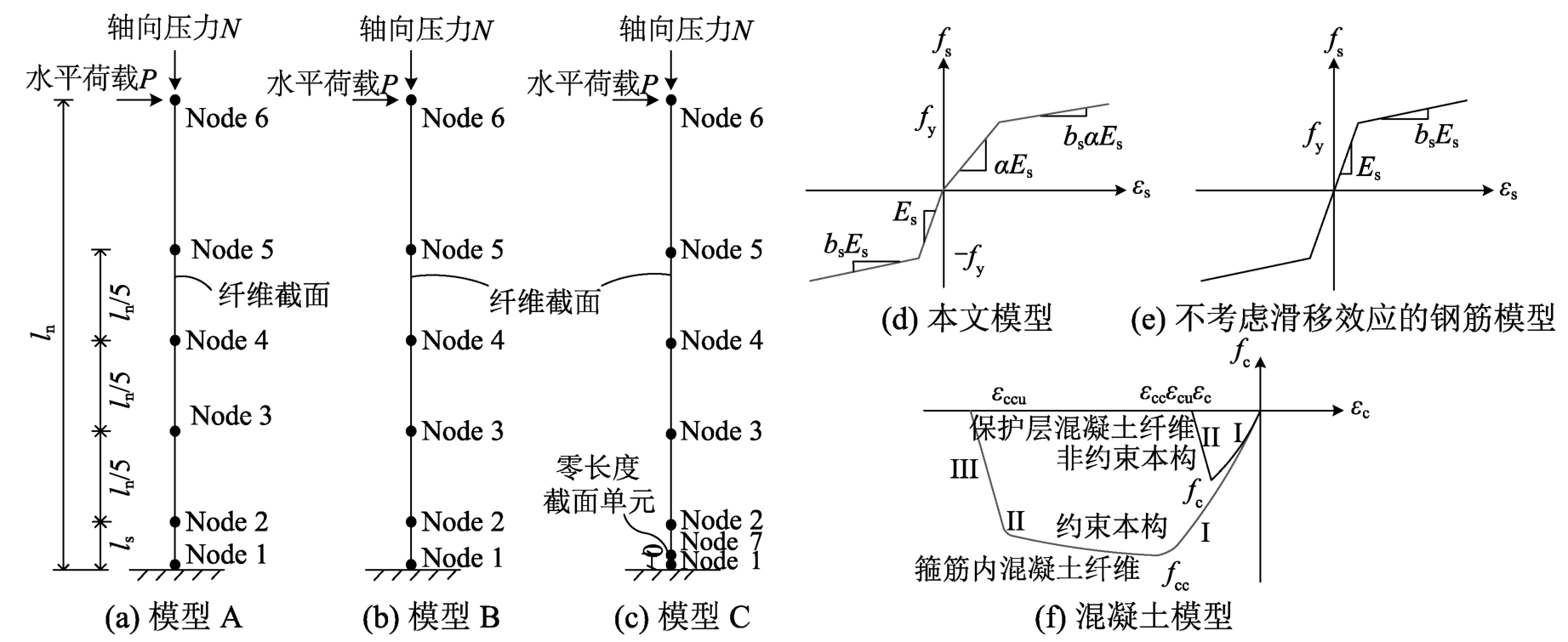
图8 宏观有限元模型
Fig.8 Macro finite element model
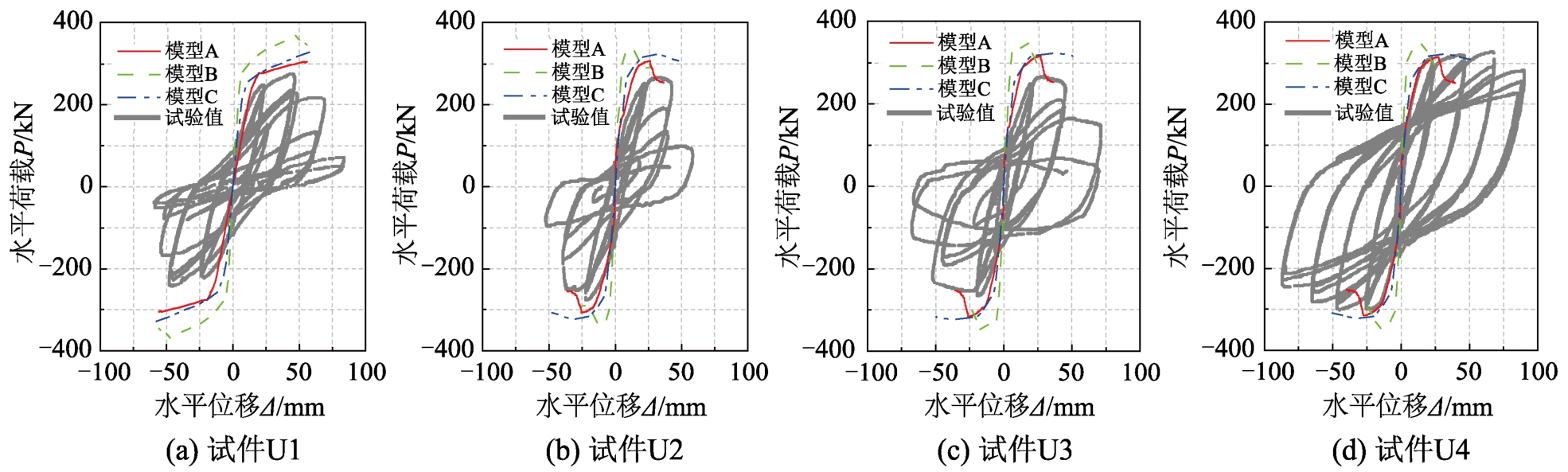
图9 模拟结果与Saatcioglu试验结果对比
Fig.9 Comparison of simulation and Saatcioglu test results
图10所示为模拟结果与Sezen试验结果的对比。由图10(a)可看到在轴压比为0.15时，模型A和模型C与试验结果的吻合精度较模型B好。对于中小轴压比的情况，3个模型与Saatcioglu试验和与Sezen试验的对比结果大致相同。但从图10(b)可看到在轴压比为0.6时，3个模型的承载力与刚度都明显大于试验结果。原因是在高轴压比情况下，混凝土框架柱往往发生由混凝土率先压溃而导致的小偏压破坏[31]，而本文模型是建立在弯曲型破坏特征的基础上。因此，在高轴压比的情况(非延性破坏)下，本文模型并不适用。
图11所示为模拟结果与Lynn、Kawashima和Lehman试验结果的对比。由图11(a)～图11(d)可看到在中小轴压比(0.07～0.26)时，模型A与模型C的计算结果与试验结果最为吻合，而模型B依然高估了柱的刚度。由图11(e)～图11(h)可看到模型A与试验结果吻合度较高，模型C次之，而模型B则高估柱的刚度。总体而言，模型A的计算结果与试验结果最为吻合，能够较好地反映RC柱承载力、刚度和位移变化。
图10 模拟结果与Sezen试验结果对比
Fig.10 Comparison of simulation and Sezen test results
基于以上14个试件的计算结果与试验结果的对比分析，可看到当构件处于弹性阶段时，由钢筋滑移变形引起的构件变形较小，但处于弹塑性阶段时，由钢筋滑移变形引起的构件变形不容忽视。基于本文钢筋模型所建立的宏观有限元模型(模型A)，可以较好地反映RC构件承载力、刚度和位移变化，计算结果优于已有模型(模型B和模型C)，同时兼具建模方便(与模型C相比)。值得注意的是，本文所提钢筋模型是以弯曲型破坏特征的RC构件为基础建立的，适用于以延性破坏为主的RC压弯剪构件，对于脆性破坏形态并不适用，如图10(b)所示的由高轴压比引起的脆性破坏。
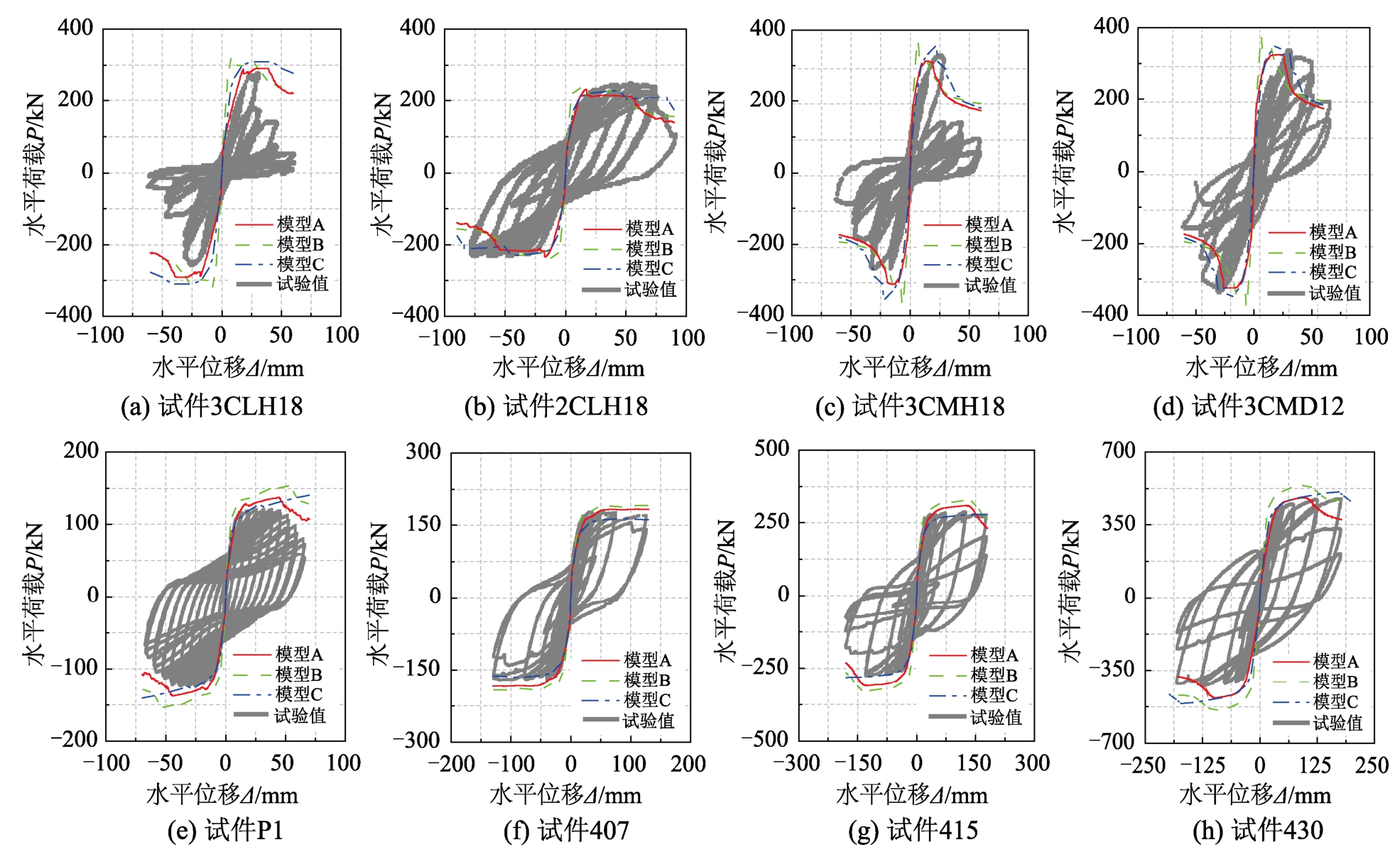
图11 模拟结果与Lynn、Kawashima和Lehman试验结果对比
Fig.11 Comparison of simulation and Lynn, Kawashima and Lehman test results
3.4 柱顶附加水平位移
由钢筋滑移变形引起的柱顶附加水平位移可表示为：
式中：Δflex+slip为弯曲变形和钢筋滑移变形引起的柱顶水平位移；Δflex为弯曲变形引起的柱顶水平位移；ΔModel,A和ΔModel,B分别为模型A和模型B计算的柱顶水平位移。
图12所示为计算的附加柱顶水平位移与试验结果的对比。在钢筋屈服前阶段，计算结果与试验数据吻合良好，随着水平荷载增加，计算结果略微低估试验结果。总体而言，由式(15)计算的附加柱顶水平位移与试验数据吻合度较好，表明模型A可反映钢筋滑移变形引起的柱顶附加水平位移。由此进一步证明了本文所提钢筋模型中通过扩大钢筋受拉状态下的应变值来反映钢筋滑移效应(截面层次)这一假设的可靠性。因此，从构件和截面层次验证了本文所提钢筋模型具有较好的精度和可靠性。
图12 柱顶附加水平位移与试验数据的比较
Fig.12 Comparison of column additional lateral displacement and test data
4 结论
本文提出了考虑滑移效应的双线性钢筋本构模型，并应用于纤维截面的宏观尺度有限元模型，对比试验结果和既有模型可以得到以下结论：
(1) 本文假设将构件中钢筋滑移变形分量的影响在钢筋应力-应变本构关系中考虑(即扩大钢筋受拉状态下的实际应变值)，提出考虑滑移效应的双线性钢筋本构模型，通过降低钢筋弹性模量来实现应变值的增大。
(2) 不考虑钢筋滑移效应的宏观有限元模型会高估RC柱刚度，且不能反映钢筋滑移变形引起的RC构件受力性能的退化。基于零长度截面单元的宏观有限元模型可反映钢筋滑移变形引起的RC构件刚度下降。
(3) 通过本文所提的钢筋模型，利用截面分析方法(纤维截面模型)来考虑RC柱的钢筋滑移效应，结果表明该方法可反映钢筋滑移行为所带来的RC构件刚度、位移和承载力退化，总体上能反映RC构件的受力特征，可为RC结构的性能化抗震数值模拟提供更多的选择。
(4) 随着RC构件从弹性阶段进入弹塑性阶段，钢筋滑移变形引起的构件变形比重不断增大，极端情况下与弯曲变形相当，因此在钢筋混凝土结构的弹塑性地震反应分析和抗震性能评估中应当考虑此钢筋滑移效应。
[1]Saatcioglu M, Ozcebe G.Response of reinforced concrete columns to simulated seismic loading[J].ACI Structural Journal, 1989, 86(6): 3－12.
[2]Sezen H, Moehle J P.Seismic tests of concrete columns with light transverse reinforcement[J].ACI Structural Journal, 2006, 103(6): 842－849.
[3]Lynn A C, Moehle J P, Mabin S A, et al.Seismic evaluation of existing reinforced concrete building columns[J].Earthquake Spectra, 1996, 12(4): 715－739.
[4]Kawashima K, Watanabe G, Hayakawa R.Seismic performance of RC bridge columns subjected to bilateral excitation[C]// Proceedings of 35th Joint Meeting, Panel on Wind and Seismic Effects, Tsukuba Science City,Japan: Tokyo Institute of Technology, 2003.
[5]Lehman D E, Moehle J P.Seismic performance of well-confined concrete bridge columns: No.PEER-1998/01[R].Berkeley: University of California-Berkeley, 2000.
[6]Brage F, Gigliotti R, Laterza M.R/C existing structures with smooth reinforcing bars: Experimental behavior of beam-column joints subject to cyclic lateral loads[J].Open Construction and Building Technology Journal,2009, 3(16): 52－67.
[7]吴涛, 魏慧, 刘喜, 等.箍筋约束高强轻骨料混凝土柱轴压性能试验研究[J].工程力学, 2018, 35(2): 203－213.Wu Tao, Wei Hui, Liu Xi, et al.Experimental study on axial compression behavior of confined high-strength lightweight aggregate concrete under concentric loading[J].Engineering Mechanics, 2018, 35(2): 203－213.(in Chinese)
[8]梁兴文, 杨鹏辉, 何伟, 等.钢筋混凝土框架-纤维增强混凝土耗能墙结构抗震性能试验研究[J].工程力学,2018, 35(1): 209－218.Liang Xingwen, Yang Penghui, He Wei, et al.Experimental study on aseismic behavior of reinforced concrete frame-energy dissipation walls made with high performance fiber reinforced concrete[J].Engineering Mechanics, 2018, 35(1): 209－218.(in Chinese)
[9]Terzic V, Schoettler M J, Restrepo J I, et al.Concrete column blind prediction contest 2010: Outcomes and observations: No.PEER-2015/01[R].California: Pacific Earthquake Engineering Research Center, 2015.
[10]Schoettler M J, Restrepo J I, Guerrini G, et al.A full-scale, single-column bridge bent tested by shake-table excitation: No.PEER-2015/02[R].California: Pacific Earthquake Engineering Research Center, 2015.
[11]Wu Y F, Zhao X M.Unified bond stress-slip model for reinforced concrete[J].Journal of Structural Engineering,2013, 139(11): 1951－1962.
[12]Tao M X, Nie J G.Fiber beam-column model considering slab spatial composite effect for nonlinear analysis of composite frame systems[J].Journal of Structural Engineering, 2014, 140(1): 04013039.
[13]陶慕轩, 丁然, 潘文豪, 等.传统纤维模型的一些新发展[J].工程力学, 2018, 35(3): 1－21.Tao Muxuan, Ding Ran, Pan Wenhao, et al.Some advances in conventional fiber beam-column model[J].Engineering Mechanics, 2018, 35(3): 1－21.(in Chinese)
[14]Tao M X, Nie J G.Element mesh, section discretization and material hysteretic laws for fiber beam–column elements of composite structural members[J].Materials and Structures, 2015, 48(8): 2521－2544.
[15]Monti G, Spacone E.Reinforced concrete fiber beam element with bond-slip[J].Journal of Structural Engineering, 2000, 126(6): 654－661.
[16]Pan W H, Tao M X, Nie J G.Fiber beam–column element model considering reinforcement anchorage slip in the footing[J].Bulletin of Earthquake Engineering, 2017,15(3): 991－1018.
[17]Zhao J, Sritharan S.Modeling of strain penetration effects in fiber-based analysis of reinforced concrete structures[J].ACI Structural Journal, 2007, 104(2): 133－141.
[18]成虎, 李宏男, 王东升, 等.考虑锈蚀黏结退化的钢筋混凝土桥墩抗震性能分析[J].工程力学, 2017, 34(12):48－58.Cheng Hu, Li Hongnan, Wang Dongsheng, et al.Seismic performance analysis of reinforced concrete bridge column considering bond deterioration caused by chloride ion induced corrosion[J].Engineering Mechanics, 2017, 34(12): 48－58.(in Chinese)
[19]朱绩超, 王响, 张勤.考虑粘结-滑移与剪切作用的钢筋混凝土柱侧向变形分析[J].工程力学, 2015, 32(7):128－135.Zhu Jichao, Wang Xiang, Zhang Qin.Lateral deformations analysis of reinforced concrete columns incorporating bond-slip and shear effects[J].Engineering Mechanics, 2015, 32(7): 128－135.(in Chinese)
[20]Sezen H, Setzler E J.Reinforcement slip in reinforced concrete columns[J].ACI Structural Journal, 2008,105(3): 280－289.
[21]Shima H, Chou L L, Okamura H.Micro and macro models for bond in reinforced concrete[J].Journal of the Faculty of Engineering, 1987, 39(2): 133－194.
[22]Viwathanatep S, Popov E, Bertero V V.Effects of generalized loadings on bond of reinforcing bars embedded in confined concrete blocks: No.UCB/EERC-79/22[R].California: Pacific Earthquake Engineering Research Center, 1979.
[23]Mathey R G, Watstein D.Investigation of bond in beam and pull-out specimens with high-yield-strength deformed bars[J].ACI Journal Proceedings, 1961, 32(9):1071－1090.
[24]Engstrom B, Mangnusson J, Huang Z.Pull-out behavior of ribbed bars in normal and high-strength concrete with various confinements[J].Special Publication, 1998, 180:215－242.
[25]Ueda T, Lin I, Hawkins N M.Beam bar anchorage in exterior column-beam connections[J].ACI Journal Proceedings, 1986, 83(3): 412－422.
[26]Bae S, Bavrak O.Plastic hinge length of reinforced concrete columns[J].ACI Structural Journal, 2008,105(3): 290－300.
[27]Mckenna F, Fenves G L, Scott M H, et al.Open system for earthquake engineering simulation (OpenSEES)[R].Berkeley, CA: Pacific Earthquake Engineering Research Center, 2000.
[28]Yassin M H M.Nonlinear analysis of prestressed concrete structures under monotonic and cyclic loads[M].Berkeley: University of California-Berkeley, 1994.
[29]Roy H E H, Sozen M A.Ductility of concrete[J].Special Publication, 1965, 12: 213－235.
[30]Mander J B, Priestley M J N, Park R.Theoretical stress-strain model for confined concrete[J].Journal of Structural Engineering, 1988, 114(8): 1804－1826.
[31]过镇海.钢筋混凝土原理[M].北京: 清华大学出版社,2013.Guo Zhenhai.Principles of reinforced concrete[M].Beijing: Tsinghua University Press, 2013.(in Chinese)