目前，混凝土及岩石断裂韧度的确定方法中，须采用含有预制裂缝的试件。比如，中国水工混凝土断裂试验规程DL/T 5332―2005[1]中，推荐楔入劈拉法、三点弯曲梁法确定混凝土断裂韧度：所用试件的预制裂缝长度a0=80 mm，试件高度W=200 mm，即初始缝高比α=a0/W=0.4；国际材料与结构研究实验联合会RILEM[2－3]推荐的确定水泥砂浆和混凝土材料断裂特性所用试件，其初始缝高比α=0.15～0.5；国际岩石力学协会ISRM[4－5]推荐确定岩石材料的断裂韧度所用试件的初始缝高比α=0.15～0.26。美国ASTM E399规范[6－7]规定确定满足线弹性断裂力学条件下的无尺寸效应的断裂韧度，相应试验试件的预制裂缝长度a0应大于2.5(KIC/ft)2 (KIC为材料的断裂韧度，ft为材料的拉伸强度)。
预制裂缝试件的制作耗时耗力，试验成本相对较高[8－10]。并且，裂缝的预制方式(预埋钢板[8－10]或切缝[11－12])、预制裂缝的尖端形状[13－16]等，都会对断裂试验结果产生一定影响[17－19]。另外，对于实际混凝土或岩石工程中受力前的结构或构件，往往不含一定长度的预制裂缝，无宏观裂缝的情况较为常见[20]。由此，若采用无缝试件去评价实际混凝土或岩石结构的断裂特性，可大大减轻试验准备工作量，降低预制裂缝对测试结果的影响权重。并且，无缝试件试验结果相对更真实贴近未预先设置人工裂缝的实际工程结构的断裂特性。
另一方面，在实验室条件下，由小尺寸试件确定的混凝土或岩石断裂韧度存在较为明显的尺寸效应[21-23]。尺寸效应产生的本质原因为[24]：实验室内所用试件的相对尺寸较小，即试件高度W与试件颗粒尺寸(混凝土的骨料最大粒径dmax[21－22]或岩石的平均颗粒尺寸gav[23])的比值W/dmax或W/gav较小，试件呈现非均质特性而为非线弹性断裂破坏，且试件裂缝尖端断裂过程区与试件前后边界的相互影响不能忽略。由此，试件处于准脆性断裂状态。而由处于准脆性断裂控制的小尺寸混凝土或岩石试件，来确定无尺寸效应的断裂韧度的理论及其相应方法，现有断裂力学模型[25－32]未能给出满意答案，目前该问题仍是混凝土与岩石断裂特性研究的难点问题[19, 33－35]。
由此，本文阐述与发展了由无缝试件确定材料无尺寸效应的断裂韧度的理论，考虑混凝土骨料或岩石颗粒对断裂韧度的重要影响，建立了由无缝试件的峰值荷载确定混凝土与岩石无尺寸效应的断裂韧度的模型与具体方法。通过相应的混凝土与岩石无缝试件的断裂试验分析，对所提模型与方法的合理性与适用性进行了验证。
1 无缝试件确定材料断裂韧度的理论
1.1 材料强度、断裂韧度及准脆性断裂三者的联系
Bažant教授[26]的断裂力学理论研究表明：材料破坏时的强度与其断裂韧度有区别但也存在关联。图1阐述了强度准则、断裂韧度准则及准脆性断裂三者的联系。
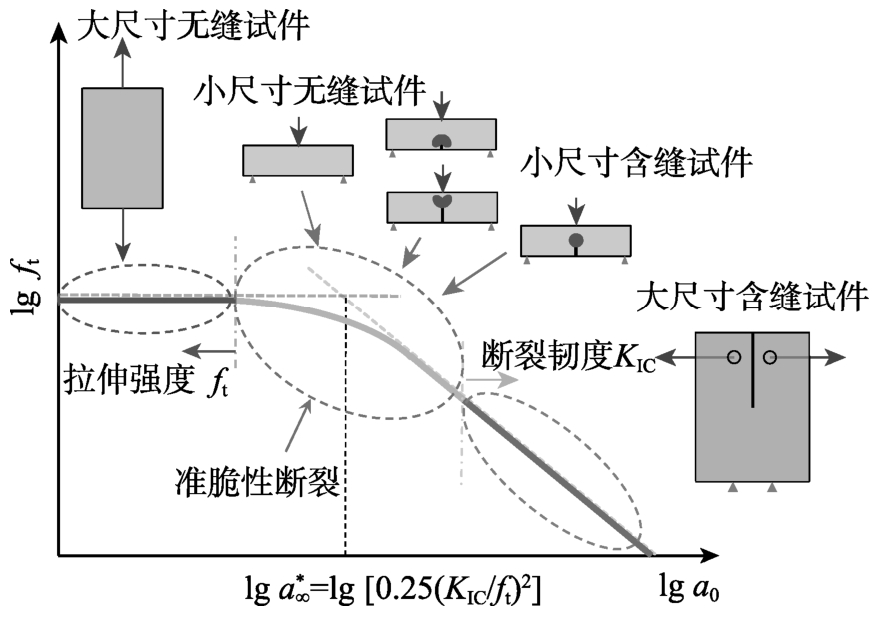
图1 强度准则、断裂韧度准则及准脆性断裂三者的联系
Fig.1 Relationship between strength, fracture toughness,and quasi-brittle fracture
如图1所示，无尺寸效应的材料参数——断裂韧度KIC，可由大尺寸含有预制长裂缝的试件确定[6－7](100%断裂韧度准则控制)；而另一无尺寸效应的材料参数——拉伸强度ft，可由大尺寸无缝试件确定[36] (100%强度准则控制)。对于实验室条件下的小尺寸试件，其断裂破坏同时受控于断裂韧度准则和强度准则(比如80%断裂韧度准则和20%强度准则控制，或者60%断裂韧度准则和40%强度准则控制等)，因此，小尺寸含浅缝与含深缝试件都处于准脆性断裂控制；小尺寸无缝试件也处于准脆性断裂状态。
若两极限准则——断裂韧度KIC和拉伸强度ft的具体数值都已知，则可描述小尺寸试件的准脆性断裂状态。另一方面，如果已知小尺寸试件的结构特性，也可以外推确定两个无尺寸效应的材料参数——KIC和ft。
1.2 描述无缝试件强度的尺寸效应理论模型
Bažant教授提出的尺寸效应理论模型——SEM (size effect model) [26,31]中，给出了无缝试件强度的名义应力公式。
对于无缝试件，即缝高比α=a0/W=0的试件，SEM的四参数模型应用公式具体为[26,31]：
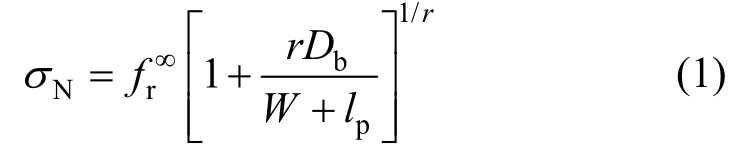
式中：σN为不考虑裂缝长度影响的名义应力；
、r、Db、lp为通过试验数据拟合确定经验参数；W为试件尺寸。
同时，SEM给出了缝高比α=a0/W＜0.1的浅缝试件的分析公式[26,31]：
1) 当不考虑试件初始缺陷时，十二参数经验方程为：
式中：E'为弹性模量；g0为能量释放率；α0为初始缝高比；da为骨料最大粒径；Gf、cf、fr∞、Db、r、k、p、q、lp、ε、ε,n、ψ为经验参数。
2) 当考虑试件初始缺陷时，十五参数经验方程为：
式中：Gf、cf、fr∞、Db、r、k、p、q、lp、ls、ε、ε,n、ψ、n、m为经验参数。
可见，SEM的无缝与浅缝公式复杂繁琐，且须通过试验数据拟合确定相应的多个参数；另外，无缝与浅缝试件须采用不同计算公式，并未统一。
1.3 确定无缝试件强度与断裂韧度的边界效应模型
当前学者们基于实验室小尺寸试件来确定无尺寸效应的混凝土与岩石断裂韧度的方法，大体可归纳为2类：第1类由于试件尺寸较小，裂缝尖端断裂过程区的影响不能忽略，则采用等效裂缝长度ac来替带初始裂缝长度a0代入线弹性断裂力学计算模型中，得出等效断裂韧度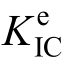
；第2类试验测定小尺寸试件的结构特性(比如峰值荷载)，基于断裂模型公式采用外推法确定断裂韧度KIC。第2类方法的代表即SEM[26,31]和边界效应模型BEM(boundary effect model) [37－42]。
以名义应力为表现形式的BEM的基本解析表达式为[37－42]：
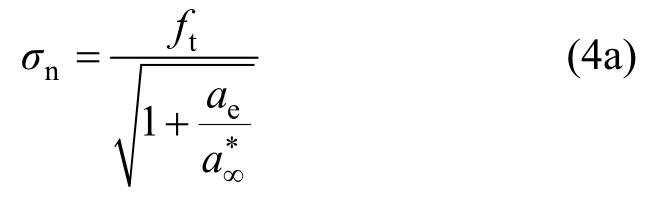
式中：σn为考虑裂缝长度影响的名义应力，对于无缝试件，σn=σN，σn相关于几何结构参数ae与峰值荷载Pmax等；ft为材料的拉伸强度；ae记为等效裂缝长度，为试件的几何结构参数，其仅与试件尺寸相关，而若对于无缝试件，ae=0；
为材料的特征裂缝长度，其值与材料的颗粒尺寸相关[21-23]，可由材料参数——断裂韧度KIC和拉伸强度ft确定[37-42]，其理论表达式为：
可见，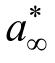
也是材料参数，并可衡量KIC和ft两者在准脆性断裂破坏中的比例权重。
1.4 无缝试件断裂韧度的解析表达式
由解析式(4)可反解出断裂韧度KIC的表达式：
若σn和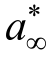
方便确定，则对于给定尺寸的试件，可由式(5)直接确定出断裂韧度KIC。
对于三点弯曲梁试件型式，考虑峰值荷载时对应的裂缝尖端虚拟裂缝扩展量Δafic，试件前、后边界以及初始裂缝长度a0等影响的名义应力σn的具体表达式为[40-42]：
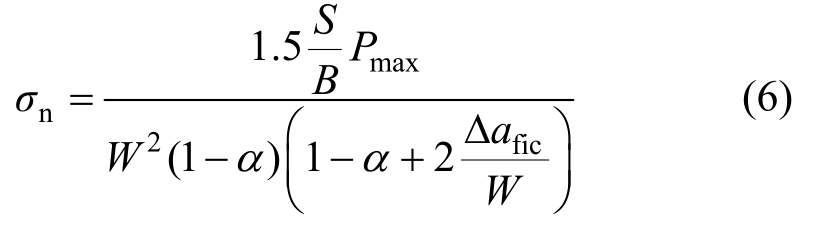
式中：S为试件有效跨长；B为试件厚度；Pmax为试件的峰值荷载；W为试件高度；α为试件缝高比。
对于无缝试件，综合式(5)与式(6)，可得断裂韧度KIC具体表达式为：
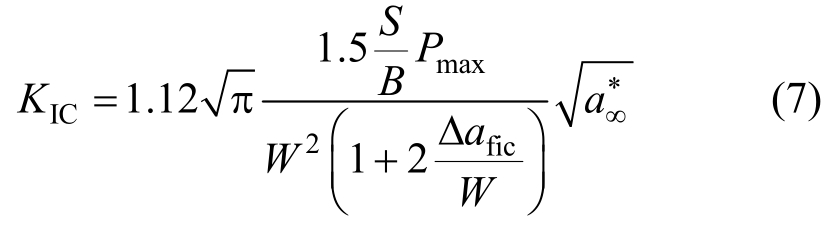
式(7)中，采用特征裂缝长度
及Pmax时的虚拟裂缝扩展量Δafic，来充分考虑岩石、混凝土的离散颗粒属性、非均质的材料特性。结合课题组对多组不同比例KIC和ft情况下的统计分析，对于混凝土材料，其特征裂缝长度
=1.5dmax[21－22]；对于岩石材料，
=3gav[23]，如考虑颗粒的最大粒径dmax大致为平均颗粒粒径gav的2倍，则混凝土与岩石材料还可采用简化关系
=3gav=1.5dmax。
为方便设计，对于实验室小尺寸试件，峰值荷载Pmax时的混凝土与岩石的虚拟裂缝扩展量Δafic可分别取Δafic=1.0dmax[21－22]和Δafic=(1.0～2.0)gav[23]。
由此，当试件尺寸S、B、W确定后，仅需测定无缝试件的峰值荷载Pmax，即可通过式(7)确定出断裂韧度KIC。
需说明, 上述推导基于三点弯曲受力型式。若采用其他受力型式，仅需建立其相应的名义应力σn表达式，并结合式(5)，即可得出该型式下的无缝试件KIC解析表达式。例如，对于传统断裂试验采用的紧凑拉伸或楔入劈拉试件，考虑Δafic，试件前、后边界，a0等影响的σn的具体表达式为[41]：
结合式(5)，即可得出，由紧凑拉伸或楔入劈拉无缝试件的Pmax确定相应材料KIC的解析表达式：
2 试验研究
本文试验材料采用芝麻灰类型的花岗岩，其密度为2727 kg/m3，抗压强度为101 MPa。通过统计分析可知：该岩石材料的颗粒尺寸集中在1.5 mm～3.0 mm(约占90%)，最大颗粒尺寸dmax=5 mm (约占0.7%)，平均颗粒尺寸gav=2.5 mm。
设计2个系列不同尺寸花岗岩试件，I系列与II系列的试件尺寸分别为S×B×W=160 mm×30 mm×40 mm和S×B×W=320 mm×30 mm×80mm，试件相对尺寸分别为 W/gav=16和W/gav=32。其中，每个系列包括4个初始缝高比α=0的无缝试件；同时，每个系列设计多组不同缝高比的预制含缝试件，目的是将由无缝试件确定的断裂韧度值与含缝试件确定值进行比较，来验证本文所提模型与方法的正确性。设计试件尺寸的详细信息见表1。
试验在量程为600 kN的SHT4605型号的电液伺服万能试验机上进行，试验过程中记录各试件的峰值荷载Pmax。试验实际加载情况见图2。
表1 花岗岩试件设计尺寸及实际缝长a0与实测峰值荷载Pmax
Table 1 Details on the size of the granite specimens,actual notch length (a0), and experimental peak loads (Pmax) in this study
设计组 编号 S/mmB/mm W/mm a0/mm Pmax/kN I-0-1 160 30 40 0 2.98无缝I-0-2 160 30 40 0 3.49 I-0-3 160 30 40 0 3.29 I-0-4 160 30 40 0 2.81 I-1-1 160 30 40 1 5.54系列I 浅缝I-1-2 160 30 40 1 5.13 I-1-3 160 30 40 1 5.27 I-1-4 160 30 40 1 4.90 I-1-5 160 30 40 1 4.83 I-1-6 160 30 40 1 5.33 I-1-7 160 30 40 1 4.91 I-1-8 160 30 40 1 5.02 8组含缝 160 30 40 2～24 II-0-1320 30 80 0 7.18无缝II-0-2320 30 80 0 6.28 II-0-3320 30 80 0 6.07 II-0-4320 30 80 0 6.59 II-1-1320 30 80 0.8 5.54系列I I 浅缝II-1-2320 30 80 1 5.13 II-1-3320 30 80 0.8 5.27 II-1-4320 30 80 1.5 4.90 II-1-5320 30 80 1.8 4.83 II-1-6320 30 80 1 5.33 II-1-7320 30 80 1.5 4.91 II-1-8320 30 80 1.5 5.02 11组含缝 320 30 80 2～56
图2 试验加载全景图
Fig.2 Test loading panorama
实测各试件的峰值荷载Pmax列入表1。基于本文解析表达式(7)，由各试件的Pmax即可直接确定断裂韧度KIC。取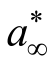
=3gav，Δafic=1.0gav、2.0gav、5.0gav对应的KIC计算结果见表2。
表2 基于本文模型确定的本文试验所用花岗岩断裂韧度KIC
Table 2 KIC of granite determined by using the proposed model
设计组 编号 KIC/(MPa•m1/2)Δafic=gav Δafic=2gav Δafic=5gav I-0-1 2.274 2.047无缝I-0-2 2.663 2.397 I-0-3 2.512 2.261 I-0-4 2.146 1.931平均值 2.399 2.159离散系数 0.097 0.097 I-1-1 2.613 2.346系列I浅缝I-1-2 2.176 1.954 I-1-3 2.302 2.067 I-1-4 2.447 2.197 I-1-5 2.111 1.896 I-1-6 2.264 2.033 I-1-7 2.566 2.304 I-1-8 2.221 1.994平均值 2.338 2.099离散系数 0.079 0.079 8组含缝 2.108 1.907 II-0-1 2.903 2.742 2.467无缝II-0-2 2.540 2.399 2.159 II-0-3 2.455 2.318 2.086 II-0-4 2.665 2.517 2.265平均值 2.641 2.494 2.245离散系数 0.074 0.074 0.074 II-1-1 2.395 2.261 2.033系列I I浅缝II-1-2 2.254 2.128 1.913 II-1-3 2.280 2.152 1.935 II-1-4 2.232 2.106 1.892 II-1-5 2.245 2.117 1.902 II-1-6 2.341 2.209 1.986 II-1-7 2.237 2.110 1.896 II-1-8 2.286 2.157 1.938平均值 2.284 2.155 1.937离散系数 0.025 0.025 0.026 11组含缝 2.582 2.236 2.108
由表2可见，分别由系列I和系列II的无缝试件确定的断裂韧度KIC基本一致(Δafic=1.0gav时，系列I确定的KIC平均值为2.399 MPa•m1/2；系列II确定的KIC平均值为2.641 MPa•m1/2)。由此表明：无缝试件确定的KIC与试件尺寸无关，是材料参数；可采用不同尺寸无缝试件确定无尺寸效应的KIC。另外，对于系列I，Δafic=2.0gav与Δafic=1.0gav时确定的KIC相差较小而基本吻合。对于系列II，即使Δafic增加到5.0gav，确定的KIC与Δafic=1.0gav相比，仍变化较小而基本一致。则为方便设计应用，对于岩石材料，可简化取Δafic=1.0gav。
采用系列I和系列II中，含有1 mm长预制裂缝的试件，基于式(5)和式(6)确定的KIC也列入表2。可见，采用浅缝试件与采用无缝试件的确定结果基本一致，从而证明了本文所提模型的准确性和合理性。
如图3所示，无缝试件裂缝出现位置随机。通过表2的比较可见，无缝试件实测试验结果及确定参数的离散性略大于浅缝试件：比如Δafic=1.0gav时，无缝试件系列I和系列II确定的KIC的离散系数分别为0.097和0.074；相应的浅缝试件确定的KIC的离散系数分别为0.079和0.025。考虑确定结果的离散性，建议由无缝试件确定断裂韧度时，采用多个或者多组试件。而若想精确控制试件裂缝的出现位置及初始扩展方向，减小试验数据的离散性，可以采用浅缝试件。
图3 试验中一组无缝花岗岩试件断裂破坏的图示
Fig.3 Failure of a set of unnotched granite specimens
基于基本理论式(4)，采用回归分析方法[21－24]，由多组不同缝高比的含缝试件，可外推确定出无尺寸效应的KIC。即对一定量的试验数据(由实测Pmax确定的σn，以及含缝试件的几何形状参数ae)进行拟合来确定KIC。数据拟合情况见图4和图5，具体确定的KIC结果也列入表2。
由表2、图4和图5的比较可见，采用无缝试件直接由本文模型表达式(7)确定的KIC，与通过回归分析方法确定的KIC基本一致，由此也证明了本文模型的合理性和适用性。
图4 由不同缝高比α试件(W/gav=16)确定花岗岩的KIC
Fig.4 Determination of KIC using granite specimens with different α (W/gav=16)
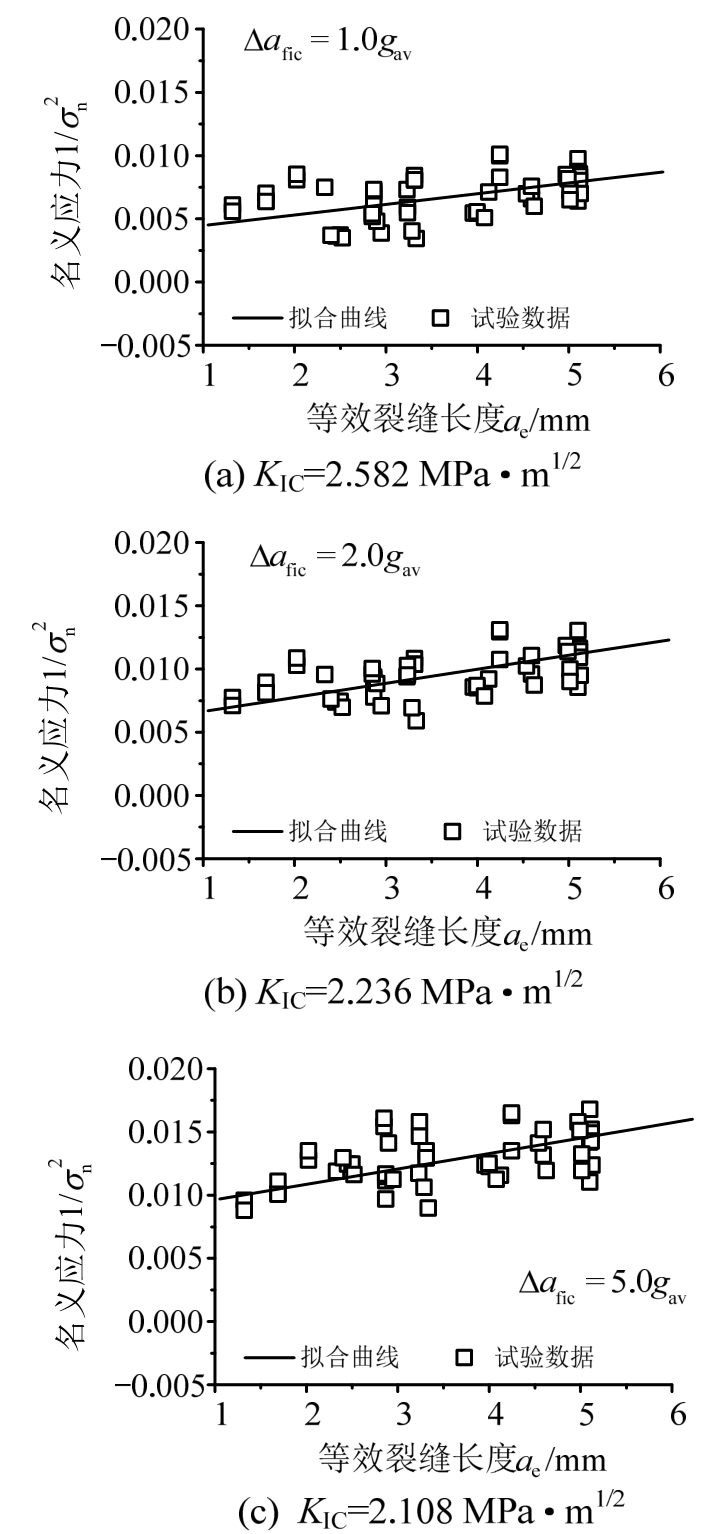
图5 由不同缝高比α试件(W/gav=32)确定花岗岩的KIC
Fig.5 Determination of KIC using granite specimens with different α (W/gav=32)
另外，本文同步进行了W=200 mm的大尺寸花岗岩试件的断裂试验，采用实测Pmax，基于ASTM规范中线弹性断裂理论公式直接确定的KIC=1.65～1.74 MPa•m1/2。虽然W=200 mm的试件相对尺寸W/gav=80，但仍小于满足线弹性断裂条件的理论尺寸W/gav≈400。因此，基于ASTM 规范，由W=200 mm试件确定的KIC值，接近但略小于I系列与II系列小尺寸试件的预测结果。
3 其他学者试验验证
3.1 文献[43]花岗岩试件的试验验证
采用文献[43]的三点弯曲花岗岩无缝试件为研究对象，该花岗岩的平均颗粒尺寸gav=2.5 mm。试件尺寸S×B×W=280 mm×25 mm×70 mm，相对尺寸W/gav=28。试件尺寸信息与实测峰值荷载Pmax见表3。
表3 文献[43]花岗岩试件尺寸及实际a0与Pmax
Table 3 Details on the size of granite specimens, actual a0 and Pmax from a previous study[43]
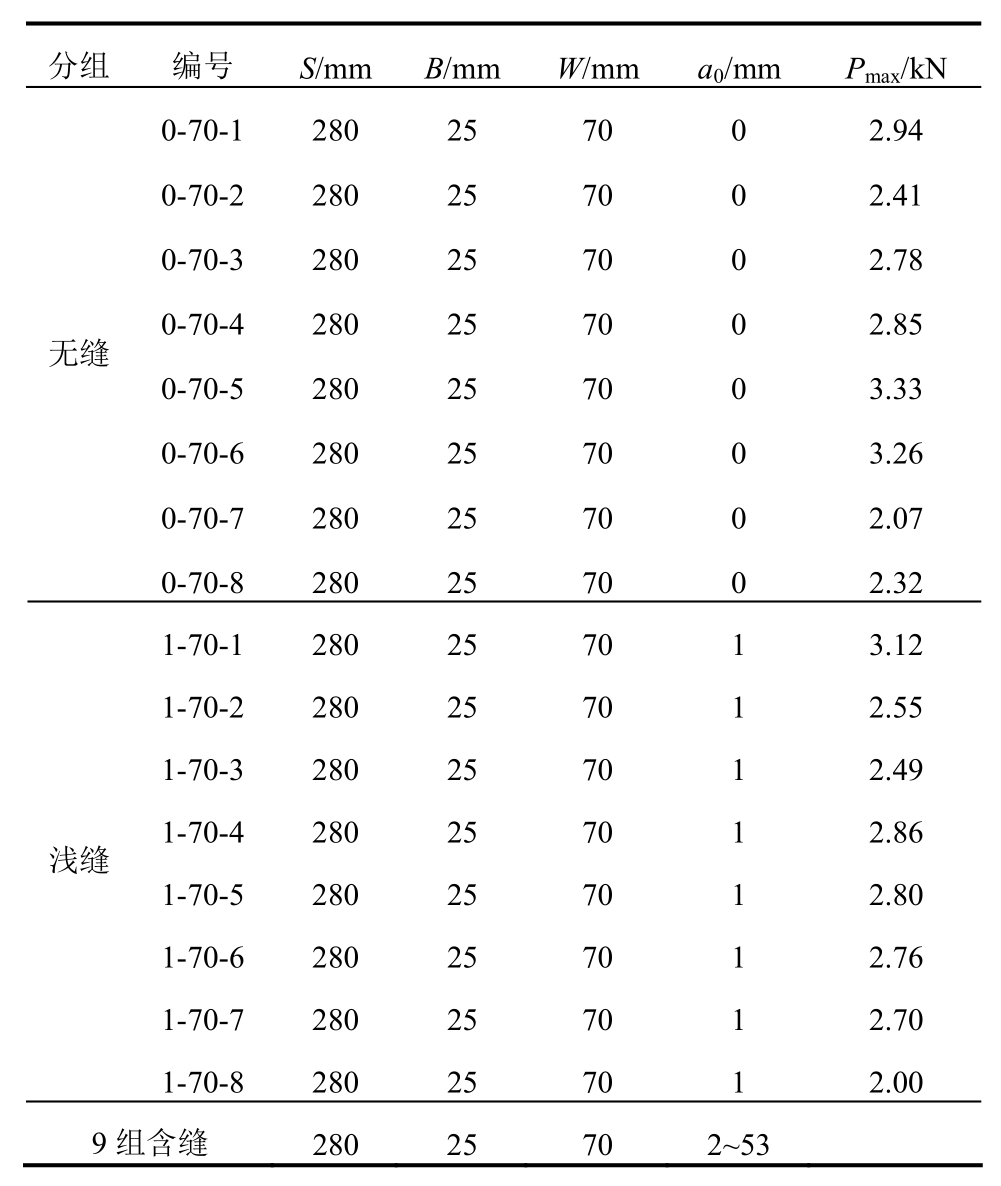
分组编号 S/mmB/mm W/mm a0/mm Pmax/kN 0-70-1280 25 70 0 2.94无缝0-70-2280 25 70 0 2.41 0-70-3280 25 70 0 2.78 0-70-4280 25 70 0 2.85 0-70-5280 25 70 0 3.33 0-70-6280 25 70 0 3.26 0-70-7280 25 70 0 2.07 0-70-8280 25 70 0 2.32 1-70-1280 25 70 1 3.12浅缝1-70-2280 25 70 1 2.55 1-70-3280 25 70 1 2.49 1-70-4280 25 70 1 2.86 1-70-5280 25 70 1 2.80 1-70-6280 25 70 1 2.76 1-70-7280 25 70 1 2.70 1-70-8280 25 70 1 2.00 9组含缝 280 25 70 2～53
基于本文模型解析表达式(7)，取a*∞=3gav，Δafic=1.0gav、2.0gav对应的KIC计算结果见表4。
由表4的比较可见，采用本文式(7)由无缝试件的确定结果，与由本文式(5)和式(6)采用浅缝试件的确定结果基本一致；其与基于边界效应基本理论表达式(4)，通过9组含缝试件，采用数据拟合方法确定的断裂韧度KIC也较吻合。
表4 基于本文模型确定的文献[43]所用花岗岩断裂韧度KIC
Table 4 KIC of granite from a previous study[43]as determined by the proposed model
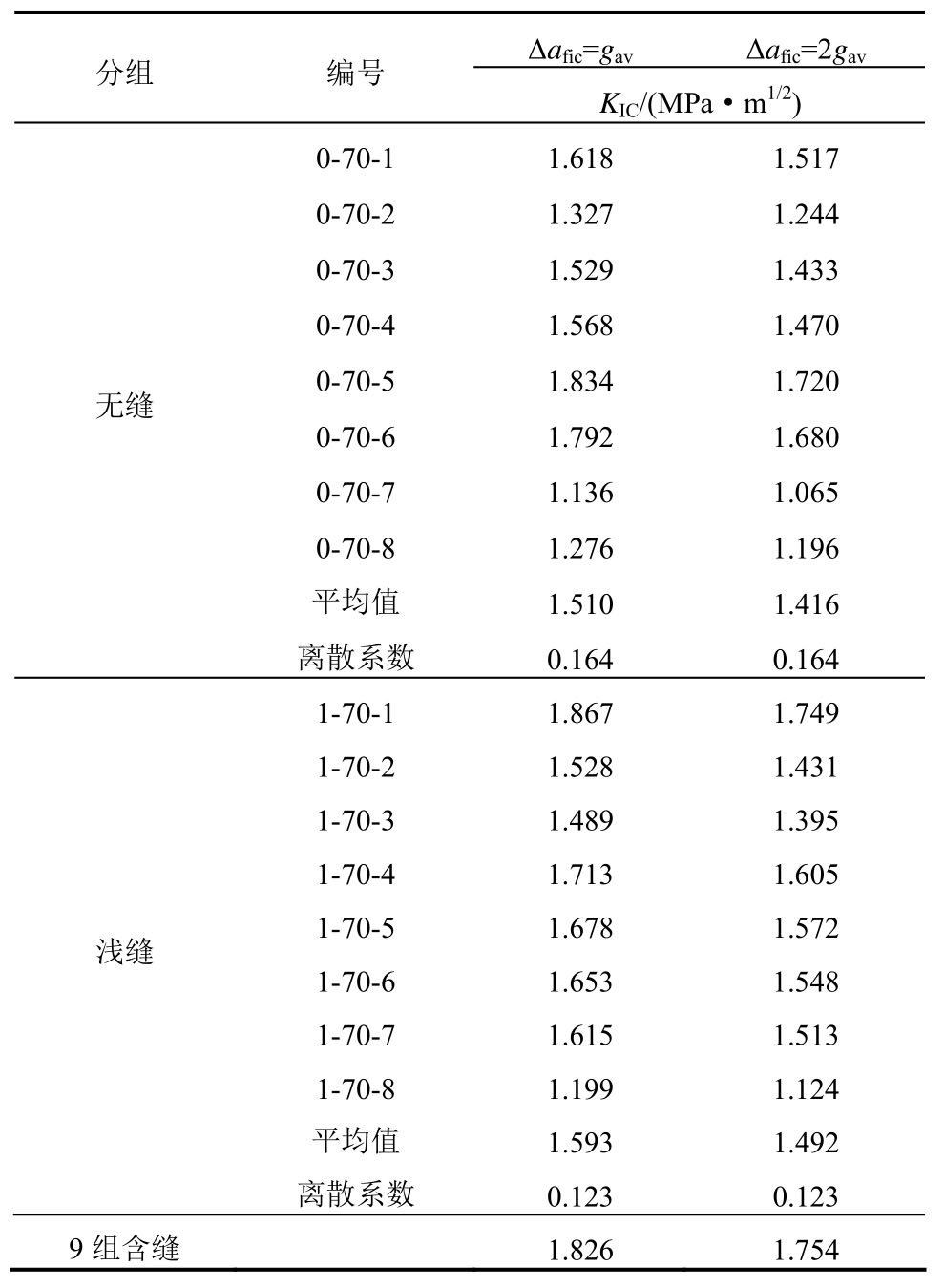
Δafic=gav Δafic=2gav分组 编号 KIC/(MPa·m1/2)0-70-1 1.618 1.517无缝0-70-2 1.327 1.244 0-70-3 1.529 1.433 0-70-4 1.568 1.470 0-70-5 1.834 1.720 0-70-6 1.792 1.680 0-70-7 1.136 1.065 0-70-8 1.276 1.196平均值 1.510 1.416离散系数 0.164 0.164 1-70-1 1.867 1.749浅缝1-70-2 1.528 1.431 1-70-3 1.489 1.395 1-70-4 1.713 1.605 1-70-5 1.678 1.572 1-70-6 1.653 1.548 1-70-7 1.615 1.513 1-70-8 1.199 1.124平均值 1.593 1.492离散系数 0.123 0.123 9组含缝 1.826 1.754
3.2 文献[12]混凝土试件的试验验证
采用文献[12]的3组不同尺寸三点弯曲混凝土无缝试件为研究对象，其试件尺寸S×B×W依次为468 mm×40 mm×215 mm、202×40×93 mm、87 mm×40 mm×40 mm。该混凝土的骨料最大粒径dmax=10mm。相对尺寸W/dmax依次为21.5、9.3、4。试件尺寸信息与实测峰值荷载Pmax见表5。
基于本文模型，取
=1.5dmax，Δafic=1.0dmax，由无缝试件确定的KIC结果见表6；同时，由浅缝试件确定的结果也列入表6。同样，为便于比较，采用回归分析方法，由多组含缝试件确定的KIC结果列入表6。
由表6的比较结果可见：基于本文模型，采用无缝试件的确定结果(3个系列KIC平均值分别为1.352 MPa·m1/2、1.436 MPa·m1/2、1.335 MPa·m1/2)，与由本文模型，采用浅缝试件的确定结果(KIC平均值为1.378 MPa·m1/2)基本一致。同时，无缝试件确定结果与通过15组含缝试件采用数据拟合方法确定的断裂韧度(KIC=1.451 MPa·m1/2)也基本吻合。
表5 文献[12]混凝土试件尺寸及实际a0与Pmax
Table 5 Details on the size of concrete specimens,actual a0 and Pmax from a previous study[12]
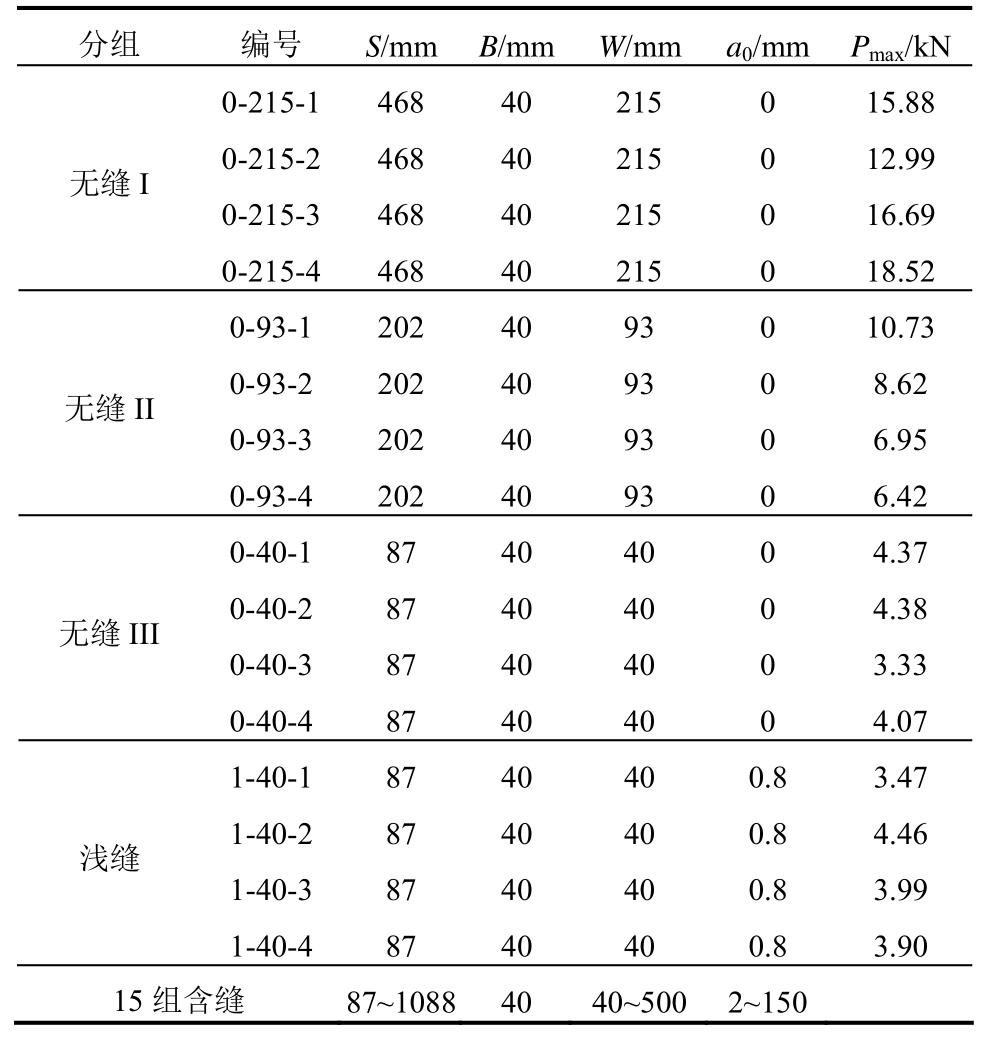
分组 编号 S/mmB/mm W/mm a0/mmPmax/kN 0-215-1468 40 215 0 15.88无缝I 0-215-2468 40 215 0 12.99 0-215-3468 40 215 0 16.69 0-215-4468 40 215 0 18.52 0-93-1202 40 93 0 10.73无缝II 0-93-2202 40 93 0 8.62 0-93-3202 40 93 0 6.95 0-93-4202 40 93 0 6.42 0-40-187 40 40 0 4.37无缝III 0-40-287 40 40 0 4.38 0-40-387 40 40 0 3.33 0-40-487 40 40 0 4.07 1-40-187 40 40 0.8 3.47浅缝1-40-287 40 40 0.8 4.46 1-40-387 40 40 0.8 3.99 1-40-487 40 40 0.8 3.90 15组含缝 87～108840 40～500 2～150
表6 基于本文模型确定的文献[12]所用混凝土断裂韧度KIC
Table 6 KIC from a previous study[12]as determined
by the proposed model
无缝I 无缝II编号 KIC/(MPa·m1/2) 编号 KIC/(MPa·m1/2)0-215-1 1.341 0-93-1 1.884 0-215-2 1.097 0-93-2 1.513 0-215-3 1.409 0-93-3 1.220 0-215-4 1.564 0-93-4 1.127平均值 1.352 1.436离散系数0.144 0.237无缝III 浅缝编号 KIC/(MPa·m1/2) 编号 KIC/(MPa·m1/2)0-40-1 1.445 1-40-1 1.209 0-40-2 1.448 1-40-2 1.554 0-40-3 1.101 1-40-3 1.390 0-40-4 1.346 1-40-4 1.359平均值 1.335 1.378离散系数0.122 0.103 15组含缝1.451
3.3 文献[11]混凝土试件的试验验证
采用文献[11]的4组不同尺寸三点弯曲混凝土无缝试件为研究对象，试件尺寸S×B×W依次为1088 mm×40 mm×500 mm、468 mm×40 mm×215 mm、202 mm×40 mm×93 mm、87 mm×40 mm× 40 mm。该混凝土的骨料最大粒径dmax=10 mm。相对尺寸W/dmax依次为50、21.5、9.3、4。试件尺寸信息与实测峰值荷载Pmax，见表7。
表7 文献[11]混凝土试件尺寸及实际a0与Pmax
Table 7 Details on the size of concrete specimens,actual a0 and Pmax from a previous study[11]
分组 编号 S/mm B/mmW/mm a0/mm Pmax/kN Ae01 1088 40 500 0 34.73无缝I Ae02 1088 40 500 0 33.94 Ae03 1088 40 500 0 34.16 Ae04 1088 40 500 0 45.19 Ae05 1088 40 500 0 35.79 Ae06 1088 40 500 0 38.59 Be01 468 40 215 0 16.65无缝II Be02 468 40 215 0 22.95 Be03 468 40 215 0 17.24 Be04 468 40 215 0 22.09 Be05 468 40 215 0 18.73 Be06 468 40 215 0 15.63 Ce01 202 40 93 0 9.86无缝III Ce02 202 40 93 0 9.48 Ce03 202 40 93 0 9.54 Ce04 202 40 93 0 10.67 Ce05 202 40 93 0 9.58 Ce06 202 40 93 0 8.55 Ce07 202 40 93 0 9.41 Ce08 202 40 93 0 9.09 De01 87 40 40 0 3.96无缝IV De02 87 40 40 0 4.11 De03 87 40 40 0 3.93 De04 87 40 40 0 3.92 De05 87 40 40 0 4.85 De06 87 40 40 0 4.33 De07 87 40 40 0 3.62 14组含缝 87～1088 40 40～500 3～150
基于本文模型，取a*∞=1.5dmax，Δafic=1.0dmax，由无缝试件确定的KIC结果见表8；同时，由浅缝试件确定的结果也列入表8。同样，为便于比较，采用回归分析方法，由多组含缝试件确定的KIC结果列入表8。
由表8的比较结果可见：基于本文模型，采用无缝试件的确定结果(四个系列KIC平均值分别为1.414 MPa·m1/2、1.594 MPa·m1/2、1.672 MPa·m1/2、1.357 MPa·m1/2)，与通过14组含缝试件采用数据拟合方法确定的断裂韧度 (KIC平均值为1.581 MPa·m1/2)基本吻合。
表8 基于本文模型确定的文献[11]所用混凝土断裂韧度KIC
Table 8 KIC from a previous study[11]as determined by the proposed model
无缝I 无缝II编号 KIC/(MPa·m1/2) 编号 KIC/(MPa·m1/2)Ae01 1.325 Be01 1.406 Ae02 1.295 Be02 1.938 Ae03 1.303 Be03 1.455 Ae04 1.724 Be04 1.865 Ae05 1.365 Be05 1.581 Ae06 1.472 Be06 1.320平均值 1.414 1.594离散系数 0.117 0.159无缝III 无缝IV编号 KIC/(MPa·m1/2) 编号 KIC/(MPa·m1/2)Ce01 1.731 De01 1.309 Ce02 1.664 De02 1.359 Ce03 1.675 De03 1.299 Ce04 1.873 De04 1.296 Ce05 1.682 De05 1.604 Ce06 1.501 De06 1.432 Ce07 1.652 De07 1.197 Ce08 1.596平均值 1.672 1.357离散系数 0.064 0.096 14组含缝 1.581
4 结论
鉴于预制裂缝试件的制作相对繁琐且其制作效果对试验结果影响较大，并且为更真实模拟实际无缝结构的断裂特性，本文发展建立了采用小尺寸无缝试件确定混凝土与岩石断裂韧度的理论模型及其相应方法。通过本文进行的不同尺寸花岗岩试件试验，以及其他学者进行的岩石与混凝土的试验成果，验证了所提模型的合理性与适用性。本文研究得出结论如下：
(1) 实验室小尺寸无缝试件同时受控于断裂韧度准则与强度准则，处于准脆性断裂状态。本文模型与方法考虑了混凝土骨料粒径与岩石颗粒尺寸对断裂破坏的重要影响，仅需处于准脆性断裂状态的小尺寸无缝试件的实测峰值荷载，即可直接确定出其无尺寸效应的断裂韧度。模型可实现对无缝与含缝试件的统一描述，表达式形式简单，且对试验条件要求较低。克服了现有尺寸效应模型对于无缝和含缝试件须采用不同计算方程，且待定参数较多，不利于推广应用的缺点。
(2) 所提模型具体应用时，对于混凝土材料，其特征裂缝长度可取为1.5倍骨料最大粒径(
=1.5dmax)；对于岩石材料，其特征裂缝长度可取为3倍平均颗粒尺寸(
=1.5dmax=3gav)。
为方便设计应用，对于实验室条件下的小尺寸混凝土与岩石试件，峰值荷载时的虚拟裂缝扩展量可分别取Δafic=dmax，Δafic=gav或2gav。
(3) 基于本文发展的理论与模型，由无缝试件确定的混凝土与岩石的断裂韧度KIC，与采用1 mm预制浅裂缝试件确定的KIC基本吻合。并且，由无缝试件确定的KIC，与由多组预制裂缝试件，通过回归分析方法确定的KIC基本一致。
(4) 由无缝试件确定材料的断裂韧度 ，可采用相同尺寸试件，也可采用不同尺寸试件。鉴于无缝试件未预设裂缝出现位置，试验数据离散性略大于含缝试件。因此建议，由无缝试件确定断裂韧度值时，采用多个或者多组试件；若想精确控制裂缝出现及初始扩展位置，可采用含浅缝试件(例如1 mm的预制裂缝)。
须说明，本文岩石试验研究对象仅为花岗岩类型, 所提模型对于其他类型岩石(如变质岩、粘土岩和碎屑岩等)的适用性，还需进一步的试验验证。
本文重点关注于三点弯曲受力型式，建立了相应的断裂韧度解析表达式，并由试验进行了验证。基于相同理论，本文也给出了由紧凑拉伸与楔入劈拉受力型式下的无缝试件确定断裂韧度的解释解。由此，可进一步推广由无缝试件确定断裂韧度的理论及方法在其他受力型式的应用：对于四点弯曲、偏心受力、立方体受压、圆柱体受压、巴西圆盘试件等其他受力型式，只需推导出相应的名义应力表达式，结合本文式(5)，即可建立相应的不同受力型式下的由无缝试件确定混凝土与岩石材料断裂韧度的解析表达式。
[1]DL/T 5332―2005, 水工混凝土断裂试验规程[S].北京: 中国电力出版社, 2006.DL/T 5332―2005, Norm for fracture test of hydraulic concrete[S].Beijng: China Electric Power Press, 2006.(in Chinese)
[2]RILEM TC-50 FMC (Draft Recommendation).Determination of the fracture energy of mortar and concrete by means of three-point bend tests on notched beams[J].Materials and Structures, 1985, 18 (6):285―290.
[3]Shah S P, Carpinteri A.Fracture mechanics test methods for concrete: Report of Technical Committee 89-FMT Fracture Mechanics of Concrete, Test Methods, RILEM[M].London; New York: Chapman and Hall, 1991.
[4]ISRM Testing Commission.Suggested methods for determining the fracture toughness of rock[J].International Journal of Rock Mechanics and Mining Sciences ＆ Geomechanics Abstracts, 1988, 25(2): 71―96.
[5]ISRM Testing Commission.Suggested method for determining mode I fracture toughness using cracked chevron notched Brazilian disc (CCNBD) specimens[J].International Journal of Rock Mechanics and Mining Sciences ＆ Geomechanics Abstracts, 1995, 32(1): 57―64
[6]ASTM E399―90, Standard test method for plane-strain fracture toughness testing of metallic materials[S].Philadelphia: American Society for Testing and Materials, 1990.
[7]ASTM E399―12e2, Standard test method for linear-elastic plane-strain fracture toughness testing of high strength metallic materials[S].Philadelphia:American Society for Testing and Material, 2013.
[8]Li Qingbin, Guan Junfeng, Wu Zhimin, et al.Fracture behavior of site-casting dam concrete[J].ACI Material Journal, 2015, 112(1): 11―20.
[9]Li Qingbin, Guan Junfeng, Wu Zhimin, et al.Equivalent maturity for ambient temperature effect on fracture parameters of site-casting dam concrete[J].Construction and Building Materials, 2016, 120(9): 293―308.
[10]Guan Junfeng, Li Qingbin, Wu Zhimin, et al.Relationship between fracture parameters of site-casting and sieved concrete[J].Magazine of Concrete Research,2016, 68(1): 43―54.
[11]Hoover C G, Bažant Z P, Vorel J, et al.Comprehensive concrete fracture tests: Description and results[J].Engineering Fracture Mechanics, 2013, 114(12): 92―103.
[12]Çağlar Y, Şener S.Size effect tests of different notch depth specimens with support rotation measurements[J].Engineering Fracture Mechanics, 2016, 157(5): 43―55.
[13]Jiang Y P, Guo W L, Shao X J.On the study of the effects of notch shape on the creep damage under cyclic loading[J].International Journal of Fatigue, 2007, 29(5):836―842.
[14]Berto F, Fergani O.A review of the notch rounding approach under in plane mixed mode loading[J].International Journal of Fatigue, 2017, 101(8): 127―136.
[15]Ayatollahi M R, Torabi A R, Bahrami B.Comprehensive notch shape factors for V-notched Brazilian disk specimens loaded under mixed mode I/II from pure opening mode to pure closing mode[J].Archive of Applied Mechanics, 2017, 87(2): 299―313.
[16]Li J, Su CY, Lu L, et al.Investigation on fatigue crack growth behavior for commercial pure titanium at different crack tip plastic deformed levels[J].Theoretical and Applied Fracture Mechanics, 2019, 100(4): 1―13.
[17]Zaitsev Y V, Kovler K L.Notch sensitiv ity of concrete and size effect.Part I: Effect of specimen size and crack length by 3-point bending[J].Cement and Concrete Research, 1985, 15(6): 979―987.
[18]Zaitsev Y V, Kovler K L.Notch sensitivity of concrete and size effect.Part II: Stress state effect[J].Cement ＆Concrete Research, 1986, 16(1): 7―16.
[19]Guan Junfeng, Li Changming, Juan Wang, et al.Determination of fracture parameter and prediction of structural fracture using various concrete specimen types[J].Theoretical and Applied Fracture Mechanics, 2019,100(4): 114―127.
[20]Lin Peng, Guan Junfeng, Peng Haoyang, et al.Horizontal cracking and crack repair analysis of a super high arch dam based on fracture toughness[J].Engineering Failure Analysis, 2019, 97(3): 72-90.
[21]管俊峰, 胡晓智, 王玉锁, 等.用边界效应理论考虑断裂韧性和拉伸强度对破坏的影响[J].水利学报, 2016,47(10): 1298―1306.Guan Junfeng, Hu Xiaozhi, Wang Yusuo, et al.Effect of fracture toughness and tensile strength on fracture based on boundary effect theory[J].Journal of Hydraulic Engineering, 2016, 47(10): 1298―1306.(in Chinese)
[22]管俊峰, 王强, 胡晓智, 等.考虑骨料尺寸的混凝土岩石边界效应断裂模型[J].工程力学, 2017, 34(12): 22―30.Guan Junfeng, Wang Qiang, Hu Xiaozhi, et al.Boundary effect fracture model for concrete and granite considering aggregate size[J].Engineering Mechanics, 2017, 34(12):22―30.(in Chinese)
[23]管俊峰, 钱国双, 白卫峰, 等.岩石材料真实断裂参数确定及断裂破坏预测方法[J].岩石力学与工程学报，2018, 37(5): 1146―1160.Guan Junfeng, Qian Guoshuang, Bai Weifeng, et al.Method for predicting fracture and determining true material parameters of rock[J].Chinese Journal of Rock Mechanics and Engineering, 2018, 37(5): 1146―1160.(in Chinese)
[24]管俊峰, 胡晓智, 李庆斌, 等.边界效应与尺寸效应模型的本质区别及相关设计应用[J].水利学报, 2017,48(8): 955―967.Guan Junfeng, Hu Xiaozhi, Li Qingbin, et al.Essential difference and design application of boundary effect model and size effect model[J].Journal of Hydraulic Engineering, 2017, 48(8): 955―967.(in Chinese)
[25]Hillerborg A, Modeer M, Petersson P E.Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J].Cement Concrete Research, 1976, 6 (6): 773―782.
[26]Bažant Z P.Size effect in blunt fracture: Concrete, rock,metal[J].Journal of Engineering Mechanics, 1984,110(4): 518―535.
[27]Jenq Y S, Shah S P.Two parameter fracture model for concrete[J].Journal Engineering Mechanics-ASCE,1985, 111(10): 1227―1241.
[28]Karihaloo B L, Nallathambi P.Effective crack model for the determination of fracture toughness (
) of Concrete[J].Engineering Fracture Mechanics, 1990, 35 (4/5):637―645.
[29]Carpinteri A.Fractal nature of material microstructure and size effects on apparent mechanical properties[J].Mechanics of Materials, 1994, 18(2): 89―101.
[30]Xu S L, Reinhardt H W.Determination of double-K criterion for crack propagation in quasi-brittle fracture,Part II: Analytical evaluating and practical measuring methods for three-point bending notched beams[J].International Journal of Fracture, 1999, 98(2): 151―177.
[31]Hoover C G, Bažant Z P.Universal size-shape effect law based on comprehensive concrete fracture tests[J].Journal Engineering Mechanics, 2014, 140(3): 473―479.
[32]管俊峰, 李庆斌, 吴智敏.采用峰值荷载法确定全级配水工混凝土断裂参数[J].工程力学, 2014, 31(8): 8―13.Guan Junfeng, Li Qingbin, Wu Zhimin.Determination of fully-grade hydraulic concrete fracture parameters by peak-load method[J].Engineering Mechanics, 2014,31(8): 8―13.(in Chinese)
[33]Hoover C G, Bažant Z P.Comparison of Hu-Duan boundary effect model to size-shape effect law for quasi-brittle fracture based on new comprehensive fracture tests[J].Journal Engineering Mechanics, 2014,140(3): 480―486.
[34]Hu Xiaozhi, Guan Junfeng, Wang Yusuo, et al.Comparison of boundary and size effect models based on new developments[J].Engineering Fracture Mechanics,2017, 175(4): 146―167.
[35]管俊峰, 姚贤华, 白卫峰, 等.由小尺寸试件确定混凝土的断裂韧度与拉伸强度[J].工程力学, 2019,36(1): 70―79, 87.Guan Junfeng, Yao Xianhua, Bai Weifeng, et al.Determination of fracture toughness and tensile strength of concrete using small specimens[J].Engineering Mechanics, 2019, 36(1): 70―79, 87.(in Chinese)
[36]Hu Xiaozhi.Size effect on tensile softening relation[J].Materials and Structures, 2011, 44(1): 129―138.
[37]Hu X Z, Wittmann F.Size effect on toughness induced by crack close to free surface[J].Engineering Fracture Mechanics, 2000, 65(2/3): 209―221.
[38]Hu X Z.An asymptotic approach to size effect on fracture toughness and fracture energy of composites[J].Engineering Fracture Mechanics, 2002, 69(5): 555―564.
[39]Hu X Z, Duan K.Size effect and quasi-brittle fracture:the role of FPZ[J].International Journal of Fracture,2008, 154 (1): 3－14.
[40]Guan Junfeng, Hu X Z, Li Qingbin.In-depth analysis of notched 3-p-b concrete fracture[J].Engineering Fracture Mechanics, 2016, 165(10): 57－71.
[41]Guan Junfeng, Hu Xiaozhi, Xie Chaopeng, et al.Wedge-splitting tests for tensile strength and fracture toughness of concrete[J].Theoretical and Applied Fracture Mechanics, 2018, 93(2): 263－275.
[42]Guan Junfeng, Hu Xiaozhi, Yao Xianhua, et al.Fracture of 0.1 and 2 m long mortar beams under threepoint-bending[J].Materials ＆ Design, 2017, 133(11):363－375.
[43]Wang Y S, Hu X Z.Determination of strength and toughness of granite using notched three-point-bend samples[J].Rock Mechanics and Rock Engineering,2017, 50(1): 1－12.