板壳单元作为数值计算分析中常见的单元类型，被广泛应用于建筑和桥梁等结构的数值模拟中[1―3]。多年来，国内外研究学者对板壳单元的计算精度和非线性求解效率两方面做了大量研究[4―5]。目前，板单元主要有两种分析理论，一种是Kirchhoff板理论[6]，该理论假定挠度和转角相互独立且要求位移为C1类连续，主要适用于由薄板组成的工程结构中[7-9]，但当板厚增加时，该理论模拟结果的精度降低甚至会导致错误的计算结果；另一种理论是Mindlin-Reissner中厚板理论[10-11]，该理论克服了Kirchhoff板理论的不足，在解决中厚板问题上具有足够的精度，被广泛应用于结构有限元非线性分析中[12-15]。针对壳单元，其理论通常包括三种：由平面膜单元和板弯曲单元组成的平板型壳元[16]、经典的曲面型壳元[17]以及三维实体退化型壳元[18]，其中，曲面型壳元和退化型壳元的有限元列式比较复杂且收敛性较差，在实际应用中难以实施。而平板型壳元具有构造简单、计算精度高等优点，被广泛应用于实际工程中[19]。近年，随着复合材料层合板壳结构的出现，单一材料的板壳单元已经无法满足工程应用需要[20-21]。因此，研究人员以复合材料力学原理和平板型壳元基本理论为基础，开发了一种分层壳单元模型，该模型将不同的材料本构行为联系起来，在模拟实际构件或者结构复杂受力方面具有明显优势。陆新征等[22]和张有佳等[23]将分层壳模型应用于钢筋混凝土剪力墙和核电预应力混凝土安全壳的非线性分析中，研究结果均表明该模型具有良好的计算精度。
在板、壳单元模型的非线性计算方面，高效的数值求解方法同样占据重要地位。Farhat和Wilson[24]、杨玉明[25]将基于预处理共轭梯度法的并行计算方法应用于板壳结构的非线性分析中，大大提高了板壳结构的并行计算效率。Li、Carrera等[26]提出一种分层壳有限元模型自适应方法，提高了分层壳结构的有限元非线性数值分析效率。尽管学者们提出的数值求解方法在很大程度上改善了板、壳单元的计算效率，但在非线性分析时仍需要对切线刚度矩阵进行合成和分解，该过程将消耗大量的计算资源。
隔离非线性有限元法[27]作为一种结构非线性分析新方法，将结构的非线性部分隔离开来，并将结构的切线刚度矩阵的逆矩阵表示成初始弹性刚度矩阵的逆与相应修正矩阵的和，从而避免了切线刚度矩阵的直接分解，实现了非线性问题的高效求解。目前，该方法已被应用于平面单元、纤维梁单元的材料非线性分析中[28]。而分层壳单元作为建筑结构数值模拟的重要组成部分，有必要建立基于隔离非线性有限元法的分层壳单元分析模型，对提高板壳单元非线性分析效率具有较大意义。本文根据隔离非线性有限元法和分层壳单元理论，将单元截面变形分解为线弹性变形和非线性变形，以高斯积分点作为非线性变形插值结点，建立了非线性变形场。依据虚功原理和积分点处的内力平衡条件建立了基于隔离非线性有限元法的分层壳单元控制方程，采用Woodbury公式和组合近似法联合求解控制方程。基于时间复杂度理论对模型的计算效率进行评价，结果表明：隔离非线性有限元法的分层壳单元模型相比于传统有限元方法的模型计算效率显著提高，数值算例验证了本文单元模型的准确性与高效性。
1 基本理论
1.1 分层壳单元
分层壳单元基于复合材料力学原理，将一个壳单元沿厚度方向上划分成若干层，各层可根据需要设置不同的厚度和材料，每一层由平板型壳单元组成，如图1所示。分层壳单元考虑了面内应变—面外弯曲之间的耦合作用，能较全面地反映壳体结构的空间力学性能[29]。
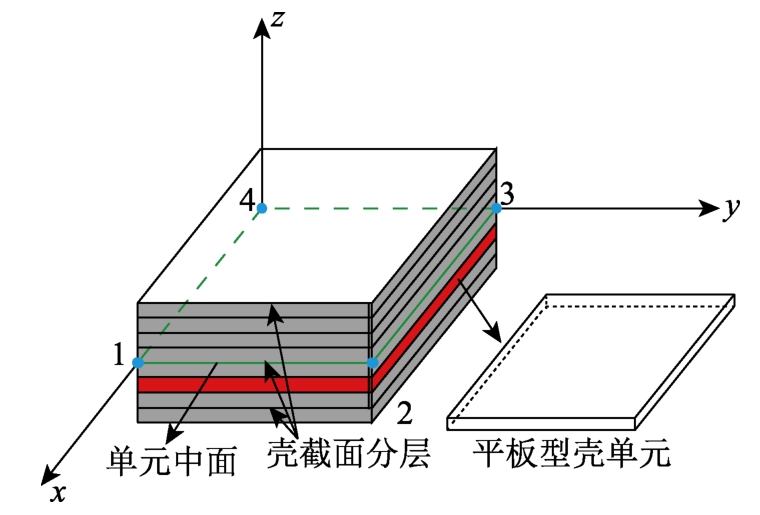
图1 分层壳单元示意图
Fig.1 Sketch of multi-layer shell elements
以常用的四节点平板型分层壳单元为例，对其基本理论和公式进行阐述，如图2所示。单元中面设置4个位移插值结点，每个位移插值结点有6个自由度，其结点位移增量可用列阵表示为[30-31]：
式中：Δqi={Δui Δvi Δwi Δθxi Δθyi Δθzi}T，其中，Δui、Δvi、Δwi分别为沿x、y及z轴方向的平动位移增量，Δθxi、Δθyi、Δθzi分别为绕x、y及z轴的转角位移增量。平板型分层壳单元面内和面外的变形行为可分别通过平面膜单元和板弯曲单元来进行模拟，其中平面膜单元提供面内位移以及面内转动的分量，即
板弯曲单元则提供面外挠度及绕x、y轴转角的分量，其节点位移分量表示为
图2 四结点平板型分层壳单元
Fig.2 Sketch of flat multi-layer shell element with four nodes
依据单元沿厚度方向的平截面假定，通过单元中面的任意一点的位移和横截面上的转角，可得单元内任意一点的位移场增量方程，具体可表示为：
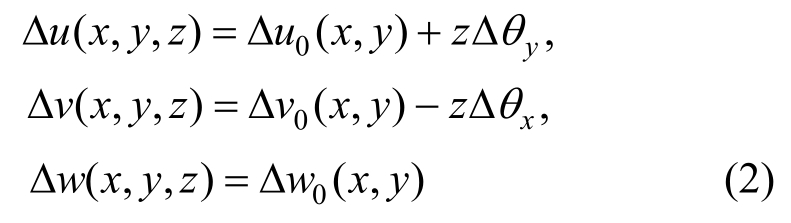
式中：Δu0、Δv0、Δw0为单元中面任意一点的位移增量；z为分层壳单元任意层与中面的距离。由弹性力学的几何方程可知，对式(2)求一阶偏导数可得到单元中面的应变和曲率增量，即：
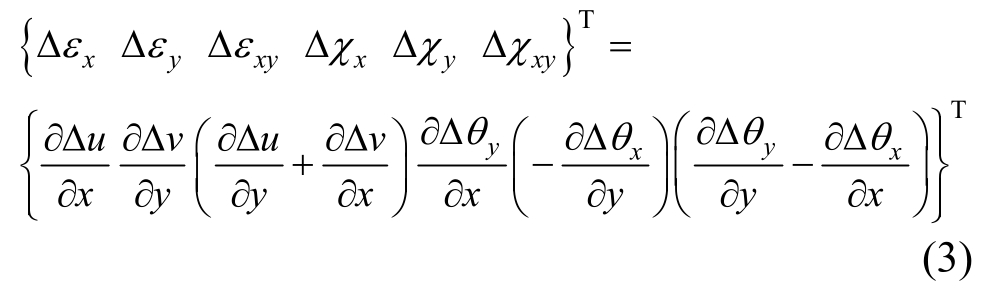
式中：Δεx、Δεy分别为x和y方向应变增量；Δεxy为面内剪切应变增量；Δχx、Δχy分别为分层壳单元中面的x和y方向曲率增量；Δχxy为中面扭转率增量。为下文表述方便，令Δdm={Δεx Δεy Δεxy}T为膜单元变形场，Δdb={Δχx Δχy Δχxy}T为板元弯曲变形场。
得到单元中面的应变和曲率后，根据各层材料之间满足平截面假定和各层在横截面上的坐标，可计算出各层的应变，分层壳单元第j层的应变增量
可表示为：
在面外荷载作用下，分层壳单元在厚度方向上通常发生面外剪切变形，而单元厚度变薄将会发生剪切闭锁现象，为解决该问题，学者采用假设剪应变法计算面外剪切应变，其基本原理是：单元内的剪切应变由插值点处的剪切应变按线性插值表示，则单元的剪切应变增量Δγxz、Δγyz可具体表示为[32]：
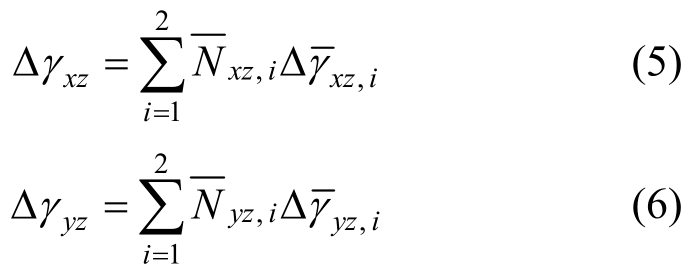
式中：
为插值函数，η和ξ为单元内任一点的局部坐标；
为插值点处的剪切应变增量。
设单元截面变形增量分布函数为：
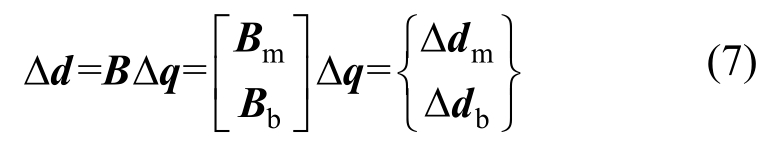
式中：Δd={Δdm Δdb}T为截面变形向量；B=[Bm Bb]T为单元的变形矩阵；Bm和Bb分别为膜单元和板弯曲单元变形矩阵。
2.2 截面变形分解
隔离非线性方法作为一种高效的非线性求解方法[27]，是将材料本构关系中的应变分解为线弹性和非线性两部分，如图3所示。
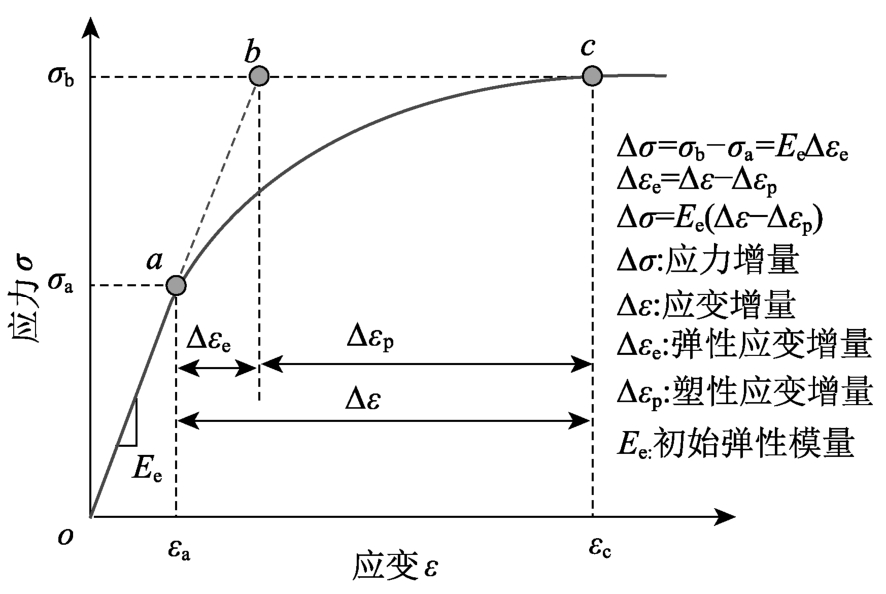
图3 应变分解
Fig.3 Strain decomposition of material
当采用分层壳单元计算材料非线性问题时，可基于隔离非线性的思想，将分层壳单元截面变形分解为线弹性及非线性两部分。由于面外剪切变形对单元非线性行为影响较小，在此不考虑面外剪切变形的非线性，认为其一直处于弹性状态，单元的膜单元变形和板元弯曲变形可分解为：
式中：Δde={Δdm,e Δdb,e}T为截面线弹性变形增量；Δdp={Δdm,p Δdb,p}T为截面非线性变形增量。
在截面内力计算方面，分层壳第j层的应力增量可通过该层的刚度矩阵和应变增量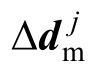
相乘得到，对截面中各层的应力增量进行积分，得到膜内力增量和弯矩增量，具体表达式为：
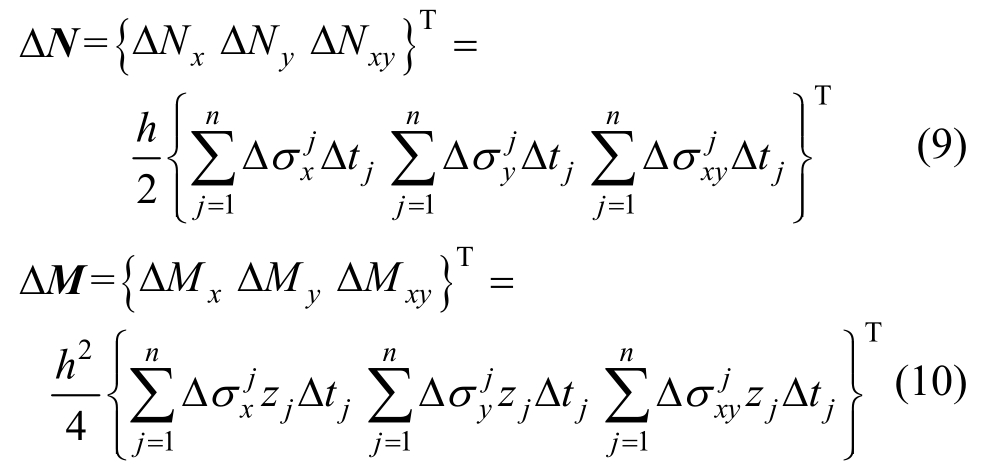
式中：
为第j层的应力增量；Δtj为第j层的等参厚度； h为单元的厚度； zj为第j层等参坐标；n为截面划分的层数。
由图3可知，材料的应力等于弹性应变和弹性模量的乘积，而分层壳单元中截面的内力可通过截面弹性变形与截面弹性刚度矩阵相乘得到，结合式(8)截面变形的分解，截面内力的表达式为：
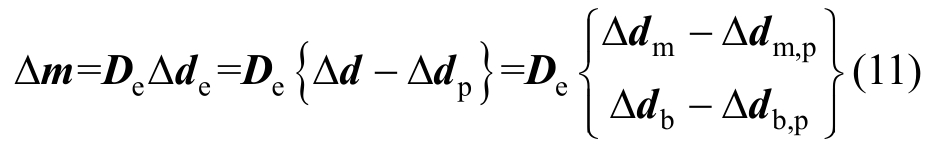
式中：Δm={ΔN ΔM}T为截面内力；De=
为弹性刚度矩阵；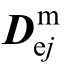
为膜单元应力状态下的第j层弹性刚度矩阵。
由式(11)可知，基于截面变形分解的方法求解截面内力时，引入了未知量Δdp，依据有限元基本理论：单元的变形场增量Δd可通过变形插值函数和结点位移增量表示，同样Δdp可通过非线性变形插值结点处的非线性变形增量Δdp进行插值得到[28]，即：
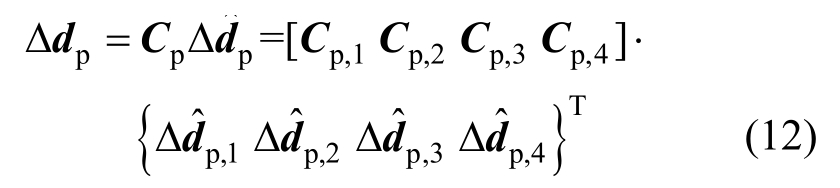
式中：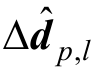
为单元第l个塑性插值结点处的非线性变形向量；Cp,l为单元第l个非线性变形插值结点处的非线性变形插值形函数矩阵。令非线性变形插值结点与4个高斯积分点重合，由于非线性变形插值形函数的Kronecker delta性质[31]，可知Cp,l=1,2,3,4=I6，I6为6阶单位矩阵。
在传统变刚度有限元方法的非线性求解迭代过程中，截面内力增量线性化表达式还可表示为[31]：
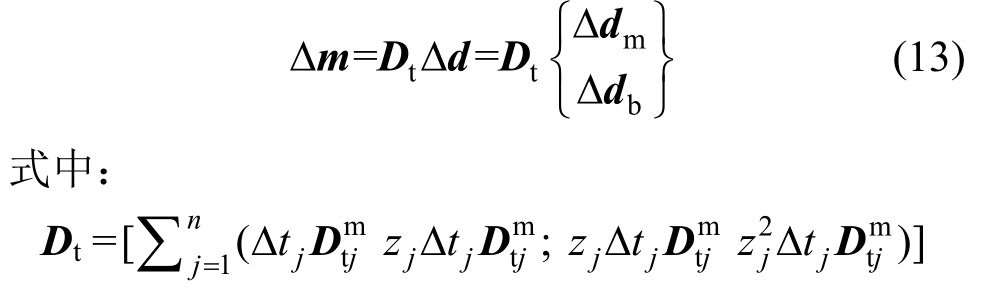
为切线刚度矩阵，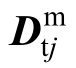
为膜单元应力状态下的第j层的切线刚度矩阵。对比式(11)和式(13)可知：在非线性分析过程中，基于变形分解的截面内力表达式可以保证截面刚度矩阵的始终不变。
3 隔离非线性分层壳控制方程
根据虚功原理，分层壳单元变分表达式为：
式中：δd为截面变形的变分；δq为单元节点位移的变分；Δf为单元节点力增量。将式(7)、式(8)、式(11)和式(12)代入虚功方程式(14)，经整理可得：
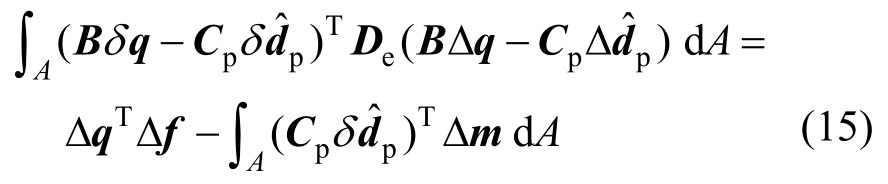
此外，考虑塑性插值点处的内力平衡条件，将式(11)和式(12)代入式(13)可得补充方程：
将式(16)代入式(15)，经整理可得基于隔离非线性方法的分层壳单元控制方程：
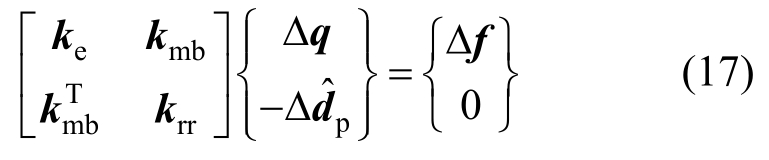
式中：ke为单元初始弹性刚度矩阵；kmb表示非线性变形与单元节点力之间的关系；krr为单元的非线性矩阵，表示了单元的非线性信息。其具体表达式分别如下：
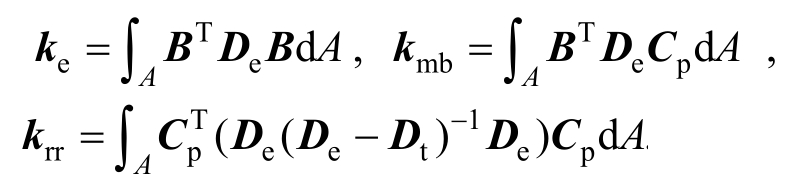
对单元控制方程集成，得到结构的整体控制方程：
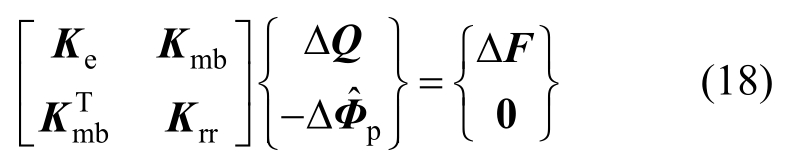
式中：ΔQ为结构的位移向量；ΔF为结构的荷载向量；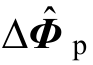
为结构中所有塑性插值点处的非线性变形向量。矩阵Krr为分块对角矩阵，每个块矩阵表示了每个高斯积分点的材料非线性信息，若该高斯积分点没有进入非线性，则该块矩阵为零矩阵。在非线性分析过程中，只更新和分解矩阵Krr，矩阵Ke和Kmb均为常数矩阵且与材料非线性状态无关。
4 控制方程求解
在结构非线性分析任意迭代步内，可利用Woodbury公式对结构的整体控制方程式(18)进行准确和高效的求解。其求解高效性主要体现为：在局部非线性分析过程中，结构中的大部分单元一般处于线弹性状态，仅有小部分单元进入非线性，因而，进入非线性的塑性自由度数p远小于结构位移自由度数n (p＜＜n)，在迭代步内仅需对p维的矩阵合成和分解，避免了对n维整体刚度矩阵实时更新和分解，降低了结构非线性分析的计算时间。而传统变刚度有限元分析中，大部分计算时间消耗在n维切线刚度矩阵的分解上。
基于此，采用Woodbury公式求解整体控制方程式(18)，其展开形式为：
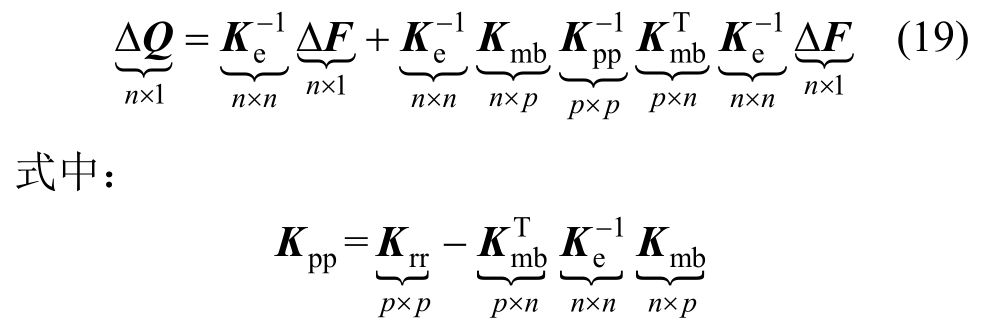
在数学上，矩阵Kpp称为整体刚度矩阵Ke的舒尔补，其矩阵维数为p×p阶，与塑性自由度数目一致[27]。从式(19)可知：Woodbury公式求解整体控制方程时，其计算量主要来自舒尔补矩阵Kpp的实时更新和分解，因而，非线性分析过程中产生塑性自由度数的多少直接影响着Woodbury公式的计算效率。以往的研究表明[33-34]：当结构局部进入材料非线性时，Woodbury公式求解效率比传统有限元方法求解效率高，对于一个位移自由度n=10000的结构，当进入塑性的塑性自由度数p≥1000时，Woodbury公式求解效率低于传统有限元方法。
4.1 Woodbury公式和CA法联合求解
在板壳单元的非线性分析中，由于单元和其周围单元联系紧密，单元与单元之间的高斯积分点相互之间影响较大，即使在局部材料非线性阶段，进入非线性的塑性自由度数也较多，所以使用Woodbury公式求解整体控制方程在板壳单元非线性分析中存在一定的局限性。组合近似法(combined approximations method， CA法)通过构造s个线性无关的基向量来线性逼近位移向量[35]，由于基向量个数s比结构位移自由度数n小很多，所以大幅度的减小了非线性分析过程中的计算量。把式(19)的求解过程具体分解为从右至左的6个计算步骤，其计算过程如图4(a)所示，由Woodbury公式求解分析可知，较大维数的矩阵Kpp直接分解计算是影响基于隔离非线性有限元法的板壳单元求解效率的关键因素，当采用CA法求解图4(a)中的步骤③时，在非线性求解过程中主要是矩阵回代与向量之间的运算，避免了矩阵Kpp的直接分解计算，提高了基于隔离非线性有限元法的板壳单元的计算效率。CA法求解步骤③的具体计算过程如图4(b)所示，图4表示了结构非线性分析过程中一个迭代步内的完整计算。
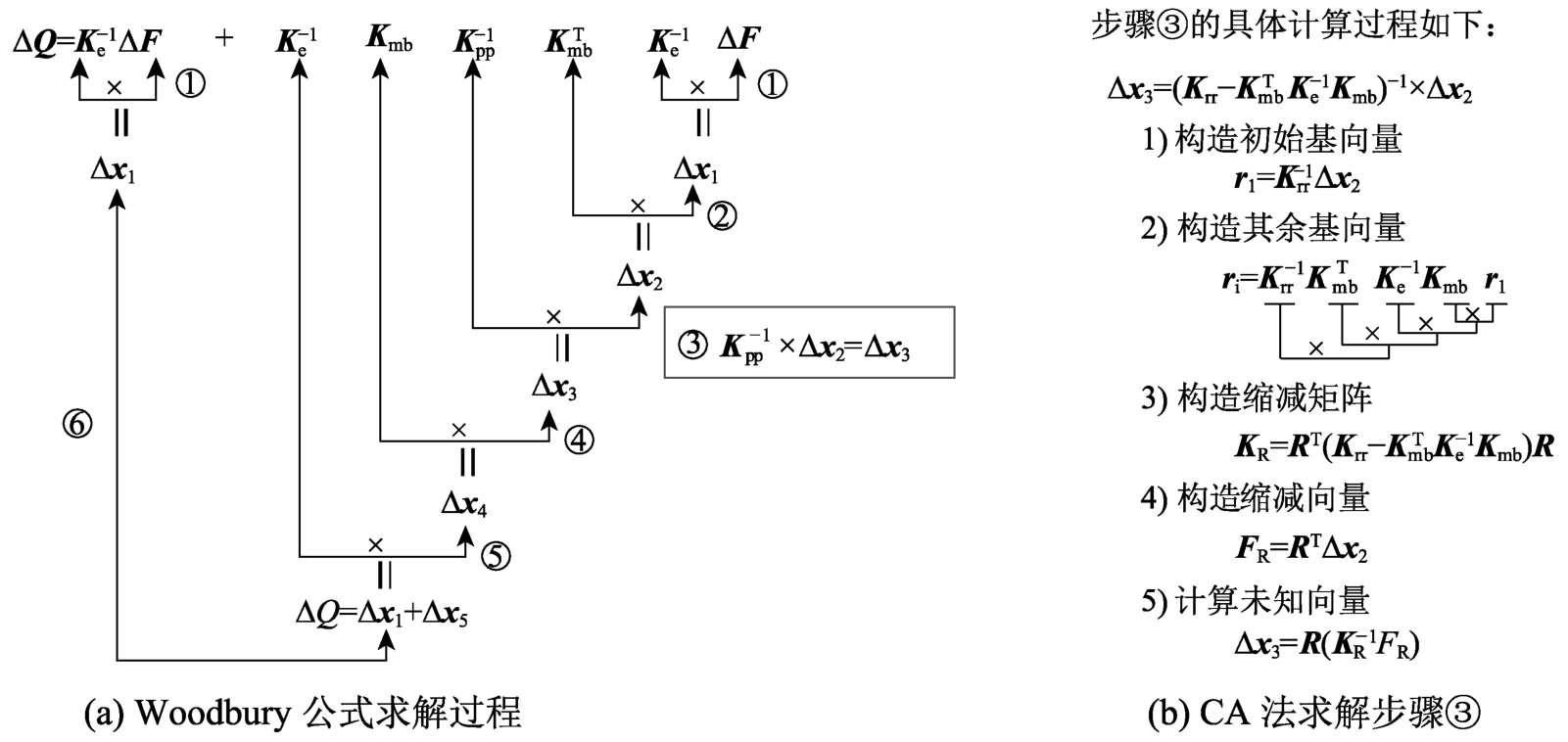
图4 Woodbury公式和CA法联合求解过程示意图
Fig.4 Sketch of Woodbury formula and CA method solving process
4.2 效率分析
时间复杂度理论[33]是一种算法计算效率定量评价的方法，仅与算法本身相关，与硬件、软件、编程语言以及程序优化等因素无关。传统有限元方法在增量步内的每个迭代步的计算过程中都需要对规模为n×n阶、带宽为m阶的整体刚度矩阵进行一次LDLT分解，一次分解和回代的时间复杂度函数为[34]：
Woodbury公式和CA法联合求解整体控制方程时，只需要在开始计算前对规模为n×n阶、带宽为m阶的刚度矩阵Ke进行一次LDLT分解。根据图4所示的求解过程，通过对Woodbury公式和CA法联合求解整体控制方程的计算量进行统计，其时间复杂度函数约为[36]：
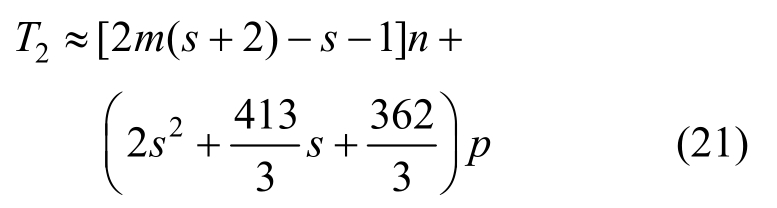
式中：m为刚度矩阵的带宽，一般可取为
s为基向量个数；p为进入塑性的塑性自由度数。
5 数值算例
5.1 空心板
板的几何尺寸及构造如图5所示，边长为2000 mm×2000 mm，厚度为30 mm，板的四周为固定支座。将板模型划分为400个单元，在厚度方向上每个单元划分20层，其中在单元中面的上、下两层为空心层。板上承受均布荷载q=6.25 N/mm2，总计1251个增量步，力加载曲线如图6所示。弹性模量为E=2×105 MPa，泊松比为ν =0.3，屈服强度为262 MPa，屈服后刚度系数为0.1。模型位移自由度总数为1323，每个单元有12个塑性自由度，塑性自由度总数为4800。
分别采用有限元软件ANSYS和隔离非线性有限元法建立分析模型，两种方法的单元数量、截面划分的层数和材料本构关系均相同，其中，ANSYS模型中的单元类型为shell181单元，与隔离非线性有限元法中使用的分层壳单元类型相同。图7(a)和图7(b)分别给出了板中心点A的挠度-荷载曲线和第80个单元的1节点x方向的应力-应变曲线对比图，可知：隔离非线性有限元法的计算结果与ANSYS的计算结果吻合较好，验证了隔离非线性分层壳有限元法的准确性。
图5 模型尺寸及分层 /mm
Fig.5 Size and layers of the model structure
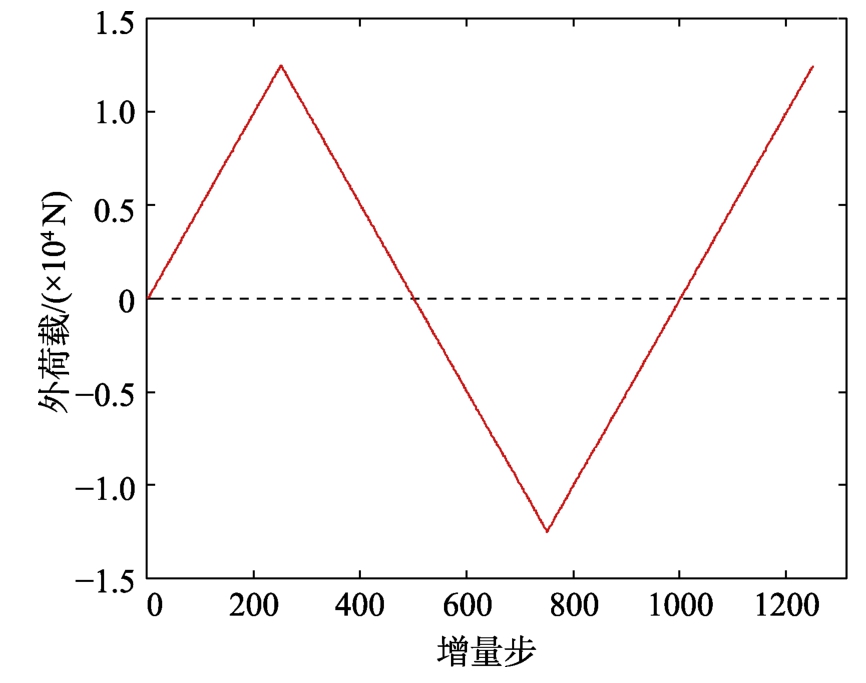
图6 力加载曲线
Fig.6 Force loading curve
图8给出了加载过程中板进入非线性状态的塑性自由度数量演变曲线，其中最大的塑性自由度数是4764，平均塑性自由度数是2498(位移自由度总数的187.96%)，表明了结构发生了很大范围的材料非线性变形，同时，板中进入非线性状态的塑性自由度数随着外荷载和加卸载条件的改变而动态变化。传统变刚度有限元方法和隔离非线性有限元法的时间复杂度曲线如图9所示，可知：有限元方法的时间复杂度保持不变，且仅与结构位移自由度有关，而隔离非线性有限元法的时间复杂度与结构自由度及产生的塑性自由度数均相关。对于大范围的材料非线性问题，即板中所有单元全部进入非线性状态，隔离非线性有限元法的时间复杂度也是低于传统有限元方法的，表明本文方法提高了分层壳单元在非线性分析过程中的数值计算效率。
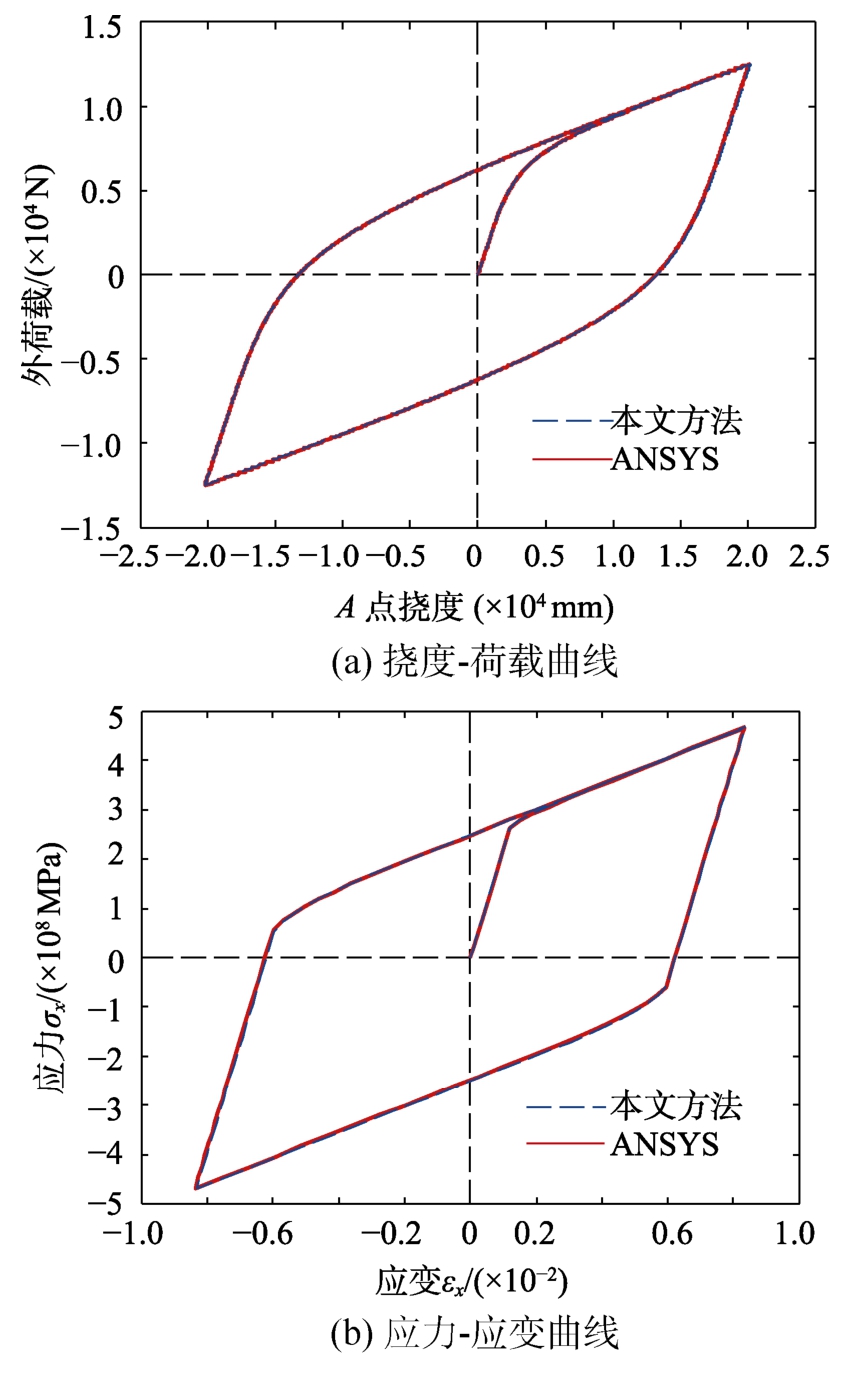
图7 结果曲线对比
Fig.7 The comparison curve of the results
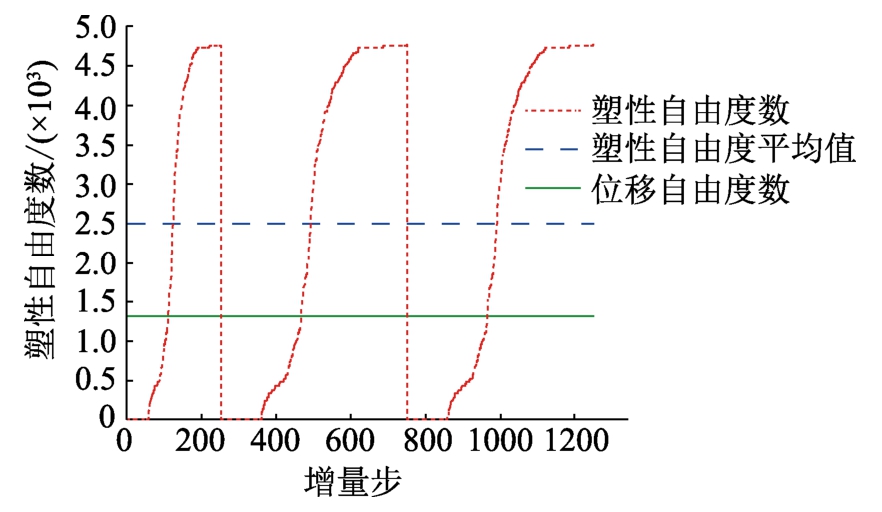
图8 塑性自由度
Fig.8 Plastic degree of freedoms
5.2 剪力墙
图10为某一单片钢板剪力墙，墙底部与基础固结，墙的宽度为1000 mm、高度为2000 mm，将墙划分为40个单元，每个单元截面在厚度方向上为100 mm并划分为10层。在节点16施加x、y和z三个方向的荷载，大小均为Fx=Fy=Fz=336000 N，力控制加载，总计500个增量步。材料本构关系采用理想弹塑性本构模型，屈服强度为235 MPa，弹性模量为E=2.1×105 MPa，泊松比为ν = 0.3。塑性自由度个数为960，位移自由度个数为330。
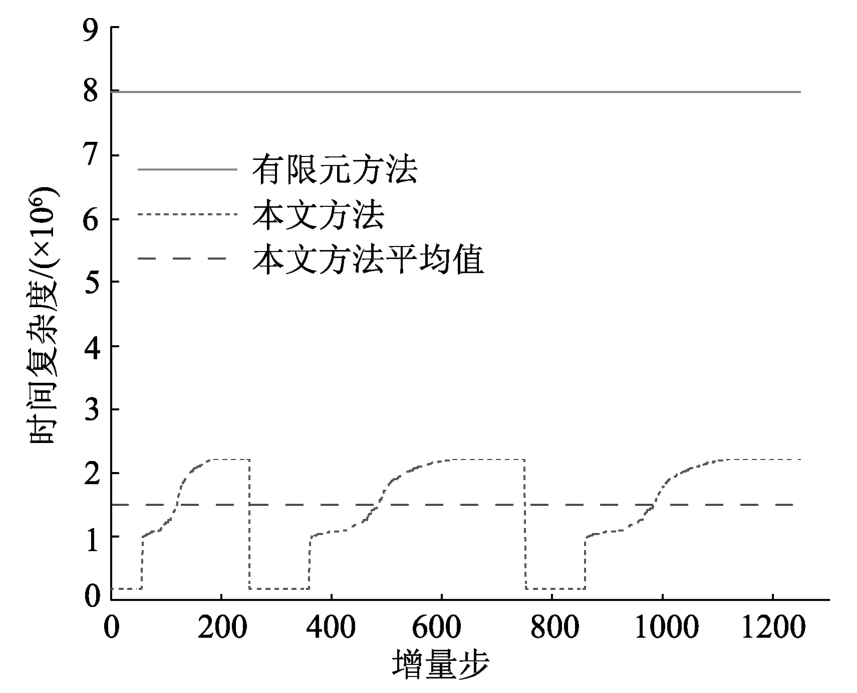
图9 时间复杂度理论
Fig.9 The comparison of time complexity theory
图10 剪力墙模型
Fig.10 The model of shear wall
分别采用有限元软件ANSYS和隔离非线性有限元法建立分析模型。图11给出了使用隔离非线性有限元法和传统有限元方法计算得到的加载点A的x、y和z三个方向的位移-荷载(F-u)曲线，从图中可知三个方向的位移吻合良好，因为剪力墙的面内刚度大于面外刚度，所以z方向的位移进入非线性程度较强，x、y方向的位移进入非线性程度较弱，表明：剪力墙三个方向相互之间的耦合受力减低了剪力墙的承载能力。图12给出了使用两种方法得到的单元11中3节点的应变和应力曲线对比图，可知：单元的应变和应力变化趋势及计算精度与传统有限元方法的基本相同，验证了本文提出分层壳单元模型的准确性。
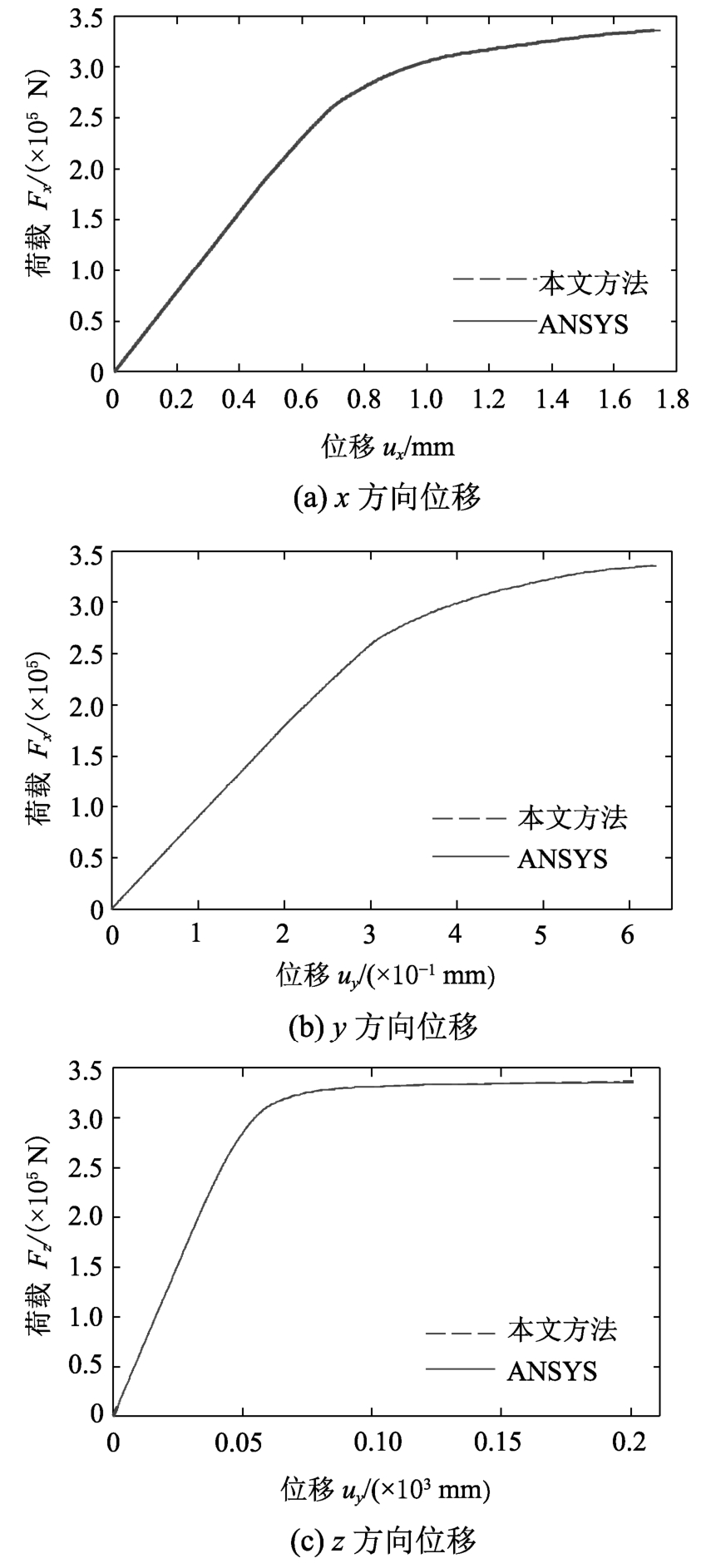
图11 位移曲线
Fig.11 The comparison of displacement curve
图13给出了塑性自由度数随增量步的变化曲线，非线性分析过程中产生的最大塑性自由度数为252，占总自由度数的76.36%，而每个增量步的平均塑性自由度数为129，占总自由度数的39.1%，表明结构较大范围的出现材料非线性。为论证其高效性，将传统有限元方法和本文方法的时间复杂度进行统计对比，如图14所示，传统有限元法和本文方法的平均时间复杂度分别为5.588×105和1.004×105，此外，传统有限元法的时间复杂度为本文方法的5.57倍，表明本文方法能够高效地求解结构复杂受力状态下的大范围材料非线性问题。
图12 应变-应力曲线
Fig.12 The comparison of stress-strain
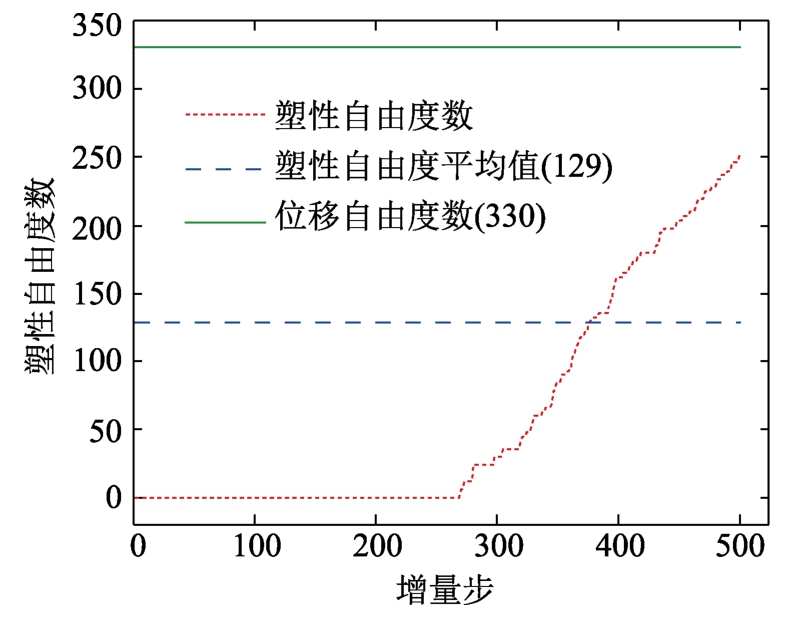
图13 塑性自由度
Fig.13 Plastic freedoms degree
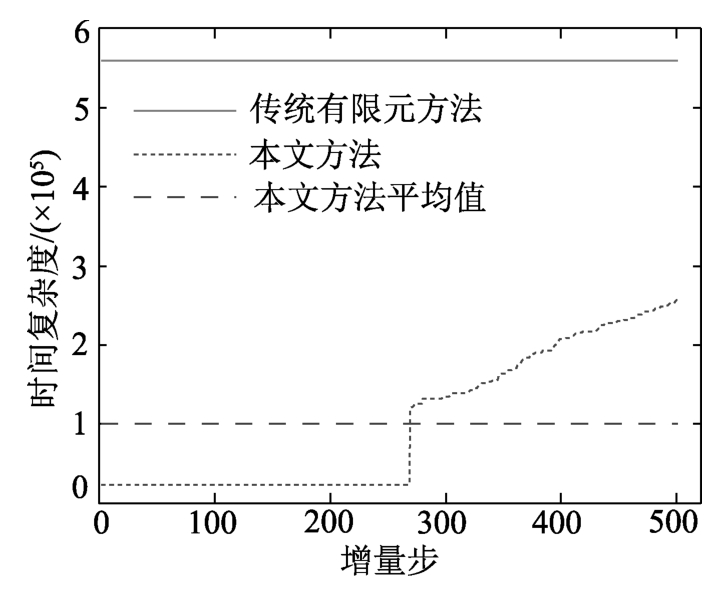
图14 时间复杂度理论
Fig.14 The curve of time complexity theory
6 结论
本文基于隔离非线性有限元法和分层壳单元的基本理论，将单元截面变形分解为线弹性及非线性两部分，推导了分层壳单元的隔离非线性控制方程，联合Woodbury公式和CA法对控制方程进行高效求解。最后，将该方法应用于板、剪力墙结构与构件的非线性分析中，并得到如下结论：
(1) 与传统的分层壳单元有限元模型相比，本文方法可保证单元初始刚度矩阵保持不变，将单元材料非线性集中于控制方程的右下角矩阵块中，实现了单元非线性性状态的隔离。
(2) 依据时间复杂度理论分析可知，隔离非线性有限元法的分层壳单元模型与传统有限元方法相比，即使结构大范围出现材料非线性行为时，本文方法也可显著提高分层壳单元的非线性求解效率。
(3) 通过与有限元软件ANSYS的结果对比分析表明，本文方法与传统有限元方法在求解分层壳单元的材料非线性问题时具有一致的计算精度。
[1]林旭川, 陆新征, 缪志伟, 等.基于分层壳单元的RC核心筒结构有限元分析和工程应用[J].土木工程学报,2009, 42(3): 49―54.Lin Xuchuan, Lu Xinzheng, Miao Zhiwei, et al.Finite element analysis and engineering application of RC core-tube structures based on the multi-layer shell elements[J].China Civil Engineering Journal, 2009,42(3): 49―54.(in Chinese)
[2]Lu X Z, Xie L L, Guan H, et al.A shear wall element for nonlinear seismic analysis of super-tall buildings using OpenSees[J].Finite Elements in Analysis and Design,2015, 98: 14―25.
[3]张大长, 野口博.考虑反复加载时混凝土损伤积累的RC平板及剪力墙的有限元分析模型的开发[J].工程力学, 2007, 24(1): 88―95.Zhang Dachang, Noguchi Hiroshi.Development of FEA models of RC slabs and shear walls considering damage accumulation under reverse cyclic loading[J].Engineering Mechanics, 2007, 24(1): 88―95.(in Chinese)
[4]Batoz J L, Tahar M B.Evaluation of a new quadrilateral thin plate bending element[J].International Journal for Numerical Methods in Engineering, 2010, 18(11):1655―1677.
[5]Nguyen-Hoang S, Phung-Van P, Natarajan S, Kim H G.A combined scheme of edge-based and node-based smoothed finite element methods for Mindlin–Reissner flat shells[J].Engineering with Computers, 2016, 32(2):267―284.
[6]Gunderson R, Haisler W E, Stricklin J A.A rapidly converging triangular plate element[J].AIAA Journal,1969, 7(1): 180―181.
[7]苏幼坡, 刘英利, 王绍杰.薄钢板剪力墙抗震性能试验研究[J].地震工程与工程振动, 2002, 22(4): 81―84.Su Youpo, Liu Yingli, Wang Shaojie.Experimental study of anti-seismic behavior of thin steel-plate shear walls[J].Earthquake Engineering and Engineering Vibration,2002, 22(4): 81―84.(in Chinese)
[8]Wegmuller A W, Amer H N.Nonlinear response of composite steel-concrete bridges[J].Computers ＆Structures, 1977, 7(2): 161―169.
[9]Hirst M J S, Yeo M F.The analysis of composite beams using standard finite element programs[J].Computers ＆Structures, 1980, 11(3): 233―237.
[10]Mindlin R D.Influence of rotatory inertia and shear on flexural motions of isotropic elastic plates[J].Journal of Applied Mechanics-Transactions of the Asme, 1951,18(1): 31―38.
[11]Reissner E.On the theory of bending of elastic plates[J].Studies in Applied Mathematics, 1944, 23(1): 184―191.
[12]Fischer F D, Rammerstorfer F G, Friedl N.Residual stress-induced center wave buckling of rolled strip metal[J].Journal of Applied Mechanics-Transactions of the Asme, 2003, 70(1): 84―90.
[13]Coman C D, Bassom A P.An asymptotic description of the elastic instability of twisted thin elastic plates[J].Acta Mechanica, 2008, 200: 59―68.
[14]董烁.基于厚板理论的梁板结构开洞对板墙受力性能的影响[D].郑州: 河南工业大学, 2017.Dong Shuo.The mechanical properties influence of beam slab structure of open hole to the wall based on plate theory[D].Zhengzhou: Henan University of Technology,2017.(in Chinese)
[15]贾程, 陈国荣.Mindlin-Reissner板屈曲分析的光滑有限元法[J].郑州大学学报(工学版), 2013, 34(5): 38―42.Jia Cheng, Chen Guorong.A smoothed finite element method for buckling analysis of Mindlin-Reissner Plates[J].Journal of Zhengzhou University (Engineering Science), 2013, 34(5): 38―42.(in Chinese)
[16]Greene B E, Strome D R, Weikei R C.Application of the stiffness method to the analysis of shell structures[C].Los Angeles: Aviation Conference of ASME, 1961:58―61.
[17]Argyris J H, Scharpf D W.The sheba family of shell elements for the matrix displacement method[J].Aeronautical Journal, 1968, 72(694): 873―883.
[18]Ahmad S, Irons B M, Zienkiewicz O C.analysis of thick and thin shell structures by curved Element[J].International Journal of Numerical Methods in Engineering, 1970, 2(3): 419―451.
[19]王丽莎, 岑松, 解琳琳, 等.基于新型大变形平板壳单元的剪力墙模型及其在OpenSees中的应用[J].工程力学, 2016, 33(3): 47―54.Wang Lisha, Cen Song, Xie Linlin, et al.Development of a shear wall model based on a new flat shell element for large deformation simulation and application in OpenSees[J].Engineering Mechanics, 2016, 33(3): 47―54.(in Chinese)
[20]刘人怀, 薛江红.复合材料层合板壳非线性力学的研究进展[J].力学学报, 2017, 49(3): 487―506.Liu Renhuai, Xue Jianghong.Development of nonlinear mechanics for laminated composite plates and shells[J].Chinese Journal of Theoretical and Applied Mechanics,2017, 49(3): 487―506.(in Chinese)
[21]张峰.复合材料层合板结构的非协调扩展逐层方法研究[D].天津: 中国民航大学, 2017.Zhang Feng.Study on composite laminated plates by incompatible extended layerwise method[D].Tianjin: Civil Aviation University of China, 2017.(in Chinese)
[22]Miao Z W, Lu X Z, Jiang J J, et al.Nonlinear FE model for RC shear walls based on multi-layer shell element and micro-plane constitutive model[C].Sanya, Hainan,China: Proc.Computational Methods in Engineering And Science, 2006: 405―411.
[23]张有佳, 李小军, 贺秋梅.基于分层壳单元的安全壳结构有限元分析[J].建筑科学, 2014, 30(5): 35―40.Zhang Youjia, Li Xiaojun, He Qiumei.Finite element analysis of a containment vessel structures based on the multi-layer shell elements[J].Building Science, 2014,30(5): 35―40.(in Chinese)
[24]Farhat C, Wilson E.A new finite element concurrent computer program architecture[J].International Journal for Numerical Methods in Engineering, 1987, 24(9):1771―1792.
[25]杨玉明.中厚板壳结构弹塑性并行有限元法[D].江苏:南京理工大学, 2005.Yang Yuming.The parallel finite method for moderate thick shell structures of elastic-plastic[D].Jiangsu:Nanjing University of Technology, 2005.(in Chinese)
[26]Li G, Carrera E, Cinefra M, De Miguel A G, Pagani A,Zappino E.An adaptable refinement approach for shell finite element models based on node-dependent kinematics[J].Composite Structures, 2019, 210: 1―19.
[27]李钢, 余丁浩, 李宏男.基于拟力法的纤维梁有限元非线性分析方法[J].建筑结构学报, 2016, 37(9): 61―68.Li Gang, Yu Dinghao, Li Hongnan.Nonlinear fiber beam element analysis based on force analogy method[J].Journal of Building Structures, 2016, 37(9): 61―68 (in Chinese)
[28]Li G, Yu D H.Efficient inelasticity-separated finiteelement method for material nonlinearity analysis[J].Journal of Engineering Mechanics, 2018, 144(4):04018008.
[29]陆新征, 蒋庆, 缪志伟, 潘鹏.建筑抗震弹塑性分析[M].第二版.北京: 中国建筑工业出版社, 2015.Lu Xinzheng, Jiang Qing, Miao Zhiwei, Pan Peng.Elasto-plastic analysis of buildings against earthquake[M].2nd ed.Beijing: China Architecture ＆ Building Press,2015 (in Chinese)
[30]王勖成.有限单元法[M].北京: 清华大学出版社,2003.Wang Xucheng.Finite element method[M].Beijing:Tsinghua University Press, 2003.(in Chinese)
[31]彭细荣, 杨庆生, 孙卓.有限单元法及其应用[M].北京: 清华大学出版社, 2012.Peng Xirong, Yang Qingsheng, Sun Zhuo.Finite element method and application[M].Beijing: Tsinghua University Press, 2012.(in Chinese)
[32]Dvorkin E N, Bathe K J.A continuum mechanics based fournode shell element for general non-linear analysis[J].Engineering Computations, 1984, 1(1): 77―88.
[33]李钢, 贾硕, 李宏男.基于算法复杂度理论的拟力法计算效率评价[J].计算力学学报, 2018, 35(2): 129―137.Li Gang, Jia Shuo, Li Hongnan.The efficiency evaluation of force analogy method based on the algorithm complexity theory[J].Chinese Journal of Computational Mechanics, 2018, 35(2): 129―137.(in Chinese)
[34]Li G, Jia S, Yu D H, Li H N.Woodbury approximation method for structural nonlinear analysis[J].Journal of Engineering Mechanics, 2018, 144(7): 04018052.
[35]Kirsch U.Reanalysis of structures: A unified approach for linear, nonlinear, static, and dynamic systems[M].New York: Springer, 2008.
[36]李佳龙, 李钢, 李宏男.基于隔离非线性的实体单元模型与计算效率分析[J].工程力学, 2019, 36(9): 40―49,59.Li Jialong, Li Gang, Li Hongnan.The inelasticityseparated solid element model and computational efficiency analysis[J].Engineering Mechanics, 2019,36(9): 40―49, 59.(in Chinese)