高强度钢材具有高强、轻质、经济等优势，开始在建筑结构和桥梁结构中得到逐步应用，并成为近期社会发展和行业需求的趋势[1－2]。然而，与普通钢材相比，高强钢材屈强比增加，延伸率降低，它的断裂破坏成为更突出和需要关注的问题。传统的断裂力学均假定裂纹已存在，不适用于强震作用下无明显缺陷部位塑性变形显著的断裂破坏[3－4]。强震作用下钢材的断裂破坏属于超低周疲劳断裂破坏的范畴[5－6]，其主要关注裂纹的起始和扩展，它的主要特点是较低的疲劳寿命和较大的塑性应变幅。
已有的研究结果表明，结构钢材作为多晶体金属材料，它在单调加载和超低周循环加载下的断裂破坏是微孔洞扩展、聚合引起的延性断裂破坏[6－8]。针对钢材的延性断裂，国内外学者提出一些断裂预测模型，如微孔扩展模型[9]和循环微孔扩展模型[6]。Liao等[10]、刘希月等[11]基于Q460钢材圆棒试样的单调拉伸试验，标定了钢材的微孔扩展模型参数。陈博林[12]、刘希月[13]标定了 Q460C高强钢材的循环微孔扩展模型参数，刘希月[13]还应用该模型对Q460C高强钢材梁柱节点的断裂破坏开展预测分析，取得了良好的预测结果。目前关于建筑高强钢材断裂破坏的研究多集中在Q460钢材[10－14]，对于Q690钢材断裂性能，尤其是在超低周循环荷载下的断裂破坏的相关研究内容还较少。
除了微孔扩展模型和循环微孔扩展模型，连续损伤模型[15]也可以用于钢材的断裂破坏预测分析。这类模型基于材料内部微观结构的变化，着重考察损伤对材料宏观力学性质的影响以及结构的损伤演化过程，通过引进内部变量，将微观结构变化映射到宏观力学变化上加以分析，即采用带有损伤变量的本构关系真实地描述受损材料的宏观力学行为。本文以 Q690D高强度钢材为研究对象，开展了缺口圆棒试样的单调拉伸试验和超低周循环加载试验，研究了不同加载方式对试样承载能力和变形能力的影响。基于试验和有限元分析的结果，标定了 Q690D钢材的连续损伤模型的参数，并对带初始间隙试样的断裂破坏进行了预测分析。
1 连续损伤模型
单调加载情况下，Lemaitre[15]最早建立了连续损伤力学模型的框架，提出用刚度的退化来描述材料的损伤程度：
式中，E0、E分别表示材料无损伤和有损伤时的弹性模量。
Bonora[16]在Lemaitre[15]的基础上，提出了材料的损伤演化方程：
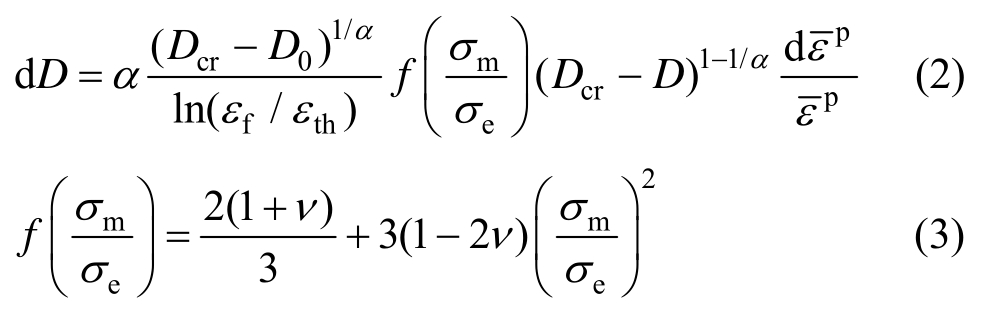
式中：α为材料参数；dD、D0、Dcr分别为累积损伤增量、初始损伤、临界损伤；
th、f分别为单调加载下的损伤应变门槛值和断裂应变；
为累积塑性应变增量，
表示应力三轴度，σm、σe分别为静水压力和Mises等效应力；v为泊松比。
在单调比例加载条件下，假定应力三轴度保持不变，Bonora[16]假设th不随应力三轴度的变化而变化，并建立了单调荷载下断裂塑性应变与应力三轴度之间的关系：
式中，
为断裂塑性应变，式(3)可用来预测不同应力三轴度情况下材料的延性断裂破坏。
已有的研究结果[17]表明，当应力三轴度小于-1/3时，材料不会发生断裂破坏，因此本文假定在循环加载过程中，有效累积塑性应变
与累积塑性应变
的关系可定义为：
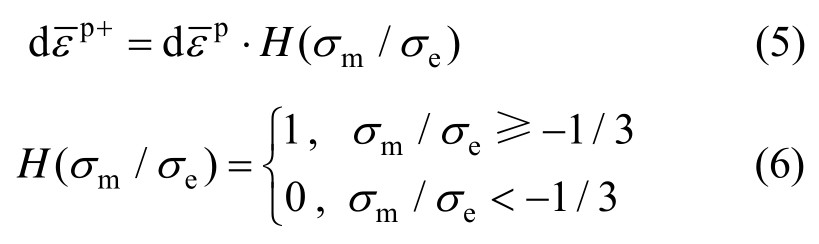
可知当应力三轴度大于等于-1/3时，有效累积塑性应变
才会随着累积塑性应变
的增大而增大。
对于材料在超低周疲劳循环荷载作用下损伤的演化规律，本文通过如下的假设，将单调加载下的损伤模型(式(2))推广应用到超低周循环加载的情况：1)当有效累积塑性应变
大于损伤应变门槛值th，并且在应力三轴度大于-1/3的情况下，损伤开始累积；2)只有在应力三轴度大于-1/3的情况下，损伤才会引起刚度的退化。超低周循环荷载下材料的损伤演化规律可以写为：
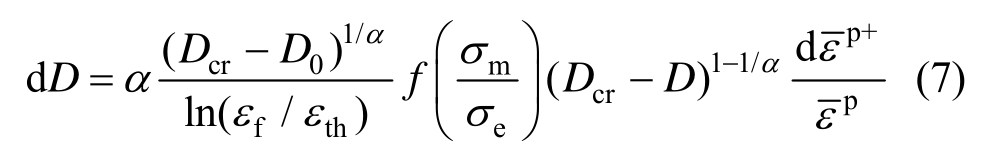
损伤对于弹性模量的影响可表述为：
单调拉伸加载情况下，式(7)可退化为式(2)。因此，该模型既可应用在超低周疲劳加载的情况，也可应用在单调加载下的情况。
2 Q690D钢材的试验结果与分析
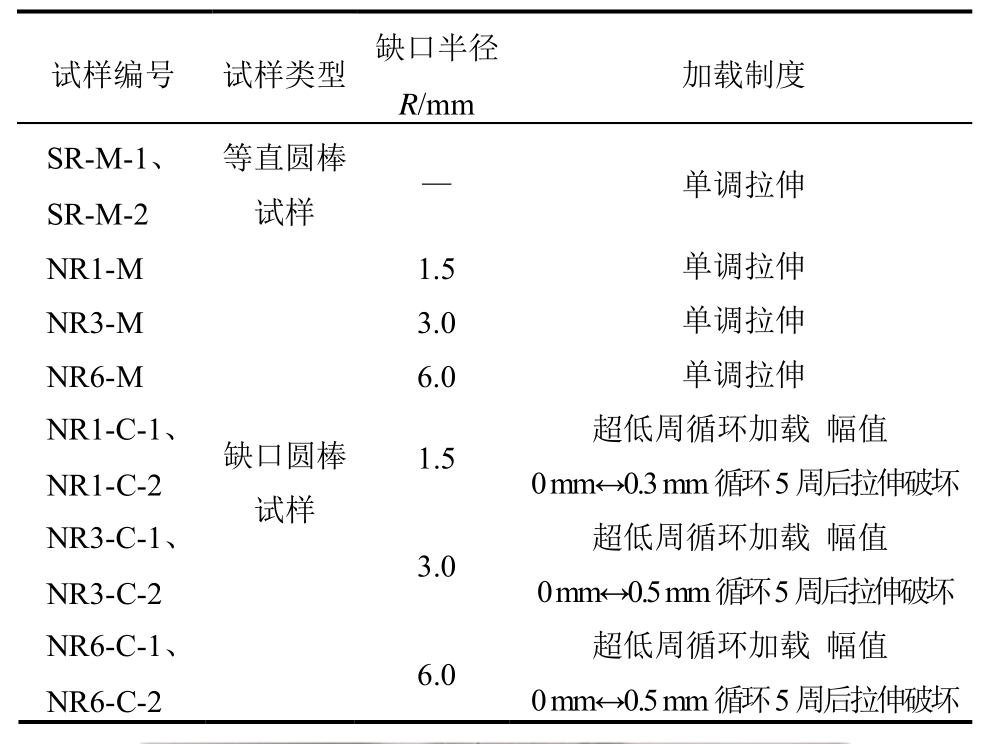
舞阳钢铁有限公司生产的 Q690D建筑结构高强度钢材，其化学组成如表1所示，钢材的交货状态为调质。从10 mm厚的热轧钢板中沿着轧制方向取样，设计并加工钢材圆棒试样，圆棒试样包含缺口圆棒试样和等直圆棒试样。缺口圆棒试样的设计几何尺寸由图1(a)给出，为研究不同应力三轴度情况下钢材的超低周疲劳断裂，试样的缺口尺寸分别为1.5 mm、3 mm和6.25 mm，相应的试样命名为NR1、NR3和NR6。等直试样的几何尺寸如图1(b)所示，试样命名为SR。为获得Q690D钢材的基本力学性能，等直圆棒试样加工2个，进行单调拉伸试样。对于缺口圆棒试样，每种试样加工3个，其中1个开展单调加载试验，2个开展超低周循环加载试验。超低周疲劳加载采用在低应变幅值下循环5周，然后单调拉伸直至断裂，试样的加载制度由表2给出。试验设备为MTS370.25轴向伺服疲劳试验系统，引伸计为MTS 634.12F-24，引伸计标距为25 mm，如图2所示。
表1 Q690D钢材的化学组成/(%)
Table 1 Chemical composition of steel Q690D
C Si Mn S P Mo Ni Cr V Cu 0.1 0.24 1.1 0.002 0.002 0.20 0.32 0.29 0.003 0.01
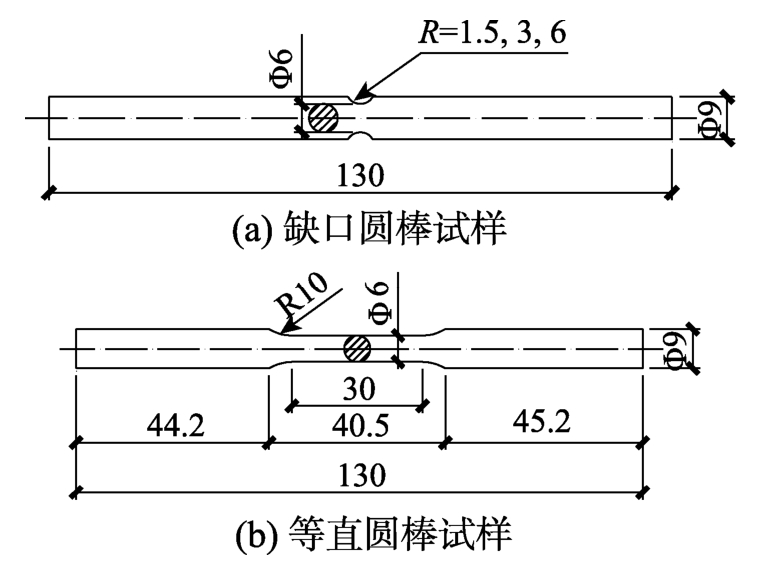
图1 圆棒试样的几何尺寸/mm
Fig.1 Round bar specimen geometry
基于SR-M-1、SR-M-2等直圆棒试样的单调拉伸试验，获得Q690D钢材的工程应力-应变关系曲线，进而得到Q690D钢材的基本力学性能，列入表3中，由于Q690D钢材没有明显的屈服平台，因此钢材的屈服极限取塑性应变为0.2%时的应力σp0.2。在等直圆棒试样的单调拉伸试验中，钢材断裂时的断裂应力σf和断裂应变f可由下式计算[10―11]：
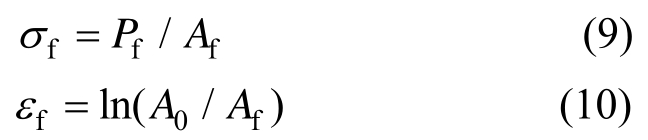
式中：Pf为钢材试样断裂时的荷载；A0、Af分别为试样的初始横截面面积和断裂后的横截面面积，计算得到Q690D钢材的断裂应力和断裂应变如表3所示。
表2 Q690D圆棒试样的加载制度
Table 2 Loading on Q690D steel specimens
?
图2 圆棒试样单调拉伸和超低周疲劳加载试验
Fig.2 Monotonic tensile and extremely low cycle fatigue tests of round bar specimens
表3 Q690D钢材的力学性能指标
Table 3 Mechanical properties of Q690D steel
?
试验获得圆棒试样的荷载-位移曲线如图3所示，可以看出在超低周循环加载情况下，缺口圆棒试样出现循环软化现象。基于缺口圆棒试样的荷载-位移曲线，得到每个缺口圆棒试样的极限荷载 Pu由表4给出。对于缺口圆棒试样，试验结果表明，裂纹起始后迅速扩展，并引起荷载的急剧下降，因此可将荷载-位移曲线中的斜率突变点作为试样裂纹起始的时刻，此时的位移定义为断裂位移
f。由此获得缺口圆棒试样在单调加载和超低周循环加载下的断裂位移列入表4。由表4可见，在单调和超低周循环加载情况下，缺口圆棒试样具有明显的缺口强化效应，缺口半径越小，试样的极限荷载越大，但试样的断裂位移越小，即缺口半径减小可以提高试样的承载能力，但也会降低试样的变形能力。另外，表4还对比了加载制度对试样极限荷载和断裂位移的影响，可以看出超低周循环加载下试样的极限荷载与单调加载基本相同，但断裂位移比单调荷载下明显减小，原因在于前5周的循环加载对试样造成了一定的损伤。因此试样再进行拉伸时，相对于直接单调拉伸的试样，其变形能力会降低。
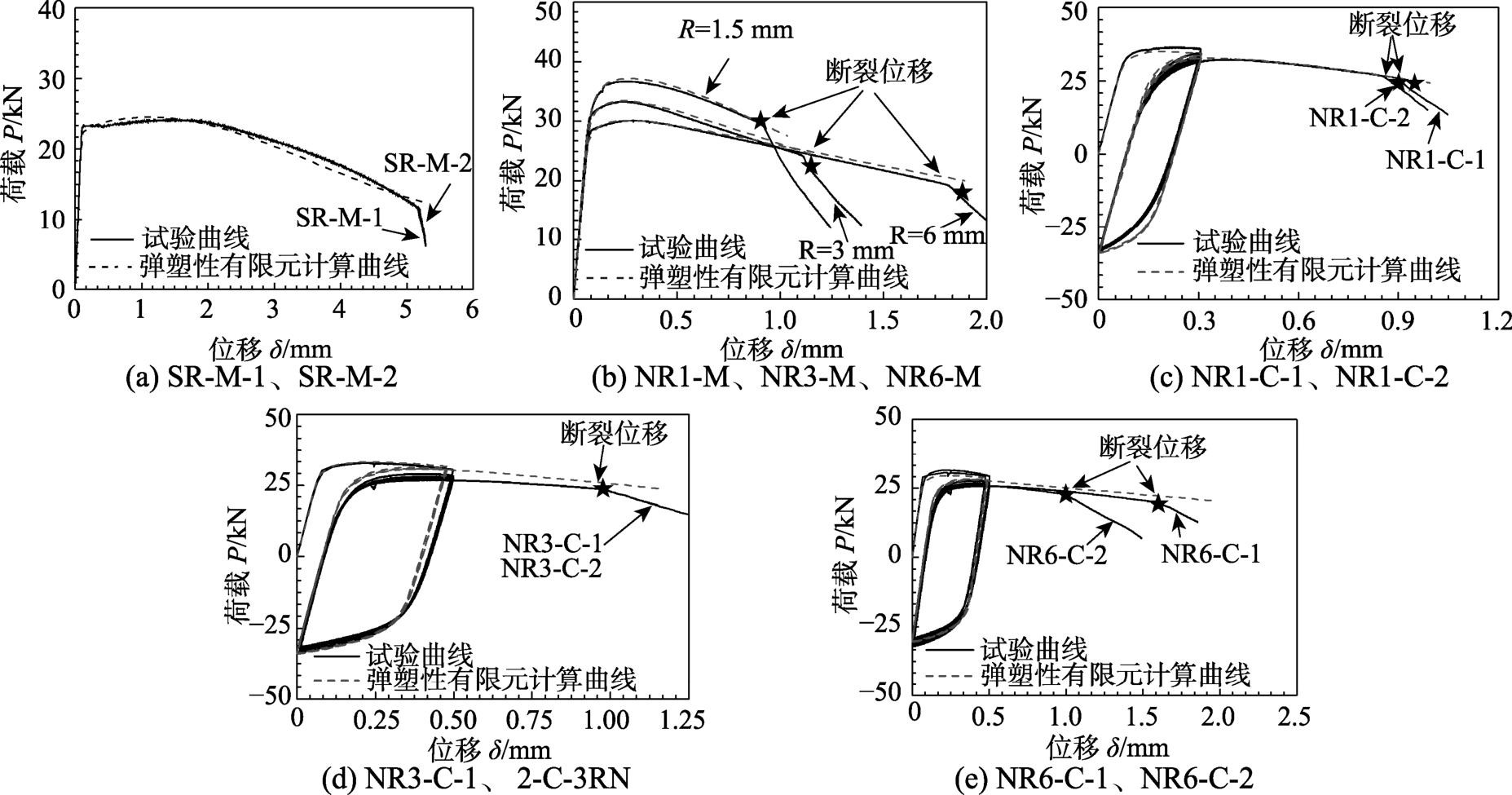
图3 圆棒试样的荷载-位移试验曲线
Fig.3 Load-displacement curves of round bar specimens
图4 圆棒试样的宏观断口形貌
Fig.4 Fracture surface of round bar specimens
表4 缺口圆棒试样断裂破坏的试验结果
Table 4 Fracture test results of notched specimens
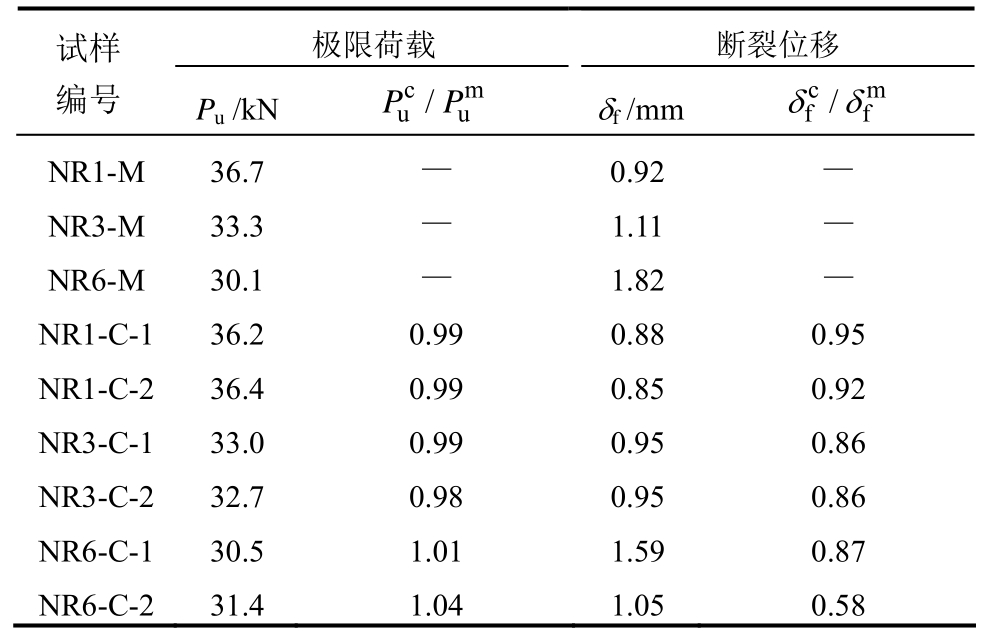
试样编号极限荷载 断裂位移P/kN Puc/Pum images/BZ_246_1077_786_1106_828.png/mm images/BZ_246_1077_786_1106_828.pngfc/images/BZ_246_1077_786_1106_828.pngfm uf NR1-M 36.7 — 0.92 —NR3-M 33.3 — 1.11 —NR6-M 30.1 — 1.82 —NR1-C-1 36.2 0.99 0.88 0.95 NR1-C-2 36.4 0.99 0.85 0.92 NR3-C-1 33.0 0.99 0.95 0.86 NR3-C-2 32.7 0.98 0.95 0.86 NR6-C-1 30.5 1.01 1.59 0.87 NR6-C-2 31.4 1.04 1.05 0.58
圆棒试样最终断裂后的宏观断口如图4所示，可见，等直圆棒试样有明显的颈缩现象，另外，在单调加载和超低周循环加载情况下，试样都呈现出杯状断口，因此圆棒试样的裂纹起始位置位于试样中心处，裂纹起始后从试样中心向边缘扩展，断口处出现明显的剪切唇。典型试样的微观断口形貌如图5所示，可以看出，断口都有明显的等轴韧窝形状，试样的断裂都是微孔洞聚合引起的延性断裂。
图5 缺口圆棒试样的微观断口形貌
Fig.5 Fracture morphology of notched specimen
3 Q690D钢材连续损伤模型参数标定
对于SR-M圆棒试样，在工程应力达到极限强度前，可将Q690D钢材的工程应力-应变关系转换为真实应力-应变关系，试样断裂时的应力-应变数据点为(f, σf)，因此，工程应力达到极限强度后，可采用线性插值的方式构造出钢材的真应力-塑性应变关系曲线，如图6所示。
图6 Q690D钢材的真应力-塑性应变曲线
Fig.6 True stress versus plastic strain curves of Q690D steel
标定 Q690D钢材的连续损伤模型参数可分两步开展：1)基于钢材的真应力-塑性应变曲线标定钢材的强化模型参数；2)根据圆棒试样单调拉伸断裂破坏试验结果标定Q690D钢材的损伤模型参数。金属材料的应变强化模型一般可采用 Chaboche非线性等向强化随动强化混合模型[18]，该模型包含非线性随动强化部分和非线性等向强化部分，随动强化部分是由线性的 Ziegler定律和非线性恢复项组合得到，背应力由多个分项叠加而成，其演化方程如下：
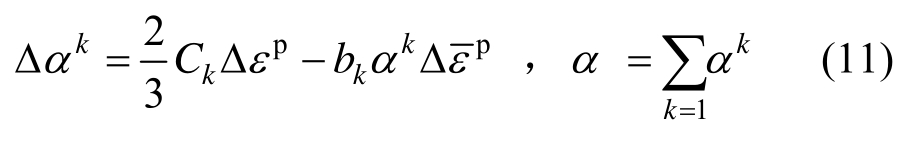
式中，Ck和bk为材料参数，Ck为初始随动强化模量，bk表示随动强化模量减小的速率。模型的等向强化部分确定了屈服面
的大小，它是累积塑性应变
的非线性函数：
式中：σ0为初始屈服极限；Q∞用于描述材料等向强化函数的饱和值；b为描述屈服面半径与累积塑性应变关系的参数。Q690D钢材的屈强比较大，在循环荷载下，钢材的屈服面大小变化较小，因此本文忽略 Q690D钢材屈服面的大小变化，钢材的应变强化采用随动强化模型。
应用ABAQUS有限元软件，为提高计算效率，采用轴对称单元建立等直圆棒试样和缺口圆棒试样的有限元模型，如图7所示，约束一端，另一端施加单调荷载或超低周循环荷载，试样裂纹易起始位置处的网格尺寸约为0.5 mm。
本文采用 Q690D钢材的随动强化模型描述钢材在单调加载和循环加载下的力学响应，因此基于图6所示的钢材的真应力-塑性应变曲线，对式(11)所示的钢材随动强化模型进行参数标定[19]，得到钢材的强化模型参数如表5，表中σ0表示钢材的初始屈服强度，钢材随动强化模型描述的钢材真应力-塑性应变曲线与试验曲线的对比也由图6给出，可见二者基本重合。另外，基于表5所示的强化模型参数，对圆棒试样在单调加载和超低周循环加载下的变形进行弹塑性有限元分析，计算得到圆棒试样的荷载-位移曲线与试验结果吻合良好，如图3所示，由于弹塑性有限元分析中没有损伤因素，因此弹塑性有限元计算结果中荷载不会出现突然下降段。
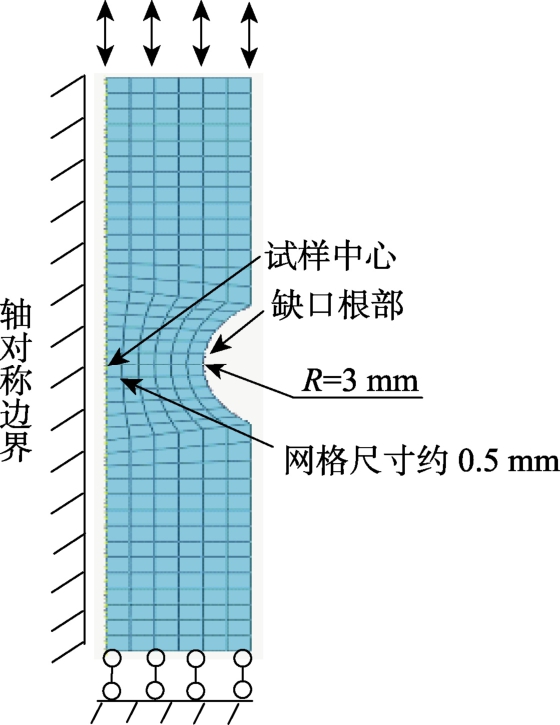
图7 NR3缺口圆棒试样的有限元模型
Fig.7 Finite element model of notched specimen NR3
表5 Q690D钢材的强化模型参数
Table 5 Hardening model parameters of Q690D steel
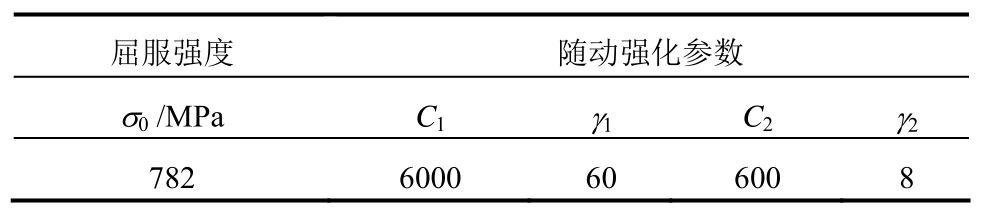
屈服强度 随动强化参数σ0/MPaC1images/BZ_31_1113_2379_1151_2425.png1C2images/BZ_31_1113_2379_1151_2425.png2 782 6000 60 600 8
Q690D钢材的连续损伤模型的损伤参数中，初始损伤 D0=0，临界损伤 Dcr=1，断裂应变f由表3给出，损伤发展指数α仅反映损伤的发展过程，不影响最终的断裂预测结果[7,16]，因此假定Q690D钢材的损伤发展指数与Q345B钢材[7]相同，α=0.198。损伤应变门槛值th可以通过试验结果和有限元计算来标定，应用 Q690D钢材的强化模型对缺口圆棒试样的单调拉伸进行弹塑性有限元分析，其钢材强化模型参数如表5所示。计算加载位移在达到断裂位移f前，试样中心处的应力-应变发展历程，并根据式(13)来计算试样中心位置在这一过程中的平均应力三轴度：
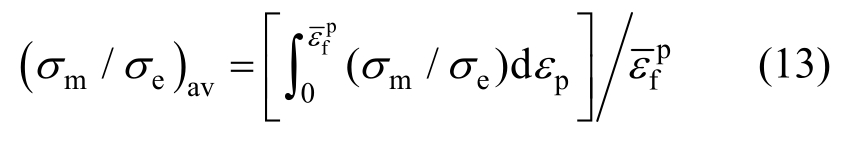
式中，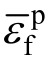
为试样中心处裂纹起始时的断裂塑性应变。等直圆棒试样的单调拉伸断裂可以看作是在应力三轴度为1/3时的破坏，因此可以将数据点(1/3，f)也列入图8中。然后可以基于式(4)对图8所示的Q690D钢材的断裂塑性应变与应力三轴度的关系进行数据回归，进而标定损伤应变门槛值th，如表6所示。
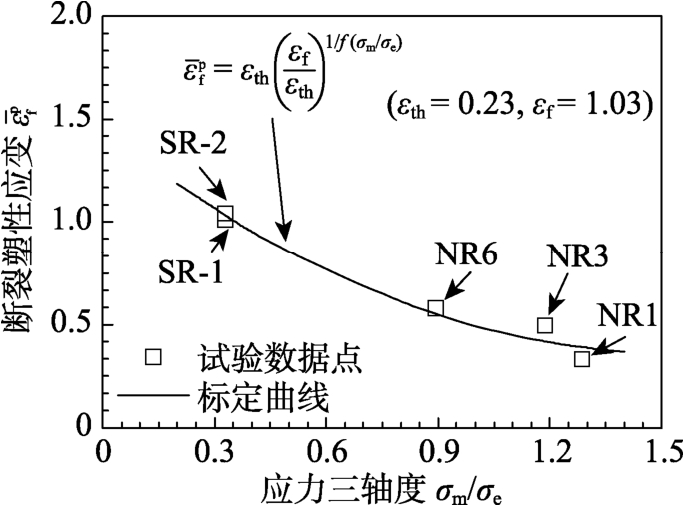
图8 损伤应变门槛值th的标定曲线
Fig.8 Calibrated curve of damage strain threshold th
表6 Q690D钢材连续损伤模型参数
Table 6 Continuum damage model parameters of Q690D steel
？
4 Q690D钢材缺口圆棒试样断裂破坏的预测分析
采用 Fortran语言编写连续损伤模型的程序，借助 ABAQUS软件的用户材料子程序，将连续损伤模型移植到 ABAQUS有限元软件中。当单元的损伤D达到临界损伤Dcr时，判断该单元失效，然后根据新的应力状态继续进行有限元计算，直到试样完全破坏。同时，可根据单元的失效顺序预测裂纹的扩展方向，并且在计算中采用准静态的分析方法，尽量减小惯性效应的影响。
为研究网格尺寸对断裂预测的影响，以NR3-M为例，在试样缺口处采用不同的网格尺寸，应用表6所示的Q690D钢材的连续损伤模型对试样的断裂破坏进行分析,得到试样的荷载-位移曲线如图9所示。可见随着网格尺寸的减小，预测的断裂位移逐渐减小，当网格尺寸小于0.5 mm后，断裂位移的减小程度明显减小，因此文中的网格尺度设定为0.5 mm。另外，在应用 Q690D钢材连续损伤模型对试件或结构进行断裂预测分析时，试件或结构裂纹易起始位置的网格尺寸也设定0.5 mm，这样可以排除网格尺寸对断裂破坏的影响。
图9 网格尺寸对NR3-M试样断裂预测的影响
Fig.9 The effect of mesh size on the fracture predicted results of Specimen NR3-M
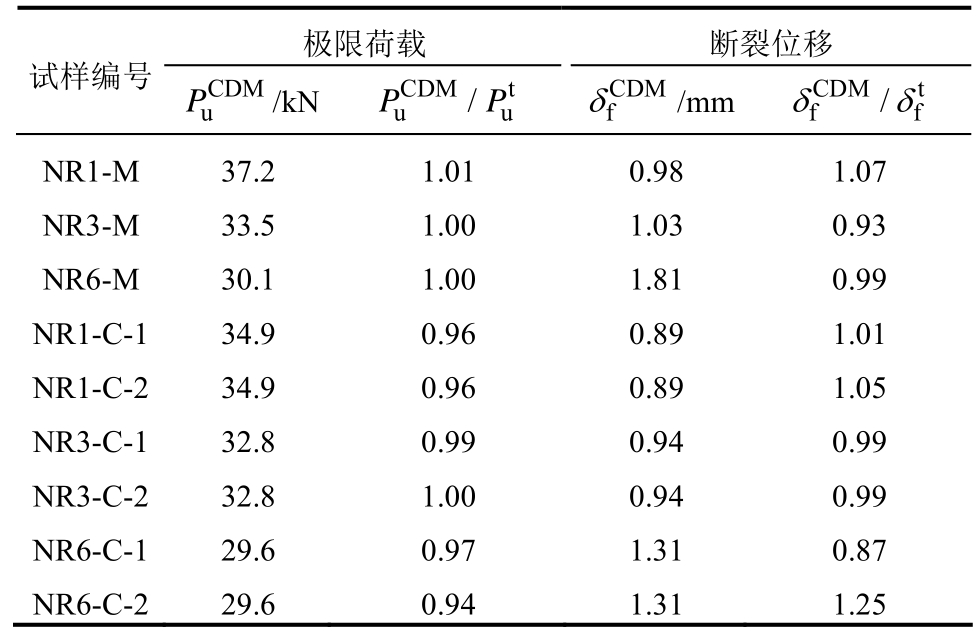
应用表6所示的Q690D钢材连续损伤模型对钢材缺口圆棒试样在单调加载和超低周加载下的断裂破坏进行有限元计算分析，计算得到试样的荷载-位移计算曲线如图10所示，可见计算曲线与试验曲线吻合良好。基于图10所示的连续损伤模型计算曲线，得到圆棒试样的极限荷载和断裂位移，如表7所示，表7还给出了圆棒试样极限荷载和断裂位移的连续损伤模型计算结果与试验结果的对比情况，由表7可见，连续损伤模型对于试样极限荷载的预测精度很好，对于试样断裂位移的预测精度也在工程允许的范围内。
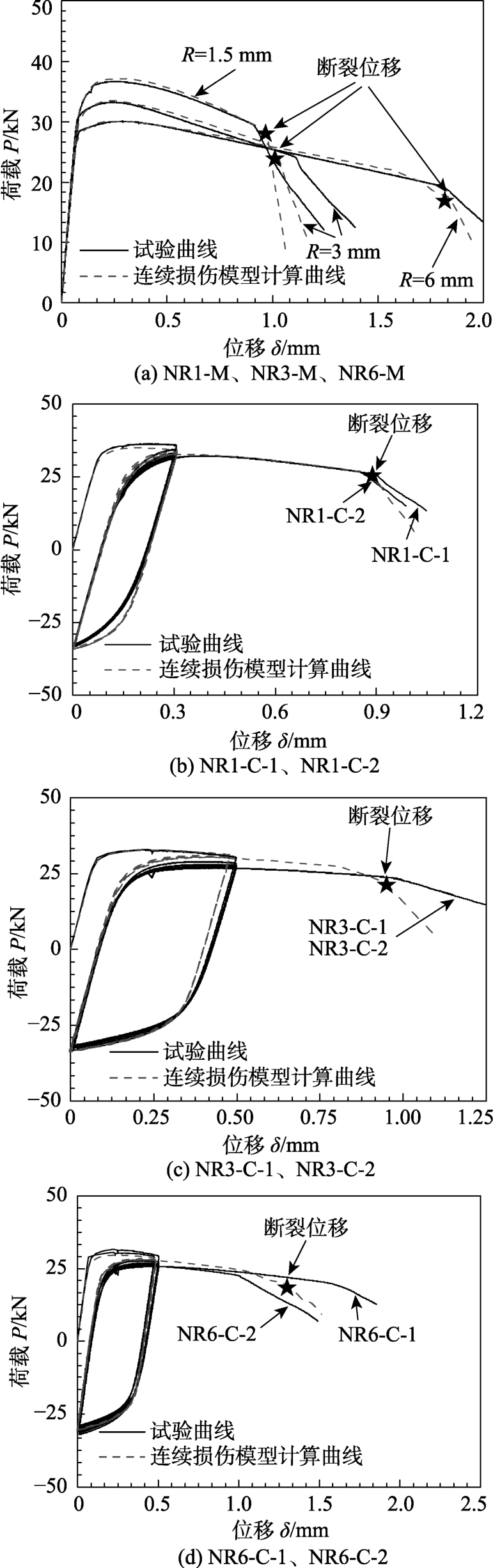
图10 缺口圆棒试样的连续损伤模型计算荷载-位移曲线
Fig.10 Load-displacement curves of notched specimens obtained from continuum damage model
表7 Q690D钢材缺口圆棒试样的断裂破坏预测结果
Table 7 Fracture prediction results of notched specimens for Q690D steel
?
为分析缺口圆棒试样的裂纹起始位置，以NR3为例，图11分析了在单调加载和超低周循环加载下试样中心和缺口根部的损伤随加载位移的发展过程，可见对于超低周循环加载工况，前5周的超低周循环加载，造成了试样中心处产生了一定的损伤，因此再拉伸时，试样中心达到临界损伤时的位移明显小于单调加载工况。另外，试样中心处的损伤最先达到临界损伤 Dcr，因此裂纹起始于试样中心处，其他试样在单调加载和超低周循环加载时的裂纹起始位置相同，裂纹都起始于试样中心处，如图12所示，这也与图4所示的试验结果一致。
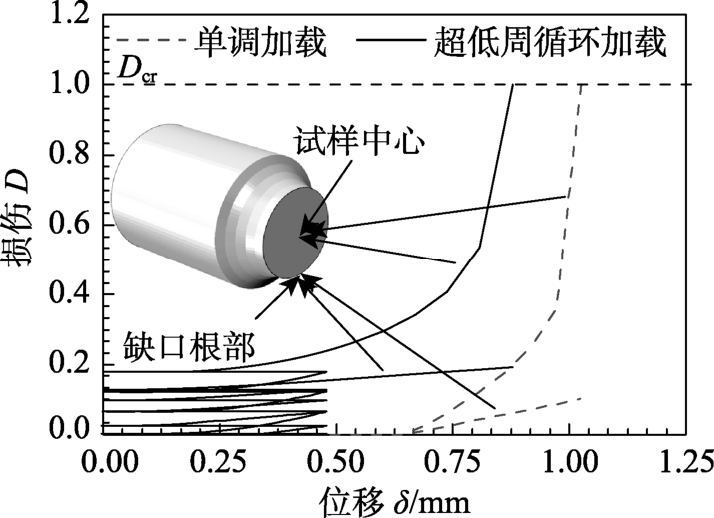
图11 NR3试样的损伤演化规律
Fig.11 Damage evolution law of Specimen NR3
图12 缺口圆棒试样裂纹起始位置的有限元计算结果
Fig.12 Crack initiation location of notched specimens obtained from finite element analyses
5 带初始间隙试样断裂破坏预测分析
为分析钢结构梁柱焊接节点处的断裂破坏，常采用十字形焊接节点来模拟实际节点处的应力状态[20]，如图13所示。为分析这种应力状态下的断裂破坏，设计了如图14所示的Q690D钢材母材试样CTC12(Connection Tension specimen with Crack)。在这类试样中设置了一条初始间隙，间隙的宽度为1 mm，长度为12 mm，该间隙用来模拟角焊缝焊接时未焊透而留下的间隙。试样加工5个，每个试样的加载工况如表8所示，其中1个试样开展单调拉伸试验，2个试样在低幅值下循环5周后拉伸断裂，另外两个 2个试样在恒定幅值下循环直至完全断裂。试样在 MTS电液伺服试验机上开展试验，如图15所示，引伸计标距为25 mm，图14给出了引伸计的放置位置。
图13 十字形焊接试件的断裂破坏[20]
Fig.13 Fracture failure of cross-shaped welded joint
图14 CTC12试样的几何尺寸/mm
Fig.14 Geometry of Specimen CTC12
图15 CTC12试样的断裂破坏试验
Fig.15 Fracture failure test of Specimen CTC12
表8 带初始间隙试样的加载工况
Table 8 Loading cases of specimens with initial gap
?
试验获得带初始间隙试样的荷载-位移曲线如图16所示，对于CTC12-M、CTC12-C-1、CTC12-C-2试样，其荷载-位移曲线的最后下降段呈现线性，因此将最后线性下降段的起点位移定义为断裂位移f，试样的断裂位移列入表9。图17给出了带初始间隙试样的断裂破坏过程，单调加载与和低循环幅值 5周后再拉断的断裂破坏过程类似，因此，图17只给出了单调加载试样的断裂破坏过程，另外，图17还给出了试样的断口情况，由断口形状可以看出，在单调加载和超低周循环加载情况下，裂纹都起始于间隙中心处，然后随着加载的进行，裂纹呈现椭圆状扩展。由CTC12-C-3、CTC12-C-4试样断口还可以明显地看到每次循环加载产生的疲劳辉纹和最后一次循环拉伸时的延性裂纹以及断口的瞬断区。
图16 带初始间隙试样的荷载-位移曲线
Fig.16 Load-displacement curves of specimens with initial gap
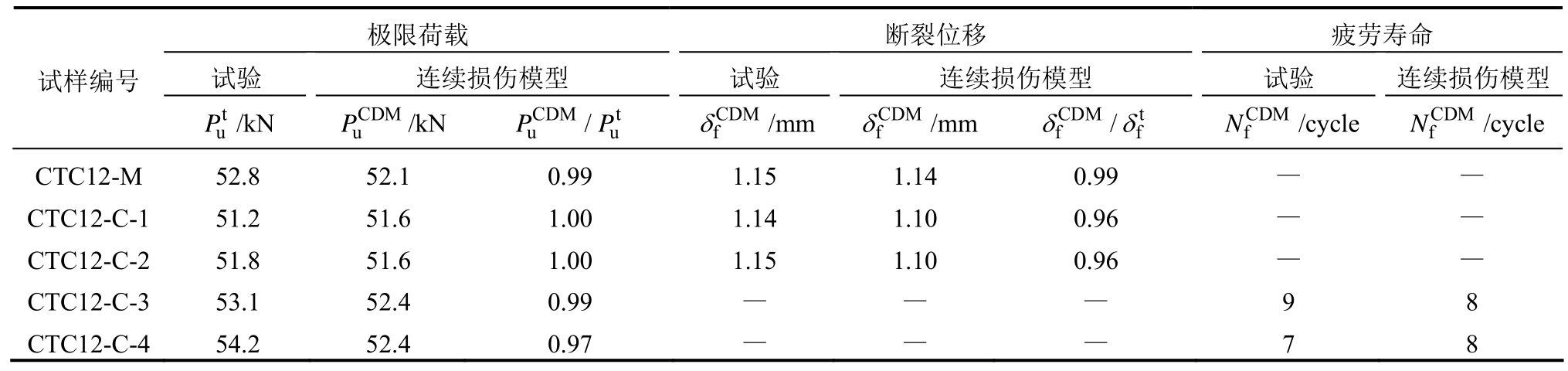
表9 带间隙试样的试验结果与连续损伤模型计算结果对比
Table 9 Comparison between test results and predicted results obtained from continuum damage mode for the specimens with initial gap
?
图17 带初始间隙试样的断裂破坏试验结果
Fig.17 Experimental fracture process of specimens with initial gap
采用 ABAQUS软件建立带初始间隙试样CTC12在引伸计标距内的有限元模型，如图18所示，间隙附近的有限元网格尺寸约为0.5 mm，这与缺口圆棒试样中心处的网格尺寸一致。基于Q690D钢材的连续损伤模型对CTC12试样在单调加载和超低周循环加载下的断裂破坏开展计算分析。为分析CTC12试样在不同加载方式下的裂纹起始位置，将间隙中心和间隙边缘两个位置处的损伤绘入图19，可以看出，间隙中心的损伤首先达到临界损伤，随后随着加载的进行，间隙边缘处的损伤也达到临界损伤，因此裂纹在间隙中心处首先产生，然后沿着试样的厚度方向扩展，在间隙边缘处也产生裂纹，这与试验结果吻合。图20给出了CTC12试样在单调加载和恒定幅值超低周循环加载下的断裂破坏数值模拟结果，可以看出数值模拟结果与 图17所示的试验结果吻合良好。带初始间隙试样在不同加载方式下的荷载-位移曲线计算结果与试验结果的对比由图16给出，基于荷载-位移曲线得到每个试样的极限荷载、断裂位移和疲劳寿命与试验结果的对比如表9所示，可以看出，数值模拟结果与试验结果吻合较好，验证了 Q690D钢材连续损伤模型具有良好的预测精度。
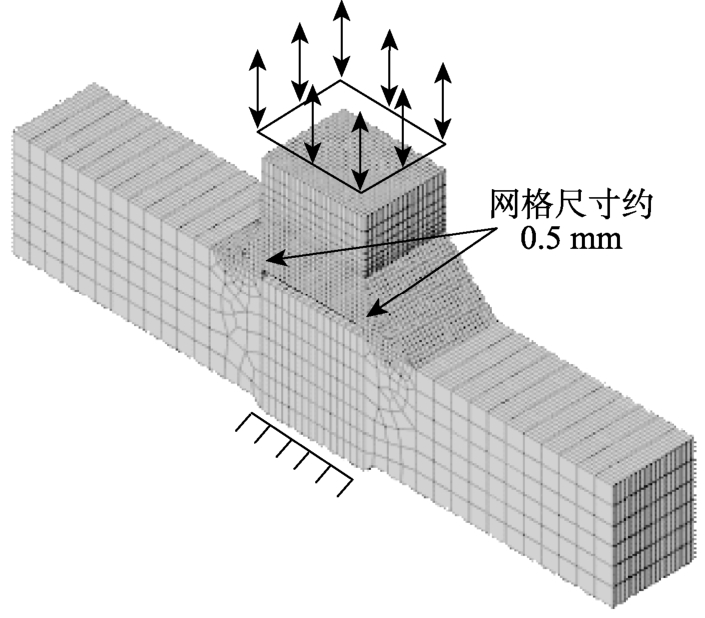
图18 带初始间隙试样有限元模型
Fig.18 Finite element model of specimen with initial gap
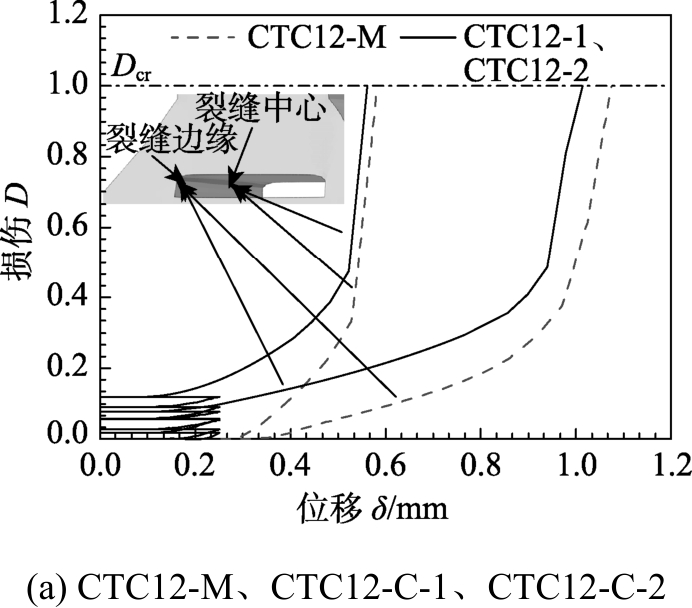
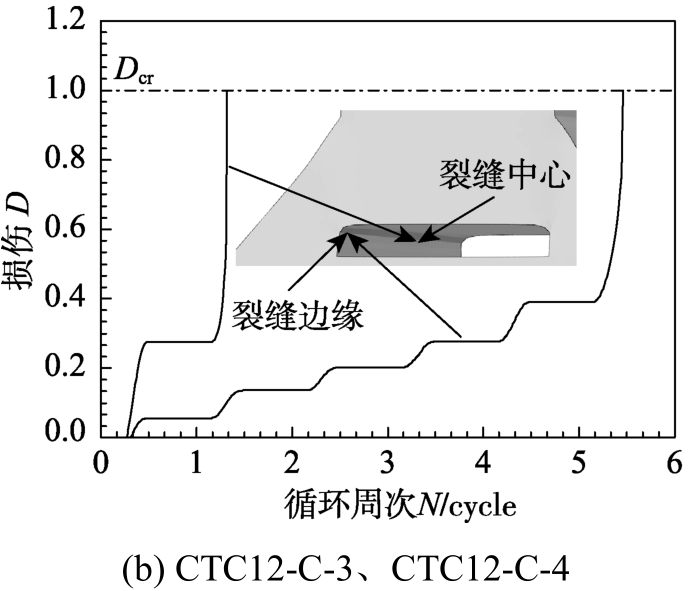
图19 带初始间隙试样裂缝处的损伤演化规律
Fig.19 Damage evolution law at the intial gap for the specimen
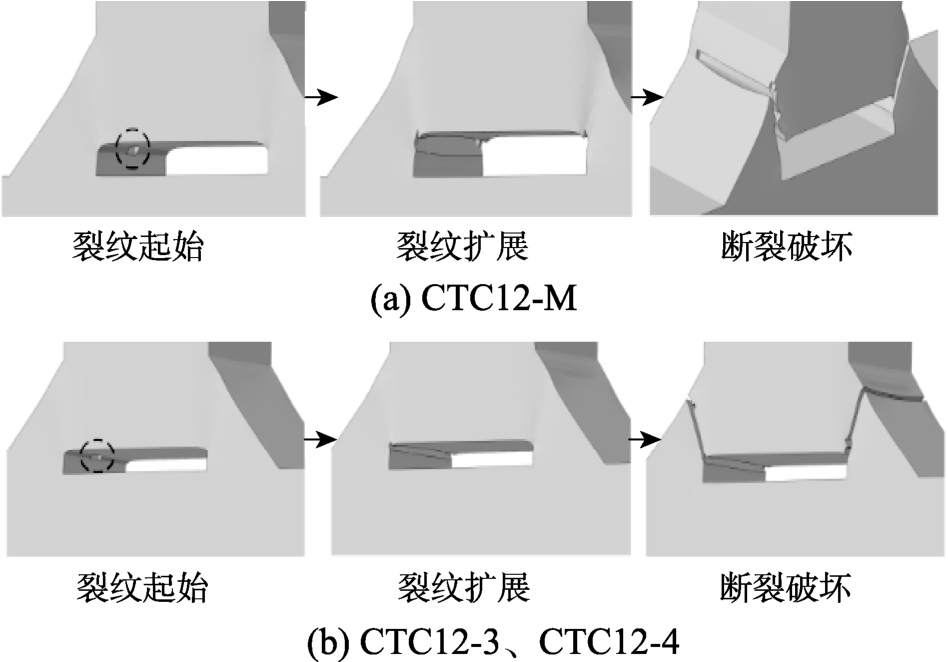
图20 带初始间隙试样断裂破坏的数值模拟结果
Fig.20 Numerical simulation of fracture process of specimens with initial gap
6 结论
(1)在单调加载和超低周循环加载下，Q690D高强钢材缺口圆棒试样具有明显的缺口强化效应，缺口半径越小，试样的极限荷载越大，但试样的断裂位移越小。Q690D钢材圆棒试样在超低周循环加载下呈现了循环软化的特点。
(2)Q690D圆棒试样在单调加载和超低周循环加载下的宏观断口和微观断口形貌表明，圆棒试样的裂纹起始于试样中心处，钢材的断裂破坏是微孔洞扩展聚合引起的延性断裂。
(3)基于Q690D圆棒试样的试验结果与相应的有限元分析，标定了 Q690D钢材的随动强化模型参数和连续损伤模型参数。对于 Q690D高强钢材圆棒试样在超低周循环荷载下的断裂破坏，连续损伤模型的预测结果与试验结果吻合良好。
(4)应用Q690D高强钢材的连续损伤模型，预测分析了含初始间隙试样在单调加载和超低周循环加载下的断裂破坏，并得到了试验结果的验证。
本文中的连续损伤模型适用于图5所示的拉伸为主的韧窝型延性断裂，当钢材发生剪切变形为主的断裂破坏时，连续损伤模型是否适用还需要进一步研究。
[1]Ban H Y, Shi G, Shi Y J, et al.Research progress on the mechanical property of high strength structural steels [J].Advanced Materials Research, 2011, 250/251/252/253:640―648.
[2]李国强, 王彦博, 陈素文, 等.高强度结构钢研究现状及其在抗震设防区应用问题[J].建筑结构学报, 2013,34(1): 1―13.Li Guoqiang, Wang Yanbo, Chen Suwen, et al.State-of-the-art on research of high strength structural steels and key issues of using high strength steels in seismic structures [J].Journal of Building Structures,2013, 34(1): 1―13.(in Chinese)
[3]廖芳芳, 王伟, 陈以一.往复荷载下钢结构节点的超低周疲劳断裂预测[J].同济大学学报(自然科学版), 2014,42(4): 539―546.Liao Fangfang, Wang Wei, Chen Yiyi.Extremely low cycle fatigue fracture prediction of steel connections under cyclic loading [J].Journal of Tongji Uinversity(Natural Science), 2014, 42(4): 539―546.(in Chinese)
[4]Huang X W, Zhao J.A cumulative damage model for extremely low cycle fatigue cracking in steel structure [J].Structural Engineering and Mechanics, 2017, 62(2):225―236.
[5]王磊, 班慧勇, 石永久, 等.基于微观断裂机理的高强钢框架梁柱节点抗震性能有限元分析[J].工程力学,2018, 35(11): 68―78 Wang Lei, Ban Huiyong, Shi Yongjiu, et al.Finite element analysis on aseismic behavior of high-strength steel beam-to-column connections in steel frame based on micromechanics of fracture [J].Engineering Mechanics,2018, 35(11): 68―78.(in Chinese)
[6]Kanvinde A M, Deierlein G G.Cyclic void growth model to assess ductile fracture initiation in structural steels due to ultra low cycle fatigue [J].Journal of Engineering Mechanics, 2007, 133(6): 701―712.
[7]Tong L W, Huang X W, Zhou F, et al.Experimental and numerical investigations on extremely-low-cycle fatigue fracture behavior of steel welded joints [J].Journal of Constructional Steel Research, 2016, 119: 98―112.
[8]黄学伟, 张旭, 苗同臣.建筑结构钢超低周疲劳断裂破坏的损伤预测模型[J].工程力学, 2017, 34(6): 101―108.Huang Xuewei, Zhang Xu, Miao Tongchen.A damage prediction model for ultra low cycle fatigue failure of building structure steel [J].Journal of Building Structures, 2017, 34(6): 101―108.(in Chinese)
[9]Kanvinde A M, Deierlein G G.Void growth model and the stress modified critical strain model to predict ductile fracture in structural steels [J].Journal of Structural Engineering, 2006, 132(12): 1907―1918.
[10]Liao F F, Wang R Z, Tu L S, et al.Micromechanical fracture model parameter influencing factor study of structural steels and welding materials [J].Construction and Building Materials, 2019, 215(10): 898―917.
[11]刘希月, 王元清, 石永久.基于微观机理的高强度钢材及其焊缝断裂预测模型研究[J].建筑结构学报, 2016,37(6): 228―235.Liu Xiyue, Wang Yuanqing, Shi Yongjiu.Micromechanical fracture prediction model of high strength steel and its weld [J].Journal of Building Structures, 2016, 37(6): 228―235.(in Chinese)
[12]陈博林.基于微观损伤模型的Q460C钢材断裂行为研究[D].北京: 北京交通大学, 2017.Chen Bolin.Fracture research of Q460C steel based on micromechanical damage models [D].Beijing: Beijing Jiaotong University, 2017.(in Chinese)
[13]刘希月.基于微观机理的高强钢结构材料与节点的断裂性能研究[D].北京: 清华大学, 2015.Liu Xiyue.Investigations on fracture behaviours of high strength steel materials and connections based on micromechanical models [D].Beijing: Tsinghua University, 2015.(in Chinese)
[14]施刚, 陈玉峰.基于微观机理的 Q460 钢材角焊缝搭接接头延性断裂研究[J].工程力学, 2017, 34(4): 13―21.Shi Gang, Chen Yufeng.Investigation on the ductile fracture behaviro of Q460 steel fillet welded joints based on micro-Mechanics [J].Engineering Mechanics, 2017,34(4): 13―21.(in Chinese)
[15]Lemaitre J.A continuous damage mechanics model for ductile fracture [J].Journal of Engineering Materials and Technology, 1985, 107(1): 83―89.
[16]Bonora N.A nonlinear CDM model for ductile failure [J].Engineering Fracture Mechanics, 1997, 58(1): 11―28.
[17]Bao Y, Wierzbicki T.On the cut-off value of negative triaxiality for fracture [J].Engineering Fracture Mechanics, 2005, 72(7): 1049―1069.
[18]Chaboche J L.Anisotropic creep damage in the framework of continuum damage mechanics [J].Nuclear Engineering and Design, 1984, 79(3): 309―319.
[19]ABAQUS.Analysis user’s manual I_V.Version 6.14 [M].USA: ABAQUS, Inc., Dassault Systèmes, 2014.
[20]刘希月, 王元清, 石永久, 等.高强度钢框架梁柱节点焊接构造的断裂性能试验研究[J].工程力学, 2018,35(5): 54―64.Liu Xiyue, Wang Yuanqing, Shi Yongjiu, et al.Experimental study on the weld fracture behavior of high strength steel beam-to-column connections [J].Journal of Building Structures, 2018, 35(5): 54―64.(in Chinese)