以布达拉宫、大昭寺等文物建筑为代表的藏式古建石砌体,雄浑壮美,气势恢宏,是人类宝贵的历史和文化遗产,同时石砌体也是藏族人民聚集地区所常采用的建筑结构类型。藏式石砌体主要采用花岗岩和粘土泥浆砌筑而成,其砌筑工艺和砌筑材料都有着鲜明而独有的特点。目前对于藏式石砌体结构性能的研究尚处于起步阶段;本文作者所在的课题组对于藏式石砌体的结构特征、材料属性和受压性能表现已进行了系统的研究,在此基础上本文重点关注藏式石砌体的抗剪性能。
砌体结构的抗剪性能主要通过试验进行研究,石砌体结构亦不例外。各类砌体结构在地震中的震害表现主要为沿着灰缝的阶梯型裂缝,或X型交叉的斜裂缝[1-2],因此能够使砌体产生相同现象的试验被认为是最有效的研究手段,其中最为广泛应用的是对角加荷试验和大尺寸墙体的压剪试验,该两类试验的试验结果经简单处理后可直接作为砌体的复合抗剪强度。其中对角加荷试验还被 ASTM E519-02[3]和国际材料与试验协会(RILEM)[4]所推荐采用。国内外许多学者采用对角加荷试验或大尺寸墙体的压剪试验对不同类型石砌体结构的抗剪性能进行了研究[5-12]。该两类试验的局限性在于,试验代价大,周期长,试验数量较少时结果往往具有较大的离散性,对于不规则的毛石砌体来说问题更为突出。
砌体的另一种常用的抗剪试验为双剪或单剪试验[8,13-16],主要用于测试叠砌小砌体的沿灰缝滑移的抗剪能力,并不能直接测试出墙体的整体抗剪能力。事实上,灰缝抗剪试验应为砌体抗剪性能的前序性、基础性的研究。重庆大学骆万康教授等[13-14]对砌体抗剪强度试验进行了深入的探讨和总结,并对摩尔和库伦两种理论计算的抗剪强度进行了适用性分析,提出了带有“变摩擦系数”的剪摩理论模式抗剪强度计算公式,该式为现行砌体结构设计规范所采用。需要注意的是,石砌体由于其石材具有较高的抗压强度,因此在剪-压复合作用下的破坏模式与其他砌体结构不同,主要以沿灰缝的滑移为主,灰缝抗剪强度具有重要意义。在石砌体抗剪性能研究方面,华侨大学[9-10,15-16]、东南大学[11-12,17-18]和葡萄牙 Minho 大学[8]等研究团队采用了这样的研究路线:先进行小试件的双剪(单剪)试验,再进行足尺墙体的拟静力试验,这样的研究方法具有较强的系统性和科学性。灰缝抗剪试验较易通过足够数量的试验来获得规律性较好的试验结果,若可以通过灰缝抗剪试验结果来推断砌体的整体性抗剪能力,势必具有广阔的应用前景,对于一些特殊工程条件下的结构性能评估也有着重要的实施意义,例如,西藏某些石砌体文物建筑,存在着修缮替换下来的保持完好的或等同的石料,进行灰缝抗剪试验是可行的,但难以重现原状墙体以进行直接性试验。
对国内外石砌体研究情况进行总结分析可见,已有的针对各类石砌体的研究成果由于粘结材料不同等因素,并不适用于藏式石砌体;另外藏式石砌体的整体抗剪性能评估急需科学依据。为研究藏式石砌体抗剪性能,进行了多组双剪试验,包括普通的三石试件和模拟藏式石砌体特征的特殊试件,获得了藏式石砌体灰缝滑移破坏机理和静力抗剪强度。然后通过两种理论模型研究了将灰缝抗剪强度转换为砌体抗剪强度的方法。
1 试验概述
1.1 藏式石砌体结构特征
藏式石砌体在垂直方向上方石层和片石层交替分布,且方石层错缝砌筑。方石一般为大块的花岗岩毛石,砌筑时石匠用石工锤等工具,对方石进行简单处理,制作成表面粗糙的六面体。片石一般为板岩片状毛石。每两个石材层之间以泥浆层进行填充。成型后的藏式石砌体有一定的分布规律性,各材料层基本保持水平,泥浆层厚度大致相同,但石材和泥浆层的尺寸方面并无统一标准。调研表明,方石短边长度一般不小于 0.2 m,长边长度从0.2 m到0.5 m不等,重量基本以一人能背运的重量为限。典型的藏式石砌体照片见图1。

图1 典型的藏式石砌体
Fig.1 Typical Tibet-style stone masonry
1.2 试件设计制作
试件设计的基本原则为石材尺寸形状和泥浆层厚度与典型藏式墙体尽量一致。出于保证试件一致性条件,以及方便加载的考虑,本次试验所用的方石均为机器切割花岗岩,尺寸统一为 400 mm 200 mm 150 mm;片石为形状随机的片状板岩,厚度普遍为15 mm~20 mm。单道泥浆层厚度在20 mm之内,兼具填充和找平的功能。为了模拟手开毛石的粗糙面,对机切方石的上、下表面进行了凿毛处理,处理后采用塞尺对粗糙度进行了测量,最大不平整度约为2.0 mm。
需要说明的是,当摩擦力成为影响抗剪强度的主要因素时,界面的粗糙程度将成为决定性因素;藏式石砌体采用的毛石千差万别,本试验显然不能代表所有的藏式石砌体。但是,为了得到具有足够规律性和可应用性的研究成果,本次试验对石块表面进行了统一的凿毛处理,处理后的石块表面粗糙程度与西藏地区某文物建筑在日常修缮中所用的砌筑用毛石块大致相仿,可以代表一种典型的砌筑工况,即使并不是普适性的。
共进行了4组总计13个试件的双剪试验,主要区别在于垂向压应力不同,以及灰缝形态不同,试件示意图和典型照片见图2,试件的详细信息见表1。本文试验中主要以三石试件为主,是因为该试件只包含两道水平泥浆灰缝,试验结果清晰直观。三石试件的制作方法为:先放置好底层方石,在其上满铺一层泥浆,手工整平后放置中间石块,然后以同样方式完成中间石块之上的泥浆层和顶端方石。在第一批试验显示试件破坏模式为界面滑移后,制作了 2个特殊试件(表1中的 S1.0-4S和S1.5-4S试件)模拟藏式石砌体带有片石层的分布特征,其两道水平灰缝可视为中间夹有片石的特殊灰缝,砌筑时先满铺一层泥浆,然后将多块形状不一的片石满铺在第一道水平灰缝上,再满铺一层泥浆,然后放置特殊灰缝上层的方石。

图2 试件示意和示例图
Fig.2 Geometry and examples of specimens
灰缝处的泥浆为西藏黄土加水搅拌制作而成,制作方法参考典型的藏族工匠砌墙工艺。粘土泥浆的配合比(水质量∶土质量)为 15%,该土水比例是经多次试配后,所选的与典型藏式石墙砌筑中所用泥浆形态最为接近的一组配合比。藏式石砌体的砌筑并无精细的泥浆配合比要求,主要依据工匠的经验,前期试验发现,在粘土塑限和液限的范围内所试配的泥浆材料标准试件的抗压强度基本一致,见图3。初始含水率对于最终固化泥浆的强度没有显著影响,泥浆本质上是土体颗粒的集合体且强度较低(3 MPa左右),可以认为用相同粘土配置的泥浆材料都是一致的,这样可以不考虑粘结材料强度不同所带来的影响,试验可得到适当简化。
表1 试验参数及主要结果汇总
Tab.1 Detailed parameters of specimens and main results
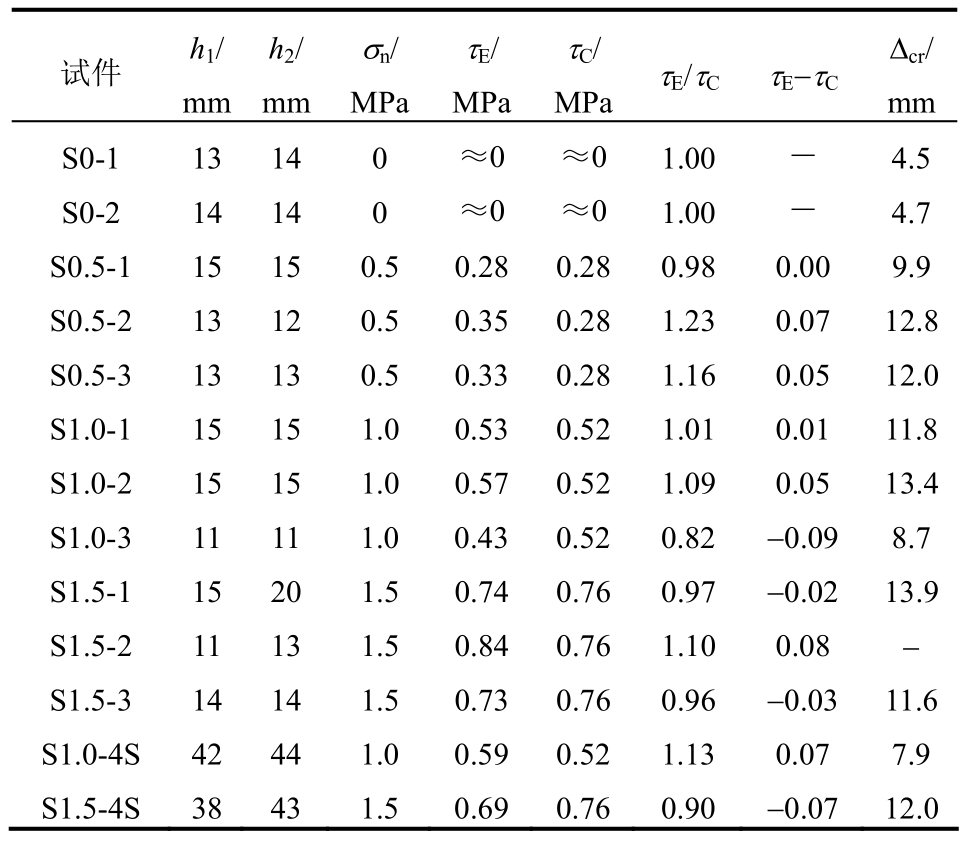
注:S1.5-2试件试验中有整体移位,未能采集到中间石块的有效位移数据。
试件 h1/mm h2/mm σn/MPa τE/MPa τC/τ/ττ-τ MPa ECEC Δcr/mm S0-1 13 14 0 ≈0 ≈0 1.00 - 4.5 S0-2 14 14 0 ≈0 ≈0 1.00 - 4.7 S0.5-1 15 15 0.5 0.28 0.28 0.98 0.00 9.9 S0.5-2 13 12 0.5 0.35 0.28 1.23 0.07 12.8 S0.5-3 13 13 0.5 0.33 0.28 1.16 0.05 12.0 S1.0-1 15 15 1.0 0.53 0.52 1.01 0.01 11.8 S1.0-2 15 15 1.0 0.57 0.52 1.09 0.05 13.4 S1.0-3 11 11 1.0 0.43 0.52 0.82 _0.09 8.7 S1.5-1 15 20 1.5 0.74 0.76 0.97 _0.02 13.9 S1.5-2 11 13 1.5 0.84 0.76 1.10 0.08 _S1.5-3 14 14 1.5 0.73 0.76 0.96 _0.03 11.6 S1.0-4S 42 44 1.0 0.59 0.52 1.13 0.07 7.9 S1.5-4S 38 43 1.5 0.69 0.76 0.90 _0.07 12.0

图3 泥浆标准试件抗压强度统计
Fig.3 Statistics of compressive strength of standard earthen mortar specimen
1.3 试验装置
为了减小弯曲应力的影响,并避免翻动重量较大的石块损坏设备,试验采用平推双剪的加载方式。上、下两块方石的侧面通过反力架和刚性限位装置限制其侧向位移,中间方石的一侧受推。为减少加载过程中上、下压板摩擦力对理想剪切试验边界条件的不利影响,在试件的上、下压板上各安装一套滚轴滑板。加载时试件中心和加载的千斤顶中心对齐,同时保证上、下钢压板与试件紧密接触,避免偏心受压。试验装置图见图4。

图4 试验装置图
Fig.4 Setup of the test
压力荷载由竖向千斤顶一次性加载完毕。水平荷载通过水平千斤顶进行加载,采用连续加荷方法,缓慢加载并减少冲击。采用位移计对中间受推石块的水平位移进行采集。本试验方法与其他学者的研究[15-18]基本一致,并参考了《砌体基本力学性能试验方法》(GB/T 50129―2011)[19]的相关规定。经测算,石块的自重远小于有压力组试件所承受的压力荷载,其影响可忽略不计。
共进行了4组不同压应力工况的双剪试验,无压应力组包括2个试件,其他组至少包括3个试件的试验。压应力σn分别为0 MPa、0.5 MPa、1.0 MPa和1.5 MPa。
2 抗剪试验结果与分析
2.1 试验现象
水平荷载开始施加后,无压应力的试件几乎立即发生了中间石块的滑移,两道水平灰缝的顶面与中间石块的水平面分离,形成滑移面。有压应力的试件,在水平荷载逐渐增大的过程中,首先发生的现象是灰缝由于受到扰动而有部分土体的掉落;然后受推的中间石块会发生细微和缓慢的位移,在此过程中灰缝并无剧烈的现象和变化;当水平荷载达到某一量值时,中间的石块的水平运动迅速加快,两道水平灰缝和中间石块的交界面基本同时发生分离,形成清晰可见的滑移表面,该水平荷载的量值即为灰缝抗剪的极限承载力。所有有压应力试件的两道滑移表面,同样均出现在灰缝的顶面。灰缝抗剪的极限承载力随着压应力的提高而增大,该规律与其他学者的试验结果一致。
体现藏式石砌体结构特征的特殊灰缝试件(S1.0-4S和S1.5-4S)试验中的破坏现象以及剪切应力-位移曲线与普通试件并无显著区别,同样为灰缝顶面形成滑移面,特殊灰缝中的片石有肉眼可见的轻微移位,表明特殊灰缝由于其厚度较大,自身的水平方向变形更大。特殊灰缝试件的极限剪切应力与相同压应力的普通试件较为接近。上述情况说明,从工程应用的角度可以将特殊灰缝视为与普通水平灰缝同等的粘结层,在剪切荷载作用下发生界面滑移破坏。这样藏式石砌体的受剪破坏分析可得到大大简化。需要说明的是,目前的研究手段为静力试验,仍需要拟静力或动力试验等方法予以验证。
试件的极限破坏状态见图5,可清晰地看到灰缝顶面所形成的滑移界面。

图5 试件的滑移破坏状态
Fig.5 Slide failure state of specimens
2.2 试验数据和损伤机理分析
各试件的剪切应力-位移曲线见图6。中间石块的受剪荷载-位移曲线中表现为,水平位移首先单调增加,曲线的斜率有一定的变化,斜率变化并无明显规律;当达到灰缝抗剪的极限承载力时,多数试件的剪切应力会有少量的下降,部分试件在后续加载过程中剪切应力又有所增大。进入滑移状态后,位移值的增长速度显著加快。试验的表观现象和数据曲线有较好的对应关系。
石砌体在双剪试验中所承受的压力荷载远小于其极限强度,因此其剪切破坏形式为剪摩破坏,是沿着特定的滑移面发生的材料相互错动。双剪试验中普遍采用库伦理论类型的表达式来计算石砌体的灰缝抗剪强度[13-16],表达式的基本形式为:
式中:c为粘结强度;σn为竖向压应力;μ为灰缝与块材间的摩擦系数。式(1)清楚地表示出抗剪强度由粘结和摩擦两个方面组成。

图6 各试件的剪切应力-相对剪切位移曲线
Fig.6 Shear stress versus relative shear slippage of specimens
在未施加压力情况下进行的抗剪试验中,抵抗滑移主要由泥浆的粘接力提供。该工况中试件的剪切应力-位移曲线几乎立刻进入平直段,结合灰缝中土体的状态分析,泥浆所组成的水平灰缝的粘结强度极低,小于0.1 MPa,从工程应用的角度来看是可以忽略不计的,即c≈0。
众所周知,物体的水平运动只有在克服了最大静摩擦力时才会发生位移。当试件的竖向压应力恒定时,最大静摩擦力也保持不变,但承受水平推力的中间石块却持续产生水平向位移,即使在水平推力小于最大静摩擦力的前期阶段。通过对试验现象的观察和荷载-位移曲线的分析可知,前期的水平位移来自两方面:首先是石材-泥浆界面的不断扩大的局部分离,其次是泥浆灰缝自身发生了以水平向为主的变形。两方面因素都是贯穿于整个承载过程,各自导致的石块间相对位移作代数和,即为位移计所采集到的水平位移。完全进入滑移阶段之前,该水平位移的量值就已达到毫米级,表明土体颗粒相互错动与作用有较大的变形潜力。该现象与泥浆体的土体颗粒聚集性质、粘结力较弱以及不均匀分布等因素有着密切的关联。在界面完全裂通、进入纯滑移阶段后,试件承受的水平荷载也没有出现急剧退化的现象,显示出藏式石砌体具备一定的耗能性能。试件达到极限状态、开始进入完全滑移时对应的变形特征值Δcr和压应力有一定的正相关性,表明最大静摩擦力增大时,会延缓完全滑移面的出现,对抗剪是有利的。
2.3 灰缝抗剪强度表达式
有压力的各工况中,试验中的最大剪应力随着压应力的增大而增大,与库伦理论相吻合。各试件的灰缝抗剪极限承载力可通过试验现象较容易地获得,c和μ可通过对数据的统计回归得到,回归分析得到的量值为:c=0.046,μ=0.48。回归所得的c≈0,与试验现象相符,验证了前面所述的猜想,泥浆提供的粘结力可忽略不计。回归曲线见图7,决定系数为0.95。

图7 各试件的极限剪切应力试验结果和回归曲线
Fig.7 Test results of ultimate shear stress and fitting culve of specimens
据此得到了藏式石砌体灰缝抗剪强度平均值的表达式为:
根据式(2)对试件的灰缝抗剪强度进行计算,对比结果见表1。表中σn为压应力,τE、τC分别为灰缝抗剪强度试验值和回归公式计算值。试验值和计算值符合较好,所有试件试验值与计算值的比值统计平均值为1.03,变异系数为0.11,除个别试件外(S0.5-2、S0.5-3、S1.0-3),大部分试件试验值和计算值的误差在 15%之内,且差值均不超过0.1 MPa。
将本文得到的灰缝抗剪强度表达式与其他学者的研究成果进行对比,见表2,藏式石砌体的库伦理论类型灰缝抗剪强度表达式中的摩擦系数μ明显小于采用了水硬性砂浆的石砌体;且由于泥浆的抗压强度较低,粘结能力可以忽略。以上均体现出采用土材粘结材料所带来的特殊性。
表2 其他研究者提出的抗剪公式参数及对比
Table 2 Parameters proposed by others and the contrast

石材 粘结材料 c/MPa μ 参考文献石灰石 灰浆 0.58 0.58 [20]花岗岩 灰浆 0.36 0.63[8]花岗岩 无 0 0.65花岗岩 砂浆 0.068images/BZ_239_292_1481_355_1522.png 灰浆 0.33 0.74 0.84 [15]花岗岩 砂浆 0.100images/BZ_239_755_1700_796_1733.png 0.92 [16]粗料石 砂浆 0.043images/BZ_239_755_1755_796_1787.png 0.89 [17]细料石 砂浆 0.100images/BZ_239_755_1809_796_1841.png 0.86 [18]花岗岩 泥浆 0.046(≈0)0.48 本文images/BZ_239_755_1863_796_1895.png
3 灰缝抗剪强度与砌体抗剪强度的关系研究
以往的研究[8_12]均表明,双剪试验所得到的砌体抗剪强度大于同等条件下的整体墙体试验所获得的结果。灰缝抗剪强度与砌体的整体抗剪强度之间是否有相关性,是本节所要探讨的内容。以下利用2个理论模型进行研究,分别为Mann-Müller的剪摩理论模型[21]和 Calderini等[22]提出的主拉应力理论向剪摩理论转换的模型。
3.1 Mann-Müller的剪摩理论模型
Mann-Müller所提出的模型[21]是目前最为普遍接受的砌体抗剪模型之一,该模型的两个基本假定为: a)块体刚度远大于灰缝;b)忽略竖向灰缝的力学性能。该模型认为砌体在剪-压复合作用下的破坏是由于水平灰缝抵抗滑移的能力不足而造成了两种材料的相互错动。
图8为Mann-Müller模型的计算示意图,以砌体中心区域的块体进行受力分析。如图8所示,在平均压应力σ和剪切应力τ的作用下,块体达到极限平衡状态;而实际情况中,为了满足弯矩平衡条件,同时由于各层砌体错缝排列,块体承受的局部正应力是不同的,分别为σ1和σ2。由静力平衡可得:
式中:
也就是:
根据摩擦原理,块体承受较小的压应力σ2的部分更易发生滑移破坏,其极限平衡方程为:
由式(3)和式(4)可得,用平均压应力表示的极限平衡方程为:
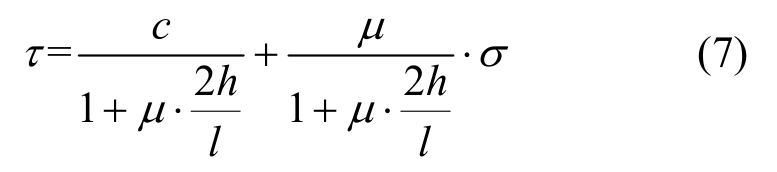
由式(7)可见,Mann-Müller模型不仅建立了平均压应力和局部压应力下滑移表达式之间的联系,也很好地解释了为何砌体在剪-压复合作用下往往发生阶梯型破坏的原因。
显然,在双剪试验中块体所承受的压应力是均匀的,因此将承受平均压应力的块体置于 Mann-Müller模型中考虑,则会出现局部应力减小、灰缝提供的摩擦力减小的情况。引入折减系数 a,则式(7)变为:
图8 Mann-Müller模型示意图
Fig.8 Calculation diagram of Mann-Müller’s model
由此可得折减系数:
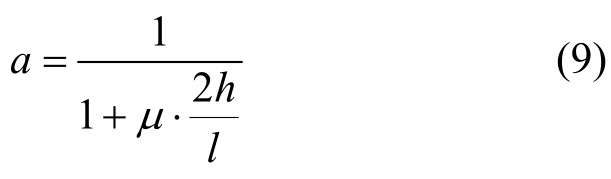
3.2 Calderini的理论模型
Calderini[22]探索了主拉应力破坏理论和剪摩破坏理论的统一,尝试利用对角加荷试验的结果来识别剪摩理论参数,建立了对角加荷试验的加载值与粘结系数、摩擦系数关系的表达式,并通过有限元模拟进行了较好的验证。对角加荷试验的加载值可以与砌体利用主拉应力破坏理论推导的整体性剪-压复合作用抗剪承载力建立联系,因此该理论模型同样可以将灰缝抗剪强度扩展为砌体抗剪强度。
如图9所示,承受对角荷载和侧向均布荷载的正方形墙体,根据主拉应力的破坏理论,当中心点的主拉应力超过容许应力时将出现受拉破坏。根据前人的研究成果[23]和有限元计算[24]可得,中心点处的应力值为:
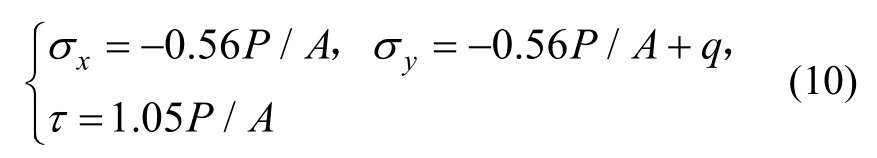
式中,受拉为正,以下均同。σx为水平向正应力,σy为垂向正应力。
在主拉应力理论下考虑整体墙体,为了向剪摩理论进行过渡,需满足两个条件:a)水平灰缝保持受压状态;b)竖向灰缝可以传递正应力,σx不为零。为了满足条件a),需有:

式中,fdt等于第一主应力,其值为:
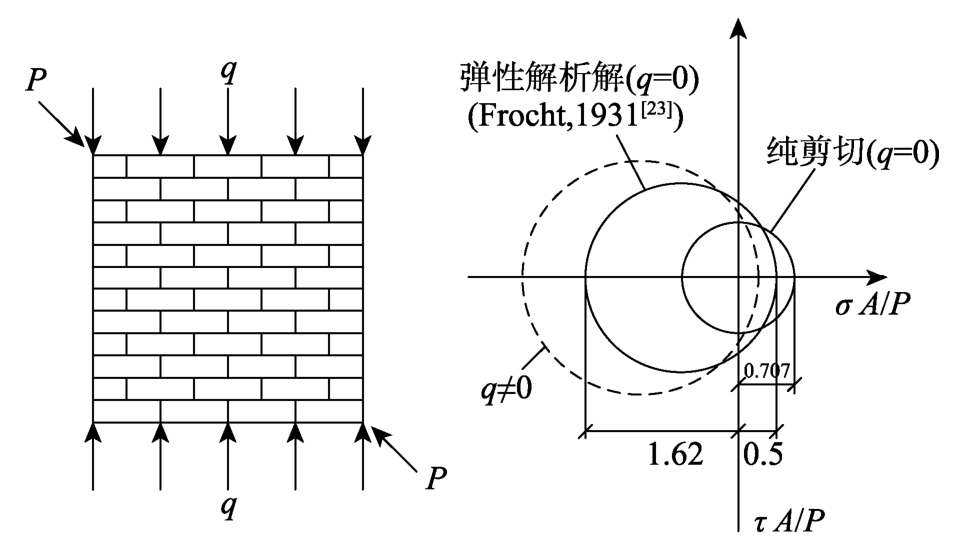
图9 对角加荷试验和中心点的莫尔圆
Fig.9 Diagonal compression test loading scheme(left)and stress state at the center of the panel in Mohr’s representation(right)
然后参见图10,在考虑σx不为零的情况下,采用剪摩理论考虑中心块体的极限平衡方程为:

式(13),![]() 代表σx使竖向灰缝闭合的极限状态。
代表σx使竖向灰缝闭合的极限状态。
将式(10)代入式(13)可得:
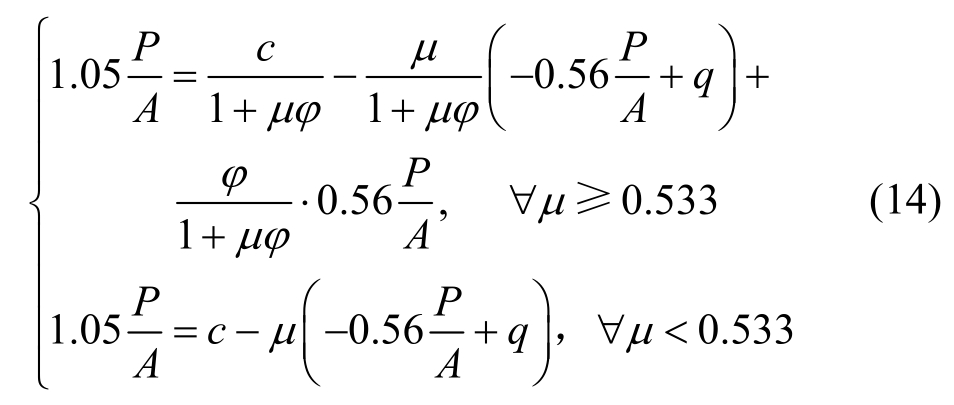
进一步变形后可得:

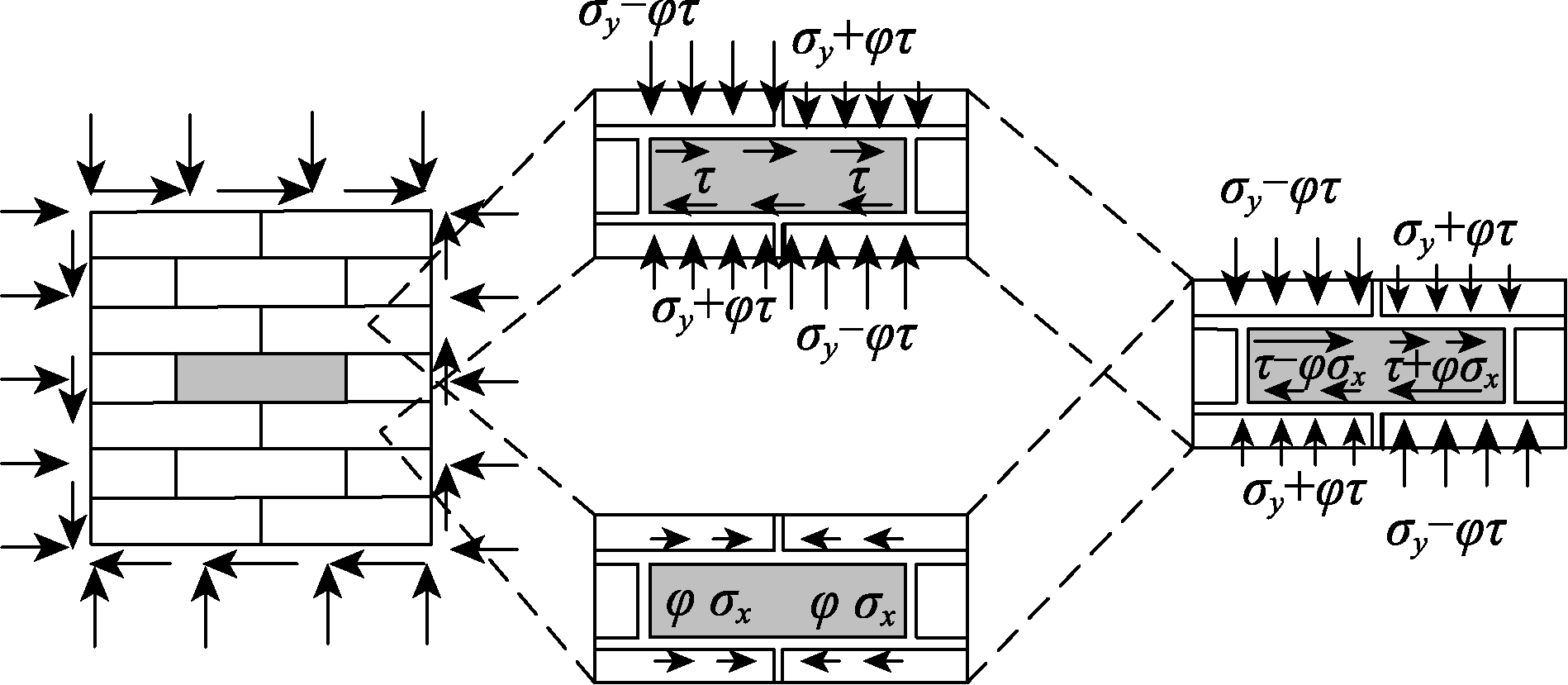
图10 剪-压复合作用下的块体应力状态
Fig.10 Stress state on a block due to shear/compression loads
3.3 试验数据验证
华侨大学、东南大学和葡萄牙Minho大学等研究团队在研究各种石砌体过程中,进行了不同类型石砌体小试件的双剪(单剪)试验,以及同等条件的足尺墙体拟静力试验,各种研究中均发现灰缝抗剪强度表达式中的摩擦系数明显小于足尺墙体抗剪强度剪摩形式表达式中的摩擦系数。利用上述研究者已发表文献的试验数据,对式(9)和式(15)进行验证,见表3。
从表3可见,理论公式计算得到的折减系数普遍低于试验结果;粗料墙体的偏差较大,说明石材的粗糙表面对于提高抗剪强度有一定的贡献,而细料墙体的结果则较为接近,说明理论计算方法有一定的可靠性,且有一定的安全富裕度。
表3 利用其他研究者的试验数据进行计算的结果
Table 3 Calculated results by others’ data through tests

墙体h/mm l/mm μ类型式(9)计算a值式(15)计算a值试验所得a值参考文献粗料石墙 200 570 0.84 0.63 0.62 0.82 [9]粗料石墙 250 500 0.89 0.53 0.54 0.86 [11]细料石墙 250 500 0.86 0.54 0.55 0.69 [12]细料石墙 150 200 0.65 0.51 057 0.59 [8]
3.4 藏式石砌体抗剪强度表达式的估计
根据前面所述的理论,式(9)是将灰缝抗剪强度延伸为以剪摩理论表达的砌体抗剪强度,式(15)是将灰缝抗剪强度延伸为以主拉应力理论表达的砌体抗剪强度。
针对本次试验,式(9)和式(15)计算得到的折减系数a分别为0.74和0.64。出于保守考虑取为0.64。对藏式石砌体的剪-压复合作用下抗剪强度进行预估,如前所述,本次藏式石砌体灰缝抗剪试验所获得强度表达式中可以忽略粘结系数,因此,以本次试验所采用的材料砌筑的藏式石砌体,其剪-压复合作用下抗剪强度平均值的表达式为:
需要再次说明的是,本文研究中的试验对象是一种典型的界面条件藏式石砌体,由于实际情况中的藏式石砌体界面粗糙程度离散性较大,在对特定建筑单体中的墙体构件进行评估时,应以同等条件材料的双剪试验结果为准,本文研究的主要意义在于提供一种研究和评估的思路。
4 结论
本文对4组共13个不同压力作用下的泥浆砌筑石墙试件进行双剪试验,分析藏式石砌体沿通缝抗剪强度和破坏机理,通过对试验数据的统计回归提出典型藏式石砌体灰缝的抗剪强度计算公式。通过 2种理论模型,分析了砌体灰缝抗剪强度与剪-压复合作用下抗剪强度表达式之间的关系,利用其他研究者的试验数据进行了验证。主要得到了如下结论:
(1)藏式石砌体水平灰缝抗剪的破坏机理是泥浆层自身变形与界面分离同步进行的延性破坏过程,最终的破坏形态是泥浆层与石材分离,形成完全的滑移界面。
(2)藏式石砌体方石层间夹有片石的灰缝可视为摩擦系数与纯泥浆层灰缝相同的水平灰缝。
(3)藏式石砌体灰缝抗剪强度表达式符合库伦破坏理论,可用τ=c+μσn 表示。本文建议的参数取值为c=0, μ=0.48。泥浆灰缝的粘结强度和摩擦系数均明显低于水硬性砂浆材料。
(4)砌体在剪-压复合作用下的抗剪强度与灰缝抗剪强度有一定的关联性,可采用乘以一个折减系数的方式进行估计,该折减系数和界面摩擦系数以及块材的尺寸有关。本文提供了两种计算折减系数的方法。对于本文双剪试验的对象,与之类似的藏式石砌体在剪-压复合作用下抗剪强度平均值的表达式为τM=0.31σn。
[1]蔡永建, 郑水明, 吴建超.2015-04-25尼泊尔M8.1地震震害特征[J].大地测量与地球动力学, 2015, 35(4):557-560.Cai Yongjian, Zheng Shuiming, Wu Jianchao.Seismic disaster characteristics of building of nepal M8.1 Earthquake on April 25, 2015 [J].Journal of Geodesy and Geodynamics, 2015, 35(4): 557-560.(in Chinese)
[2]巴桑次仁, 曹忠权, 邓桂英, 等.西藏当雄6.6级地震与尼木 6.5级地震震害特征分析[J].震灾防御技术,2009, 4(2): 233-239.Basang Ciren, Cao Zhongquan, Deng Guiying, et al.Damage analysis of dangxiong Ms6.6 and nimu Ms6.5 earthquakes in Tibet [J].Technology for Earthquake Disaster Prevention, 2009, 4(2): 233-239.(in Chinese)
[3]ASTM E 519-02, Standard test method for diagonal tension(shear)in masonry assemblages [S].West Conshohocken, PA: ASTM International, 2002.
[4]RILEM TC 76, Diagonal tensile strength tests of small wall specimens [S].Bagneux: International Union of Laboratories and Experts in Construction Materials,Systems and Structures, 1994.
[5]Milosevic J, Gago A S, Lopes M, et al.Experimental assessment of shear strength parameters on rubble stone masonry specimens [J].Construction & Building Materials, 2013, 47(10): 1372-1380.
[6]Pinho F F S, Lúcio V J G, Baião M F C.Experimental analysis of rubble stone masonry walls strengthened by transverse confinement under compression and compression-shear loadings [J].International Journal of Architectural Heritage, 2018, 12(1): 91-113.
[7]Corradi M, Tedeschi C, Binda L, et al.Experimental evaluation of shear and compression strength of masonry wall before and after reinforcement: deep repointing [J].Construction and Building Materials, 2008, 22(4): 463-472.
[8]Vasconcelos G.Experimental investigations on the mechanics of stone masonry: characterization of granites and behavior of ancient masonry shear walls [D].Braga,Portugal: University of Minho, 2005.
[9]郭子雄, 柴振岭, 胡奕东, 等.条石砌筑石墙抗震性能试验研究[J].建筑结构学报, 2011, 32(3): 57-63.Guo Zixiong, Chai Zhenling, Hu Yidong, et al.Experimental study on seismic behavior of stone masonry wall [J].Journal of Building Structures, 2011, 32(3): 57-63.(in Chinese)
[10]郭子雄, 柴振岭, 胡奕东, 等.机器切割料石砌筑石墙灰缝构造及抗震性能试验研究[J].建筑结构学报,2011, 32(3): 64-68.Guo Zixiong, Chai Zhenling, Hu Yidong, et al.Experimental study on seismic behavior and mortar joint detail of machine sawing stone masonry wall [J].Journal of Building Structures, 2011, 32(3): 64-68.(in Chinese)
[11]徐明, 赵娜, 时丹, 等.粗料石墙体抗震性能试验研究[J].土木工程学报, 2014(9): 29-37.Xu Ming, Zhao Na, Shi Dan, et al.Experimental study on seismic behavior of block stone masonry wall [J].China Civil Engineering Journal, 2014(9): 29-37.(in Chinese)
[12]徐明, 时丹, 赵娜, 等.足尺细料石墙体抗震性能试验研究[J].建筑结构学报, 2014, 35(6): 145-152.Xu Ming, Shi Dan, Zhao Na, et al.Experimental research on seismic behavior of smooth block stone masonry walls[J].Journal of Building Structures, 2014, 35(6): 145-152.(in Chinese)
[13]骆万康, 朱希诚, 廖春盛.砌体抗剪强度研究的回顾与新的计算方法[J].土木建筑与环境工程, 1995, 17(4):41-49.Luo Wankang, Zhu Xicheng, Liao Chunsheng.A review on the study on shear strength of masonry and a new calculating method [J].Journal of Civil and Environmental Engineering, 1995, 17(4): 41-49.(in Chinese)
[14]骆万康, 李锡军.砖砌体剪压复合受力动、静力特性与抗剪强度公式[J].土木建筑与环境工程, 2000, 22(4):13-19.Luo Wankang, Li Xijun.A study on the response of brick masonry structure under dynamic and static shear-compression loading and suggested shearing equation [J].Journal of Civil and Environmental Engineering, 2000, 22(4): 13-19.
[15]柴振岭, 郭子雄, 胡奕东, 等.干砌甩浆砌石墙通缝抗剪强度试验研究[J].建筑结构学报, 2010, 31(增刊 2):340-345.Chai Zhenling, Guo Zixiong, Hu Yidong, et al.Experimental study on shear strength of mortar joint of dry-laid stone masonry walls [J].Journal of Building Structures, 2010, 31(Suppl 2): 340-345.(in Chinese)
[16]郭子雄, 柴振岭, 刘阳, 等.机器切割条石砌筑石墙灰缝抗剪性能试验研究[J].工程力学, 2012, 29(6): 92-97.Guo Zixiong, Chai Zhenling, Liu Yang, et al.Experimental study on the mortar joint shear behavior of machine-cutting stone walls [J].Engineering Mechanics,2012, 29(6): 92-97.(in Chinese)
[17]时丹.东南地区细料石墙体抗震性能试验研究[D].南京: 东南大学, 2013: 13-28.Shi Dan.Experimental research on seismic behavior of smooth block stone masonry wall in south-east of China[D].Nanjing: Southeast University, 2013: 13-28.(in Chinese)
[18]赵娜.东南地区粗料石墙体抗震性能试验研究[D].南京: 东南大学, 2013: 17-24.Zhao Na.Experimental research on seismic behavior of rough block stone masonry wall in the southeast of China[D].Nanjing: Southeast University, 2013: 17-24.(in Chinese)
[19]GB/T 50129-2011, 砌体基本力学性能试验方法[S].北京: 中国建筑工业出版社, 2011.GB/T 50129-2011, Standard of experiment method for mechanical properties of masonry [S].Beijing: China Architecture & Building Press, 2011.(in Chinese)
[20]Binda L, Tiraboschi C, Abbaneo S.Experimental research to characterize masonry materials [J].Masonry International, 1997, 10(3): 92-101.
[21]Mann W, Muller H.Failure of shear-stressed masonry—an enlarged theory, tests and application to shear-walls [C]//Proceedings of the International Symposium on Load bearing Brickwork, London, 1980: 1-13.
[22]Calderini C, Cattari S, Lagomarsino S.The use of the diagonal compression test to identify the shear mechanical parameters of masonry [J].Construction and Building Materials, 2010, 24(5): 677-685.
[23]Frocht M.Recent advances in photoelasticity [J].ASME Transactions, 1931, 55: 135-153.
[24]Brignola A, Frumento S, Lagomarsino S, et al.Identification of shear parameters of masonry panels through the in-situ diagonal compression test [J].International Journal of Architectural Heritage, 2008,3(1): 52-73.