颤振导数是表征桥梁断面气动特性的重要参数之一，对于一般的桥梁断面，目前多通过风洞试验[1]或流体动力学模拟[2_3]来得到颤振导数。在风洞试验中，识别桥梁节段模型颤振导数的主要方法有均匀流风场的自由振动法[4_7]和强迫振动法[8_9]以及紊流风场的随机激励法[10_11]；其中均匀流风场自由振动法识别颤振导数是其中较为简便的方法。1998年，张若雪[12]提出了基于竖弯信号和扭转信号总体误差最小的总体最小二乘法(ULS)，用于识别颤振导数。为了解决竖弯信号和扭转信号幅值差异所造成的识别误差问题，丁泉顺[13]基于 ULS法在整体误差函数中引入了一个平衡竖弯和扭转信号权重的加权因子，提出了修正最小二乘法(MLS)。2017年，李加武等[14]通过加权矩阵对加权因子进行细化，提出了加权矩阵最小二乘法(WLS)，对高噪声处信号取较小权值，低噪声处信号取较大权值。在自由振动试验中，通常在同一风速下对节段模型进行多次激振，采集多组同风速下的自由振动衰减信号，以提高识别精度[15]。为了解决同一风速下多次激振的自由振动信号识别误差问题，李永乐等[16]提出了加权整体最小二乘法(WELS)，对相同风速下N次采样的各时程信号进行加权，避免了识别过程中弱信号被强信号所“淹没”。除了基于最小二乘原理的识别方法，部分学者还提出了基于特征系统实现理论的识别算法[17_18]。
使用最小二乘原理对桥梁断面的颤振导数进行识别时，所构造的目标函数是含有多个待求参数的非线性函数，在求解该优化问题时，可以使用梯度下降算法[19]或者随机搜索方法[20]。使用传统迭代算法求解时需要使用迭代初值，且初值对识别结果具有一定的影响，欠佳的初值可能只得到一个局部最优解。为解决这一难题，可采用生物启发类的全局优化算法，人工蜂群算法就是其中性能较为优异的一种。人工蜂群算法最先由土耳其学者Karaboga[21]于 2005年提出，是一种模拟蜂群群体寻找优良蜜源的智能仿生计算方法。从算法寻优机理来看，该方法是一种进行广义邻域搜索的智能算法，通过采蜜蜂、观察蜂和侦察蜂三种蜂的转换，不仅能有效地进行局部邻域搜索，还具有全局寻优能力。人工蜂群算法对待优化的目标函数无特殊要求，也不需要特定的初值，算法本身具有全局收敛能力，因此初值可设为特定值或者随机值，参数可搜索的范围较广，算法适应性比较强。本文基于最小二乘原理，将竖弯和扭转信号的整体残差平方和作为目标函数，使用人工蜂群算法对中间参数进行识别，进而识别出桥梁断面的颤振导数。
1 节段模型自由衰减振动的数学模型
根据Scanlan桥梁颤振导数理论，桥梁断面的自激升力和自激力矩的表达式为[22]：
式中：Lse、Mse分别为自激升力和自激力矩；ρ为空气密度；U为平均风速； K=Bω/U为折算频率；B为模型宽度；h、α分别为模型的竖向线位移和扭转角位移；
为颤振导数。
在气动自激力的作用下，弯扭两自由度桥梁节段模型运动微分方程为：
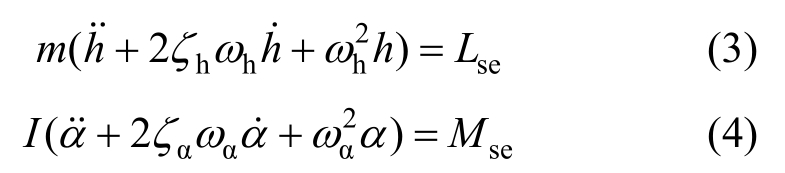
式中：m、I分别为单位长度模型质量和质量惯性矩；ζh、ζα分别为竖弯和扭转阻尼比；
、
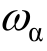分别为竖弯和扭转圆频率。
将式(1)、式(2)分别代入式(3)、式(4)，经整理后可得：
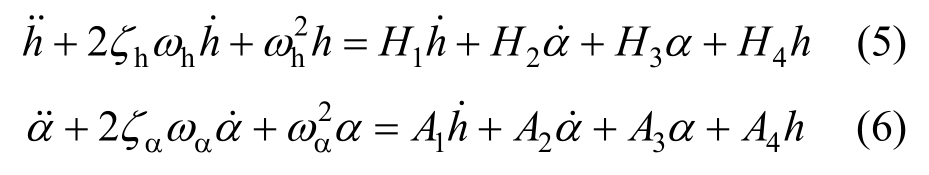
式中：
将式(5)和式(6)写成矩阵形式：
式中：
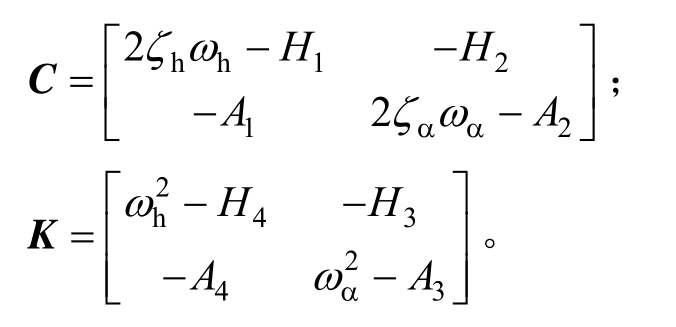
令状态向量
则系统的状态方程为：
式中，系数矩阵
E为单位矩阵。
求解方程式(8)可得到自由振动响应。
矩阵A具有复共轭特征值
以及复共轭特征向量
令：
则自由振动竖弯h和扭转α信号时程响应估计值为：
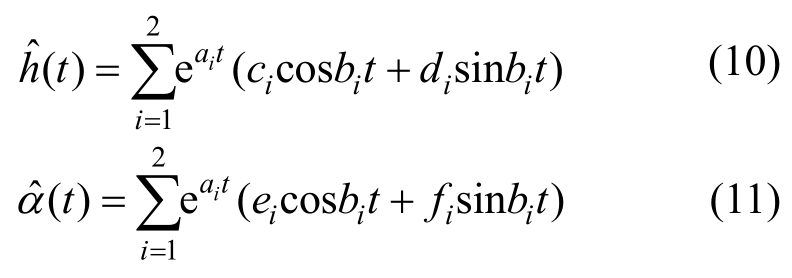
式中，ci、di、ei、 fi(i=1,2)是由初始条件决定的常数。
式(10)和式(11)中的 ai、 bi、 ci、 di、 ei、 fi(i=1, 2)为 12个待求中间参数，其中ci、di、ei、fi(i=1, 2)为8个线性参数，ai、bi(i=1, 2)为4个非线性参数。通过人工蜂群算法求出这 12个参数，进而识别出颤振导数。
设竖弯信号h和扭转信号α的时程长度为m，h和α时程实测值和估计值之间误差分别为：
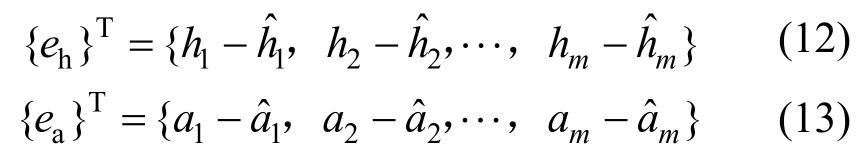
相应地，竖弯信号和扭转信号实际值和估计值之间误差的权值分别为：
竖弯信号的权值可取扭转信号的最大值，扭转信号的权值可取竖弯信号的最大值[13]。
竖弯信号和扭转信号误差平方和函数分别为：
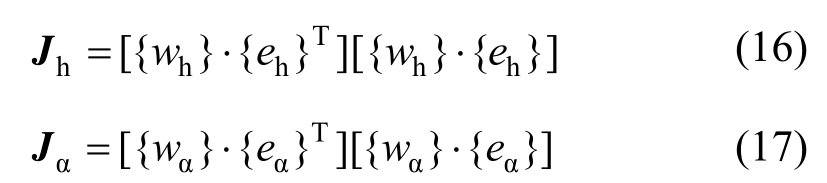
总体误差平方和函数为：
下面讨论如何求解12个待求中间参数。
由 λi＝ai+ibi ，记：
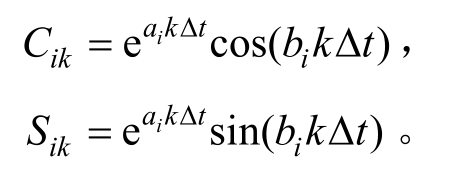
式中，k=1, 2, …，m，m为振动采样记录总点数。
则总体误差平方和函数为：
式中，
令
可得以下方程：
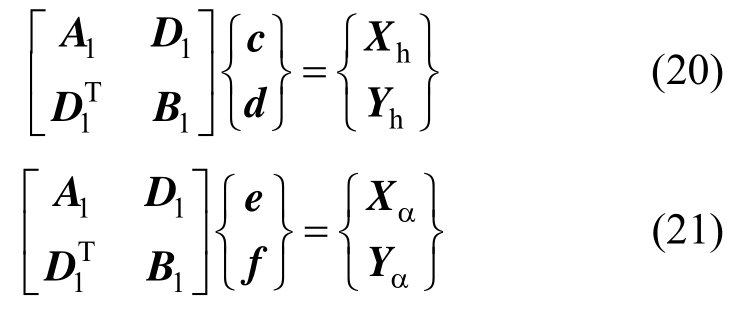
式中：
通过交叉迭代的方法可以求解 12个中间参数ai、bi、ci、di、ei、 fi(i=1, 2)。该问题本质上属于优化问题，本文采用人工蜂群算法得到使总体误差目标函数J最小的最优解。
将式(8)中的状态向量Y写成Y=
的形式，将状态向量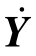
写成
的形式。矩阵P和Q由12个中间参数组成，且
系统矩阵A=QP-1，从系统矩阵中可确定颤振导数。
2 人工蜂群算法基本原理及求解步骤
人工蜂群算法是受自然界中蜜蜂采蜜行为启发而产生的一种生物启发式算法。人工蜂群算法的寻优过程参照了蜜蜂寻找最优蜜源的机理。负责寻找新蜜源的侦察蜂外出随机寻找蜜源，一旦寻找到蜜源，侦察蜂就转变为采蜜蜂。采蜜蜂记录所采的蜜源信息(蜜源好坏和蜜源位置)并与观察蜂分享。观察蜂接收采蜜蜂分享的蜜源信息并依据蜜源的好坏对蜜源进行选择，较好的蜜源吸引到观察蜂的概率较大，被蜜源吸引的观察蜂转化为采蜜蜂。采蜜蜂分享蜜源信息后，根据记忆，在原蜜源附近选择一个新的蜜源，若在附近找不到更好的蜜源，采蜜蜂则放弃该蜜源，成为侦察蜂，随机寻找新的蜜源[23]。
将人工蜂群算法应用到颤振导数识别上，蜜源对应于由参数确定的桥梁振动数学模型，蜜源的好坏与数学模型对桥梁断面响应预测的精确程度相对应，本文由最小二乘总体误差平方和函数来度量。误差函数值越小，数学模型对真实系统的预测越精确，相对应蜜源越好，最好的蜜源则对应已有信息下数学模型对真实系统的最佳估计。
基于自由振动响应信号将人工蜂群算法应用于桥梁断面颤振导数识别的基本步骤如下(见图1)。
1)蜜蜂种群的初始化：蜜蜂的总数为 N(其中采蜜蜂为Ne，观察蜂为Nu)，蜜蜂个体向量维度为4(a1, b1, a2, b2)，S为个体搜索的待定参数空间。
是Ne个个体，则 X=(X1, X2, …,
代表一个采蜜蜂种群。用X(0)表示初代采蜜蜂种群，X(n)表示第n代采蜜蜂种群。
2)n=0时刻，在搜索空间内随机生成Ns个可行解
可行解Xi为：
式中，j取值于{1，2，3，4}，为 4维解向量的某个分量。
3)计算[C]，[S]，A1，B1，D1，Xh，Yh，Xα ，Yα。计算ci、di、ei、 fi(i=1, 2)。计算总体误差平方和函数J，根据蜜源的收益度
计算各向量的“收益度”函数值，将排名靠前一半的蜜蜂作为初代采蜜蜂X(0)。
4)对于第n代的采蜜蜂X(n)，在搜索空间内从其位置向附近邻域搜索新位置，所采用的搜索公式为：
式中，j取自于{1，2，3，4}，k取自于
且k不等于i，k和i随机生成。
图1 人工蜂群算法流程
Fig.1 The flowchart of the ABC algorithm
5)在采蜜蜂搜索到的新向量 new-Xi和原位置向量Xi中，选取“收益度”较大的，保留给下一代，这保证了种群能够保留精英个体，使得进化方向不会后退。
6)观察蜂依据采蜜蜂“收益度”的大小选择其所要跟随的采蜜蜂，并在邻域内搜索。
7)同步骤 4)和步骤 5)，并记下种群更新后的最优“收益度”值，以及相应的参数。
8)在某只采蜜蜂的周围，若搜索次数Bas达到一定的阈值 Limit仍然没有搜索到更优的位置时，则初始化该采蜜蜂，随机搜索新的位置。
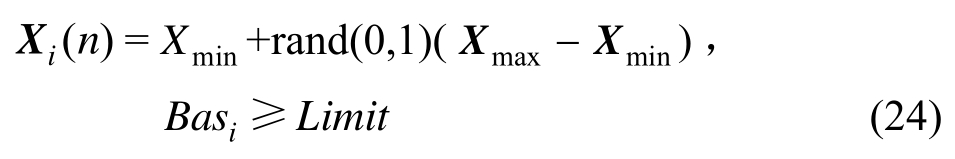
9)若满足停止准则，则停止计算并输出最优适应度值对应的参数，否则转向步骤3)。
10)将人工蜂群算法识别出的 12个参数代入系统矩阵，计算出颤振导数。
3 理想平板模型仿真
3.1 仿真模型
为验证人工蜂群算法识别桥梁断面颤振导数的可行性，设计理想平板仿真模型，节段模型气动自激力采用Theodorsen理论解[24]。模型参数为：平板宽0.45 m，单位长度质量11.94 kg，单位长度质量惯性矩0.532 kg·m2，竖弯基频1.488 Hz，扭转基频2.966 Hz，竖弯阻尼比ζh=0.007，扭转阻尼比ζα=0.002。竖弯信号的权值取扭转信号的最大值，扭转信号的权值取竖弯信号的最大值。将计算的理论参数代入式(7)中进行求解，得到仿真模型在各个风速下自由衰减时程。
3.2 颤振导数识别
3.2.1 添加白噪声的识别结果
仿真计算风速增量为 2 m/s，为考察人工蜂群算法在混有测量噪声时的识别精度，对无噪声，添加 2%白噪声、5%白噪声、10%白噪声水平的情况进行仿真，由于无噪声的结果和理论解完全吻合，这里不再单独列出。各个工况颤振导数识别结果如图2所示。
从图2可以看出，在2%小噪声情况下，各个风速下用人工蜂群算法识别出的颤振导数和Theodorsen理论解非常吻合，识别值几乎完全等于理论值；在 5%中等噪声情况下，识别值与理论值有较少的偏差，其中
识别值与理论值在低风速区间有一定的偏差，
的识别值和理论值在高风速区间有一定的偏离；在10%大噪声情况下，除颤振导数
在部分风速下偏差较大外，其余颤振导数的识别值与理论值相差较小，且所有识别值与理论值趋势性完全相同。在中高等白噪声水平下，颤振导数中有部分识别结果与理论值出现了一些偏差，其余颤振导数识别值与理论值偏差很小。颤振导数仿真识别的结果表明，人工蜂群算法具有较好的抵抗白噪声能力。
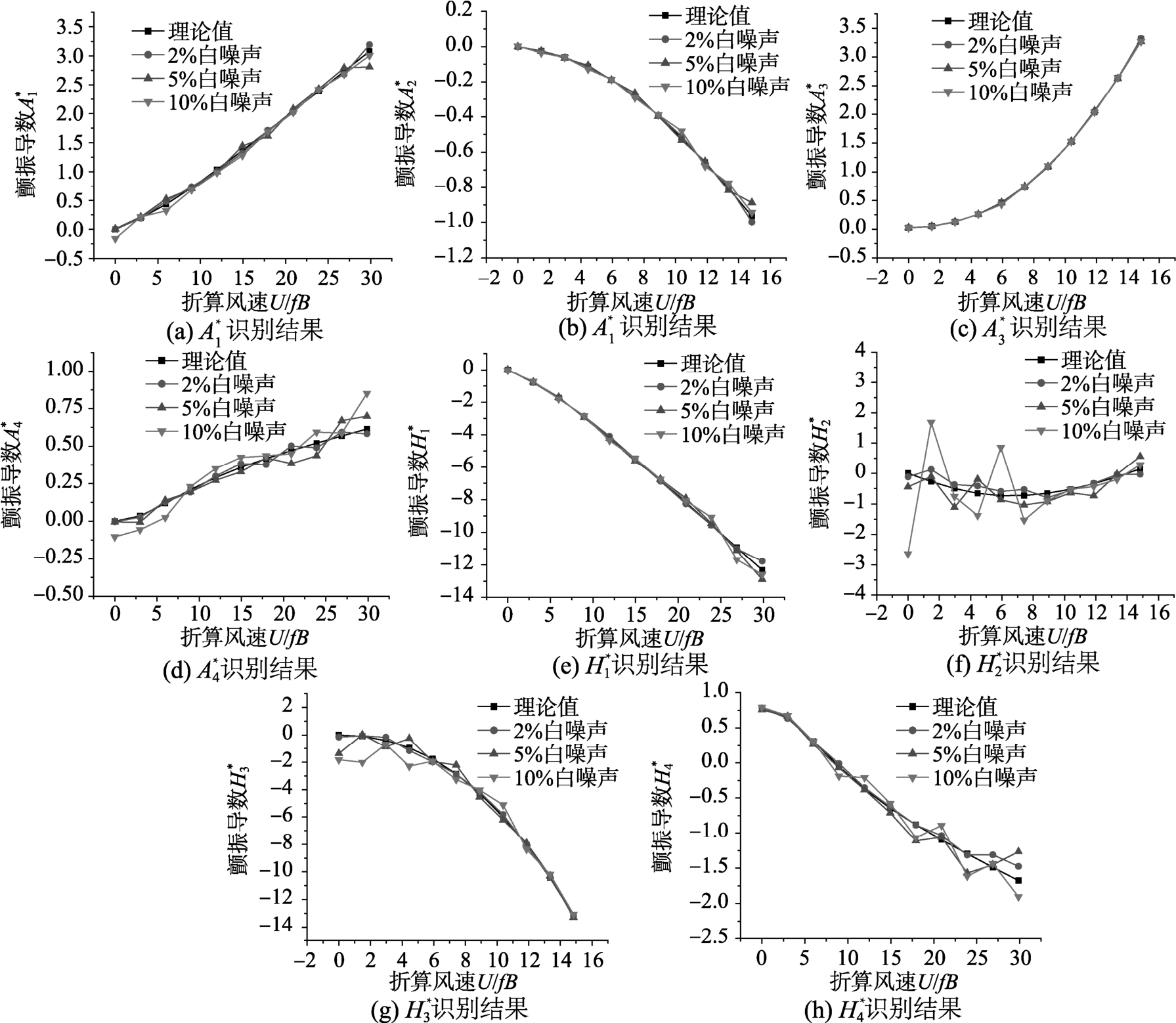
图2 不同白噪声水平下识别的颤振导数和Theodorsen理论解的对比
Fig.2 Comparison on the flutter derivatives for Theodorsen’s theoretical solutions and identified results with different white noise levels
在计算效率方面，利用同一计算平台(酷睿i5-6500CPU，内存 12G，MATLABR2017a)，分别采用ABC法和MLS法对某一风速下的颤振导数进行识别，识别结果收敛至同一精度，重复 20次计算，ABC算法平均用时为0.074 s，MLS法平均用时为0.017 s，采用ABC算法计算时无须提供初值，但会增加一定的计算时间，由于两种方法的计算时间均较短，ABC法计算时间的增加几乎可以忽略不计。
3.2.2 添加有色噪声的识别结果
为多方面验证人工蜂群算法的抗噪能力，对添加 2%有色噪声、5%有色噪声、10%有色噪声水平的情况进行仿真，5%有色噪声信号的功率谱如图3所示。识别结果如图4所示。
从图4中可以看出，在添加2%有色噪声的情况下，各颤振导数的识别值与Theodorsen理论解十分吻合，除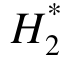
的个别值出现一定的偏离外，其余识别值几乎完全等于理论值；在添加 5%有色噪声的情况下，
、
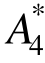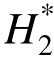和
有一定的偏离，其余识别值仍能与理论值吻合较好；在添加10%有色噪声的情况下，A4*和 H2*与理论解偏离较大，其余识别值只在高风速下有稍大的偏离，且所有识别值与理论值都具有相同的趋势性。识别结果表明，人工蜂群算法也具有较好的抗有色噪声能力。
图3 添加有色噪声的功率谱
Fig.3 Power spectrum of the non-white noise
图4 不同有色噪声水平下识别的颤振导数和Theodorsen理论解的对比
Fig.4 Comparison on the flutter derivatives for Theodorsen’s theoretical solutions and identified results with different non-white noise levels
4 某大桥主梁断面颤振导数
某大桥节段模型测振试验在湖南大学风工程试验研究中心 HD－2号风洞第一试验段边界层风洞中进行。模型设计参数为：缩尺比 1∶40；风速比1∶8；模型宽度B=0.28 m；质量m=14.327 kg/m；惯性矩I=0.6543 kg·m2/m。实桥主梁断面和节段模型见图5和图6。
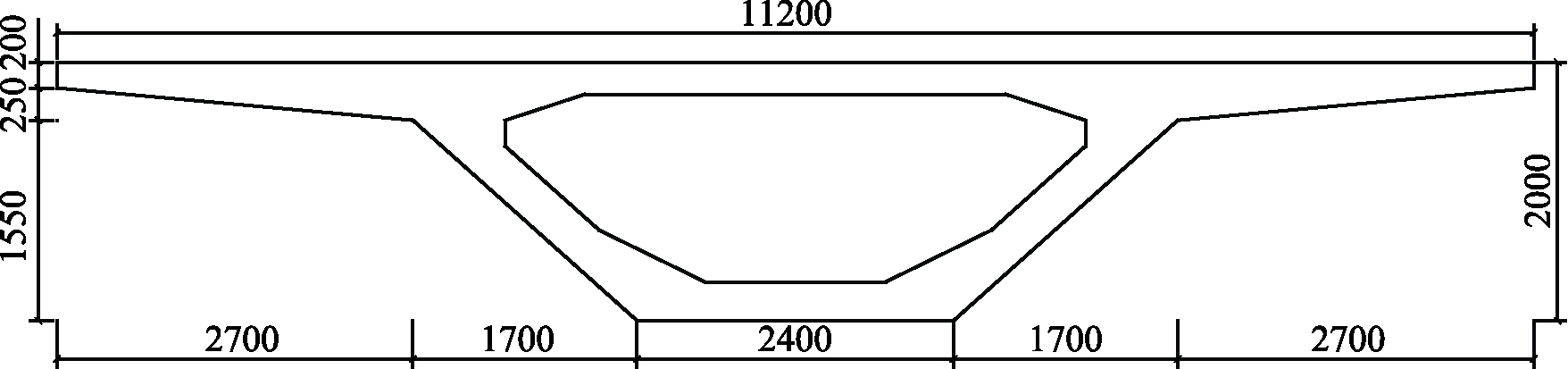
图5 主梁标准断面/mm
Fig.5 Typical cross section of main girder
风洞试验进行了0°风攻角下的测振试验，分别使用人工蜂群算法和 MLS算法对颤振导数进行识别，竖弯信号的权值取扭转信号的最大值，扭转信号的权值取竖弯信号的最大值，识别结果如图7所示。基于识别出的颤振导数，采用 M-S搜索法[22]计算颤振临界风速，计算值为11.8 m/s，节段模型风洞试验测得的颤振临界风速为12 m/s，两者相差1.56%，从而验证了识别结果的准确性。从识别结果中可以看出：
图6 风洞中的节段模型
Fig.6 Sectional model in wind tunnel
图7 ABC法和MLS法识别结果对比
Fig.7 Comparison on the identified results for ABC method and MLS method
(1)人工蜂群算法与已有 MLS法的识别结果几乎完全一致，且由识别的颤振导数计算出的颤振临界风速与风洞试验结果吻合较好，说明了人工蜂群算法在识别桥梁断面颤振导数上的有效性。
(2)相比MLS迭代法，人工蜂群算法对初值没有要求，识别精度与需要设定初值的迭代算法一致，这体现了群体智能算法在全局寻优方面的优势。
(3)由于
和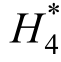
对误差比较敏感，使得识别结果相对离散。
5 结论
本文首先介绍了桥梁断面弯扭两自由度自由振动的数学模型，并建立了基于最小二乘原理的目标函数，进而将人工蜂群算法应用到颤振导数的识别，最后采用理想平板数值仿真和节段模型风洞试验验证了该方法的有效性。本文的数值仿真和试验结论如下：
(1)应用人工蜂群算法对仿真理想平板进行识别，在无噪声时，得到的颤振导数与Theodorsen理论解完全一致，表明在高风速下人工蜂群算法仍能精确地识别出颤振导数，可以克服风速较高时，信号衰减快，有效竖弯信号短对颤振导数识别带来的困难。
(2)在2%小噪声情况下，理想平板的识别结果与理论解几乎完全吻合；在 5%中等噪声情况下，识别结果有微小偏差；在10%大噪声情况下识别结果与理论值的趋势仍完全相同。这表明，人工蜂群算法具有较好的抗噪能力。
(3)对某大桥节段模型进行了风洞试验，并分别采用人工蜂群算法和 MLS迭代法进行了颤振导数的识别，结果表明，人工蜂群算法与 MLS迭代法具有相同的精度，且不需要提供初值，体现了群体智能算法的优势。
综上所述，识别桥梁断面颤振导数的人工蜂群算法具有稳定可靠、抗噪声能力强、识别精度高的特点，可以作为桥梁断面颤振导数识别的有效新工具。
[1]徐昕宇, 李永乐, 廖海黎, 等.双层桥面桁架梁三塔悬索桥颤振性能优化风洞试验[J].工程力学, 2017, 34(5):142―147.Xu Xinyu, Li Yongle, Liao Haili, et al.Flutter optimization of a double-deck truss-stiffened girder three-tower suspension bridge by wind tunnel tests [J].Engineering Mechanics, 2017, 34(5): 142―147.(in Chinese)
[2]祝志文, 顾明, 陈政清.桥梁断面颤振导数的 CFD全带宽识别法[J].工程力学, 2007, 24(9): 80―87.Zhu Zhiwen, Gu Ming, Chen Zhengqing.Extraction of flutter derivatives of bridge deck among full bandwidth of reduced wind speeds [J].Engineering Mechanics,2007, 24(9): 80―87.(in Chinese)
[3]Xu F Y, Zhang Z B.Free vibration numerical simulation technique for extracting flutter derivatives of bridge decks [J].Journal of Wind Engineering and Industrial Aerodynamics, 2017, 170: 226―237.
[4]Andersen M S, Ole Johansson J, Brandt A.Flutter derivatives from free decay tests of a rectangular B/D=10 section estimated by optimized system identification methods [J].Engineering Structure, 2018, 156: 284―293.
[5]Ding Q S, Dong S H, Zhou Z Y.Identification of aerodynamic derivatives of bridge decks at high testing wind speed [J].Canadian Journal of Civil Engineering,2018, 45(11): 1004―1014.
[6]Ding Q S, Zhou Z Y, Zhu L D, et al.Identification of flutter derivatives of bridge decks with free vibration technique [J].Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(12): 911―918.
[7]Bartoli G, Contri S, Mannini C, et al.Toward an improvement in the identification of bridge deck flutter derivatives [J].Journal of Engineering Mechanics, 2009,135(8): 771―785.
[8]陈政清, 胡建华.桥梁颤振导数识别的时域法与频域法对比研究[J].工程力学, 2005, 22(6): 127―133.Chen Zhengqing, Hu Jianhua.A comparative study between time-domain method and frequencydomain method for identification of bridge flutter derivatives [J].Engineering Mechanics, 2005, 22(6):127―133.(in Chinese)
[9]王骑, 李郁林, 李志国, 等.不同风攻角下薄平板的颤振导数[J].工程力学, 2018, 35(10): 13―19.Wang Qi, Li Yulin, Li Zhiguo, et al.Flutter derivatives of a thin plate model under different attack angles [J].Engineering Mechanics, 2018, 35(10): 13―19.(in Chinese)
[10]秦仙蓉, 顾明.紊流风场中桥梁气动导数识别的随机方法 [J].土木工程学报, 2005, 38(4): 73―77.Qin Xianrong, Gu Ming.Stochastic system method for identification of aerodynamic derivatives of bridge decks in turbulent flow [J].China Civil Engineering Journal,2005, 38(4):73―77.(in Chinese)
[11]Boonyapinyo V, Janesupasaeree T.Data-driven stochastic subspace identification of flutter derivatives of bridge decks [J].Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(12): 784―799.
[12]张若雪.桥梁结构气动参数识别的理论和试验研究[D].上海: 同济大学, 1998: 1―112.Zhang Ruoxue.Theoretical and experiment study on identification of aerodynamic derivatives of bridge decks[D].Shanghai: Tongji University, 1998: 1―112.(in Chinese)
[13]丁泉顺.大跨度桥梁耦合颤抖振响应的精细化分析[D].上海: 同济大学, 2001: 10―90.Ding Quanshun.Refinement of coupled flutter and buffeting analysis for long-span bridges [D].Shanghai: Tongji University, 2001: 10―90.(in Chinese)
[14]李加武, 张斐, 吴拓.桥梁断面颤振导数识别的加权最小二乘法[J].振动工程学报, 2017, 30(6): 993―1000.Li Jiawu, Zhang Fei, Wu Tuo.Weighted least square method for identification of flutter derivatives of bridge section [J].Journal of vibration engineering, 2017, 30(6):993―1000.(in Chinese)
[15]Gu M, Zhang R X, Xiang H F.Identification of flutter derivatives of bridge decks [J].Journal of Wind Engineering and Industrial Aerodynamics, 2000, 84(2):151―162.
[16]李永乐, 廖海黎, 强士中.桥梁断面颤振导数识别的加权整体最小二乘法[J].土木工程学报, 2004, 37(3):80―84.Li Yongle, Liao Haili, Qiang Shizhong.Identification for flutter derivatives of bridge deck cross section by weighting ensemble least-square method [J].China Civil Engineering Journal, 2004, 37(3): 80―84.(in Chinese)
[17]祝志文, 顾明.基于自由振动响应识别颤振导数的特征系统实现算法[J].振动与冲击, 2006, 25(5):28―31.Zhu Zhiwen, Gu Ming.Identification of flutter derivatives by using eigensystem realization algorithm[J].Journal of Vibration and Shock, 2006, 25(5): 28―31.(in Chinese)
[18]李友祥, 祝志文, 陈政清.识别桥梁断面颤振导数的快速相关特征系统实现算法[J].振动与冲击, 2008(8):117―120.Li Youxiang, Zhu Zhiwen, Chen Zhengqing.Implementation of eigensystem realization algorithm with data correlation to identify flutter derivatives of bridges [J].Journal of Vibration and Shock, 2008(8): 117―120.(in Chinese)
[19]许福友, 陈艾荣, 张哲.识别桥梁断面 18个颤振导数的梯度下降算法[J].工程力学, 2008, 25(6): 81―87.Xu Fuyou, Chen Airong, Zhang Zhe.Identification of 18 flutter derivatives of bridge decks using gradient declining algorithm [J].Engineering Mechanics, 2008,25(6): 81―87.(in Chinese)
[20]许福友, 陈艾荣, 马如进.桥梁断面颤振导数识别的随机搜索方法[J].土木工程学报, 2006, 39(7): 63―68.Xu Fuyou, Chen Airong, Ma Rujin.Identification of flutter derivatives of bridge decks on the basis of stochastic search technique [J].China Civil Engineering Journal, 2006, 39(7): 63―68.(in Chinese)
[21]Karaboga D.An idea based on honey bee swarm for numerical optimization.Technical Report-TRo6 [R].Kayseri: Erciyes University, 2005: 1―10.
[22]陈政清.桥梁风工程[M].北京: 人民交通出版社,2005: 5.Cheng Zhengqing.Bridge wind engineering [M].Beijing:China Communications Press, 2005: 5.(in Chinese)
[23]江铭炎, 袁东风.人工蜂群算法及其应用[M].北京:科学出版社, 2014: 11.Jiang Mingyan, Yuan Dongfeng.Atificial bee colony algorithm and its application [M].Beijing: Science Press,2014: 11.(in Chinese)
[24]Theodorson T.General theory of aerodynamic instability and mechanism of flutter [R].Washington: NACA Report No.496, 1935: 413―433.