直立锁边屋面系统是将相邻屋面板的卷边借助专用设备与T型支座依次咬合,然后连接到支承结构的屋面系统。凭借其优良的防水性能、抗变形能力以及多样化的板面形式得到了越来越多设计者的喜爱,因此被广泛应用于大跨建筑的屋面围护结构中。由于直立锁边屋面系统在咬合处的抗风承载能力较低,在台风影响区等风力较大的地区,该类屋面系统在强风作用下的风揭破坏事故时有发生,如图1所示。

图1 直立锁边金属屋面系统风揭破坏事故
Fig.1 Wind uplift accident of standing seam roof system
Schroter[1]与Sinno[2]分别通过空气静压试验与空气动力学试验研究了直立锁边屋面系统的受力性能,确定了相应型号屋面系统抗风承载能力。Damatty等[3]与Ali和Senseny[4]分别用弹簧单元与接触单元模拟屋面连接接缝建立直立锁边屋面系统的有限元模型。其中Damatty等[3]通过施加静力荷载得到了屋面系统的抗风承载力,而Ali和Senseny[4]通过动力分析得到阻尼对夹子反力的影响不大。通过一系列的试验与模拟研究,国外已提出关于屋面系统抗风揭的标准试验方法[5_6],并且已经得到了很多国家的认可。需要指出,国外的直立锁边屋面系统在形式和构造细节上与国内的直立锁边屋面系统存在较大的差异,所取得的研究成果无法直接用于国内的直立锁边屋面系统设计中。国内学者则多数集中于屋面板的抗风承载力的研究,秦国鹏等[7]与孙成疆[8]基于美国FM4471标准,借助空气压力箱对直立锁边屋面系统验开展了抗风揭试验屋面系统的抗风承载力,同时指出锁缝是该类型屋面系统的薄弱环节。考虑到屋面型号众多,国内学者同时进行了数值模拟研究,陈玉[9]借助有限元分析软件对屋面系统的受力性能、破坏形式、承载力、变形等响应开展了参数研究,并拟合得到了承载力计算公式。尽管开展了大量试验与数值研究,仍未阻止风揭破坏事故的发生。为此国内学者们[10]设计了抗风夹用来加强锁缝处的咬合作用,但在目前的多数研究中并没有考虑抗风夹的影响。
为研究带抗风夹的直立锁边屋面系统在风荷载下的受力性能,使用沙袋进行静力堆载试验,并借助有限元软件ANSYS进行静力荷载下带抗风夹的直立锁边屋面系统的参数模拟研究,确定了屋面系统的破坏准则,通过分析不同型号屋面系统的破坏形式、承载力、变形及应力变化特点,提出了直立锁边屋面系统的承载力计算公式,为工程中需要采用抗风夹进行局部加强时的设计提供参考。
1 静力试验研究
1.1 静力试验介绍
试验中使用沙袋对屋面系统进行反向静力加载,每次加载将9个或18个沙袋(分别对应0.25 kPa或0.5kPa)均匀平铺在屋面系统上,持压1 min后进行下一次加载,直至屋面系统破坏。试验加载装置如图2所示,其中立柱、钢梁和檩条均采用I20a钢。设计时,檩条两端腹板均进行了延伸,使其可以与钢梁腹板接触。连接檩条与钢梁时,借助预先加工的角钢,采用12个M20高强螺栓将檩条与钢梁连接。试验时先将所有T型支座均用4个直径5 mm的螺栓与檩条连接,然后借助专业设备将屋面板与T型支座咬合,最后将整个装置翻转,试验框架长3000 mm,宽1350 mm。

图2 试验加载装置图/mm
Fig.2 Experimental loading frame
试验中使用的屋面板型号为 400/65、300/65,即板宽分别为400 mm和300 mm,竖向板高度为65 mm,厚度均为1 mm,图3中给出了所使用的屋面板、T型支座和抗风夹的几何信息。
试验中采用的直立锁边屋面板材料为铝镁锰合金,型号为 3004-H36,材料的性能参数信息见表1。共进行了4组工况的静力试验研究,工况参数信息见表2。
试验主要测量屋面板的变形及抗风夹处的受力情况,根据以往国内学者[7, 9]的研究结果,屋面系统的竖向板及跨中屋面板应力往往较大,因此在竖向板和跨中屋面板布置应变片,同时也在抗风夹上布置了应变片。应变片采用BX120-2AA。为了测抗风夹与屋面直立锁边卡口的相对变形,用激光位移计进行测量,激光位移计采用KEYENCE 公司生产的LKG-400,量程为10 mm,精度为0.001 mm。图4为使用的应变片与激光位移计,图5给出激光位移计测点的布置示意图,其中图5(a)中a点与b点的横向位移即为卡口位移。

图3 组件基本信息/mm
Fig.3 Component basic information
表1 屋面板材料信息
Table 1 Material properties of roof plate

屈服强度/MPa极限强度/MPa弹性模量/MPa密度/泊松比(t/mm3)220 280 70000 2.7×10-9 0.3
表2 试验工况表/mm
Table 2 Experimental cases

工况 屋面板宽度 檩条间距 抗风夹间距1 300 1000 无2 300 1000 1000 3 400 1000 1000 4 400 500 500

图4 测量装置图
Fig.4 Measuring device

图5 位移测点布置示意图
Fig.5 Displacement measurement point layout
1.2 试验结果分析
在上述4组静力加载试验中,工况1和工况3分别在3.6 kPa和6.5 kPa时由于卡口侧向位移达到1.8 mm左右而发生脱扣破坏,工况2和工况4则分别在7.9 kPa和12.5 kPa时由于屋面最大应力超过极限强度而发生撕裂破坏。
试验表明,直立锁边屋面系统在荷载作用下的破坏形式主要是脱扣破坏(如图6(a))和撕裂破坏(如图6(b))。前者是由于卡口位移过大,T型支座对屋面卷边的约束作用消失,屋面板脱离T型支座被掀翻,工况1和工况3正是这种破坏形式;后者是由于抗风夹对屋面竖向板横向位移的限制,抗风夹附近竖向板发生应力集中,产生较大的应力值,工况2、工况4即发生撕裂破坏。

图6 直立锁边屋面系统主要破坏形式
Fig.6 Main failure modes of the standing seam roof system
取4组工况的卡口位移与竖向板最大测点应力变化曲线进行分析,如图7和图8所示。图9给出了应变测点的位置。工况1和工况3分别在3.6 kPa、6.5 kPa时发生脱扣破坏,观察此时的屋面应力分别为220 MPa、250 MPa,均低于极限强度280 MPa。而此时的卡口位移则均为1.8 mm左右,可以认为,由于卡口位移过大,T型支座的约束作用消失,引起屋面系统的脱扣破坏;工况2和工况4分别在7.9 kPa和12.5 kPa时发生撕裂破坏,此时的卡口位移仅为1 mm左右,低于发生脱扣破坏的临界卡口位移值(1.8 mm)。观察屋面竖板的应力发现此时的屋面最大应力均已接近 300 MPa,超过极限强度280 MPa,导致了屋面系统在竖向板处发生撕裂破坏。取屋面系统破坏前的一级荷载作为屋面系统的承载力,4组工况的承载力分别为 3.4 kPa、7.6 kPa、6.0 kPa、12.0 kPa。同时可以得出,当卡口位移达到1.8 mm左右时,T型支座对屋面系统的约束作用已消失,屋面系统将发生脱扣破坏;由于屋面板材料的极限强度为280 MPa,因此可以认为当屋面的最大应力超过280 MPa时将会发生撕裂破坏。
对试验结果的卡口位移曲线(图7)和竖向板测点应力曲线(图8)进一步分析,可以发现由于工况1、工况 2和工况 3的支座间距为100 mm,大于工况4的500 mm,因此在加载初期工况1、工况2和工况3的卡口位移增长明显快于工况4。在荷载达到2 kPa时,工况1、工况2和工况3的卡口位移均达到了1 mm左右。而随着荷载的继续增加,工况1由于未采用抗风夹对相邻屋面板的卷边处进行附加约束,卡口位移继续快速增长,在达到1.8 mm后发生脱扣破坏。工况3虽然使用了抗风夹,但由于其板宽(400 mm)较大,单个抗风夹承受的荷载增加。因此随着荷载增加,工况3的卡口位移也继续快速增长,同样在达到1.8 mm后引起了脱扣破坏。工况2由于使用了抗风夹,并且板宽(300 mm)较小,这使得工况2在卷边处的约束作用相较于工况1和工况3有很大的提升。工况2在2 kPa的荷载作用下卡口位移达到1 mm后继续施加荷载,由于卷边处较强的约束作用,卡口位移并未快速增长,而是缓慢增长维持在1 mm左右。工况4对抗风夹密度进行了加密,卷边处的约束作用因此十分明显,在整个加载过程中卡口位移均增长缓慢并最终维持在 1 mm左右。从屋面应力来看,在 2 kPa之前,4组工况的屋面应力增长比较一致。在此之后,工况1和工况3由于在卷边处的约束作用弱,在荷载继续增加的过程中屋面产生了较大的变形,屋面最大应力也随之快速增加,在破坏时刻分别达到220 MPa与250 MPa。工况2和工况4由于卷边处的约束作用强,在随后的加载中屋面变形相对较小,屋面最大应力增加也相对较慢,随着应力增加超过极限强度接近300 MPa,屋面发生撕裂破坏。
由试验结果可知抗风夹的受力很小,基本不超过100 MPa,跨中屋面板的应力也多处于弹性阶段,应力值不超过200 MPa。
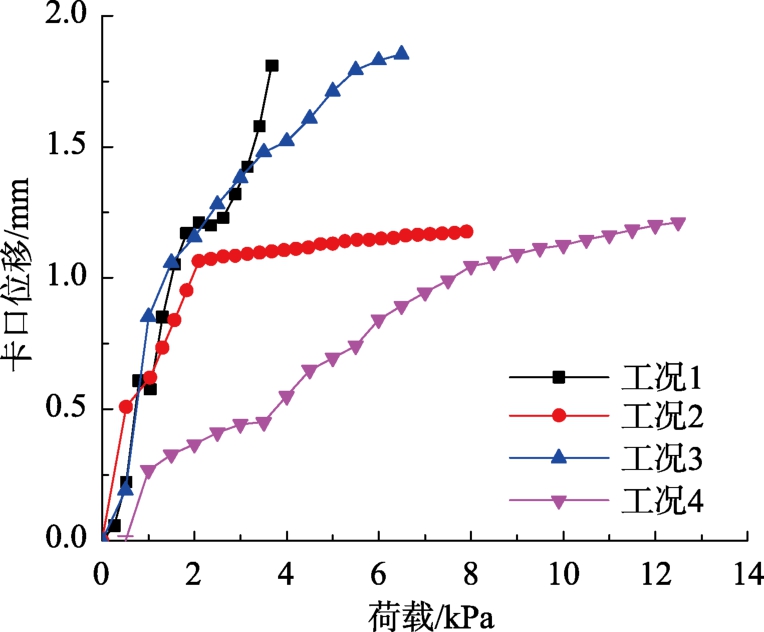
图7 卡口位移曲线
Fig.7 Seam displacement curves

图8 竖向板应力曲线
Fig.8 Stress curves at vertical plate
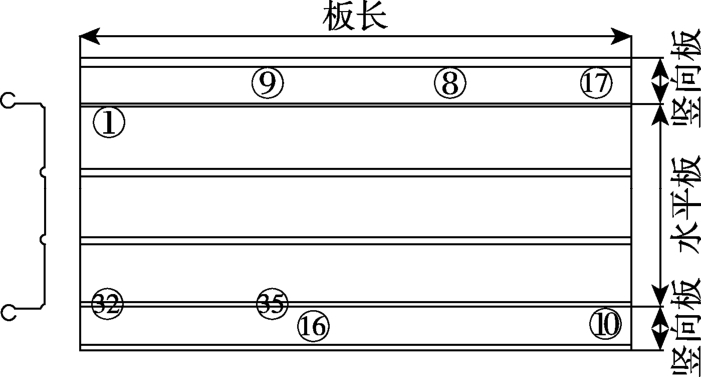
图9 竖向板处应变测试点布置图
Fig.9 Strain measuring points layout at vertical plate
2 数值模拟研究
2.1 数值模拟方法概况
直立锁边屋面系统型号众多,逐一进行静力加载试验会消耗大量人力和财力。所以借助有限元分析软件 ANSYS开展工况补充分析。屋面板的材性同前。屋面板使用Shell181单元,T型支座和抗风夹使用Solid187单元,另通过指定线的分段数,对屋面系统进行映射网格划分,有限元模型见图10。

图10 屋面系统有限元模型
Fig.10 Finite element model of roof system
有限元模型两侧的z向边界条件设定为固结,x向边界不做约束,T型支座底部同样设置为固结。相邻屋面板在卷边处相互咬合,在此处同时有T型支座的顶紧作用和抗风夹的限制作用,约束条件比较复杂。参考文献[3_4],采用耦合、法向约束及接触单元模拟卷边处的约束作用,如图11所示。在建立上述有限元模型时,忽略下部檩条的影响,并且假定采用耦合、法向约束的卷边不产生相对位移。

图11 屋面系统卷边处约束设置
Fig.11 Constraint setting at the seaming of roof system
参考上述模拟方法对 32组屋面系统建立有限元模型,进行了数值模拟研究。
2.2 数值模拟方法有效性的验证
为验证上述数值模拟方法的有效性,将模拟工况3(板宽400 mm、厚1 mm,抗风夹间距1000 mm)的模拟结果与试验工况3的结果进行了对比。根据试验中布置的竖向板、屋面板跨中、抗风夹测点,选取有限元模型中相近区域的单元节点,绘制荷载-应力曲线进行对比。对比结果如图12所示,可以发现模拟中屋面系统的极限承载力是5.4 kPa,试验中为6.0 kPa,极限承载力仅相差0.6 kPa。卡口位移方面,破坏时刻模拟与试验的卡口位移结果均在1.8 mm左右,且在加载过程中相差也较小,最大误差仅为0.15 mm,不足10%;在应力方面,加载过程中抗风夹处应力误差最大为6 MPa,误差仅为 9%。竖向板和跨中屋面板应力虽然在加载初期应力值较小的情况下存在较大的误差,但随着荷载的增加,误差逐渐缩小,当荷载达到2.5 kPa后,应力误差均小于10%。从变化趋势上看,模拟与试验在三处的测点应力变化趋势较为一致。由此采用本文的数值模拟方法可以较好地模拟屋面系统的受力性能,其参数分析的结果可供工程设计参考。图13为加载过程中屋面应力与卡口位移分布云图。

图12 数值模拟与试验结果对比
Fig.12 Comparison between numerical simulation and experimental results

图13 屋面系统响应分布云图
Fig.13 Response distribution of roof system
3 研究结果的参数分析
32组数值模拟工况的参数信息见表3,通过对各工况的抗风承载力、屋面最大应力和卡口位移等响应进行分析,确定板厚、板宽、抗风夹间距等参数对屋面系统受力性能的影响。同时通过讨论无量纲参数与抗风承载力的相关性,确定与抗风承载力相关性最强的参数,并拟合得到承载力计算公式。
表3 数值模拟工/mm
Table 3 Numerical simulation cases

工况 板厚 板宽 檩条间距 抗风夹间距 抗风夹尺寸1~5 0.8~1.2 400 1000 1000 正常6~12 1 300~600 1000 1000 正常13~23 1 400 500~1500 同檩条间距 正常24~32 1 400 1000 1000 厚度: 2~4长度: 3~5
3.1 屋面板厚度的影响
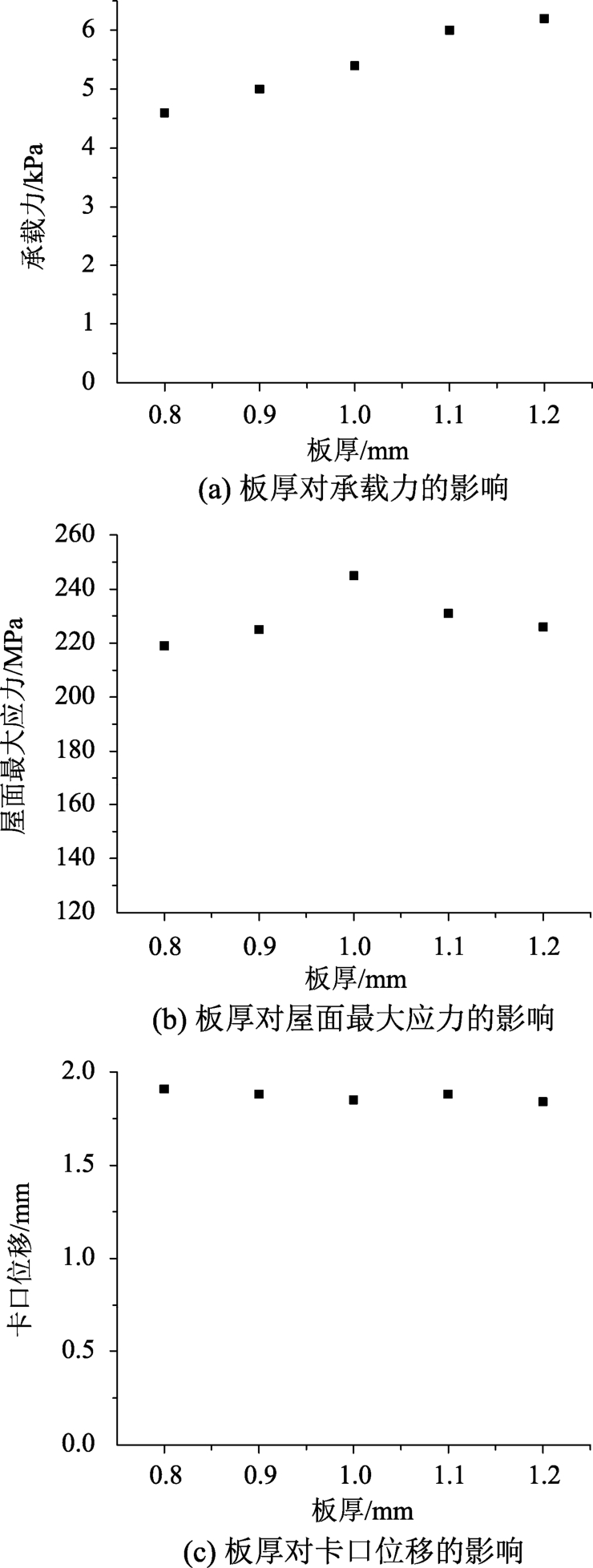
图14 板厚的影响
Fig.14 The influence of plate thickness
数值模拟工况1~工况5对屋面板厚的影响进行了研究,结果见图14。数值模拟结果表明板厚的改变对屋面最大应力和卡口位移影响较小,5组工况均由于卡口位移达到1.8 mm而发生脱扣破坏,在破坏时刻屋面竖向板处局部最大应力均刚刚达到屈服强度,在屋面板的多数位置材料尚处于弹性阶段,材料的利用率较低。当然板厚的增加使屋面板的刚度得到提升,屋面系统的抗风承载力得到一定的提高,但依靠增加板厚来提高屋面系统的承载力并不经济。
3.2 屋面板宽度的影响
工况6~工况12研究了屋面板宽对屋面系统的影响,关键响应受板宽影响的变化情况见图15,由图15可以看出板宽的变化对屋面系统有较大的影响。板宽的增加使屋面系统的刚度降低,因而导致极限承载力由板宽 300 mm时的 7.4 kPa降低为板宽600 mm时的2 kPa,承载力降幅达到73%。同时屋面系统的破坏形式也因板宽的改变发生了转变,在板宽300 mm与350 mm时为撕裂破坏,随着板宽增加转变为脱扣破坏,对应最大应力和卡口位移变化图(见16(b)和图16(c))上出现了明显的改变。在撕裂破坏时,屋面应力超过了极限强度280 MPa,但卡口位移仅 1.2 mm左右。在脱口破坏时,卡口位移突增至 1.8 mm以上,而屋面应力则突降到250 MPa以下。
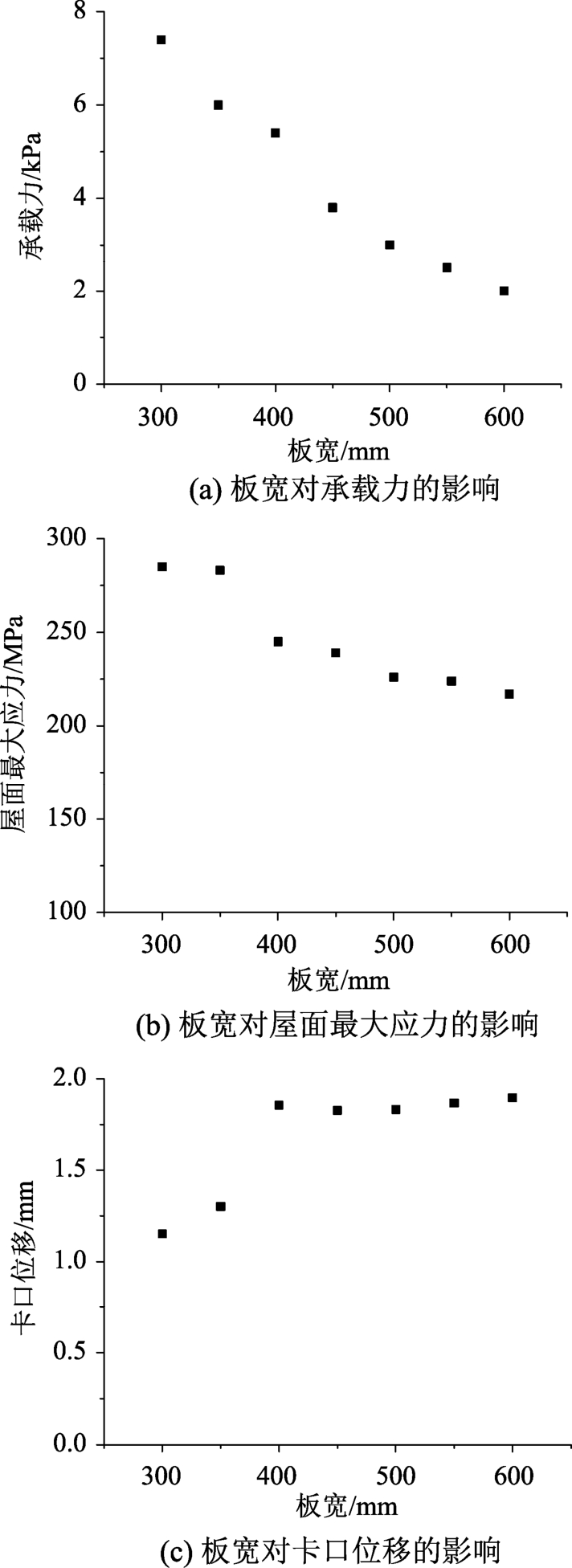
图15 板宽的影响
Fig.15 The influence of plate width
3.3 抗风夹间距的影响
数值模拟工况13~工况23针对的是抗风夹间距对屋面系统受力性能的影响,将破坏时刻各工况的响应结果整理成图16。可以发现抗风夹间距对屋面系统的破坏形式与极限承载力均有较大影响,在抗风夹间距分别为500 mm、600 mm和700 mm时,屋面系统刚度大,产生的变形小,主要发生撕裂破坏,极限承载力均在9 kPa以上。而随着抗风夹间距的增加,屋面系统的刚度有所下降,变形随之加大,破坏形式也转化为脱扣破坏,极限承载力基本在4 kPa左右。同时注意到抗风夹间距的增加,并未使屋面系统的最大应力出现较大幅度的下降,即使发生脱口破坏时,屋面最大应力也维持在245 MPa左右。
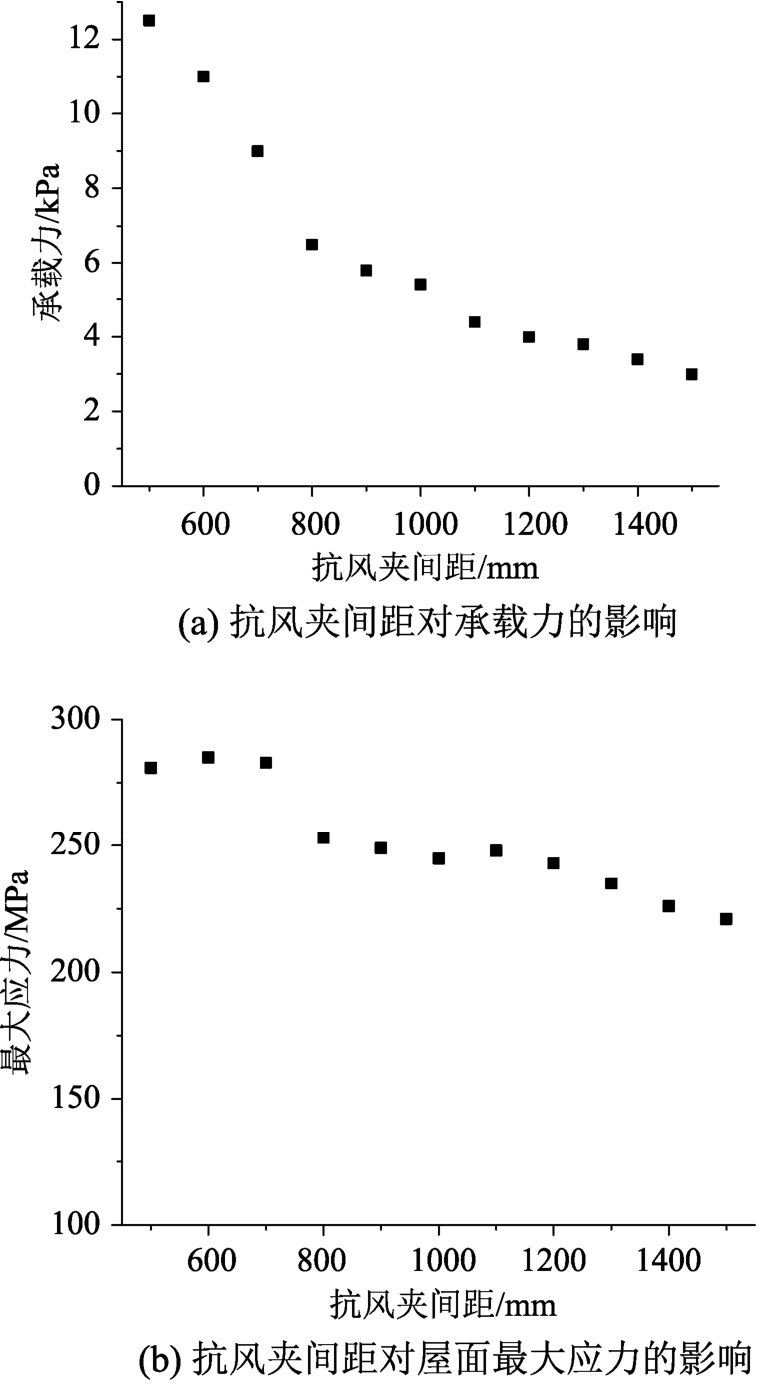
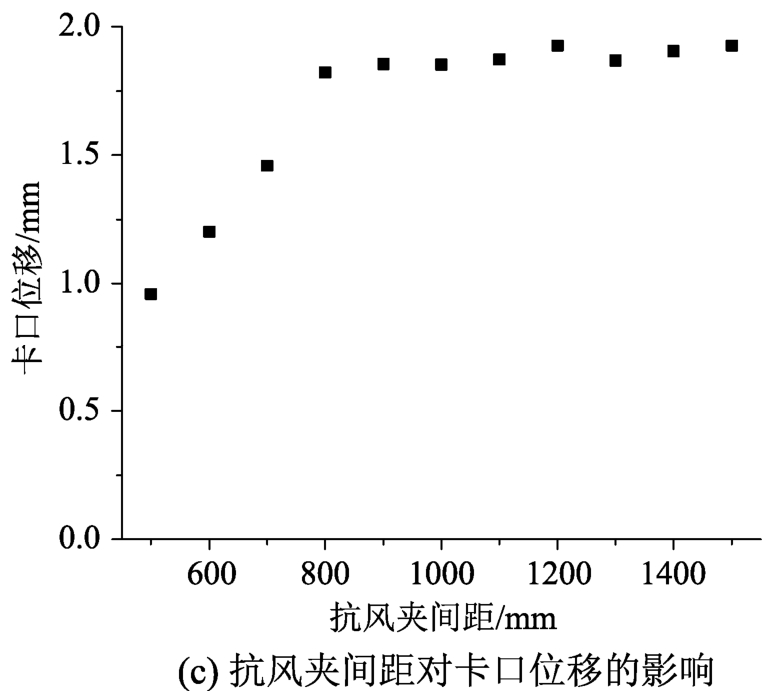
图16 抗风夹间距的影响
Fig.16 The influence of anti-wind clip spacing
3.4 抗风夹尾端厚度与长度的影响
工况24~工况32对抗风夹尺寸对屋面系统的影响进行了对比研究,相关结果汇总于表4。分析表4中数据可以发现,抗风夹尺寸的改变对屋面系统的影响有限。首先,所有模拟工况的破坏形式均为脱扣破坏。其次,各工况的极限承载力均位于4 kPa~6 kPa的荷载区间内,变化较小。最后,屋面最大应力也多集中在245 MPa左右。所以抗风夹尺寸的改变对屋面系统受力性能的影响有限。
表4 抗风夹尺寸的影响
Table 4 The influence of the size of the anti-wind clip
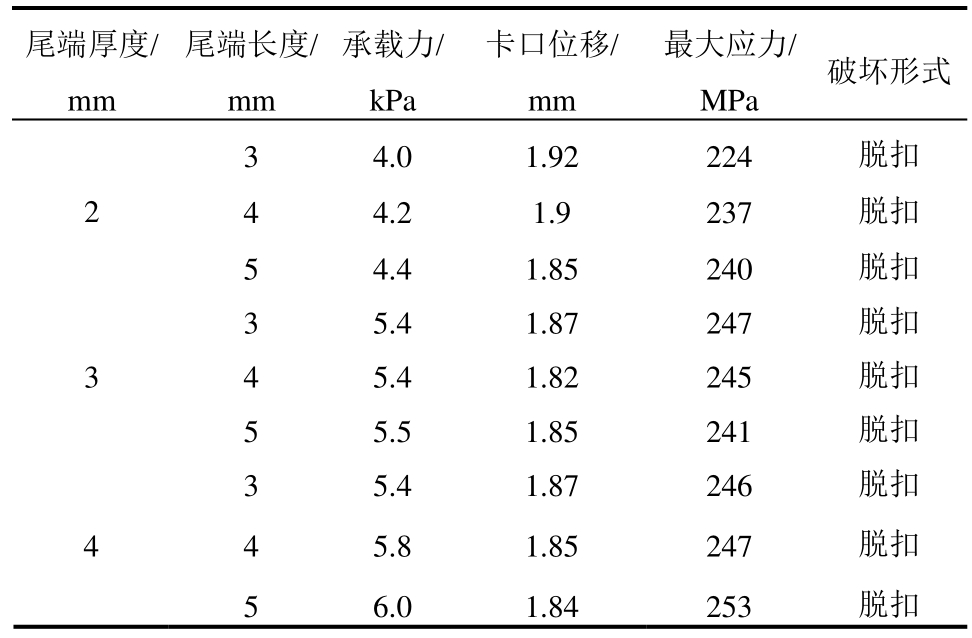
尾端厚度/mm尾端长度/mm承载力/kPa卡口位移/mm最大应力/破坏形式MPa 3 4.0 1.92 224 脱扣2 4 4.2 1.9 237 脱扣3 5 4.4 1.85 240 脱扣3 5.4 1.87 247 脱扣4 5.4 1.82 245 脱扣5 5.5 1.85 241 脱扣3 5.4 1.87 246 脱扣4 4 5.8 1.85 247 脱扣5 6.0 1.84 253 脱扣
4 直立锁边屋面系统抗风承载力
通过前述参数分析可以发现,除抗风夹尺寸外,屋面板厚、板宽及抗风夹间距均对屋面系统的抗风承载力有较大影响,因此选择板厚 d、板宽 b和抗风夹间距l作为自变量,拟合它们与抗风承载力之间的关系。
为确定板宽、板厚、抗风夹间距与屋面系统承载力的相关性,采用相关分析法对前述参数模拟结果进行统计分析,绘制各参数间的相关分析图,相关分析图是由每两个参数间的相关系数构成的矩阵图(见表5),本文对该矩阵中的元素定义如下:
1)矩阵图的下三角元素定义为两参数(X1、X2)的皮尔森(Pearson)相关系数 Rps,按式(1)计算。Rps是标准的线性相关系数,其绝对值越接近1则两参数的线性关系越明显。
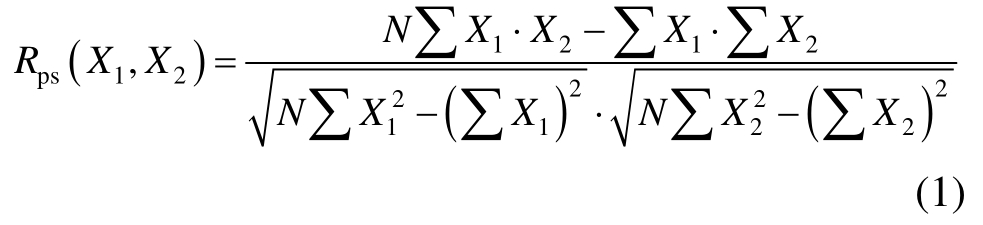
式中, N表示参数分析的工况数。
2)矩阵图中的上三角元素定义为两参数(X1、X2)的斯皮尔曼(Spearman)秩相关系数 Rsp,按式(2)计算。Rsp不仅可以识别线性相关性,也能识别单调的非线性相关性,可用于挖掘参数间潜在的非线性函数关系。
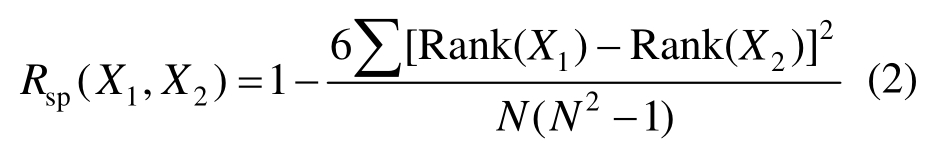
式中,Rank(·)表示取参数的秩。
本文主要关注板宽、板厚、抗风夹间距与屋面系统承载力的相关性,因此只采用上述方法计算了无量纲参数 b/l、bl/d2、b/d、l/d、bd/l2与抗风承载力的相关性,相关性分析结果见表5。
表5 不同参数对抗风承载力的相关性分析
Table 5 Correlation analysis of different parameters against bearing capacity

无量纲参数 b/lb/dl/dbd/l2bl/d2 承载力b/l 1 0.34 b/d 1 _0.68 l/d 1 _0.74 bd/l2 1 0.47 bl/d2 1 _0.94承载力 0.298 _0.67 _0.74 0.53 _0.94 1
从表5可以发现,无论是Rps还是Rsp都表明与屋面系统抗风承载力相关性最强的参数为bl/d2。然后借助MATLAB拟合该参数和抗风承载力的关系曲线,如图17所示。同时得到了直立锁边屋面系统抗风承载力F的计算式(3)。需要指出,该公式主要适用于带抗风夹的直立锁边屋面系统抗风承载力的预估。
式中:F为抗风承载力,kPa;b为板宽,mm;l为抗风夹间距,mm;d为板厚,mm。
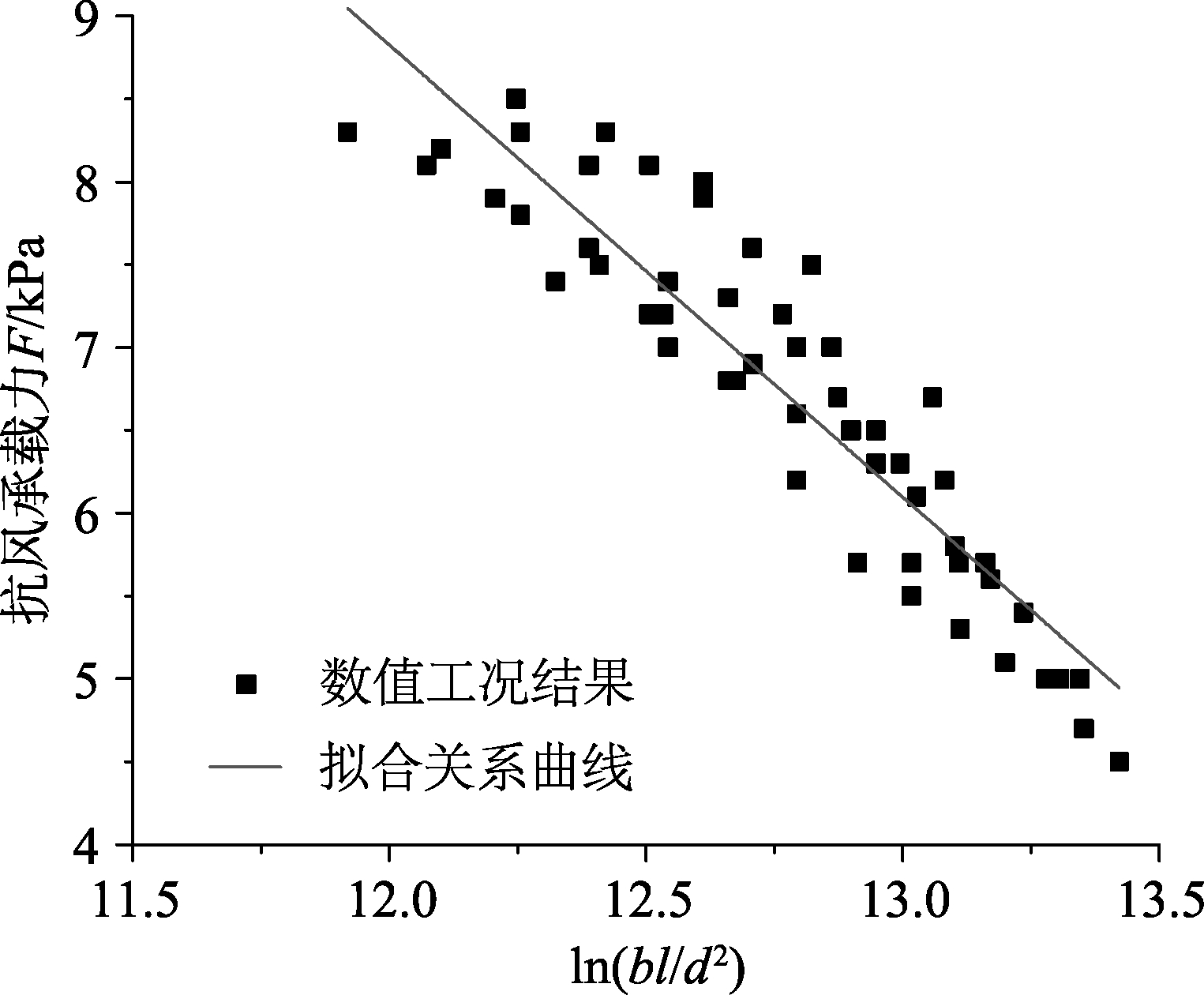
图17 参数ln(bl/d2)与承载力F的关系曲线
Fig.17 Relationship curve between ln(bl/d2)and bearing capacity F
5 结论
通过对带抗风夹的直立锁边屋面系统开展的参数研究可以发现:
(1)直立锁边屋面系统的破坏形式主要是脱扣破坏与撕裂破坏。脱扣破坏是由于屋面卷边处约束作用弱,荷载作用下卡口位移过大;撕裂破坏则是由于屋面卷边处约束作用强,材料应力充分发展超过极限强度。
(2)破坏形式方面,板宽与抗风夹间距的变化会使屋面系统的破坏形式发生改变,板厚与抗风夹尺寸的变化不会影响屋面系统的破坏形式;承载力方面,板宽与抗风夹间距的变化会使屋面系统的承载力有较大幅度的改变,抗风夹尺寸对屋面承载力的影响有限,板厚的变化对屋面系统的承载力有较大影响,但也会使成本提高。
(3)通过相关性分析与数据拟合得到直立锁边屋面系统的抗风承载力计算公式,通过该公式可以近似得到各型号屋面系统的抗风承载力,为直立锁边屋面系统的抗风设计提供参考。
(4)需要指出,文中采用的静荷载并未考虑风荷载对屋面系统的疲劳损伤影响。而长时间的风荷载作用会使屋面系统的疲劳效应更加明显,造成屋面系统承载力、受力性能等的变化。因此在后续研究中有必要考虑真实风荷载的动力特性。
[1]Schroter R C.Air pressure testing of sheet metal roofing[C]//Proceedings of the Second International Symposium on Roofing and Technology, Gaithersburg, MD, 1985: 1-6.
[2]Sinno R R.Response of metal roofs to uniform static and true hurricane wind loads [C]//Proceedings of the Nineteenth International Specialty Conference on Cold-Formed Steel Structures, St.Louis, Missouri,U.S.A, 2008: 281-305.
[3]Damatty A A E, Rahman M, Ragheb O.Component testing and finite element modeling of standing seam roofs [J].Thin-Walled Structures, 2003, 25(41): 1053-1072.
[4]Ali H M, Senseny P E.Models for standing seam roofs[J].Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(12/13/14/15): 1689-1702.
[5]ANSI/FM 4474_2004, American national standard for evaluating the simulated wind uplift resistance of roof assemblies using static positive and negative differential pressures [S].Norwood, USA: FM Approval, 2004.
[6]EOTA 006, Guideline for European technical approval of systems of mechanically fastened flexible roof waterproofing membranes [S].Brussels: EOTA, 2000.
[7]秦国鹏, 张晓旭, 孙超.铝合金屋面系统抗风揭性能试验研究及数值分析[J].工业建筑, 2016, 46(10):169-173.Qin Guopeng, Zhang Xiaoxu, Sun Chao.Experimental research and numerical analysis of an aluminum-alloy roof system under wind uplift load [J].Industrial Construction, 2016, 46(10): 169-173.(in Chinese)
[8]孙成疆.直立锁缝金属屋面系统在模拟极端暴风工况下抗风揭能力测试与分析[J].建筑结构, 2011, 41(增刊 1): 1438-1442.Sun Chengjiang.Simulated wind uplift pressure analysis and tests of the standing seam metal roof system [J].Building Structure, 2011, 41(Suppl 1): 1438-1442.(in Chinese)
[9]陈玉.直立锁边屋面系统抗风承载能力研究[D].北京:北京交通大学, 2015.Chen Yu.Loading bearing capacity of the standing seam roof system under the wind load [D].Beijing: Beijing Jiaotong University, 2015.(in Chinese)
[10]范亚娟.金属屋面系统抗风吸力的静力性能和疲劳性能研究[D].北京: 北京交通大学, 2016.Fan Yajuan.Study on the static and fatigue performance of metal roof system under wind suction [D].Beijing:Beijing Jiaotong University, 2016.(in Chinese)