RC剪力墙是框架剪力墙和剪力墙结构的主要承压与抗侧力构件，其地震作用下的抗震性能将直接影响剪力墙和框架剪力墙结构抗震性能的优劣[1－4]。近年来，RC剪力墙的数值模拟方法受到了研究人员的广泛关注，并针对其提出了多种计算模型，如：纤维模型、分层壳模型、多垂直杆模型等。而这些数值模型均存在一定的不足，如：纤维模型忽略了构件的剪切效应，这将导致构件在非线性分析中出现偏差，尤其对发生剪切和弯剪破坏的RC剪力墙，其偏差较大，甚至可能改变其整体结构的塑性受力特征[5]。鉴于此，杨红等[5]、Vásquez等[6]、臧登科[7]、解琳琳[8]采用组合剪切效应的纤维模型，对 RC剪力墙进行数值建模分析，发现组合剪切效应的纤维模型能较为准确的模拟剪切效应显著RC剪力墙的非线性反应。
然而，值得指出的是，上述数值模型均是针对完好RC剪力墙提出的，难以反映剪力墙由于环境侵蚀作用引起的抗震性能劣化问题，因而无法直接用于在役RC剪力墙结构的数值建模及其抗震性能评估中。事实上，在中国、日本、加拿大、俄罗斯和北美的部分严寒地区，大量在役RC构件与结构处于冻融环境之中。且已有研究表明，冻融作用将使混凝土材料产生物理损伤，导致其力学性能及其与钢筋间的粘结性能发生退化[9－11]，进而致使 RC剪力墙的力学性能、变形性能以及抗震性能发生不同程度的劣化[12－14]，从而加剧在役RC剪力墙结构的地震灾害风险。因此，忽略在役RC剪力墙的抗震性能退化特性，将极大的影响在役RC剪力墙结构抗震性能评估结果的准确性。
综上，为实现冻融环境下在役RC剪力墙结构抗震性能的科学合理评估，本文基于8榀低矮RC剪力墙拟静力试验结果[14－15]，通过理论分析与试验回归相结合的方法得到了冻融损伤剪切恢复力模型，进而结合考虑不均匀冻融损伤的纤维模型，建立了冻融损伤低矮RC剪力墙数值模拟方法，并与试验结果进行了对比，验证了该模型的准确性，其将为冻融环境下在役RC剪力墙结构的抗震性能评估提供理论支撑。
1 冻融低矮RC剪力墙试验概况
为研究冻融循环作用下低矮RC剪力墙的抗震性能，课题组以冻融循环次数、混凝土强度、轴压比为试验变量，根据国家规程和规范[16－17]，设计制作了8榀剪跨比均为1.14，尺寸与配筋均相同的矩形截面低矮RC剪力墙试件。试件尺寸及配筋见图1，试验具体变量设置见表1，混凝土与钢筋力学性能参数见表2和表3，其中以SW-1为对比试件即不对其进行冻融试验，其余试件均在制作完成且经标准养护28 d后，将其移入人工气候实验室进行快速冻融试验，具体冻融方案见文献[7,14]。待冻融试验完成后，采用力-位移混合加载模式对各剪力墙试件进行拟静力加载[14－15]，详细加载制度见图3。并通过布置在不同位置处的位移计与力传感器分别量测墙体剪切变形以及墙顶水平位移与荷载(测点布置见图2)。
观察拟静力加载试验中试件的破坏过程可以发现(试件破坏照片见文献[14－15])，不同设计参数下各试件的剪切斜裂缝开展较为充分，其最终破坏模式均为典型的剪切型破坏。同时，根据拟静力加载过程中所测得的试验数据得到各试件开裂、屈服、峰值状态下剪切骨架曲线特征点参数列于表4。
图1 低矮RC剪力墙试件尺寸及配筋/mm
Fig.1 Dimensions and reinforcement details of the squat RC shear wall
表1 RC剪力墙试件试验变量
Table 1 Design parameters of shear wall specimens
试件编号 冻融循环次数 混凝土强度等级 轴压比SW-1 0 C50 0.2 SW-2 100 C50 0.2 SW-3 200 C30 0.2 SW-4 200 C40 0.2 SW-5 200 C50 0.1 SW-6 200 C50 0.2 SW-7 200 C50 0.3 SW-8 300 C50 0.2
表2 混凝土力学性能
Table 2 Mechanical properties of concrete
混凝土强度等级 立方体抗压强度fcu/MPa轴心抗压强度fc/MPa弹性模量Ec/MPa C30 32.00 24.32 30447.2 C40 40.30 30.63 32686.8 C50 55.08 41.86 35335.7
表3 钢筋力学性能
Table 3 Mechanical properties of reinforcement
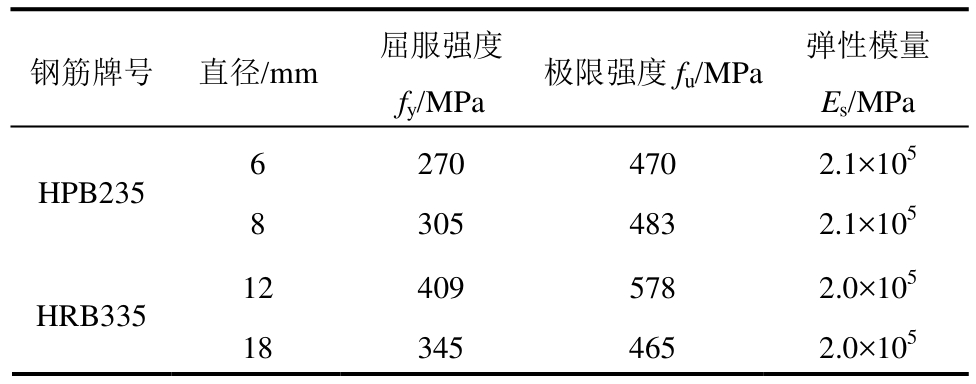
钢筋牌号 直径/mm 屈服强度 极限强度f/MPa 弹性模量f/MPa uE/MPa ys HPB235 5 8 305 483 2.1×10 6 270 470 2.1×105 HRB335 12 409 578 2.0×105 18 345 465 2.0×105
图2 加载装置及测点布置
Fig.2 Test setup and arrangement of instruments
图3 水平加载制度
Fig.3 Horizontal loading protocol
表4 剪切骨架曲线特征点参数值
Table 4 Characteristic parameters of shear skeleton curves
试件编号 荷载/kN 剪应变/( 10-3rad)荷载/kN 剪应变/( 10-3rad)荷载/kN 剪应变/( 10-3rad)开裂点 屈服点 峰值点images/BZ_85_1054_1264_1067_1319.pngimages/BZ_85_1648_1264_1660_1319.pngimages/BZ_85_1054_1320_1067_1375.pngimages/BZ_85_1648_1320_1660_1375.pngSW-1 168.892 0.383 276.766 1.353 330.348 2.179 SW-2 151.663 0.538 248.408 1.451 302.919 3.117 SW-3 158.701 0.516 213.004 0.961 250.029 2.400 SW-4 156.802 0.291 214.546 1.493 256.603 3.430 SW-5 121.613 0.488 214.028 2.125 260.908 3.891 SW-6 151.374 0.542 238.624 2.038 288.502 4.373 SW-7 209.741 1.010 242.066 1.461 279.049 2.673 SW-8 149.313 1.328 188.747 2.696 231.604 5.790
2 组合剪切效应的纤维模型
为精确模拟各剪切破坏冻融损伤RC剪力墙的非线性反应，本文通过OpenSEES有限元分析软件，采用组合剪切效应的纤维模型，并结合不均匀冻融损伤模型以考虑冻融循环对混凝土构件力学性能的影响，从而实现对8榀低矮RC剪力墙试件拟静力加载的数值建模分析。
组合剪切效应的纤维模型基本思路是将纤维截面的弯曲、轴向效应与截面剪切恢复力模型所定义的剪切效应利用 OpenSEES中 Section Aggregator命令组合起来，形成新的组合截面以实现纤维截面的抗剪。其中，弯曲、轴向效应通过材料本构模型实现，剪切效应则通过非线性剪切恢复力模型实现，如图4所示。基于此，准确建立考虑冻融影响的剪切恢复力模型成为本文建立数值模拟方法的关键。
图4 结合不均匀冻融损伤考虑剪切效应的纤维模型
Fig.4 Fiber model considering shear effect and combined with uneven freeze-thaw damage
3 低矮RC剪力墙剪切恢复力模型
构件恢复力模型的建立方法主要有理论方法和试验拟合方法等[18]。对于未冻融低矮 RC剪力墙，可通过已有理论成果[5,7]建立其剪切恢复力模型。然而，对于冻融损伤低矮RC剪力墙，由于其抗剪性能的劣化不仅受混凝土材料本身力学性能降低的影响，还受到钢筋与混凝土间黏结性能退化、构件内部微裂缝增多等诸多因素的影响，因此通过理论方法建立其剪切恢复力模型难度较大。而试验拟合方法能够在保证一定精度条件下，综合考虑上述各因素对RC剪力墙抗剪性能的影响。鉴于此，本文首先借鉴国内外已有理论成果[7,19－21]建立了未冻融低矮RC剪力墙剪切恢复力模型，进而根据第1章所述剪力墙试验结果，拟合得到考虑冻融损伤影响的低矮
RC剪力墙剪切恢复力模型骨架曲线特征点修正函数，并据此对未冻融低矮RC剪力墙剪切恢复力模型骨架曲线特征点进行修正，从而建立了考虑冻融损伤影响的低矮RC剪力墙剪切恢复力模型。
3.1 未冻融低矮RC剪力墙剪切恢复力模型
剪力墙剪切恢复力模型是描述墙体剪力 V(即墙顶所受水平荷载 P)与剪应变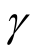
滞回关系的抽象数学模型，主要包括骨架曲线和滞回规则两部分。OpenSEES有限元分析软件中的滞回模型(Material Hysteretic)能够较准确的反映 RC剪力墙剪力与剪应变的滞回关系，因此，本文采用该模型建立未冻融与冻融损伤低矮RC剪力墙剪切恢复力模型，并重点介绍其骨架曲线控制参数的标定方法。
基于 Hysteretic模型，本文将未冻融及冻融低矮 RC剪力墙剪切恢复力模型骨架曲线简化为图4(b)所示的三折线，各转折点分别对应剪力剪应变关系的开裂点(Pc，
)、屈服点(Py，
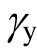)和峰值点(Pm，
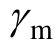)，因此，仅需确定上述各特征点对应的剪力P和剪应变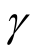就能确定剪切恢复力模型的骨架曲线。对于未冻融低矮RC剪力墙各特征点剪力P剪应变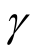本文采用经验证准确性[5,8,19]的计算式对其进行计算，公式详见表5。
表5 未冻融低矮RC剪力墙剪切骨架曲线参数计算式
Table 5 Calculation formula of shear skeleton curve parameters of unfrozen squat RC shear wall
特征点 计算公式参数说明开裂荷载[7] c m P＝PPm为峰值荷载0.53开裂点 开裂剪应变[19]v＝＝＝++ ，各参数表征意义见文献[19]屈服荷载[20]c P Ka c Ka为剪力墙初始弹性剪切刚度，参考Hirosawa(广泽)公式计算，其表达式为 a w ss cc KGAEAEAx/( )/[2(1 )]X＝__ ρt为有效受拉钢筋百分率；n为轴压比屈服点屈服剪应变[19]P P y m 1.24 0.15 0.5n ρtimages/BZ_31_1113_2379_1151_2425.png＝+Kb为剪力墙开裂后剪切刚度，其表达式为Kb=αsKa，αs计算见文献[19]y cr y PP K-images/BZ_31_1113_2379_1151_2425.pngc b峰值荷载[21]PAFFN w sv sbe m＝+++1.500.25 0.20 0.40images/BZ_86_849_2460_899_2501.png峰值点images/BZ_86_988_2509_1112_2550.pngfc为混凝土轴心抗压强度(psi)；Aw为墙体截面面积(in2)；Fsv与Fsbe分别为竖向分布筋、暗柱纵筋承担的力(lbf)，其具体计算见文献[21]；N为轴压力；Hw为剪力墙高度(in)；hw为剪力墙截面高度(in)峰值剪应变[19]images/BZ_31_1113_2379_1151_2425.pngm y m＝+Ks为剪力墙屈服后抗剪刚度，本文结合试验结果取为0.045Ka PP K-images/BZ_31_1113_2379_1151_2425.pngy s
3.2 冻融低矮RC剪力墙剪切恢复力模型
课题组基于材性试验结果并参考文献[22－23]，以相对动弹性模量(Relatively Dynamic Elasticity of Modulus，RDME)为冻融损伤指标定量表征混凝土冻融损伤程度，建立了混凝土冻融损伤参数D表达式：
式中：N为冻融循环次数；fcu为混凝土立方体抗压强度。依据式(1)计算得出本文涉及参数下混凝土冻融损伤值，列于表6。
表6 混凝土冻融损伤值
Teble 6 Freeze-thaw damage value of concrete
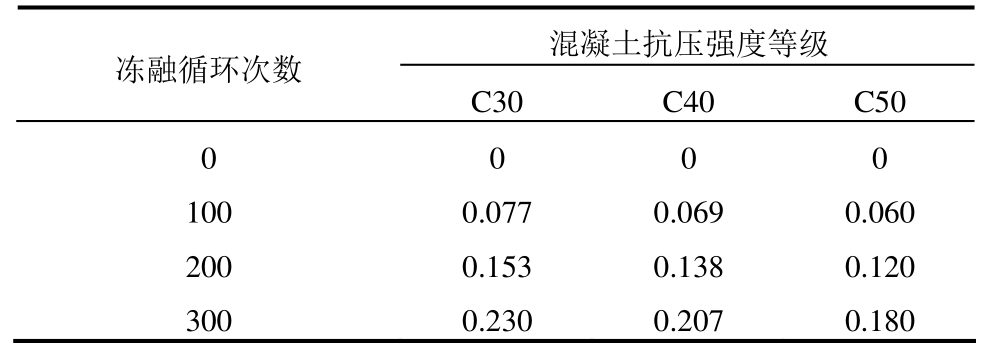
冻融循环次数 混凝土抗压强度等级C30 C40 C50 0 0 0 0 100 0.077 0.069 0.060 200 0.153 0.138 0.120 300 0.230 0.207 0.180
此外，由表4可见：冻融损伤程度相同时，随轴压比的变化，RC剪力墙不同受力状态下的抗剪承载力与剪应变均发生不同程度的改变。因此，本文综合考虑冻融损伤参数D与轴压比n对RC剪力墙力学及变形性能的影响，选取D和n为参数，对未冻融低矮RC剪力墙剪切骨架曲线特征点进行修正，修正公式如下：
式中：
分别为考虑冻融损伤影响的墙体特征点i的墙顶水平荷载与剪应变；Pi、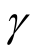i分别为未冻融墙体特征点i的墙顶水平荷载与剪应变； fi(D,n)、ri(D,n)分别为特征点i考虑冻融损伤与轴压比影响的荷载和剪应变修正函数，由剪切骨架曲线各特征点试验值(见表4)归一化处理后的系数经多参数非线性曲面拟合得到，具体确定方法如下：
将表4中冻融低矮RC剪力墙试件各特征点的荷载与剪应变分别除以相同轴压比下未冻融试件相应特征点的荷载与剪应变得到相应的修正系数即归一化处理。进而分别以冻融损伤参数D、轴压比n为横坐标，修正系数为纵坐标，绘制出各特征点荷载和剪应变修正系数随冻融损伤参数 D及轴压比n的变化规律图(见图5~图6)。由图可以看出：轴压比相同时，随冻融损伤参数D的增大，剪力墙各特征点荷载与剪应变修正系数近似呈幂函数型变化趋势；冻融损伤程度相等时，随轴压比n的增大，剪力墙各特征点荷载与剪应变修正系数无明显函数ri(D,n)假定为关于冻融损伤参数D的指数函数规律。鉴于此，为保证拟合结果具有较高精度，本文将各特征点的荷载修正函数fi(D,n)与剪应变修正形式，关于轴压比n的二次函数形式；并考虑边界条件，得到修正函数表达式如下：
式中，a、b、c、d均为拟合参数，其值见拟合结果图7。结合拟合结果及上述分析得到考虑冻融损伤影响的低矮RC剪力墙剪切骨架曲线特征点荷载、剪应变计算式及其拟合优度R2如下：
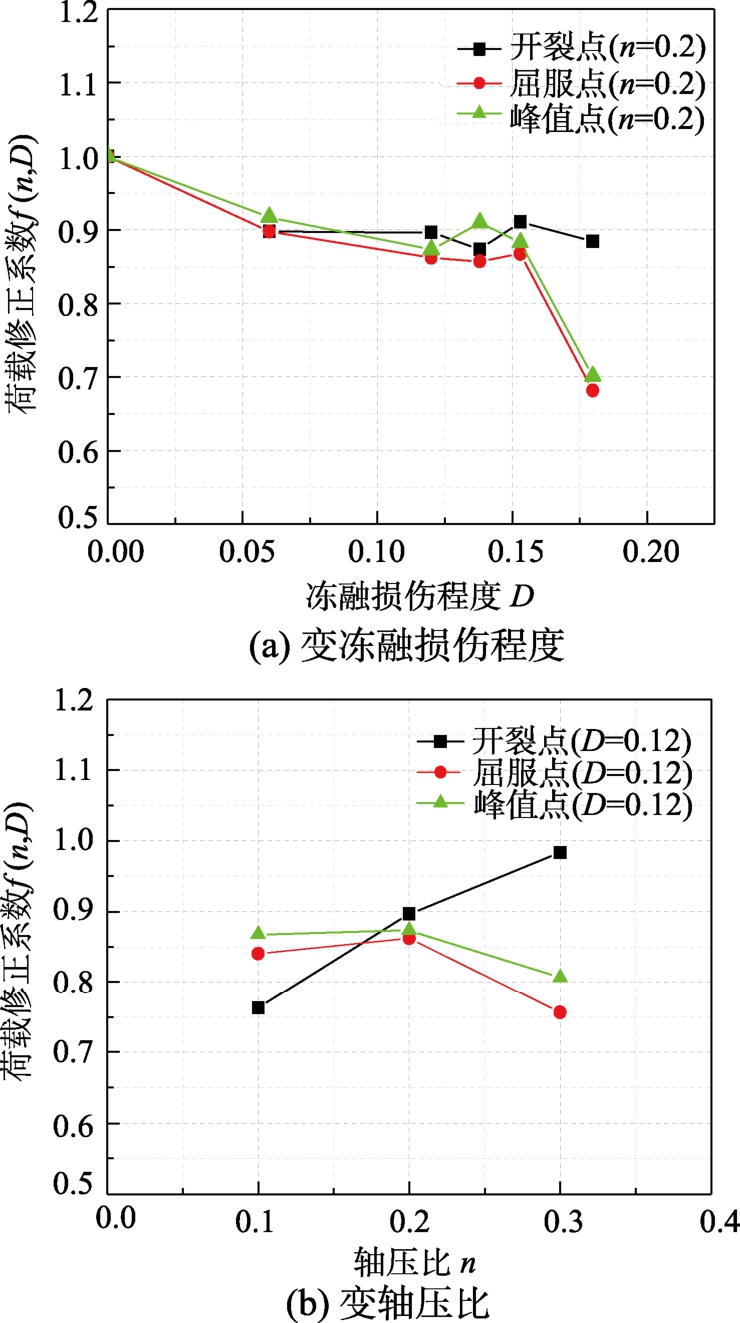
图5 荷载修正系数变化规律
Fig.5 Variation of load correction coefficient
图6 剪应变修正系数变化规律
Fig.6 Variation of shear distortion correction coefficien
图7 拟合结果
Fig.7 Fitting results
1)开裂荷载与开裂剪应变：
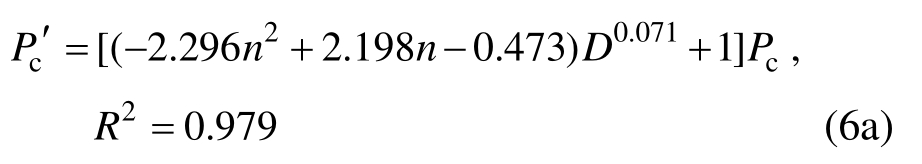
2)屈服荷载与屈服剪应变：
3)峰值荷载与峰值剪应变：
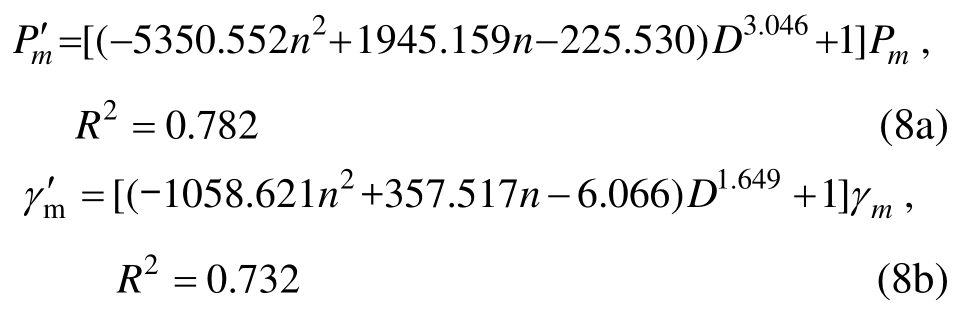
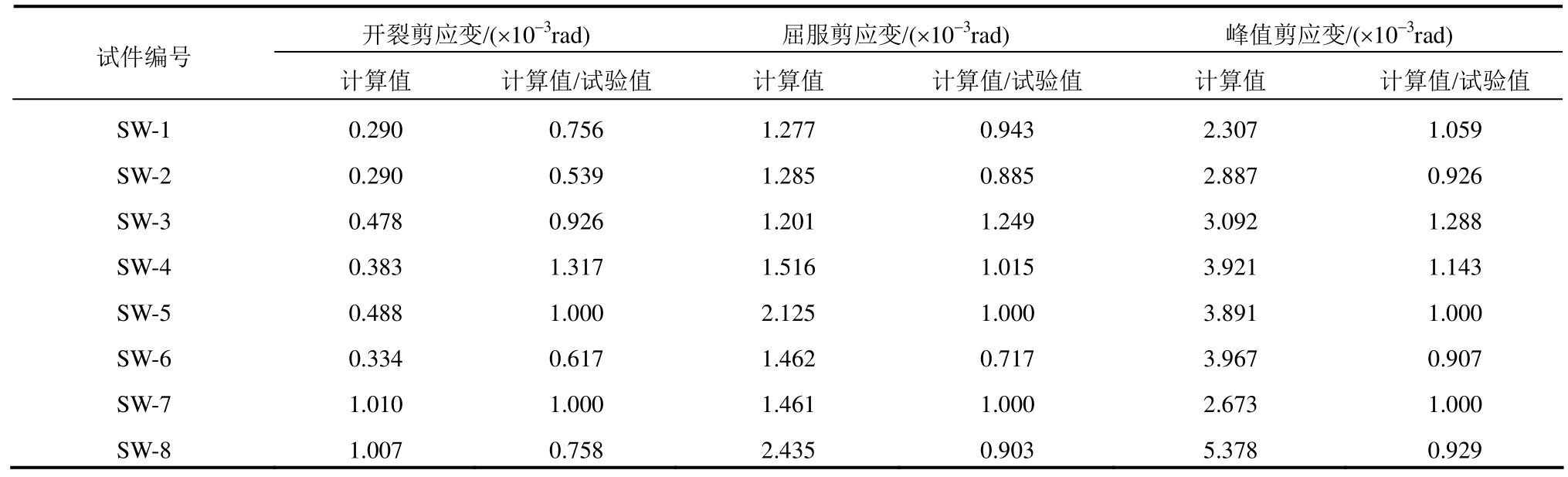
根据式(6)~式(8)计算得到第1章各榀RC剪力墙试件剪切骨架曲线特征点荷载与剪应变理论值及其与试验值之比，列于表7~表8。由表7~表8可见：各特征点荷载计算值与试验值吻合良好，所有误差均不超过12%；开裂剪应变、屈服剪应变、峰值剪应变计算值与试验值之比的均值分别为0.864、0.964、1.032，标准差分别为0.062、0.023、0.017；综上，采用本文所提出的承载力与剪应变计算模型能较好地反映冻融损伤低矮RC剪力墙实际受力与变形性能。个别试件剪应变计算值与试验值吻合较差这主要是由于文章所采用的剪应变理论计算式是由试验数据回归而来，即公式及试验数据本身存在一定的离散性所致。
表7 剪切骨架曲线特征点荷载计算值及其与试验值之比
Teble 7 Load calculated at characteristic point of shear skeleton curve and its ratio to test value
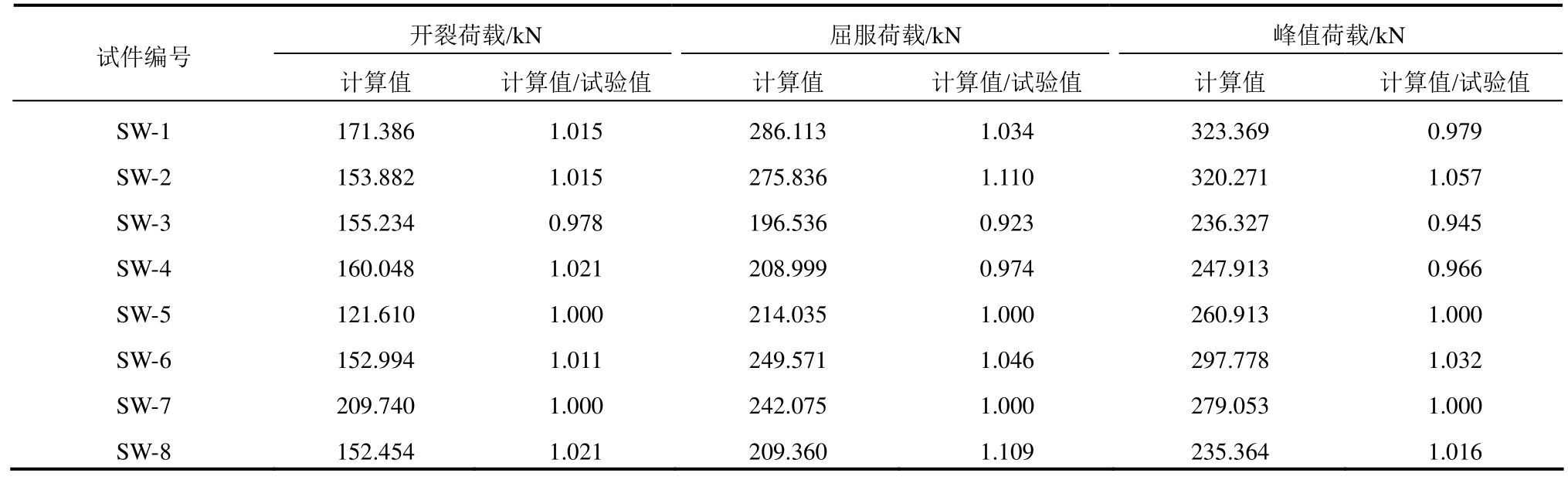
试件编号 开裂荷载/kN 屈服荷载/kN 峰值荷载/kNimages/BZ_89_1656_1242_1669_1301.png计算值 计算值/试验值 计算值 计算值/试验值 计算值 计算值/试验值images/BZ_89_1656_1303_1669_1362.pngSW-1 171.386 1.015 286.113 1.034 323.369 0.979 SW-2 153.882 1.015 275.836 1.110 320.271 1.057 SW-3 155.234 0.978 196.536 0.923 236.327 0.945 SW-4 160.048 1.021 208.999 0.974 247.913 0.966 SW-5 121.610 1.000 214.035 1.000 260.913 1.000 SW-6 152.994 1.011 249.571 1.046 297.778 1.032 SW-7 209.740 1.000 242.075 1.000 279.053 1.000 SW-8 152.454 1.021 209.360 1.109 235.364 1.016
表8 剪切骨架曲线特征点剪应变计算值及其与试验值之比
Teble 8 Shear distortion calculated at characteristic point of shear skeleton curve and its ratio to test value
试件编号 计算值 计算值/试验值 计算值 计算值/试验值 计算值 计算值/试验值开裂剪应变/( 10-3rad)屈服剪应变/( 10-3rad)峰值剪应变/( 10-3rad)SW-1 0.290 0.756 1.277 0.943 2.307 1.059 SW-2 0.290 0.539 1.285 0.885 2.887 0.926 SW-3 0.478 0.926 1.201 1.249 3.092 1.288 SW-4 0.383 1.317 1.516 1.015 3.921 1.143 SW-5 0.488 1.000 2.125 1.000 3.891 1.000 SW-6 0.334 0.617 1.462 0.717 3.967 0.907 SW-7 1.010 1.000 1.461 1.000 2.673 1.000 SW-8 1.007 0.758 2.435 0.903 5.378 0.929
剪切滞回模型的输入参数包括骨架曲线控制参数和滞回规则控制参数两部分。其中，骨架曲线控制参数按式(6)~式(8)计算确定；对于滞回规则控制参数，由于目前鲜有针对其定量方法的研究，且各低矮RC剪力墙试件滞回曲线的捏缩程度与刚度退化速率相差较多，同时滞回曲线的捏缩程度受混凝土强度、配筋方式与配筋率等诸多因素影响。因此，在参考 OpenSEES官网以及文献[24]的取值范围及建议并结合前述拟静力试验结果经多次试算调整后，本文取基于延性的损伤退化参数damage1=0.00，基于能量的损伤退化参数damage2=0.02，刚度退化参数beta以及变形(力)捏缩控制参数取值见表9所示，更合理的取值有待进一步研究。
表9 捏缩与刚度退化控制参数取值
Teble 9 Control parameters of pinch and stiffness degradation
试件编号 Pinchx Pinchy beta SW-1 0.70 0.30 0.70 SW-2 0.70 0.30 0.60 SW-3 0.65 0.35 0.60 SW-4 0.70 0.30 0.70 SW-5 0.70 0.30 0.70 SW-6 0.70 0.30 0.50 SW-7 0.51 0.50 0.70 SW-8 0.80 0.20 0.50
4 冻融损伤低矮RC剪力墙数值模型建立与验证
4.1 模型建立
4.1.1 不均匀冻融损伤混凝土模型
Petersen等[22－23]以相对动弹性模量为冻融损伤指标衡量混凝土构件的冻融损伤程度并量测了冻融后混凝土棱柱体试件不同位置处的相对动弹性模量，试验验证了冻融损伤在混凝土构件截面内的分布具有不均匀性。基于此，本文将低矮RC剪力墙构件截面按冻融程度划分不同部分，各部分由不同损伤程度的混凝土纤维和忽略冻融影响的钢筋纤维组成，(截面划分见图4(c)，不同颜色代表不同损伤程度)，并以相对动弹性模量RDME为冻融损伤系数作为联系混凝土强度和不同冻融损伤程度的桥梁，计算冻融损伤后的混凝土强度与弹性模量，其详细计算方法参见文献[25]，具体计算流程见图4(a)(图4(a)中，相对动弹性模量简化为R表示)。
此外，需要指出的是上述不均匀冻融损伤模型是基于 RILEM TC176-IDC[26]冻融条件，与本文人工气候快速冻融技术所采用的冻融试验方法不同。因此，为合理准确的使用上述不均匀冻融损伤模型，以导致相同动弹性模量退化程度为原则将本文冻融循环次数与文献[23]中的冻融循环次数进行等效，得到不同冻融条件下的等效冻融循环次数计算式[27]：
式中，Np、N分别为文献[23]与本文的冻融循环次数。
4.1.2 材料本构与截面划分以及单元类型
本文采用基于柔度法的非线性梁柱单元(Force-Based Beam-Column Element)模拟竖向悬臂低矮RC剪力墙，并沿墙体高度方向设置5个数值积分点，同时结合不均匀冻融损伤模型将墙体截面划分为具有不同损伤程度的5个部分，每个部分由边长为5 mm的正方形混凝土纤维和钢筋纤维组成。其中：非约束混凝土纤维本构采用 OpenSEES中的Concrete01模型，其峰值应力与弹性模量取值见表2；约束混凝土纤维本构采用Concrete02模型以考虑受拉混凝土作用；钢筋纤维本构采用SteelMPF模型，其应变硬化率取0.01，屈服强度与弹性模量取值见表3。
4.2 模型验证
为验证本文建议考虑不均匀冻融损伤影响组合剪切效应的纤维模型的准确性与适用性，采用上述方法对第1章中的8榀低矮RC剪力墙试件拟静力加载试验进行了模拟分析，所得模拟滞回曲线与试验滞回曲线对比见图8所示。由图8可见：基于所建议的冻融RC剪力墙数值模拟方法模拟所得各试件滞回曲线在骨架曲线、强度退化、刚度退化以及捏缩效应方面均与试验结果吻合较好；而试件SW-1的负向、SW-7的正向与试验滞回的吻合程度则相对较差，这主要是由于冻融的不均匀性以及初始加载的方向性使得正、负向加载时试件损伤累积不同导致试验滞回曲线呈现出较为明显的不对称分布所致。
模拟骨架曲线、滞回环面积与试验结果的接近程度是判别数值模拟结果准确性的重要条件。鉴于此，对模拟滞回曲线进行处理后得到各低矮RC剪力墙屈服和峰值状态下的荷载与位移模拟值、最终破坏时的累积耗能模拟值，及其与试验值的比值，列于表10。由表10计算得到：各试件屈服荷载、峰值荷载模拟值与试验值之比的均值分别为1.030、1.024，标准差分别为0.012、0.011；屈服位移、峰值位移模拟值与试验值之比的均值分别为 0.832、1.021，标准差分别为0.034、0.001；各试件最终破坏时的累积耗能模拟值与试验值之比的均值分别为1.033，标准差分别为0.017。
综上，采用本文建议的数值模拟方法所得各试件的滞回曲线、骨架曲线以及耗能能力均与试验结果符合较好，表明本文所建议的考虑不均匀冻融损伤分布的组合剪切效应的纤维模型能够较准确地模拟冻融损伤低矮RC剪力墙的滞回性能，较为精准的反映冻融大气环境下低矮RC剪力墙构件的力学性能与抗震性能。
图8 模拟与试验滞回曲线对比
Fig.8 Comparisons of the simulated and tested hysteretic curves
表10 累积耗能与骨架曲线特征点参数模拟值及其与试验值之比
Table 10 Simulation value of cumulative energy dissipation and skeleton curve characteristic parameter and its ratio with text value
注：试件各特征点荷载试验值见表4。
屈服荷载 屈服位移 峰值荷载 峰值位移 累积耗能试件 模拟值/编号 kNimages/BZ_91_661_2465_673_2519.pngimages/BZ_91_1096_2465_1109_2519.pngimages/BZ_91_1376_2465_1388_2519.pngimages/BZ_91_1736_2465_1749_2519.png模拟值/试验值试验值/mm模拟值/mm模拟值/试验值模拟值/kN模拟值/试验值试验值/mm模拟值/mm模拟值/试验值试验值/(kN·mm)模拟值/(kN·mm)模拟值/试验值SW-1 263.110 0.951 3.252 2.010 0.618 311.539 0.943 5.861 5.860 1.000 7100.311 6066.172 0.854 SW-2 256.071 1.031 2.973 2.439 0.820 311.844 1.029 5.970 5.973 1.001 5307.521 6112.814 1.152 SW-3 221.752 1.041 2.941 2.779 0.945 261.832 1.047 5.255 5.251 0.999 2966.100 2472.110 0.833 SW-4 222.600 1.038 2.703 2.221 0.822 262.500 1.023 5.413 5.890 1.088 3632.721 3690.547 1.016 SW-5 197.600 0.923 2.592 1.739 0.671 234.807 0.900 4.611 4.610 1.000 3077.616 3333.058 1.083 SW-6 242.825 1.018 3.151 3.140 0.996 292.768 1.015 5.892 5.885 0.999 5134.217 6110.28 1.190 SW-7 233.234 0.964 2.311 1.490 0.645 275.143 0.986 4.541 4.600 1.013 5937.918 6625.068 1.116 SW-8 240.035 1.272 2.772 3.154 1.139 289.948 1.252 5.511 5.890 1.069 6420.919 6554.482 1.021
5 结论
本文基于8榀冻融低矮RC剪力墙试件拟静力试验结果，对剪切破坏型RC剪力墙数值模拟方法进行了深入系统的研究，得到如下结论：
(1)通过理论分析与试验回归相结合的方法对8榀冻融损伤低矮RC剪力墙拟静力试验结果进行分析，建立了综合考虑冻融损伤参数和轴压比影响的低矮RC剪力墙剪切恢复力模型，并通过与试验值对比验证了该模型的准确性。
(2)结合不均匀冻融损伤模型，采用组合剪切效应的纤维模型，提出了冻融损伤低矮RC剪力墙数值模拟方法，并通过与试验结果对比表明：采用该模拟方法模拟所得各试件的滞回曲线、骨架曲线以及最终破坏时的累积耗能均与试验结果符合较好。
(3)本文所建立的数值模型能较准确的反映冻融环境下低矮RC剪力墙的力学和抗震性能，可用于该环境下在役RC剪力墙结构的抗震性能评估。
[1]Hidalgo P A, Ledezma C A, Jordan R M.Seismic behavior of squat reinforced concrete shear walls[J].Earthquake Spectra, 2002, 18(2): 287―308.
[2]纪晓东, 程小卫, 徐梦超.小剪跨比钢筋混凝土墙拉剪性能试验研究[J].工程力学, 2018, 35(增刊1): 53―61.Ji Xiaodong, Cheng Xiaowei, Xu Mengchao.Experimental study on tension-shear behavior of lowaspect-ratio RC walls [J].Engineering Mechanics, 2018,35(Suppl 1): 53―61.(in Chinese)
[3]白国良, 秦朝刚, 徐亚洲, 等.装配整体式与现浇剪力墙结构抗震性能对比分析[J].工程力学, 2019, 36(2):39―47.Bai Guoliang, Qin Chaogang, Xu Yazhou, et al.Contrastive analysis on aseismic performances between momolithic precast concrete and cast-in-place shear wall structure.[J].Engineering Mechanics, 2019, 36(2): 39―47.(in Chinese)
[4]邓明科, 寇佳亮, 梁兴文, 等.延性纤维混凝土剪力墙抗震性能试验研究[J].工程力学, 2014, 31(7): 170―177.(in Chinese)Deng Mingke, Kou Jialiang, Liang Xingwen, et al.Experimental investigation on aseismic behavior of dutile fiber reinforced concrete shear walls [J].Engineering Mechanics, 2014, 31(7): 170―177.
[5]杨红, 张睿, 臧登科, 等.纤维模型中非线性剪切效应的模拟方法及校核[J].工程科学与技术, 2011, 43(1):8―16.Yang Hong, Zhang Rui, Zang Dengke, et al.Simulating method and checking of nonlinear shear effect in fiber model [J].Engineering Science and Technology, 2011,43(1): 8―16.(in Chinese)
[6]Vásquez, Jorge A, De l L J C , Hube, Matías A.A regularized fiber element model for reinforced concrete shear walls [J].Earthquake Engineering & Structural Dynamics, 2016 45(13): 2063―2083.
[7]臧登科.纤维模型中考虑剪切效应的 RC结构非线性特征研究[D].重庆: 重庆大学, 2008.Zang Dengke.Study on nonlinear characteristics of rcstructures considering shear effect in fiber model [D].Chongqing: Chongqing University, 2008.(in Chinese)
[8]解琳琳.基于OpenSEES的RC构件抗震性能数值模拟及验证[D].安徽: 合肥工业大学, 2012.Xie Linlin.Numerical simulation and verification of seismic performance of RC members based on OpenSEES [D].Anhui: Hefei University of Technology,2012.(in Chinese)
[9]Hanjari K Z, Utgenannt P, and Lundgren K.Experimental study of the material and bond properties of frostdamaged concrete [J].Cement and Concrete Research.2011, 41(3): 244―254.
[10]Duan A, Jin W L, Qian J R.Effect of freeze-thaw cycles on the stress-strain curves of unconfined and confined concrete [J].Materials & Structures, 2011, 44(7): 1309―1324.
[11]冀晓东.冻融后混凝土力学性能及钢筋混凝土粘结性能的研究[D].辽宁: 大连理工大学, 2007.Ji Xiaodong.Experimental study and theoretical analysis on the mechanical performance of concrete and bond behaviour between concrete and stall bar after freezing and thawing [D].Liaoning: Dalian University of Technology, 2007.(in Chinese)
[12]郑山锁, 荣先亮, 张艺欣， 等.冻融损伤钢筋混凝土剪力墙恢复力模型研究[J].华中科技大学学报(自然科学版), 2019, 47(6): 109―114.Zheng Shansuo, Rong Xianliang, Zhang Yixin, et al.Restoring force model of freeze-thaw injury reinforced concrete shear walls [J].Journal of Huazhong University of Science and Technology(Natural Science Edition)2019, 47(6): 109―114.(in Chinese)
[13]郑山锁, 董晋琦, 荣先亮, 等.不同轴压比冻融 RC剪力墙抗震性能试验[J].天津大学学报(自然科学与工程技术版), 2019, 52(7): 690―698.Zheng Shansuo, Dong Jinqi, Rong Xianliang, et al.Experiment on the seismic behavior of freeze-thaw RC shear walls with different axial compression rations [J].Journal of Tianjin University(Science and Technology)2019, 52(7): 690―698.(in Chinese)
[14]Yang W, Zheng S S, Zhang D Y, et al.Seismic behaviors of squat reinforced concrete shear walls under freezethaw cycles: A pilot experimental study [J].Engineering Structures, 2016, 124: 49―63.
[15]郑山锁, 甘传磊, 秦卿, 等.冻融循环后一字形短肢剪力墙抗震性能试验研究[J].工程力学, 2016, 33(12):94―103.Zheng Shansuo, Gan Chuanlei, Qin Qing, et al.Experimental study on the seismic behavior of short-pier shear walls subjected to freeze-thaw cycles [J].Engineering Mechanics, 2016, 33(12): 94―103.(in Chinese)
[16]JGJ3―2002, 高层建筑混凝土结构技术规程[S].北京:中国建筑工业出版社, 2003.JGJ3―2002, Technical specification for concrete structures of tall buildings [S].Beijing: China Architecture & Building Press, 2003.(in Chinese)
[17]GB 50010―2002, 混凝土结构设计规范[S].北京: 中国建筑工业出版社, 2003.GB 50010―2002, Code for design of concrete structures[S].Beijing: China Architecture and Building Press,2003.(in Chinese)
[18]姚谦峰, 常鹏.工程结构抗震分析 [M].北京: 北京交通大学出版社, 2012: 180―183.Yao Qianfeng, Chang Peng.Seismic analysis of engineering structure [M].Beijing: Beijing Jiaotong University Press, 2012: 180―183.(in Chinese)
[19]Hirosawa M.Past experimental results on reinforced concrete shear walls and analysis on them [R].Tokyo,Japan: No 6 Building Research Institute, Ministry of Construction, 1975.
[20]Park Y J, Ang H S.Mechanistic seismic damage model for reinforced concrete [J].Journal of Structural Engineering, 1985, 111(4): 722―739.
[21]Cevdet Kerem Gulec.Performance-based assessment and design of squat reinforced concrete shear wall [D].Buffalo: The State University of New York, 2009.
[22]Petersen L.Influence of material deterioration processes on mechanical behavior of reinforced concrete structures[D].Germany: University of Hannover, 2004.
[23]Petersen L, Lohaus L, Polak M A.Influence of freezing-and-thawing damage on behavior of reinforced concrete elements [J].ACI Materials Journal, 2007,104(4): 369―378.
[24]秦卿.近海大气环境下多龄期 RC剪力墙结构抗震性能试验研究及地震易损性分析[D].陕西: 西安建筑科技大学, 2017.Qin Qing.Experimental study on seismic behavior of multi-age RC shear wall structures in offshore atmospheric environment and seismic vulnerability analysis [D].Shaanxi: Xi’an University of Architecture and Technology, 2017.(in Chinese)
[25]Qin Qing, Zheng Shansuo, Li Lei, et al.Experimental study and numerical simulation of seismic behavior for RC columns subjected to freeze-thaw cycles [J].Advances in Materials Science and Engineering, 2017,2017: 1―13.
[26]Setzer M J, Heine P, Kasparek S, et al.Test methods of frost resistance of concrete: CIF-test: capillary suction,internal damage and freeze thaw test-reference method and alternative methods A and B [J].Materials and Structures, 2004, 37(274): 743―753.
[27]张艺欣, 郑山锁, 裴培, 等.钢筋混凝土柱冻融损伤模型研究[J].工程力学, 2019, 36(2): 78―86.Zhang Yixin, Zheng Shansuo, Pei Pei, et al.Research on the modeling method of reinferced concrete column subjected to freeze-thaw damage [J].Engineering Mechanics, 2019, 36(2): 78―86.(in Chinese)