幂强化弹塑性材料在工程领域中的应用十分广泛，这种材料的受力及变形行为分析具有重要的理论价值和实际工程意义。幂强化弹塑性材料的特点是材料的变形规律会根据应力状态而改变，正是这种性质导致材料在达到屈服点后呈现非线性的本构关系，使得相关的力学问题难以解析求解。在工程问题中，材料的本构参数和结构的边界条件往往不容易确定，在这种情况下，反问题为确定这些参数提供了一种新思路。
反问题研究主要分为两个部分：正问题求解和反问题求解。幂强化材料的平面应变正问题的求解方法主要包括解析方法和数值方法，解析解[1-3]比较难获得，而数值解[4]主要是借助商业软件或者编写源程序。编写源程序需要深厚的理论基础并且花费大量时间和精力，不太适合工程技术人员，相比之下，商用软件的精度与效率都比较高，工程应用范围更广。
关于反问题的研究，国内外学者已经做了不少的研究工作，提出很多方法。何永勇等[5]基于遗传算法，实现了转子裂纹的识别。郭红玲等[6]基于蚁群算法求解弹性本构参数区间。姜绍飞等[7]对传统多粒子群协同优化(MPSCO)算法进行分布式并行化改进，开发了基于云计算的 PMPSCO 算法，提出了基于 PMPSCO 算法的框架结构物理参数辨识方法。Guo等[8]提出了一种基于猫群优化(CSO)算法的单、双二极管模型参数估计优化技术，结果表明该方法性能良好，CSO算法可以有效地解决太阳能电池模型参数辨识的优化问题。杨海天等[9]采用Levenberg-Marquardt(LM)算法对弹性支撑与本构参数进行单一/组合反演，以及基于梯度法求解平面双模问题确定本构参数[10]。郭力等[11]针对非线性参数反演过程中灵敏度计算困难的问题，提出了灵敏度分析和弹塑性参数反演的一种新方法。Astroza等[12]提出了一种新的框架，将基于高保真度力学的非线性(滞后)有限元模型和非线性随机滤波技术相结合，用于框架结构中未知材料参数的估计。韩阳等[13]基于LM算法对向家坝岩石的三轴压缩蠕变试验曲线进行拟合及参数识别。Cui等[14]基于最小二乘法，进行瞬态热传导反问题中的参数辨识，他们还基于改进的LM算法[15]求解瞬态非线性热传导的多重边界参数。薛齐文等[16]引入Bregman距离函数及其加权函数，应用正则化技术，建立了一种非定常热力耦合反问题的数值求解模式。韩雯雯等[17]基于共轭梯度法，利用圆管外壁面可测的有限温度信息，同时反演出第三类边界条件。大体上看，这些方法可以分为两种：随机法和梯度法。随机法可以实现全局搜索，但是计算时间长、收敛慢、效率低，通常在实际工程中很少采用；而梯度法效率高、计算时间短，在研究中被广泛使用。
综上所述，考虑到ABAQUS有限元商用软件具有强大的建模和计算能力，并且非常适于求解非线性问题，本文应用ABAQUS软件对幂强化材料的平面应变问题进行数值求解，然后采用梯度法对反问题进行求解。在梯度法中，灵敏度矩阵的准确确定非常重要，文献[18]验证了复变量求导法相对差分法的优越性。然而在本文以前，能够准确确定灵敏度矩阵的复变量求导法很难与ABAQUS有限元软件相结合，这是因为普通用户无法获得ABAQUS有限元软件中的全部源程序代码。为此，本文将ABAQUS中的用户单元子程序(UEL)与复变量求导法相结合[19]，首次用于力学反问题的求解。既保证正问题求解的高效率与高精度，同时采用复变量求导法准确确定灵敏度矩阵。最后，采用最小二乘法对反问题进行求解。据笔者目前所知，并未有其他文献涉及本文研究内容。
1 正问题的有限元推导
1.1 基本控制方程
本文研究的是幂强化弹塑性材料的平面应变问题的反问题分析。在正问题中，模型的变形存在两个阶段：线弹性变形阶段与塑性变形阶段。
有限单元法中，单元需要满足静力平衡方程[20]：
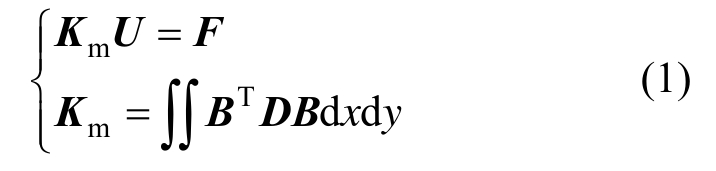
式中：B为应变位移矩阵；D为单元的应力应变矩阵；Km为单元刚度阵；U为单元节点的位移向量；F为单元的节点载荷列向量。
位移边界条件：
式中：us、vs为单元节点的已知位移；
为已知边界的位移分量。
应力边界条件：
式(3)中：
为已知边界的应力分量；l和m为边界的方向余弦。
1.2 弹性变形阶段
线弹性阶段的本构矩阵表达式为：
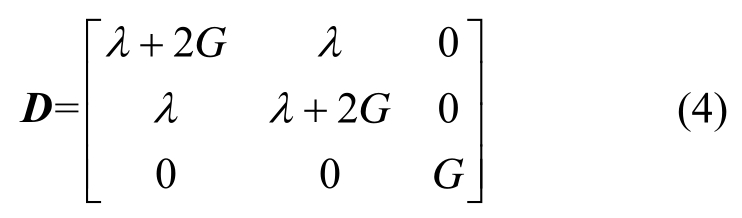
其中：
为弹性模量，ν为泊松比。
1.3 塑性变形阶段
当物体内某一点的Von Mises应力
超过了材料的初始屈服应力σ0，材料开始进入屈服状态，物体的变形开始出现塑性变形。此时，材料的屈服应力可以表示为：
式中：E1为材料的强化系数；p为等效塑性应变；n为材料的强化指数，一般是介于0～1的正数。
由于材料本构关系的非线性，在材料发生塑性变形时，应力-应变关系很难通过解析解求得。因此，本文利用Newtown迭代法求解单元的等效塑性应变增量Δp，在屈服阶段，单元要满足屈服方程[21]：
将屈服方程进行泰勒展开，可得：
则可以得到：
式中，H=npn-1为当前屈服过程中应变强化系数。
在Newtown迭代完成后，需要对各种变量进行更新，更新的方法如式(10)～式(18)所示：
式中：
为试探应力σtr 的应力偏量；Δεp为塑性应变增量；Δεe 为弹性应变增量；εp为塑性应变；εe为弹性应变；I为单位矩阵。
计算塑性变形下的Jacobian矩阵：
Jacobian矩阵的表达式为：
求得Jacobian矩阵后，将J中与z方向无关的元素提取出来，组成新的矩阵D。
将D代入式(1)中，即可求解当前载荷下单元的静力平衡方程。
2 反问题理论基础
2.1 反问题中的目标函数
在反问题中，材料的杨氏模量、泊松比、位移边界条件与载荷边界条件的大小是未知的，其他条件与正问题一样给定，所需要的额外信息是物理量测量值，这些测量值可以通过实验仪器测量所得。在本文中，这些测量信息是测点的位移值，通过数值模拟得到。
二维平面应变的反问题的优化目标函数可以表示为：
式中：M为测量点的数量；N为待反演参数的个数；z=(z1,z2,z3,…,z N )T为待反演的参数向量；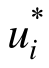
和ui分别为测点位移的测量值和计算值，i=1,2,…,M。
2.2 最小二乘法
全局余量矢量为R，其表达如式(23)所示。
式中，R为残余矢量，代表u*和u的差距。
经过推导，残余矢量与参数增量的关系可以表示为如下矩阵形式。具体推导见文献[14]。
式中，[∂u/∂z]为灵敏度矩阵，由位移对各反演参数的一阶偏导数组成，详见文献[14]。
由于式(24)为病态方程组，应用最小二乘法可以得到稳定的解，表达式如下所示：
式(25)利用高斯消元法求解，可以得到更新的z的值。
式中，w为松驰因子[14]。
2.3 复变量求导法
1967 年，Lyness和Moler[22]提出了复变量求导法，该方法一般是将实数函数f(x)中的自变量x替换成复数变量x+ih，其中h取值很小，一般取10-20，通过泰勒级数展开后，f(x+ih)可以表示为：
由于h的取值很小，所以f(x)的一阶导数可以表示如下：
式中，Im代表虚部。
在复变量求导法中，由于直接计算，所以一阶偏导数的计算与空间步长大小无关，不涉及截断误差。因此，复变量求导法在一阶偏导数的计算精度方面，总体上要优于传统的差分法[23]。本文的各灵敏度系数均采用复变量求导法获得。
2.4 复变量求导法与ABAQUS有限元方法的结合
由于ABAQUS有限元软件对复杂不规则或大型结构的非线性力学问题的适应性强，本文采用ABAQUS有限元软件对正问题进行求解。现有的ABAQUS软件只能实现实数值的求解，而没有对复数进行运算的求解器。为了采用复变量求导法获得反演计算所需的灵敏度系数，本文采用ABAQUS的UEL子程序，这涉及实数变量与复数变量的形式转换。
对于每个单元，需要将单元的每个节点变成一个实数节点和一个虚数节点相结合的复数节点，则二维复数单元的节点位移矢量具有如下形式：
式中：uRe=(ux,uy )T代表传统单元节点的位移值；uIm代表虚数节点的位移。
通常可以将uIm表示为参数θ的扰动h对节点位移uRe的影响：
式中，u′为位移uRe对于参数θ的偏导数。
由于将传统实单元转换成了复数单元，那么相应地，静力平衡方程(1)的复数形式为：
式中，B*和D*分别是B和D的复数形式。
为了利用ABAQUS求解器求解这些方程，对于形如n×n的复数矩阵就必须化成2n×2n的实数矩阵，例如复数单元刚度阵的实数化如下所示：
静力平衡方程的实数形式为：
将式(33)传递给ABAQUS求解，就能求出单元上虚值节点的位移，从而求出该点位移对被扰动参数的灵敏度系数，组成反演过程中的灵敏度矩阵。
2.5 反问题的收敛准则
当反演计算过程中目标函数的值小于一个给定的足够小的正数，或者前后两次的目标函数几乎不变化时，迭代结束，可以表示为：
式中，ξ为给定的足够小的正数，本文取ξ=10-5。
反问题的计算过程可以总结为以下几步：
1) 假设待辨识的各参数的初始值为z0，假设初始迭代步k=0。
2) 将当前的参数值zk传递进被调用的正问题求解程序，获得该迭代步下的计算值uk。
3) 检查目标函数是否满足收敛准则，如果满足，则迭代过程结束，计算停止；如果不满足，继续以下步骤。
4) 采用复变量求导法计算各参数的灵敏度系数[∂u/∂z]，测量值与计算值的差。通过最小二乘法求解得到Δz。
5) 计算得到zk+1。
6) 当前迭代步为k=k+1，返回第(2)步，继续计算。
3 数值算例1
3.1 复数有限元方法用于求解正问题的精度验证
本文的算例由正问题和反问题组成，其中正问题是利用ABAQUS用户单元子程序(UEL)求解幂强化弹塑性材料的非线性平面应变问题。本文选取的算例模型为带椭圆孔的六边形，如图1所示。其中模型的尺寸如图1所示，椭圆孔位于模型中心，模型一共由2346个单元组成(图2)，单元类型为8节点的完全积分平面应变单元。
图1 算例1的模型尺寸和测点位置 /mm
Fig.1 Model dimensions and measurement points in example 1
a、b边为固支边，c边的初始位移条件为
初始的载荷边界条件为椭圆孔墙壁d受到了与外法线方向相反的均布载荷P|d=20MPa，材料的弹性模量为5 2.1×10MPa，泊松比为0.3，初始屈服应力为100 MPa。
图2 算例1模型的网格划分形式
Fig.2 The grid division form of model in example 1
材料的屈服应力表达式为：
为了验证分别使用ABAQUS的自带CPE8单元与使用本文建立的自定义复变量UEL计算弹塑性问题的结果一致性，从模型上随机提取10个节点，节点位置如图1所示，节点的位移值如表1所示。
表1 两种单元下节点位移的对比以及误差
Table 1 Comparison of node displacements and errors between the two elements
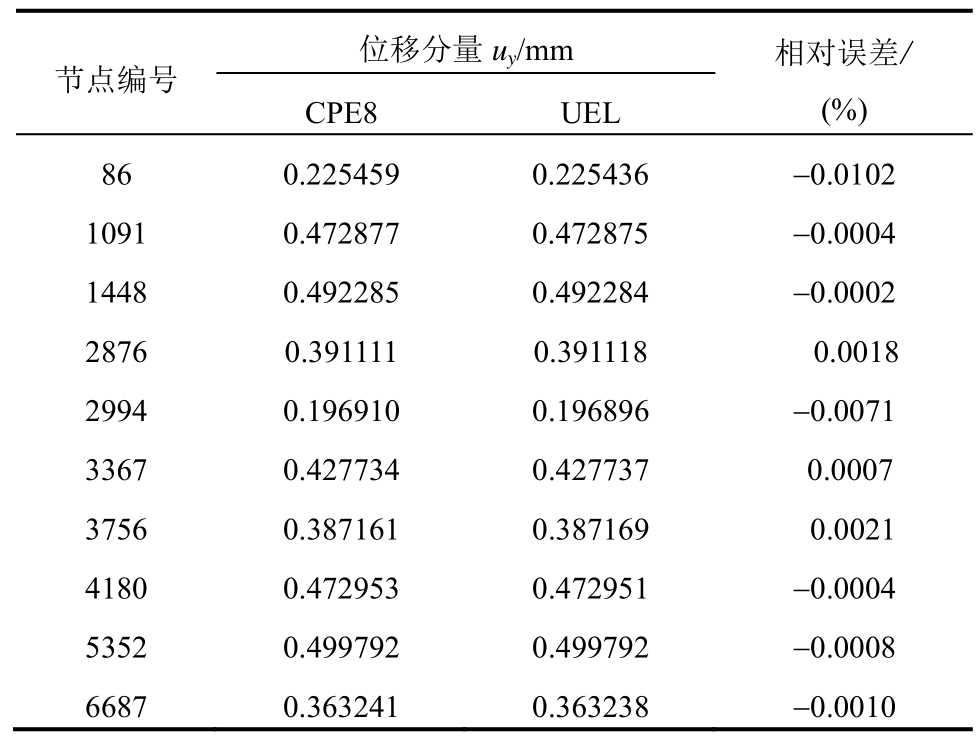
节点编号 位移分量uy/mm 相对误差/(%)CPE8 UEL 86 0.225459 0.225436 -0.0102 1091 0.472877 0.472875 -0.0004 1448 0.492285 0.492284 -0.0002 2876 0.391111 0.391118 0.0018 2994 0.196910 0.196896 -0.0071 3367 0.427734 0.427737 0.0007 3756 0.387161 0.387169 0.0021 4180 0.472953 0.472951 -0.0004 5352 0.499792 0.499792 -0.0008 6687 0.363241 0.363238 -0.0010
此外，本文还比较了应力结果。随机选取5个单元，单元中心积分点的y方向正应力的结果如表2所示。
从表1和表2可以看出，无论是将节点位移还是将积分点应力分量进行比较，利用ABAQUS传统单元计算的结果与利用复变量UEL计算的结果非常接近，两者计算结果相对误差均小于0.05%。可见，将复变量引入到UEL中以后，对计算结果的实数部分没有影响。
表2 单元中心积分点应力的比较
Table 2 Comparison of stresses at the central integral point of the element
单元编号 应力分量σy/MPa 相对误差/(%)CPE8 UEL 40 115.962 115.962 0.0000 220 60.4363 60.4354 -0.0015 420 115.602 115.600 -0.0014 640 -4.39954 -4.39801 -0.0349 1100 77.0797 77.0863 0.0086
采用应力或者位移作为测量物理量进行反演，都是有效的，本文将位移作为测量物理量进行后文的反演。
3.2 本构参数与边界条件的反演
当结构处于塑性变形阶段，材料的本构参数很难确定，因此，反演方法提供了一种新手段。在本文的反问题中，弹性模量、泊松比以及边界条件的值未知，需要进行反演，其他的计算条件均已知，与3.1节正问题模型相同。将正问题中一些节点x方向上的位移作为测量值，测量点选取的个数为100个，选取的方法为，以单元编号为参考，初始单元编号为40，此后每隔20个单元再选为下一个单元，依此类推，最后一个被选中的单元编号为2020。将被选中单元的第五个节点的x方向位移作为测点测量值。需要反演的各参数的初始值为：弹性模量E=2×105MPa，泊松比ν=0.2，边界位移
为[0.2,0.2]Tmm，均布载荷P为2 MPa。
图3显示了各参数的收敛过程，经过13次迭代后，各参数分别收敛于真实值，收敛时目标函数为1.35×10-6，可见本文提出的方法对于力学参数的反演具有较高的精度。同时，从图4可以观察到，优化目标函数的值总体上下降得比较快，这说明本文使用的算法不仅具有高精度，而且具有较高的效率。
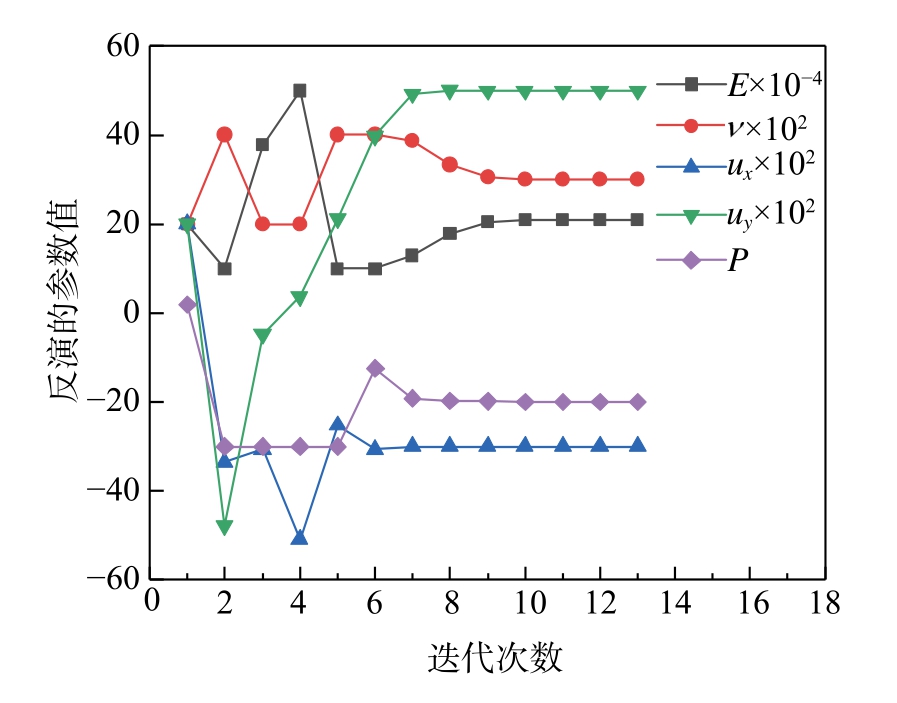
图3 各参数的收敛过程
Fig.3 The convergence process of each parameter
图4 目标函数的变化过程
Fig.4 Change process of objective function
3.3 反演初值的影响
为了研究参数反演初值的选取对反演过程的影响，选取4组参数初值，除初值的选取不同以外，其他条件均与3.2节相同。研究在不同初值情况下，迭代的收敛情况以及迭代次数，如表3所示。
表3 不同初值对收敛过程的影响
Table 3 The influence of different initial values on the process of convergence
参数和迭代情况第1组 第2组 第3组 第4组弹性模量E/MPa2×105 3×105 4×105 2×105泊松比ν 0.2 0.3 0.4 0.2 x方向位移边界/mm u 0.2 0.3 0.4 10 y方向位移边界/mm x P 2 3 4 10收敛与否 是 是 是 否迭代总次数 13 12 13 ―u 0.2 0.3 0.4 10均布荷载/MPa y
如表3显示，收敛情况与初值有关。如果初值选取不当，如第4组，可能会导致反演过程不收敛，而当初值选取合适，如第1组～第3组，收敛迭代的总次数与初值没有明显的关系。所以在反演过程中，已知辨识参数的大致范围对成功反演有帮助。
4 数值算例2
4.1 反演效率和精度分析
为了验证本文反演算法对不同模型和不同参数的适应性，考虑另一个模型，即一个带孔的圆环模型，如图5所示，圆环的内半径为40 mm，外半径为100 mm，在圆环的周向方向上，存在着4个均匀分布的半径为10 mm的圆孔。圆环内壁受到P1=100 MPa的压强，圆孔受到P2=30 MPa的压强。由于模型的对称性，在有限元的数值分析中将模型的1/4取出作为分析对象。
图5 算例2模型的尺寸 /mm
Fig.5 Model size of example 2
有限元模型的网格划分如图6所示，模型一共由404个单元组成，单元类型为8节点的完全积分平面应变单元。模型两条直边为对称边界条件。材料的杨氏模量5 5×10MPa，泊松比为0.35，弹塑性参数与算例1保持一致。测点为随机选取的20个单元的第五个节点，测量物理量为该测点的x方向位移。
图6 算例2模型的网格划分形式
Fig.6 The grid division form of model in example 2
在反问题中，待反演的参数为弹性模量E，泊松比ν，压强P1和P2。初值的的选取E=2.5MPa ×106MPa，ν=0.25，P1=200 MPa，P2=50 MPa，松弛因子w取1。图7为在无误差测量值下的参数反演过程。
4.2 测量误差的影响
在实验过程和实际的工程中，位移的大小是通过仪器测量得到的。不可避免地，测量中会存在误差，为了研究测量误差对于最后反演结果的影响，定义相对误差Erel为：
图7 各参数的收敛过程
Fig.7 The convergence process of each parameter
式中：z为待反演的参数；zestimated和zexact分别为在有/无测量误差时参数反演的结果。
为了定量地分析测量误差的大小对于反演参数的影响，假设测点的误差分别为1%、5%、10%，所以测量的位移值可以表示为：
式中：umeasured代表位移的测量值；ζ为测量误差；γ为-1～1的随机数。
计算条件与4.1节相同，分别在20个测点上施加随机误差，测量误差分别为1%、5%、10%。
表4 三种测量误差对反演结果的影响
Table 4 The influence of three kinds of measurement errors on inversion results
结果相对误差Erel/(%)反演参数测量误差ζ=1测量误差ζ=5测量误差ζ=10弹性模量E/MPa 0.28 1.36 1.23泊松比ν 0.73 0.87 1.37压强P1/MPa 0.03 0.06 0.31压强P2/MPa 0.16 1.19 0.82
从表4可以看出，测量误差对反演结果有影响，测量误差越大，反演的参数与真实值的差距也越大。在一定的测量误差内，应用本文的方法仍然可以反演出较为准确的结果，同时可以发现Erel的值都小于相应给定的测量误差。
5 结论
本文首次将ABAQUS的用户单元子程序(UEL)与复变量求导法结合起来，用于幂强化弹塑性材料的平面应变反问题。该方法可以准确求出反演所需要的计算值与灵敏度矩阵，并且验证了复变量UEL求解力学问题的精度。在反问题中，以计算值与测量值之间的残差作为优化目标函数，在上一步得到了灵敏度矩阵后，利用最小二乘法求解优化参数的增量，进行多次迭代直到收敛。可以得出如下结论：
(1) ABAQUS中的UEL与复变量求导法相结合是确定求解反问题的梯度法中灵敏度矩阵的一种有效方法，所建立的复单元既不影响实数部分的计算，又能得到精确的灵敏度系数。
(2)本文建立的反问题求解算法是有效的，可以同时反演多个不相关的参数，包括材料本构参数和边界条件。
(3)反演参数初值影响反演结果：在合适的范围内，不同的初值对于总迭代次数和辨识结果没有明显影响；超过该范围，可能会导致反演发散。
(4)当存在一定的测量误差时，本文建立的反演方法仍然具有较高的精度。
本文为解决复杂结构非线性材料的力学反问题提供了一种新方法。
[1]樊森清, 王坤哲, 文良凡, 等.膨胀管技术中膨胀力的理论计算[J].石油机械, 2012, 40(8): 34―37.Fan Senqing, Wang Kunzhe, Wen Liangfan, et al.Theoretical calculation of the expansive force of the expandable tubular material [J].China Petroleum Machinery,2012, 40(8): 34―37.(in Chinese)
[2]侯公羽, 李晶晶, 杨悦, 等.基于幂强化本构模型的轴对称圆巷弹塑性解[J].岩土力学, 2014, 35(01): 134―142.Hou Gongyu, Li Jingjing, Yang Yue, et al.Elastoplastic solution of axisymmetric circular tunnel based on power-hardening model [J].Rock and Soil Mechanics,2014, 35(01): 134―142.(in Chinese)
[3]唐胜兰, 俞缙, 张建智, 等.顾及沉积岩应变强化与扩容效应的围岩弹塑性力学状态理论分析[J].华侨大学学报(自然科学版), 2016, 37(06): 691―697.Tang Shenglan, Yu Jin, Zhang Jianzhi, et al.Analytical research for elastoplastic mechanical response considering strain-hardening and dilatancy of sedimentary rock[J].Journal of Huaqiao University (Natural Science),2016, 37(06): 691―697.(in Chinese)
[4]任志乾, 于宗乐, 陈循.钢丝绳弹塑性损伤本构模型研究[J].机械工程学报, 2017, 53(1): 121―129.Ren Zhiqian, Yu Zongyue, Chen Xun.Study on wire rope elastic-plastic damage constitutive model [J].Journal of Mechanical Engineering, 2017, 53(1): 121―129.(in Chinese)
[5]何永勇, 褚福磊, 郭丹, 等.基于遗传算法的旋转机械转子裂纹识别的研究[J].机械工程学报, 2001,(10):69―74.He Yongyong, Chu Fulei, Guo Dan, et al.Study on genetic algorithms based rotor crack detection for rotating machin[J].Journal of Mechanical Engineering, 2001(10):69―74.(in Chinese)
[6]郭红玲, 杨海天, 赵潇.蚁群算法求解弹性本构参数区间反问题[J].工程力学, 2012, 29(1): 7―12.Guo Hongling, Yang Haitian, Zhao Xiao.Solving an inverse problem of intervals of elastic constitutive parameters via ant colony algorithm [J].Engineering Mechanics, 2012, 29(1): 7―12.(in Chinese)
[7]姜绍飞, 任晖, 骆剑彬.基于云计算的框架结构参数并行辨识算法[J].工程力学, 2018, 35(4): 135―143.Jiang Shaofei, Ren Hui, Luo Jianbin.A parallel identification algorithm on physical parameters of frame structures based on cloud computing [J].Engineering Mechanics, 2018, 35(4): 135―143.(in Chinese)
[8]Guo Lei, Meng Zhuo, Wang Libiao, et al.Parameter identification and sensitivity analysis of solar cell models with cat swarm optimization algorithm [J].Energy Conversion & Management.2016, 108(Jan.): 520―528.
[9]杨海天, 杨博, 李哈汀.带有弹性边界支撑梁的多宗量反问题数值求解[J].大连理工大学学报, 2011(4):469―472.Yang Haitian, Yang Bo, Li Hating.Numerical solution of multi-variables inverse problem for a beam with elastic boundary supports [J].Journal of Dalian University of Technology, 2011, (4): 469―472.(in Chinese)
[10]Ran Chunjiang, Yang Haitian, Zhang Guoqing.A gradient based algorithm to solve inverse plane bimodular problems of identification [J].Journal of Computational Physics, 2018, 355: 78―94.
[11]郭力, 高效伟.复变量求导法灵敏度分析及弹塑性参数反演[J].东南大学学报(自然科学版), 2008(1): 141―145.Guo Li, Gao Xiaowei.Sensitivity analysis and elasto-plastic parameter inversing via complex-variable differentiation method [J].Journal of Southeast University (Natural Science Edition), 2008(1): 141―145.(in Chinese)
[12]Astroza Rodrigo, Ebrahimian Hamed, Conte Joelp.Material parameter identification in distributed plasticity fe models of frame-type structures using nonlinear stochastic filtering [J].Journal of Engineering Mechanics,2015, 141(5): 04014149.
[13]韩阳, 谭跃虎, 李二兵, 等.岩石非定常Burgers蠕变模型及其参数识别[J].工程力学, 2018, 35(3): 210―217.Han Yang, Tan Yuehu, Li Erbing, et al.Non-stationary burgers creep model of rock and its parameter identification [J].Engineering Mechanics, 2018, 35(3): 210―217.(in Chinese)
[14]Cui Miao, Duan Weiwei, Gao Xiaowei.A new inverse analysis method based on a relaxation factor optimization technique for solving transient nonlinear inverse heat conduction problems [J].International Journal of Heat and Mass Transfer, 2015, 90: 491―498.
[15]Cui Miao, Zhao Yi, Xu Bingbing, et al.A new approach for determining damping factors in Levenberg-Marquardt algorithm for solving an inverse heat conduction problem[J].International Journal of Heat and Mass Transfer,2017, 107: 747―754.
[16]薛齐文, 张雪珊.热力耦合反问题研究[J].机械工程学报, 2010, 46(18): 157-161.Xue Qiwen, Zhang Xueshan.Research of inverse problem of thermo-mechanical coupling[J].Journal of Mechanical Engineering, 2010, 46(18): 157―161.(in Chinese)
[17]韩雯雯, 吴健, 刘长亮, 等.基于导热反问题的二维圆管内壁面第三类边界条件的反演[J].机械工程学报,2015, 51(16): 171―176.Han Wenwen, Wu Jian, Liu Changliang, et al.Inversion of the third boundary condition on the inner wall of atwo-dimensional pipe based on inverse heat conduction problems [J].Journal of Mechanical Engineering, 2015,51(16): 171―176.(in Chinese)
[18]Cui Miao, Yang Kai, Xu Xiaoliang, et al.A modified Levenberg–Marquardt algorithm for simultaneous estimation of multi-parameters of boundary heat flux by solving transient nonlinear inverse heat conduction problems [J].International Journal of Heat and Mass Transfer, 2016, 97: 908―916.
[19]Fielder Randal, Montoya Arturo, Millwater Harry, et al.Residual stress sensitivity analysis using a complex variable finite element method [J].International Journal of Mechanical Sciences, 2017, 133: 112―120.
[20]王勖成.有限单元法[M].北京: 清华大学出版社,2003: 62.Wang Xucheng.Finite Element Method[M].Beijing:Tsinghua University press, 2003: 62.(in Chinese)
[21]Dunne, Fionn, Nik Petrinic.Introduction to computational plasticity [M].New York: Oxford University press, 2005: 17.
[22]Lyness J N, Moler C B.Numerical differentiation of analytic functions [J].Siam Journal on Numerical Analysis, 1967, 4(2): 202―210.
[23]Gao X W, Liu D D, Chen P C.Internal stresses in inelastic BEM using complex-variable differentiation [J].Computational Mechanics, 2002, 28(1): 40―46.