桁架具有拆装运输方便、能充分利用材料强度等优点,且该类结构仅考虑轴力作用,因而相对框架等结构而言,优化的设计变量和状态变量相对较少,相关的结构分析较容易实施,因而新提出的结构优化方法通常选择理想桁架结构模型作为验证方法适用性的结构载体,使得桁架结构优化成为结构优化设计的基本问题。
桁架结构优化设计方法主要有优化准则法[1]和数学规划法[2]。优化准则法基于工程经验、力学概念和数学原理设定一组准则,据此建立结构优化设计的迭代公式,简单实用。而且,由于准则法中设计变量的数量与优化迭代次数的关系不大,较数学规划法具有更高的计算效率[1],因而得到广泛的应用。当前常用的结构优化设计方法[3-5]大多采用结构在设计荷载下根据弹性理论求得的内力分布状态确定各构件的强度需求,并据此开展优化设计。此类方法能够有效满足构件层面的强度需求,是当前结构优化设计的主流方法。但由于未考虑结构在罕遇荷载下进入弹塑性状态乃至塑性极限状态(形成体系失效模式)时内力重分布的影响,因而不能满足结构体系强度需求。为研究结构在罕遇荷载下的体系强度,文献[6-8]开展了抗震结构失效模式的识别和优化研究。进一步地,结构塑性设计理论[9-10]以及在此基础上发展起来的直接设计法(也称为高等分析法)[11-12]按照结构进入塑性极限状态(形成体系失效模式)时的内力分布状态确定结构体系强度需求,由此建立的设计方案能够阻止体系失效模式的形成,满足结构体系层面的强度需求。在塑性设计基础上文献[9]尝试开展桁架结构体系强度的优化设计。目前,直接设计法(或称为高等分析法)也陆续引入欧美国家以及我国最新的钢结构设计规范[13-14]中。然而,基于塑性设计和直接设计法理论发展而来的结构体系强度优化设计方法不能阻止部分高承载构件中出现塑性铰[15-16],因而难以保证满足构件层面的强度需求。
合理的结构设计方案既要满足设计荷载下构件层面的强度需求,也要满足罕遇荷载下体系层面的强度需求[17]。Wang等[18]基于常规塑性铰法确定桁架结构体系强度需求,并利用遗传算法搜索确定能够同时满足构件和体系强度需求的优化设计方案,计算格式复杂且耗时,究其原因在于该方法不能给出结构体系强度与构件强度之间的显式关系,因而难以通过正常的构件设计满足结构在构件和体系两个层面的强度要求。为此,文献[19-20]采用弹性模量缩减法(elastic modulus reduction method,简记为EMRM)分析工程结构体系层面的承载力,据此确定结构在构件和体系两层面强度需求之间的显性关系式。在此基础上,文献[21-22]研究建立了结构两层面强度优化设计的均匀承载准则法,由此建立的结构设计和优化方案能够同时满足结构在构件和体系两个层面的强度需求,从而解决了传统优化设计理论的难题。但是该方法依据基准承载比[19-20]确定构件强度的调整量,导致低承载构件和部分高承载构件的强度富余量较大,优化效果得不到保障,而且文献[21-22]没有考虑稳定性对杆件强度的影响,导致优化设计方案不满足安全性要求。
鉴于此,本文考虑细长杆稳定性对桁架结构两层面强度的影响,研究建立钢桁架结构两层面强度优化设计的改进均匀承载准则法。首先在单元承载比中引入轴压杆稳定性影响,然后利用EMRM的迭代首步和末步的单元承载比建立了桁架在构件强度与体系强度之间的显性关系式,并按照两层面强度系数的目标值调整各构件强度,据此建立桁架结构两层面强度优化设计的改进均匀承载准则法。
1 桁架结构两层面强度需求
单元承载比(EBR)是EMRM的控制参数,用于综合评估单元在荷载作用下接近于全截面塑性屈服状态的程度,取值区间为[0,1],用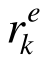 表示,其中k表示迭代步,e表示单元编号。对于桁架结构,由于各杆件仅受轴力Ne作用,可据此定义
表示,其中k表示迭代步,e表示单元编号。对于桁架结构,由于各杆件仅受轴力Ne作用,可据此定义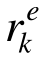 :
:

式中,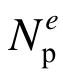 表示单元e全截面塑性抗拉/压强度,当忽略材料受拉、受压屈服强度σs的区别时,有:
表示单元e全截面塑性抗拉/压强度,当忽略材料受拉、受压屈服强度σs的区别时,有:
式中,A为杆件横截面面积。中长杆受压时,需要考虑稳定性对抗压强度的影响:
式中,φ为轴心受压构件的稳定系数,由《钢结构设计规范》(GB 50017―2017)[14]附录G确定,且与构件长细比(或换算长细比)等因素密切相关,其中的长细比取决于轴压杆的计算长度,且需要考虑平面内和平面外两种不同的受力状态,具体按《钢结构设计规范》(GB 50017―2017)表5.3.1确定。
单元承载比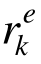 随着迭代的进展而在结构空间的分布越来越均匀。为便于描述
随着迭代的进展而在结构空间的分布越来越均匀。为便于描述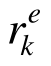 在结构空间分布的状态,定义承载比均匀度dk:
在结构空间分布的状态,定义承载比均匀度dk:
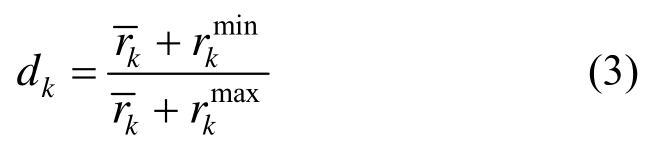
式中:下标k表示EMRM迭代步;![]() 分别表示结构中单元承载比的平均值、最大值和最小值。据此,可进一步定义基准承载比
分别表示结构中单元承载比的平均值、最大值和最小值。据此,可进一步定义基准承载比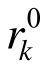 :
:
根据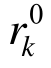 可以建立判别高承载单元的动态准则:满足
可以建立判别高承载单元的动态准则:满足![]() 的单元,属于高承载单元,否则称为低承载单元。
的单元,属于高承载单元,否则称为低承载单元。
通过缩减高承载单元的弹性模量可以模拟加载过程中结构的刚度损伤和衰减:
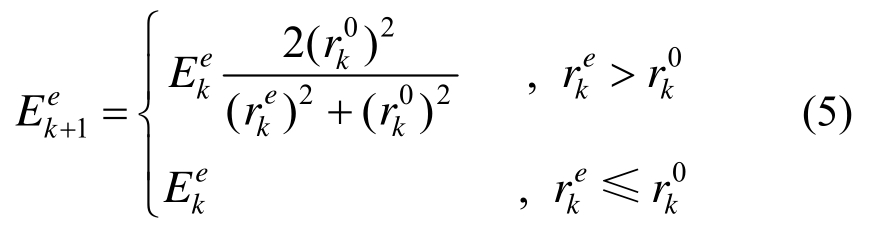
式中,![]() 表示单元e的弹性模量在两相邻迭代步k+1和k时的取值。
表示单元e的弹性模量在两相邻迭代步k+1和k时的取值。
由式(1)可见,结构加载中单元承载比随着外荷载呈比例增大,当![]() 增大到1时,
增大到1时,![]() 所在单元达到全截面塑性屈服,此时对应的外荷载为第k迭代步的极限荷载
所在单元达到全截面塑性屈服,此时对应的外荷载为第k迭代步的极限荷载![]()
式中,P0为外荷载初始值,在两层面强度设计中取荷载设计值。
重复以上迭代计算,直至第M迭代步的计算结果![]() 满足收敛条件:
满足收敛条件:
式中,ε表示容许误差,取值范围为10-5~10-2。
第M步是迭代末步,根据该步的计算结果![]() 可以得到结构极限强度PLim:
可以得到结构极限强度PLim:
式中,PLim是塑性极限荷载的下限,对应于结构体系能够承受的罕遇荷载。大型工程结构的极限承载力难以精确计算,通常可利用塑性极限荷载的下限近似表达。结构极限承载力也称为结构体系强度。
上述计算结构体系强度的方法称为弹性模量缩减法[19-20],简记为EMRM。文献[19-20]研究表明,EMRM通过线弹性迭代分析确定结构体系强度,与常见的弹塑性方法相比能够取得更高的计算效率。
EMRM首步迭代(k=1)分析得到的单元承载比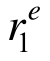 对应于桁架结构在设计荷载下的弹性内力Ne,据此可确定桁架在构件层面的强度需求
对应于桁架结构在设计荷载下的弹性内力Ne,据此可确定桁架在构件层面的强度需求![]() 同时EMRM迭代末步(k=M)得到的单元承载比
同时EMRM迭代末步(k=M)得到的单元承载比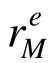 对应于桁架结构在罕遇荷载下进入塑性极限状态时的内力,利用此时的最大单元承载比
对应于桁架结构在罕遇荷载下进入塑性极限状态时的内力,利用此时的最大单元承载比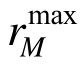 可以确定桁架在体系层面的强度需求PLim。
可以确定桁架在体系层面的强度需求PLim。
2 桁架结构两层面强度设计
结构设计方案既要保证结构在设计荷载下处于弹性状态,避免结构在重复荷载下发生塑性积累;而且为了节省材料、控制造价,应允许结构在预定的罕遇荷载作用下进入弹塑性状态,甚至逼近塑性极限状态,但不能发生倒塌破坏,从而保证结构的安全性。这两个“保证”可以通过两层面强度设计来实现:首先通过结构在设计荷载下的弹性分析确定构件层面的强度需求,然后通过罕遇荷载下的塑性极限分析确定结构在体系层面的强度需求,据此开展结构两层面强度设计。由于EMRM迭代分析的首步和末步分别对应结构弹性分析和塑性极限分析状态[19-20],因而,这里选择EMRM作为两层面设计的工具。
2.1 构件层面的强度设计
由于桁架结构模型中同一构件c的轴力通常不发生变化,因此桁架结构分析的有限元模型中每个等截面构件通常为一个单元e,此时的单元承载比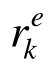 等同于构件承载比
等同于构件承载比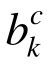 。特殊地,当同一构件上需要划分为多个单元时,取其中最大的
。特殊地,当同一构件上需要划分为多个单元时,取其中最大的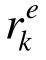 作为该构件的
作为该构件的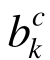 ,即有:
,即有:![]() 其中,Nc表示构件c上离散单元的数量。
其中,Nc表示构件c上离散单元的数量。
桁架结构开展EMRM迭代首步时,各单元的弹性模量都取其初始值,由此可确定结构在设计荷载下的线弹性内力,进而利用式(1)确定EMRM首步迭代中各构件的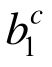 ,并据此确定设计荷载下各构件的强度系数
,并据此确定设计荷载下各构件的强度系数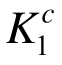 :
:
构件强度系数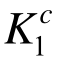 不同于传统的安全系数,在计算中已经考虑了荷载系数、材料系数以及结构重要性系数等三个分项系数的取值,因而
不同于传统的安全系数,在计算中已经考虑了荷载系数、材料系数以及结构重要性系数等三个分项系数的取值,因而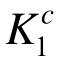 的目标值通常取[K0]=1.0。当
的目标值通常取[K0]=1.0。当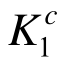 ≥[K0]时,表明构件c的原有强度能够满足需求,处于安全状态。反之,当
≥[K0]时,表明构件c的原有强度能够满足需求,处于安全状态。反之,当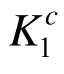 <[K0]时,表明该构件的强度储备不足,存在失效风险,需按照下式调整该构件的截面强度:
<[K0]时,表明该构件的强度储备不足,存在失效风险,需按照下式调整该构件的截面强度:
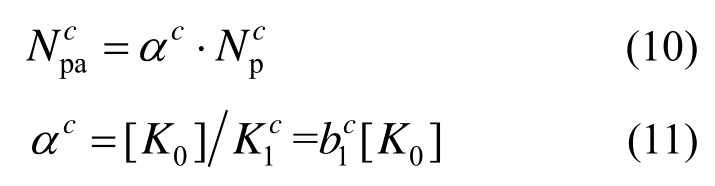
式中:![]() 分别表示调整前、后的构件截面强度;cα为构件强度系数比。
分别表示调整前、后的构件截面强度;cα为构件强度系数比。
2.2 体系层面的强度设计
罕遇荷载是指能够使结构进入塑性极限状态,甚至发生坍塌破坏的罕遇工况下的极限荷载,在美国荷载设计规范ASCE/SEI 7-10 [23]中称为罕遇工况下的荷载组合(load combinations for extraordinary events)。EMRM迭代末步结构在罕遇荷载下进入塑性极限状态。根据该迭代步的构件承载比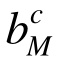 可以确定各构件在迭代末步的强度系数:
可以确定各构件在迭代末步的强度系数:
进一步地,根据式(1)和式(8),利用EMRM迭代末步的最大构件承载比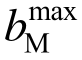 确定桁架的体系强度需求:
确定桁架的体系强度需求:
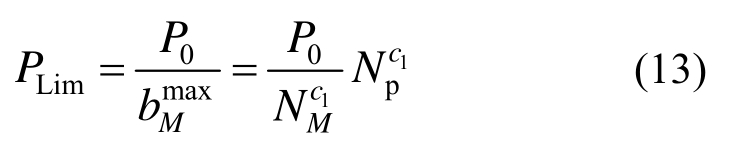
式中: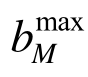 表示EMRM迭代末步的最大构件承载比;
表示EMRM迭代末步的最大构件承载比;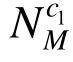 是与
是与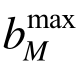 相应的杆件轴向内力,上标c1是迭代末步承受最大承载比的构件编号。
相应的杆件轴向内力,上标c1是迭代末步承受最大承载比的构件编号。
式(13)给出了体系强度PLim与构件强度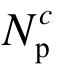 之间的定量关系,在此基础上可建立结构优化调整方法,为此需根据
之间的定量关系,在此基础上可建立结构优化调整方法,为此需根据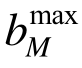 定义结构体系强度系数Ks:
定义结构体系强度系数Ks:
结构体系强度系数Ks反映了结构体系强度的富余状况。通常在结构设计之初可根据预定的荷载设计水平P0和罕遇水平PL确定体系强度系数的目标值[Ks]:
当前的结构设计规范通常没有给出荷载罕遇水平PL,因而在设计之初难以预先确定[Ks]。为此,可根据目前国内外对既有工程结构极限承载力PLim的研究结果[12,24-25]并结合式(15)确定结构体系强度系数目标值的取值。Zhang等[24]通过对9个钢框架结构进行承载力试验,得到不同可靠度水平下的结构体系强度系数取值。Albermani等[25]在对大型钢输电塔架进行承载力试验的基础上指出,新建输电塔结构的体系强度系数处于1.10~1.78之间。本文取[Ks]=1.4。
当迭代末步各构件的强度系数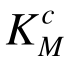 大于体系强度系数目标值[Ks]时,有Ks≥[Ks],表明结构满足体系强度需求,在遭遇罕遇荷载时能够避免坍塌破坏。反之若任一构件在迭代末步的强度系数
大于体系强度系数目标值[Ks]时,有Ks≥[Ks],表明结构满足体系强度需求,在遭遇罕遇荷载时能够避免坍塌破坏。反之若任一构件在迭代末步的强度系数![]() 则有Ks<[Ks],表明桁架结构不能满足体系强度需求,难以抵御罕遇荷载的袭击。另一方面,为了减少耗材,节省工程造价,各构件的强度系数
则有Ks<[Ks],表明桁架结构不能满足体系强度需求,难以抵御罕遇荷载的袭击。另一方面,为了减少耗材,节省工程造价,各构件的强度系数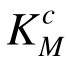 也不能太大,应尽可能接近[Ks]。因此,可按下式调整构件截面强度:
也不能太大,应尽可能接近[Ks]。因此,可按下式调整构件截面强度:
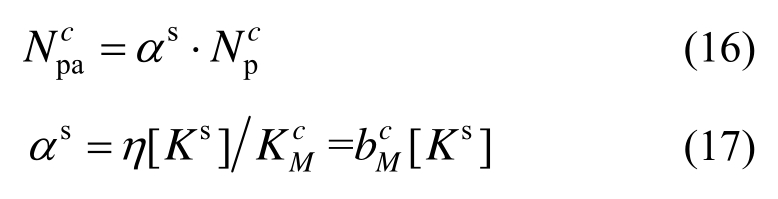
式中:αs为体系强度系数比;η为加速因子,大于1时可加快优化迭代的收敛速度,本文取η=1.001。
在桁架结构两层面强度设计中,每次调整构件c截面强度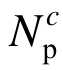 之后,要根据调整后的强度
之后,要根据调整后的强度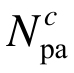 确定其截面面积Ac:
确定其截面面积Ac:

式中:σs表示构件c的材料设计强度;Ac表示构件c的截面面积。
进一步地,根据Ac更新构件的截面几何尺寸。本文算例均采用圆管构件,圆管截面外径R1的调整公式为:
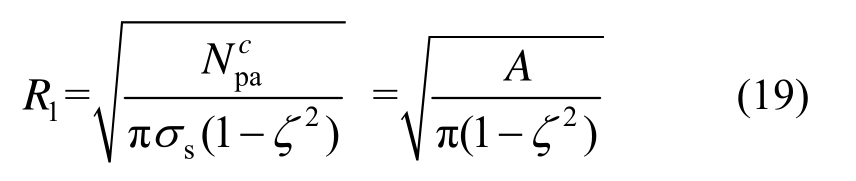
其中,ζ为圆管截面内外径之比,可根据构造要求确定[26]。
2.3 结构两层面强度优化设计
罕遇荷载作用下桁架结构一旦形成失效模式,将不能继续承载。如果此时仍有较多杆件的单元承载比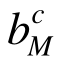 较低,将造成过多的材料浪费。为此,需要开展结构优化设计,力图使每根构件都能充分发挥其承载能力,理想状态是桁架结构进入塑性极限状态时,全部构件都同时进入失效临界状态,即全部构件的
较低,将造成过多的材料浪费。为此,需要开展结构优化设计,力图使每根构件都能充分发挥其承载能力,理想状态是桁架结构进入塑性极限状态时,全部构件都同时进入失效临界状态,即全部构件的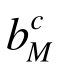 相等,此时承载比均匀度dM达到最大值。因此,两层面优化设计的迭代过程应满足收敛条件:
相等,此时承载比均匀度dM达到最大值。因此,两层面优化设计的迭代过程应满足收敛条件:
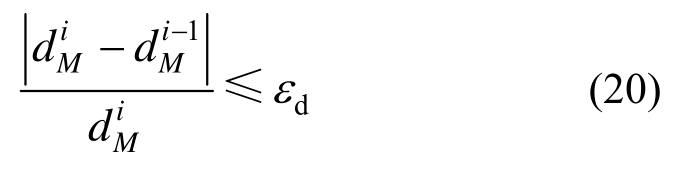
式中: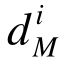 和
和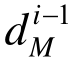 分别为当前(即第i次)和上一次(即第i-1次)两层面优化设计循环计算中EMRM迭代末步的构件承载比均匀度;εd为收敛容差,取值范围为0.001~0.05。
分别为当前(即第i次)和上一次(即第i-1次)两层面优化设计循环计算中EMRM迭代末步的构件承载比均匀度;εd为收敛容差,取值范围为0.001~0.05。
需要注意的是,最终的优化方案需根据模数要求确定各构件的截面几何尺寸。
经过上述优化循环分析,不仅能够充分发挥各构件的承载能力,节省材料,而且能够满足桁架在构件和体系两个层面的强度需求,从而得到承载性能和经济性能均优的结构优化设计方案,称之为桁架结构两层面优化设计的改进均匀承载准则法,其流程如图1所示。
3 算例分析
本节结合3个桁架算例,对本文建立的改进均匀承载准则法、原均匀承载准则法、满应力准则法等优化设计方法进行对比分析,其中:算例1是承受集中荷载作用的10杆平面桁架,文献[27]利用数学规划法建立了该桁架的优化方案;算例2为承受分布荷载作用的平面桁架桥;算例3为空间桁架结构。这里采用ANSYS有限元软件进行建模和计算分析,其中平面桁架结构采用平面2节点杆单元Link1单元建模,空间桁架结构采用空间2节点杆单元Link8单元建模。使用的PC机基本配置为:Intel (R) Pentium (R) G630 2.70GHz, 4G内存。
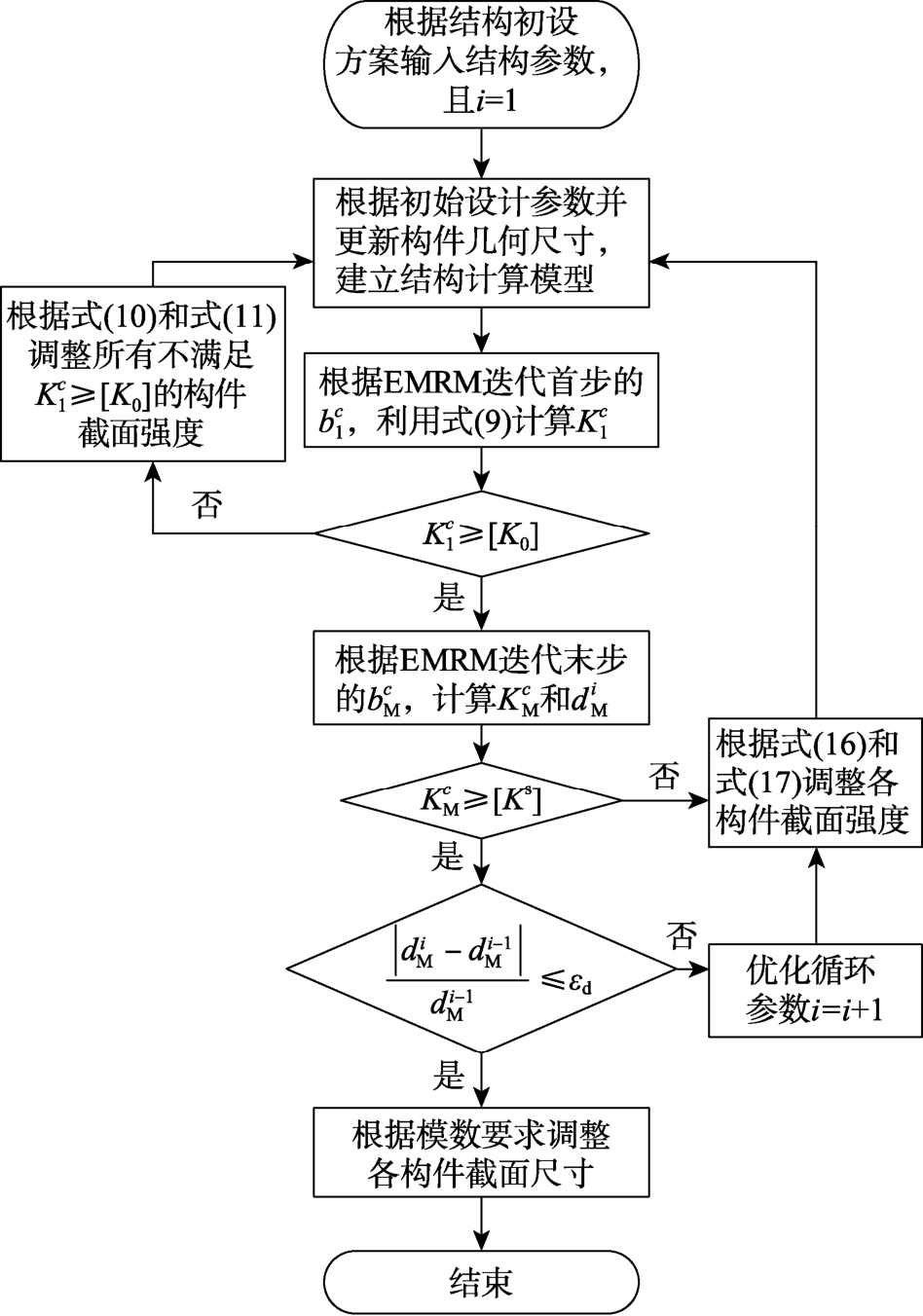
图1 改进均匀承载准则法流程图
Fig.1 Flow chart for improved uniform bearing criterion
3.1 算例1∶10杆平面桁架
由10根杆件组成的平面桁架结构承受2个大小相等的集中荷载F=444.8 kN,如图2所示。材料容许应力[σ]=170MPa ,弹性模量为200 GPa。构件均采用圆管型截面形式,桁架的计算模型及杆件编号如图2所示。初始设计方案中,弦杆和直腹杆(编号为1~6)的截面外径为20 cm,斜腹杆(编号为7~10)的截面外径为10 cm,各杆内外径之比均为0.9。文献[27]利用数学规划法确定了该桁架的优化设计方案。这两个设计方案中各构件的截面积Ac分别见表1。这里分别取构件强度系数和体系强度系数的目标值[K0]=1.0、[Ks]=1.4。同时构件横截面积最小限值为1 cm2。
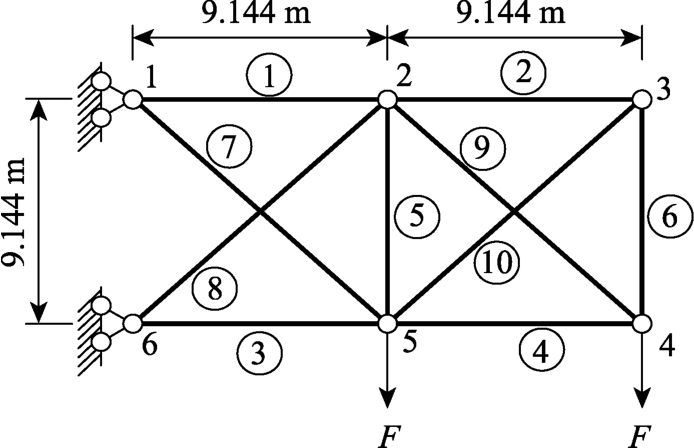
图2 十杆桁架
Fig.2 Ten-bar truss
3.1.1 不考虑稳定性影响
考虑到文献[27]中的数学规划法没有考虑压杆稳定性影响,本节采用式(2a)定义单元承载比,然后分别利用原均匀承载法[21-22]和本文改进均匀承载法建立十杆桁架两层面优化设计方案,求得各杆的截面面积Ac 、构件强度系数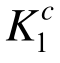 、
、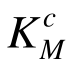 及桁架体系强度系数Ks,结果分别见表1中“原均匀承载法”和“本文改进方法”下面的数据。为了便于对比分析各设计方案,这里利用EMRM计算初始设计方案和数学规划法优化设计方案迭代首步和末步的单元承载比,并代入式(9)和式(14)求得这两个方案的构件强度系数
及桁架体系强度系数Ks,结果分别见表1中“原均匀承载法”和“本文改进方法”下面的数据。为了便于对比分析各设计方案,这里利用EMRM计算初始设计方案和数学规划法优化设计方案迭代首步和末步的单元承载比,并代入式(9)和式(14)求得这两个方案的构件强度系数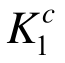 、
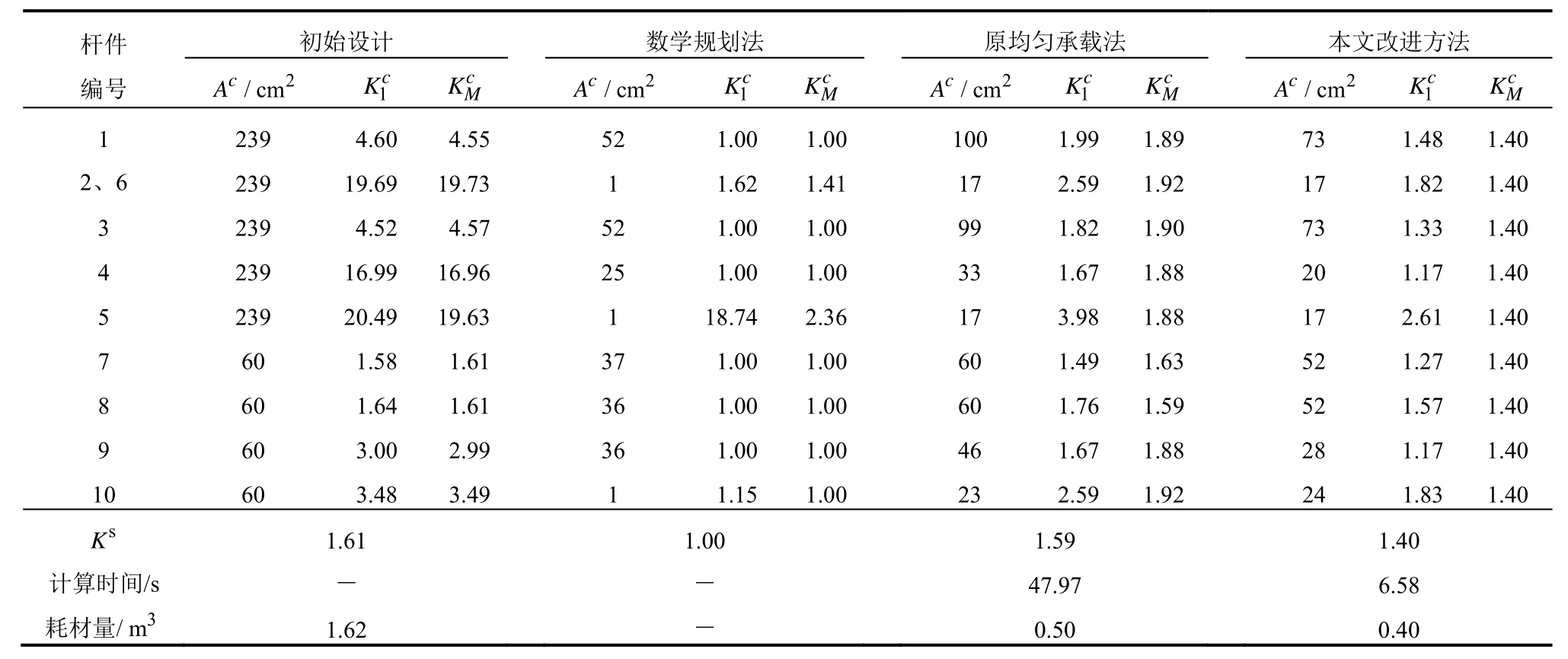
、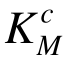 和体系强度系数Ks,结果如表1所示。从表1可以看出,在不考虑压杆稳定影响时,桁架初始设计方案、原均匀承载法和本文改进方法的优化设计方案中,构件强度系数和体系强度系数分别满足
和体系强度系数Ks,结果如表1所示。从表1可以看出,在不考虑压杆稳定影响时,桁架初始设计方案、原均匀承载法和本文改进方法的优化设计方案中,构件强度系数和体系强度系数分别满足![]() 表明这三个设计方案均能够满足桁架在构件层面和体系层面的强度需求,符合安全性要求。但是数学规划法的优化设计方案尽管迭代首步的构件强度系数满足
表明这三个设计方案均能够满足桁架在构件层面和体系层面的强度需求,符合安全性要求。但是数学规划法的优化设计方案尽管迭代首步的构件强度系数满足![]() 但体系强度系数Ks<[Ks](其原因在于构件1、3、4、7~10在迭代末步的强度系数
但体系强度系数Ks<[Ks](其原因在于构件1、3、4、7~10在迭代末步的强度系数![]() 由此可见,传统的数学规划法优化设计方案能够满足构件层面强度需求,但不能保证体系层面强度也满足要求。
由此可见,传统的数学规划法优化设计方案能够满足构件层面强度需求,但不能保证体系层面强度也满足要求。
同时,从表1的初始设计方案中可以看出大多数构件的强度系数 远大于其目标值[Ks],导致材料浪费。原均匀承载法方案降低了大部分杆件的截面积Ac,从而节省了材料,耗材量从原方案的1.62 m3减少到0.5 m3。而本文改进方法进一步将十杆桁架结构用材量减少到0.40m3,与原均匀承载法相比不仅减少了20%的耗材,而且计算用时降低了86%。表明本文提出的改进均匀承载准则法在优化效果和计算效率方面都优越于原均匀承载准则法。并且,本文改进方法的优化方案中各构件在迭代末步具有相同的强度系数
远大于其目标值[Ks],导致材料浪费。原均匀承载法方案降低了大部分杆件的截面积Ac,从而节省了材料,耗材量从原方案的1.62 m3减少到0.5 m3。而本文改进方法进一步将十杆桁架结构用材量减少到0.40m3,与原均匀承载法相比不仅减少了20%的耗材,而且计算用时降低了86%。表明本文提出的改进均匀承载准则法在优化效果和计算效率方面都优越于原均匀承载准则法。并且,本文改进方法的优化方案中各构件在迭代末步具有相同的强度系数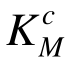 ,且都等于[Ks],满足均匀承载的目标,从而能够最大限度节省耗材。
,且都等于[Ks],满足均匀承载的目标,从而能够最大限度节省耗材。
3.1.2 压杆稳定性影响
为了反映稳定性对结构设计方案的影响,这里利用式(2b)代替式(2a)计算单元承载比,在此基础上利用本文改进均匀承载法研究建立该十杆桁架的系数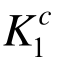 、
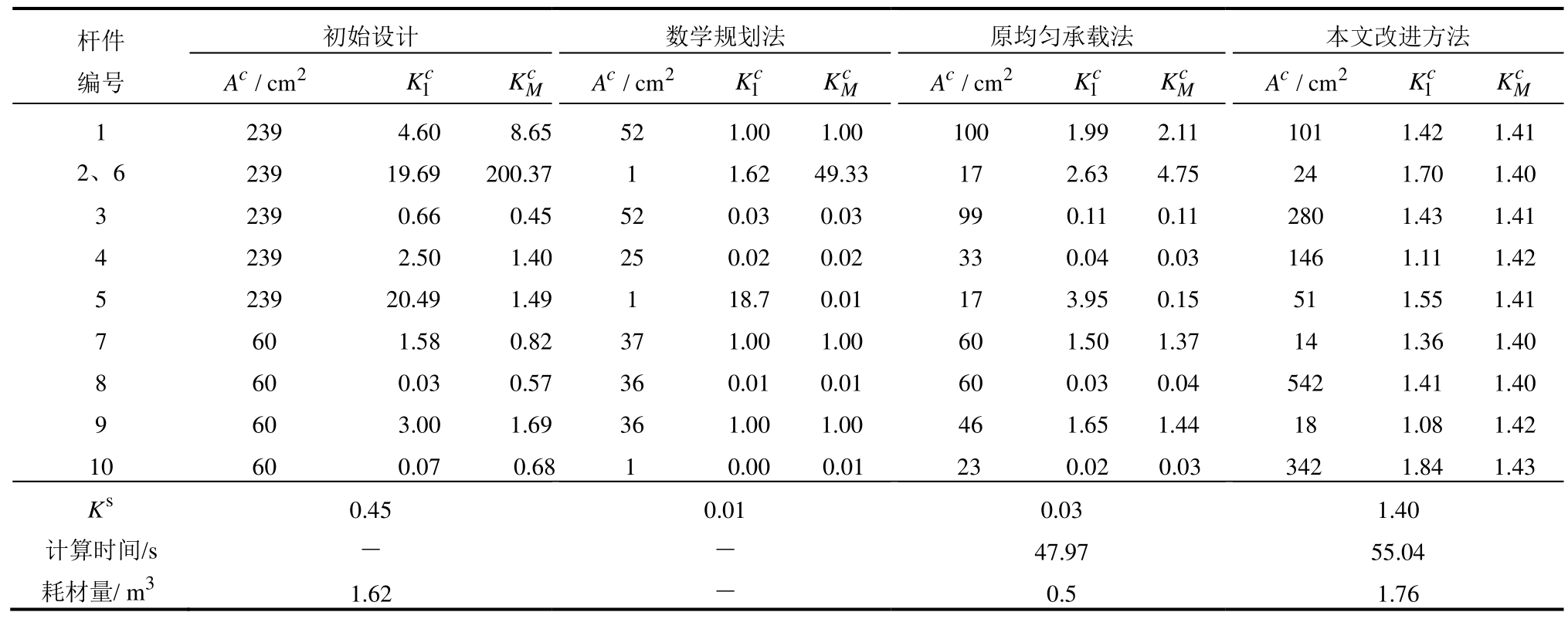
、 及桁架体系强度系数Ks,结果见表2。为了便于对比分析,这里利用基于式(2b)的两个层面的强度需求,其原因在于这三个设计方案都没有考虑稳定性影响。由此可知,稳定性对桁架结构在构件和体系两个层面的强度都有显著影响,不考虑稳定性将高估桁架的承载力,导致设计方案存在安全性不足的问题。
及桁架体系强度系数Ks,结果见表2。为了便于对比分析,这里利用基于式(2b)的两个层面的强度需求,其原因在于这三个设计方案都没有考虑稳定性影响。由此可知,稳定性对桁架结构在构件和体系两个层面的强度都有显著影响,不考虑稳定性将高估桁架的承载力,导致设计方案存在安全性不足的问题。
表1 优化设计方案对比
Table 1 Results from four design and optimization methods
杆件编号 初始设计 数学规划法 A/2 c cm K1c KcM c A/2 cm K1cKcM 1 239 4.60 4.55 521.001.00 2、6 239 19.69 19.73 1 1.621.41 3 239 4.52 4.57 521.001.00 4 239 16.99 16.96 251.001.00 5 239 20.49 19.63 1 18.742.36 7 60 1.58 1.61 371.001.00 8 60 1.64 1.61 361.001.00 9 60 3.00 2.99 361.001.00 10 60 3.48 3.49 1 1.151.00 s K 1.61 1.00计算时间/s - -耗材量/3 m 1.62 -原均匀承载法 本文改进方法 c A/2 cmK1cKcM c A/2 cm K1cKcM 1001.991.89 73 1.481.40 172.591.92 17 1.821.40 991.821.90 73 1.331.40 331.671.88 20 1.171.40 173.981.88 17 2.611.40 601.491.63 52 1.271.40 601.761.59 52 1.571.40 461.671.88 28 1.171.40 232.591.92 24 1.831.40 1.59 1.40 47.97 6.58 0.50 0.40
表2 考虑稳定性的优化设计方案对比
Table 2 Comparison of different optimal design based on stability
杆件编号 初始设计 数学规划法 原均匀承载法 本文改进方法 A/2 c cm K1cKcMc A/2cm K1c KcM c A/2cm K1c KcM c A/2cm K1c KcM 1 239 4.608.65521.001.001001.992.11 101 1.421.41 2、6 239 19.69200.3711.6249.33172.634.75 24 1.701.40 3 239 0.660.45520.030.03990.110.11 280 1.431.41 4 239 2.501.40250.020.02330.040.03 146 1.111.42 5 239 20.491.49118.70.01173.950.15 51 1.551.41 7 60 1.580.82371.001.00601.501.37 14 1.361.40 8 60 0.030.57360.010.01600.030.04 542 1.411.40 9 60 3.001.69361.001.00461.651.44 18 1.081.42 10 60 0.070.6810.000.01230.020.03 342 1.841.43 s K 0.45 0.010.031.40计算时间/s - - 47.9755.04耗材量/3m 1.62 - 0.51.76
同时从表2可见,本文改进方法的优化设计方案中所有构件强度系数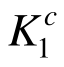 、
、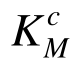 和体系强度系数Ks都不小于各自的目标值[K0]和[Ks],使桁架两层面满足强度的需求,从而克服了初始设计方案、数学规划法和原均匀承载法优化设计方案的缺陷。
和体系强度系数Ks都不小于各自的目标值[K0]和[Ks],使桁架两层面满足强度的需求,从而克服了初始设计方案、数学规划法和原均匀承载法优化设计方案的缺陷。
3.1.3 优化设计方案的校核
进一步地,利用弹塑性增量分析法(EPIA) 检验数学规划法、原均匀承载准则法以及本文改进方法的优化设计方案能否满足桁架结构的体系强度需求。此时,计算模型中压杆的容许应力仍需利用式(2b)中的稳定系数φ进行折减[28]。首先利用EPIA求得上述三种优化设计方法分别确定的桁架结构优化设计方案的极限承载力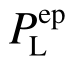 ,然后将
,然后将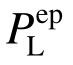 代替式(14)中的PLim可以求得上述三种优化设计方案的体系强度系数Ks,结果见表3。从表3可以看出,数学规划法和原均匀承载准则法由于没有考虑稳定性的影响,因此,所得优化设计方案的结构体系强度系数均小于目标值[Ks]=1.40,无法满足桁架结构体系强度需求,相比之下本文改进方法在考虑稳定性影响时所得优化设计方案的体系强度系数等于目标值1.40,且其迭代末步的构件强度系数
代替式(14)中的PLim可以求得上述三种优化设计方案的体系强度系数Ks,结果见表3。从表3可以看出,数学规划法和原均匀承载准则法由于没有考虑稳定性的影响,因此,所得优化设计方案的结构体系强度系数均小于目标值[Ks]=1.40,无法满足桁架结构体系强度需求,相比之下本文改进方法在考虑稳定性影响时所得优化设计方案的体系强度系数等于目标值1.40,且其迭代末步的构件强度系数 均接近于1.40,表明本文提出的设计方法不仅满足了体系强度需求,而且不浪费材料,与3.1.2节得出结论基本一致。综上所述,通过与EPIA进行对比,再次验证了本文改进方法的合理性。
均接近于1.40,表明本文提出的设计方法不仅满足了体系强度需求,而且不浪费材料,与3.1.2节得出结论基本一致。综上所述,通过与EPIA进行对比,再次验证了本文改进方法的合理性。
表3 塑性极限荷载及体系安全系数
Table 3 Plastic ultimate load and system safety factor
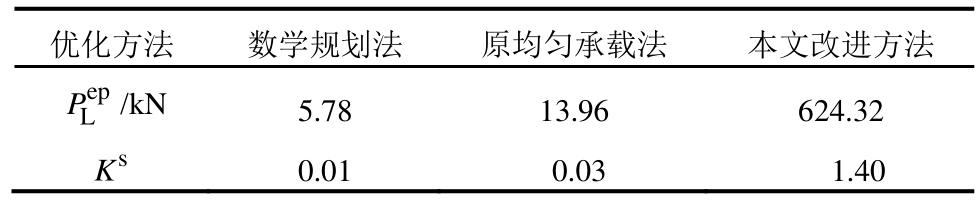
优化方法 数学规划法 原均匀承载法 本文改进方法P/kN 5.78 13.96 624.32 ep L K 0.01 0.03 1.40 s
3.2 算例2:平面桁架结构
图4所示为一平面桁架,荷载施加于桁架上弦的6个节点上,两端的节点荷载为450 kN,其余节点荷载为900 kN。构件材料为Q235,其容许应力[σ]=215MPa ,弹性模量为200 GPa,构件均采用圆管型截面。初始设计方案已考虑了稳定性影响,所有杆件的截面外径均为30 cm,各杆内外径之比均为0.8,各杆截面Ac见表4。这里分别取构件和体系强度系数目标值[K0]=1.0、[Ks]=1.4。同时构件横截面积最小限值为56 cm2。
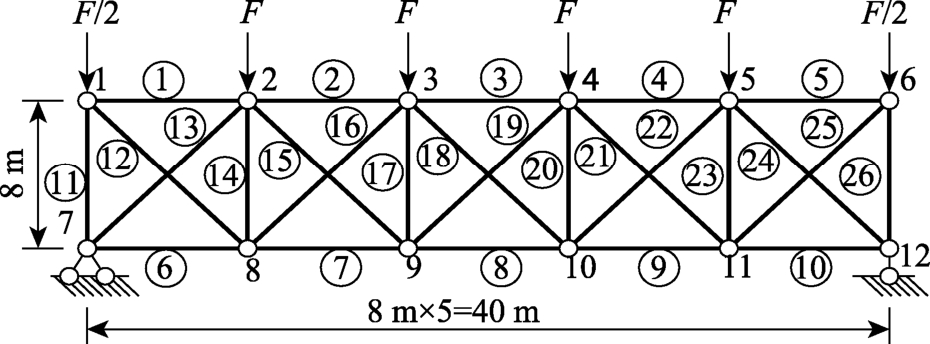
图4 平面桁架
Fig.4 Plane truss
3.2.1 优化设计方案及其比较
根据算例1可知,稳定性对桁架结构优化设计有显著影响,为此采用式(2b)定义单元承载比,在此基础上利用原均匀承载准则法和本文改进方法分别建立该桁架的优化设计方案,确定各构件的截面积Ac 、构件强度系数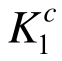 和
和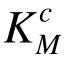 及体系强度系数Ks,结果见表4。为便于对比分析,表中还列出了满应力准则法建立的设计方案,确定各构件的截面积Ac。对于满应力准则法而言,当考虑压杆稳定性影响时,需要根据式(2b)中的稳定系数φ折减容许应力[σ],即用φ[σ]代替[σ]作为容许应力[28]。进一步地,利用EMRM迭代首步和末步的单元承载比求得初始设计方案和满应力法优化设计方案的构件强度系数
及体系强度系数Ks,结果见表4。为便于对比分析,表中还列出了满应力准则法建立的设计方案,确定各构件的截面积Ac。对于满应力准则法而言,当考虑压杆稳定性影响时,需要根据式(2b)中的稳定系数φ折减容许应力[σ],即用φ[σ]代替[σ]作为容许应力[28]。进一步地,利用EMRM迭代首步和末步的单元承载比求得初始设计方案和满应力法优化设计方案的构件强度系数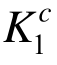 、
、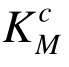 及体系强度系数Ks,结果见表4。从表4可以看出,结构初始设计方案满足
及体系强度系数Ks,结果见表4。从表4可以看出,结构初始设计方案满足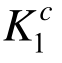 ≥[K0]和Ks≥[Ks],表明该方案满足结构两层面强度需求。但是,该方案中大多数构件的
≥[K0]和Ks≥[Ks],表明该方案满足结构两层面强度需求。但是,该方案中大多数构件的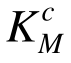 均远大于目标值[Ks],说明初始设计方案的体系强度富裕量较大,有必要优化。同时可见,表4中满应力法优化设计方案各构件的截面积Ac明显减少,大幅降低了桁架的耗材量。但是,该优化设计方案中Ks<[Ks ],表明其不满足桁架体系层面强度需求。
均远大于目标值[Ks],说明初始设计方案的体系强度富裕量较大,有必要优化。同时可见,表4中满应力法优化设计方案各构件的截面积Ac明显减少,大幅降低了桁架的耗材量。但是,该优化设计方案中Ks<[Ks ],表明其不满足桁架体系层面强度需求。
进一步地从表4可见,原均匀承载法和本文改进方法的优化设计方案均满足![]() 和
和![]() 表明这两个优化设计方案均能满足桁架两层面的强度需求,从而克服了初始方案和满应力法优化方案不能满足体系层面强度需求的缺陷。同时由表4可知,原均匀承载法设计方案耗材量为15.12 m3,相对初始设计方案耗材量减少38.36%;而本文改进方法设计方案的耗材量仅为7.54 m3,相比原均匀承载法设计方案进一步降低耗材50.13%,而且计算耗时间也明显减少,证明本文改进方法相比原均匀承载法在优化效果和效率方面的优越性。
表明这两个优化设计方案均能满足桁架两层面的强度需求,从而克服了初始方案和满应力法优化方案不能满足体系层面强度需求的缺陷。同时由表4可知,原均匀承载法设计方案耗材量为15.12 m3,相对初始设计方案耗材量减少38.36%;而本文改进方法设计方案的耗材量仅为7.54 m3,相比原均匀承载法设计方案进一步降低耗材50.13%,而且计算耗时间也明显减少,证明本文改进方法相比原均匀承载法在优化效果和效率方面的优越性。
由上述分析结果可以看出,满应力法优化方案不能保证桁架在体系层面的强度需求,因此不满足结构安全性要求,其原因在于该优化方法没有考虑结构加载过程中应力再分布的影响;原均匀承载法尽管能够保证桁架两层面强度需求,克服满应力法的缺陷,但是由于该方法采用EMRM迭代末步的基准承载比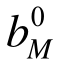 作为低承载构件截面强度的调整目标,导致低承载构件强度富余量大,部分高承载构件强度有富余,但得不到调整,从而造成其优化设计方案仍具有较大的强度富裕量;本文建立的改进均匀承载法采用[Ks]作为构件截面强度的调整目标,不仅能够满足桁架结构在构件和体系两个层面的强度需求,而且各构件的
作为低承载构件截面强度的调整目标,导致低承载构件强度富余量大,部分高承载构件强度有富余,但得不到调整,从而造成其优化设计方案仍具有较大的强度富裕量;本文建立的改进均匀承载法采用[Ks]作为构件截面强度的调整目标,不仅能够满足桁架结构在构件和体系两个层面的强度需求,而且各构件的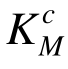 基本接近体系强度系数的目标值1.40,能够充分发挥各构件的材料强度,从而得到更经济的优化设计方案。
基本接近体系强度系数的目标值1.40,能够充分发挥各构件的材料强度,从而得到更经济的优化设计方案。
表4 考虑稳定性的不同优化方案对比
Table 4 Comparison different optimal design based on stability
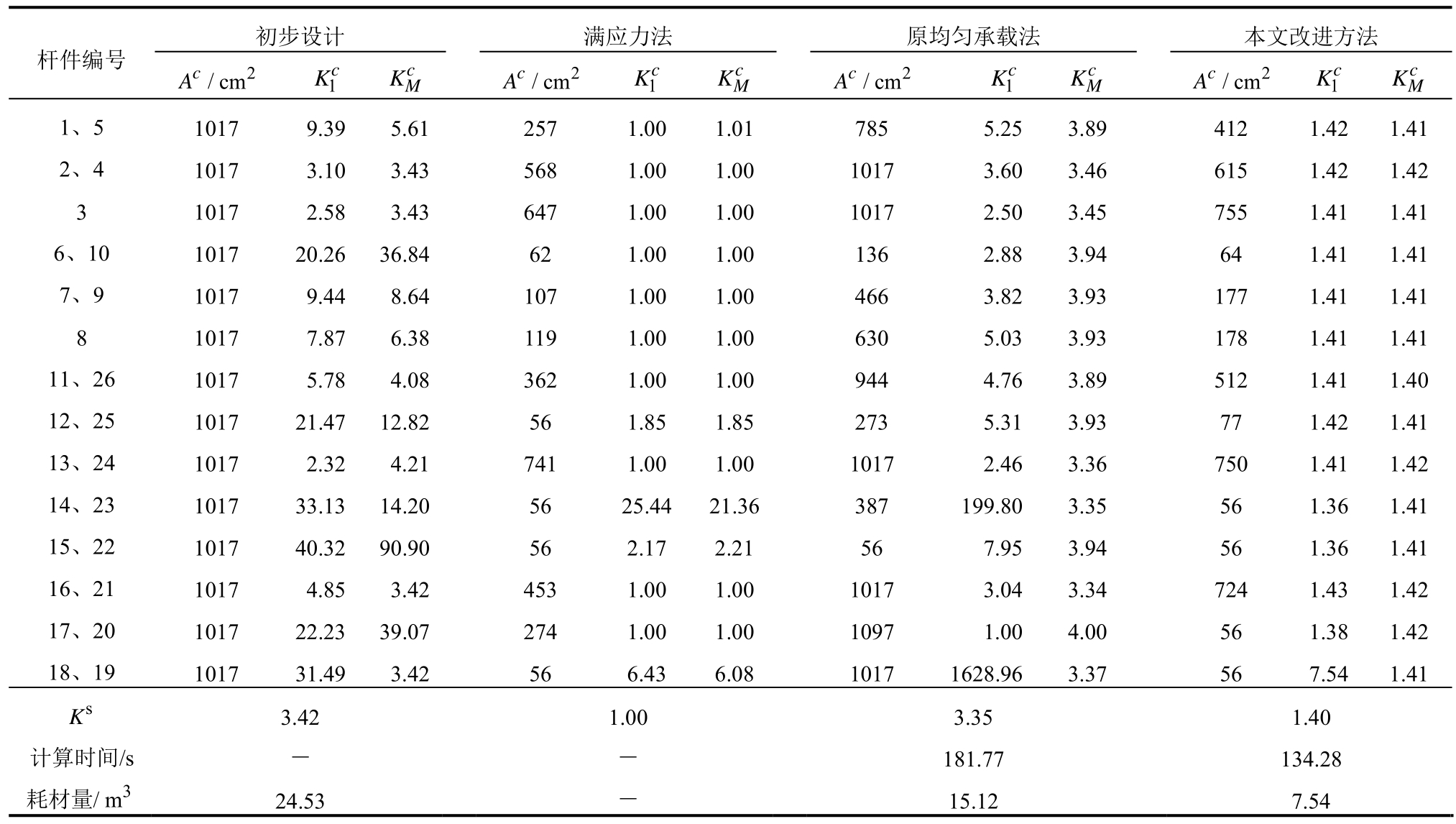
杆件编号初步设计 满应力法 原均匀承载法 本文改进方法A/2c cm K1c KcM c A/2 cmK1c KcMc A/2 cmK1cKcM c A/2 cm K1cKcM 1、5 1017 9.39 5.61 257 1.00 1.01 785 5.253.89 412 1.421.41 2、4 1017 3.10 3.43 568 1.00 1.00 1017 3.603.46 615 1.421.42 3 1017 2.58 3.43 647 1.00 1.00 1017 2.503.45 755 1.411.41 6、10 1017 20.26 36.84 62 1.00 1.00 136 2.883.94 64 1.411.41 7、9 1017 9.44 8.64 107 1.00 1.00 466 3.823.93 177 1.411.41 8 1017 7.87 6.38 119 1.00 1.00 630 5.033.93 178 1.411.41 11、26 1017 5.78 4.08 362 1.00 1.00 944 4.763.89 512 1.411.40 12、25 1017 21.47 12.82 56 1.85 1.85 273 5.313.93 77 1.421.41 13、24 1017 2.32 4.21 741 1.00 1.00 1017 2.463.36 750 1.411.42 14、23 1017 33.13 14.20 56 25.4421.36387 199.803.35 56 1.361.41 15、22 1017 40.32 90.90 56 2.17 2.21 56 7.953.94 56 1.361.41 16、21 1017 4.85 3.42 453 1.00 1.00 1017 3.043.34 724 1.431.42 17、20 1017 22.23 39.07 274 1.00 1.00 1097 1.004.00 56 1.381.42 18、19 1017 31.49 3.42 56 6.43 6.08 1017 1628.963.37 56 7.541.41 s K 3.421.00 3.351.40计算时间/s - - 181.77 134.28耗材量/3m 24.53 - 15.12 7.54
3.2.2 优化设计方案的校核
进一步地,利用EPIA检验满应力法、原均匀承载准则法以及本文改进方法的优化设计方案能否满足桁架结构的体系强度需求。首先利用EPIA求得上述三种优化设计方案的极限承载力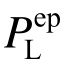 ,然后利用
,然后利用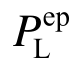 代替式(14)中的PLim求得上述三种方案的体系强度系数Ks,结果见表5。从表5可以看出:满应力法优化设计方案的体系强度系数小于目标值1.40,无法满足桁架结构体系强度要求;原均匀承载准则法优化设计方案的体系强度系数远大于目标值1.40,表明此时设计方案富裕量过大;相比之下本文改进方法优化设计方案的体系强度系数与其目标值大体相等,不仅满足了桁架结构体系强度的需求,而且基本没有浪费材料,具有较好的经济性,再次验证了本文改进方法的合理性。
代替式(14)中的PLim求得上述三种方案的体系强度系数Ks,结果见表5。从表5可以看出:满应力法优化设计方案的体系强度系数小于目标值1.40,无法满足桁架结构体系强度要求;原均匀承载准则法优化设计方案的体系强度系数远大于目标值1.40,表明此时设计方案富裕量过大;相比之下本文改进方法优化设计方案的体系强度系数与其目标值大体相等,不仅满足了桁架结构体系强度的需求,而且基本没有浪费材料,具有较好的经济性,再次验证了本文改进方法的合理性。
表5 塑性极限荷载及体系安全系数
Table 5 Plastic ultimate load and system safety factor

优化方法 满应力法 原均匀承载法 本文改进方法P/kN 451.80 1510.38 633.87 ep L K 1.00 3.36 1.41 s
3.3 算例3:空间桁架结构
图5所示承受分布荷载P的空间桁架,荷载均匀作用于桁架上弦的6个节点上,且P=1500 kN。构件材料为Q235,容许应力为215 MPa,弹性模量为200 GPa。为便于清楚表示各构件及节点编号,将该结构展开为如图6所示。
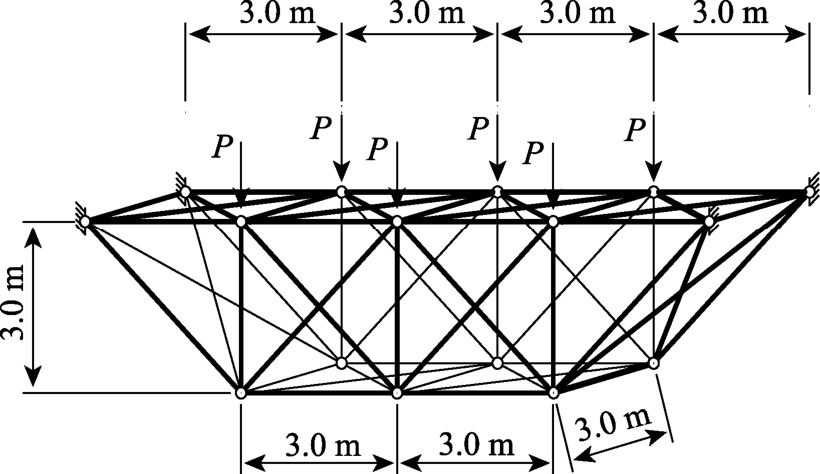
图5 空间桁架
Fig.5 Space truss
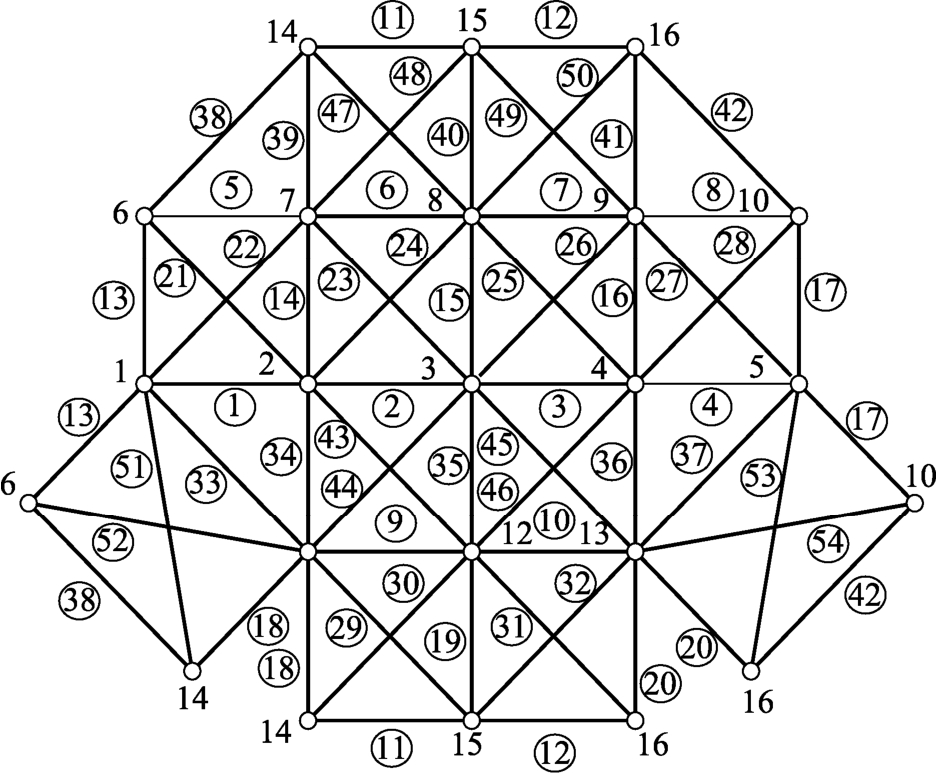
图6 构件编号
Fig.6 The serial number of components
构件均采用圆管型截面,初始设计方案已经考虑稳定性影响,上弦杆和交叉系杆(编号为1~8、13~32和51~54)的截面外径为10 cm,下弦杆和竖杆(编号为9~12和33~50)的截面外径为20 cm,各杆内外径之比均为0.9。该方案中各杆的截面积Ac见表6。这里分别取构件和体系强度系数目标值[K0]=1.0、[Ks]=1.4。同时构件横截面积最小限值为12 cm2。
3.3.1 优化设计方案及其对比
首先利用式(2b)计算单元承载比,在此基础上通过原均匀承载法和本文改进方法建立该空间桁架结构的优化设计方案,确定各构件的Ac、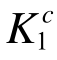 、
、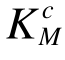 及桁架的Ks,结果见表6。表6还列出了满应力准则法建立的该桁架优化设计方案的Ac,并利用EMRM迭代首步和末步的单元承载比求得初始设计方案和满应力法优化设计方案中各构件的
及桁架的Ks,结果见表6。表6还列出了满应力准则法建立的该桁架优化设计方案的Ac,并利用EMRM迭代首步和末步的单元承载比求得初始设计方案和满应力法优化设计方案中各构件的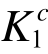 、
、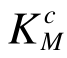 及桁架的Ks。从表6可以看出,该空间桁架结构初始设计方案满足
及桁架的Ks。从表6可以看出,该空间桁架结构初始设计方案满足![]() 表明该方案满足桁架两层面强度需求。但是,初始设计方案中大多数构件的
表明该方案满足桁架两层面强度需求。但是,初始设计方案中大多数构件的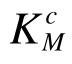 远大于其目标值[Ks],说明该方案的强度富裕量较大,需要进行优化。进一步地,由表6满应力法优化设计方案中各构件的截面积Ac可以看出,该优化方案能够大大减少桁架的耗材量,满应力法不能满足体系层面强度需求的缺陷。同时由表6可知,原均匀承载法设计方案耗材量为1.96 m3,相对初始设计方案耗材量减少25.76%;而本文改进方法设计方案的耗材量仅为1.31 m3,相比原均匀承载法设计方案进一步降低耗材33.16%,计算时间也有所减少,再次证明了本文改进方法在空间桁架结构优化设计效果和计算效率方面具有显著优越性。
远大于其目标值[Ks],说明该方案的强度富裕量较大,需要进行优化。进一步地,由表6满应力法优化设计方案中各构件的截面积Ac可以看出,该优化方案能够大大减少桁架的耗材量,满应力法不能满足体系层面强度需求的缺陷。同时由表6可知,原均匀承载法设计方案耗材量为1.96 m3,相对初始设计方案耗材量减少25.76%;而本文改进方法设计方案的耗材量仅为1.31 m3,相比原均匀承载法设计方案进一步降低耗材33.16%,计算时间也有所减少,再次证明了本文改进方法在空间桁架结构优化设计效果和计算效率方面具有显著优越性。
表6 考虑稳定性的不同优化设计方案法对比
Table 6 Comparison different optimal design based on stability
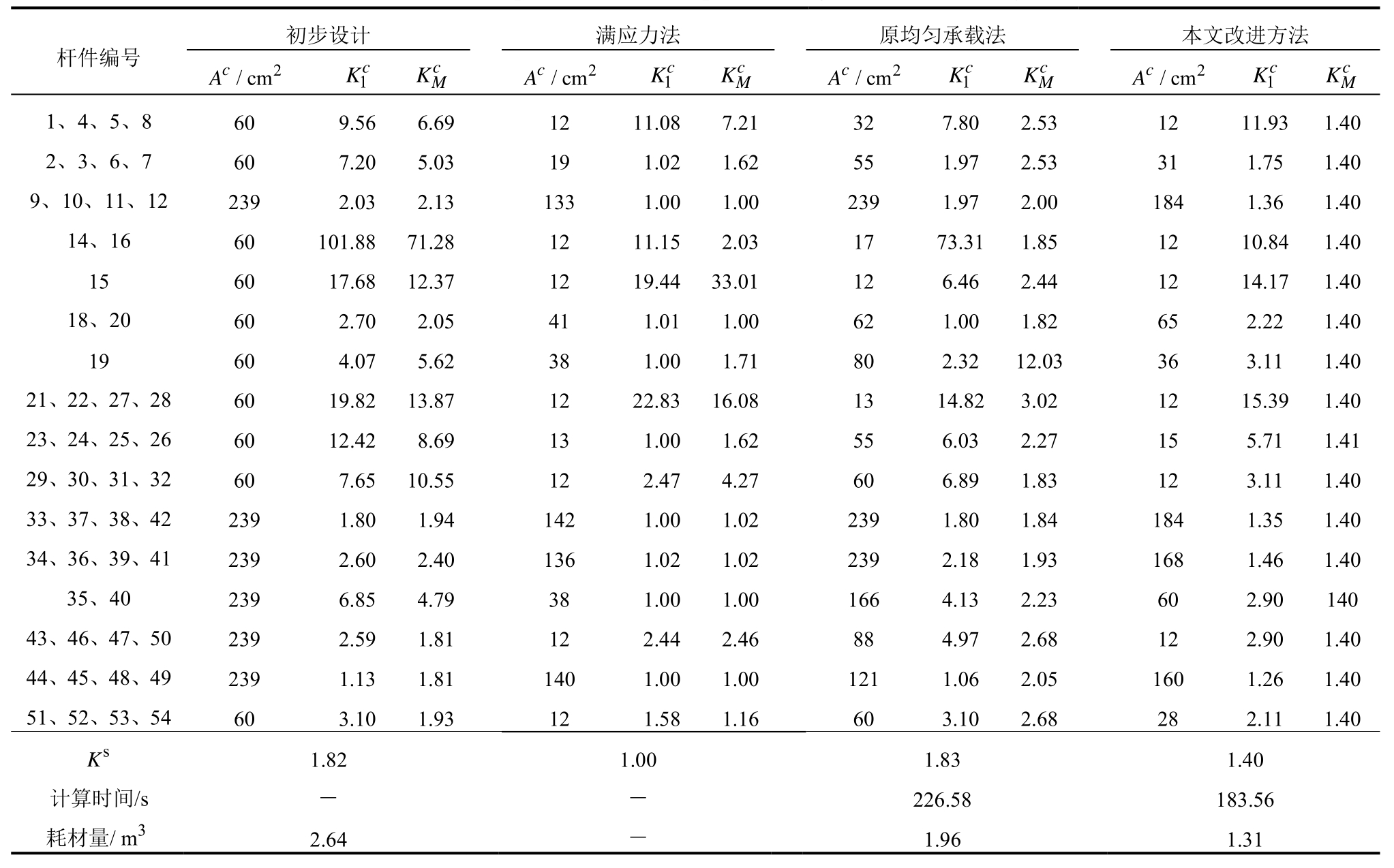
杆件编号初步设计 满应力法 原均匀承载法 本文改进方法A/2 c cm K1c KcM c A/2 cmK1cKcMc A/2 cmK1c KcM c A/2 cm K1c KcM 1、4、5、8 60 9.56 6.69 12 11.087.2132 7.802.53 12 11.931.40 2、3、6、7 60 7.20 5.03 19 1.021.6255 1.972.53 31 1.751.40 9、10、11、12 239 2.03 2.13 133 1.001.00239 1.972.00 184 1.361.40 14、16 60 101.88 71.28 12 11.152.0317 73.311.85 12 10.841.40 15 60 17.68 12.37 12 19.4433.0112 6.462.44 12 14.171.40 18、20 60 2.70 2.05 41 1.011.0062 1.001.82 65 2.221.40 19 60 4.07 5.62 38 1.001.7180 2.3212.03 36 3.111.40 21、22、27、28 60 19.82 13.87 12 22.8316.0813 14.823.02 12 15.391.40 23、24、25、26 60 12.42 8.69 13 1.001.6255 6.032.27 15 5.711.41 29、30、31、32 60 7.65 10.55 12 2.474.2760 6.891.83 12 3.111.40 33、37、38、42 239 1.80 1.94 142 1.001.02239 1.801.84 184 1.351.40 34、36、39、41 239 2.60 2.40 136 1.021.02239 2.181.93 168 1.461.40 35、40 239 6.85 4.79 38 1.001.00166 4.132.23 60 2.90140 43、46、47、50 239 2.59 1.81 12 2.442.4688 4.972.68 12 2.901.40 44、45、48、49 239 1.13 1.81 140 1.001.00121 1.062.05 160 1.261.40 51、52、53、54 60 3.10 1.93 12 1.581.1660 3.102.68 28 2.111.40 s K 1.821.00 1.831.40计算时间/s - - 226.58 183.56耗材量/3m 2.64 - 1.96 1.31
3.3.2 优化设计方案的校核
这里利用EPIA检验满应力法、原均匀承载准则法以及本文改进方法的优化设计方案的合理性。首先利用EPIA计算各优化设计方案的极限承载力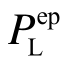 ,然后利用
,然后利用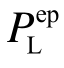 代替式(14)中的PLim可得上述三种优化方案的体系强度系数Ks,结果见表7。从表7结果可以看出:满应力法优化设计方案的体系强度系数小于目标值1.40,无法满足桁架结构体系强度要求;原均匀承载准则法优化设计方案的体系强度系数明显大于目标值1.40,表明该设计方案富裕量过大;相比之下本文改进方法优化设计方案的体系强度系数恰好等于目标值,从而不仅满足了桁架结构体系强度的需求,还充分发挥了材料强度,具有较好的经济性,再次验证了本文改进方法在空间桁架结构优化设计中的合理性。
代替式(14)中的PLim可得上述三种优化方案的体系强度系数Ks,结果见表7。从表7结果可以看出:满应力法优化设计方案的体系强度系数小于目标值1.40,无法满足桁架结构体系强度要求;原均匀承载准则法优化设计方案的体系强度系数明显大于目标值1.40,表明该设计方案富裕量过大;相比之下本文改进方法优化设计方案的体系强度系数恰好等于目标值,从而不仅满足了桁架结构体系强度的需求,还充分发挥了材料强度,具有较好的经济性,再次验证了本文改进方法在空间桁架结构优化设计中的合理性。
需要说明的是,本文限于篇幅尚未讨论工程应用的细节问题。但从图1的计算流程图可以看出,对于不同的工程对象,正确建立单元承载比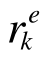 和构件承载比
和构件承载比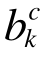 的表达式是利用EMRM开展结构两层面强度分析和优化设计的关键。
的表达式是利用EMRM开展结构两层面强度分析和优化设计的关键。
表7 塑性极限荷载及体系安全系数
Table 7 Plastic ultimate load and system safety factor
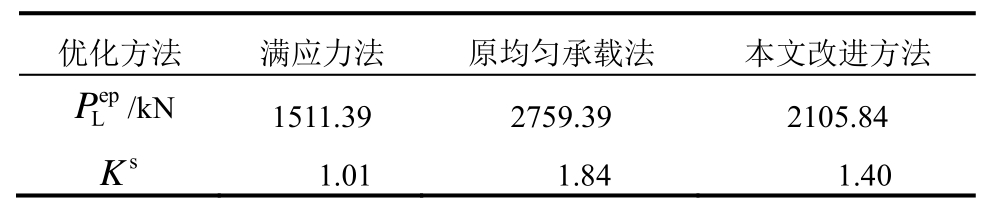
优化方法 满应力法 原均匀承载法 本文改进方法P/kN 1511.39 2759.39 2105.84 ep L K 1.01 1.84 1.40 s
4 结论
为克服现行结构优化设计方法的缺陷,提出了考虑压杆稳定性影响的改进均匀承载准则法。通过与现行多种优化设计方法对比分析得到如下结论:
(1) 本文建立的均匀承载准则以体系强度系数为目标调整各构件强度,克服了原均匀承载准则法利用基准承载比建立构件强度调整公式导致的缺陷,优化效果更佳,且提高了计算效率。
(2) 不考虑稳定性将高估桁架的承载力,导致设计方案安全性不足。本文改进方法通过在单元承载比表达式中引入稳定系数合理考虑压杆稳定性对桁架结构两层面强度的影响,并利用弹塑性方法验证了本文优化设计方案的合理性。
(3) 传统的满应力准则法和数学规划法难以保证桁架结构在体系层面的强度需求。原均匀承载准则法的优化设计方案具有较大的强度富裕量。本文建立的改进方法不仅满足桁架结构在构件和体系两个层面的强度需求,而且大大降低耗材,达到优化经济性能的效果。
[1]Schevenels M, Mcginn S, Rolvink A, et al.An optimality criteria based method for discrete design optimization taking into account buildability constraints [J].Structural and Multidisciplinary Optimization, 2014, 50(5): 755-774.
[2]Kanno Y.Global optimization of trusses with constraints on number of different cross-sections: A mixed-integer second-order cone programming approach [J].Computational Optimization and Applications, 2016,63(1): 203-236.
[3]易桂莲, 隋允康.基于应力约束全局化策略的板壳结构强度拓扑优化[J].工程力学, 2015, 32(8): 211-216.Yi Guilian, Sui Yunkang.Topology optimization for plate and shell structures based on stress constraint globalization [J].Engineering Mechanics, 2015, 32(8):211-216.(in Chinese)
[4]Greiner D, Emperador J M, Galván B, et al.Comparing the fully stressed design and the minimum constrained weight solutions in truss structures [M]// Evolutionary Algorithms and Metaheuristics in Civil Engineering and Construction Management.Springer, Cham, 2015: 17-32.
[5]Zhou M, Sigmund O.On fully stressed design and p-norm measures in structural optimization [J].Structural and Multidisciplinary Optimization, 2017, 56(3): 731-736.
[6]徐龙河, 吴耀伟, 李忠献.基于概率的钢框架结构地震失效模式识别方法[J].工程力学, 2016, 33(5): 66-73.Xu Longhe, Wu Yaowei, Li Zhongxian.Probability based seismic failure modes identification method for steel frame structure [J].Engineering Mechanics, 2016, 33(5):66-73.(in Chinese)
[7]白久林, 金双双, 欧进萍.防屈曲支撑-钢筋混凝土框架结构基于能量平衡的抗震塑性设计[J].建筑结构学报, 2017, 38(1): 125-134.Bai Jiulin, Jin Shuangshuang, Ou Jinping.Seismic plastic design of buckling-restrained braced-RC frame structures based on energy balance [J].Journal of Building Structures, 2017, 38(1): 125-134.
[8]徐龙河, 于绍静, 卢啸.基于损伤控制函数与失效概率的结构抗震性能多目标优化与评估[J].工程力学,2017, 34(10): 61-67.Xu Longhe, Yu Shaojing, Lu Xiao.Damage control
[9]function and failure probability based structural seismic performance multi-objective optimization and assessment[J].Engineering Mechanics, 2017, 34(10): 61-67.(in Chinese)
[10]Prager W, Shield R T.A general theory of optimal plastic design [J].Journal of Applied Mechanics, 1967, 34(1):184-186.
[11]Rozvany G I N, Pomezanski V.Fundamentals of exact multi-load topology optimization stress based least volume trusses (generalized Michell structures) - Part I:Plastic design [J].Structural & Multidisciplinary Optimization, 2014, 50(6): 1051-1078
[12]Buonopane S G, Schafer B W.Reliability of steel frames designed with advanced analysis [J].Journal of Structural Engineering, 2006, 132(2): 267-276.
[13]Zhang H, Shayan S, Rasmussen K J R, et al.System-based design of planar steel frames, I: Reliability framework [J].Journal of Constructional Steel Research.2016, 123: 135-143.
[14]ANSI/AISC 360-10, Specification for structural steel buildings [S].Chicago: American Institute of Steel Construction, 2010.
[15]GB50017-2017, 钢结构设计规范[S].北京:中国计划出版社, 2017.GB50011-2017, Design code for steel structures [S].Beijing: China Architectural Industry Press, 2017.(in Chinese)
[16]Iu C K.Nonlinear analysis for the pre- and post-yield behavior of a composite structure with the refined plastic hinge approach [J].Journal of Constructional Steel Research, 2016, 119: 1-16.
[17]Feng X, Guo S.Geometrical nonlinear elasto-plastic analysis of tensegrity systems via the co-rotational method [J].Mechanics Research Communications,2017, 79: 32-42.
[18]Rahman M K.Ultimate strength estimation of ships transverse frames by incremental elastic plastic finite element analysis [J].Marine Structures, 1988, 11(7):291-317.
[19]Wang H, Ohmori H.Elasto-plastic analysis-based truss optimization using genetic algorithm [J].Engineering Structures, 2013, 50(3): 1-12.
[20]Yang L F, Li Q, Zhang W, et al.Homogeneous generalized yield criterion based elastic modulus reduction method for limit analysis of thin-walled structures with angle steel [J].Thin-walled Structures,2014, 80(9): 153-158.
[21]Yang L F, Yu B, Ju J W.Incorporated strength capacity technique for limit load evaluation of trusses and framed structures under constant loading [J].Journal of Structural Engineering, 2015, 141(11): 04015023-1-04015023-11
[21]杨绿峰, 李琦, 张伟.工程结构整体承载力设计与优化的弹性模量缩减法研究[J].土木工程学报, 2015, 48(5):62-70.Yang Lufeng, Li Qi, Zhang Wei.Elastic modulus reduction method for design and optimization of global load bearing capacity of engineering structures [J].China Civil Engineering Journal, 2015, 48(5): 62-70.(in Chinese)
[22]杨绿峰, 欧伟, 张伟.桥梁结构两层面承载力设计与优化的策略和方法[J].中国公路学报, 2016, 29(7):62-71.Yang Lufeng, Ou Wei, Zhang Wei.Investigation on strategy and method of two-level load carrying capacity design and optimization for bridge structures [J].China Journal of Highway and Transport, 2015, 48(5): 62-70.(in Chinese)
[23]ASCE /SEI 7-10, Minimum Design Loads for Buildings and Other Structures [S].America: American Society of Civil Engineers, 2010.
[24]Zhang H, Shayan S, Rasmussen K J R, et al.System-based design of planar steel frames, II: Reliability results and design recommendations [J].Journal of Constructional Steel Research, 2016, 123: 154-161.
[25]Albermani F G A, Kitipornchai S.Numerical simulation of structural behaviour of transmission towers [J].Thin-Walled Structures, 2003, 41(2/3): 167-177.
[26]柴昶, 刘迎春.冷成型焊接圆钢管径厚比限值合理取值的讨论[J].建筑结构, 2015, 45(3): 44-47.Cai Chang, Liu Yingchun.Discussion on reasonable value of cold-formed welded round steel pipe diameter ratio [J].Building Structure, 2015, 45(3): 44-47.(in Chinese)
[27]Kirsch U.On singular topologies in optimum structural design [J].Structural & Multidisciplinary Optimization.1990, 2(3): 133-142.
[28]钱令希.工程结构优化设计[M].北京: 科学出版社,2011: 12-13.Qian Lingxi.Engineering structure optimization design[M].Beijing: Science Press, 2011: 12-13.(in Chinese)