2016 年初印发的《中共中央国务院关于进一步加强城市规划建设管理工作的若干意见》，提出大力推广装配式建筑，力争用10年左右时间，使装配式建筑占新建建筑的比例达到30%，为装配式建筑的发展提供了强力的政策保障。预制混凝土剪力墙结构作为装配式建筑的重要形式，具有优越的抗震性[1-2]，是我国发展装配式建筑的重要技术手段。
预制构件间的连接技术是预制混凝土剪力墙结构的关键[3]。预制剪力墙的钢筋连接技术有直接连接和间接连接，直接连接中连接钢筋与被连接钢筋直接连接在一起，钢筋应力直接传递，主要有套筒挤压连接技术[4]、搭接连接技术[5]、U型套箍连接技术[6]、U型闭合筋连接技术[7]、环筋扣合锚连技术[8]、接缝连接梁连接技术[9]以及整体箍筋插销连接技术[10]等；间接连接是钢筋间依靠混凝土或灌浆料作为传力介质传递钢筋应力，主要有插入式预留孔灌浆连接技术[11]、套筒浆锚连接技术[12]、间接搭接技术[13]、波纹管浆锚连接技术[14-15]、螺栓连接技术[16]等。研究表明，构造合理的直接连接和间接连接技术均能有效传递应力，保证预制构件间的整体性。
空心模剪力墙结构在竖直方向采用间接连接技术；水平装配单元间通过穿插水平钢筋，实现了直接连接。周剑等[17]对空心模剪力墙结构竖向连接位置处的竖向插筋进行了试验研究，结果表明竖向插筋能够传递钢筋应力，满足墙体的受力要求。刘继良等[18]研究了空心模剪力墙结构竖向接缝在弯曲破坏时的连接性能，结果表明，竖向接缝能够保证不同装配单元水平连接的整体性。Xiong等[19]对空心模剪力墙的受剪承载力进行了对比分析，提出了能够预测空心模剪力墙受剪承载力的计算模型。初明进等[20]按照强弯弱剪的原则设计了4个带竖向接缝的空心模剪力墙试验，研究了剪切破坏时不同构造竖向接缝的连接性能，结果表明宽度为20 mm的竖向接缝构造合理，能够保证墙体在发生剪切破坏时预制构件间的有效连接。以上研究主要针对空心模剪力墙的受力性能或接缝的构造形式，而轴压比、剪跨比、空心模内水平分布钢筋等参数对带竖向接缝的空心模剪力墙影响缺乏研究。
本文按照强弯弱剪的原则设计了5个带竖向接缝的空心模剪力墙试件(图1)，进行恒定轴力作用下的拟静力试验，对墙体的滞回性能、承载力、变形能力、刚度以及接缝连接性能等指标进行对比分析，以期为该结构的推广应用提供理论参考。
图1 预制混凝土空心模
Fig.1 Precast two-way hollow slab
1 试验概况
1.1 试件设计
设计了5个剪力墙试件，分别为试件DW1、DW2-N、DW3-L1、DW4-L2和DW5-H，几何尺寸及配筋如图2所示。试件由加载梁、墙体和地梁三部分组成；墙体为矩形截面，截面尺寸为1440 mm×180 mm，包括边缘构件、竖向接缝、空心模以及浇筑于空心模内的后浇混凝土；边缘构件长度为200 mm，竖向接缝宽度为20 mm，竖向接缝两侧的空心模宽度皆为510 mm；加载梁截面尺寸为280 mm×280 mm，地梁截面尺寸为500 mm×600 mm。
试件按照强弯弱剪的原则设计，边缘构件纵向钢筋为
箍筋为
墙体竖向分布钢筋配置于空心模内，为双层
水平钢筋由2部分组成，一部分配置于空心模内，称为“水平分布钢筋”，除试件DW5-H为双层
外，其余均为双层
该部分水平钢筋在竖向接缝处断开(图2)；另一部分配置于空心模水平孔洞内，称为“水平连接钢筋”，每一水平孔洞内配置
穿过竖向接缝，钢筋两端分别锚入两侧边缘构件内。
各试件参数如表1所示。为保证墙体发生剪切破坏，墙体基准剪跨比为1.5。试件DW1为基准试件，剪跨比为1.5，墙体高度为2160 mm，试验轴压比为0.15，空心模内水平分布钢筋为双层φ8@200；试件DW2-N的轴压比变化为0.25；试件DW3-L1和试件DW4-L2的剪跨比分别为1.0和2.0，对应的墙体高度分别为1440 mm和2880 mm(图2(b)、图2(c))；试件DW5-H的水平分布钢筋变化为双层φ10@200。
图2 试件几何尺寸及配筋情况(阴影部分为预制混凝土)
Fig.2 Dimension and reinforcement layout of specimens(the shadow part is precast concrete)
表1 试件参数
Table 1 Parameters of specimens
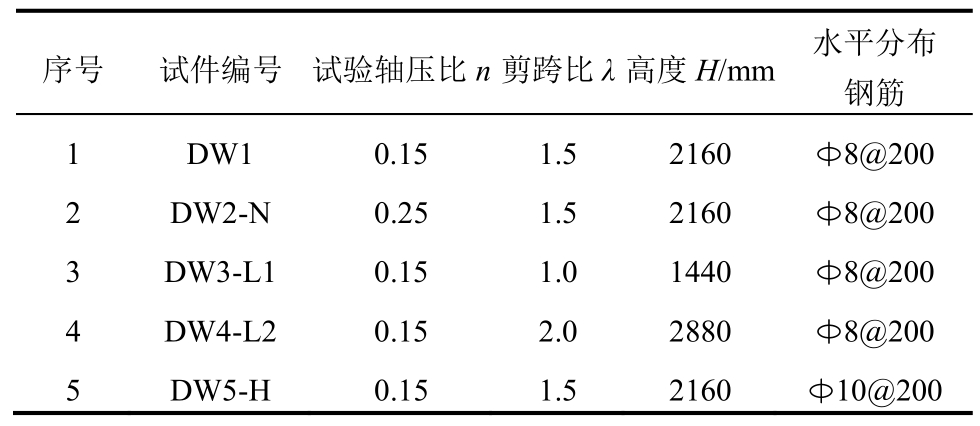
序号试件编号试验轴压比n 剪跨比λ 高度H/mm 水平分布钢筋1 DW1 0.15 1.5 21608@200 2 DW2-N 0.25 1.5 21608@200 3 DW3-L1 0.15 1.0 14408@200 4 DW4-L2 0.15 2.0 28808@200 5 DW5-H 0.15 1.5 216010@200
1.2 试件制作
工厂制作的空心模尺寸为2700 mm(长度)×1180 mm(宽度)×180 mm(厚度)，如图3所示，水平孔洞直径89 mm，间距200 mm；竖向孔洞直径140 mm，间距180 mm。空心模内水平分布钢筋为双层φ8@200或φ10@200(用于试件DW5-H)，竖向分布钢筋为双层φ8@180。
为模拟实际工程中的竖向接缝，试件制作时将空心模沿纵向中轴线剖开，安装时使两原始纵向侧边相对。此外，将空心模剖切面凿除宽度为80 mm的预制混凝土(图4)，露出的水平分布钢筋伸入边缘构件内；同时，凿除空心模顶部长度为120 mm的预制混凝土，露出的竖向分布钢筋伸入加载梁内。
制作剪力墙试件时，首先制作地梁，地梁内预埋边缘构件纵向钢筋和竖向插筋，竖向插筋为C12，空心模每一竖向孔洞内设置1根，伸入孔洞内的长度为410 mm；待地梁达到预定强度后，将其与上部墙体相交处的混凝土凿毛；然后安装空心模，空心模底部距地梁上表面20 mm；在水平孔洞内穿插水平连接钢筋，随后支护模板；最后在边缘构件、空心模水平孔洞和竖向孔洞、竖向接缝以及加载梁内浇筑混凝土，形成剪力墙试件。现浇混凝土为掺加微膨胀剂的自密实混凝土。
1.3 材料强度
制作空心模和剪力墙试件时预留标准立方体试块，与试件同条件养护；试验前一天测得混凝土立方体抗压强度平均值fcu,m如表2所示。每种类型钢筋预留一组试样，测得钢筋屈服强度fy,m、抗拉强度fu,m和伸长率δ如表3所示。
图3 空心模几何尺寸及配筋图
Fig.3 Dimension and reinforcement layout of precast two-way hollow slab
图4 空心模凿边处理
Fig.4 Edge chiseling of precast two-way hollow slab
表2 混凝土实测抗压强度
Table 2 Tested compressive strength of concrete
注：N=n(fc,p·δc,p+fc,c·δc,c )A ，其中：fc,p、fc,c分别为预制混凝土和现浇混凝土的轴心抗压强度；δc,p和δc,c分别为预制混凝土和现浇混凝土所占体积比；A为墙体截面面积。
试件编号 fcu,m /MPa 试验轴向荷载N/kN预制混凝土 现浇混凝土DW1 43.11 35.20 1257 DW2-N 43.11 35.20 1928 DW3-L1 45.14 37.24 1217 DW4-L2 45.14 37.24 1217 DW5-H 43.05 32.27 1113
表3 钢筋实测强度
Table 3 Tested strength of reinforcements
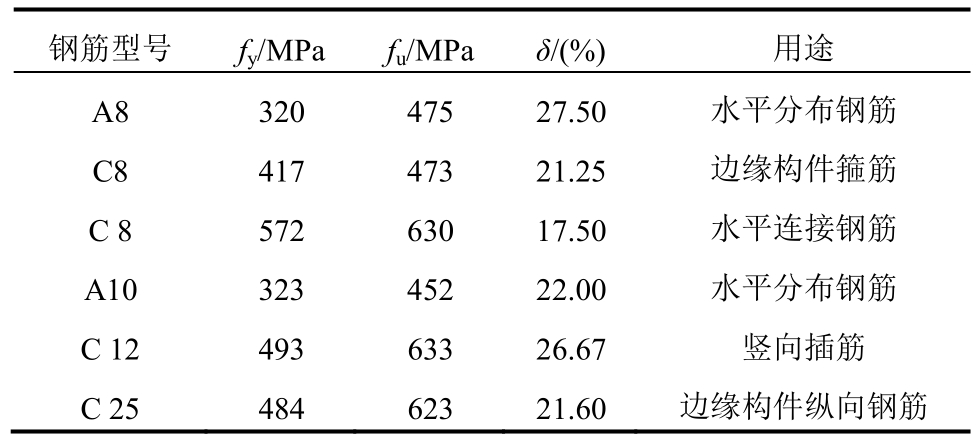
钢筋型号 fy/MPa fu/MPa δ/(%) 用途A8 320 475 27.50 水平分布钢筋C8 417 473 21.25 边缘构件箍筋C 8 572 630 17.50 水平连接钢筋A10 323 452 22.00 水平分布钢筋C 12 493 633 26.67 竖向插筋C 25 484 623 21.60 边缘构件纵向钢筋
1.4 加载和测量方案
试验为恒定轴力作用下的拟静力试验。试验时，先通过竖向千斤顶施加轴向荷载，在试验过程中保持恒定，然后采用拉压千斤顶施加水平荷载。
水平荷载采用荷载-位移混合控制，剪跨比为1.0、1.5和2.0试件的加载级差分别为300 kN、250 kN和200 kN，每级荷载反复加载1次；当试件出现斜裂缝后改用位移控制，以斜裂缝出现时的荷载级对应的位移为初始位移，以初始位移的倍数作为控制位移进行加载，每级控制位移反复加载2次，直至试件顶点水平位移角达到1/40左右，试验结束。
试验中测量了墙体的荷载、位移和钢筋应变。采用力传感器量测竖向荷载和水平荷载；在加载梁侧面中心设置位移计测量顶点水平位移；在墙体两侧各设置3～5个位移计测量墙体不同高度处水平位移，并设置竖向位移计测量相邻水平位移测点之间的相对变形；在墙体竖向接缝、空心模与边缘构件相交处以及空心模竖向孔洞位置处各设置4组相对变形测量装置，测量竖向相对变形和水平相对变形；在墙体与地梁相交处设置5个位移计测量墙体与地梁间的竖向张开变形，设置1个位移计测量墙底水平滑移变形。在边缘构件纵向钢筋、竖向插筋和空心模水平分布钢筋上设置电阻应变片，用于测量钢筋应变。剪跨比为1.5的试件测点布置如图5所示。
图5 剪跨比为1.5的试件的测点布置图
Fig.5 Layout of measurement points of specimens with shear span ratio 1.5
2 破坏过程与破坏形态
峰值荷载时，各墙体边缘构件纵向钢筋处于弹性阶段，边缘构件根部混凝土基本完好，空心模内配置的水平分布钢筋受拉屈服，墙体未发生受弯破坏，达到受剪承载力。
2.1 基准试件DW1
当水平荷载达到-310 kN/+350 kN(千斤顶先推后拉，推为“负”，拉为“正”)时，试件顶点水平位移角为-1/1213/+1/1785，墙体与地梁相交位置出现细微水平裂缝；当水平荷载达到-376 kN/+350 kN时(位移角为-1/964/+1/1785)，竖向接缝位置处出现短细斜裂缝，两方向短细斜裂缝交叉，如图6(a)所示；当水平荷载达到-550 kN/+597 kN(水平位移角为-1/558/+1/452)时，距墙底400 mm～600 mm高度范围内出现斜裂缝，墙体进入位移控制阶段。
当顶点水平位移角达到-1/315/+1/403时，距墙体西侧边缘约400 mm位置处空心模竖向孔洞位置出现多条短细斜裂缝，两方向斜裂缝交叉，交叉点位于空心模预制混凝土最薄处，构成宏观竖向裂缝(见图6(b))；随着控制位移的增加，空心模各竖向孔洞位置处均出现宏观竖向裂缝。当控制位移角达到1/138时，宏观竖向裂缝处预制混凝土起皮、掉渣，两侧预制混凝土间的相对变形(包括竖向错动和水平张开相对变形)突然增大，空心模内配置的水平分布钢筋屈服，墙体达到峰值承载力-751 kN/+804 kN；此时竖向接缝处混凝土轻微剥落，边缘构件纵向钢筋依然处于弹性阶段，根部混凝土基本完好，未出现明显压溃现象，如图6(b)所示。
图6 试件DW1破坏过程和破坏形态
Fig.6 Failure process and pattern of specimen DW1
峰值荷载后，宏观竖向裂缝处预制混凝土剥落发展为竖向裂缝；竖向接缝和竖向裂缝两侧预制混凝土间的相对变形增大，墙体被分割为多个墙柱，边缘构件纵向钢筋应变、墙体根部水平裂缝宽度逐渐减小，演变为墙柱组合体；当水平荷载下降至峰值荷载的85%时，水平位移角为1/72，如图6(c)所示；继续加载至水平位移角达到1/36时停止试验，此时墙体根部混凝土基本完好，竖向裂缝处的预制混凝土破坏较为严重，但墙体依然保持良好的竖向承载力，如图6(d)所示。
2.2 变化参数试件
各试件在破坏点和试验结束时的裂缝开展情况如图7、图8所示；破坏点为骨架曲线上水平荷载下降至峰值荷载85%时所对应的状态点[15]。
荷载作用下，各墙体相继出现根部水平裂缝、竖向接缝处短细斜裂缝、空心模竖向孔洞位置处宏观竖向裂缝，最后宏观竖向裂缝发展为竖向裂缝。墙体参数不同，破坏形态存在差异。
2.2.1 变化轴压比试件DW2-N
试件DW2-N的试验轴压比为0.25，墙体的裂缝出现荷载显著提高，裂缝宽度明显减小：根部水平裂缝的出现荷载为-476 kN和+568 kN，比试件DW1分别提高了53.5%和62.2%；竖向接缝处短细斜裂缝的出现荷载以及宏观竖向裂缝的构成荷载比试件DW1分别提高了69.9%和27.4%。
2.2.2 变化剪跨比试件DW3-L1、DW4-L2
与基准试件DW1相比，试件DW3-L1的裂缝出现荷载较高；出现了从墙体左下角到右上角的整体对角斜裂缝，与水平轴约呈45°；另一方向未形成整体斜裂缝，而是在左半部分空心模出现右下部到左上部的斜裂缝，与水平轴约呈60°；试件DW3-L1的斜裂缝数量明显多于其他试件，斜裂缝将预制混凝土分割为多个大小不一的菱形区块；当水平荷载达到峰值荷载时，菱形混凝土区块发生剥落；水平位移角达到1/37时，预制混凝土剥落严重，但墙体依然保持良好的竖向承载力，如图8(b)所示。
图7 各试件在破坏点时裂缝开展情况
Fig.7 Crack development situation of specimens at the failure point
图8 各试件在试验结束时裂缝开展情况
Fig.8 Crack development situation of specimens at off-test
试件DW4-L2的裂缝出现顺序与试件DW1略有差异，其出现根部水平裂缝后，相继出现斜裂缝、竖向接缝处短细斜裂缝以及竖向孔洞处短细斜裂缝；裂缝的出现荷载明显小于试件DW1。由于试件DW4-L2空心模竖向孔洞内和竖向接缝处的现浇混凝土存在浇筑不密实的现象，因此竖向接缝处现浇混凝土破坏较快，竖向接缝下部的斜裂缝开展较大；墙体水平位移角达到1/40时，竖向接缝下部斜裂缝相交处混凝土压溃而停止试验，如图8(c)所示。
2.2.3 变化水平分布钢筋试件DW5-H
试件DW5-H的空心模内水平分布钢筋为双层φ10@200，在竖向接缝处断开。试件DW5-H的裂缝开展过程与试件DW1基本相同，但斜裂缝宽度明显减少。
3 试验结果及分析
3.1 顶点水平力-位移角滞回曲线
图9为各试件顶点水平力-位移角滞回曲线，其中纵轴是剪压比P/fcbh0，P为试件所受水平荷载，b为墙体截面厚度，h0为墙体截面有效高度；位移角是顶点水平位移Δ与墙体高度H的比值。通过滞回曲线的对比可以发现：试验加载初期，滞回曲线基本表现为直线，残余变形很小，试件基本处于弹性状态；随着水平位移的增加，裂缝数量增多、宽度增大，墙体刚度退化，卸载后残余变形增大，承载力减小；提高剪跨比和水平分布钢筋配筋量可减缓承载力退化；峰值荷载后，各试件滞回曲线捏拢现象明显增加。
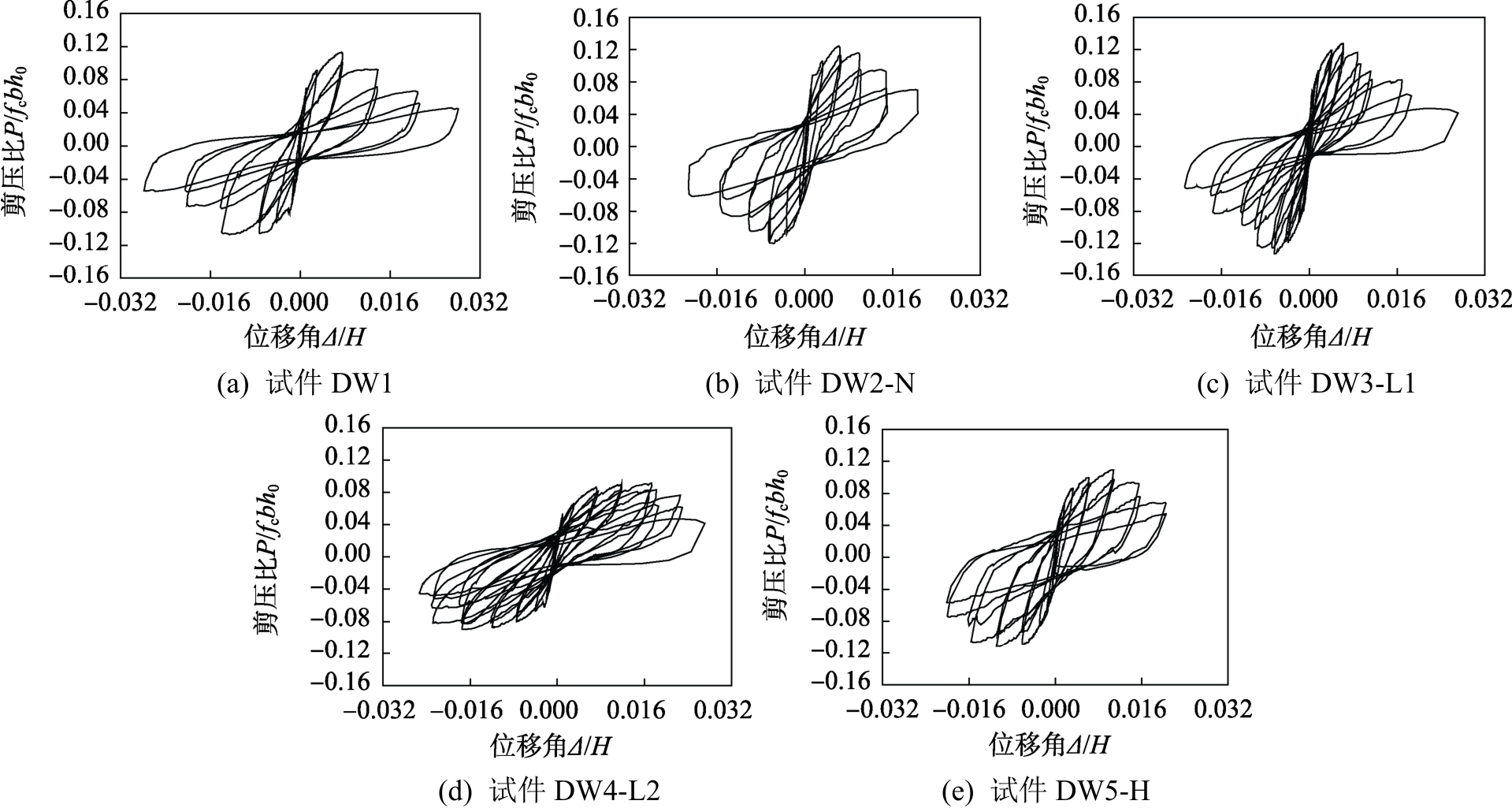
图9 顶点水平力-位移滞回曲线
Fig.9 Top lateral force-displacement hysteretic loops
3.2 骨架曲线和延性
图10为各试件顶点水平力-位移角骨架曲线，表4为各试件名义屈服点、峰值荷载点、破坏点等特征点对应的荷载、位移特征值及位移延性系数。试件的名义屈服点采用几何作图法确定[15]。位移延性系数μΔ为破坏点位移Δu与名义屈服点位移Δy的比值。由图10和表4可知：
1) 提高轴压比，墙体的受剪承载力提高，峰值位移角减小，峰值荷载后承载力退化速率加快。试件DW2-N 受剪承载力比试件DW1提高了11.8%，峰值位移角减小了22.5%。
2) 随着剪跨比的提高，墙体受剪承载力降低，峰值位移增加，承载力退化速率减缓。与试件DW1相比，试件DW3-L1的受剪承载力提高了19.2%，试件DW4-L2降低了17.0%；试件DW4-L2在峰值位移角达到1/57时的前后骨架曲线基本接近水平，承载力比较稳定。
3) 增加空心模内水平分布钢筋配筋量可提高墙体的受剪承载力和峰值位移角。空心模内水平分布钢筋虽然在竖向接缝处断开，但提高该部分钢筋配筋量，可提高墙体的峰值荷载和峰值位移角。试件DW5-H的受剪承载力比试件DW1提高了11%；峰值位移角为1/94，远大于试件DW1的1/138。
4) 空心模剪力墙试件具有良好的延性。虽然试件未发生弯曲破坏，但除试件DW2-N的延性系数接近5.0外，其余试件(包括剪跨比1.0的试件DW3-L1)的延性系数均大于6.0。空心模剪力墙可避免脆性破坏；且在位移角超过1/40时，墙体依然具有良好的竖向承载力。
3.3 竖向接缝处的相对变形
在往复荷载作用下，竖向接缝处现浇混凝土先出现两方向相互交叉的短细斜裂缝，然后竖向接缝两侧墙体出现相对变形，使墙体逐渐演变为分缝墙。
竖向接缝两侧墙体的相对变形如图11所示。试验加载初期，竖向接缝两侧未发生相对变形，墙体整体性良好。随着水平荷载的增加，水平和竖向相对变形逐渐增大，墙体整体性降低，实际剪跨比提高；峰值荷载时，各试件竖向接缝两侧墙体的水平相对变形为0.23 mm～1.86 mm，竖向相对变形为1.53 m～8.27 m。峰值荷载后，相对变形持续增加，竖向接缝处的现浇混凝土被挤出墙面。提高轴压比可减小相对变形；而随着剪跨比的提高，相对变形随之显著增大。
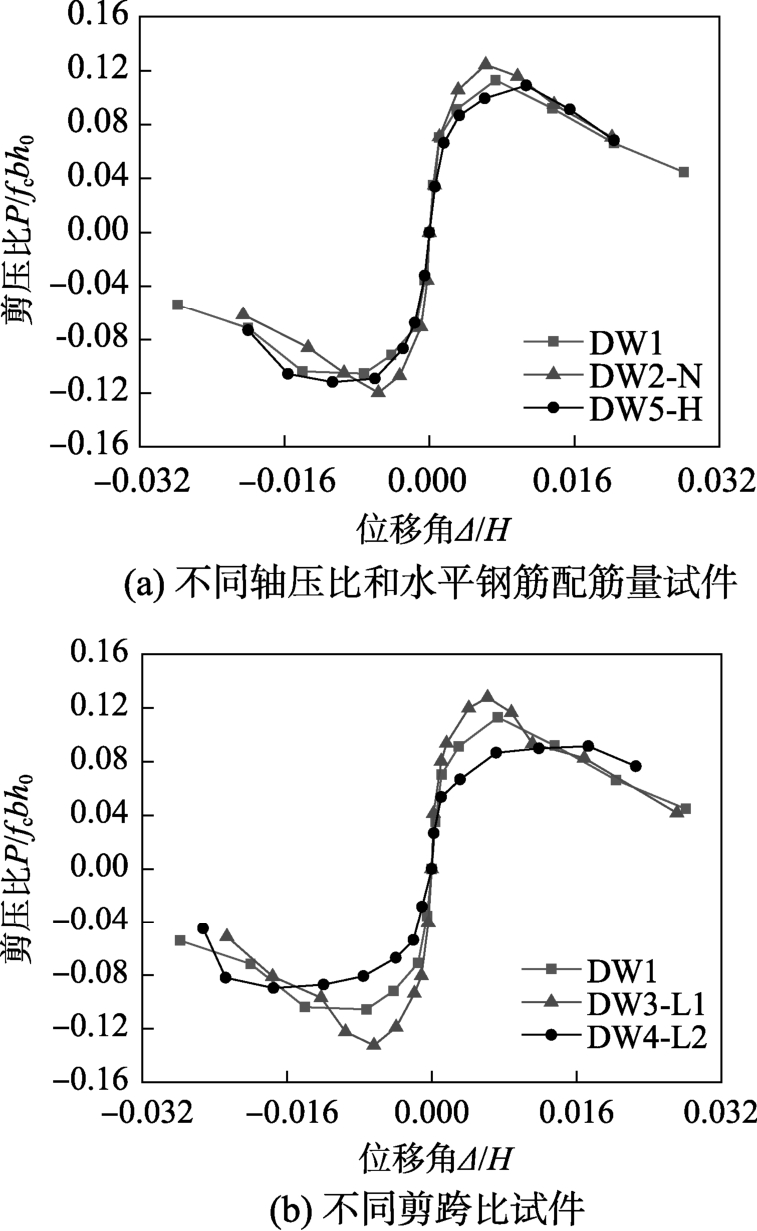
图10 顶点水平荷载-水平位移骨架曲线
Fig.10 Top lateral force-displacement skeleton curves of walls
表4 屈服点、峰值点和破坏点荷载-位移特征值
Table 4 Characteristic of yield point, peak point and ultimate point of load and displacement
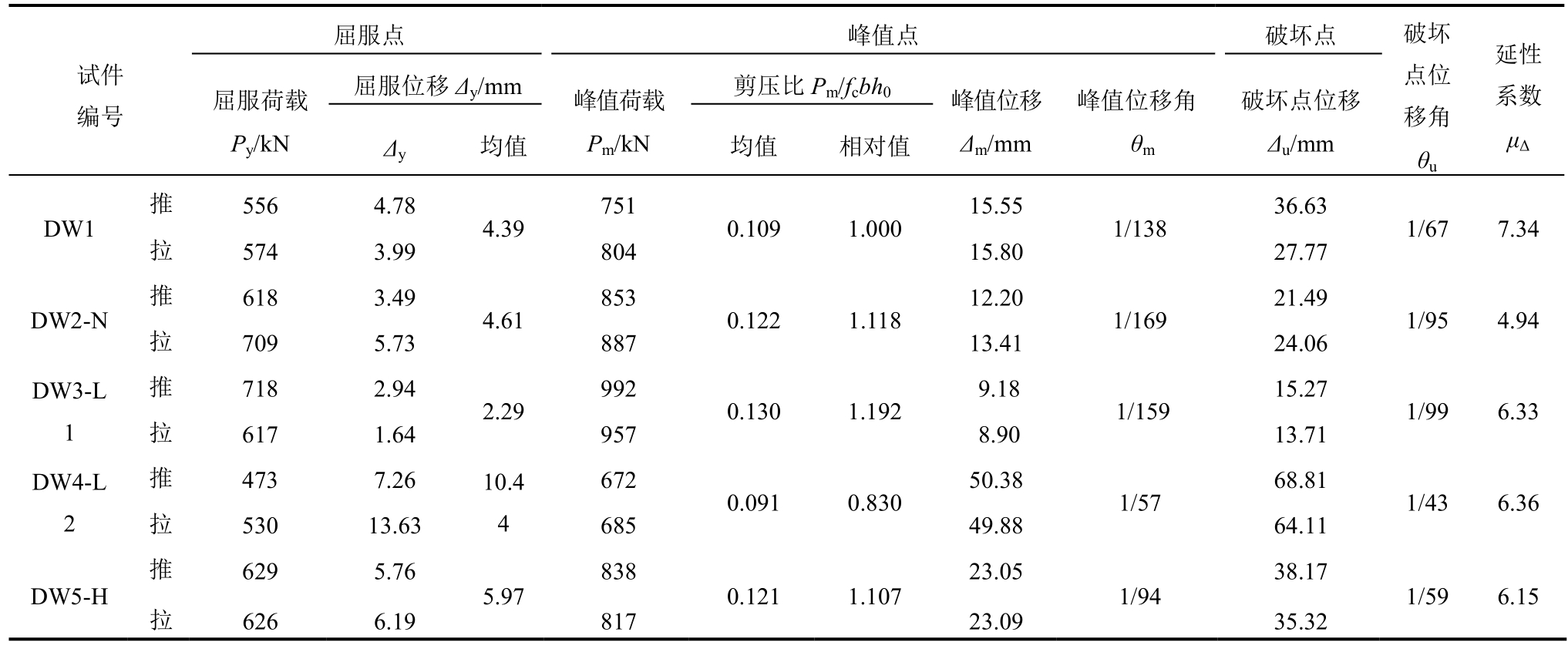
试件编号屈服荷载Py/kN屈服点 峰值点 破坏点 破坏点位移角θu屈服位移Δy/mm 峰值荷载Pm/kN Δy 均值 均值 相对值剪压比Pm/fcbh0 峰值位移Δm/mm峰值位移角θm破坏点位移Δu/mm延性系数μΔ拉 574 3.99 804 15.80 27.77 DW2-N 推 618 3.49 4.61 853 0.122 1.118 12.20 1/169 21.49 1/95 4.94拉 709 5.73 887 13.41 24.06 DW3-L 1 DW1推 556 4.78 4.39 751 0.109 1.000 15.55 1/138 36.63 1/67 7.34推 718 2.94 2.29 992 0.130 1.192 9.18 1/159 15.27 1/99 6.33拉 617 1.64 957 8.90 13.71 DW4-L 2推 473 7.26 10.4 4 672 0.091 0.830 50.38 1/57 68.81 1/43 6.36拉 530 13.63 685 49.88 64.11 DW5-H推 629 5.7683823.0538.17 1/596.15拉 626 6.19 817 23.09 35.32 5.970.121 1.1071/94
3.4 受剪承载力计算
由前述试验现象可知，峰值荷载时沿墙体竖向接缝以及边缘构件与空心模相交位置形成的新、旧混凝土结合面均出现开裂现象，使墙体进入分缝墙工作阶段。因此，基于该现象以竖向接缝和边缘构件与空心模相交位置为界限提出了针对带竖向接缝的空心模剪力墙的四单元计算模型，用于预测带竖向接缝的空心模剪力墙的受剪承载力。
3.4.1 计算模型
计算带竖向接缝的空心模剪力墙的受剪承载力时，根据墙体的破坏过程和破坏状态，对四单元计算模型进行了以下4项基本假设：
1) 在整个墙片达到峰值承载力前，每个混凝土墙片条带的顶部截面与底部截面分别达到截面的峰值抗弯承载力；
2) 墙肢构件达到峰值承载力时，竖向裂缝滑移区提供的总剪力达到最大值；
图11 竖向接缝两侧墙体相对变形
Fig.11 Relative deformation at vertical joint of walls
3) 墙体中部的破坏状况明显大于其顶部和底部，因此假设滑移量在墙片中间高度处最大，在条带顶部和底部滑移量为0；
4) 不同条带承担的竖向荷载与其截面面积成正比，并且轴力作用于每个混凝土条带的轴心处。
表5为各试件峰值荷载时，宏观竖向裂缝、竖向接缝以及边缘构件与空心模相交位置处新、旧混凝土结合面的竖向相对变形。通过数据对比可以看出，宏观竖向裂缝处的滑移变形非常小，墙体滑移变形主要集中于竖向接缝处和空心模与边缘构件相交位置处。文献[21]中指出，界面处的相对滑移量是影响界面剪应力的主要因素之一。因此在进行受剪承载力计算时，可将各试件划分为4个计算单元，如图12所示；各单元简化计算模型如图13所示，因界面处的正应力叠加之和为0，对墙体受剪承载力无影响，故在图13中未予表示。根据弯矩平衡可以得到各单元的受剪承载力计算公式：
式中：Ti为单元界面总剪力；li为单元截面宽度；Mi、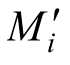
为单元上、下端部承担最大弯矩；Hw为单元高度。
表5 峰值荷载时不同位置处的相对滑移
Table 5 Relative slip deformation of different direction at peak-loading
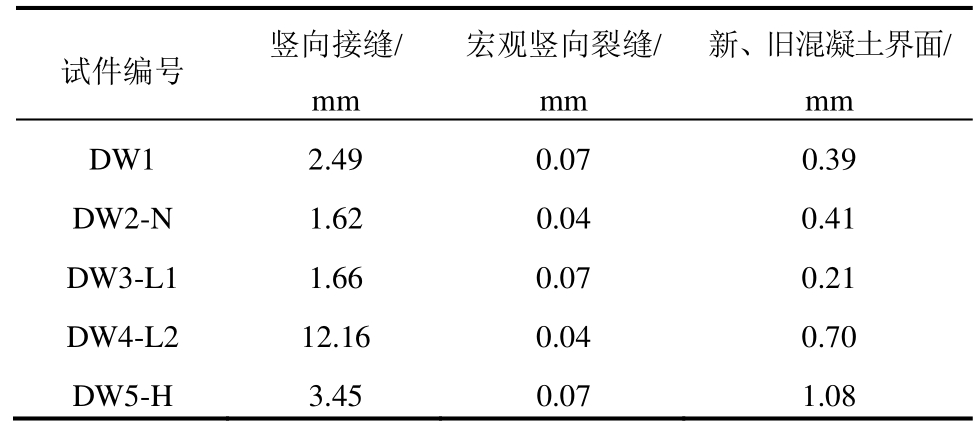
试件编号 竖向接缝/mm宏观竖向裂缝/mm新、旧混凝土界面/mm DW1 2.49 0.07 0.39 DW2-N 1.62 0.04 0.41 DW3-L1 1.66 0.07 0.21 DW4-L2 12.16 0.04 0.70 DW5-H 3.45 0.07 1.08
3.4.2 界面总剪力
为便于计算剪切滑移产生的总剪力，文献[19]对滑移界面处的剪应力进行了简化计算，认为各界面处的剪应力τ相同。由图12可以看出滑移界面1、4的构造与滑移界面2、3显著不同，且两种情况的界面均包括现浇界面和新、旧混凝土界面，因此结合文献[21]提出的剪应力计算方法，采用式(2)求取界面处最大平均剪应力：
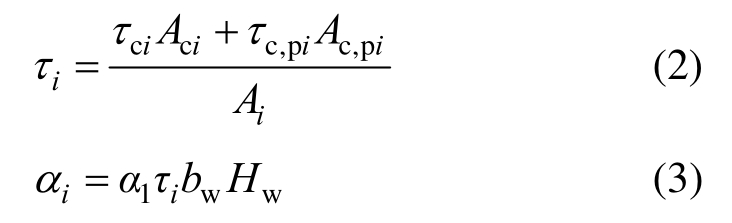
式中：τci为界面处现浇混凝土产生的界面剪应力；τc,pi为界面处新、旧混凝土结合面产生的界面剪应力；Aci为滑移界面处现浇混凝土截面面积，如图12界面虚线位置所示；Ac,pi为滑移界面处新、旧混凝土结合面截面面积，如图12界面实线位置所示；Ai为滑移界面截面面积，取A=bw·Hw；αi为剪应力界面系数。
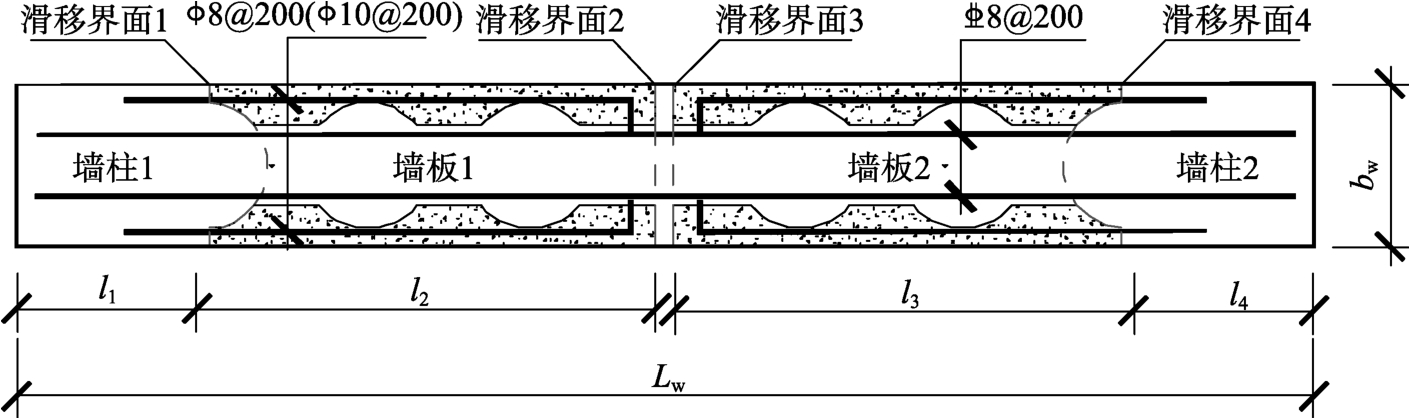
图12 截面划分示意图
Fig.12 Schematic of the division of section
计算得到的界面剪应力如表6所示。基于假设3)，本文提出了剪应力界面系数α，对两种不同界面的剪应力界面系数进行了计算，由此可采用式(3)求取界面处的最大总剪力，计算结果见表6。
图13 计算模型示意图
Fig.13 Schematic of the computational model
表6 各试件界面剪应力、界面系数以及最大总剪力
Table 6 Shear stress of specimens, factor and total shear of the interface
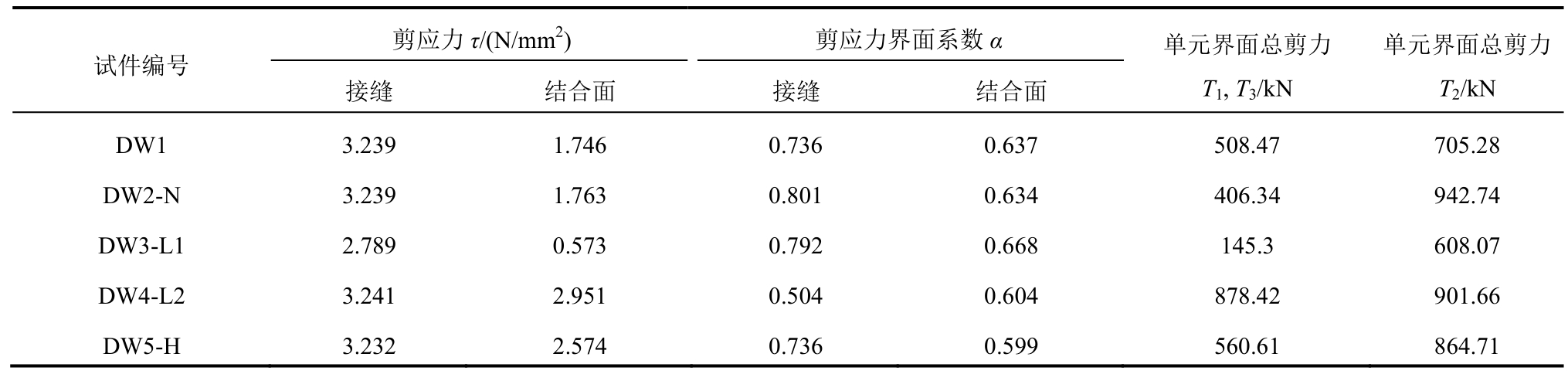
试件编号接缝 结合面 接缝 结合面剪应力τ/(N/mm2) 剪应力界面系数α 单元界面总剪力T1, T3/kN单元界面总剪力T2/kN DW1 3.239 1.746 0.736 0.637 508.47 705.28 DW2-N 3.239 1.763 0.801 0.634 406.34 942.74 DW3-L1 2.789 0.573 0.792 0.668 145.3 608.07 DW4-L2 3.241 2.951 0.504 0.604 878.42 901.66 DW5-H 3.232 2.574 0.736 0.599 560.61 864.71
3.4.3 端部弯矩求取
式(1)中提出需要考虑端部弯矩对墙体受剪承载力的贡献。各单元的端部弯矩除受配筋、截面以及混凝土强度的影响外，还受轴向荷载的影响。在进行上部弯矩求取时，仅需按照假设4)求取轴向荷载即可；而求取下部弯矩时，还应考虑界面最大总剪力以及单元自重对轴向荷载的作用。本文采用XTRACT软件对各单元端部弯矩进行计算，计算结果如表7所示。根据式(1)计算得到各单元的受剪承载力，并将其进行叠加计算，计算结果如表7所示。图14为计算结果与试验结果的对比分析，可以看出，计算结果较为保守，均小于试验结果，这是由于上部加载梁和下部地梁对各单元的约束作用，使得各单元的实际高度Hw小于计算高度。由此表明本文建立的墙体计算模型适用于带竖向接缝模剪力墙受剪承载力的预测。
图14 受剪承载力对比
Fig.14 Comparison of shear capacity
表7 端部弯矩及受剪承载力计算结果
Table 7 Result of flexural strengths of the end section and shear capacity
项目 M1/(kN·m)M′(kN·m)1/M(kN·m)2/M′(kN·m)2/M(kN·m)3/M′(kN·m)3/M(kN·m)4/M′(kN·m)4/∑(kN·m)Tl/2/ii ∑(kN·m)M/i M′∑i /∑iF/(kN·m)kN单元截面宽度li/mm 200 510 510 200 - - - -单元截面厚度bw/mm 180- - - -DW1 99.46 95.90 111.80 76.83 116.90 145.8090.03 96.16 720.71 418.19 414.69769.10 DW2-N 98.83 93.99 145.50 57.17 151.00 190.9093.61 96.14 769.29 488.94 438.20839.82 DW3-L1 100.30 95.070 110.20 17.55 115.40 177.2093.61 91.60 413.28 419.51 381.42934.01 DW4-L2 100.30 71.31 110.10 106.90 115.40 120.6089.72 79.87 1083.53 415.52 378.68685.30 DW5-H 97.67 91.63 102.50 45.58 151.40 116.8088.88 91.38 839.04 440.45 345.39804.39
4 结论
本文按照强弯弱剪的原则设计了5个带竖向接缝的空心模剪力墙试件，进行了恒定轴力作用下的拟静力试验，研究了轴压比、剪跨比、水平分布钢筋配筋量等关键参数对竖向接缝连接性能和墙体受力性能的影响，主要结论如下：
1) 竖向接缝和空心模竖向孔洞内新、旧混凝土结合面对墙体破坏过程和破坏形态影响显著。在荷载作用下，墙体沿竖向接缝以及空心模竖向孔洞处开裂、发生相对变形，显著提高了墙体的变形能力，除试件DW2-N的延性系数接近5.0外，其余试件的延性系数均大于6.0。
2) 提高轴压比可提高墙体的受剪承载力，减小峰值位移角，降低延性系数；随着剪跨比的提高，墙体受剪承载力降低，峰值荷载稳定性和墙体变形能力增强。
3) 空心模内水平分布钢筋在竖向接缝处不连续，但提高其配筋量依然可提高墙体的受剪承载力、延性，减小裂缝宽度。
4) 竖向接缝构造合理，满足墙体受力要求。
5) 本文提出的四单元计算模型充分了考虑界面构造差异性，适用于计算带竖向接缝的空心模剪力墙受剪承载力，计算结果表明该模型计算结果保守，可用于预测带竖向接缝的空心模剪力墙的受剪承载力。
[1]Fintel M.Performance of buildings with shear walls in earthquakes of the last thirty years [J].PCI Journal, 1995,40(3): 62-80.
[2]Ghosh S K.Observation on the performance of structures in the Kobe earthquake of January 17, 1995 [J].PCI Journal, 1995, 40(2): 14-22.
[3]Han W L, Zhao Z Z, Qian J R.Global experimental response of a 3-story full-scale precast concrete shear wall structure with rebars spliced by grouted coupler [J].PCI Journal, 2019, 64(1): 51-65
[4]李宁波, 钱稼茹, 叶列平, 等.竖向钢筋套筒挤压连接的预制钢筋混凝土剪力墙抗震性能试验研究[J].建筑结构学报, 2016, 37(1): 31-40.Li Ningbo, Qian Jiaru, Ye Lieping, et al.Tests on seismic behavior of precast RC shear walls with vertical rebar splicing by pressed sleeve [J].Journal of Building Structures, 2016, 37(1): 31-40.(in Chinese)
[5]刘家彬, 陈云钢, 郭正兴, 等.竖向新型连接装配式剪力墙抗震性能试验研究[J].湖南大学学报(自然科学版), 2014, 41(4): 16-24.Liu Jiabin, Chen Yungang, Guo Zhengxing, et al.Test on the seismic performance of precast shear wall with vertical reinforcement lapping in pore-forming on steel plate [J].Journal of Hunan University (Natural Sciences),2014, 41(4): 16-24.(in Chinese)
[6]余志武, 彭晓丹, 国巍, 等.装配式剪力墙U型套箍连接节点抗震性能[J].浙江大学学报(工学版)，2015,49(5): 975-984.Yu Zhiwu, Peng Xiaodan, Guo Wei, et al.Seismic performance of precast concrete shear wall with U-type reinforcements ferrule connection [J].Journal of Zhejiang University (Engineering Science), 2015, 49(5): 975-984.(in Chinese)
[7]刘家彬, 陈云钢, 郭正兴, 等.装配式混凝土剪力墙水平拼缝U型闭合筋连接抗震性能试验研究[J].东南大学学报(自然科学版), 2013, 43(3): 565-570.Liu Jiabin, Chen Yungang, Guo Zhengxing, et al.Test on seismic performance of precast concrete shear wall with U-shaped closed reinforcements connected in horizontal joints [J].Journal of Southeast University (Natural Science Edition), 2013, 43(3): 565-570.(in Chinese)
[8]焦安亮, 张鹏, 李永辉, 等.环筋扣合锚接连接预制剪力墙抗震性能试验研究[J].建筑结构学报, 2015, 36(5):103-109.Jiao Anliang, Zhang Peng, Li Yonghui, et al.Tests on seismic behavior of pre-cast shear walls with annular closed reinforcements [J].Journal of Building Structures,2015, 36(5): 103-109.(in Chinese)
[9]王墩, 吕西林, 卢文胜.带接缝连接梁的预制混凝土剪力墙抗震性能试验研究[J].建筑结构学报, 2013,34(10): 1-11.Wang Dun, Lü Xilin, Lu Wensheng.Experimental study on seismic performance of precast concrete shear wall with joint connecting beam [J].Journal of Building Structures, 2013, 34(10): 1-11.(in Chinese)
[10]姜洪斌, 陈再现, 张家齐, 等.预制钢筋混凝土剪力墙结构拟静力试验研究[J].建筑结构学报, 2011, 32(6):34-40.Jiang Hongbin, Chen Zaixian, Zhang Jiaqi, et al.Quasi-static test of precast reinforced concrete shear wall structure [J].Journal of Building Structures, 2011, 32(6):34-40.(in Chinese)
[11]姜洪斌, 张海顺, 刘文清, 等.预制混凝土结构插入式预留孔灌浆钢筋锚固性能[J].哈尔滨工业大学学报,2011, 43(4): 28-31.Jiang Hongbin, Zhang Haishun, Liu Wenqing, et al.Experimental study on plug-in filling hole for steel bar anchorage of the PC structure [J].Journal of Harbin Institute of Technology, 2011, 43(4): 28-31.(in Chinese)
[12]种迅, 张蓝方, 万金亮, 等.两层带开洞预制剪力墙抗震性能试验研究与数值模拟分析[J].工程力学, 2019,36(5): 176-183.Zhong Xun, Zhang Lanfang, Wan Jinliang, et al.Experimental study and numerical simulation on seismic performance of two-story precast shear walls with opening[J].Engineering Mechanics, 2019, 36(5): 176-183.(in Chinese)
[13]张微敬, 钱嫁茹, 于检生, 等.竖向分布钢筋单排间接搭接的带现浇暗柱预制剪力墙抗震性能试验[J].土木工程学报, 2012, 45(10): 89-97.Zhang Weijing, Qian Jiaru, Yu Jiansheng, et al.Test on seismic behavior of precast shear walls with cast-in-situ boundary elements and vertical distributed reinforcements spliced by a single row of steel bars [J].China Civil Engineering Journal, 2012, 45(10): 89-97.(in Chinese)
[14]朱张峰, 郭正兴.装配式混凝土剪力墙结构空间模型抗震性能试验[J].工程力学, 2015, 32(4): 153-159.Zhu Zhangfeng, Guo Zhengxing.Research on seismic performance of a spatial model of a mew precast concrete shear wall structure [J].Engineering Mechanics, 2015,32(4): 153-159.(in Chinese)
[15]朱张峰, 郭正兴.考虑竖向与水平接缝的工字形装配式混凝土剪力墙抗震性能试验研究[J].工程力学,2019, 36(3): 139-148.Zhu Zhangfeng, Guo Zhengxing.Aseismic experimental research on I-shaped precast concrete shear walls with vertical and horizontal joints [J].Engineering Mechanics,2019, 36(3): 139-48.(in Chinese)
[16]薛伟辰, 古徐莉, 胡翔, 等.螺栓连接装配整体式混凝土剪力墙低周反复试验研究[J].土木工程学报, 2014,47(增刊2): 221-226.Xue Weichen, Gu Xuli, Hu Xiang, et al.Experimental study of assembles monolithic concrete shear wall with bolted connection under low reversed cyclic loading[J].China Civil Engineering Journal, 2014, 47(Suppl2):221-226.(in Chinese)
[17]周剑, 赵作周, 侯建群, 等.预制混凝土空心模剪力墙上下层插筋连接抗震性能试验研究[J].建筑结构学报,2015, 36(6): 44-52.Zhou Jian, Zhao Zuozhou, Hou Jianqun, et al.Experimental study on seismic behavior of splice rebar connection between upper and lower floors of shear walls with precast concrete hollow moulds [J].Journal of Building Structures, 2015, 36(6): 44-52.(in Chinese)
[18]刘继良, 初明进, 侯建群, 等.带竖向接缝的预制空心模剪力墙受弯性能试验研究[J].建筑结构学报, 2017,38(3): 84-92.Liu Jiliang, Chu Mingjin, Hou Jianqun, et al.Experimental study on flexural performance of precast concrete shear walls built with precast two-way hollow slabs with vertical joints [J].Journal of Building Structures, 2017, 38(3): 84-92.(in Chinese)
[19]Xiong C, Chu M J, Liu J L, et al.Shear behavior of precast concrete wall structure based on two-way hollow-core precast panels [J].Engineering Structure,2018, 176: 74-89.
[20]初明进, 刘继良, 崔会趁, 等.不同构造竖缝的装配式空心模板剪力墙抗震性能试验研究[J].建筑结构学报,2014, 35(1): 93-102.Chu Mingjin, Liu Jiliang, Cui Huichen, et al.Experimental study on seismic behaviors of assembled monolithic concrete shear walls built with precast two-way hollow slabs with various details [J].Journal of Building Structures, 2014, 35(1): 93-102.(in Chinese)
[21]Xu J C, Wu C Q, Li Z X, et al.Numerical analysis of shear transfer across an initially uncrack reinforced concrete member [J].Engineering Structure, 2015, 102:296-309.