作为典型的颗粒材料，砂土具有显著的压硬性，其刚度表现受到实际应力水平的影响。土体刚度的这种特性在工程应用中需要得到充分的重视，尤其是在土体应力有较大变化时的应用场景中，例如基坑的开挖/回填[1-2]、土石坝的蓄水/泄水[3]、地震波沿深度方向的传递[4-5]和地下结构抗震[6]等。基坑开挖相关的研究表明，如果不考虑土体刚度随深度(即应力水平)的变化，将大幅度低估挡土墙的侧向变形[1]。膨胀土地基中的桩-土共同作用研究发现，土体刚度对于桩身轴力和桩头位移都有很大影响[7]。
室内实验(波速法、共振柱、扭剪和三轴等)研究表明，土体在极小应变(小于10-5)条件下处于准弹性状态，其模量为常数[8-10]。可记此时的剪切模量为极小应变剪切模量G0或最大剪切模量Gmax。土体的极小应变模量是深入研究小应变模量或者动模量的前提，具有极为重要的科研及应用价值。
土体的极小应变模量受到许多因素的影响，主要有固结应力水平、密实度、颗粒形状、粒径级配、微观结构等。对于同一种砂土而言，主要是密实度和固结应力水平的影响，最常用的回归公式是Hardin-Richart公式[11]：
式中，F(e)是孔隙率e的函数，主要反映了堆积密度对于土体刚度的影响，常取为(eg-e)2/(1+e)。A、m和eg是土体参数，综合反映了颗粒形状、粒径级配、微观结构等因素的影响。(p′)m主要反映了土体刚度随应力水平而非线性增长的特征。理想弹性球的经典赫兹接触给出G0～(p′)13的关系，但是天然土体颗粒之间的接触与理想弹性球体相互间的接触有一定区别，土力学实验得出的m值大多分布在1/3~3/5的区间内[12-13]。
实验室实验中的相关研究大多是基于等向固结状态，而实际地基大都处于非等向固结状态。因此，基于实验室实验的Hardin-Richart公式直接应用于实际工程中，会带来一定的误差。许多实验研究表明，非等向固结下的土体刚度并不符合Hardin-Richart公式的预测，从而需要增加一定的修正系数。
Hardin-Richart等经验公式属于Cauchy弹性模型，在循环荷载等复杂应力路径下可能表现出能量非保守特性，即弹性能量是与应力路径相关的，这在理论上不正确，同时也会引起不正确的残余变形[14]。而弹性力学中的超弹性模型也称为Green弹性模型，其应力-应变关系始终从一个自由能函数的微分形式给出，完全满足热力学基本定律的要求，在不同材料的本构关系研究中得到广泛应用[15-16]。另外，超弹性模型在处理正剪耦合时比较方便，例如剪胀性、应力引起的各向异性、主应力旋转等[17-18]。因此研究非等向固结，尤其是高度非等向状态下的土体刚度，采用超弹性模型更为合适。Houlsby等研究了能反映土体刚度随平均应力变化的超弹性模型[16]，但非等向固结状态的影响并没有得到讨论。
本文首先对以往学者完成的非等向固结状态下的砂土极小应变刚度实验进行研究分析，得出有较多实验数据支持的经验规律；然后针对3种能够反映土体刚度随应力水平增大规律的超弹性模型进行研究，发现其中仅有HE1模型对砂土非等向固结状态下的刚度规律趋势预测正确；最后，对于HE1模型进行了参数影响分析。
1 非等向固结实验研究分析
关于非等向固结状态的研究，一般是考虑常规三轴固结状态，即
记此时的固结应力比
非等向固结状态下的土体极小应变剪切模量，可以由下列形式的修正Hardin-Richart公式给出：
其中：R为修正系数，取值由k13决定。实验研究发现，土体剪切刚度主要受相应平面内的两个主应力的影响[19]，因此Yu和Richart[20]建议采用
来代替p′对刚度做归一化：
并基于Ottawa砂和Toyoura砂实验数据给出了经验公式：
其中，归一化固结应力比
是土体能达到的最大固结应力比。可以看出，该修正系数R*随固结应力比k13是单调递减的。
另外，也有人采用
来进行归一化。为了便于统一比较，我们将这些实验数据(参见表1)以及经验公式统一换算为式(2)，然后研究其修正系数R随k13的变化规律，如图1所示，显然经典Hardin-Richart公式意味着R恒定为1。
在使用p′进行归一化时，Yu-Richart公式(式(3)和式(4))换算为式(2)后给出的修正系数R随着固结应力比k13的增大先是略微增大，而后较大幅度下降。总的来说，当固结应力比小于某阈值时，修正系数R基本为1；当固结应力比相对较大时，修正系数R迅速降低，降低幅值可超过20%。这与Kuribayashi等关于Toyoura砂[21](图中三角符号)、Tatsuoka等关于Toyoura砂[22](图中未列出)以及Bellotti等关于Ticino砂[23](图中方块符号)的实验研究结果相一致。另外，DEM数值模拟[24]、极小应变条件下的弹性模量的实验研究[25]和循环荷载条件下的剪切模量的实验研究[26]同样得出了类似的结论。
表1 前人实验总结
Table 1 Summary of previous experiments
序号 归一化参量 非线性参数m固结应力比k13 m值 实验方法 实验所用砂 土样状况 k13范围 参考文献1 p′ 0.5 共振柱 Toyoura砂 饱和 1~4.3 Kuribayashi等[19]+ 0.5 共振柱 Ottawa砂、Toyoura砂干 1~4.5 Yu和Richart[18]3 σ13σ′′ ≈0.5 波速法 Ticino砂 干 1~3.03 Bellotti等[21]4 p′ ≈0.5 波速法 Blue砂 饱和 1~2.5 Payan等[24]2 13()2 σ′σ′
图1 不同固结应力比下的土体极小应变模量修正系数
Fig.1 Comparison of the relationships between shear modules ratio and stress ratio by various investigations
虽然也有实验研究认为修正系数R随着k13的增大而增大[27-29]，如Payan等[27]关于Blue砂的实验 (图中圆形符号)，但这些研究的k13值范围普遍较小，一般小于2.5。鉴于Yu-Richart的研究系统性更强，且得到多数相关研究的重复验证，因此我们主要采用其研究结果来作为参考。考虑到Yu-Richart建议了新的归一化方式，因此，本文中两种归一化方式的结果都予以呈现。
2 超弹性模型
2.1 超弹性模型简介
本文所有应力均指有效应力，所有应变均指弹性应变(极小应变条件下，弹性应变等于总应变)。σij为Cauchy有效应力张量，εij为弹性应变张量；δij为Kronecker delta记号，上述2阶张量均遵循哑标的爱因斯坦求和约定。应力不变量有平均应力
及剪应力
其中
为偏应力张量。同样，应变不变量有体积应变
及剪应变
其中
为偏应变张量。在常规三轴条件下，一般采用如下形式
的简写；此时的应力和应变不变量有
超弹性模型是指材料具有Helmholtz自由能F(又可称为弹性势能)或Gibbs自由能E(又可称为应变余能)，其应力-应变关系可以从相应的自由能函数的微分中推导得出。这两种形式的自由能可以通过勒让德变换来互相推导，但是对于某些函数形式的自由能，可能并不存在简单函数形式的另一种对应的自由能函数形式。
对于Helmholtz自由能形式的超弹性模型有：
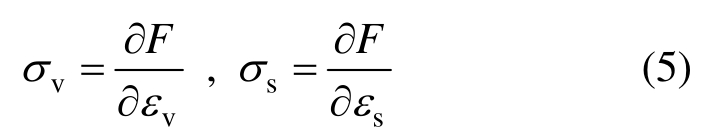
进而得出其应力-应变关系为：
切线刚度矩阵中体积模量
剪切模量
剪胀模量
极小应变剪切模量G0就等于该切线剪切模量G。
对于Gibbs自由能形式的超弹性模型有：
进而得出其应力-应变关系为：
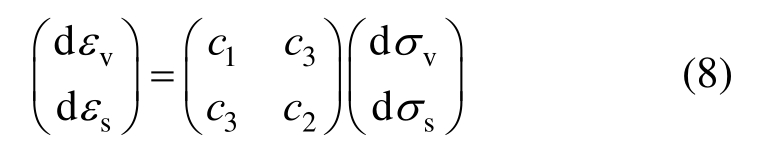
切线柔度矩阵中
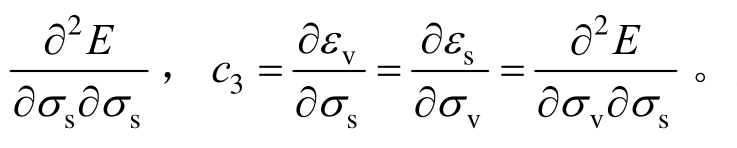柔度矩阵求逆得出刚度矩阵：
考虑Hardin-Richart公式给出的刚度随平均应力的幂律关系，其对应的超弹性模型大致有3种[16]，如表2所示。其中应力和应变不变量的定义及其与三轴状态下的不变量的关系参见2.1节；参数n反映了土体刚度随应力水平的增长，与Hardin-Richart公式中的m有关，具体关系2.1.1节、2.1.2节、2.1.3节将推导给出；ξ或ς与泊松比有关；B或C影响着土的刚度模量的大小。
表2 3种能反映Hardin-Richart公式的超弹性模型
Table 2 Three types of hyperelastic models compatible to the Hardin-Richart formula
模型 Helmholtz自由能 Gibbs自由能 剪切应力比FBεε ξε vv ()n =+ 无简单形式2 q 3 HE12 s pnnξ′+≤2(2)HE2 FBε ξε)n=+ 22/(21)vs ′HE3 无简单形式 22vvs()2v 2s(ECσςσ-=+()nn v 62 q p =ξε ε s EBσσξσ=+n +qn pnξ′-≤3(2)2
2.1.1 HE1模型
首先得出HE1超弹性模型的应力不变量为：
进而可以得出其切向刚度矩阵，其中：
如果考虑等向固结状态下：
式中，
相当于Hardin-Richart公式中的m，
相当于A·F(e)，其中密实度的影响可通过将B设定为密实度相关函数来体现。可见，HE1模型对于等向固结土体，能够给出完全符合Hardin-Richart公式的预测结果。
接下来我们推导三轴条件下的刚度规律，记
则剪切应力比
可以看出HE1模型对于土体能达到的最大剪切应力比有一个限值。土体相应的固结应力比为：
将土体剪切模量中的应变项消去，得出：
与式(2)对比，可以得出HE1模型给出的Hardin-Richart公式修正系数为：
和式(14)共同绘图可以得出其随固结应力比变化的规律。
2.1.2 HE2模型
对于HE2超弹性模型，其两种自由能形式给出的结果是等价的，在此仅给出Helmholtz自由能形式的结果。首先得出其应力不变量为：
进而得出其切向刚度矩阵，其中：
在等向固结状态下同样可以得出与HE1类似的符合经典Hardin-Richart公式的结果，在此不再重复。
常规三轴条件下，剪切应力比
可见HE2模型对于土体能达到的最大剪切应力比没有限制。将p′和q的公式代入刚度式中消去应变，即可得出剪切刚度与剪切应力比的关系：
式中，
相当于Hardin-Richart公式中的m，将
代入其中，即可得出其与固结应力比k13的关系。
2.1.3 HE3模型
首先得出HE3超弹性模型的应变不变量为
进而得出其切向柔度矩阵，求逆可得出其切向刚度矩阵，其中
式中：-n相当于Hardin-Richart公式中的m，因此n的取值一般为-1/3~3/5，即小于0。考虑到体应变不能为负，则由式(20)可知
即
可以看出HE3模型对于土体能达到的最大剪切应力比也有一个限值。
2.2 模拟对比分析
式(16)、式(19)、式(21)中给出了修正Hardin-Richart公式中的修正系数R，将其随固结应力比k13的变化绘制出来如图2所示。图中同时给出了经典Hardin-Richart公式以及Yu-Richart经验公式的结果。
HE1模型给出的修正系数R随着固结应力比k13的增大而衰减，与Yu-Richart经验公式给出的趋势较为一致；而HE2和HE3模型给出的R都随着固结应力比k13的增大而持续增大，与实验规律不一致。需要说明的是，图示曲线具体数值仍然受到模型参数的影响，但并不改变这种明显不同的趋势。从模型本身角度而言，这些不同的趋势主要受到两个因素的影响：一个是弹性剪胀或剪缩特性，另一个是剪切刚度的影响因素。从式(10)可以看出，HE1模型具有弹性剪胀特性，即保持平均应力不变条件下剪切，能使得弹性体积应变减小；而式(11)表明其剪切刚度仅受弹性体积应变影响，因而非等向固结这种剪切能够使得剪切刚度变小。式(17)显示HE2模型同样具有弹性剪胀特性，但式(18)显示其剪切刚度同时受到弹性体积应变和弹性剪切应变的影响，非等向固结状态下这两者共同作用使得剪切刚度增大。而式(20)显示HE3模型则具有弹性剪缩特性，不能反映非等向固结状态下土体刚度的衰减规律。
图2 不同固结应力比下的土体极小应变模量修正系数
Fig.2 The relationships between shear modules ratio and stress ratio
考虑到HE2和HE3预测的趋势与实验结果有较大差异，因此我们仅对HE1进行定量的参数分析。在做此分析时，主要对比一下HE1的预测与Yu-Richart公式的结果，因此在绘图时采用Yu-Richart的建议：纵坐标刚度的归一化时采用
即为式(3)中的R*；横坐标固结应力比的归一化时采用式(4)中的kn。HE1模型对土体能达到的最大固结应力比有一个限值，我们采用这个限值对其固结应力比进行归一化，从而得到HE1模型中相应的kn。
HE1模型的3个参数中：B只影响土体刚度的大小，不影响该相对规律；n的具体数值可通过实验数据很精确地标定，且对于表1所总结的砂土都大致为1；ξ的具体数值难以通过常规土力学实验来精确标定，所以有必要进行参数分析。将Yu-Richart公式与HE1模型的结果对比，如图3所示。HE1模型的结果受到其参数ξ的影响：ξ越大时，修正系数R*整体越小。HE1的结果与Yu-Richart公式总体比较吻合。在较低应力比时，HE1的结果要略小于Yu-Richart公式；在较高应力比时，HE1的结果要略大于(ξ=2或ξ=3)或略小于(ξ=4)Yu-Richart公式。
图3 HE1模型不同固结应力比下的模量修正系数
Fig.3 The relationships between shear modules ratio and stress ratio by HE1 model
3 结论
(1) 3种类型的超弹性模型能够反映等向固结状态下土体刚度随应力水平增大而增大的幂律关系，但仅有HE1模型对土体非等向固结状态下的刚度规律趋势预测正确。这主要是因为其具有包括弹性剪胀在内的特殊的正剪耦合特性。
(2) HE1模型对土体非等向固结状态下的刚度规律预测结果受到其参数ξ取值的影响，但总体而言与实验结果总结的规律一致。
(3) 下一步工作，考虑具有非线性刚度地基与地下结构的弹性动力相互作用，以便反映在边界条件下的地基非等向固结极小应变刚度对地下结构抗震性能的影响。
[1]Clayton C R I.Stiffness at small strain: research and practice [J].Géotechnique, 2011, 61(1): 5-37.
[2]温科伟, 刘树亚, 杨红坡.基于小应变硬化土模型的基坑开挖对下穿地铁隧道影响的三维数值模拟分析[J].工程力学, 2018, 35(增刊): 80-87.Wen Kewei, Liu Shuya, Yang Hongpo.Threedimensional numerical simulation analysis of theinfluence of pit excavation based on Hardening soil-smallstrain model for metro tunnel [J].Engineering Mechanics, 2018, 35(Suppl): 80-87.(in Chinese)
[3]张凌凯, 王睿, 张建民, 等.不同应力路径下堆石料的动力变形特性试验研究[J].工程力学, 2019, 36(3):114-120.Zhang Lingkai, Wang Rui, Zhang Jianmin, et al.Experimental study on dynamic deformation characteristics of rockfill materials under differentstress paths [J].Engineering Mechanics, 2019, 36(3): 114-120.(in Chinese)
[4]Towhata I.Seismic Wave Propagation in Elastic Soil with Continuous Variation of Shear Modulus in the Vertical Direction [J].Journal of the Japanese Geotechnical Society Soils & Foundation, 1996, 36(1):61-72.
[5]李志远, 李建波, 林皋, 等.饱和层状地基条形基础动刚度的精细积分算法[J].工程力学, 2018, 35(6):15-23.Li Zhiyuan, Li Jianbo, Lin Gao, et al.Precise integration method for dynamic stiffness of strip foundation on saturatedsoil [J].Engineering Mechanics, 2018, 35(6):15-23.(in Chinese)
[6]刘晶波, 王东洋, 谭辉, 等.隧道纵向地震反应分析的整体式反应位移法[J].工程力学, 2018, 35(10): 17-26.Liu Jingbo, Wang Dongyang, Tan Hui, et al.Integral response displacement method for longitudinalseismic response analysis of tunnel structure [J].Engineering Mechanics, 2018, 35(10): 17-26.(in Chinese)
[7]张大峰, 杨军, 李连友, 等.考虑膨胀土地基膨胀率和刚度沿深度变化的桩-土共同作用解析解[J].工程力学, 2016, 33(12): 86-93.Zhang Dafeng, Yang Jun, Li Lianyou, et al.Analytical solution of pile-soil interaction in expansive soil foundation with expansion rate and stiffness variation along the pile [J].EngineeringMechanics, 2016, 33(12):86-93.(in Chinese)
[8]顾晓强, 杨峻, 黄茂松, 等.砂土剪切模量测定的弯曲元、共振柱和循环扭剪试验[J].岩土工程学报, 2016,38(4): 740-746.Gu Xiaoqiang, Yang Jun, Huang Maosong, et al.Combining bender element, resonant column and cyclic torsional shear tests to determine small strain shear modulus of sand [J].Chinese Journal of Geotechnical Engineering, 2016, 38(4): 740-746.(in Chinese)
[9]杨同帅, 叶冠林, 顾琳琳.上海软土小应变三轴试验及本构模拟[J].岩土工程学报, 2018, 40(10): 1930-1935.Yang Tongshuai, Ye Guanlin, Gu Linlin.Small-strain triaxial tests and constitutive modeling of Shanghai soft clays [J].Chinese Journal of Geotechnical Engineering,2018, 40(10): 1930-1935.(in Chinese)
[10]Kong G, Li H, Yang G, et al.Investigation on shear modulus and damping ratio of transparent soils with different pore fluids [J].Granular Matter.2018, 20(1):1-8.
[11]Hardin B O, Richart F E.Elastic wave velocities in granular soils [J].Journal of the Soil Mechanics & Foundations Division, 1963, 89(2): 33-66.
[12]Oztoprak S, Bolton M D.Stiffness of sands through a laboratory test database [J].Géotechnique, 2013, 63(1):54-70.
[13]王海波, 徐明, 宋二祥.考虑土体小应变特性的一种实用本构模型[J].工程力学, 2011, 28(6): 60-65.Wang Hai-bo, Xu Ming, Song Erxiang.A practical constitutive model of soil considering thebehavior at small strains [J].Engineering Mechanics, 2011, 28(6):60-65.(in Chinese)
[14]郭晓霞, 迟世春, 林皋.邓肯E-B模型弹性部分能量守恒的探讨[J].岩石力学与工程学报, 2007, 26(增刊1):3114-3121.Guo Xiaoxia, Chi Shichun, Lin Gao.Discussion on energy conservation for elastic component of Duncan-Chang E-B model [J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Suppl1): 3114-3121.(in Chinese)
[15]李雪冰, 危银涛.一种改进的Yeoh超弹性材料本构模型[J].工程力学, 2016, 33(12): 38-43.Li Xuebing, Wei Yintao.An improved Yeoh constitutive model for hyperelastic material [J].Engineering Mechanics, 2016, 33(12): 38-43.(in Chinese)
[16]Houlsby G T, Amorosi A, Rojas E.Elastic moduli of soils dependent on pressure: a hyperelastic formulation[J].Géotechnique, 2005, 55(5): 383-392.
[17]陈志辉, 程晓辉.饱和黏土不排水抗剪强度各向异性的热力学本构模型研究[J].岩土工程学报, 2014, 36(5):836-846.Chen Zhihui, Cheng Xiaohui.Thermodynamic constitutive model for anisotropic undrained shear strength of saturated clays [J].Chinese Journal of Geotechnical Engineering, 2014, 36(5): 836-846.(in Chinese)
[18]程晓辉, 陈志辉.纯主应力旋转条件下饱和黏土累积变形的热力学模型分析[J].岩土工程学报, 2015, 37(9):1581-1590.Cheng Xiaohui, Chen Zhihui.Thermodynamic modeling of accumulated deformation of saturated clays under pure principal stress rotation [J].Chinese Journal of Geotechnical Engineering, 2015, 37(9): 1581-1590.(in Chinese)
[19]Roesler S K.Anisotropic shear modulus due to stress anisotropy[J].Journal of the Geotechnical Engineering Division, 1979, 105(7): 871-880.
[20]Yu P, Richart F E.Stress ratio effects on shear modulus of dry sands [J].Journal of Geotechnical Engineering,1984, 110(3): 331-345.
[21]Kuribayashi E, Iwasaki T, Tatsuoka F.Effects of stress-strain conditions on dynamic properties of sands[J].Proceedings of the Japan Society of Civil Engineers,1975(242): 105-114.
[22]Tatsuoka F, Iwasaki T, Fukushima S, et al.Stress conditions and stress histories affecting shear modulus and damping of sand under cyclic loading [J].Soils and Foundations, 1979, 19(2): 29-43.
[23]Bellotti R, Jamiolkowski M, Presti D C F L, et al.Anisotropy of small strain stiffness in Ticino sand [J].Géotechnique, 1996, 46(1): 115-131.
[24]Gu X, Yang J, Huang M.DEM simulations of the small strain stiffness of granular soils: effect of stress ratio [J].Granular Matter, 2013, 15(3): 287-298.
[25]Hoque E, Tatsuoka F.Effects of stress ratio on small-strain stiffness during triaxial shearing [J].Géotechnique, 2004, 54(7): 429-439.
[26]Ueno K, Kuroda S, Hori T, et al.Elastic shear modulus variations during undrained cyclic loading and subsequent reconsolidation of saturated sandy soil [J].Soil Dynamics and Earthquake Engineering, 2019,2019(116): 476-489.
[27]Payan M, Khoshghalb A, Senetakis K, et al.Small-strain stiffness of sand subjected to stress anisotropy [J].Soil Dynamics and Earthquake Engineering, 2016, 2016(88):143-151.
[28]袁晓铭, 孙静.非等向固结下砂土最大动剪切模量增长模式及Hardin公式修正[J].岩土工程学报, 2005,27(3): 264-269.Yuan Xiaoming, Sun Jing.Model of maximum dynamic shear modulus of sand under anisotropic consolidation and revision of Hardin’s formula [J].Chinese Journal of Geotechnical Engineering, 2005, 27(3): 264-269.(in Chinese)
[29]Jafarian Y, Javdanian H, Haddad A.Dynamic properties of calcareous and siliceous sands under isotropic and anisotropic stress conditions [J].Soils and Foundations.2018, 58(1): 172-184.