在1994年美国北岭地震和1995年日本神户地震中,抗弯钢框架的焊接部位多次出现脆性破坏,研究[1]表明,这些焊接部位的破坏是由高应力约束区的延性断裂引起的。此后许多学者对焊缝或焊接节点的断裂机理作了大量研究,以更好提高焊接连接的抗震性能。
Kanvinde等[2-3]利用传统断裂力学方法和微观损伤模型SMCS对比分析了钢结构焊接节点的韧性断裂。Zhou等[4]完成了9个梁柱节点试件的超低周疲劳试验,采用CVGM断裂模型对钢结构梁柱节点的超低周疲劳延性断裂进行了研究。王磊等[5]采用CVGM断裂模型对高强钢梁柱节点的抗震性能进行了研究。刘希月等[6]设计了20个局部焊缝构造的十字型接头试件,并进行了单调拉伸和循环荷载试验,研究了高强钢焊接构造断裂机理。Liao等[7]进行了Q345钢母材、熔敷金属、热影响区3种材料试件的断裂性能试验,采用微观损伤模型VGM研究了Q345钢焊接节点的断裂性能。王伟等[8]完成了在单调荷载作用下10个钢管柱-梁翼缘焊接节点试验,采用SMCS和VGM断裂模型对各试件进行了断裂预测,研究表明,微观断裂判据用于预测节点延性断裂具有良好的适用性。张沛[9]设计了Q235B无缝钢管和焊接钢管的母材、熔敷金属、热影响区的光滑和缺口圆棒试件,进行了单向拉伸和低周循环加载试验,并采用了GTN损伤模型对单向拉伸缺口试件进行了有限元模拟和断裂预测分析。
而近年来在断裂力学领域的很多研究表明,除了应力三轴度外,洛德角是影响金属材料塑性流动和韧性破坏的另一重要参数。在之前以孔洞成长聚合理论建立的VGM、CVGM和GTN等模型只考虑了应力三轴度的影响,无法准确模拟偏应力和低应力三轴度状态下的延性断裂。Bao等[10]试验研究发现仅采用应力三轴度不能很好地预测在纯剪和受压状态下的金属延性断裂。Barsoum等[11]研究也表明在材料的延性断裂中洛德角参数起着重要作用。Xue[12]提出了考虑应力三轴度和洛德角参数的塑性模型,此模型能很好描述金属材料在断裂点区域的塑性发展,完成了一系列单调加载下铝合金试件的延性断裂试验,并进行了塑性模型的验证分析。Bai和Wierzbicki[13-14]提出了考虑应力三轴度和洛德角参数的塑性模型和改进的Mohr-Coulomb(MMC)断裂模型,设计了分别用于研究平面应变状态的槽板试件和剪切状态的蝴蝶型试件,并进行试验验证。Lou等[15-16]提出了由微观机理引起的宏观断裂准则,并进行多种应力状态试验以验证其准确性。Smith等[17]在VGM模型基础上,引入洛德角参数,提出了用于预测延性断裂的SWDM模型(应力加权损伤模型)。Wen等[18]提出了包含应力三轴度和洛德角的新模型,并以Bao等[10]的试验数据验证新模型的预测精度。Ma等[19]在VGM模型基础上,提出了考虑洛德角影响的简化断裂模型,并用来预测焊接钢管节点的剪切断裂。Liu等[20]提出了考虑应力三轴度和洛德角参数的延性断裂模型,设计了不同应力状态分布的11个试件,并进行了试验研究和数值分析的验证。王俊杰等[21]提出了考虑罗德角参数的钢材薄板延性断裂标定方法。
综上所述,目前在结构工程中对单调荷载下延性断裂预测主要采用VGM和SMCS两种模型。而近十多来年提出的考虑应力三轴度和洛德角参数的断裂模型应用不多。基于此,本文通过设计不同的应力三轴度和洛德角参数分布范围的焊缝金属试件,进行单调荷载作用下Q345钢焊缝金属的断裂性能试验研究。用自编的UVARM子程序,对VGM模型、改进SWDM模型和Lou模型进行各试件的延性断裂预测,比较各模型的预测精度。
1 断裂模型的理论基础
1.1 VGM模型
基于微观机制的金属延性断裂通常表现为空穴形核、扩张和聚合的演变过程,其中最具代表性的模型是VGM模型。该模型是在Rice等[22]理论基础上提出的,通过应力三轴度的变化来描述材料的应力状态,假定孔洞扩张速率是应力三轴度的指数函数。VGM模型的表达式如下:
式中:T为应力三轴度,![]() 为静水应力,σe为等效应力或Mises应力;
为静水应力,σe为等效应力或Mises应力;![]() 为等效塑性应变增量;η为表示临界空穴扩张比的材料参数,是材料的固有参数;A取1.5,A值是Rice基于刚塑性材料推导得到的,因本文研究的焊缝金属为弹塑性材料,因而把A作为变量进行考虑。
为等效塑性应变增量;η为表示临界空穴扩张比的材料参数,是材料的固有参数;A取1.5,A值是Rice基于刚塑性材料推导得到的,因本文研究的焊缝金属为弹塑性材料,因而把A作为变量进行考虑。
用损伤变量D的形式来表达断裂模型,其增量表达式为:
式中,A和C为材料参数。当D值达到1时,材料开始发生断裂。
1.2 改进SWDM模型
Smith[17]在CVGM模型基础上,通过引入洛德角参数项,并将应力三轴度项用双曲正弦函数表达,提出了应力加权损伤模型SWDM,其损伤变量D增量表达式见式(3)。

式中:![]() 是材料参数,可以通过试验校准得到;ξ是洛德角参数,θ为洛德角;J2、J3分别为偏应力张量第2、第3不变量。当D值达到1时,材料开始发生断裂。
是材料参数,可以通过试验校准得到;ξ是洛德角参数,θ为洛德角;J2、J3分别为偏应力张量第2、第3不变量。当D值达到1时,材料开始发生断裂。
式(3)引入承载力退化函数,可用于循环荷载下的断裂预测。因SWDM模型是在CVGM模型[16]基础上修正得到的,本文参照VGM模型与CVGM模型的推导关系,将式(3)进行改进,得到用于单调荷载下的断裂预测模型,见式(5)。
1.3 Lou模型
Lou等[15]提出了基于微观机理的延性断裂准则,本文称为Lou模型。在该准则中,假定孔洞形核是等效塑性应变的函数,孔洞成长为应力三轴度的函数,孔洞的剪切聚合依赖于正则化的最大剪应力![]() 。断裂模型采用损伤变量D增量表达形式如式(6)所示。
。断裂模型采用损伤变量D增量表达形式如式(6)所示。

Lou[16]后来将准则中的最大剪应力项用洛德参数L表示,新准则可以用应力三轴度、洛德参数和等效塑性应变三维空间来表示,断裂模型转换成式(7),其全量表达式见式(8)。当D到达1时,材料开始发生断裂。

式中,L为洛德参数,见式(9)。
式中,σ1、σ2和σ3分别为第1、第2和第3主应力。
2 试验设计
所有试件均取材于35 mm×420 mm×1500 mm对接焊缝接头,焊缝金属采用焊丝H08MnMoA。试件取样示意图如图1所示,所取试件的标距段或缺口段都在焊缝处,以保证试验破坏均发生在焊缝处。焊前坡口两侧打磨,采用埋弧焊,焊剂采用SJ101G,电流为650 A~750 A,电压为28 V~34 V,焊接速度为40 cm/min~50 cm/min。

图1 试件取样示意图
Fig.1 Sample schematic diagram of specimens
本文设计了12个试件。图2(a)为3个相同尺寸的光滑圆棒试件WTRA、WTRB和WTRC。图2(b)为2个圆周缺口WCNT系列试件,其中试件WCNTA缺口半径为2 mm,试件WCNTB缺口半径为5 mm,这2个试件的缺口根部直径都为5 mm。图2(c)为1个槽板试件WGP。图2(d)为3个矩形缺口WRN系列试件,缺口中心面积基本保持不变,通过改变缺口中心宽度与厚度的比值来控制洛德角参数的大小,其中试件WRNA缺口中心尺寸a×b=7.5 mm×6 mm,试件WRNB缺口中心尺寸a×b=9 mm×5 mm,试件WRNC缺口中心尺寸a×b=11 mm×4 mm。为了研究中低应力三轴度状态,本文设计了3种剪切WIN系列试件,分别为图2(e)所示的纯剪试件WINA以及图2(f)~图2(g)所示的2种剪拉试件WINB和WINC。3种剪切试件通过改变缺口部分轴向与荷载方向之间的角度来获得不同的应力三轴度。纯剪试件WINA的缺口部分轴向与加载方向成90°,可得到本文中最低的应力三轴度状态,另外2种剪拉试件WINB和WINC的角度为70°和45°,逐渐偏向于轴拉试件,应力三轴度相应增大。试验采用MTS试验机,加载过程中,位移采用引伸计测得。

图2 试件设计图 /mm
Fig.2 Geometry and dimensions of specimens
3 试验结果及有限元模拟
3.1 单向拉伸下钢材的真实应力-应变曲线及校准方法
对光滑圆棒试件WTRA、WTRB和WTRC进行单向拉伸试验,随着加载过程的进行,试件在标距段内某处发生颈缩现象,之后引伸计测量的标距段伸长量将不再适用,该时刻之前的工程应力应变值为有效数据,得到的工程应力-应变曲线见图3。试验测得的3个光滑圆棒试件的平均弹性模量E为209778 MPa,屈服强度fy为358.80 MPa,抗拉强度fu为525.43 MPa。因下文中所分析的部分试件发生断裂时,其塑性应变会超出光滑圆棒试件颈缩前的塑性应变,因而需要对其颈缩后的应力-应变关系进行外推拟合,这样才能准确模拟直至断裂前试件的塑性发展过程。对颈缩后的真实应力和应变可以根据外推模型来估测,本文采用Voce、Swift和Swift-Voce混合模型对3个光滑圆棒试件试验颈缩前的真实应力应变数据进行拟合,并外推得到颈缩后的真实应力-应变曲线。Voce模型见式(10),Swfit模型见式(11),Swift-Voce混合模型引入加权系数w,将Voce和Swift模型进行线性组合,模型形式见式(12)。
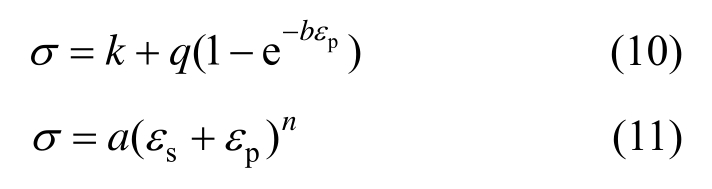
式中:εs为材料的屈服应变;εp为塑性应变;k、q、b、a、n均为待拟合参数。
根据3根光滑圆棒的试验数据,拟合得到Voce、Swift、Swift-Voce混合模型系数,拟合结果见表1。真实应力-真实塑性应变曲线如图4所示。
表1 Voce、Swift和Swift-Voce混合模型拟合系数
Table 1 Fitting coefficient of Voce, Swift and mixed Swift-Voce model

Voce Swift Swift-Voce k q b a n k q b a n w 366 261 16 865 0.18 453 183 24 1443 0.50 0.28
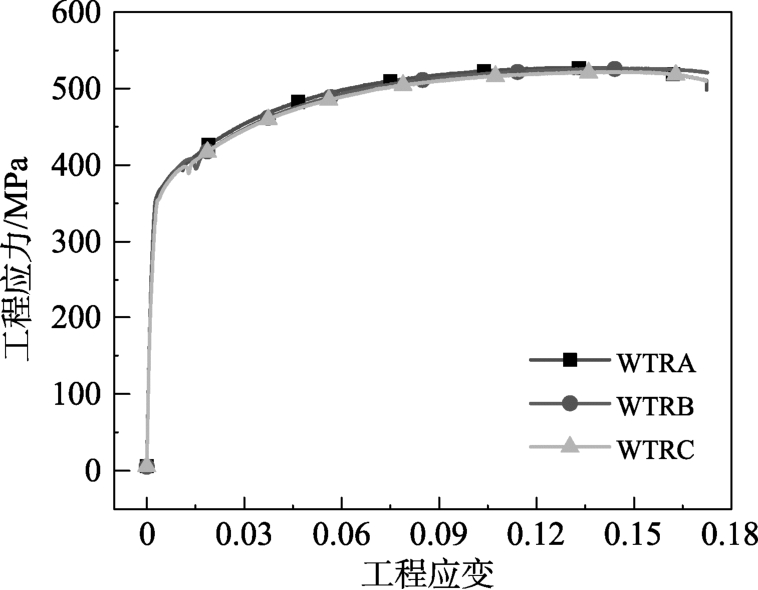
图3 工程应力-应变曲线
Fig.3 Engineering stress-strain curves
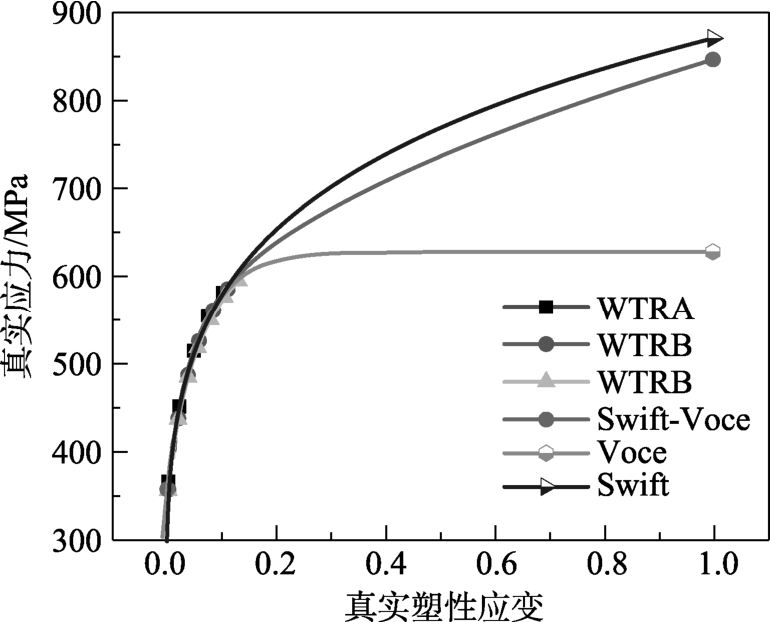
图4 真实应力-真实塑性应变曲线
Fig.4 True sress-true plastic strain curves
3.2 有限元网格精度
圆周缺口WCNT系列试件采用轴对称模型建模,单元类型CAX8R,试件缺口部位的细化网格尺寸为0.2 mm;槽板试件WGP与矩形缺口WRN系列试件采用1/4模型建模,单元类型C3D8R,缺口部位的细化网格尺寸为0.3 mm;剪切和剪拉WIN系列试件采用1/2模型建模,单元类型C3D8R,缺口部位的细化网格尺寸为0.3 mm。
3.3 试验及有限元分析结果
图5 (a)~图5(i)为单调荷载下9个试件试验与有限元模拟的荷载-位移曲线。由于试验采用位移控制加载,所以选取试验曲线刚度突变点(初始断裂点)处的位移作为有限元模拟曲线的终止位移。
图5(a)和图5(b)为圆周缺口试件WCNTA和WCNTB的荷载-位移曲线。可看出,缺口半径越小,荷载值越大,断裂时刻的位移越小。WCNTA缺口半径为2 mm,WCNTB缺口半径为5 mm,WCNTA在缺口处截面变化梯度更大,因而应力集中现象更明显,在最小截面上的静水应力较大,提高了应力三轴度水平,试件的变形能力相对变差。
槽板试件WGP的荷载-位移曲线见图5(c),断裂位移约1.2 mm,变形能力较差。图5(d)~图5(f)为矩形缺口WRN系列试件的试验荷载-位移曲线,可看出,由于缺口中心面积基本保持不变,最小净截面长宽比的改变对荷载的影响很小,而对断裂位移会有一定的影响,WRNC的断裂位移比WRNA和WRNB提前了20%以上,说明试件越接近于平面应变状态其变形能力越差。
图5(g)为纯剪试件WINA的荷载-位移曲线,荷载峰值出现在断裂位移附近,从纯剪试件的位移值可以看出,试件的延性很好,断裂位移接近17 mm,缺口部位剪切变形非常明显。
图5(h)为剪拉试件WINB的荷载-位移曲线,在约75%断裂位移处达到极限荷载,继续加载后的刚度下降速度介于纯剪试件WINA和剪拉试件WINC之间,断裂位移同样在两试件之间,说明随着缺口部位轴线与加载方向的夹角增大,试件达到极限荷载的位移将会延后,试件变形量增大,断裂位移增大,刚度下降更快。
图5(i)为剪拉试件WINC的荷载-位移曲线,在65%断裂位移附近达到荷载峰值,缺口部位轴线与荷载方向呈45°,为剪拉应力状态。到加载后期更接近于轴拉应力状态。延性是剪切系列试件中最差的。
由图5比较试验与有限元模拟的荷载-位移曲线,Swift硬化模型计算的曲线偏高,Voce硬化模型曲线偏低,与Voce模型比较,Swift模型的误差更小。Swift-Voce混合模型计算的曲线介于Swift与Voce之间,与试验曲线拟合精度是最好的。除剪切试件外,Swift和Voce硬化模型,对极限荷载的预测比较准确,初始断裂荷载误差较大,主要原因是前期模型的应力-应变曲线差异较小,均是颈缩前的数据。随着塑性应变的增大,开始采用颈缩后外推数据,真实应力的差距逐渐变大,最终反映到模拟结果上,导致初始断裂荷载值产生不同程度的误差。根据3种模型的模拟精度,本文采用拟合精度最好的Swift-Voce混合模型进行模拟各试件的荷载-位移曲线。
3.4 断口破坏形式分析
选取几个典型试件分析断口破坏形式。由图6(a)可看出,圆周缺口试件WCNTA断口呈杯锥状,有相对明显的纤维区和剪切唇区,断口表面为纤维状,颜色灰暗,具备延性断裂的断口特征。由图6(b)、图6(c)可看出,槽板WGP试件与矩形缺口试件WRNC类似,断口呈纤维状,颜色灰暗,四周剪切唇区较小。由图6(d)可看出,剪切试件WINA断口比较平整,剪切唇区较大,可以看出剪切试件主要是在剪应力作用下发生断裂。
图7为UVARM子程序计算得到的部分试件损伤累积云图,损伤值D是按照Lou模型公式(8)计算得到的,损伤值最大处为起始开裂点,据此可确定圆周缺口试件、矩形缺口试件、槽板试件以及剪拉试件的起始开裂位置在最小截面中心点,纯剪试件的起始开裂位置在缺口处最小截面顶部和底部。与试验破坏位置对比,可以看出,有限元模拟可以很好地预测试件的破坏位置。

图5 试验与数值模拟结果对比
Fig.5 Results comparison between numerical simulation and experiment

图6 试件断口
Fig.6 Fracture modes of specimens

图7 有限元模拟与试验的破坏形式对比
Fig.7 Comparison of failure modes between FE simulations and experiments
4 断裂预测
4.1 各类试件的应力状态分析
对每个试件进行有限元数值模拟,用UVARM子程序提取最小截面中心点处的等效塑性应变、应力三轴度和洛德参数L,并从应力三轴度和洛德参数L两个维度对试件的应力状态进行对比分析,见图8和图9。
由图8和图9可看出,圆周缺口WCNT系列试件是研究应力三轴度的变化。WCNTA的应力三轴度在1.1附近,WCNTB应力三轴度在0.7~0.9之间变化。2个试件的最小截面面积相同,区别之处在于圆周缺口的半径不同,缺口半径越小,截面变化梯度更大,应力三轴度越大。圆周缺口WCNT系列试件在整个加载过程中的洛德参数值恒定为-1,即轴对称拉伸状态。
槽板试件WGP的应力三轴度超过1.0,洛德参数值基本保持为0,即平面应变状态。

图8 应力三轴度T-等效塑性应变曲线
Fig.8 Stress triaxiality - equivalent plastic strain curves
3种矩形缺口试件的应力三轴度在1.0~1.1,应力三轴度相差不大。在设计试件过程中,保持最小截面的面积相同,只改变截面的长宽比,目的是研究洛德参数的影响。WRNA的洛德参数为-0.5~-0.6,WRNB的洛德参数为−0.2~−0.4,WRNC最小截面的长宽比越大,其洛德参数接近于0,接近平面应变状态。

图9 洛德参数L-等效塑性应变曲线
Fig.9 Lode parameter - equivalent plastic strain curves
对于WINA、WINB和WINC,属于中低应力三轴度范围,应力三轴度范围在0~0.6变化。通过改变缺口轴线与加载方向的夹角,试件的应力状态发生较为明显变化。在加载初期,WINA试件应力三轴度和洛德参数基本为0,在加载过程中,随着等效塑性应变的增大,应力三轴度主要从0向0.4增加,洛德参数从0不断向-1靠近,说明在加载过程中,WINA试件能一直处于低应力状态,随着加载的进行,试件出现较大的剪切变形,其受力状态由纯剪向剪拉转变。对于WINB和WINC试件,在加载初期,应力三轴度不超过0.2,洛德参数在-0.15和-0.3附近变化,且WINB较WINC更接近于剪切状态,说明这个阶段试件受力接近于以剪为主状态,且缺口轴线与加载方向夹角越大,其受剪切程度越高。随着加载进行,应力三轴度和洛德参数都有较大的变化,这是因为,随着加载的进行,剪切变形越来越大,试件缺口轴线与加载方向的夹角不断减小,以剪为主状态逐渐转变为以拉为主状态,这两个试件的应力三轴度水平由不到0.2变化到0.4左右,罗德参数则不断向-1靠近,即向拉伸应力状态靠近。
4.2 断裂预测
提取9类试件起始断裂点的应力三轴度、等效塑性应变、洛德角参数以及洛德参数,用以校准VGM、改进SWDM和Lou模型的材料参数。按照最小二乘法原理,用自编的MATLAB程序进行各模型材料参数校准,校准的目标是使得每个试件的损伤变量D值在起始断裂时刻等于1。校准后材料参数如表2所示。
表2 3种断裂预测模型校准参数
Table 2 Calibration parameters of three fracture prediction models
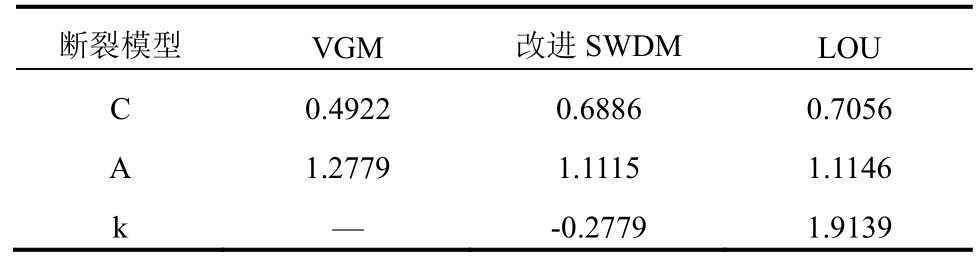
断裂模型 VGM 改进SWDM LOU C 0.4922 0.6886 0.7056 A 1.2779 1.1115 1.1146 k — -0.2779 1.9139
图10为3种断裂模型预测结果与试验结果的比较,图中的圆点和三角形标识为3种模型的起始断裂位置。为了更准确地对比这3种断裂预测模型的模拟结果,将各个试件试验和模拟结果的断裂位移进行统计,并分别计算误差,见表3。将误差大小分成3个误差区间,分别为0%~2%、0%~10%、10%以上,对每个误差区间内的试件个数进行统计,如表4所示。
从表3和表4看出,VGM模型仅通过应力三轴度一个变量来调整损伤积累量,对于平面应变状态或接近于平面应变状态WGP和WRN系列的试件,预测结果不如Lou模型和改进SWDM模型准确,说明偏应力状态对于材料的断裂性能具有一定的影响。VGM模型没有引入洛德角项,在模型的适用范围上不及Lou模型和改进SWDM模型广泛。
表3 3种模型预测结果
Table 3 Prediction results of three fracture models

试件 试验断裂位移/mm预测断裂位移/mm VGM 误差 改进SWDM 误差 Lou 误差WCNTA 1.03 1.00 3.49 1.09 5.23 1.15 11.63 WCNTB 1.88 1.68 10.53 1.75 7.02 1.77 5.85 WGP 1.17 1.28 9.62 1.16 1.28 1.19 1.28 WRNA 1.68 1.59 5.36 1.65 1.79 1.59 5.36 WRNB 1.25 1.38 10.84 1.35 8.43 1.31 5.42 WRNC 1.03 1.11 7.59 1.01 1.27 1.01 1.27 WINA 16.65 16.83 1.08 16.65 0.00 16.38 1.62 WINB 14.67 14.04 4.29 13.92 5.14 14.10 3.85 WINC 7.83 7.31 6.68 7.26 7.24 7.35 6.13

图10 3种断裂模型预测结果与试验结果比较
Fig.10 Comparison of fracture prediction between three fracture models and experiments
表4 预测误差统计
Table 4 Prediction error

断裂预测模型 不同误差范围内试件个数0%~2% 0%~10% 10% 以上VGM 1 7 2改进SWDM 4 9 0 Lou 3 8 1
Lou和改进SWDM模型在0%~2%、0%~10%误差区间内的试件个数都比VGM多,在10%+区间的试件个数都比VGM少,预测精度优于VGM模型,说明了改进SWDM和Lou模型分别引入了偏应力状态变量的罗德角参数和洛德参数,对不同应力分布状态预测结果较好,模型适用性更好。
5 结论
(1) 圆周缺口试件和槽板试件分别适用于研究高应力三轴度下的轴对称应力状态和平面应变状态;矩形缺口试件位于前两者之间,通过变化缺口中心最小截面的长宽比可以获得不同的偏应力状态;剪切试件适用于中低应力三轴度应力状态。
(2) 采用Siwft、Voce和Swift-Voce混合模型校准颈缩后真实应力-应变曲线,Swift-Voce混合模型得到的荷载-位移曲线与试验曲线吻合度最好。
(3) 校准了VGM模型、改进SWDM模型以及Lou模型的材料参数,用校准好的参数能对各试件进行了较为准确地断裂预测模拟。
(4) VGM模型仅通过应力三轴度一个变量来调整损伤积累量,对于平面应变状态或接近于平面应变状态WGP和WRN系列的试件,预测结果不如Lou模型和改进SWDM模型准确。改进SWDM和Lou模型分别引入了偏应力状态变量的罗德角参数和洛德参数,其对不同应力分布状态的预测结果较好,模型适用性更好。
[1]Kuwamura H, Yamamoto K.Ductile crack as trigger of brittle fracture in steel [J].Journal of Structural Engineering, 1997, 123(6): 729―735.
[2]Chi W M, Kanvinde A M, Deierlein G G.Prediction of ductile fracture in steel connections using SMCS criterion[J].Journal of Structural Engineering, 2006, 132(2):171―181.
[3]Kanvinde A M, Fell B V, Gomez I R, et al.Predicting fracture in structural fillet welds using traditional and micromechanical fracture models [J].Engineering Structures, 2008, 30(11): 3325―3335.
[4]Zhou H, Wang Y Q, Shi Y Y, et al.Extremely low cycle fatigue prediction of steel beam-to-column connection by using a micro-mechanics based fracture model [J].International Journal of Fatigue, 2013, 48: 90―100.
[5]王磊, 班慧勇, 石永久, 等.基于微观断裂机理的高强钢框架梁柱节点抗震性能有限元分析 [J].工程力学,2018, 35(11): 68―78.Wang Lei, Ban Huiyong, Shi Yongjiu, et al.Finite element analysis of aseismic behavior of high-strength steel beam-to-column connections in steel frames based on micromechanics of fracture [J].Engineering Mechanics, 2018, 35(11): 68―78.(in Chinese)
[6]刘希月, 王元清, 石永久, 等.高强度钢框架梁柱节点焊接构造的断裂性能试验研究[J].工程力学, 2018,35(5): 54―64.Liu Xiyue, Wang Yuanqing, Shi Yongjiu, et al.Experimental study on the weld fracture behavior of high strength steel beam-to-column connections [J].Engineering Mechanics, 2018, 35(5): 54―64.(in Chinese)
[7]Liao F F, Wang W, Chen Y Y.Parameter calibrations and application of micromechanical fracture models of structural steels [J].Structural Engineering and Mechanics, 2012, 42(2): 1―22.
[8]王伟, 廖芳芳, 陈以一.基于微观机制的钢结构节点延性断裂预测与裂后路径分析[J].工程力学, 2014, 31(3):101―108.Wang Wei, Liao Fangfang, Chen Yiyi.Ductile fracture predition and post-fracture path tracing of steel connections based on micromechanics-based fracture criteria [J].Engineering Mechanics, 2014, 31(3): 101―108.(in Chinese)
[9]张沛.基于GTN损伤模型的钢节点断裂预测研究[D].北京: 北京交通大学, 2014: 37―54.Zhang Pei.Study on fracture prediction of steel joints using micromechanical GTN model [D].Beijing: Bejing Jiaotong University, 2014: 37―54.(in Chinese)
[10]Bao Y B, Wierzbicki T.On fracture locus in the equivalent strain and stress triaxiality space [J].International Journal of Mechanical Sciences, 2004, 46: 81―98.
[11]Barsoum I, Faleskog J.Rupture mechanisms in combined tension and shear—Experiments [J].International Journal of Solids and Structures, 2007, 44: 5481―5498.
[12]Xue L.Damage accumulation and fracture initiation in uncracked ductile solids subject to triaxial loading [J].International Journal of Solids and Structures, 2007, 44:5163―5181.
[13]Bai Y L, Wierzbicki T.Application of extended Mohr-Coulomb criterion to ductile fracture [J].International Journal of Fracture, 2010, 161: 1―20.
[14]Bai Y L, Wierzbicki T.A new model of metal plasticity and fracture with pressure and Lode dependence [J].International Journal of Plasticity, 2008, 24: 1071―1096.
[15]Lou Y S, Huh H, Lim S, et al.New ductile fracture criterion for prediction of fracture forming limit diagrams of sheet metals [J].International Journal of Solids and Structures, 2012, 49: 3605―3615.
[16]Lou Y S, Huh H.Prediction of ductile fracture for advanced high strength steel with a new criterion:Experiments and simulation [J].Journal of Materials Processing Technology, 2013, 213: 1284―1302.
[17]Smith C M, Deierlein G G, Kanvinde A M.A stress-weighted damage model for ductile fracture initiation in structural steel under cyclic loading and generalized stress states [R].CA: Stanford University,2014: 161―244.
[18]Wen H J, Mahmoud H.New model for ductile fracture of metal alloys.Ⅰ: Monotonic loading [J].Journal of Engineering Mechanics, 2016, 142(2): 04015088.
[19]Ma X X, Wang W, Chen Y Y, et al.Simulation of ductile fracture in welded tubular connections using a simplified damage plasticity model considering the effect of stress triaxiality and Lode angle [J].Journal of Constructional Steel Research, 2015, 114: 217―236.
[20]Liu Y, Kang L, Ge H B.Experimental and numerical study on ductile fracture of structural steels under different stress states [J].Journal of Constructional Steel Research, 2019, 158: 381―404.
[21]王俊杰, 王伟.考虑罗德角参数的钢材薄板延性断裂标定方法 [J].工程力学, 2019, 36(5): 37―43.Wang Junjie, Wang Wei.Ductile fracture locus validation method of thin steel plates considering the Lode angle parameter [J].Engineering Mechanics, 2019, 36(5): 37―43.(in Chinese)
[22]Rice J R, Tracey D M.On the ductile enlargement of voids in triaxial stress fields [J].Journal of the Mechanics and Physics of Solids, 1969, 17: 201―217.