钢筋混凝土结构在桥梁、大坝、核设施、军事建筑及防护工程领域应用广泛。大量研究表明[1-3],混凝土具有显著的拉压不对称特性,其拉伸强度远低于压缩强度;其压缩以及拉伸强度显著依赖于加载率,且在高应变率区域强度的强化趋势更加明显[4]。在爆炸/冲击载荷作用下,结构承受应力波载荷,这类材料结构的破坏往往是由于反射卸载波引起[5],即发生层裂破坏。工程中一般在混凝土中铺设钢筋来承受拉伸载荷[6],不管是进行建筑物抗暴设计,还是进行爆炸破坏效果评估,准确测量钢筋混凝土材料的动态拉伸性能及研究损伤破坏演化特性,都具有重要的理论意义和工程价值。
近年,针对加筋混凝土和钢纤维混凝土等改良型混凝土材料的研究越来越多[7-14]。Low等[7]分析了钢筋混凝土板在爆炸载荷作用下的剪切和弯曲失效。Chung等[8]、Landon等[9]通过实验和数值模拟等方法研究了固支方板在爆炸载荷作用下的响应。汪维等[10]对方形钢筋混凝土板在单向支撑条件下进行了近场爆炸加载实验。此类实验主要依据试件在爆炸后的总体破坏形貌来对其抗震塌能力进行分级,而不能很好地测量钢筋混凝土材料的层裂强度以及研究层裂过程中的损伤演化特征。
Klepaczko等[15]提出的一维应力层裂实验可以很好的研究混凝土等脆性材料在一维应力条件下的动态拉伸强度及损伤演化特征。该实验是基于弹性波在一维杆中的传播和反射理论,杆中的压缩波到达自由面,反射成拉伸波后,拉伸波达到动态拉伸强度时即发生层裂破坏。Forquin等[16-17]基于一维应力层裂实验平台研究了混凝土的动态破碎过程,给出了混凝土材料的层裂强度及断裂能;Diaz-Rubio等[18]研究了3种陶瓷材料在一维应力条件下的层裂现象;张磊等[19]利用大直径SHPB进行了钢纤维增强混凝土的层裂实验,其结果表明钢纤维混凝土具有更高的层裂强度以及更好的阻止损伤演化和裂纹扩展的能力。
为了研究钢筋在增强混凝土中所起的力学效应,本文设计了分别在轴心位置布置光圆钢筋和螺纹钢筋的单向增强(unidirectional)钢筋混凝土(UDRC) 细长杆,并基于74 mm直径分离式Hopkinson压杆(SHPB)实验平台进行了杆的一维应力波层裂实验,研究其在冲击拉伸载荷作用下的层裂特性。通过超高速相机结合数字图像相关法(DIC),记录杆表面的位移场实时变化情况,分析试样表面的应变场演化,并基于作者在文献[20]中提出的关于一维杆应力层裂实验以裂纹左右2点速度趋势变化来判断裂纹起裂的判据,研究UDRC试件的拉伸强度的应变率效应,并结合有限元分析钢筋在层裂过程中所起的作用。
1 实验设计及材料
1.1 材料及试件制备
采用圆杆状钢筋混凝土试件进行测试,分别在试件轴心位置布置一根φ6 mm的光圆钢筋或者螺纹钢筋,试件尺寸为:直径φ74 mm,长1000 mm;钢筋混凝土圆柱试件的长径比超过10,近似认为其沿轴向处于一维应力状态。混凝土标号为C40,采用海昌P·O52·5级水泥,掺合CL-19聚羧酸减水剂、F类Ⅱ级粉煤灰及Ⅱ区中砂、以及10 mm连续级配石子骨料,在特制钢模具中浇注成型,经饱和水环境中保养28 d后,放入干燥箱中直至重量稳定。首先在MTS材料试验机上测量了标准立方体块混凝土试件的压缩性能,并利用准静态巴西圆盘实验获得材料的静态拉伸强度,得到的材料准静态性能参数如表1所示。
表1 混凝土物理参数
Table 1 Physical parameters of concrete

弹性模量/GPa 泊松比 压缩强度/MPa拉伸强度/MPa密度(kg/m3)32 0.2 60 4.6 2379
1.2 实验方法及设计
实验在φ74 mm SHPB上完成,图1(a)为一维应力层裂实验布置示意图。子弹直径同样为φ74 mm,长100 mm,在入射杆撞击端设置紫铜整形片,以延缓升时、拉长加载波形,实际得到的入射杆中传播的入射应力波为不对称钟形,如图1(b)所示,脉冲上升沿的升时为150 μs,脉冲下降沿历时为75 μs,在钢杆中的入射波波长λ约为1.1 m,其a/λ=0.033(a为杆半径),远小于一维应力波初等理论[17]要求的a/λ<0.7。因此,本实验可以用一维应力波的初等理论进行分析。图1(b)的压缩入射波被导入混凝土或钢筋混凝土试件,在试件中产生层裂。试件撞击端界面上涂抹润滑剂并紧贴入射杆,以保证入射杆与试件打击端具有良好平面接触。
采用超高速相机记录试件变形及层裂过程,为保证DIC分析具有足够的像素分辨率,相机记录混凝土杆试件距离自由端的100 mm~400 mm区段,多重层裂主要发生在该段范围内。实验采用英国Specialised Imaging公司的Kirana-05M超高速像增强成像系统,采集帧率为500000 fps(采样时间间隔2 μs)。作为对比,分别在距试件打击端30 cm、60 cm的环向位置对称贴一对应变片,记录轴向应变的时程曲线,以便与DIC测试结果进行标对,验证实验记录的可靠性。

图1 钢筋增强混凝土一维应力层裂SHPB实验设计图
Fig.1 SHPB experimental setup for measuring the spall strength of a one-dimensional UDRC bar
同时,采用激光高速测速仪记录试件自由端面的质点速度历史,激光高速测速仪为德国Polytec公司HSV-E-100型红外测速仪,该激光测速仪光斑直径2 mm,速度范围0 m/s~24 m/s,采样率为4 points/μs。
1.3 DIC测试
DIC方法通过对变形前后试件表面的数字散斑图像进行处理获得被测物体的表面位移场和应变(即位移空间梯度)信息。DIC位移测量精度首先取决于所拍摄区域图像的像素数量,像素越多,测量精度越大。由理论分析和预备实验可知,对于本次实验的钢筋混凝土长杆来说,多重层裂发生在距自由端100 mm~300 mm范围内。因此相机拍摄范围为距自由端100 mm~400 mm。单位像素对应试件上的长度为0.334 mm。
DIC位移测量精度受图像子区的灰度梯度影响。混凝土试件的自然纹理和对比度,不足以使DIC计算获得足够高的精度。因此,有必要在混凝土杆的表面人工制作散斑团。由于混凝土表面存在大量空隙和细小颗粒,首先在混凝土表面上涂抹均匀的白色涂料,待白色涂料完全干燥后再喷洒黑色斑点。散斑图像如图2所示。

图2 钢筋混凝土试件表面喷涂的散斑及真实与虚拟应变片示意图(virtual strain gauge(VSG)区域是后面进行DIC应变场分析的区域)
Fig.2 Speckle distribution and strain gauge on the surface of the concrete bar
在DIC计算时采用MatchID软件,图像相关算法为(zero-normalized sum of squared differences,ZNSSD)算法,子集大小(Subset size)为31像素,步长尺寸(Step size)为5像素。图3为试件上应变片(图2所示)测得的应变时程曲线与DIC方法在该点分析得到的应变比较,可见两者符合良好。
2 实验结果及分析
2.1 钢筋混凝土层裂过程特征
为探究UDRC的层裂过程,首先使用高速相机拍摄钢筋混凝土的整个层裂过程。相机的采集帧率为25000 fps(采样时间间隔40 μs)。结果如图4所示。UDRC在压缩脉冲波作用下共有3个位置发生了层裂破坏,如图4所示。与混凝土杆的层裂现象不同,UDRC发生层裂后,并未观察到层裂片飞离基体的现象,其断口是先张开后又闭合的。图5是图4(a)裂纹的张开闭合过程。

图3 DIC方法测试得到的轴向应变与应变片测量数值的比较
Fig.3 Comparisons of the strain histories measured by the DIC approach and the strain gauge

图4 光圆钢筋增强混凝土杆的一维应力层裂过程
Fig.4 Thecrack process of the plain steel reinforced concrete in one-dimensional stress spallingtest

图5 裂纹的发展演化过程
Fig.5 The evolution of crack
2.2 钢筋混凝土层裂演化特征
2.1 节的结果表明UDRC在强压缩载荷作用下,将发生多重层裂,且其断口是反复张开闭合的。为研究钢筋混凝土的层裂演化特征,采用激光高速测速仪记录试件自由端面的质点速度历史,并采用超高速相机记录试件变形及层裂过程。试件自由端面的质点速度历史如图6所示。可以发现,当混凝土发生层裂时,层裂片与母体脱离;在陷入层裂片内的应力波几个来回反射后,混凝土飞片速度趋向稳定,残余速度约为峰值速度的1/2。而钢筋混凝土发生层裂后,虽然自由面速度也出现了回跳现象,但是从速度后续发展上发现自由表面的速度并未趋向稳定,而是快速下降,接近0。这表明钢筋增强混凝土并未形成完整的层裂片,反射应力波通过钢筋回传到整根UDRC试件中,也说明钢筋和混凝土的接触良好,未发生拔出现象。

图6 混凝土及UDRC自由端质点速度时程曲线
Fig.6 The particle velocity at rear end of concrete and UDRC
结合超高速相机和DIC技术,可以分析试件表面的位移场和应变场。图7~图9分别给出了混凝土及UDRC表面的位移场和应变场等高线图。等高线图是按X轴为杆状试件轴向拉格朗日坐标,Y轴为时间,根据杆状试件上像素点的位移、应变历史画出的。在一维杆理论中,当杆状试件发生层裂时,层裂处将生成新的自由面,并将向其两侧发出卸载波,从而使其中裂纹左边质点速度不断增大,而另一边的质点速度不断减小。层裂位置左、右两边的位移场将发生强间断,而层裂点的名义应变将快速增大。据此,可以判断应变场等高线形成尖峰凸起时,杆状试样在该点处发生了层裂破坏,并同时可以获得裂纹起裂的时刻。图6表明:混凝土发生层裂后,层裂片与母体的距离越来越大,即两者出现了分离;而光圆钢筋混凝土及螺纹钢筋混凝土发生层裂后,虽然层裂片与母体的距离在一定范围内增大,但增加到一定范围之后,又出现了缩小。其原因是钢筋混凝土轴心位置的钢筋未出现断裂,层裂片所携带的能量通过钢筋传递到母体,从而使两者距离缩小。从试件表面的应变场等高线图可以发现,混凝土表面发生了明显的3个层裂,并且层裂位置的应变一直增大。而钢筋混凝土,尤其是螺纹钢筋混凝土出现了多处层裂,但是,层裂位置的应变先增大,后减少,形成一个纺锥体。位移场和应变场的等高线图说明钢筋混凝土断裂试件中的裂纹在拉压应力波交替作用下反复张开闭合,随着应力波在杆中的衰减而趋于稳定。
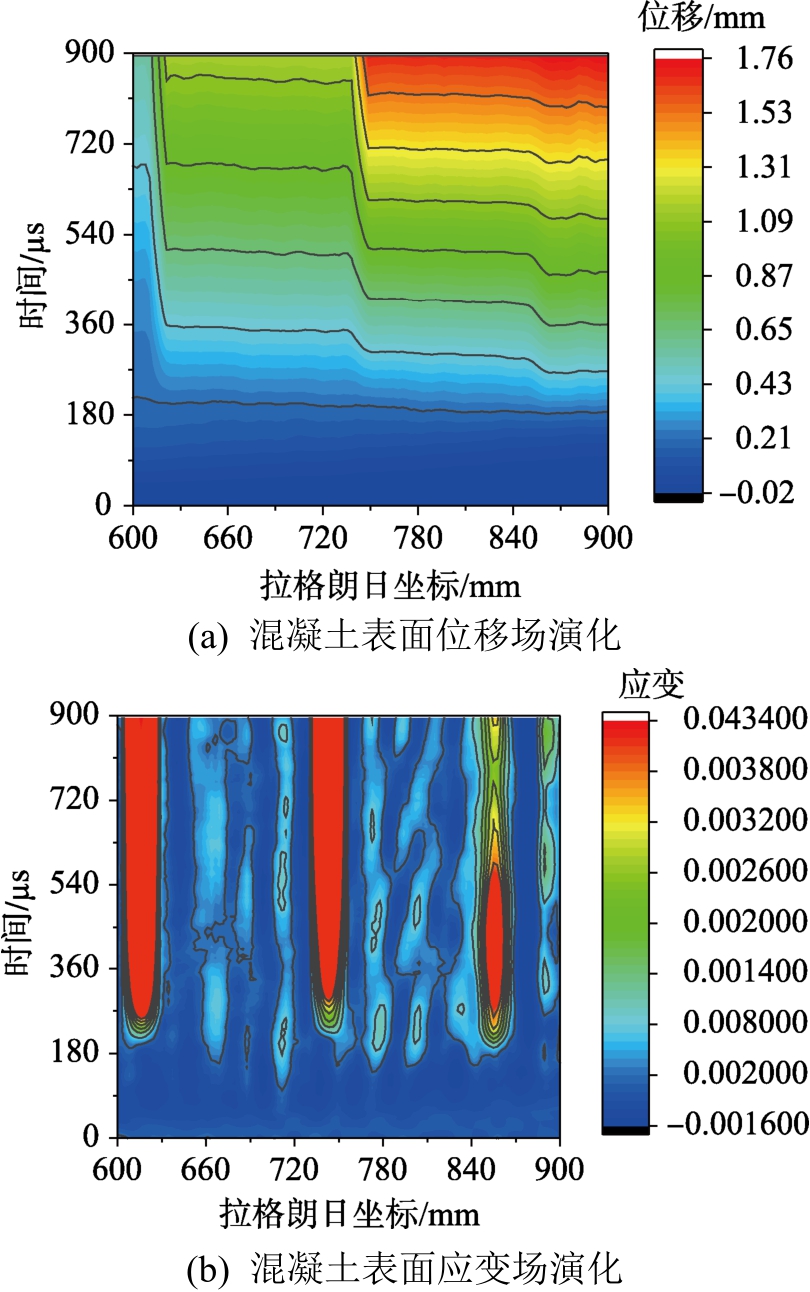
图7 混凝土表面位移场和应变场演化
Fig.7 The evolution of the displacement and strain field on concrete surface

图8 光圆钢筋UDRC表面位移场和应变场演化
Fig.8 The evolution of the displacement and strain field on plain steel UDRC surface

图9 螺纹钢筋UDRC表面位移场及应变场演化
Fig.9 The evolution of the displacement and strain field on deformed steel UDRC surface
2.3 UDRC细长杆层裂模拟
超高速相机结合DIC分析给出了UDRC细长杆表面的位移场及应变场演化特征。这2类场的结果表明,在UDRC发生层裂后,层裂飞片并未脱离母体,而是通过钢筋将陷入飞片内的能量传递到母体中,从而使两者速度趋向一致。但实验不能给出UDRC内部的演化特征,而有限元方法可以探讨钢筋在UDRC发生层裂时所起的作用。
利用有限元软件Lsdyna建立了SHPB实验平台的轴对称二维模型,其中UDRC细长杆杆长1000 mm,直径74 mm,钢筋长1000 mm,直径6 mm。单元采用平面4节点单元,单元尺寸为1 mm。钢筋与混凝土的接触采用共节点。在模型中,混凝土采用KCC模型,该模型考虑了混凝土的应变率效应、静水压效应及剪胀效应,可以较好的模拟混凝土在动态下的材料响应。钢筋采用弹性模型,其材料参数如表2、表3所示。其中混凝土参数为基于Lsdyna自动生成的参数。为简化模型,在试件的边界直接施加图1(b)所示的UDRC试件上第二个应变片所记录的载荷波形。
表2 混凝土的材料参数
Table 2 Material parameters of concrete

密度/(kg/m3) 泊松比拉伸强度/MPa B1 B2 B3 Ω 2379 0.2 4.6 1.6 5.5 1.15 0.5 A0 A1 A2 A0Y A1Y A2Y A1F A2F 22.38 0.463 1.067×10-3 16.90 0.625 3.402×10-3 0.44171.563×10-3 λ1 λ2 λ3 λ4 λ5 λ6 λ7 λ8 0 8×10-6 2.4×10-5 4×10-5 5.6×10-5 7.2×10-5 8.8×10-53.2×10-4 λ9 λ10 λ10 λ12 λ13 μ1 μ2 μ3 5.2×10-4 5.7×10-4 1 10 100 0 0.85 0.97 μ4 μ5 μ6 μ7 μ8 μ9 μ10 μ11 0.99 1 0.99 0.97 0.5 0.1 0 0 μ12 μ13 0 0
表3 钢筋的材料参数
Table 3 Material parameters of steel
弹性模量/GPa 泊松比 密度/(kg/m3)210 0.3 7800
在本次分析中,分别模拟了混凝土和UDRC细长杆的层裂。图10分别给出了距打击端60 cm位置的应变历史及自由端质点速度历史与UDRC实验数据的比较。结果表明三者的应变及速度历史在未发生破坏(速度发生回跳)前基本重合;这表明钢筋的存在不影响混凝土的层裂强度;而在此之后出现了分岔,结合图11所给出的不同时刻应变发展云图可见,混凝土发生层裂后,飞片与母体分离,陷入飞片中的应力波只能在飞片中来回传播,而单向钢筋增强混凝土却由于钢筋未发生断裂,陷入飞片内的应力波可以通过钢筋传递到母体,从而使两者的距离缩小,甚至裂纹发生“愈合”,保持了结构的完整性。
图11给出了不同时刻混凝土和UDRC细长杆的应变云图。可见全部裂纹在10 μs内出现,并且裂纹的发生是有顺序的,首先是距打击端80 cm的位置发生层裂,依次向两端发展。然而混凝土与钢筋连接的界面并未破坏,陷入层裂片的应力波通过钢筋在整根UDRC试件中传播,裂纹右端的能量通过钢筋传递到了裂纹左端,从而使两者的相对距离缩小,裂纹“愈合”。
而混凝土发生层裂时,由于不存在钢筋,陷入飞片内的应力波会在飞片内来回传播,从而导致自由端速度在开始有加大的震荡,在多个来回反射之后趋于平衡,并远离母体。

图10 有限元模型及实验中混凝土及UDRC应变及质点速度比较
Fig.10 The particle velocity at rear end of concrete and UDRCby CAE

图11 不同时刻混凝土和UDRC细长杆的有限元应变云图
Fig.11 The velocity contour maps of concrete and UDRC surface at different times by CAE
2.4 轴向钢筋增强混凝土的层裂强度
第2.3节的论述表明了轴向钢筋增强混凝土杆仍然满足一维波理论的假设,且钢筋的存在不影响混凝土的层裂强度。另外,受益于超高速摄影技术及DIC分析,可以得到试件的全场应变历史,结合作者在文献[17]中提出的根据层裂位置左、右两点速度趋势变化判断层裂发生时刻的判据,可以方便地得到同一试件上不同位置的断裂应变及应变率。因此得到的层裂应变仍然可以作为一维应力下的断裂应变。
实验针对混凝土及光圆钢筋和螺纹钢筋增强混凝土各进行了3发实验,共获得19个动态强度,其与静态加载下的混凝土拉伸强度(4.6 MPa)之比,即动态扩大系数(DIF)与应变率的关系如图12所示。可以看到,混凝土和钢筋混凝土的拉伸强度相差不大,均有明显的应变率效应。在应变率为30 s-1程度,其拉伸强度DIF能达到5左右。且从已有的实验数据[21-31]观察,钢筋混凝土的应变率效应与混凝土的应变率效应区别不大。

图12 混凝土及钢筋混凝土材料拉伸强度的应变率效应
Fig.12 Strain rate influence on tensile strength of plain concrete and reinforced concrete
3 结论
本文基于φ74 mmSHPB一维应力层裂实验平台,设计了分别在轴心布置光圆钢筋和螺纹钢筋的轴向钢筋增强混凝土(UDRC)细长杆以进行钢筋混凝土的层裂强度研究。通过超高速相机结合数字图像相关法(DIC),对钢筋混凝土的一维层裂实验开展分析,探讨了应力波在钢筋混凝土中传播的特性,并分析了试件表面的位移场和应变场演化特征,并于准静态的结果比较。结果显示:
(1) 轴向钢筋增强混凝土虽然是复合材料,但在试件的横向尺寸远小于加载波长时,仍满足一维应力波假设。
(2) 钢筋在混凝土起裂时不起作用,而保持了结构的完整性。钢筋在RC起裂时的作用可以忽略,而在起裂后由于轴心位置的钢筋未出现断裂,层裂片所携带的能量通过钢筋传递到母体,从而整体未发生破坏,在断裂后将使结构保持完整。断裂试件中的裂纹在拉压应力波交替作用下反复张开闭合,随着应力波在杆中的衰减而趋于稳定。
(3) 钢筋混凝土的层裂强度与混凝土的层裂强度相差不大,且钢筋混凝土与混凝土的层裂强度均体现出明显的应变率效应,且其规律基本相似。
[1]Reinhardt H W.Concrete under impact loading, tensile strength and bond [J].HERON, 1982, 27(3): 1―48.
[2]Lu D, Wang G, Du X, et al.A nonlinear dynamic uniaxial strength criterion that considers the ultimate dynamic strength of concrete [J].International Journal of Impact Engineering, 2017, 103(5): 124―137.
[3]Malvar L J, Ross C A.Review of strain rate effects for concrete in tension [J].Materials Journal, 1998,95(6): 735―739.
[4]Malvar L J, Crawford J E.Dynamic increase factors for concrete [R].Orlando, FL: Twenty-eighth DDESB Seminar, 1998.
[5]王礼立, 胡时胜, 杨黎明, 等.材料动力学[M].合肥:中国科学技术大学出版社, 2017: 227―228.Wang Lili, Hu Shisheng, Yang Liming, et al.Material dynamics [M].Hefei: University of Science and Technology of China of Press, 2017: 227―228.(in Chinese)
[6]Reynolds C E, Steedman J C, Threlfall A J.Reinforced concrete designer’s handbook [M].London: E & FN Spon, Taylor & Francis Group Press, 2007: 37―48.
[7]Low H Y, Hao H.Reliability analysis of direct shear and flexural failure modes of RC slabs under explosive loading[J].Engineering Structures, 2002, 24(2): 189―198.
[8]Yuen S C K, Nurick G N.Experimental and numerical studies on the response of quadrangular stiffened plates.Part I: Subjected to uniform blast load [J].International Journal of Impact Engineering, 2005, 31(1): 55―83.
[9]Langdon G S, Yuen S C K, Nurick G N.Experimental and numerical studies on the response of quadrangular stiffened plates.Part II: Localized blast loading [J].International Journal of Impact Engineering, 2005, 31(1):85―111.
[10]汪维, 张舵, 卢芳云, 等.方形钢筋混凝土板的近场抗爆性能[J].爆炸与冲击, 2012, 32(3): 251―258.Wang Wei, Zhang Duo, Lu Fangyun, et al.Antiexplosion performances of square reinforced concrete slabs under close-in explosions [J].Explosion and Shock Waves, 2012, 32(3): 251―258.(in Chinese)
[11]孙珊珊, 赵均海, 贺拴海, 等.爆炸荷载下钢管混凝土墩柱的动力响应研究[J].工程力学, 2018, 35(5): 27―35.Sun Shanshan, Zhao Junhai, He Shuanhai, et al.Dynamic response of concrete-filled steel tube piers under blast loadings [J].Engineering Mechanics, 2018: 35(5): 27―35.(in Chinese)
[12]陶慕轩, 丁然, 潘文豪, 等.传统纤维模型的一些新发展[J].工程力学, 2018, 35(3): 1―21.Tao Muxuan, Ding Ran, Pan Wenhao, et al.Some advances in conventional fiber beam-column model [J].Engineering Mechanics, 2018, 35(3): 1―21.(in Chinese)
[13]邓明科, 吕浩, 宋恒钊.外包钢板-高延性混凝土组合连梁抗震性能试验研究[J].工程力学, 2019, 36(3):192―202.De Mengke, Lü Hao, Song Hengzhao.Experimental research on aseismic behavior of high ductile concrete filled steel plate composite coupling beams [J].Engineering Mechanics, 2019, 36(3): 192―202.(in Chinese)
[14]Liu J I N, Wenxuan Y U, Xiuli D U, et al.Meso-scale modelling of the size effect on dynamic compressive failure of concrete under different strain rates [J].International Journal of Impact Engineering, 2019,125(3): 1―12.
[15]Klepaczko J R, Brara A.An experimental method for dynamic tensile testing of concrete by spalling [J].International Journal of Impact Engineering, 2001, 25(4):387―409.
[16]Forquin P, Erzar B.Dynamic fragmentation process in concrete under impact and spalling tests [J].International Journal of Fracture, 2010, 163(1―2): 193―215.
[17]Forquin P, Lukić B.On the processing of spalling experiments.Part I: Identification of the dynamic tensile strength of concrete [J].Journal of Dynamic Behavior of Materials, 2018, 4(1): 34―55.
[18]Diaz-Rubio F G, Perez J R, Galvez V S.The spalling of long bars as a reliable method of measuring the dynamic tensile strength of ceramics [J].International Journal of Impact Engineering, 2002, 27(2): 161―177.
[19]张磊, 胡时胜, 陈德兴, 等.钢纤维混凝土的层裂特征.爆炸与冲击, 2009, 29(2): 119―124.Zhang Lei, Hu Shisheng, Chen Dexing, et al.Spall fracture properties of steel-fiber-reinforced concrete [J].Explosion and Shock Waves, 2009, 29(2): 119―124.(in Chinese)
[20]俞鑫炉, 付应乾, 董新龙, 等.混凝土一维应力层裂实验的全场DIC分析[J].力学学报, 2019(4): 1064―1072.Yu Xinlu, Fu Yingqian, Dong Xinlong, et al.Full field DIC analysis method for one-dimensional spall strength measurement of concrete [J].Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(4): 1064―1072.(in Chinese)
[21]Rossi P, Van M J G M, Toutlemonde F, et al.Effect of loading rate on the strength of concrete subjected to uniaxial tension [J].Materials & Structures, 1994, 27(5):260―264.
[22]Zielinski, A J, Reinhardt H W, Körmeling H A.Experiments on concrete under uniaxial impact tensile loading [J].Matériaux et Construction.
[23]Mellinger F M, Brikimer D L.Measurements of stress and strain on cylindrical test specimens of rock and concrete under impact loading [R].Department of the Army, Ohio River Division Laboratories, 1966,Tech Rep No.4―46.
[24]Birkimer D L.Critical normal fracture strain of Portland cement concrete [D].Cincinnati, OH: University of Cincinnati, 1968: 3731―3731.
[25]Birkimer D L, Robert L.Dynamic tensile strength of concrete materials [J].Journal of Proceedings, 1971,68(1): 47―49.
[26]McVay, Mark K.Spall damage of concrete structures [R].US Army Corps of Engineers, Waterways Experiment Station, Vicksburg, Miss., USA, Technical Report SL―88―22, 1988.
[27]Brara A, Klepaczko J R.Experimental characterization of concrete in dynamic tension [J].Mechanics of Materials,2006, 38(3): 253―267.
[28]Erzar B, Forquin P.Experiments and mesoscopic modelling of dynamic testing of concrete [J].Mechanics of Materials, 2011, 43(9): 505―527.
[29]Cowell, Walter L.Dynamic properties of plain Portland cement concrete [R].Technical Report No.R447,DASA130181, Us Naval Civil Engineering Laboratory,California, 1966.
[30]Takeda J.Deformation and fracture of concrete subjected to dynamic load [J].Mechanical Behavior of Materials,1972, 4(739): 77―86.
[31]John R, Antoun T, Rajendran A M.Effect of strain rate and size on tensile strength of concrete [C].Shock Compression of Condensed Matter-1991, Elsevier Science Publishers, 1991: 501―504.