高层及超高层建筑中，常出现低矮剪力墙。由于混凝土材料的脆性特征，在强地震作用下低矮剪力墙容易发生剪切破坏，其延性和耗能能力较低，破坏后危及整个结构的安全。采用钢板和混凝土组合的形式，可充分发挥两种材料的各自优势，有效提高剪力墙的延性和耗能能力。研究表明[1-3]，双钢板-混凝土组合剪力墙和内置单钢板-混凝土组合剪力墙均有较高的延性和耗能能力，当钢板-混凝土组合应用于剪跨比较低(小于等于1)的剪力墙时，墙体虽能承受较高的剪应力，但其变形能力仍然较差，其根本原因是混凝土的脆性和开裂软化特性。
高延性混凝土(high ductile concrete，HDC)[4-7]是一种具有高韧性、高抗裂性能和耐损伤能力较好的新型结构材料，在拉伸和剪切荷载作用下具有多裂缝开展和应变硬化特征，能显著改善混凝土材料的韧性和抗裂能力，在土木工程领域具有广阔的应用前景。研究表明，在短柱[8]、梁[9-10]、钢框架组合剪力墙[11]及低矮剪力墙[12]等承受较高剪应力的构件中采用HDC替换混凝土，显著改善构件的变形能力，实现具有延性的剪切破坏。
基于以上研究，为提高低矮剪力墙的抗震性能和剪切变形能力，本文设计并制作了5片HDC低矮剪力墙试件，考虑轴压比、水平分布筋数量和配置钢板对剪力墙试件破坏形态、延性和耗能的影响，为HDC低矮剪力墙的工程应用提供依据。
1 试验概况
1.1 试件设计及制作
试验设计并制作了5片尺寸相同的剪力墙，其中3片HDC剪力墙(试件HDCW-01、HDCW-02和HDCW-03)和2片内置钢板HDC组合剪力墙(试件SHDCW-03和SHDCW-04)，试件参数见表1。试件尺寸及配筋情况见图1。
所有试件由加载梁、墙身和底梁三部分组成。剪力墙截面尺寸均为100 mm×1000 mm，剪跨比λ=1.0，采用高延性混凝土浇筑，HDC强度等级按C50混凝土设计。顶部加载梁高度为200 mm，采用C50普通混凝土浇筑。由于低矮剪力墙试件对底梁承载力和刚度要求较高，本文采用可替换式钢底梁装置，并在底梁与墙板试验区之间设置高度为200 mm的外包钢板HDC刚性过渡区域，并采用栓钉进行有效连接。
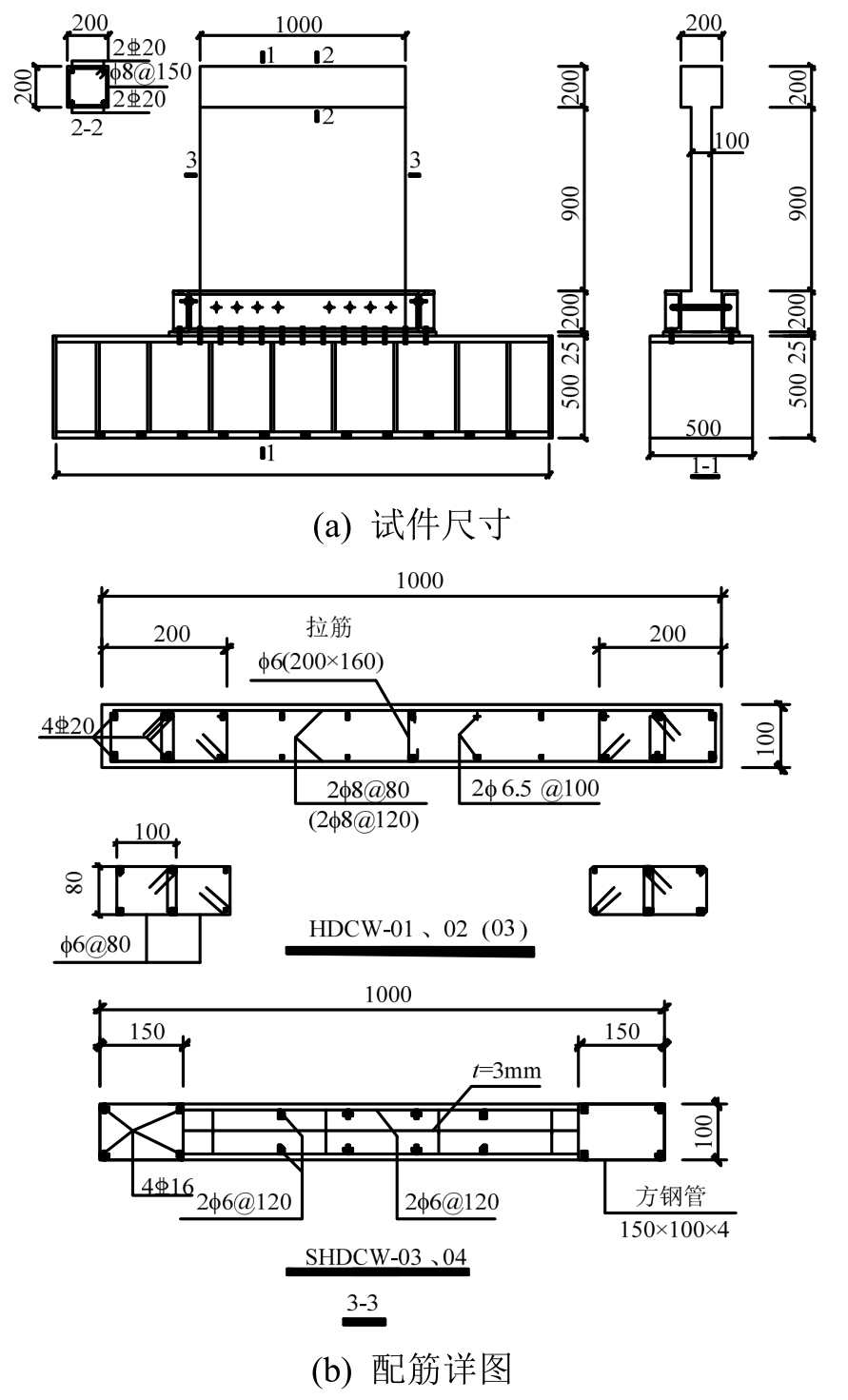
图1 试件尺寸及配筋
Fig.1 Dimension and reinforcement details of the specimens
表1 试件参数
Table 1 Parameter of the specimens
试件编号 边缘约束构件 水平分布筋纵筋 箍筋 方钢管厚度/mm竖向分布筋 钢板厚度/mm剪跨比 试验轴压比 竖向荷载/kN HDCW-01 4■20 2φ6@80 — 2φ8@80 2φ6.5@100 — 1.0 0.34 1110 HDCW-02 4■20 2φ6@80 — 2φ8@80 2φ6.5@100 — 1.0 0.28 924 HDCW-03 4■20 2φ6@80 — 2φ8@120 2φ6.5@100 — 1.0 0.28 924 SHDCW-03 4■16 — 4 2φ6.5@1202φ6.5@120 3 1.0 0.40 1294 SHDCW-04 4■16 — 4 2φ6.5@1202φ6.5@120 3 1.0 0.28 924
1.2 材料力学性能
本试验所采用的HDC主要成分由水泥、粉煤灰、精细河砂、矿物掺合料、水、高效减水剂和PVA纤维组成。其中水泥采用P.O42.5R的普通硅酸盐水泥，粉煤灰为某电厂一级灰，砂为灞河河砂，最大粒径为1.18 mm。PVA纤维力学性能指标见表2。
表2 PVA纤维各项性能指标
Table 2 Performance indicators of PVA
长度/mm直径/μm长径比/(×103)抗拉强度/MPa弹性模量/GPa伸长率/(%)密度/(g/cm3)12 39 0.31 1600 40 7 1.3
对试验同条件HDC材料预留立方体试块，试块尺寸为100 mm×100 mm×100 mm，对其进行力学性能试验，得到抗压和抗拉强度试验结果如表3所示。试件制作时采用的钢筋、方钢管和钢板型号和强度指标如表4所示。
表3 HDC的强度试验结果
Table 3 The test results of the strength of HDC
材料 ft/MPa 极限拉应变εt0 fdu/MPa fc/MPa 峰值压应变εc0 HDC 5.08 0.008 52.12 45.19 0.0039
表4 钢材的材料性能
Table 4 Material properties of steel
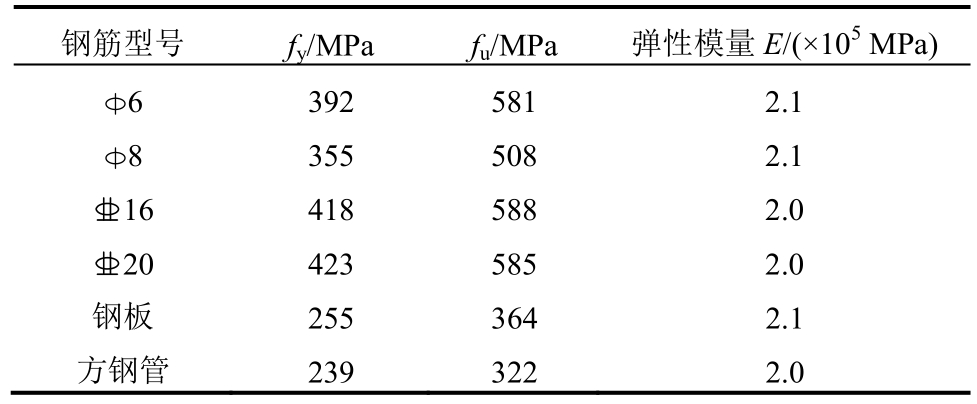
钢筋型号 fy/MPafu/MPa 弹性模量E/(×105 MPa)6 392 581 2.1 8 355 508 2.1 16 418 588 2.0 20 423 585 2.0钢板 255 364 2.1方钢管 239 322 2.0
本试验采用哑铃型试件，测试了HDC的单轴拉伸应力-应变曲线如图2所示，可见，HDC的极限拉应变可达到0.8%，具有明显的拉伸应变硬化效应。其裂缝开展如图3所示。
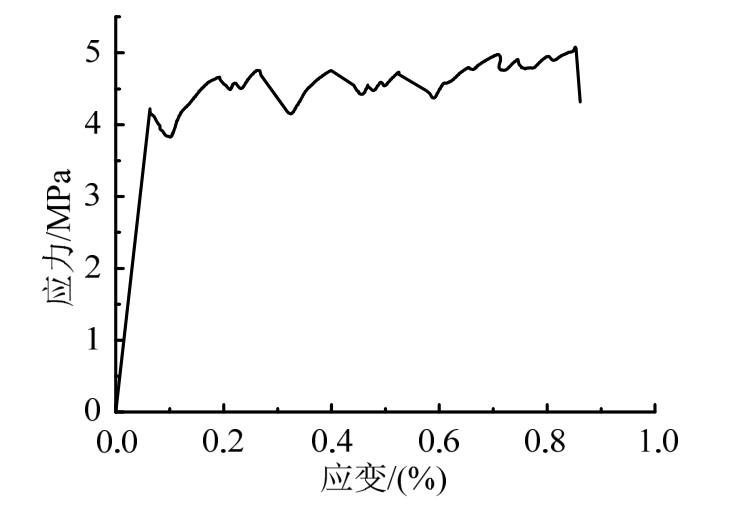
图2 HDC单轴拉伸应力-应变曲线
Fig.2 Tensile stress-strain curves of HDC
图3 HDC试件多裂缝开展
Fig.3 Multi crack development of HDC specimen
1.3 加载方案
本试验采用低周反复水平加载，加载装置如图4和图5所示。首先施加预定的竖向荷载，通过刚性垫梁均匀施加在试件加载梁顶部，并在试验过程中保持不变。为防止试件发生平面外失稳，试验采用2个1000 kN的液压伺服作动器并行施加水平荷载。
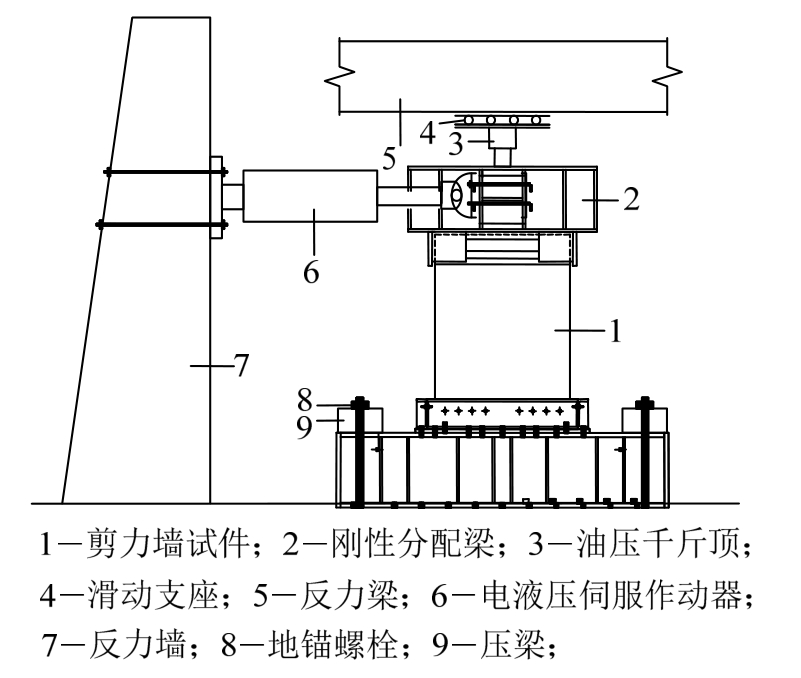
图4 试验加载装置
Fig.4 Test setup
图5 试验加载现场
Fig.5 Photo of test
试件水平加载采用荷载-位移混合控制方法，试件屈服前采用荷载控制加载，屈服后改为位移控制，以4 mm为级差进行逐级往复加载，每级位移循环三次，直至荷载下降到峰值荷载的85%以下停止加载。
1.4 试件破坏形态
本文5个试件的破坏过程都经历了弹性阶段、带裂缝工作阶段和破坏阶段，最终破坏形态如图6所示，对试件破坏过程与破坏形态的描述见表5。
图6 试件破坏形态
Fig.6 Failure modes of the specimens
表5 试件破坏过程与破坏形态
Table 5 Failure modes and failure mechanisms of the specimens
试件编号破坏过程弹性阶段 带裂缝工作阶段 破坏阶段破坏形态HDCW-01 HDCW-02 HDCW-03 SHDCW-03 SHDCW-04 HDC和钢筋很好的协同工作，承受水平力，墙体底部出现细微斜裂缝和水平裂缝；荷载-位移滞回曲线基本呈线性变化HDC和钢筋很好的协同工作，承受水平力，墙体底部出现细微斜裂缝；荷载-位移滞回曲线基本呈线性变化HDC和钢筋很好的协同工作，承受水平力，墙体底部出现细微的水平裂缝；荷载-位移滞回曲线基本呈线性变化HDC、钢板和钢筋很好的协同工作，承受水平力，墙体基本没有裂缝出现；荷载-位移滞回曲线基本呈线性变化HDC、钢板和钢筋很好的协同工作，承受水平力，墙体底部出现细微的水平裂缝；荷载-位移滞回曲线基本呈线性变化墙体腹部及底部出现多条斜向裂缝，随着荷载的增加，墙面出现大量细密剪切斜裂缝；纵筋、水平分布筋及箍筋发生屈服墙体腹部及底部出现较多的斜向裂缝，西侧墙脚出现新的水平裂缝；随着荷载的增加，墙面继续出现较多细长的斜裂缝，原有的斜裂缝分叉延伸较明显；水平分布筋、箍筋及纵筋发生屈服墙体底部裂缝密集发展，部分逐渐贯穿至墙底；加载至500 kN时，箍筋和水平分布筋被拉断；继续加载，纵筋基本发生屈服墙体底部出现细密的水平裂缝，东侧墙角出现斜裂缝，且逐渐延伸分叉，部分裂缝继续下延与原有裂缝贯通；钢管、钢板及钢筋发生屈服；加载位移至21.5 mm时 ，钢管发生屈曲墙体腹部出现较多细长斜向裂缝，且原有裂缝变宽延伸；钢管、钢板及钢筋发生屈服；加载位移至17 mm时，钢管发生屈曲破坏过程中，墙体斜裂缝增多，与原有斜裂缝形成交叉裂缝，裂缝细而密，且墙体伴随有“嗞嗞”的响声；墙体底部水平裂缝延伸、变宽、贯通形成水平剪切滑移裂缝；脚部HDC保护层受压外鼓破坏过程中，少量原有斜裂缝继续延伸；墙板底部斜裂缝快速发展、贯通形成剪切滑移裂缝，且墙体伴随有“嗞嗞”的响声。墙体底部HDC保护层出现轻微压碎、剥落现象随着位移幅值的不断增大，墙体中部出现交叉斜裂缝，斜裂缝逐渐发展、变宽形成主裂缝；底部HDC压碎外鼓，荷载迅速下降，试件破坏以后具有较好的完整性墙体腹部剪切斜裂缝变宽，墙体下部HDC保护层压酥并轻微外鼓；墙体底部钢管受压屈曲外鼓，斜裂缝贯通发展；试件破坏时底部水平裂缝贯通，底部钢板两侧HDC受压外鼓墙体中部多条斜裂缝变宽，墙体底部钢管受压屈曲外鼓，同时墙体底部HDC保护层有轻微压酥现象；试件破坏时，墙体底部钢板两侧HDC受压外鼓弯曲屈服后的剪切滑移破坏弯曲屈服后的剪切滑移破坏弯曲屈服后的剪切破坏弯剪破坏弯剪破坏
1.5 破坏形态分析
5个HDC低矮剪力墙试件的裂缝分布及破坏形态进行比较，具有以下特点。
1) 试件HDCW-01和HDCW-02的裂缝出现破坏过程相似，墙内钢筋均发生屈服以后，剪力墙底部塑性区弯曲裂缝贯通形成一条水平通缝，从而使剪力墙强度降低，发生弯曲屈服后的剪切滑移破坏。不同之处在于，试件屈服以后，随轴压比增大，斜裂缝与墙体中和轴的夹角变小。
2) 试件HDCW-03由于配置的水平分布筋较少，水平分布筋和箍筋较早被拉断，而发生弯曲屈服后的剪切破坏。与试件HDCW-02相比，水平分布筋间距增大，剪切斜裂缝越明显。
3) 钢板-HDC组合剪力墙SHDCW-03和SHDCW-04均由于角部HDC受压外鼓发生弯剪破坏。不同之处在于，随轴压比增大，墙体脚部HDC压酥现象严重，钢管较晚发生屈曲。
4) 与HDCW试件相比，钢板-HDC组合试件发生延性较好的弯剪破坏，承载力显著增加。
5) 文献[13]中试件SHPCW-06发生剪切破坏时，斜裂缝数量较少，承载力下降突然，塑性铰区混凝土压碎剥落严重，带有明显的脆性(见图6)。本文HDC低矮剪力墙试件破坏时均保持较好的完整性，斜裂缝沿整个墙面细密开展，未出现明显的脆性破坏，表明HDC良好的受拉应变硬化特征能显著提高低矮剪力墙的耐损伤能力，改善其脆性剪切破坏模式。
2 试验结果分析
2.1 荷载-位移滞回曲线
试件的顶点水平荷载-位移滞回曲线见图7。由图7可以看出：
1) 5个HDC低矮剪力墙试件的滞回曲线均比较饱满，无明显捏缩现象。加载初期，各试件滞回曲线呈线性变化，基本无残余变形，处于弹性工作状态；屈服后随着加载位移的增加，试件刚度下降，卸载后残余变形逐渐增大。
图7 荷载-位移滞回曲线
Fig.7 Load-displacement hysteretic loops
2) 对HDC剪力墙试件，随轴压比增大，滞回环面积减小，峰值荷载之后承载力下降突然；随水平分布钢筋间距增大，滞回环面积减小，耗能能力降低。
3) 与HDC试件相比，2个钢板-HDC组合剪力墙试件的滞回性能明显提高，滞回环更饱满，峰值荷载后承载力降低和刚度退化缓慢，表现出较好的抗震性能。
2.2 骨架曲线
5个HDC低矮剪力墙试件的骨架曲线如图8所示，由图8可以看出：
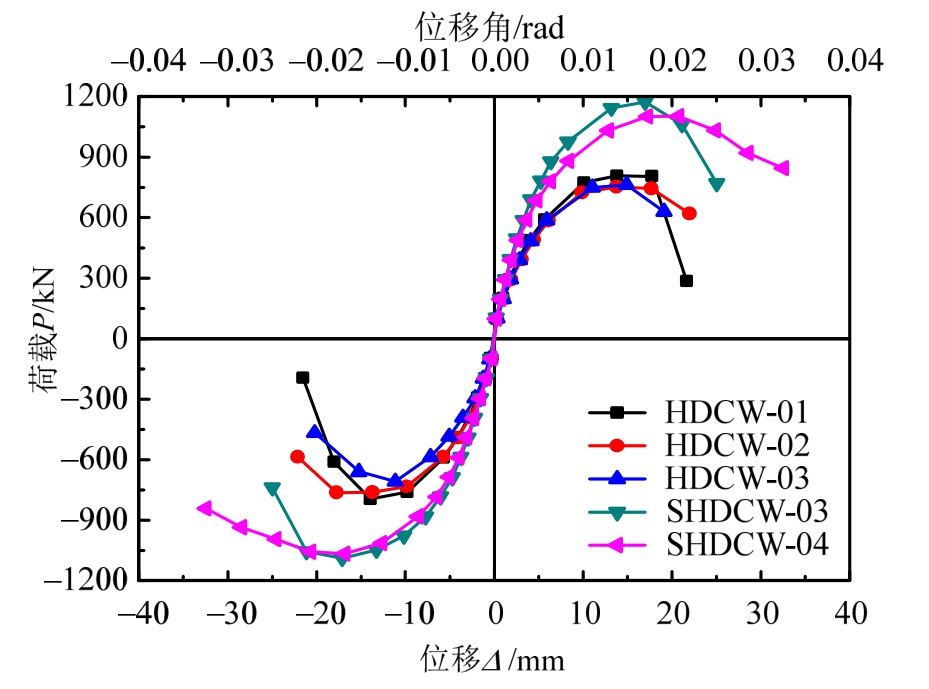
图8 试件骨架曲线
Fig.8 Skeleton curves of the specimen
1) 3个HDC剪力墙试件的骨架曲线在试件开裂前基本重合。试件达到峰值荷载后，随轴压比增大，承载力下降突然；随水平分布钢筋间距增大，试件极限位移减小。
2) 与HDC剪力墙试件相比，2个钢板-HDC组合剪力墙试件的骨架曲线弹性段明显变长，峰值荷载显著提高，主要原因是HDC开裂后，钢板承受更多剪力。其中，试件SHDCW-04和SHDCW-03相比，轴压比降低，达到峰值点以后，承载力下降更为平缓，表现出较好的延性。
2.3 变形能力及延性分析
本文采用极限位移角θ(构件的极限位移与试件高度的比值)作为其延性指标来分析低矮剪力墙的延性；采用“能量等值法”来确定试件的屈服点。根据《建筑抗震试验方法规程》[14]规定，取荷载下降至峰值荷载的85%所对应的点为极限位移点[14]，H取值为加载点到剪力墙底部截面的高度。各试件的特征点和位移延性的计算结果如表6所示。表6给出了文献[13]中2个型钢高性能混凝土低矮剪力墙试件以及文献[15]中的2个高强混凝土剪力墙的特征点取值，由表6可以看出：
表6 试件的特征点比较
Table 6 Comparison of characteristic point
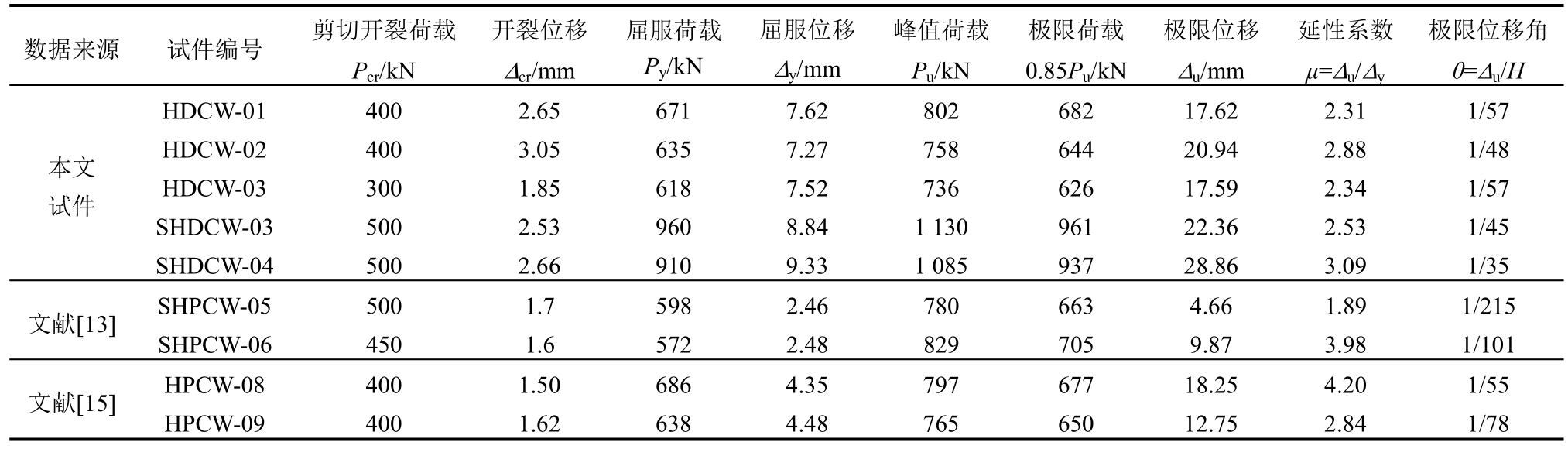
数据来源 试件编号 剪切开裂荷载Pcr/kN开裂位移Δcr/mm屈服荷载Py/kN屈服位移Δy/mm峰值荷载Pu/kN极限荷载0.85Pu/kN极限位移Δu/mm延性系数μ=Δu/Δy极限位移角θ=Δu/H HDCW-01 400 2.65 671 7.62 802 682 17.62 2.31 1/57 HDCW-02 400 3.05 635 7.27 758 644 20.94 2.88 1/48 HDCW-03 300 1.85 618 7.52 736 626 17.59 2.34 1/57 SHDCW-03 500 2.53 960 8.84 1 130 961 22.36 2.53 1/45 SHDCW-04 500 2.66 910 9.33 1 085 937 28.86 3.09 1/35文献[13]SHPCW-05 500 1.7 598 2.46 780 663 4.66 1.89 1/215本文试件SHPCW-06 450 1.6 572 2.48 829 705 9.87 3.98 1/101文献[15]HPCW-08 400 1.50 686 4.35 797 677 18.25 4.20 1/55 HPCW-09 400 1.62 638 4.48 765 650 12.75 2.84 1/78
1) 试件HDCW-02的极限位移为试件HDCW-01的1.19倍，试件SHDCW-04的极限位移为试件SHDCW-03的1.29倍，说明随着轴压比减小，试件的极限变形能力明显提高；当水平分布筋数量变小，试件HDCW-03的变形能力比试件HDCW-02有所降低。
2) 与HDC试件相比，钢板-HDC组合剪力墙试件的屈服荷载平均增加了46%，峰值荷载平均增加了45%，说明内置钢板有效的提高了HDC低矮剪力墙的抗剪承载力；屈服位移平均增加了22%，极限位移角平均增加了35%，说明在HDC剪力墙内置钢板后，有效提高了变形能力。
3) 与文献[13]和文献[15]中剪跨比为1.0的剪力墙相比，本文试件的屈服位移和极限位移显著提高，说明HDC良好的拉伸性能和纤维桥联作用，显著提高了HDC低矮剪力墙试件的变形能力。
2.4 耗能分析
各试件在低周反复荷载作用下各特征点的累积耗能如表7所示。由表7可得：
表7 累积耗能
Table 7 Energy dissipation of the specimens
试件编号 累积耗能E/(kN·mm)屈服荷载 峰值荷载 极限位移HDCW-01 10 462 26 003 100 440 HDCW-02 11 050 54 025 118 649 HDCW-03 12 035 28 828 75 987 SHDCW-03 11 270 59 308 238 452 SHDCW-04 24 372 95 248 314 356
1) 与HDCW-01相比，HDCW-02峰值荷载对应的累积耗能增加了1.08倍，可见HDC低矮剪力墙试件的耗能能力随着轴压比的降低而增加；与试件HDCW-03相比，试件HDCW-02峰值荷载和极限位移时对应的累积耗能分别增加了87%和56%，可以得到HDC低矮剪力墙试件的耗能能力随着水平分布钢筋间距的减小而增大。
2) 与HDC剪力墙试件相比，钢板-HDC组合剪力墙试件达到峰值荷载时对应的累积耗能平均提高了1.88倍，达到极限位移时对应的累积耗能平均提高了2.07倍，表明在HDC低矮剪力墙内置钢板后，试件的耗能能力大幅度提升。
2.5 刚度与损伤分析
本文采用刚度退化曲线来描述试件的刚度退化现象。等效刚度K值计算如式(1)，根据试验结果所得低矮剪力墙的刚度退化曲线如图9所示：
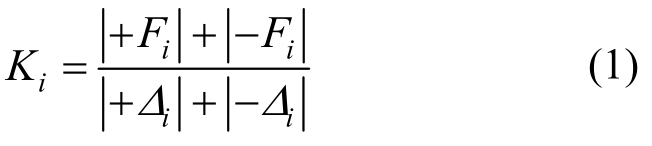
式中：Fi、Δi分别为第i次循环的最大荷载及其对应的位移。图9为5个试件的刚度退化曲线，由图9可以看出：
图9 刚度退化曲线
Fig.9 Curves of stiffness degradation
1) 五个HDC剪力墙的初始刚度退化较快，试件屈服后，刚度退化曲线逐渐平缓，说明试件在破坏阶段的损伤程度基本趋于稳定。
2) 两个组合剪力墙的刚度退化曲线均高于其余三个试件，说明HDC与钢板的组合作用，可以提高HDC低矮剪力墙的耐损伤能力。
3 抗剪承载力分析
3.1 基于软化拉-压杆模型的抗剪承载力计算
3.1.1 软化拉-压杆模型
软化拉-压杆模型是Hwang等[16―17]在拉-压杆模型的基础上考虑混凝土的受压软化特性发展起来，该模型满足平衡条件、变形协调条件和物理方程，用于计算钢筋混凝土受剪构件承载力有较好的效果。下面以剪力墙为例，简述采用软化拉-压杆模型分析受剪构件承载力的原理。
当剪力墙出现斜裂缝后，钢筋承受拉力，裂缝间的混凝土承受压力，形成拉-压杆作用。软化拉压杆模型通过3个传力机构传递荷载，分别为斜向机构、水平机构和竖向机构，如图10所示。
斜向机构为一对角混凝土斜压杆(图10(a))，斜向压杆与水平轴向夹角θ为：
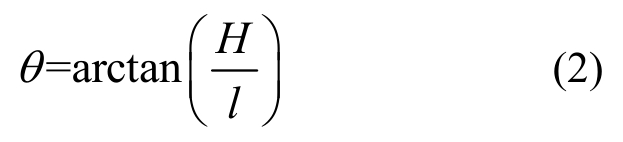
式中：H为加载点到剪力墙底部截面的高度；l为剪力墙受压、受拉合力作用点之间的距离。
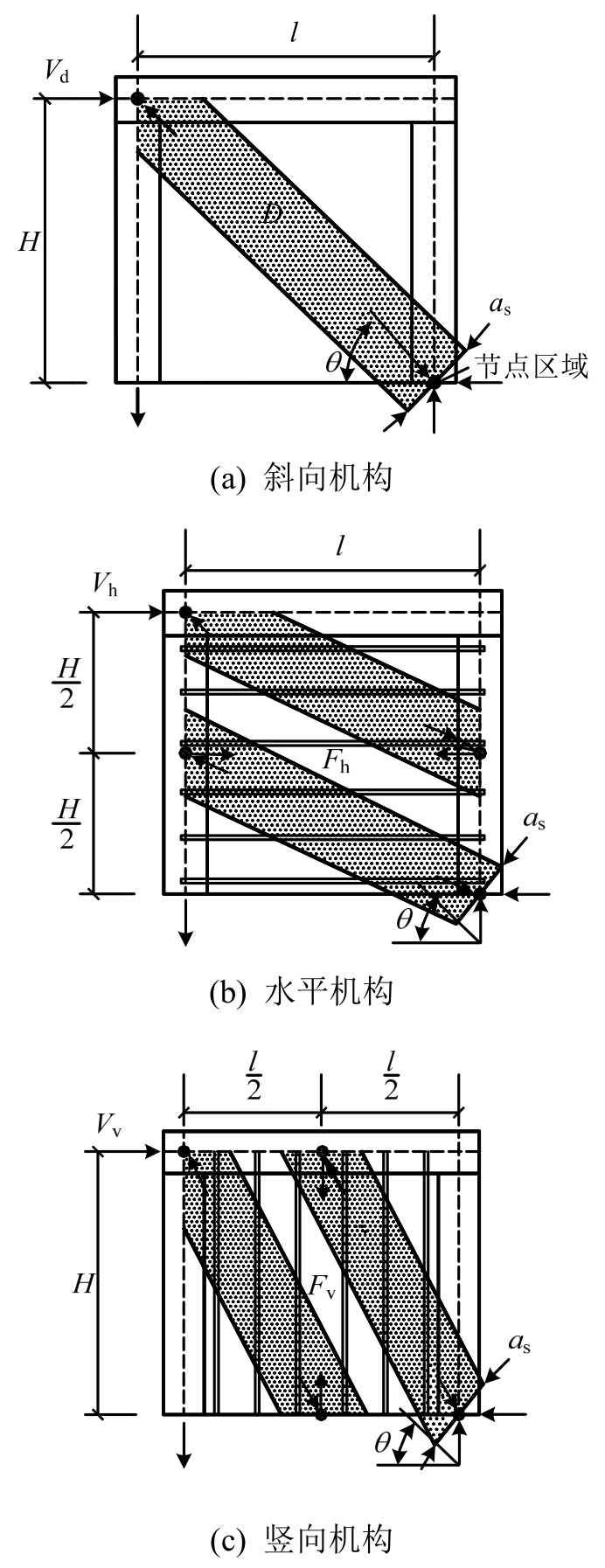
图10 剪力墙软化拉-压杆模型
Fig.10 Softened strut-and-tie model of shear wall
其有效面积Astr为：
式中，as为剪力墙斜向压杆高度，as≈aw ，
为剪力墙承受的竖向荷载，Aw为墙体截面面积，
为混凝土圆柱体抗压强度，h为剪力墙高度；bs为剪力墙斜向压杆宽度，本文取剪力墙厚度。
水平机构包含一个水平拉杆和两个平缓压杆(图10(b))，由墙体内水平分布钢筋组成。
竖向机构包含一个竖向拉杆和两个陡峭压杆(图10(c))，由墙体内竖向分布钢筋组成。
在软化拉-压杆模型中，RC剪力墙的抗剪强度取决于节点区域混凝土的受压承载力，其承载力由斜向机构、竖向机构和水平机构三者承担的剪力叠加所得。
3.1.2 软化拉-压杆模型方法的简化算法
由于采用软化拉-压杆模型计算构件的抗剪承载力需编程后反复迭代获得，不易于推广应用。因此，Hwang将软化拉压杆模型进一步简化[16]，得到该模型的简化计算方法。下面以RC剪力墙为例给出简化算法的公式。
剪力墙的承载力V为[16]：
式中：K为拉杆贡献系数[16]；ζ为混凝土抗压强度软化系数。
3.1.3 HDC低矮剪力墙的软化拉压-杆模型
采用软化拉-压杆模型计算HDC低矮剪力墙抗剪承载力时，本文对HDC受压软化系数、斜向压杆的有效面积及水平机构、竖向机构承担的拉力进行了修正。
1) HDC受压软化系数
Suwada和Fukuyama[19]基于试验数据提出了混凝土中掺入PVA纤维的软化系数计算公式如下：
由式(5)可得：HDC材料的软化系数在0.6和1之间，软化性能明显高于混凝土。但该公式认为HDC材料的软化性能只与垂直于主压应变方向的主拉应变有关，并未考虑材料强度对软化性能的影响。故本文在式(5)基础上，参考Zhang和Hsu[20]提出的混凝土软化系数计算式的强度因素，提出考虑材料强度的HDC的受压软化系数，计算如下：
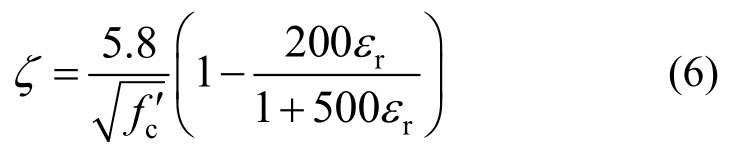
从式(16)可以看出，HDC材料的软化系数存在一个下限值，由于主拉应变的求解需要繁琐的迭代过程，因此为方便计算，本文取软化系数的下限值，即：
2) 钢板-HDC组合剪力墙斜向压杆的有效面积
本文在计算钢板-HDC组合剪力墙的抗剪承载力时，将钢板简化为等强度的HDC墙板，则内置钢板后HDC剪力墙斜向压杆的有效面积计算如下：
式中：d为钢板的厚度；αE为钢板和HDC的弹性模量比。
3) 水平、竖向机构承担的拉力Fyh、Fyv
采用软化拉-压杆模型计算HDC低矮剪力墙抗剪承载力时，水平拉杆由水平分布钢筋组成，竖向拉杆由竖向分布钢筋、暗柱纵筋和方钢管组成，则水平机构、竖向机构承担的拉力Fyh、Fyv计算如下:
式中：Ash、
分别为剪力墙水平分布钢筋作为水平拉杆的总截面面积、屈服强度；As、
分别为暗柱纵筋作为竖向拉杆的总截面面积、屈服强度；Asv、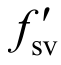
分别为剪力墙竖向分布钢筋作为竖向拉杆的总截面面积、屈服强度；Avf、
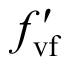分别为方钢管作为竖向拉杆的总截面面积、屈服强度。
4) 基于软化拉-压杆模型计算HDC低矮剪力墙抗剪承载力的过程
① 通过式(2)计算θ；
② 通过式(3)计算HDC剪力墙斜向压杆有效面积Astrc；通过式(8)计算钢板-HDC组合剪力墙斜向压杆有效面积Astrc；
③ 通过式(7)计算HDC的受压软化系数ζ；
④ 通过式(9)计算拉力Fyh、Fyv；
⑤ 参照文献[16]中关于计算节点拉杆贡献系数K的公式，计算本文拉压杆系数K；
⑥ 通过式(4)计算HDC剪力墙抗剪承载力V。
3.2 基于规范的抗剪承载力计算
根据《高层建筑混凝土结构技术规程》[21]中关于计算混凝土剪力墙偏心受压时斜截面抗剪承载力公式，计算HDC剪力墙抗剪承载力，计算公式如下：
根据《组合结构设计规范》[22]中关于计算内置钢板混凝土组合剪力墙偏心受压时斜截面抗剪承载力的公式，计算钢板-HDC组合剪力墙的抗剪承载力，计算公式如下：
3.3 理论计算值与试验结果对比分析
结合试件的各项参数以及本文的材性试验结果，利用本文建议的基于软化拉-压杆模型及式(10)、式(11)分别对本文HDC低矮剪力墙试件的抗剪承载力进行计算，结果如表8所示。
表8 试件抗剪承载力对比
Table 8 Comparison of shear capacity
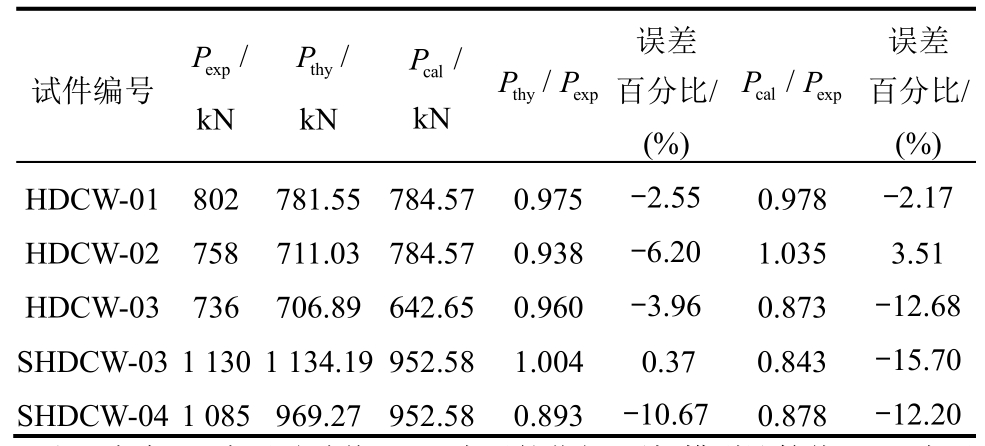
注：表中Pexp表示试验值；Pthy表示软化拉-压杆模型计算值；Pcal表示规范计算值。
试件编号Pexp/kN P/kN thy P/kN cal P/Pexp thy误差百分比/(%)P/Pexp cal误差百分比/(%)HDCW-01 802 781.55 784.57 0.975 -2.55 0.978 -2.17 HDCW-02 758 711.03 784.57 0.938 -6.20 1.035 3.51 HDCW-03 736 706.89 642.65 0.960 -3.96 0.873 -12.68 SHDCW-03 1 130 1 134.19 952.58 1.004 0.37 0.843 -15.70 SHDCW-04 1 085 969.27 952.58 0.893 -10.67 0.878 -12.20
从表8对比分析结果可以看出：基于软化拉-压杆模型的抗剪承载力计算结果与本文试验所得结果比较吻合，误差在10%以内。主要是由于在计算抗剪承载力时，现行规范仅考虑各影响项的单纯叠加，而本文基于软化拉-压杆模型将钢板作为斜压杆的一部分，同时考虑了竖向分布钢筋和方钢管作为拉杆对抗剪承载力的贡献，在计算理论中充分考虑了HDC材料的受压软化特性，为HDC低矮剪力墙抗剪承载力的计算提供较为精确的理论。
4 结论
通过对5片HDC低矮剪力墙进行水平低周反复荷载试验，对其各项抗震性能指标及抗剪承载力进行分析，结论如下：
(1) 与相关文献相比，HDC低矮剪力墙比普通混凝土低矮剪力墙的极限位移角、承载力均得到明显提高。纤维的掺入能够有效抑制裂缝的开展，推迟试件的破坏。
(2) 与HDC剪力墙试件相比，钢板与HDC的组合效应能够有效提高低矮剪力墙的承载能力和变形能力。
(3) 试件随着轴压比增大，累积耗能减小；随着水平分布钢筋间距增大，耗能能力下降。钢板与HDC的协同作用使HDC剪力墙的耗能能力大大提高。
(4) 基于软化拉-压杆模型，将钢板简化为斜压杆的一部分，同时考虑了水平分布钢筋、竖向分布钢筋和方钢管作为拉杆对抗剪承载力的贡献，在计算理论中考虑了HDC材料的强度软化性能，为HDC低矮剪力墙抗剪承载力计算提供较为精确的理论。
[1]聂建国, 卜凡民, 樊健生.低剪跨比双钢板-混凝土组合剪力墙抗震性能试验研究[J].建筑结构学报, 2011,32(11): 74-81.Nie Jianguo，Bu Fanmin，Fan Jiansheng.Experimental research on seismic behavior of low shear-span ratio composite shear wall with double steel plates and infill concrete [J].Journal of Building Structures, 2011, 32(11): 74-81.(in Chinese)
[2]聂建国, 卜凡民, 樊健生.高轴压比、低剪跨比双钢板-混凝土组合剪力墙拟静力试验研究[J].工程力学,2013, 30(6): 60-66, 76.Nie Jianguo，Bu Fanmin，Fan Jiansheng.Qusi-static test on low shear-span ratio composite shear wall with double steel plates and infill concrete under high axial compression ratio [J].Engineering Mechanics, 2013,30(6) : 60-66, 76.(in Chinese)
[3]吕西林, 干淳洁, 王威.内置钢板钢筋混凝土剪力墙抗震性能研究 [J].建筑结构学报, 2009, 30(5): 89―96.Lü Xilin, Gan Chunjie, Wang Wei.Study on seismic behavior of steel plate reinforced concrete shear walls[J].Journal of Building Structures, 2009, 30(5): 89-96.(in Chinese)
[4]邓明科, 常云涛, 梁兴文, 等.高延性水泥基复合材料抗压强度尺寸效应的正交试验研究[J].工业建筑,2013, 43(7): 80-85.Deng Mingke, Chang Yuntao, Liang Xingwen, et al.Orthogonal test research on compressive strength size effect of engineered cementitious compisites [J].Industrial Construction, 2013, 43(7): 80-85.(in Chinese)
[5]邓明科, 孙宏哲, 梁兴文, 等.延性纤维混凝土抗弯性能的试验研究[J].工业建筑, 2014, 44(5): 85-90.Deng Mingke, Sun Hongzhe, Liang Xingwen, et al.Experimental study of flexural behavior of ductile fiber reinforced concrete [J].Industrial Construction, 2014,44(5): 85-90.(in Chinese)
[6]邓明科, 刘海勃, 秦萌, 等.高延性纤维混凝土抗压韧性试验研究[J].西安建筑科技大学学报(自然科学版),2015, 47(5): 660-665.Deng Mingke, Liu Haibo, Qin Meng, et al.Experimental research on compressive toughness of the high ductile fiber reinforced concrete [J].Xi’an University of Architecture and Technology (Natural Science Edition),2015, 47(5): 660-665.(in Chinese)
[7]李艳, 梁兴文, 邓明科.高性能PVA纤维增强水泥基复合材料常规三轴受压本构模型[J].工程力学, 2012,29(1): 106-113.Li Yan, Liang Xingwen, Deng Mingke.A constitutive model for high performance PVA fiber reinforced cement composites under conventional triaxial compression [J].Engineering Mechanics, 2012, 29(1): 106-113.(in Chinese)
[8]邓明科, 张辉, 梁兴文, 等.高延性纤维混凝土短柱抗震性能试验研究[J].建筑结构学报, 2015, 36(12): 62-69.Deng Mingke, Zhang Hui, Liang Xingwen, et al.Experimental study on seismic behavior of high ductile fiber reinforced concrete short column [J].Journal of Building Structures, 2015, 36(12): 62-69.(in Chinese)
[9]邓明科, 卢化松, 杨开屏, 等.型钢高延性混凝土短梁抗剪性能试验研究[J].建筑结构学报, 2015, 36(10):73-80.Deng Mingke, Lu Huasong, Yang Kaiping, et al.Experimental study on shear behavior of steel reinforced high ductile concrete short beams [J].Journal of Building Structures, 2015, 36(10): 73-80.(in Chinese)
[10]邓明科, 代洁, 梁兴文, 等.高延性混凝土无腹筋梁受剪性能试验研究[J].工程力学, 2016, 33(10): 208-217.Deng Mingke, Dai Jie, Liang Xingwen, et al.Experimental study on the shear behavior of high ductile fiber reinforced concrete beams without stirrups [J].Engineering Mechanics, 2016, 33(10): 208-217.(in Chinese)
[11]孙宏哲, 邓明科, 孙飞, 等.半刚接钢框架内填高延性纤维混凝土剪力墙结构抗震性能试验研究[J].土木工程学报, 2015, 31(3): 42-51.Sun Hongzhe, Deng Mingke, Sun Fei, et al.Experimental study on seismic behavior of semi-rigid steel frames with ductile fiber reinforced concrete infill walls [J].China Civil Engineering Journal, 2015, 31(3):42-51.(in Chinese)
[12]邓明科, 方超, 代洁, 等.高延性纤维混凝土低矮剪力墙抗震性能试验研究[J].建筑结构, 2017, 47(2): 57-63.Deng Mingke, Fang Chao, Dai Jie, et al.Experimental study on seismic behavior of high ductile fiber reinforced concrete low-rise shear walls [J].Building Structure,2017, 47(2): 57-63.(in Chinese)
[13]梁兴文, 白亮, 杨红楼, 等.型钢高性能混凝土剪力墙抗震性能试验研究[J].工程力学, 2010, 27(10): 131-138.Liang Xingwen, Bai Liang, Yang Honglou, et al.Experimental study on the seismic behavior of high performance steel-concrete shear walls [J].Engineering Mechanics, 2010, 27(10): 131-138.(in Chinese)
[14]JGJ 101-96, 建筑抗震试验方法规程[S].北京: 中国建筑工业出版社, 1997.JGJ 101-96, Specification of testing methods for earthquake resistant building [S].Beijing: China Archi-tecture Industry Press, 1997.(in Chinese)
[15]梁兴文, 辛力, 邓明科, 等.高强混凝土剪力墙抗震性能及其性能指标试验研究[J].土木工程学报, 2010 43(11): 37-45.Liang Xingwen, Xin Li, Deng Mingke, et al.Experimental study on the seismic behavior and performance indexes of high-strength concrete shear walls [J].China Civil Engineering Journal, 2010, 43(11):37-45.(in Chinese)
[16]Hwang Shyh-Jiann, Lee Hung-Jen.Strength prediction for discontinuity regions by softened strut-and-tie model[J].Journal of Structural Engineering, 2002, 128(12),1519-1526.
[17]Hwang Shyh-Jiann, Fang Wen-Hung, Lee Hung-Jen, et al.Analytical model for predicting shear strength of squat walls [J].Journal of Structural Engineering, 2001,127(1), 43-50.
[18]Paulay T, Priestley M J N.Seismic design of reinforced concrete and masonry buildings [M].New York: John Wiley & Sons, Inc., 1992: 273-285.
[19]Suwada H, Fukuyama H.Nonlinear finite element analysis on shear failure of structural elements using high performance fiber reinforced cement composite [J].Journal of Advanced Concrete Technology 2006, 4(1):45-57.
[20]Zhang L X B, Hsu T T C.Behavior and analysis of 100 MPa concrete membrane elements [J].Journal of Structrural Engineering, 1998, 124(1): 24-34.
[21]JGJ 3―2010, 高层建筑混凝土结构技术规程[S].北京: 中国建筑工程出版社, 2010.JGJ 3―2010, Technical specification for concrete structures of tall building [S].Beijing: China Architecture Industry Press, 2010.(in Chinese)
[22]JGJ 138―2012, 组合结构设计规范[S].北京: 中国建筑工程出版社, 2012.JGJ 138―2012, Code for design of composites structures [S].Beijing: China Architecture Industry Press, 2012.(in Chinese)