航空航天结构在服役时面临着高温、振动、噪声等极为严酷的多场复杂力学环境[1],纤维增强复合材料由于具有比强度和比刚度高、密度低、耐高温和耐腐蚀等优点,被广泛用于航空航天结构中[2―3]。然而复合材料结构在复杂力学环境下易发生分层、断裂等现象,严重威胁着结构的完整性和可靠性,因此强度问题成为复合材料力学性能研究和结构设计的核心问题之一。由于缺乏成熟完善的强度理论,航空航天结构中复合材料的强度预测仍以试验为主,但试验往往具有成本较高、无法准确模拟复杂工况等缺点。纤维增强复合材料是一种多相材料,呈现不均匀和各向异性的特点,刚度、强度等宏观力学性能由细观结构以及组分材料的力学性能决定,宏观结构的损伤演化过程也与细观组分材料的失效机理密切相关。因此,基于宏-细观尺度的纤维增强复合材料结构多尺度强度分析具有重要的理论意义和工程应用价值。
针对复合材料失效的多尺度模拟,国内外已有一定的研究成果。陈滨琦等[4]建立了宏观层合板结构与细观单胞模型协同分析的多尺度方法,通过均匀化和局部化实现宏细观模型间的跨尺度联系,深入研究了纤维压缩失效模式,并进行了试验验证。杨强等[5]基于协同多尺度分析方法对T型梁试验件的拉伸失效过程进行了多尺度模拟,分析结果与试验结果具有良好的一致性。李星等[6]提出了一种新的基于应力的复合材料多尺度失效准则,同时引入应力放大系数,建立了完整的损伤演化方法和多尺度分析流程。Montesano等[7]针对风力涡轮机叶片结构建立了基于物理学的多尺度渐进损伤模型,评估了叶片结构的亚临界损伤演化和刚度退化。Jiang等[8]针对二维编织复合材料提出了一种多尺度有限元模型,模拟了结构在冲击载荷作用下的界面剥离和层间剥离,建立了细观损伤机制。Tashkinov等[9]在分析编织复合材料层合板L形试件的损伤累积过程时重点考虑了微观结构参数对层合板分层过程的影响。Souza等[10]提出了一种用于预测冲击载荷下复合材料多尺度损伤演化的模型,提高了复合材料结构高速冲击下的失效预测能力。Ha等[11]开发了一种结合虚拟细观尺度体积单元和微观尺度有限元代表单元的混合多尺度方法,用于短纤维增强复合材料的渐进失效预测。Daghia等[12]提出了一种基于离散化模型和连续性模型的细观-微观尺度计算方法,提高了计算精度和效率。Tao等[13]针对传统离散有限元模型不利于结构变形机理分析的问题开发了一种多尺度建模方法,用于复合材料连接子结构的变形机制评估。熊波等[14]为提高复合材料桁架等复杂结构的分析精度,引入了结构多尺度有限元思想,可用于分析大尺度复杂复合材料结构的强度。
复合材料的损伤需要强度失效理论来判定。近年来,国内外学者对不同的强度失效准则进行了大量研究,验证其对不同工况下不同结构的损伤预测精度。强度准则分为不区分失效模式的准则和可预测失效模式的准则。前者基于唯象学[15],根据试验数据,通过构建基于应力分量的函数来近似表征材料的损伤[16]。应用广泛的失效准则有最大应力-应变准则、蔡-希尔(Tsai-Hill)准则、蔡-吴(Tsai-Wu)准则[17]。其中,最大应力-应变准则只考虑了单一方向的应力-应变影响;Tsai-Hill准则和Tsai-Wu准则考虑到了不同应力、不同强度之间的相互作用,对实体型复合材料结构损伤的预测精度较高,但无法预测损伤模式。可预测失效模式的准则有Hashin准则[18]、Puck准则[19]等。传统的Hashin准则基于宏观应力状态预测失效模式,包含纤维拉伸失效、纤维压缩失效、基体拉伸失效和基体压缩失效等。Puck准则以Hashin准则为基础,不仅可以预测微裂纹的出现,还可以确定微裂纹的方向。
以上失效准则均建立在宏观尺度上,以宏观平均应力判断细观尺度下纤维和基体的失效模式,存在一定误差。由于复合材料的损伤失效实质上是纤维、基体以及界面的失效,有必要开展细观强度理论研究。张博明等[20]对Hashin准则进行了改进,将原准则中的宏观应力修改为细观组分应力,用于判断细观尺度下纤维和基体的失效模式,强度的预报结果与试验值吻合。陈滨琦等[4]基于Mohr-Coulomb断裂理论建立了一种新的基于物理失效机理的复合材料细观失效准则,主要考虑了压缩载荷下组分材料的损伤模式和失效机理。
为准确预测纤维增强复合材料层合板在复杂载荷作用下的损伤演化过程,本文提出了一种新的细观组分刚度退化模型,并基于细观尺度下的三维Hashin失效准则和Mohr-Coulomb断裂理论的相关失效准则[4],开展碳纤维增强树脂基复合材料层合板的多尺度交互渐进损伤分析和试验研究,验证多尺度方法在复合材料层合板损伤分析中的可行性和准确性。
1 多尺度渐进损伤分析方法
1.1 多尺度交互方法
多尺度有限元分析方法的原理是通过在宏观单元上求解子问题,利用数值方法构造可以反映结构细观非均质特性的多尺度基函数[21],使其在求解宏观结构时得到高精度解。本文通过基于节点位移的子模型法[22]建立复合材料宏观数据与细观数据之间的联系,多尺度单元的子节点位移x和宏观节点位移X之间存在以下关系:
式中,N为与子网格单元节点坐标有关的形函数矩阵。以六面体单元为例,如图1所示,单元边长分别为2a、2b和2c,当坐标轴原点位于单元体心时,已知单元内任意一点n的坐标值x、y、z,可根据式(2)求解得到该点的形函数Ni(i=1, 2, …, 8):
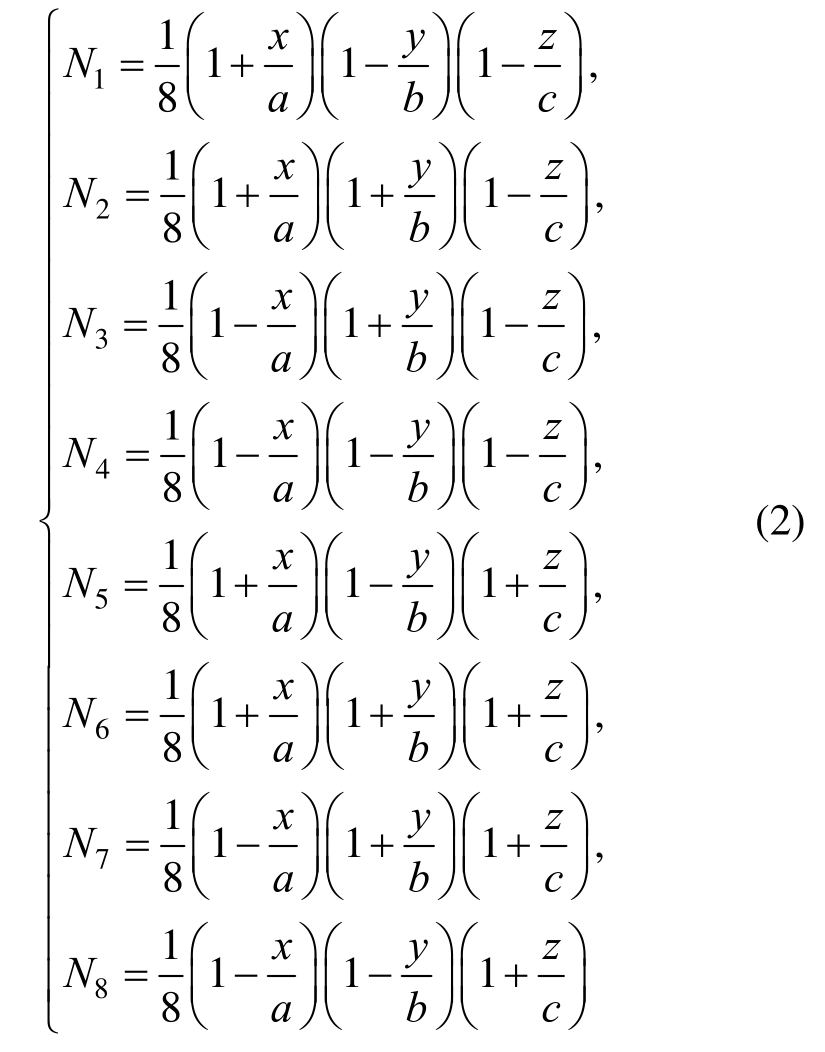
然后可根据8个节点ni (i=1,2,…,8)的位移分量求解得到该点的3个位移分量:
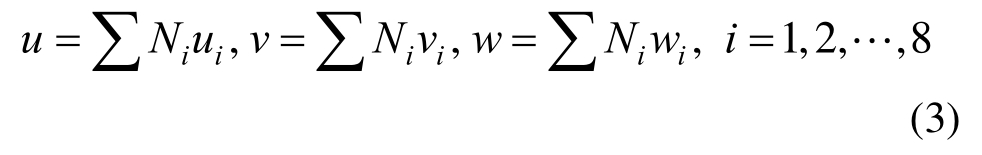
纤维增强复合材料的多尺度交互渐进损伤分析流程如图2所示。建立复合材料层合板有限元模型,对结构施加载荷,求解得到该载荷下的结构位移、应力等响应;选择应力响应较大的宏观单元建立其细观单胞模型,提取宏观单元的节点位移作形函数插值,插值结果作为单胞模型的位移边界条件,求解得到单胞中纤维和基体的应力响应并进行强度分析,对发生损伤的组分材料进行刚度折减;将宏观失效单元的材料参数更新为刚度折减后的等效弹性参数,在保持原有载荷不变的前提下重新建立平衡方程,再次判断宏观单元的损伤状态;当不再有单元损伤时增大载荷,重复上述步骤,直至结构完全损伤。

图1 8节点实体单元
Fig.1 Solid element with 8 nodes

图2 多尺度渐进损伤分析流程图[23]
Fig.2 Multi-scale progressive damage analysis procedure
1.2 面内失效准则
1.2.1 基体压缩失效
宏观尺度下的Hashin强度准则[18]认为,在复合材料结构中,1方向(沿纤维轴向)载荷主要由纤维承担,该方向上纤维主导破坏,而2方向(沿纤维径向)由基体主导破坏,即分析时不考虑1方向的基体破坏和2方向的纤维破坏。实际上,复合材料基体的有效刚度和强度显著影响着材料在1方向上对压缩载荷的承载能力[24],因此在基于细观尺度的复合材料结构损伤分析中,应考虑1方向的基体破坏对整体结构的影响,本文将Hashin强度准则引入细观尺度[20]并作改进,得到基体不同方向的压缩失效准则:

式中:![]() 分别表示基体的压缩强度和剪切强度;σm、τm分别表示基体正应力和剪切应力。当fmci≥1时,基体在i方向(i=1,2)发生压缩失效。
分别表示基体的压缩强度和剪切强度;σm、τm分别表示基体正应力和剪切应力。当fmci≥1时,基体在i方向(i=1,2)发生压缩失效。
1.2.2 基体拉伸失效
与基体的压缩失效准则类似,基体的拉伸失效准则为:

式中:![]() 分别表示基体的拉伸强度和剪切强度;σm、τm分别表示基体正应力和剪切应力。当fmti≥1时,基体在i方向(i=1,2)发生拉伸失效。
分别表示基体的拉伸强度和剪切强度;σm、τm分别表示基体正应力和剪切应力。当fmti≥1时,基体在i方向(i=1,2)发生拉伸失效。
1.2.3 纤维压缩失效
纤维的压缩失效模式有微屈曲和折断,其中折断是基体局部剪切变形伴随的纤维断裂。本文采用基于Mohr-Coulomb准则的纤维压缩失效准则[4]:

式中:![]() 表示纤维的剪切强度;μβ表示断裂面的摩擦系数;
表示纤维的剪切强度;μβ表示断裂面的摩擦系数;![]() 分别表示断裂面上的正应力、横向剪切应力和纵向剪切应力;β为折断角。当ffc≥1时,纤维发生压缩失效。
分别表示断裂面上的正应力、横向剪切应力和纵向剪切应力;β为折断角。当ffc≥1时,纤维发生压缩失效。
1.2.4 纤维拉伸失效
试验结果说明,双轴或多轴应力状态下纤维拉伸失效采用最大应力准则是合理的[4]。纤维拉伸失效主要是由拉伸应力![]() 引起的,因此采用最大应力失效准则:
引起的,因此采用最大应力失效准则:

式中:![]() 为纤维的拉伸强度;
为纤维的拉伸强度;![]() 为纤维轴向应力。当fft≥1时,纤维在1方向发生拉伸失效。
为纤维轴向应力。当fft≥1时,纤维在1方向发生拉伸失效。
1.3 层间失效准则
在宏观尺度下,复合材料层合板的破坏模式除面内失效外,还有层间失效,本文采用二次应力准则来判断胶层单元的损伤[25]:

式中:<σn>=(σn+|σn|)/2;σn、σt、σs分别表示胶层法向应力和两个方向的剪切应力;![]() 分别表示胶层在三个方向上的强度。
分别表示胶层在三个方向上的强度。
1.4 刚度退化模型
复合材料刚度退化分为宏观尺度下的等效刚度退化和细观尺度下的组分材料刚度退化,在多尺度渐进损伤分析中,损伤判断建立在细观尺度上,因此需要建立宏观与细观之间刚度退化的等效关系。在满足相应的失效准则后,细观尺度上的组分材料性能需要退化,退化方法一般分为三类:一是完全退化,即失效后刚度降为0;二是有限退化,即材料损伤后按百分比折减刚度;三是建立刚度折减系数随损伤程度变化的函数[26―27]。
综合考虑分析精度和计算效率,本文基于有限退化的刚度退化方法提出一种在1方向上考虑不同失效模式的细观组分刚度退化模型,在该方向上,复合材料层合板的失效模式分为仅纤维失效、仅基体失效和全部失效,不同的失效模式对应不同的宏观刚度折减系数,反映不同的力学性能。这种刚度退化模型能充分模拟复合材料层合板在外部载荷作用下的损伤演化过程。
2 算例研究
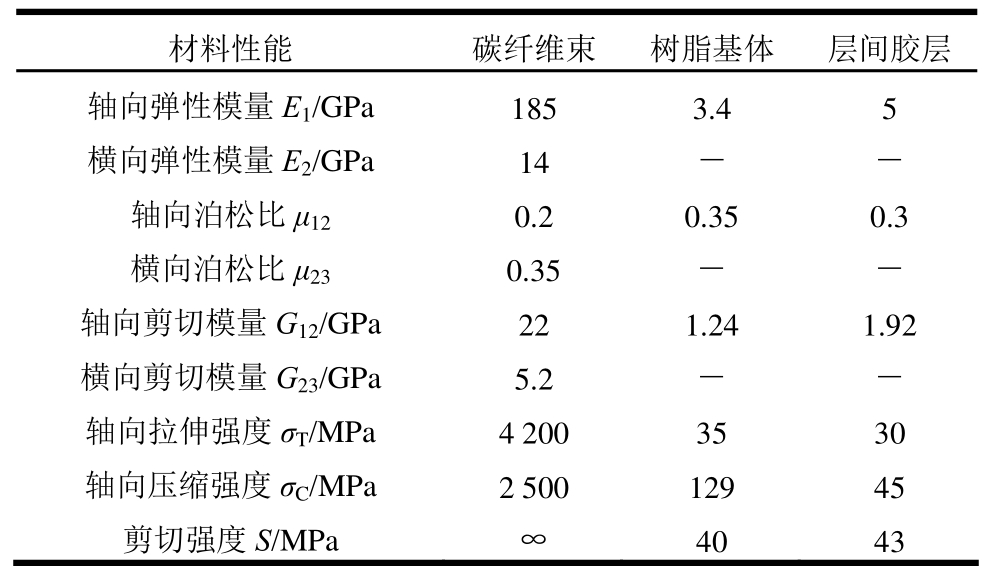
以碳纤维增强树脂基复合材料单向层合板四点弯模型为研究对象,如图3所示,层合板几何尺寸为250 mm×50 mm×6 mm,铺层角度为0°,单层厚度设为1 mm,复合材料中纤维束、基体以及层间胶层的材料属性如表1所示,纤维体积分数为50%。对单胞模型施加不同的位移边界可求解得到单胞的等效刚度矩阵[28-31],根据矩阵系数可得到层合板宏观等效弹性参数,如表2所示。
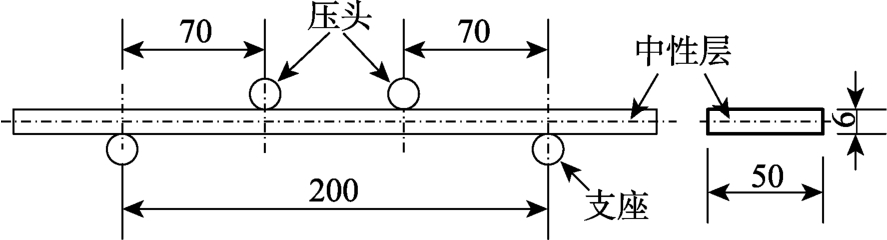
图3 四点弯结构
Fig.3 Four-point bending structure
表1 组分材料和胶层性能
Table 1 Properties of component materials and adhesive
材料性能 碳纤维束 树脂基体 层间胶层轴向弹性模量E1/GPa 185 3.4 5横向弹性模量E2/GPa 14 ― ―轴向泊松比μ12 0.2 0.35 0.3横向泊松比μ23 0.35 ― ―轴向剪切模量G12/GPa 22 1.24 1.92横向剪切模量G23/GPa 5.2 ― ―轴向拉伸强度σT/MPa 4 200 35 30轴向压缩强度σC/MPa 2 500 129 45剪切强度S/MPa ∞ 40 43
表2 单向纤维增强复合材料宏观等效弹性参数
Table 2 Unidirectional fiber reinforced composite macroequivalent elastic parameters
E1/GPa E2/GPa G12/GPa G23/GPa μ12 μ23 98.65 7.17 3.30 2.09 0.27 0.42
2.1 层合板有限元模型
复合材料层合板宏观有限元模型如图4所示,沿厚度方向共建有6层0°铺层单元,对结构纯弯段适当网格加密,层间为胶层单元,单元类型为C3D8R,胶层厚度0.05 mm。细观单胞有限元模型如图5所示,单胞尺寸与宏观模型纯弯段单元尺寸相同。单胞边界上任意一点的位移约束由宏观单元上8个节点位移通过式(2)和式(3)插值得到。
2.2 刚度退化
当纤维束在1方向上发生损伤时,折减其在该方向上的刚度 (对应参数为Ef11、μf12、μf13、Gf12、Gf13),其余方向的刚度(Ef22、Ef33、μf23、Gf23)保持不变;当基体在1方向上发生损伤后,对其他方向承载能力的影响较小,此时基体可视作正交各向异性材料,刚度折减方式与纤维束相同。通过求解等效刚度阵的方式可得到折减后的宏观等效刚度。1方向上不同失效模式下的细观刚度折减系数和对应的宏观等效刚度折减系数如表3所示。
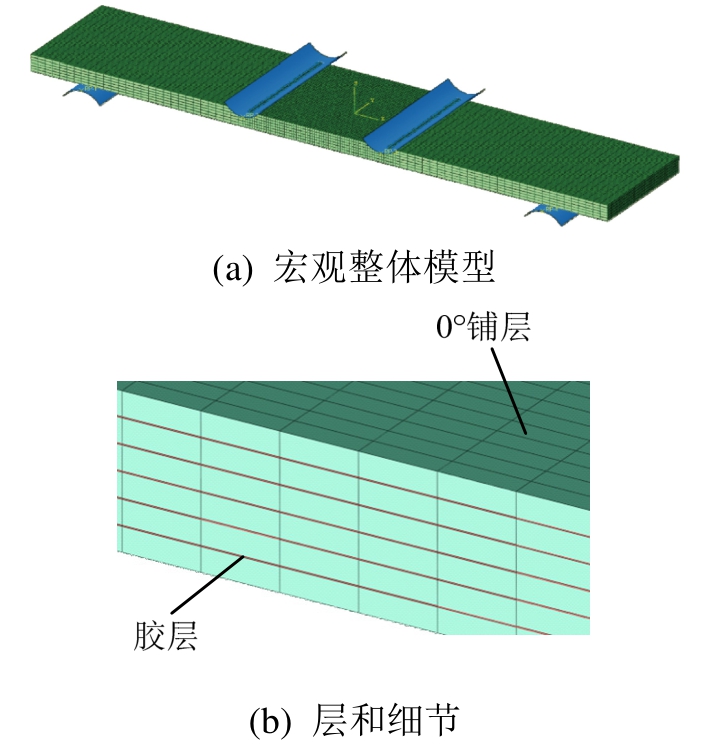
图4 层合板宏观有限元模型
Fig.4 Laminate macroscopic FEM model
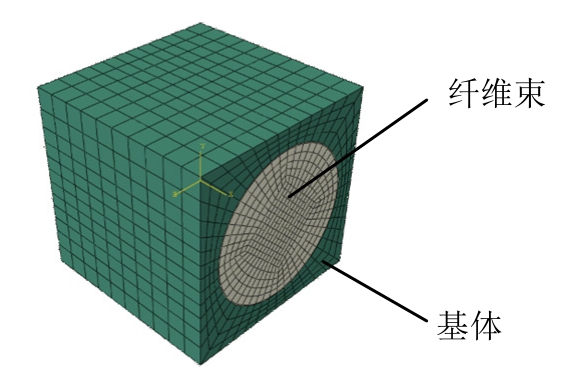
图5 细观单胞模型
Fig.5 Mesoscopic cell model
表3 宏观、细观刚度折减系数
Table 3 Stiffness reduction factors of macroscopic and mesoscopic scales

宏观失效模式 细观失效模式 细观刚度折减 宏观刚度折减1方向拉伸失效仅纤维失效Ef11d=0.01 Ef11 μf12d=μf13d=0.05 μf12 Gf12d=Gf13d=0.01 Gf12仅基体失效Em11d=0.01 Em11 μm12d=μm13d=0.09886 μm12 Gm12d=Gm13d=0.01 Gm12全部失效 同上仅纤维失效Ef11d=0.1 Ef11 μf12d=μf13d=0.1 μf12 Gf12d=Gf13d=0.1 Gf12 E11d=0.03E11 μ12d=μ13d=0.61026 μ12 G12d=G13d=0.18378 G12 E11d=0.98264 E11 μ12d=μ13d=0.48715 μ12 G12d=G13d=0.01067 G12 E11d=0.01 E11 μ12d=μ13d=0.08111 μ12 G12d=G13d=0.01 G12 E11d=0.11839 E11 μ12d=μ13d=0.62695 μ12 G12d=G13d=0.50083 G12 1方向压缩失效仅基体失效Em11d=0.1 Em11 μm12d=μm13d=0.31143 μm12 Gm12d=Gm13d=0.1 Gm12 E11d=0.9837 E11 μ12d=μ13d=0.6084 μ12 G12d=G13d=0.11475 G12全部失效 同上E11d=0.1 E11 μ12d=μ13d=0.22529 μ12 G12d=G13d=0.1 G12
2.3 损伤演化过程
基于多尺度方法分析碳纤维增强树脂基复合材料单向层合板四点加载下的损伤演化过程,得到结构的载荷-位移曲线,如图6所示,从载荷-位移曲线中选取4个参考点Pi (i=1, 2,…,4)得到对应载荷下结构各铺层Lj、各胶层Ik的损伤演化(j=1, 2,…,6;k=1, 2,…,5从板上表面开始编号),如表4和表5所示。由于结构和载荷具有对称性,在分析过程中胶层取整体结构的1/4,位置如图7中实线框所示,铺层取图7中虚线框所示的部分。
分析可知:1) 层合板没有发生破坏时,载荷与位移呈线性关系;2) 压头位移超过6 mm后载荷出现小幅下降,在纯弯段上表面局部靠近压头处出现基体压缩损伤,纤维保持完好,在中性层上侧的胶层出现局部压缩损伤,但对整体结构的影响可忽略;3) 位移增大至6.2 mm时,上表面出现局部破坏,同时L2层开始出现损伤;4) 位移超过6.2 mm后,L1层损伤有向中部扩展的趋势,L3层开始出现损伤,中性层上侧的胶层在纯弯段出现大面积损伤,整体结构发生破坏,承载能力下降,载荷位移曲线出现陡降;5) 载荷继续增大后,层合板的破坏集中在胶层,在整个加载过程中,层合板中性层下侧没有出现明显损伤。仿真结果显示,复合材料四点弯模型最终的破坏形式为多模式破坏,在前期以压缩破坏为主,后期以分层破坏为主。
表4 0°铺层损伤演化过程
Table 4 Damage evolution process of 0° laminate layers

铺参考点铺参考点层 P1 P2 P3 P4层P1 P2 P3 P4 L1images/BZ_260_336_1161_524_1417.pngimages/BZ_260_566_1162_753_1415.pngimages/BZ_260_796_1162_986_1415.pngimages/BZ_260_1029_1162_1220_1415.pngL2images/BZ_260_1341_1161_1528_1417.pngimages/BZ_260_1570_1162_1757_1415.pngimages/BZ_260_1800_1162_1991_1415.pngimages/BZ_260_2033_1162_2224_1415.pngL3images/BZ_260_336_1417_524_1674.pngimages/BZ_260_566_1417_753_1674.pngimages/BZ_260_796_1419_986_1672.pngimages/BZ_260_1029_1419_1220_1672.pngL4images/BZ_260_1341_1417_1528_1674.pngimages/BZ_260_1570_1417_1757_1674.pngimages/BZ_260_1800_1417_1988_1674.pngimages/BZ_260_2034_1417_2221_1674.pngL5images/BZ_260_336_1673_524_1930.pngimages/BZ_260_566_1673_753_1930.pngimages/BZ_260_796_1673_984_1930.pngimages/BZ_260_1030_1673_1217_1930.pngL6images/BZ_260_1341_1673_1528_1930.pngimages/BZ_260_1570_1673_1757_1930.pngimages/BZ_260_1800_1673_1988_1930.pngimages/BZ_260_2034_1673_2221_1930.pngimages/BZ_260_655_1933_736_1984.png未损伤images/BZ_260_923_1933_1008_1984.png仅纤维损伤images/BZ_260_1257_1933_1338_1984.png仅基体损伤images/BZ_260_1604_1933_1685_1984.png完全损伤
表5 胶层损伤演化过程
Table 5 Damage evolution process of adhesive layers

胶参考点 参考点 参考点胶胶层 P1 P2 P3 P4层 P1 P2 P3 P4层P1 P2 P3 P4 I1images/BZ_260_335_2241_570_2712.pngimages/BZ_260_481_2241_716_2712.pngimages/BZ_260_627_2241_862_2712.pngimages/BZ_260_773_2241_1008_2712.pngI2images/BZ_260_996_2241_1231_2712.pngimages/BZ_260_1142_2241_1377_2712.pngimages/BZ_260_1288_2241_1523_2712.pngimages/BZ_260_1435_2241_1670_2712.pngI3images/BZ_260_1657_2241_1892_2712.pngimages/BZ_260_1804_2241_2039_2712.pngimages/BZ_260_1953_2241_2188_2712.pngimages/BZ_260_2111_2241_2211_2712.pngI4images/BZ_260_335_2712_571_3184.pngimages/BZ_260_481_2712_717_3184.pngimages/BZ_260_627_2712_863_3184.pngimages/BZ_260_773_2712_1009_3184.pngI5images/BZ_260_996_2712_1232_3184.pngimages/BZ_260_1142_2712_1378_3184.pngimages/BZ_260_1288_2712_1524_3184.pngimages/BZ_260_1436_2712_1672_3184.pngimages/BZ_260_1647_2897_1728_2947.png未损伤images/BZ_260_1647_2948_1729_2998.png已损伤images/BZ_260_1979_2729_2064_3156.png分析位置

图6 载荷-位移曲线
Fig.6 Load-displacement curve

图7 损伤演化的分析位置
Fig.7 Analysis position of damage evolution process
3 试验验证
以碳纤维增强环氧树脂单向板为例,对第2节的仿真结果进行验证。试验中所用试件的尺寸和材料与第2节相同,纤维轴向为长度方向,试验装置如图8所示。

图8 四点弯试验装置
Fig.8 Four-point bending test device
3.1 试验结果
进行复合材料四点弯曲试验,测得5组有效数据,得到准静态加载工况下的载荷位移曲线如图9所示,极限载荷与对应的压头位移如表6所示。由试验结果可知:1) 当试件未出现明显的破坏迹象时,载荷与位移呈线性关系;2) 当载荷超过极限载荷的90%以后,在试件纯弯段上表面靠近一端压头处出现清晰的局部破坏现象;3) 达到极限载荷后,试件出现数条分层裂纹,多分布在中性层以上受压一侧,下表面未有明显破坏的迹象,该过程中,载荷陡降至极限载荷的50%左右后下降速度明显变缓,表明层合板仍具有一定的承载能力。由于5组试件的最终破坏形貌相似,图10给出了编号为CL5的试件在压头位移达到8 mm时的破坏形貌。

图9 载荷-位移曲线
Fig.9 Load-displacement curves
表6 极限载荷与对应的位移
Table.6 Limit load and corresponding displacement
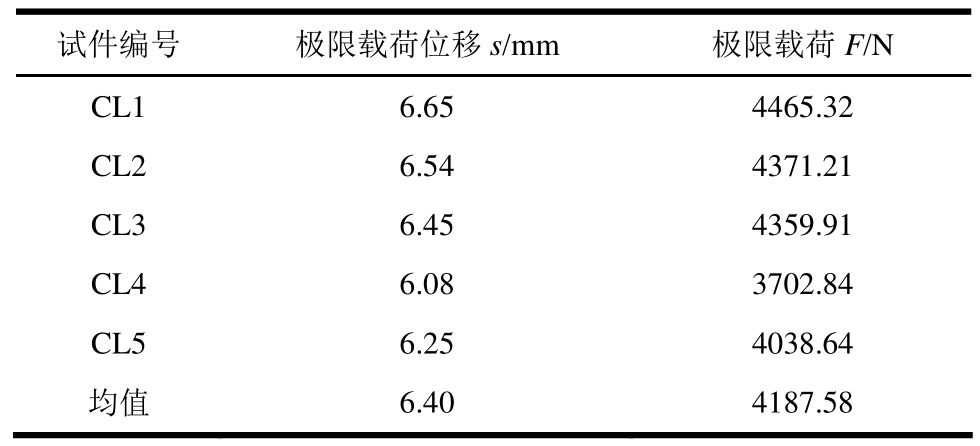
试件编号 极限载荷位移s/mm 极限载荷F/N CL1 6.65 4465.32 CL2 6.54 4371.21 CL3 6.45 4359.91 CL4 6.08 3702.84 CL5 6.25 4038.64均值 6.40 4187.58

图10 压头位移为8mm时CL5号层合板的破坏形貌
Fig.10 Damage feature of CL5 laminate at 8 mm displacement of indenter
3.2 对比分析
对比试验和仿真中复合材料层合板的损伤演化过程和破坏模式,可知:1) 试验中复合材料层合板在弯曲过程中表现为多模式破坏,上表面出现纤维和基体的局部破坏,下表面无明显的破坏现象,仿真中当载荷达到峰值后,在纯弯段上表面靠近压头处出现局部破坏,下表面保持完好,与试验结果吻合;2) 试件在加载过程中产生分层现象,破坏集中在中性层上侧,发生破坏后结构的承载能力下降,仿真中当载荷超过峰值后,四点弯模型的损伤形式主要为分层破坏,中性层上侧的胶层出现大面积损伤,但中性层下侧的胶层保持完好,与试验结果基本一致。
对比试验和仿真的载荷位移曲线,如图11所示,可知:1) 仿真得到的极限载荷与试验值接近,误差为3.28%,极限载荷对应的位移略低于试验值,误差为6.25%;2) 试验得到部分试件的载荷-位移曲线在峰值附近下降后会有小幅回弹,仿真也存在这种现象,仿真结果显示该现象是由结构的局部损伤造成的;3) 超过载荷极限后,由于中性层下侧的胶层未发生明显破坏,整体结构仍具有一定的承载能力,但此时仿真得到的载荷-位移曲线与试验曲线不完全吻合,原因是不同试件之间存在缺陷上的差异,导致试件在载荷超过极限后体现出的力学性能不完全相同,目前的仿真工作可以较为准确地模拟层合板的细观失效过程,但还无法准确反映缺陷造成的影响。

图11 试验与仿真结果对比
Fig.11 Comparison of experimental and simulation results
4 结论
本文基于多尺度分析方法,针对纤维增强复合材料层合板四点弯结构开展了准静态多尺度交互渐进损伤分析和试验验证:
(1)建立了碳纤维增强树脂基复合材料单向层合板宏观有限元模型和细观单胞模型,通过求解等效刚度阵的方法建立了复合材料层合板弹性参数和刚度折减系数在宏观尺度和细观尺度上各组分的等效关系;
(2)基于细观Hashin失效准则和Mohr-Coulomb断裂准则开展复合材料层合板四点弯模型多尺度交互渐进损伤分析,在细观尺度上考虑了1方向上不同的失效模式对宏观力学性能的影响,并在宏观尺度上考虑了分层损伤;
(3)开展了准静态工况下复合材料层合板四点弯试验,对有限元仿真的结果进行了验证,结果显示仿真结果与试验吻合较好,基于多尺度方法进行复合材料结构跨尺度渐进损伤分析具有较高精度,可较为准确地模拟层合板的细观失效过程,同时可以解释载荷-位移曲线回弹等试验现象。
[1]李彦斌, 张鹏, 吴邵庆, 等.复合材料加筋板计及热效应的声-固耦合分析[J].振动工程学报, 2015, 28(4):531―540.Li Yanbin, Zhang Peng, Wu Shaoqing, et al.Structural-acoustic coupling analysis of a composite stiffened panel in a thermal environment [J].Journal of Vibration Engineering, 2015, 28(4): 531―540.(in Chinese)
[2]吴邵庆, 范刚, 李彦斌, 等.复合材料梁弹性参数不确定性量化及试验验证[J].东南大学学报(自然科学版),2018, 48(6): 1004―1012.Wu Shaoqing, Fan Gang, Li Yanbin, et al.Uncertainty quantification on elastic parameters of composite beams and its experimental verification [J].Journal of Southeast University (Natural Science Edition), 2018, 48(6):1004―1012.(in Chinese)
[3]秦福溶, 姜东, 曹芝腑, 等.基于灵敏度分析的复合材料组分参数识别方法[J].复合材料学报, 2018, 35(12):3350―3359.Qin Furong, Jiang Dong, Cao Zhifu, et al.Parameter identification for components of composites based on sensitivity analysis [J].Acta Materiae Compositae Sinica,2018, 35(12): 3350―3359.(in Chinese)
[4]陈滨琦, 曾建江, 王玉青, 等.三向受压下单向复合材料层板破坏的细观力学分析[J].复合材料学报, 2017,34(4): 573―583.Chen Binqi, Zeng Jianjiang, Wang Yuqing, et al.Micro-mechanics analysis of damage for unidirectional composite laminates under tri-axial compression [J].Acta Materiae Compositae Sinica, 2017, 34(4): 573―583.(in Chinese)
[5]杨强, 解维华, 孟松鹤, 等.复合材料多尺度分析方法与典型元件拉伸损伤模拟[J].复合材料学报, 2015,32(3): 617―624.Yang Qiang, Xie Weihua, Meng Songhe, et al.Multi-scale analysis method of composites and damage simulation of typical component under tensile load [J].Acta Materiae Compositae Sinica, 2015, 32(3): 617―624.(in Chinese)
[6]李星, 关志东, 刘璐, 等.复合材料跨尺度失效准则及损伤演化[J].复合材料学报, 2013, 30(2): 152―158.Li Xing, Guan Zhishan, Liu Lu, et al.Composite multiscale failure criteria and damage evolution [J].Acta Materiae Compositae Sinica, 2013, 30(2): 152―158.(in Chinese)
[7]Montesano J, Hao C, Singh C V.Development of a physics-based multi-scale progressive damage model for assessing the durability of wind turbine blades [J].Composite Structures, 2016, 141: 50―62.
[8]Hongyong Jiang, Yiru Ren, Songjun Zhang, et al.Multi-scale finite element analysis for tension and ballistic penetration damage characterizations of 2D triaxially braided composite [J].Journal of Materials Science, 2018, 53(14): 10071―10094.
[9]Tashkinov M, Ershova D.Shalimov A.Computational multi-scale analysis of simultaneous processes of delamination and damage accumulation in laminated composites [J].Frattura e Integrita Strutturale, 2019, 49:396―411.
[10]Souza F V, Allen D H, Kim Y R.Multiscale model for predicting damage evolution in composites due to impact loading [J].Composites Science & Technology, 2008,68(13): 2624―2634.
[11]Ha S K, Lei Xu, Chao Zhao, et al.Progressive failure prediction of short fiber reinforced composites using a multi-scale approach [J].Journal of Composite Materials,2018, 52(27): 3785―3801.
[12]Daghia F, Ladeveze P.A micro-meso computational strategy for the prediction of the damage and failure of laminates [J].Composite Structures, 2012, 94(12):3644―3653.
[13]Muxuan Tao, Jianguo Nie.Multi-scale modeling for deformation mechanism analysis of composite joint substructures [J].Engineering Structures, 2016, 118:55―73.
[14]熊波, 罗锡林, 谭惠丰.考虑接头作用的全复合材料桁架结构多尺度分析[J].工程力学, 2015, 32(8): 229―235.Xiong Bo, Luo Xilin, Tan Huifeng.Multi-scale analysis of all-composite truss considering joint effects [J].Engineering Mechanics, 2015, 32(8): 229―235.(in Chinese)
[15]Bo Wang, Guiqiong Jiao, Wenge Pan, et al.Tensile and compress experimental investigation of three dimensionally braided C/SiC composites [J].Acta Materiae Compositae Sinica, 2004, 21(3): 110―114.
[16]张承承, 王建军.基于刚度退化的复合材料结构损伤研究进展[J].材料导报, 2016, 30(21): 8―13.Zhang Chengcheng, Wang Jianjun.Research advances in damage of composite structures on stiffness degradation[J].Material Review, 2016, 30(21): 8―13.(in Chinese)
[17]Pengfei Liu, Jinyang Zheng.Recent developments on damage modeling and finite element analysis for composite laminates: A review [J].Materials and Design,2010, 31(8): 3825―3834.
[18]Libin Zhao, Wen Yang, Tiancheng Cao, et al.A progressive failure analysis of all-C/SiC composite multi-bolt joints [J].Composite Structures, 2018, 202:1059―1068.
[19]Shi Y, Swait T, Soutis C.Modelling damage evolution in composite laminates subjected to low velocity impact [J].Composite Structures, 2012, 94(9): 2902―2913.
[20]张博明, 赵琳.基于单胞解析模型的复合材料层合板渐进损伤数值分析[J].工程力学, 2012, 29(4): 36―42.Zhang Boming, Zhao Lin.Numerical analysis for progressive damage of composite laminates based on analytic model of unit cell [J].Engineering Mechanics,2012, 29(4): 36―42.(in Chinese)
[21]卓小翔, 刘辉, 楚锡华, 等.非均质材料动力分析的广义多尺度有限元法[J].力学学报, 2016, 48(2):378―386.Zhuo Xiaoxiang, Liu Hui, Chu Xihua, et al.A generalized multiscale finite element method for dynamic analysis of heterogeneous material [J].Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(2): 378―386.(in Chinese)
[22]于士甲, 张鹏, 李彦斌, 等.基于动态子模型法的结构动响应预示方法[J].东南大学学报(自然科学版), 2017,47(2): 325―330.Yu Shijia, Zhang Peng, Li Yanbin, et al.Structural response prediction based on dynamic sub-modelling method [J].Journal of Southeast University (Natural Science Edition), 2017, 47(2): 325―330.(in Chinese)
[23]相超, 周丽, 宋恩鹏, 等.拉伸载荷下贴补复合材料层合板的渐进损伤分析[J].工程力学, 2014, 31(10):234―241.Xiang Chao, Zhou Li, Song Enpeng, et al.Progressive damage analysis of bonding patch-repaired composite laminates under tension loading [J].Engineering Mechanics, 2014, 31(10): 234―241.(in Chinese)
[24]Park I K, Park K J, Kim S J.Rate-dependent damage model for polymeric composites under in-plane shear dynamic loading [J].Computational Materials Science,2015, 96: 506―519.
[25]古兴瑾, 许希武.不同形状弹体高速冲击下复合材料层板损伤分析[J].工程力学, 2013, 30(1): 432―440.Gu Xingjin, Xu Xiwu.Analysis of damage in composite laminates under high velocity impact by projectiles of different shapes [J].Engineering Mechanics, 2013, 30(1):432―440.(in Chinese)
[26]王成华, 杨阳, 康强, 等.一种新型刚度退化模型及复合材料结构渐进损伤分析的通用方法实现[J].工程力学, 2016, 33(4): 17―23.Wang Chenghua, Yang Yang, Kang Qiang, et al.A stiffness degradation model and a general method for progressive failure analysis of composite structures [J].Engineering Mechanics, 2016, 33(4): 17―23.(in Chinese)
[27]Yiru Ren, Songjun Zhang, Hongyong Jiang, et al.Meso-scale progressive damage behavior characterization of triaxial braided composites under quasi-stable load [J].Applied Composite Material, 2017, 25(2): 335―352.
[28]Dong Jiang, Rui Ma, Shaoqing Wu, et al Numericalexperimental method for elastic parameters identification of a composite panel [J].Theoretical and Applied Mechanics Letters, 2014, 4(6): 26―31.
[29]陈素芳, 谭志勇, 姜东, 等.高温环境下纤维增强复合材料等效参数预测[J].振动与冲击, 2018, 37(11):216―224, 258.Chen Sufang, Tan Zhiyong, Jiang Dong, et al.Equivalent parametric prediction for fiber reinforced composites under high temperature condition [J].Journal of Vibration and Shock, 2018, 37(11): 216―224, 258.(in Chinese)
[30]Sufang Chen, Qingguo Fei, Dong Jiang, et al.Determination of thermo-elastic parameters for dynamical modeling of 2.5D C/SiC braided composites[J].Journal of Mechanical Science & Technology, 2018,32(1): 231―243.
[31]费庆国, 姜东, 陈素芳, 等.高温下编织复合材料热相关参数识别方法研究[J].力学学报, 2018, 50(3):497―507.Fei Qingguo, Jiang Dong, Chen Sufang, et al.Thermal-related parameter identification of braided composites at high temperature [J].Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(3): 497―507.(in Chinese)