纤维增强复合材料具有优异的力学性能，目前正在被越来越多地应用于航空、航天、船舶、兵器工业等领域[1―3]，其材料参数通常包括纤维纵向、横向弹性模量、损耗因子、剪切模量及泊松比等[4]，它们是深入研究复合材料结构静力学及动力学问题的基础[5]，准确确定上述基本性能参数，对于复合材料及其结构的力学行为分析与强度评价至关重要。
目前，国内外学者和研究人员针对该类型复合材料参数的辨识开展了大量工作。常见的辨识方法包括三点弯曲试验法、双轨剪切试验法、拉伸试验法等[6]，但上述方法都是建立在材料疲劳或破坏的基础上，测试周期长、试验成本也较为高昂。进入20世纪60年代后，人们逐步从振动学角度研究纤维复合材料的无损辨识与测试方法。例如，Schultz和Tsai[7]对玻璃纤维/树脂复合材料的弹性模量进行了辨识，发现在电磁激振器给予的外激振幅度不大时，0°、22.5°和90°的复合悬臂梁的弹性模量基本保持不变，但45°复合悬臂梁的动态弹性模量随着频率的增加约有15%的改变。Araújo等[8]通过模态力锤振动测试法和有限元法分别获得纤维复合板结构的固有频率，并构造带权重系数的最小二乘估计函数，进而辨识获得不同方向的弹性模量、剪切模量和泊松比。Visscher等[9]提出了一种基于小型扬声器振动激励(局部振动)与理论计算的混合算法，实现了对碳纤维/环氧树脂复合材料阻尼参数的有效辨识。Bledzki等[10]利用激振器获得了玻璃纤维/树脂复合薄板的振动数据，并将有限元和响应面法相结合获得了材料在纤维纵向、横向等方向的弹性模量和泊松比。Hwang[11]提出了一种结合基因优化算法与力锤脉冲激励技术的混合方法，实现了玻璃纤维/树脂基复合材料弹性常数的辨识，还提出了两步法来弥补测试过程中固有频率丢失或者存在较大误差的问题。Matter等[12]也用小型扬声器对自由边界下复合薄板的局部进行振动激励，同时利用有限元法获得固有频率、阻尼比等振动参数，并提出了一种数值-实验混合法来辨识复合材料的弹性参数和损耗参数。李双蓓等[13]以商用ABAQUS有限元软件为计算平台，将材料参数辨识转化为极小化目标函数的求解问题，并辨识获得了硼/环氧简支梁的材料参数。
虽然国内外学者和研究人员针对复合材料参数的辨识开展了大量工作，但绝大多数实验测试方法多采用模态力锤、电磁激振器或振动台作为激励手段，上述接触式激励方式常常会给具有轻质特点的复合材料带来一系列问题，进而影响振动响应测试精度和材料参数辨识精度。例如，锤击方式的激励力道难以控制，容易对结构产生局部非线性振动影响；激振器配套的柔性杆和力传感器会带来较大的附加质量和刚度影响；振动台夹具也不可避免对结构产生边界阻尼的影响。另外，也有部分文献采用了小型扬声器来产生振动，但由于声能量只能作用于被测结构的局部，一方面其产生的激励能量十分有限，测试信噪比不高；另一方面，复合材料结构在局部声学激励下的响应计算，很难通过解析法获得，还需借助商用有限元软件进行模拟，不利于开发具有自主知识产权的辨识算法。
平面声波激励是一种新型的大功率、非接触激励方式，具有激励能量充足可控、激励精度高等优势。本文在定制的平面式大功率扬声器的基础上，结合激光多普勒测振仪，针对纤维增强复合材料薄板，组建了一套完整的非接触激振-测振系统。在理论结合实际的基础上，通过粒子群迭代求解方式，成功辨识获得了该类型复合材料在纤维纵向、横向和剪切方向的弹性模量、泊松比和损耗因子等材料参数。本文的研究可以为复合材料参数的无损检测及识别提供一种新思路。
1 复合材料薄板理论模型
以纤维增强复合材料薄板为例，建立其理论模型，如图1所示。该板由β层具有正交各向异性特点的纤维和基体材料组合而成的，首先将其中面作为参考平面，建立xoy坐标系。假设纤维方向与整体坐标系x轴方向的夹角为θ，板长、宽、厚为a、b、h，每一层位于z坐标轴较低表面hk-1和较高表面hk之间，每层的厚度均相同。图中的1、2和3分别代表纤维纵向、横向和垂直于1-2平面的方向。假设其处于自由边界条件，受到的平面声波激励载荷为P(t)，声波作用的整个面积为A，关注的振动响应位于R(x1,y1)点。
图1 平面声波激振下纤维增强复合材料薄板的理论模型
Fig.1 Theoretical model of fiber-reinforced composite thin plate under planar acoustic wave excitation
假设纤维增强悬臂薄板平行纤维方向的弹性模量和损耗因子分别为E1和η1，垂直纤维方向的弹性模量和损耗因子分别为E2和η2，1-2平面内的剪切弹性模量和损耗因子分别为G12和η12，1方向作用应力引起1、2方向应变的泊松比为ν12，2方向作用应力引起1、2方向应变的泊松比为ν21。
基于经典层合板理论[14]，可将复合薄板的位移场写为：
式中：u、ν、w代表梁内任意一点的位移；u0、ν0、w0代表中面位移；t表示时间。
据参考文献[15]，可将其应变和位移的关系表示如下：
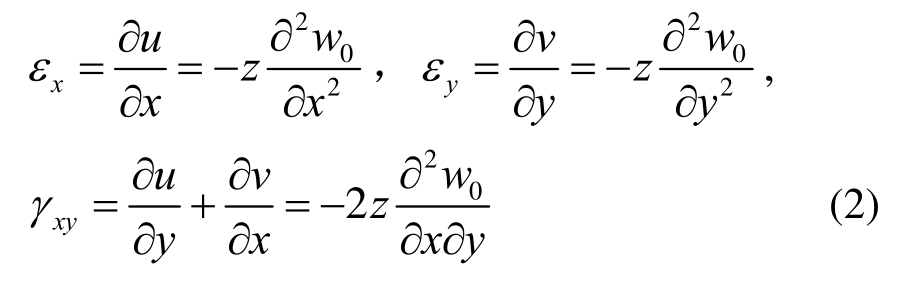
复合薄板中面弯曲挠曲率和扭曲率可表示为：
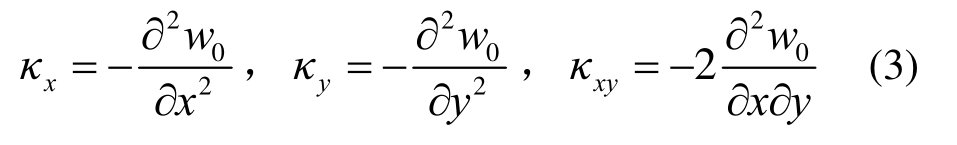
对于正交各向异性材料，当材料主轴方向与整体坐标系之间有一定夹角θ时，用应力-应变转轴公式计算得到复合薄板第k层在整体坐标系下的应力-应变关系如下：
式中：
表达式见于文献[15]；k表示复合薄板的第k层。
复合薄板所受弯矩和扭矩为：
式中，
表达式见于文献[16]。
复合薄板的动能可以用下式表示：
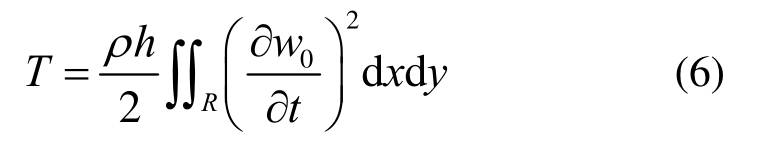
式中：ρ为复合薄板的密度；h为复合薄板的厚度。
相应地，复合薄板的弯曲应变能为：
假设复合薄板横向振动的位移w0可以表示为：
式中：ω为圆频率，与激励频率相同；W(ξ,η)为振型函数，有如下形式：
式中：qmn为待定系数；pm (ξ)(m=1,2,…,M)和qn(η)(n=1,2,…,N)为一系列的正交多项式。
通过对满足边界条件的多项式函数进行正交化处理，可获得一系列正交多项式，具体表达式可见文献[16]。由于本文关注的是自由边界条件，所以取p=0，r=0，q=0，s=0。
然后，根据Ritz法，定义能量函数L的表达式为：
式中，Tmax和Umax分别为复合薄板的最大动能和最大应变能，具体表达式参见文献[16]。
通过使能量函数L对待定系数qmn的偏导数为零，即：
进而得到复合薄板自由振动的特征方程，有如下形式：
式中：K和M分别为复合薄板的刚度矩阵和质量矩阵；特征向量
对式(12)进行求解，由此便可实现固有频率ωmn 和模态振型Wmn(x,y)的求解。
由于复合薄板受到平面声波载荷P(t)的作用，假设激励信号类型为脉冲信号，这里可将其简化为一个周期极短的简谐半波，其数学表达式为：
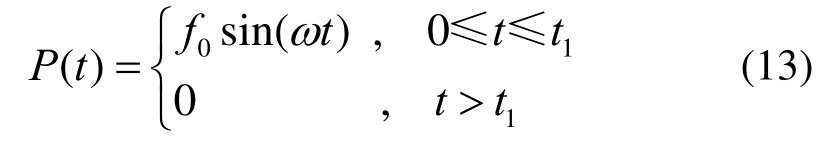
式中：f0为激励声压；ω为激励角频率；t1为激励作用的时间。
接着，采用振型叠加法求解在平面声波载荷作用下的振动响应X(t)，假设其表达式为：
式中，Tmn为各阶振型分量。
考虑复合薄板微元动力平衡，忽略阻尼及惯性力矩有：
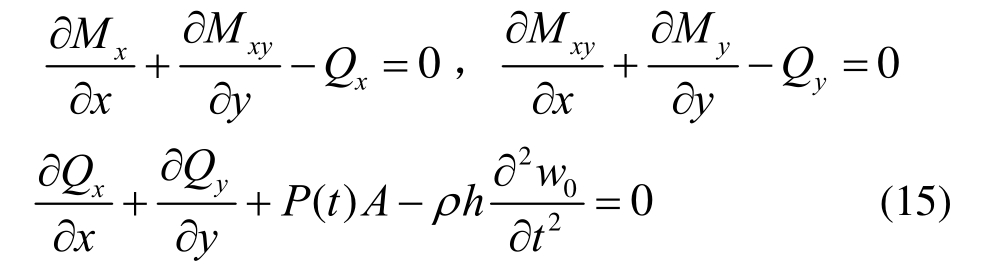
式中，Qx和Qy分别为与x轴和y轴垂直面所受的剪力。
将薄板所受弯矩代入式(14)和式(15)，经化简可得到声波载荷P(t)作用下无阻尼复合薄板的强迫振动微分方程为：
根据位移变分原理，振型Wmn需满足振型方程，即满足下列表达式：
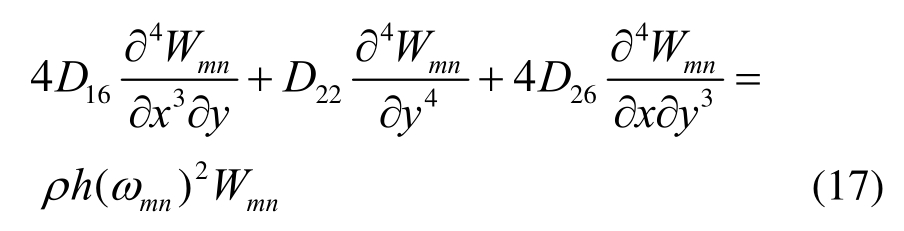
将式(17)代入式(16)，化简得：
将式(18)左右同时乘以Wcd(x,y)(其中c,d=1,2,3,··)，并沿x-y面积分，得：
利用复合薄板振型的正交性：
进一步，可将无阻尼情况下的广义振动微分方程表示为：
式中，Pmn(t)和Mmn分别为第(m,n)阶广义力和广义质量，他们各自的表达式分别为：
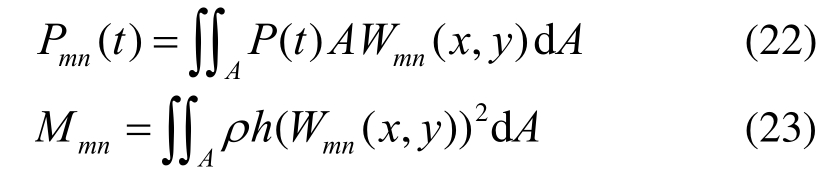
类似地，在假设小阻尼的情况下，可以将有阻尼情况下复合薄板的广义振动微分方程表示为：
式中，ζr为复合薄板的第r阶模态阻尼比。
根据模态阻尼比ξ和模态损耗因子η的关系，可以将模态损耗因子表示为：
根据模态应变能法，假设纤维纵向、纤维横向和剪切方向的模态应变能U1、U2和U12分别为：
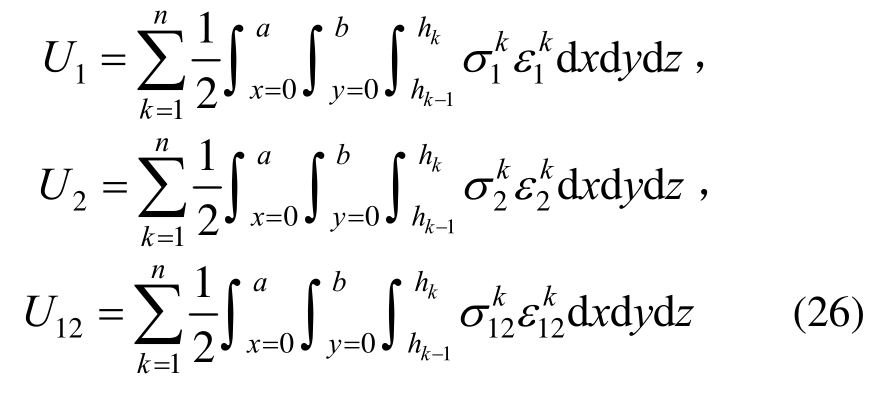
模态损耗因子和纤维各个方向的损耗因子有如下关系：
式中，Ut为薄板总的模态应变能。
在零初始条件下，式(28)的解可用杜哈梅(Duhamel)积分表示成如下形式：
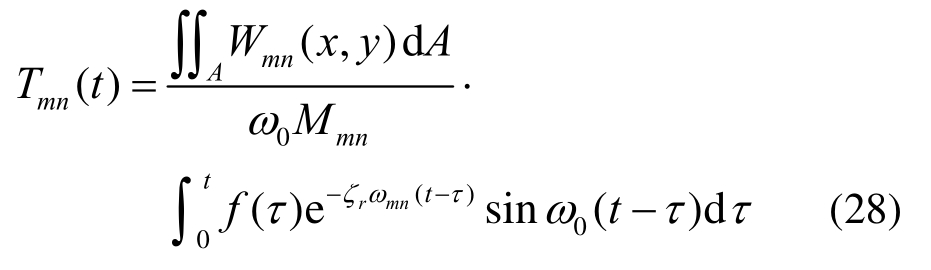
式中，ω0为有阻尼系统的角频率，其表达式为
利用Simpson数值积分法可求解式(28)，并再将其代回式(14)，即可采用振型叠加法求得平面脉冲声波P(t)激励下复合薄板的振动响应。
2 材料参数辨识原理
假设纤维增强复合材料参数未知或者不准确(虽然厂商可提供弹性模量和泊松比，但通常不能提供损耗因子，且该类型材料的分散性很大，再加上制备工艺的影响，即使在同一批次成型的材料，材料参数都可能相差很大)。下面，引入取值系数Rerr1和Rerr2，并以厂商提供的
为中心，考虑待求解弹性系数的最大和最小值，使其取值范围如下：
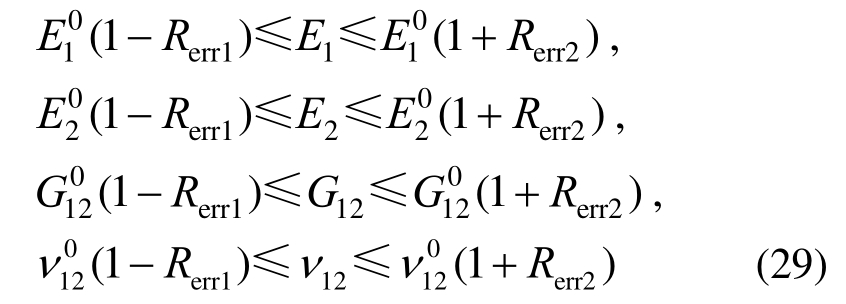
另外，由于纤维增强复合材料的损耗因子η1、η2、η12通常不超过5%，因此给出其取值范围为：
首先，利用粒子群算法[17]对材料的4个弹性系数E1、E2、G12和ν12进行迭代计算。将其作为该算法在4维目标搜索空间中由S个粒子组成的1个种群，即看作4×S维矩阵Q：
式中，第δ个粒子表示为1个4维向量Qδ为：
第δ个粒子的“飞行”速度也是1个4维向量，记为：
接下来，在粒子群算法迭代计算中，该粒子的位置和速度可根据下式进行更新：
式中：ts为当前迭代次数；c1和c2分别为自我和群体学习因子；r1和r2分别为在区间[0,1]内，服从均匀分布的随机数；
为第δ个粒子至今迭代搜索到的个体最佳位置，
为整个粒子群至今迭代搜索到的全局最佳位置。
一方面，假设可通过平面声波激励和非接触激光测振方式准确测试获得复合薄板的某阶固有频率
另一方面，利用在第1部分推导的求解公式，不断迭代计算理论固有频率fσ。当理论计算获得的固有频率的迭代误差efre达到设定值时(相对于测试结果)，则停止迭代计算。此时，可认为满足于迭代精度要求的E1、E2、G12、ν12便是辨识出的材料弹性系数。
式中：σ表示模态阶次；Rm为参与迭代计算的最大模态阶次。
类似地，根据粒子群算法，将材料在3个方向的损耗因子η1、η2和η12构造为S×3维矩阵R，其表达式为：
分别在相同的激励幅度和测点位置，对复合薄板的振动响应进行测试和计算。当计算获得的时域振动响应的峰峰值λψ，与测试响应的峰峰值
在设定的一段时间tn(假设包含多个时域峰值)内的误差erec满足迭代终止条件时，也停止计算。此时，可认为满足于迭代精度要求的η1、η2和η12便是辨识出的材料损耗因子。
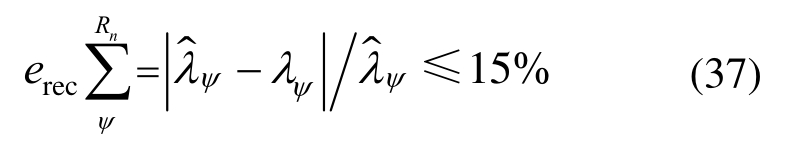
式中：ψ表示为第ψ个时域峰峰值；Rn为参与迭代计算的时域振动响应的峰峰值的最大个数。
3 辨识实例
以CF140碳纤维/环氧树脂复合材料薄板为例，如图2所示，对其材料参数进行辨识研究。该类型薄板为对称正交铺设，即[(0/90)s/0/(90/0)s]，共有21层，每个铺层具有相同的厚度和纤维体积分数，密度ρ=1778kg/m3，长、宽、厚尺寸为260 mm×130 mm×2.36 mm。
图2 复合材料薄板非接触激振-测振一体化测试系统
Fig.2 Non-contact vibration excitation-measuring integrated test system for composite thin plates
图2给出了复合材料薄板非接触激振-测振一体化测试系统，主要由平面式大功率扬声器、UTG 2025A信号发生器、VBA-202前置功率放大器、VBA-31000纯后级功率放大器、BK 2671声压传感器、Polytec PDV-100激光测振仪、LMS数据采集仪和笔记本电脑等组成。测试时，用两根轻质弹性绳将薄板悬挂，以模拟自由边界条件，如图2所示。接下来，调整声压传感器和激光测点的位置，用于测试激励信号和响应信号，并在信号发生器中设置脉冲信号的激励强度、持续时间等参数，经由两类功率放大器放大后，传输给大功率扬声器。该扬声器则会以能量充足的平面声波激励方式，激发被测薄板产生振动。通过数据采集仪和笔记本电脑，可分别记录和储存声波激励信号和响应信号的时域波形。
图3给出了在薄板下边位置处测试获得的平面声波脉冲激励信号的时域波形。实际中，用声压传感器共获得了9个测点位置对应的声波激励信号(按照3×3的网格划分原则进行确定，且经过线性平均处理后，需乘以薄板的面积才可获得计算激振力的大小)。图4给出了在激光测点位置获得的平面声波激振下复合薄板的时域响应信号。然后，基于VMD法对该时域响应信号进行分解处理，以前2阶固有频率辨识为例，图5和图6分别给出了分解后的包含第1阶和前2阶固有频率的时域波形及频谱图。表1给出了测试获得的前3阶固有频率结果。
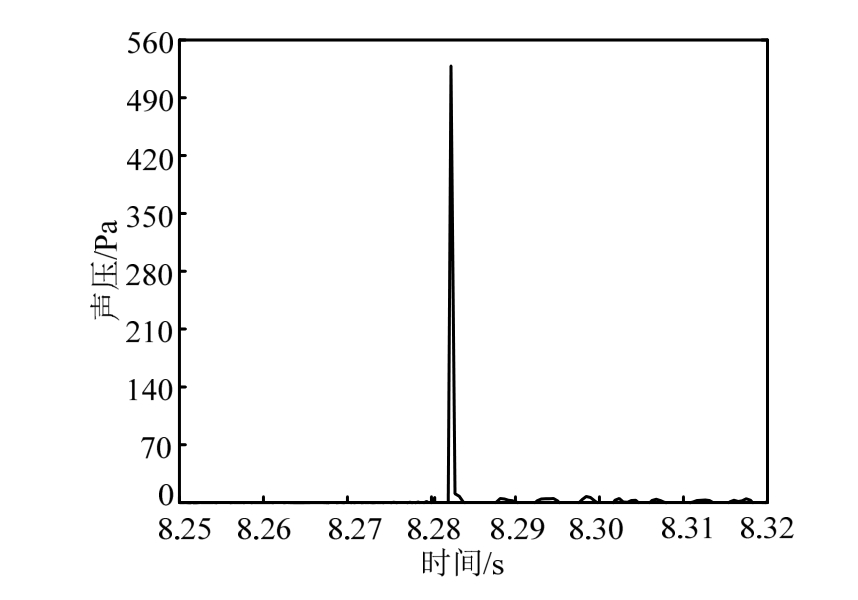
图3 测试获得的平面声波脉冲激励信号的时域波形
Fig.3 Time domain waveform of planar acoustic pulse excitation signal obtained by experimental test
图4 激光测点位置获得的时域振动响应信号
Fig.4 Time-domain waveform of the response signal obtained at the laser measuring point
图5 分解后获得的第1阶固有频率的时域波形及频谱
Fig.5 Time-domain waveform and spectrum with the 1st natural frequency obtained after decomposition
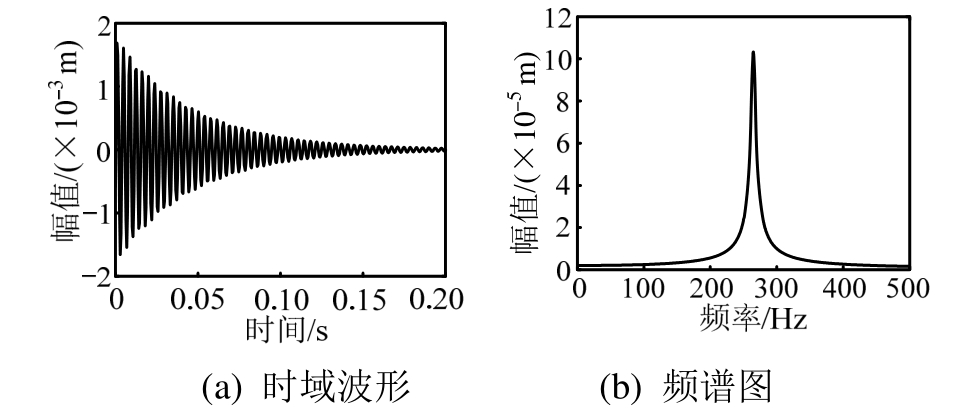
图6 分解后获得的第2阶固有频率的时域波形及频谱
Fig.6 Time-domain waveform and spectrum with the 2nd natural frequency obtained after decomposition
接下来，设定粒子群算法的迭代终止条件，并利用自行编写的MATLAB程序，分别在相同的激励幅度和测点位置，对平面声波激振下复合薄板的固有频率和振动响应开始进行迭代计算。图7给出了理论计算前3阶固有频率时迭代误差的收敛过程图，图8给出了最终迭代计算获得的理论与试验的时域振动响应。为了方便与测试结果比较，将最终迭代计算获得的复合薄板的前3阶固有频率及其误差也一并列入表1。
表1 测试及迭代计算获得的复合薄板的前3阶固有频率及误差
Table 1 The first 3 natural frequencies and errors of the composite thin plate obtained by testing and iterative calculation
模态阶次 1 2 3实验测试A/Hz 140.20 264.80391.00理论计算B/Hz 143.30 278.00401.90误差(%) |A―B| /A 2.21 4.98 2.79
图7 前3阶固有频率迭代误差的收敛过程图
Fig.7 Convergence process diagram of iterative error of the first 3 natural frequencies
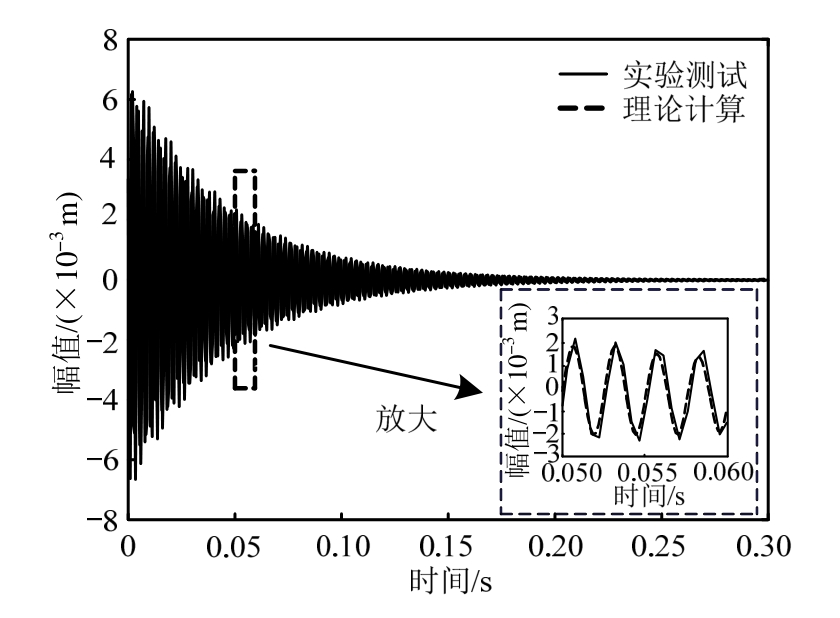
图8 理论迭代计算与实验测试获得的时域振动响应信号的对比图及放大图
Fig.8 The compared and enlarged pictures of time-domain vibration response signals obtained by theoretical iterative calculation and experimental test
最后，将理论计算后满足迭代终止条件要求的纤维纵向、横向及剪切方向的弹性模量、损耗因子及泊松比等材料参数列入表2。同时，在相同的表中还给出了厂家提供的纤维各个方向的弹性模量和泊松比结果，并对两者的偏差进行了比较。对上述结果进行分析可知，两种方法获得的时域振动响应波形吻合较好，且迭代计算获得的前3阶固有频率误差之和不超过10%。此外，辨识获得的材料参数相对于厂家提供的材料参数的最大偏差也不超过9.82%，基本上可以证明本文所提出的辨识方法的可靠性及相关算法的正确性。需要强调的是，利用该方法还可辨识获得材料在纤维纵向、横向和剪切方向的损耗因子(通常厂家利用疲劳试验机难以获得该项参数)。
表2 辨识获得的纤维增强复合材料参数及其与厂家提供的材料参数的偏差
Table 2 The identified material parameters and the related errors compared with the ones provided by the manufacturer
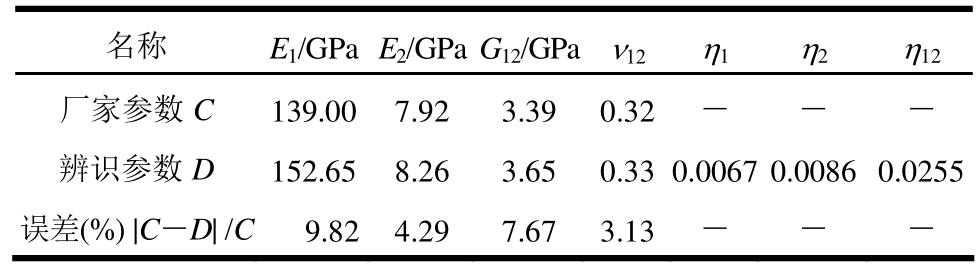
名称 E1/GPaE2/GPaG12/GPa ν12 η1 η2 η12厂家参数C 139.007.923.39 0.32 ― ― ―辨识参数D 152.658.263.65 0.33 0.0067 0.00860.0255误差(%) |C―D| /C9.824.297.67 3.13 ― ― ―
4 结论
本文采用理论与实践相结合的方式，研究了基于非接触激振-测振一体化技术的纤维增强复合材料参数的辨识方法。通过对CF140碳纤维/环氧树脂薄板进行实际辨识，并与厂家提供的材料参数进行对比后发现，两者在弹性模量、泊松比的偏差最大不超过9.82%，可以证明该辨识方法的可靠性。此外，利用该方法还可辨识出材料在纤维纵向、横向和剪切方向的损耗因子。本文的研究可以为复合材料参数的无损检测及识别提供一种新思路和新手段。
[1]Shokrieh M M, Lessard L B.Progressive fatigue damage modeling of composite materials, Part II: material characterization and model verification [J].Journal of Composite Materials, 2000, 34(13): 1081―1116.
[2]Navarro M, Ginebra M P, Planell J A, et al.In vitro degradation behavior of a novel bioresorbable composite material based on PLA and a soluble CaP glass [J].Acta Biomaterialia, 2005, 1(4): 411―419.
[3]吴振, 刘子茗.湿热力载荷下复合材料层合板力学行为[J].工程力学, 2016, 33(11): 11―19.Wu Zhen, Liu Ziming.Mechanical behaviors of laminated composite plate subjected to hygro-thermo-mechanical loading [J].Engineering Mechanics, 2016,33(11): 11―19.(in Chinese)
[4]Li H, Xue P, Guan Z, et al.A new nonlinear vibration model of fiber-reinforced composite thin plate with amplitude-dependent property [J].Nonlinear Dynamics,2018, 94(3): 2219―2241
[5]O’Dwyer D, O’Dowd N, Mccarthy C.Numerical micromechanical investigation of interfacial strength parameters in a carbon fibre composite material [J].Journal of Composite Materials, 2013, 48(6): 749―760.
[6]Michaud D J, Beris A N, Dhurjati P S.Thick-Sectioned RTM composite manufacturing: Part I - in situ cure model parameter identification and sensing [J].Journal of Composite Materials, 2002, 36(10): 1175―1200.
[7]Schultz A B, Tsai S W.Dynamic moduli and damping ratios in fiber-reinforced composites [J].Journal of Composite Materials, 1968, 2(3): 368―379.
[8]Araújo A L, Soares C M M, Freitas M J M D.Characterization of material parameters of composite plate specimens using optimization and experimental vibrational data [J].Composites Part B Engineering,1996, 27(2): 185―191.
[9]Visscher J D, Sol H, Wilde W P D, et al.Identification of the damping properties of orthotropic composite materials using a mixed numerical experimental method[J].Applied Composite Materials, 1997, 4(1): 13―33.
[10]Bledzki A K, Kessler A, Rikards R, et al.Determination of elastic constants of glass/epoxy unidirectional laminates by the vibration testing of plates [J].Composites Science & Technology, 1999, 59(13):2015―2024.
[11]Hwang.Identification of effective elastic constants of composite plates based on a hybrid genetic algorithm [J].Composite Structures, 2009, 90(2): 217―224.
[12]Matter M, Gmür T, Cugnoni J, et al.Numericalexperimental identification of the elastic and damping properties in composite plates [J].Composite Structures,2009, 90(2): 180―187.
[13]李双蓓, 周小军, 黄立新, 等.基于有限元法的正交各向异性复合材料结构材料参数识别[J].复合材料学报,2009, 26(4): 197―202.Li Shuangbei, Zhou Xiaojun, Huang Lixin, et al.Material parameter identification for orthotropic composite by the finite element method [J].Acta Materiae Composite Sinica, 2009, 26(4): 197―202.(in Chinese)
[14]Ng Y C.Deriving composite lamina properties from laminate properties using classical lamination theory and failure criteria [J].Journal of Composite Materials, 2005,39(39): 1295―1306.
[15]李晖, 梁晓龙, 常永乐, 等.纤维增强复合薄板非线性内共振表征测试方法研究[J].工程力学, 2018, 35(11):197―205, 222.Li Hui, Liang Xiaolong, Chang Yongle, et al.Study on characterization test method of nonlinear internal resonance of fiber-reinforced composite thin plate [J].Engineering Mechanics, 2018, 35(11): 197―205, 222.(in Chinese)
[16]薛鹏程, 李晖, 常永乐, 等.悬臂边界下纤维增强复合材料薄板固有频率计算及验证[J].航空动力学报,2016, 31(7): 1754―1760.Xue Pengcheng, Li Hui, Chang Yongle, et al.Natural frequency calculation and validation of fiber reinforced composite thin plate under cantilever boundary [J].Journal of Aerospace Power, 2016, 31(7): 1754―1760.(in Chinese)
[17]Jiang S, Wang Y, Ji Z.A new design method for adaptive IIR system identification using hybrid particle swarm optimization and gravitational search algorithm[J].Nonlinear Dynamics, 2015, 79(4): 2553―2576.