钢桥由于重量较轻、跨越长度大、施工便捷等优点被广泛使用，桥面沥青铺装层作为钢桥面板与车辆轮胎接触的结构层，其性能的好坏直接影响铺装层的使用状态，同时还会危及钢桥的耐久性与安全性。由于钢桥柔度大，力学响应较为复杂，在车辆荷载作用下部分铺装层很快就出现较为严重的病害。同时，钢桥面沥青铺装层相比于普通沥青路面，其病害类型具有自身显著的特点，主要表现为铺装层表面疲劳开裂和层间滑移[1]。因此，有必要建立车辆、沥青铺装层和钢桥之间的耦合动力学模型，对车桥耦合下钢桥面沥青铺装层的动力响应问题进行深入研究。
对于车桥耦合下动力响应的研究，最早由Willis等[2]提出将车辆模拟为一个常质量，并得到匀速运动车辆与简支梁耦合下动力响应的近似解。Kriloff、Timoshenko、Biggs等[3－5]在其基础上进行演化，将车辆分别模拟为移动常量力模型、周期荷载模型和移动簧上质量模型，得到相应车桥耦合下的动力响应。随着计算机时代的来临，学者们逐步开始建立更为复杂的车桥耦合模型，并采用数值模拟方式求解分析。项海帆等[6]将车辆模拟为由弹簧和阻尼器组成的体系，由此建立车桥耦合下简支梁桥的放大谱。Li等[7]将车桥耦合振动响应分为静态响应与动态响应，以此方法对车辆的加速度响应和桥梁的挠性响应进行了定性的推导。徐勋倩[8]将车辆等效为2自由度、5参数模型，将钢桥面等效为梁-板结构，研究了不同车速、桥面不平顺等级和桥面损伤程度下车辆荷载对铺装层的动力效应。Deng等[9]采用有限元软件将桥梁和车辆荷载分别模拟成不同类型的网格，分别得到桥梁跨径、车速以及桥面不平度的动态影响因子表达式，以此为依据对AASHTO规范中公式进行修正。Liu等[10]采用有限元模型进行模拟，并采用隐式Euler向后算法进行求解，最终得到双轮荷载作用下钢桥面板的非弹性响应。蔡军哲等[11]采用5自由度的重车车辆模型，并用160个梁单元模拟简支梁桥，对桥梁结构振动的位移弯矩响应进行了研究。Rezaiguia等[12]利用Fortran语言进行计算，研究了多跨连续正交异性桥面在卡车荷载作用下的响应。Gao等[13]对三跨变截面连续梁桥的车桥耦合振动进行动力响应分析。Yang等[14]通过研究得到在不考虑轨道不平顺的情况下，车辆的侧倾对桥梁响应的影响一般可以忽略的结论。İsmail Esen[15]采用1/4车模型与Euler-Bernoulli梁进行建模，在建模时考虑Euler-Bernoulli梁的前四阶振型，利用振型叠加法得到车桥动力响应。谭子翼等[16]采用Euler-Bernoulli梁，结合模态坐标分析法，对车桥耦合的动力响应进行分析，此方法考虑了桥梁的几何非线性。Zhou等[17]研究了简谐波激励下车桥耦合系统的非线性动力学行为。经薇等[18]在前人研究的基础上建立车桥耦合模型，分别从时域和频域分析，得到多车相比于单车对桥梁产生的振动作用更加强烈的结论。李慧乐等[19]基于车桥耦合系统随机振动分析，得到一种对于铁路钢桥疲劳可靠度的评估方法。谢伟平等[20]对“公轨合一”型高架桥进行了汽车-列车-桥梁耦合振动分析，为桥梁设计作出参考。李岩等[21]提出一种时变维度的随机车流与桥梁耦合振动分析方法，拓展了车桥振动整体分析方法的适用范围。
综上，对于车桥耦合下动力响应的研究已基本形成完善体系，但很少有学者将铺装层作为车桥耦合模型的一部分，来研究钢桥面沥青铺装层的动力响应。因此，建立简化且符合实际振动的车辆-沥青铺装层-钢桥耦合动力学模型，来研究钢桥面沥青铺装层的车桥耦合动力响应特性和规律十分必要。
本文在已有研究基础上，以双轴车为例，合理考虑车辆在桥面上的运动，铺装层和钢桥间的相互作用关系，支座对钢桥的支撑作用以及轮胎与铺装层表面的接触模型，建立车辆-沥青铺装层-钢桥耦合动力学模型。并基于现场测试结果验证程序计算结果的准确性和可靠性，进而分析车辆类型、后轴轴重、行车速度、桥梁跨径和桥面宽度对铺装层表面应变幅值和钢板与沥青铺装层间最大剪应力的影响。
1 耦合动力学模型的建立
1.1 建模思路
车辆通过钢桥时，一方面钢桥受到激励产生振动，反过来钢桥的振动对车辆也产生激励，两者相互耦合形成一个系统。整个系统分为三大部分：车辆振动模型、沥青铺装层-钢桥振动模型以及车辆-沥青铺装层相互作用关系。
在建立车辆振动模型时，将车体模拟为刚体，并以匀速进行运动，采用弹簧和阻尼器并联的方式模拟出车辆的悬架与轮胎，同时考虑车辆行驶过程中车体的侧倾、点头、垂向运动以及轮胎的垂向运动。沥青铺装层-钢桥振动模型中，假定其在水平方向上无间断，考虑到沥青铺装层-钢桥结构的宽高比，并考虑到钢桥支座的刚度远大于铺装层与钢板的刚度，同时为简化模型减小计算量，将钢桥面沥青铺装层与钢板视为支撑于粘弹性支座上的双层连续粘弹性薄板模型，其中上层为铺装层，下层为钢桥面板。车辆-沥青铺装层的相互作用关系以铺装层表面不平度为激励，并假设车辆轮胎与铺装层表面之间为点接触。
以7自由度的双轴六轮车为例，其振动模型如图1所示。模型中，v为车辆行驶速度；Mc为车体满载质量；Jc为车辆点头惯量；Ic为车辆侧倾惯量；Zc为车辆竖向位移；βc为车辆点头位移；φc为车辆侧倾位移；li(i=1,2,3,4)分别为各轴至车辆质心的距离；df、dri(i=1,2)分别为前、后轴轮距的1/2；Kci(i=1,2,3,4)、Cci(i=1,2,3,4)分别为各悬架弹簧刚度和阻尼；Kti(i=1,2,3,4)、Cti(i=1,2,3,4)分别为各车轮轮胎刚度和阻尼；Mwi(i=1,2,3,4)分别为各车轮质量；Zwi(i=1,2,3,4)分别为车轮竖向位移；L、W分别为桥梁长度与宽度；wp(x,y,t)为桥面竖向位移；Pti(i=1,2,3,4)分别为各轮胎接地压力；Ep1为铺装层弹性模量；μp1为铺装层泊松比；χp1为铺装层粘滞阻尼系数；ρp1为铺装层质量密度；hp1为铺装层厚度；Ep2为钢板等效弹性模量；μp2为钢板等效泊松比；χp2为钢板等效粘滞阻尼系数；ρp2为钢板等效质量密度；hp2为钢板等效厚度；Ks为桥梁支点等效竖向刚度；Cs为桥梁支点等效竖向阻尼。
1.2 车辆振动模型
根据达朗贝尔理论，车辆的振动方程为：
式中：Mc、Cc和Kc分别为车辆的质量矩阵、阻尼矩阵和刚度矩阵；
和Zc分别为集中质量的加速度、速度和位移；Fc为车辆自重矢量；Ft为车轮与桥面间垂向作用力矢量，详见文献[22―23]。
图1 车辆-沥青铺装层-钢桥耦合动力学模型
Fig.1 Dynamics model of coupled vehicle-bridge deck asphalt pavement-steel bridge
1.3 沥青铺装层-钢桥振动模型
车辆荷载作用下钢桥面沥青铺装层垂向振动微分方程式为：
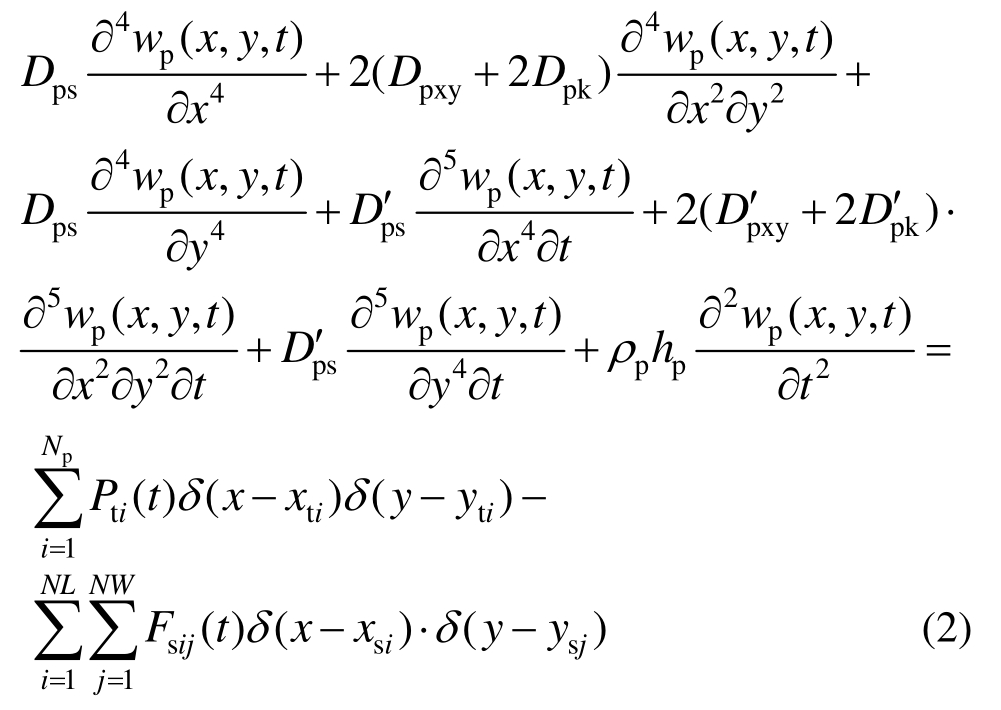
其中：
式中：Np为作用在钢桥面沥青铺装层上荷载的数量；NL、NW分别为x、y向离散支点数；Pti为车辆荷载对桥面的垂向作用力，
分别为各轮胎振动位移；qwi(i=1,2,3,4)分别为各轮胎对应铺装层表面不平度位移；wpi(i=1,2,3,4)分别为各轮胎对应铺装层表面振动位移；
分别为各轮胎垂向振动速度；
分别为各轮胎质心下铺装层表面不平度速度；
分别为各轮胎质心下铺装层表面垂向振动速度；Fsij为t时刻钢桥支座的竖向支撑力
为桥面竖向振动速度；xti、yti分别为钢桥面上第i个荷载的纵、横坐标；xsi、ysj分别为钢桥下第i个支点的纵、横坐标
为弹性抗弯刚度，根据式(4)计算[24]；
为阻尼抗弯刚度，根据式(5)计算[24]。
式中，Gpi(i=1,2)分别为铺装层与钢板的剪切模量。
为了模拟车辆在钢桥面沥青铺装层上的运动状态，建立匀速移动车辆坐标，沥青铺装层-钢桥的受力分析模型见图2。
模型中，沥青铺装层-钢桥上的固定坐标为ox，以速度v匀速运动的移动坐标为o′x′。t时刻两坐标转换关系为：
式中：x0为初始时刻后轴距原点的水平距离；y0为初始时刻后轴左侧轮胎距原点的水平距离；df和dr分别为前轴和中、后轴的轮距的1/2。
图2 沥青铺装层-钢桥受力分析模型
Fig.2 Mechanical analysis model of bridge deck asphalt pavement-steel bridge
钢桥两侧各支点坐标为：
式中：ls为x向离散间距；lw为y向离散间距。
利用Ritz法将式(2)简化，并采用双向梁函数组合级数逼近法对矩形板的振动进行分析[24]，其振型表示为：
式中：Xm(x)为钢桥面沥青铺装x向的振型函数；Yn(y)为钢桥面沥青铺装y向的振型函数。
本文以常见简支梁为例，钢桥采用x方向简支、y方向自由的边界条件，因此钢桥面沥青铺装的垂向位移表示为：
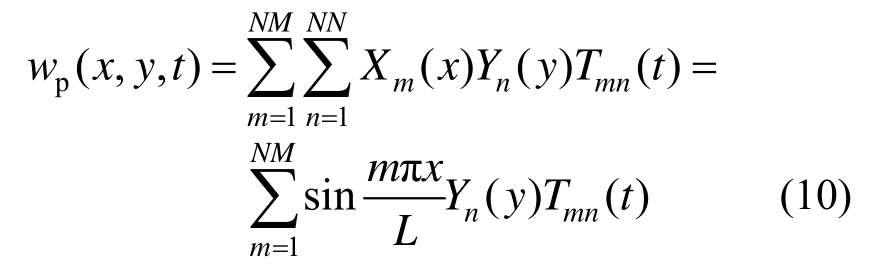
其中：
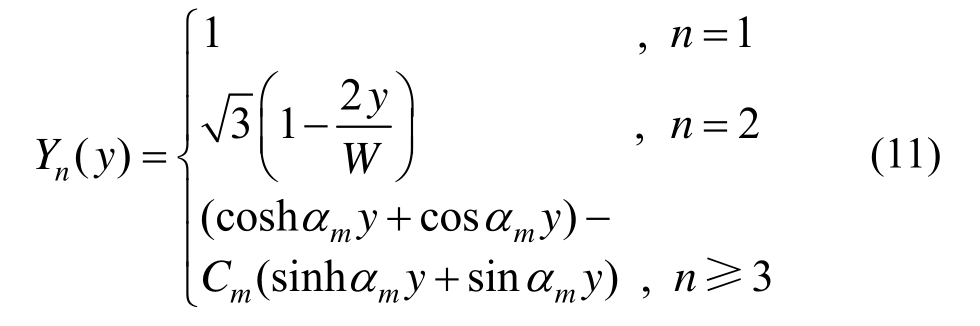
式中：Tmn为正则坐标；NM、NN分别为x、y方向模态阶数；αm为频率系数，由式(12)计算；Cm为函数系数，由式(13)计算。
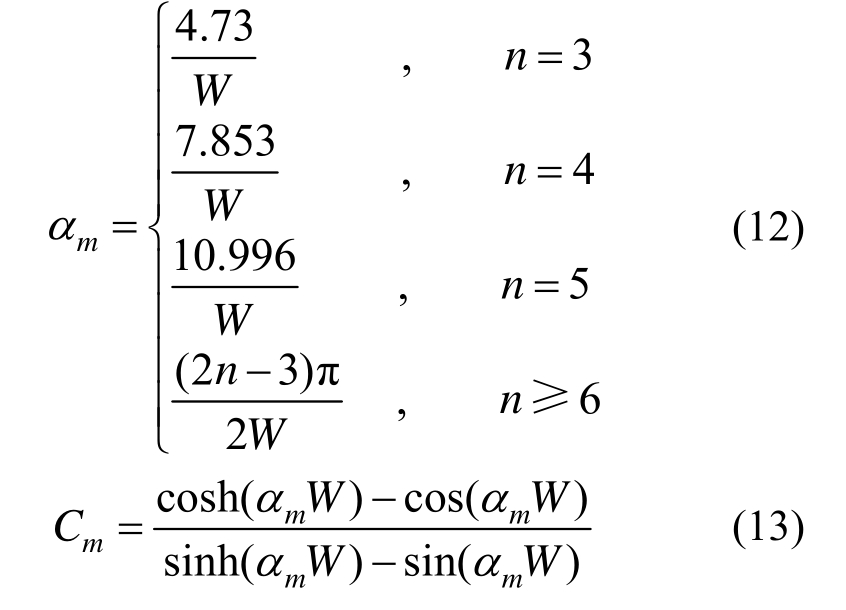
将式(10)代入式(2)，整理后得到正则坐标下钢桥面沥青铺装垂向振动的二阶常微分方程为：
1.4 铺装层表面不平顺激励
铺装层表面不平度作为模型的附加激励，其计算的准确性会影响模型的最终结果，我国采用功率谱密度来描述其特性，其位移及速度功率谱密度应分别采用式(15)和式(16)表示[25]。
式中：n/m-1为空间频率；n0为参考空间频率，取n0=0.1；w为频率指数，取w=2；Gd/m3为铺装层表面不平度系数。
16×10 -6 m3、64×10-6 m3、256×10-6 m3和1024×10-6 m3分别为A、B、C和D级铺装层表面不平度系数，根据文献[26]，可采用MATLAB模拟，分别获得铺装层表面不平度空间分布曲线。
1.5 求解模型
将式(1)和式(14)联立后，得到车辆-沥青铺装层-钢桥耦合动力学模型矩阵形式的振动方程，可表述为：
式中：M、C和K分别为车辆-沥青铺装层-钢桥系统质量、阻尼和刚度矩阵；
、X和
分别为系统的加速度、速度和位移；P为系统载荷。
采用Wilson-θ法求解式(17)，并确定θ=1.4时满足计算精度要求，其求解步骤见文献[22]。
2 模型验证
2.1 测试概况
刘秀[27]对采用单车经过的方式，对沈阳市后丁香大桥四号桥上61 m跨的中点断面进行振动检测。四号桥为连续钢箱梁桥，主梁平均高度为3 m，桥梁表面采用ERS树脂沥青组合铺装体系，具体铺装层结构自上而下分别为：40 mm高粘高弹沥青玛蹄脂碎石混合料SMA-13，热喷聚合物改性沥青粘层，30 mm树脂沥青混凝土RA05和环氧粘结碎石抗滑层EBCL。
试验汽车采用前轴为单轮、中轴后轴为双轮的三轴十轮东风普通载货车EQ1166G2，其轮距均为2 m，前轴与中轴轴距为5.8 m，中、后轴间轴距为1.2 m。
2.2 结果比较
假定铺装层表面不平度取A级，沥青铺装层-钢桥的离散尺寸为1 m×1 m，仿真与时间步长均为5.0×10-4 s。车辆模型参数根据实际测试车辆信息并参考文献[23]选取，具体数值见表1。
钢桥及铺装层模型的几何及力学参数根据经验并参考文献[1]进行选取，具体数值见表2。由于四号钢桥为三室箱梁结构，但模型为双层实心板结构，因此应对钢桥的厚度、弹性模量、质量密度、两端支撑弹簧刚度和阻尼进行数值等效。
将采样点位置设为车辆右侧轮迹线与桥梁跨中的交点，采用46 km/h的行车速度进行模拟，得到该点沥青铺装层表面的位移时程曲线。铺装层表面位移时程曲线的实测值与计算值如图3所示，由图3可得，钢桥表面实测振动位移峰值为4.6 mm，计算得到的位移峰值为4.1 mm，相对误差为11%。计算的位移时程曲线与实测曲线结果基本相同，两者振动形状相似。
表1 测试车辆计算参数
Table 1 Calculation parameters of testing vehicle
项 目 数 值车身重量/kN 200车辆长度/m 11.4前悬/m 1.3后悬/m 3.1轴距/m 5.8/1.2轮距/m 2前轴悬架刚度/(N/m) 242 604前轴悬架阻尼/(N·s/m) 800前轴轮胎质量/kg 200前轴轮胎刚度/(N/m) 875 082前轴轮胎阻/(N·s/m) 500中、后轴悬架刚/(N/m) 1 903 172中、后轴悬架阻尼/(N·s/m) 1 500中、后轴轮胎质量/kg 400中、后轴轮胎刚度/(N/m) 3 503 307中、后轴轮胎阻尼/(N·s/m) 1000
表2 钢桥及铺装层参数
Table 2 Parameters of steel bridge and bridge deck pavement
项 目 数 值钢桥等效尺寸/m 61×20×0.1钢桥等效弹性模量/GPa 0.21钢桥泊松比 0.3钢桥等效质量密度/(kg/m3) 5 000钢桥质量粘滞阻尼系数 0钢桥等效两端支撑弹簧刚度/(N/m) 1×1011钢桥等效两端支撑阻尼/(N·s/m) 1×105桥面铺装层厚度/mm 70桥面铺装层弹性模量/GPa 2桥面铺装层泊松比 0.25桥面铺装层质量密度/(kg/m3) 2 000桥面铺装层粘滞阻尼系数 0.1
采用FFT频谱分析的方法对钢桥铺装层表面位移时程曲线数据进行变换，可以得到铺装层表面位移频谱分析如图4所示。由图4可以看出，钢桥的实测一阶自振频率为2.97 Hz，而计算所得频率为3.09 Hz，相对误差0.4%，说明根据所建模型得到的时程曲线和频谱分析曲线具有正确性和可靠性。
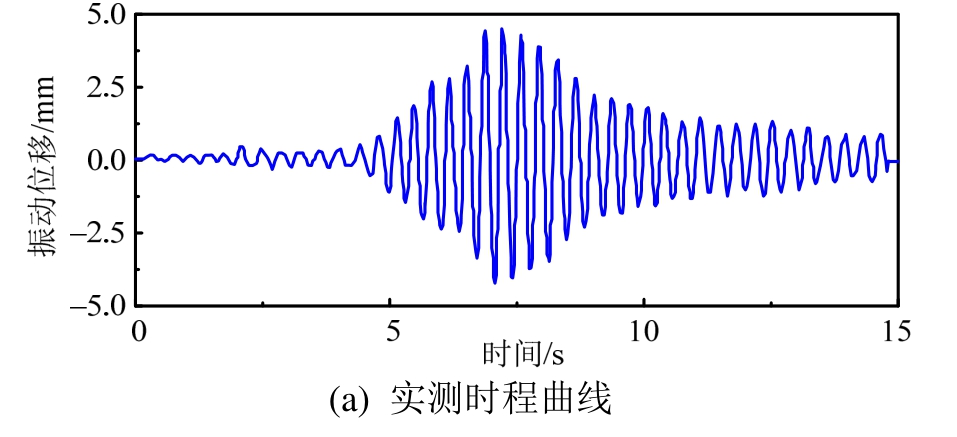
图3 钢桥铺装层表面位移时程曲线
Fig.3 Time history curves of surface displacement of steel bridge deck pavement
图4 钢桥铺装层表面位移频谱分析曲线
Fig.4 Spectrum analysis curves of surface displacement of steel bridge deck pavement
经过分析，时程曲线和频谱分析曲线的误差主要源自：1) 计算中采用的车辆模型虽根据实际测试车辆并参考文献选取，但其在数值上与实测车辆参数仍不是完全一致，而且模型参数的非线性也存在影响。2) 计算中假设桥面不平度为A级，与实际情况仍存在一定区别。3) 由于实测值为车辆经过48 m+61 m+38 m的三跨连续钢桥，但为简化计算量，模型中只考虑车辆经过中跨61 m时的情况，因此两者在形状、时间、位移峰值和振动位移幅值上存在偏差。
3 动力响应分析
以典型双轴六轮车为例，其计算参数见表3，桥梁及铺装层参数见表2，同时取模型离散间距为1 m×1 m，仿真与积分步长为5.0×10-4 s。分别分析车辆类型、后轴轴重、行车速度、桥梁跨径和桥面宽度对铺装层表面应变幅值和钢板与沥青铺装层间最大剪应力的影响规律。
表3 车辆计算参数
Table 3 Calculation parameters of vehicle
项 目 数 值前轴悬架刚度/(N/m) 242 604前轴悬架阻尼/(N·s/m) 800前轴轮胎质量/kg 200前轴轮胎刚度/(N/m) 875 082前轴轮胎阻尼/(N·s/m) 500后轴悬架刚度/(N/m) 1 903 172后轴悬架阻尼/(N·s/m) 1 500后轴轮胎质量/kg 400后轴轮胎刚度/(N/m) 3 503 307后轴轮胎阻尼/(N·s/m) 1000
3.1 车辆类型的影响
对于1+2型、1+5型、1+1+5型、1+5+5型和1+5+7型车辆(车辆类型说明具体见表4)，当后轴轴重为100 kN，以速度60 km/h匀速行驶在铺装层表面不平度为A级，跨径60 m、宽度20 m的钢桥上时，车辆类型对轮胎接地压力放大倍数、铺装层表面应变幅值和层间最大剪应力的影响如图5所示。
表4 车辆类型说明
Table 4 Description of vehicle type
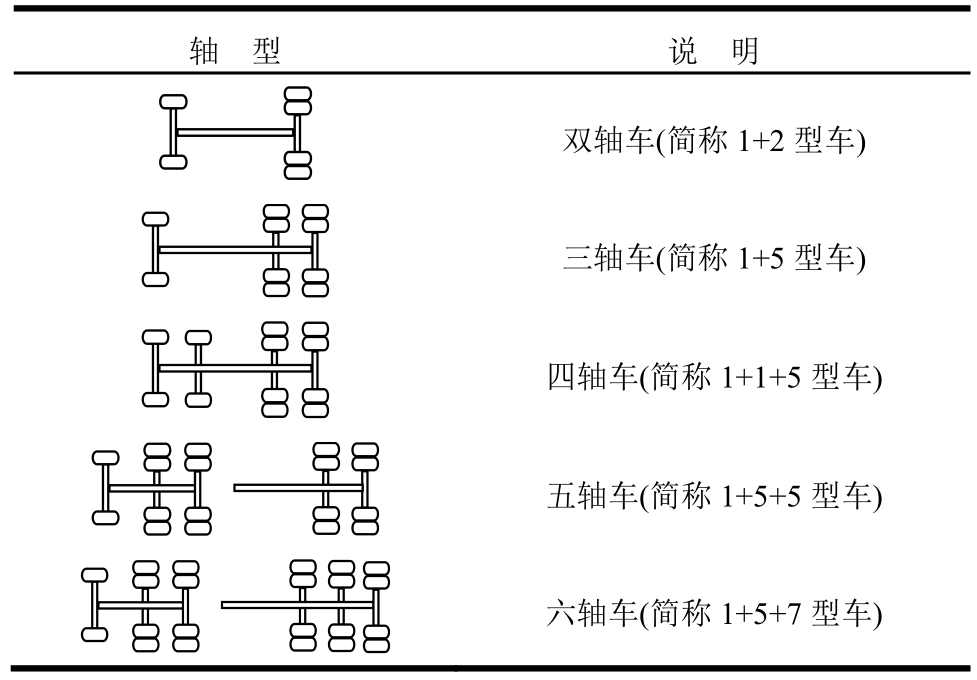
轴 型 说 明双轴车(简称1+2型车)三轴车(简称1+5型车)四轴车(简称1+1+5型车)五轴车(简称1+5+5型车)六轴车(简称1+5+7型车)
轮胎接地压力放大倍数是轮胎动态压力与静态压力的比值。由图5(a)可见，各车辆类型对应的轮胎接地压力放大倍数相差不大，但1+2型车所对应的数值最小为1.83倍，1+1+5型车所对应的数值最大为2.18倍。同时，所有车辆类型的轮胎接地压力放大倍数均大于1，即车辆动态行驶过程中，轮胎接地力大于其所分配的静态压力，可以看出车辆动力作用与静力作用的区别。由图5(b)可知，随着车辆轴数的增加，应变幅值和最大剪应力的数值都不断增大。具体来说，随着车辆轴数的增加，铺装层表面应变幅值增大了1.8倍，而钢板与铺装层间最大剪应力增大了1.7倍。
图5 车辆类型对轮胎接地压力放大倍数、铺装层表面应变幅值和层间最大剪应力的影响
Fig.5 Influences of vehicle type on amplification factor of tire pressure, surface strain amplitude of pavement and maximum shear stress between bridge deck pavement and steel plate
3.2 后轴轴重的影响
以双轴车为例，图6(a)和图6(b)分别为后轴轴重对铺装层表面应变幅值和对钢板与沥青铺装层间最大剪应力的影响。可以看出，整体上两者数值都随后轴轴重的增加而不断增大。发生此现象的原因为，随着后轴轴重的增加，车身重量也不断增加，这会导致车辆对桥梁的作用不断增大，桥梁的动力响应也随之增大。
同时可见，随着后轴轴重的不断增大，铺装层表面应变幅值从52.94με增加到185.2με，增大了2.5倍左右，而铺装层与钢板间的最大剪应力从0.35 MPa增大到了1.14 MPa，增长为原来的2.3倍。说明后轴轴重对铺装层表面应变幅值及钢板与铺装层间最大剪应力的影响较大。
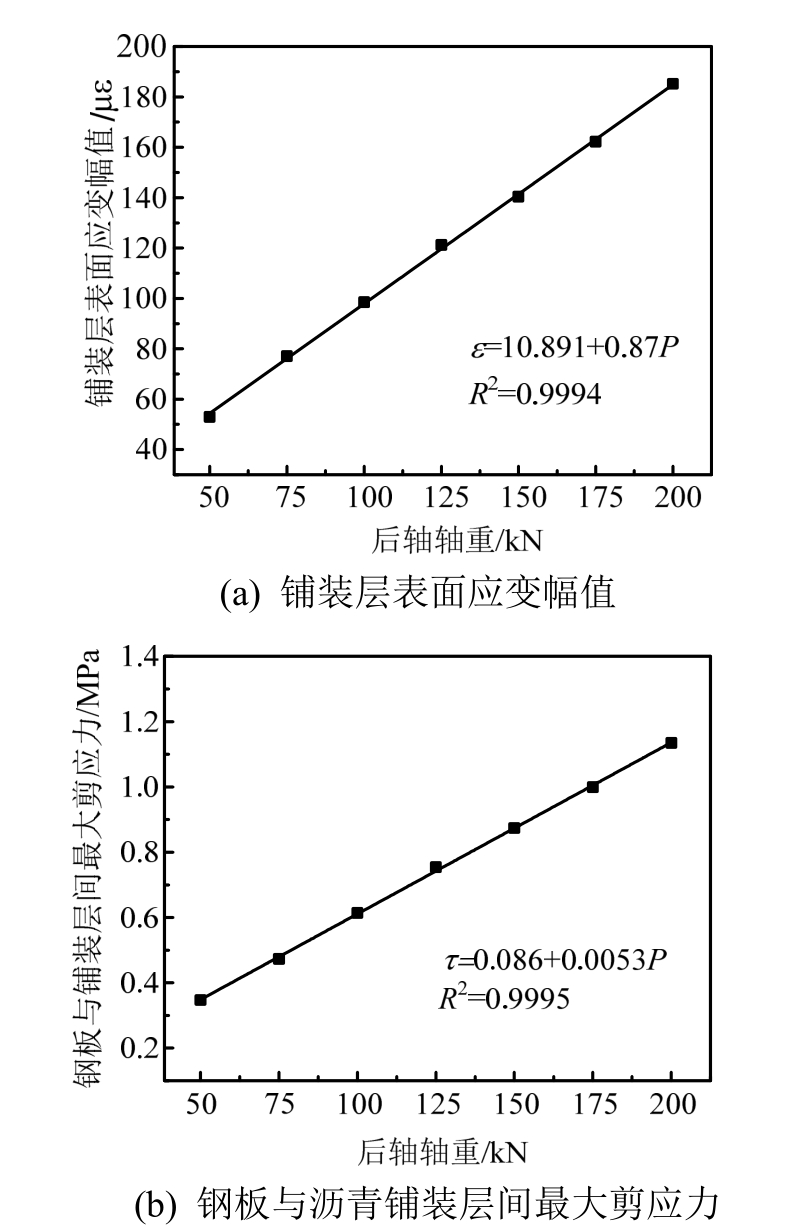
图6 后轴轴重对铺装层表面应变幅值和钢板与沥青铺装层间最大剪应力的影响
Fig.6 Influences of rear axis load on surface strain amplitude of pavement and maximum shear stress between bridge deck pavement and steel plate
3.3 行车速度的影响
同样以双轴车为例，得到行车速度与铺装层表面应变幅值、钢板与沥青铺装层间最大剪切应力的关系图，如图7所示。
可以看出，行车速度对铺装层表面应变幅值及铺装层和钢板间最大剪应力的影响较为复杂。随着行车速度的增大，两者的数值不断上下波动。但在车速为60 km/h时两者数值均达到最大，70 km/h时数值均达到最小。同时除这两个行车速度以外，当车辆以其他速度行驶时，两种动力响应在数值上相差较小，尤其在20 km/h～50 km/h的低速区间行驶时，基本可忽略行车速度带来的影响。并且当车辆以高于80 km/h的速度行驶时，两种动力响应的变化规律基本相同。
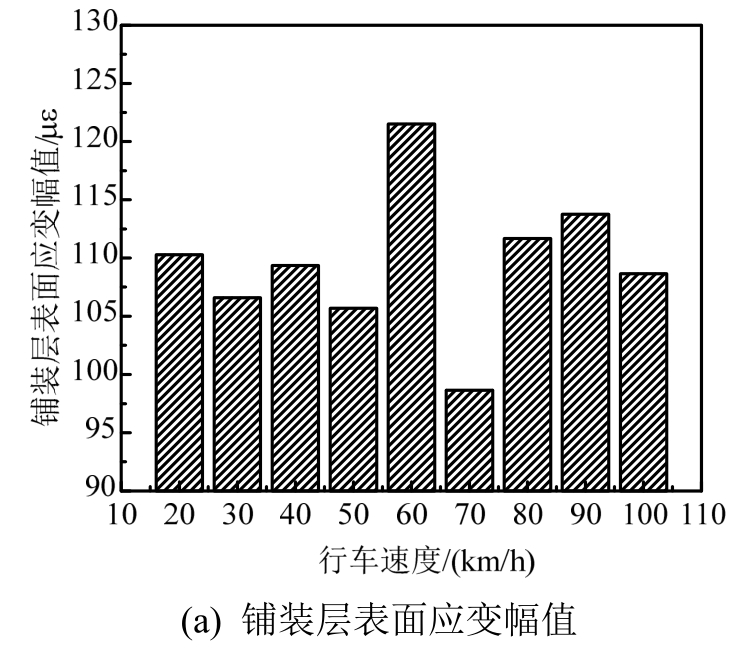
图7 行车速度对铺装层表面应变幅值和钢板与沥青铺装层间最大剪应力的影响
Fig.7 Influences of running speed on surface strain amplitude of pavement and maximum shear stress between bridge deck pavement and steel plate
3.4 桥梁跨径的影响
图8(a)为桥梁跨径对铺装层表面应变幅值的影响。由图8(a)可见，随着桥梁跨径的不断增大，铺装层表面应变幅值呈现出增大的趋势，且呈幂函数规律进行变化。随着桥梁跨径的不断增大，铺装层表面应变幅值由0.916 με增加至121.514 με，增大幅度高达132倍。图8(b)为桥梁跨径对钢板与沥青铺装层间最大剪应力的影响。由图8(b)可见，当桥梁跨径从30 m增大到60 m时，钢板与铺装层间的最大剪应力同样呈幂函数趋势增加，由0.0195 MPa增大至0.79 MPa，增大了40倍，可见桥梁跨径对钢桥面沥青铺装层的动力响应影响非常之大。
同时，随着桥梁跨径从30 m增大到60 m的过程中，铺装层表面位移峰值也不断增大，由0.0204 cm增大到1.776 cm。其原因在于，当车辆通过跨径较小的钢桥时，其对桥梁的作用时间相比于以相同行车速度行驶的车辆通过跨径较大钢桥时的作用时间较为短暂，因此对桥梁产生的动力响应较小。
图8 桥梁跨径对铺装层表面应变幅值和钢板与沥青铺装层间最大剪应力的影响
Fig.8 Influences of bridge span on surface strain amplitude of pavement and maximum shear stress between bridge deck pavement and steel plate
另外，当桥梁跨径分别为30 m、40 m、50 m和60 m时，采用傅里叶变换的方法计算出铺装层表面位移峰值时程曲线的一阶优势频率分别为2.78 Hz、2.5 Hz、2.38 Hz和2.22 Hz，如图9所示。说明桥梁的自振频率与铺装层表面位移峰值和桥梁跨径呈现出相反的变化趋势。
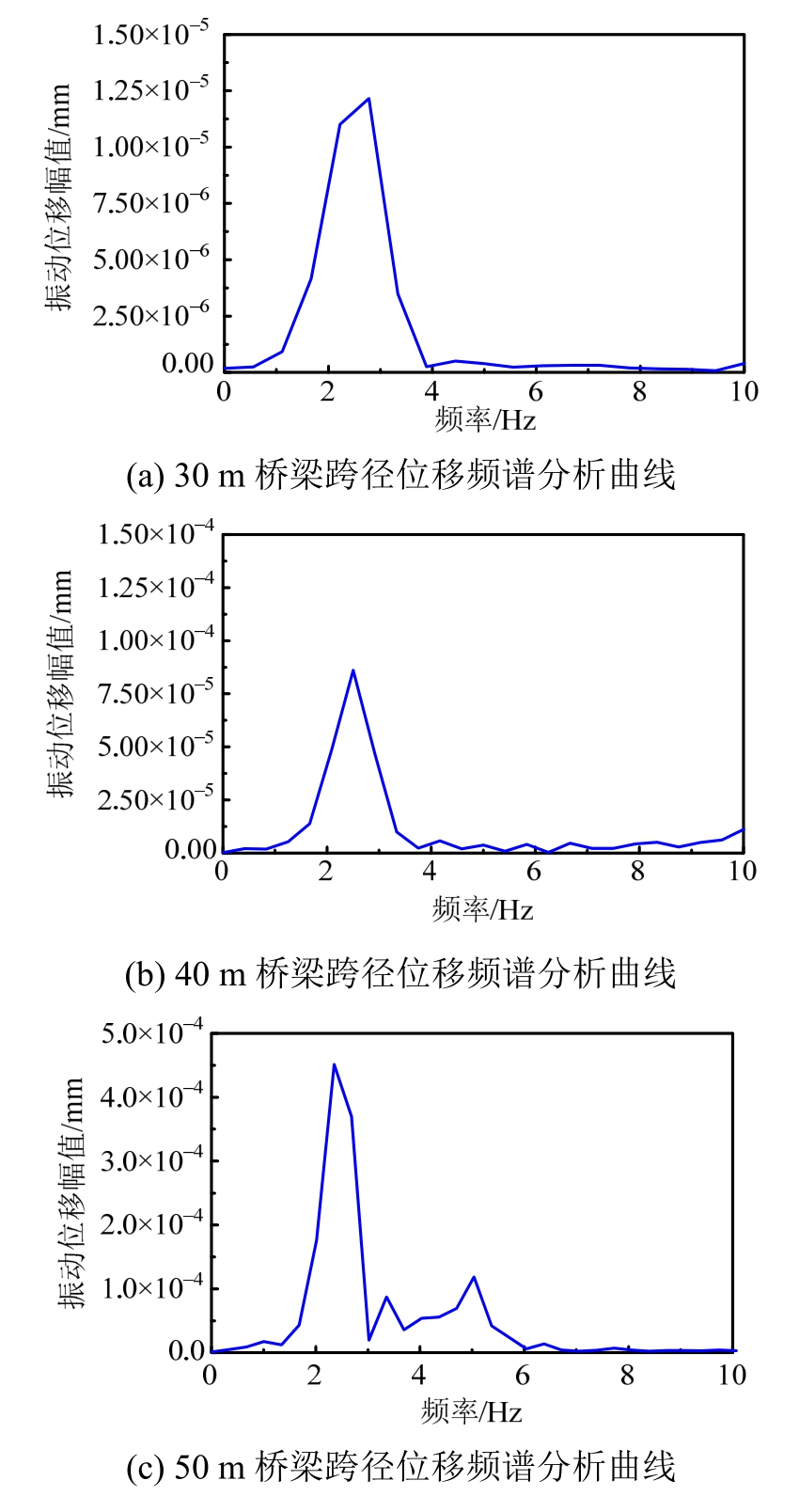
图9 不同跨径的位移频谱曲线
Fig.9 Displacement spectrum curves of different span
3.5 桥面宽度的影响
图10(a)为桥面宽度对铺装层表面应变幅值的影响。由图10(a)可见，随着桥面宽度的不断增大，铺装层表面应变幅值逐渐减小，且呈指数函数关系进行变化。随着桥面宽度不断增大，铺装层表面应变幅值由246.53με减小至19.23με，减小幅度为92.2%。
图10(b)为桥面宽度对钢板与沥青铺装层间最大剪应力的影响。由图10(b)可见，当桥面宽度从10 m增大到40 m的过程中，钢板与沥青铺装层间最大剪应力同样呈指数函数变化趋势，其数值由2.01 MPa减小至0.241 MPa，减小幅度为88%，可见桥面宽度对铺装层表面应变幅值以及钢板与沥青铺装层间最大剪应力的影响较大。
图10 桥面宽度对铺装层表面应变幅值和钢板与沥青铺装层间最大剪应力的影响
Fig.10 Influences of bridge width on surface strain amplitude of pavement and maximum shear stress between bridge deck pavement and steel plate
同时，当桥面宽度分别为10 m、20 m、30 m及40 m时，铺装层表面位移峰值时程曲线的一阶优势频率分别为2.21 Hz、2.22 Hz、2.76 Hz及2.76 Hz，如图11所示。说明桥面宽度与桥梁一阶自振频率的变化趋势相同。
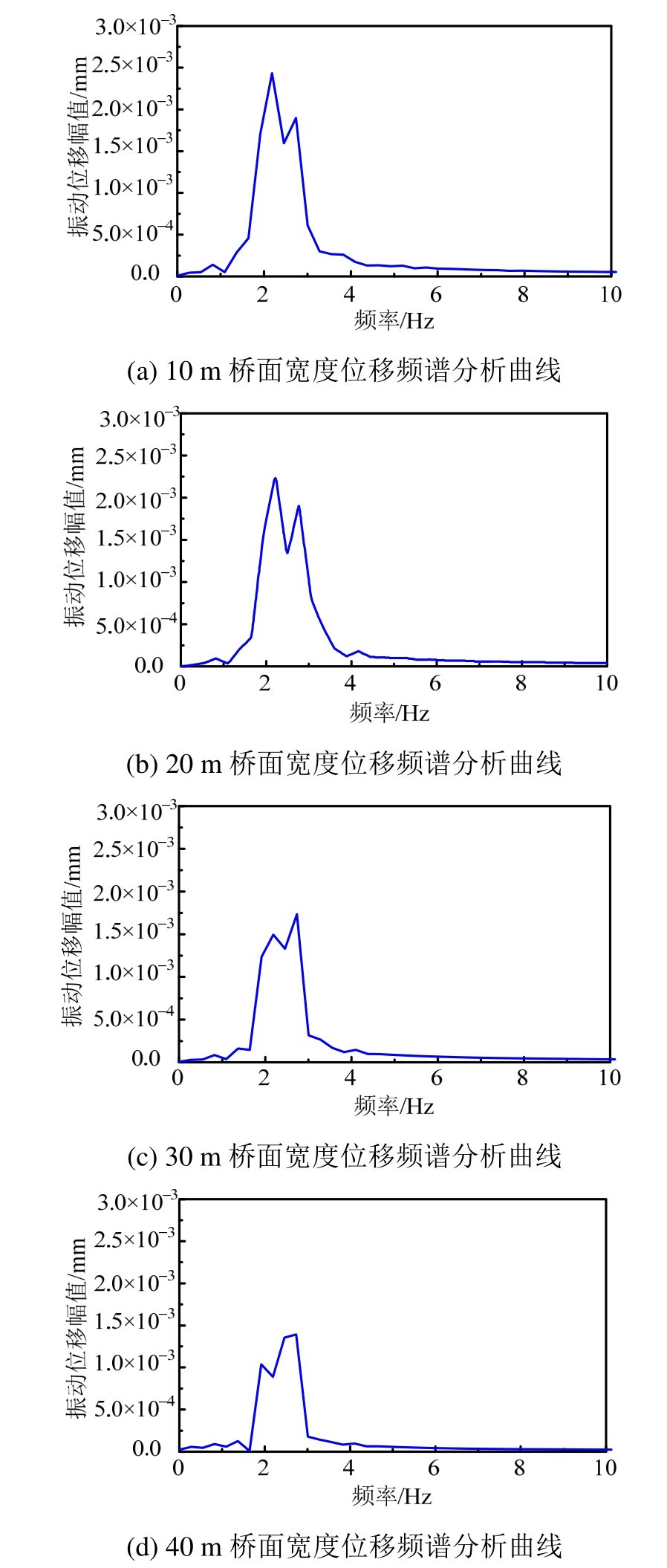
图11 不同宽度的位移频谱曲线
Fig.11 Displacement spectrum curves of different bridge width
4 结论
(1)建立车辆-沥青铺装层-钢桥耦合动力学模型，并采用Wilson-θ法求解，结果表明，根据该模型得到的时程曲线和频谱分析曲线具有较高的正确性和可靠性。
(2)所有车型的轮胎接地压力均大于其所分配的静压力，且四轴车的数值最大，可达到2.18倍。同时随着车辆轴数的增加，铺装层表面应变幅值和钢板与铺装层间最大剪应力均逐渐增大。双轴车后轴轴重从50 kN增大到200 kN的过程中，铺装层表面应变幅值和铺装层与钢板间的最大剪应力均有较大增长，前者增大为原来的2.5倍左右，后者增大了2.3倍。随着车速的增加，铺装层表面应变幅值以及铺装层与钢板间最大剪应力上下波动变化，但在车速为60 km/h时两者数值均达到最大。
(3)桥梁跨径对铺装层表面应变幅值和铺装层与钢板间最大剪应力的影响非常大，尤其对铺装层表面应变幅值的影响更为显著。桥面宽度由10 m增加到40 m时，铺装层表面应变幅值和铺装层与钢板间最大剪应力均呈指数函数逐渐减小，前者减小幅度为92.2%，后者减小幅度为88%。
[1]Liu X, Zhou C, Feng D, et al.Experimental study on interlayer shear properties of ERS pavement system for long-span steel bridges [J].Construction & Building Materials, 2017, 143: 198―209.
[2]Wrottesley, Robert Willis, Henry James, et al.Report of the commissioners appointed to inquire into the application of iron to railway structures [J].Civil Engineering, 1849, 19(5): 289―302.
[3]Kriloff A.Über die erzwungenen Schwingungen von gleichförmigen elastischen Stäben [J].Mathematische Annalen, 1905, 61(2): 211―234.
[4]Timoshenko S P.On the forced vibrations of bridges [J].Philosophical Magazine, 1922, 43(257): 1018―1019.
[5]John M.Biggs Introduction to structural dynamics[M].New York: McGraw-Hill, 1964: 315―323
[6]项海帆, 毛清华.车辆荷载作用下简支梁桥振动的研究[J].同济大学学报, 1989, 17(4): 457―465.Xiang Haifan, Mao Qinghua.Research on simply supported beam bridge vibration due to vehicular loads[J].Journal of Tongji University, 1989, 17(4): 457―465.(in Chinese)
[7]Li J Q, Leng X L, Fang T.Evolutionary random response problem of a coupled vehicle-bridge system [J].Archive of Applied Mechanics, 2002, 72(6/7): 536―544.
[8]徐勋倩.车-钢桥面铺装耦合振动系统动力效应分析[J].应用力学学报, 2009, 26(3): 501―506.Xu Xunqian.Dynamic analysis of coupled vibration system for vehicle and steel bridge deck surfacing [J].Chinese Journal of Applied Mechanics, 2009, 26(3):501―506.(in Chinese)
[9]Deng L, Cai C S.Development of dynamic impact factor for performance evaluation of existing multi-girder concrete bridges [J].Engineering Structures, 2010, 32(1):21―31.
[10]Liu X, Medani T O, Scarpas A, et al.Characterization of surfacing materials for orthotropic steel deck bridges.Part 2: Numerical work [J].International Journal of Pavement Engineering, 2010, 11(3): 255―265.
[11]蔡军哲, 何伟, 边陇超, 等.车-桥耦合振动的动力响应分析[J].大连交通大学学报, 2015, 36(4): 22―26.Cai Junzhe, He Wei, Bian Longchao, et al.Dynamic response study of vehicle-bridge coupling vibration [J].Journal of Dalian Jiaotong University, 2015, 36(4): 22―26.(in Chinese)
[12]Rezaiguia A, Ouelaa N, Laefer D F, et al.Dynamic amplification of a multi-span, continuous orthotropic bridge deck under vehicular movement [J].Engineering Structures, 2015, 100: 718―730.
[13]Gao Q, Wang Z, Liu C, et al.Dynamic responses of a three-span continuous girder bridge with variable cross-section based on vehicle-bridge coupled vibration analysis [J].Ies Journal Part A Civil & Structural Engineering, 2015, 8(2): 121―130.
[14]Yang Y B, Chang C H, Yau J D.An element for analyzing vehicle-bridge systems considering vehicle's pitching effect [J].International Journal for Numerical Methods in Engineering, 2015, 46(7): 1031―1047.
[15]İsmail Esen.Analysis of vehicle bridge dynamic interaction using quarter car model [C]// 1st International Conference on Engineering Technology and Applied Sciences.Turkey: Afyon Kocatepe University, 2016.
[16]谭子翼, 唐雪松, 盛国刚.车桥耦合系统的非线性动力响应分析[J].长沙理工大学学报(自然科学版),2016, 13(1): 49―55.Tan Ziyi, Tang Xuesong, Sheng Guogang.Analysis of the nonlinear dynamic behavior of the bridge under moving load system [J].Journal of Changsha University of Science & Technology, 2016, 3(1): 49―55.(in Chinese)
[17]Zhou S, Song G, Ren Z, et al.Nonlinear dynamic analysis for coupled vehicle-bridge system with harmonic excitation [J].Meccanica, 2017, 52(9): 2219―2243.
[18]经薇, 李松, 李强, 等.多车车桥耦合振动特性研究[J].科学技术与工程, 2017, 17(6): 111―116.Jing Wei, Li Song, Li Qiang et al.The characteristics of multi-vehicle bridge coupling systems research [J].Science Technology & Engineering, 2017, 17(6): 111―116.(in Chinese)
[19]李慧乐, 夏禾.基于车桥耦合随机振动分析的钢桥疲劳可靠度评估[J].工程力学, 2017(2): 75―83.Li Huile, Xia He.Fatigue reliability evaluation of steel bridges based on coupling random vibration analysis of train and bridge [J].Engineering Mechanics, 2017(2):75―83.(in Chinese)
[20]谢伟平, 刘亨.城市轨道交通“公轨合一”型高架桥车桥耦合振动分析[J].工程力学, 2016, 33(2): 119―126.Xie Weiping, Liu Heng.Vehicle-bridge interaction analysis of a super bridge in urban railway system [J].Engineering Mechanics, 2016, 33(2): 119―126.(in Chinese)
[21]李岩, 吴志文, 蔡明, 等.一种随机车流与桥梁耦合振动的分析方法[J].哈尔滨工业大学学报, 2018, 50(3):46―52.Li Yan, Wu Zhiwen, Cai Ming, et al.An analysis method for coupled vibration random traffic flow and bridge [J].Journal of Harbin Institute of Technology, 2018, 50(3):46―52.(in Chinese)
[22]李梦琪.基于车桥耦合振动效应的钢桥面沥青铺装层轴载换算方法[D].哈尔滨: 哈尔滨工业大学, 2018:16―28.LI Mengqi.Axle load conversion method for steel deck asphalt pavement based on coupling vibration effect of vehicle-bridge [D].Harbin: Harbin Institute of Technology, 2018: 16―28.(in Chinese)
[23]张锋, 冯德成, 凌贤长, 等.重载汽车-路面-路基垂向耦合动力学模型[J].中国公路学报, 2015, 28(4): 1―12.Zhang Feng, Feng Decheng, Ling Xianzhang, et al.Vertical coupling dynamics model of heavy truck-pavement-subgrade [J].China Journal of Highway & Transport, 2015, 28(4): 1―12.(in Chinese)
[24]曹志远.板壳振动理论[M].北京: 中国铁道出版社,1989: 13―59.Cao Zhiyuan.Vibration theory of plate and shell [M].Beijing: China Railway Press, 1989: 13―59.(in Chinese)
[25]GB/T 7031―2005, 机械振动道路路面谱测量数据报告[S].2005.GB/T 7031―2005, Mechanical vibration-road surface profiles-reporting of measured data [S].2005.(in Chinese)
[26]刘献栋, 邓志党, 高峰.公路路面不平度的数值模拟方法研究[J].北京航空航天大学学报, 2003, 29(9):843―846.Liu Xiandong, Deng Zhidang, Gao Feng.Research on the method of simulating road roughness numerically [J].Journal of Beijing University of Aeronautics & Astronautics, 2003, 29(9): 843―846.(in Chinese)
[27]刘秀.寒区沥青混凝土铺装体系力学分析与试验研究[D].哈尔滨: 哈尔滨工业大学, 2016: 125―131.Liu Xiu.Mechanical analysis and experimental study on asphalt pavement system on steel bridges in cold region[D].Harbin: Harbin Institute of Technology, 2016: 125―131.(in Chinese)