钢板剪力墙作为一种相对较新的抗侧力结构具有用钢量小、抗侧刚度大、延性好、自重轻、占用面积小、经济性好等众多优点。早期的厚钢板剪力墙由于耗钢量太大,目前已很少使用[1-2]。从20世纪80年代开始,薄钢板剪力墙成为北美地区应用的主要类型[2-3]。薄钢板剪力墙的抗侧依赖于墙板屈曲后形成的拉力场(图1(a)),研究发现其滞回曲线存在着捏缩现象、耗能能力欠理想(图1(b)),同时拉力场的反作用力可能造成柱子发生整体或者局部破坏[3-7](图1(c))。由于传统的薄钢板剪力墙存在的问题,现行的《高层民用建筑钢结构技术规程》(JGJ 99―2015)[7]将非加劲薄钢板剪力墙的应用范围限于非抗震结构以及抗震要求较低的4类高层民用钢结构。

图1 薄钢板剪力墙的抗侧性能
Fig.1 Lateral-load-resisting performance of thin plate steel shear wall
自20世纪80年代以来,国际上对钢板剪力墙的受力性能进行了大量的研究[2-4]。针对传统薄钢板剪力墙存在的问题,研究人员从抑制墙板的屈曲、降低拉力场对周边梁柱的不利影响出发提出了多种解决方案。其中,带竖缝钢板剪力墙[8-13]通过在薄钢板剪力墙上开设若干平行竖缝,将墙板分成众多狭长的缝间钢板小柱(图2(a)),从而将侧向荷载作用下墙板的剪切变形转化为缝间钢板小柱的弯曲变形,利用缝间钢板小柱端部的塑性变形来获得优良的抗震性能(图2(b))。
尽管,类似的思路在带竖缝钢筋混凝土剪力墙中获得了很大的成功,但是由于缝间钢板小柱的刚度和强度不足,带竖缝钢板剪力墙的实际性能与预期存在很大的差距,试验中甚至发现其延性比普通薄钢板剪力墙差[2,9-10],这给这种钢板剪力墙的实用性带来了许多质疑[2]:1) 由于竖缝的开设,剪力墙的抗侧刚度和承载力大大降低,对高层结构在风和多遇地震下的侧移控制非常不利,因此不能作为结构的主要抗侧力结构[2],一般只能承担10%~25%的基底剪力[13];2) 由于缝间钢板小柱的平面外弯曲和扭转刚度小,在两端形成塑性铰之前易发生弯扭失稳破坏[2](图2(c);3) 由于缝间钢板小柱的两侧边自由,面外约束弱,需要采用较厚的钢板(文献[9]建议宽厚比取8~14)才能满足局部稳定性的要求。


图2 带竖缝钢板剪力墙的受力性能[8]
Fig.2 Lateral-load-resisting performance of thin plate steel shear wall
借鉴带竖缝钢筋混凝土和钢板剪力墙的思路,本文提出了一种新型带竖向缝隙的矩形钢管排柱剪力墙结构[1](简称新型钢管排柱剪力墙)。新型钢管排柱剪力墙采用矩形钢管横向排列成排,相邻钢管之间利用连接焊缝相连,形成剪力墙整体结构(基本形式见图3)。竖向缝隙均设置在相邻钢管之间,可简单地在制作中通过间断预定区域的连接焊缝实现。在竖向缝隙高度范围内,两相邻竖向缝隙之间的矩形钢管形成缝间钢管小柱。

图3 新型剪力墙构成及几何参数示意图
Fig.3 Composition and geometric parameters of SWSS
新型钢管排柱剪力墙利用密排的矩形钢管作为墙板,将墙板的剪切变形转化为缝间钢管小柱的弯曲变形,可以为剪力墙提供足够的平面外抗弯刚度;通过性能化设计,可以保证缝间钢管小柱端部塑性铰的形成先于墙板的平面外失稳、缝间钢管小柱的平面外失稳以及钢管壁的局部失稳,从而防止墙板的剪切失稳和屈曲后拉力场的形成,避免对周边框架梁柱产生的附加荷载。与带竖缝钢板剪力墙相比,新型钢管排柱剪力墙采用矩形钢管代替钢板条作为缝间小柱,可以显著提高缝间小柱的平面外弯曲和扭转刚度,避免缝间小柱在端部的塑性变形过程中发生弯扭失稳,确保剪力墙获得理想的滞回耗能能力;可以大大提高缝间小柱的平面内弯曲刚度和截面塑性抵抗矩,有效提高剪力墙的抗侧刚度和承载能力;矩形钢管截面的翼缘和腹板可以相互提供约束作用,有利于板件的局部稳定性。
本文通过有限元分析,对这种新型剪力墙的抗侧性能进行分析和验证,并在此基础上提出各主要性能参数的计算方法,以期为相关的研究提供参考。
1 新型剪力墙的抗侧性能
1.1 计算模型及参数确定
新型钢管排柱剪力墙的各项参数如图3所示,包括墙高H,钢管截面高度hs,宽度bs,钢管壁厚度t,连接焊缝高度l,缝间小柱高度h和缝间小柱个数m。参考常用民用建筑的层高,计算模型中取剪力墙的高度H=3200 mm,总宽度为B=mhs。考虑到实际完成后墙体厚度在200 mm左右较为合适,取剪力墙厚度(即钢管截面宽度)bs=160 mm。
相邻钢管间连接焊缝的高度,按照对接焊缝计算为:
式中:![]() 为焊缝的抗剪强度设计值;V为每条焊缝所承担的剪力。假定相连钢管之间仅翼缘和腹板交界处位置相连,根据小柱端部形成塑性铰时的弯矩Mp计算获得:
为焊缝的抗剪强度设计值;V为每条焊缝所承担的剪力。假定相连钢管之间仅翼缘和腹板交界处位置相连,根据小柱端部形成塑性铰时的弯矩Mp计算获得:

按式(2)计算所得焊缝高度l的下限值lmin如表1所示。对各算例统一取焊缝高度l=600 mm,此时小柱高度h=2000 mm。
为了保证缝间小柱端部形成塑性铰先于小柱平面外失稳、墙板平面外失稳和钢管壁局部失稳,对新型钢管排柱剪力墙的各项参数应进行性能化设计。钢结构设计规范(GB 50017―2017)[14]指出,对于受弯截面,S1级和S2级两种截面均可以达到全截面塑性的要求,其中S1级截面可以获得较大的塑性转动能力,而S2级截面的塑性变形能力有限。根据规范[14],S1级截面的腹板和翼缘的宽厚比限值分别为65和25,S2级截面的宽厚比限值分别为72和32。本文按照S1级和S2级分别设计了算例(表1),其中SW8和SW6按S1截面设计,SW5按S2截面设计,SW5-6与SW5基本相同,仅两外侧钢管按S1级截面加厚。表1中λw为腹板宽厚比,λf为翼缘宽厚比,λw,R和λf,R分别为按照规范[14]计算获得的这两个参数的取值。
表1 模型几何参数
Table 1 Geometric parameters of specimens

算例 钢管截面长度hs/mm钢管截面宽度bs/mm钢管壁厚t/mm腹板宽厚比λw规范中腹板宽厚比限值λw,R翼缘宽厚比λf规范中翼缘宽厚比限值λf,R焊缝高度l/mm焊缝高度下限值lmin/mm SW5 5 70 30 318.2 S2∶72S2∶32 SW5-6 5(6)70(58)377.2 SW6 6 58 24.7 316.0 SW8 360 160 30(24.7)600 S1∶65S1∶25 8 4318311.6
分析采用ABAQUS有限元软件,考虑大变形和材料弹塑性。其中,剪力墙的钢管采用4节点单元S4R,这是一种双曲线带有沙漏控制的减缩积分通用壳单元,可用于大变形和大应变分析。框架梁柱均采用3节点二次空间梁单元(B32)。钢管材料的应力-应变采用理想弹塑性本构模型(屈服强度取fy=235 N/mm2,弹性模量E=206000 N/mm2)。为了避免外框架本身的受弯对结构抗侧性能的影响,将框架梁柱节点和柱底均设为铰接,同时出于收敛性考虑取框架梁柱的材料为线弹性。相邻钢管之间的连接通过绑定约束(tie)连接焊缝高度范围内相邻钢管角部位置的节点来模拟。边界条件如图4所示,其中对梁节点约束其平面外平动(y方向)自由度以及绕自身轴(x方向)转动自由度,对柱节点约束其绕自身轴(z方向)转动自由度,以消除结构整体和构件本身的刚体运动。水平荷载采用位移加载,单向加载时加载至柱顶侧移达到200 mm(侧移角6.25%),施加往复荷载时根据《建筑试验抗震规程》(JGJ 101―2015)[15]以屈服位移的倍数为各级荷载增量,每级循环3次,直至位移达到6倍屈服位移。

图4 边界条件
Fig.4 Boundary condition
计算分析中,外框架的柱截面选用□600×600×30,梁截面选用H650×300×16×10。为了评估外钢框架对剪力墙抗侧性能的影响,本文以SW6为例采用不同的框架梁柱截面(表2)来分析这一影响。分析表明,框架梁的抗弯刚度对结构的抗侧性能有一定的影响(图5(a)),特别是当侧移比较大时,框架梁刚度的增大有利于结构维持较高的后期承载能力,但由于梁柱节点和柱底均为铰接,框架柱对抗侧能力的影响非常有限(图5(b))。
考虑实际工程中,楼板对梁刚度的提高作用,同时避免不同框架梁对剪力墙抗侧性能的影响,在下面的分析中采用框架5(表2)的梁截面,同时在剪力墙的顶面加刚性面,使得整个剪力墙顶面的竖向位移保持一致,这样实际上是将框架梁的抗弯刚度取为无穷大。
表2 周边框架梁柱模型
Table 2 Cross-sections of beams and columns

ID 梁截面 柱截面 有无刚性面框架1H300×150×16×10框架2H650×300×16×10框架3H1200×600×16×10□ 600×600×30 无框架4□ 400×400×20框架5□ 600×600×30框架6 H650×300×16×10有□ 800×800×40


图5 框架梁柱截面对抗侧性能的影响
Fig.5 Influence of beam and column sections on lateral-load-resisting performance
1.2 有限元模型验证
由于目前未有新型钢管排柱剪力墙的试验结果,本文通过与带竖缝剪力墙的现有研究来验证有限元模型的可靠性。
文献[16]在试验结果的基础上进行了有限元分析,模型K1以试验试件SPWS III-2(框架-带缝钢板剪力墙)为原型,只施加水平荷载进行水平推覆分析。
利用与上述新型剪力墙建模类似的方法对试件SPWS III-2进行建模,试件SPWS III-2的组成和部分几何参数见图6,墙板厚度12 mm,钢板开缝缝宽12 mm,梁柱截面见表3,材料参数按材性试验结果取值,如表3所示。如图7所示为本文有限元分析得到了剪切荷载(Q)-位移(d)曲线其与文献[16]的对比,可见两者非常吻合,由此可以说明本文有限元方法的可靠性。

图6 文献[16]算例示意图
Fig.6 Composition and geometric parameters of SPWS III-2
表3 框架梁柱截面及材料参数取值
Table 3 Cross-sections of beams and columns and measured mechanical properties

构件 截面 屈服应力fy /MPa梁 H400×200×8×13 424.0柱 □ 350×350×12 423.3钢板 — 271.4

图7 有限元结果比较
Fig.7 Comparison of load-displacement curves
1.3 弹性稳定分析
现有部分研究通过将剪力墙仅与横梁连接来消除墙板对框架柱的附加作用力,但是这种连接方式会使得墙板的两侧自由边极易发生失稳,通常需要在墙板两侧设加劲肋[17-18]。文献[19]的研究也表明,带竖缝钢板剪力墙的两侧边需采取合理的加强措施才能避免过早发生弹性失稳。由于新型钢管排柱剪力墙的两侧边为矩形钢管,具有较大的平面外刚度,因而无须再设加劲肋。
利用特征值方法对剪力墙进行弹性稳定性分析,结果显示新型剪力墙的弹性稳定均由钢管壁的局部稳定性控制(表4,图8),这与带竖缝剪力墙的墙板整体平面外失稳或缝间墙肢的弯扭失稳这两种主要失稳模式不同[9]。这主要是由于新型钢管排柱剪力墙的缝间小柱的截面为箱型截面,具有很大的平面外弯曲和抗扭刚度,不易发生弯扭失稳。由表4可知,算例SW5、SW6和SW8的局部屈曲均发生在边缘位置的钢管的接近端部的位置(角部位置),这是因为水平剪力会在剪力墙中合成一个倾覆弯矩,这一倾覆弯矩会在剪力墙中产生两侧大中间小分布的竖向应力(图9),因此易在边缘钢管的端部附近形成较大的主压应力。考虑这一因素,算例SW5-6中将算例SW5的两边缘钢管的厚度增加到6 mm,结果显示剪力墙的弹性稳定性获得了显著提高(临界荷载提高了44%),并且局部失稳的位置转移到由外向内的第2根钢管的端部位置附近。可见,对于新型剪力墙来说,加强边缘钢管对提高剪力墙的稳定性是非常有效的。
表4 剪力墙的弹性屈曲
Table 4 Elastic buckling of SSWS

算例 临界荷载/kN屈曲模态SW5 5430.18 角部局部屈曲SW5-6 7889.36 边缘钢管内侧相邻钢管端部附近局部屈曲SW6 9312.88 角部局部屈曲SW8 21784.3 角部局部屈曲

图8 剪力墙的1阶屈曲模态
Fig.8 First buckling mode of SSWS

图9 线弹性分析下剪力墙SW6竖向应力分布
Fig.9 Vertical stress distribution of SW6 obtained by linear elastic analysis
1.4 弹塑性抗侧与滞回性能
1.4.1 弹塑性抗侧性能
考虑大变形和弹塑性的影响,对表1中各算例进行了单调弹塑性抗侧分析。结果表明,剪力墙的变形主要来自缝间小柱的平面内弯曲变形:在加载的初始阶段,缝间小柱主要发生弹性弯曲变形,变形形式与两端转动约束梁类似;随着荷载的加大,由于应力集中的存在,缝间小柱两端焊缝端部位置附近最先进入塑性,随后塑性由缝端逐渐向内扩展,最后柱端截面形成塑性铰。
如图10所示,各算例在达到极限承载能力后,抗侧能力均有一个缓慢的下降,下降的幅度与钢管截面的宽厚比密切相关:宽厚比越小,下降幅度越小。
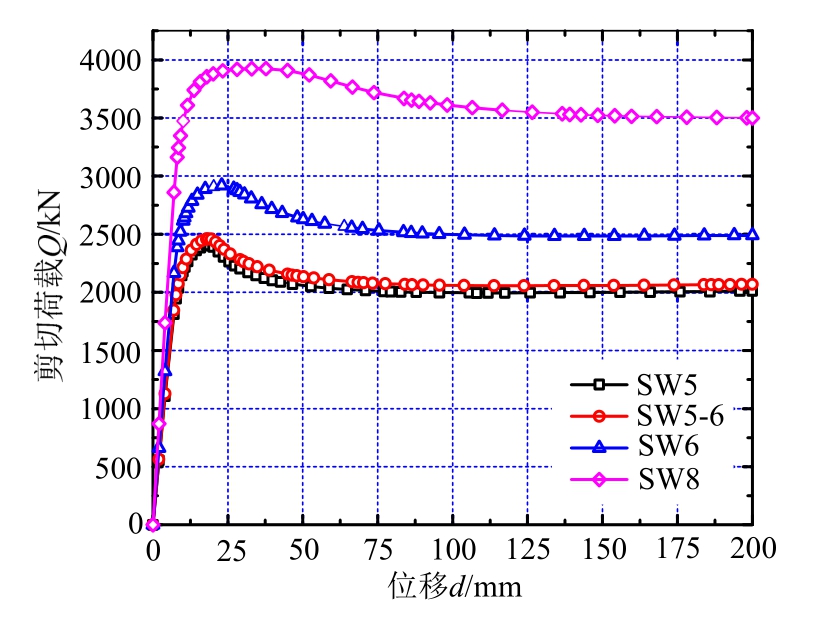
图10 荷载-位移曲线比较
Fig.10 Comparison of load-displacement curves
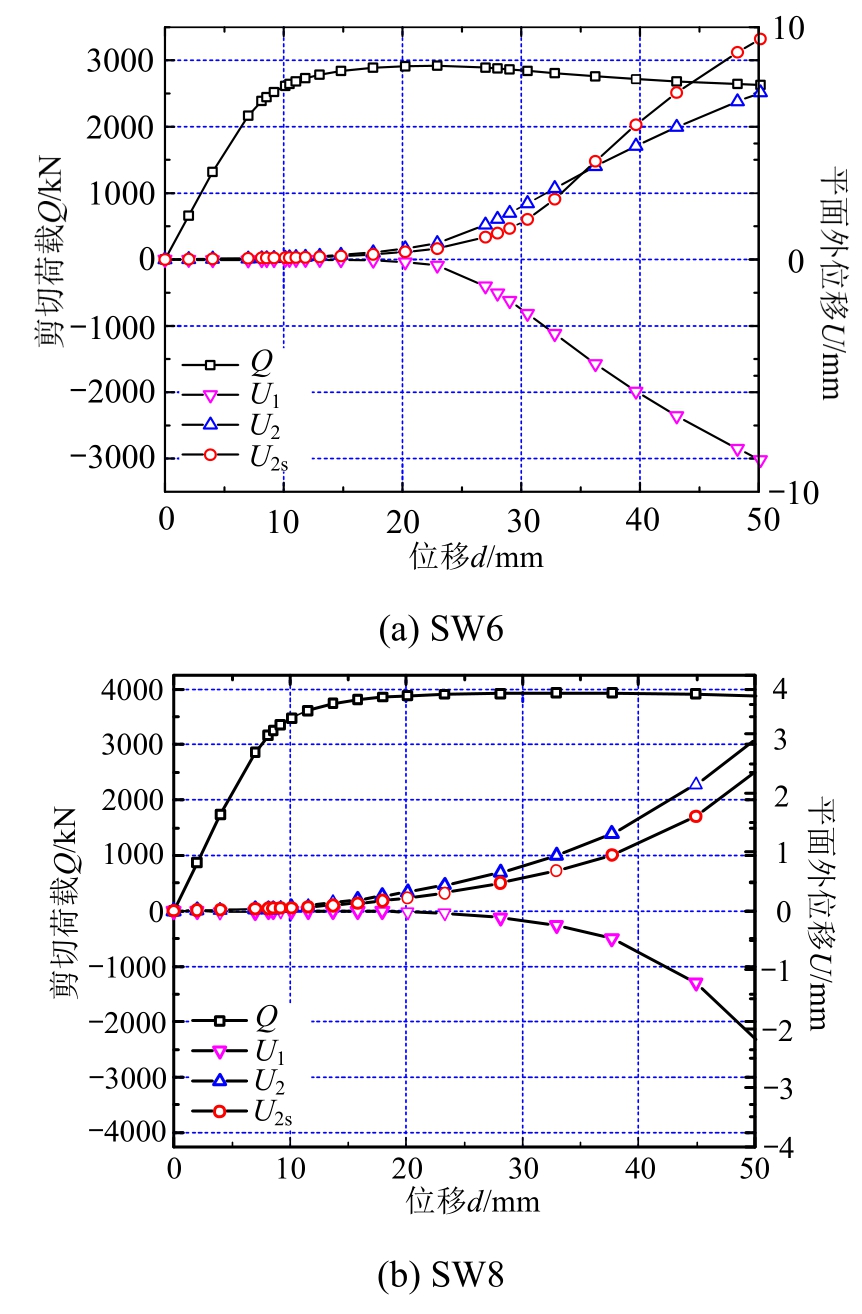
图11 荷载-位移曲线及局部变形-位移曲线
Fig.11 load-displacement curves and local-deformation-displacement curves

图12 SW6面外变形图
Fig.12 Localized out-of-plane deformation of SW6
为了分析这一现象,图11对算例SW6和算例SW8在加载过程中钢管壁的平面外变形进行了跟踪。其中,Q为剪力墙整体的剪切荷载,U2s为边缘构件腹板的平面外位移(即图12中Ⓐ点),U2为中间位置钢管腹板的平面外位移(即图12中Ⓑ点),U1为边缘钢管的翼缘位置的局部变形。从图12可以看出,剪力墙后期抗侧承载能力的降低伴随着钢管截面板件的面外变形的逐渐发展,这可以说明图11中剪力墙承载能力下降的主要原因是缝间小柱的端部位置在塑性开展较为充分后,截面板件的局部鼓曲变形导致。同时,比较图12(a)和图12(b)可以看出,在相同侧向位移情况下,壁厚较厚的构件的平面外位移相对较小。
各算例的延性系数见表5。表5中Qy和Qu分别为剪力墙的屈服荷载和极限承载力,延性系数μ=δu/δy,其中δy为屈服位移(本文选用比较常用的通用屈服弯矩法[20]从荷载位移曲线求得),δu为极限位移(取承载力下降至峰值的0.85倍时的位移)。由图10和表5可知,各算例均具有优良的延性性能,即便是按照S2截面设计的SW5的延性系数也达到5以上,而按照S1截面设计的SW6的延性系数达到12以上,SW8的延性系数更是达到19以上。对比各试件的结果,可以发现增大钢管壁厚、减小宽厚比,对改善结构的延性,增大结构的延性系数μ非常有效。比较图10和表5中SW5和SW5-6的结果可以发现,尽管加厚边缘钢管可以使得剪力墙的弹性临界荷载获得很大的提高,但是对提高极限承载力的作用较小。
表5中还通过φp/φy这一比值对钢管小柱端部的塑性变形能力进行了分析,其中φp指截面达到全塑性时的弯矩对应的截面曲率,φy指截面达到全塑性时的弯矩除以初始刚度得到的截面曲率。我国钢结构规范[14]条文说明指出S1级截面的φp为φy的8倍~15倍,S2级截面为2倍~3倍,从表5的结果来看,S2(SW5)的塑性曲率比值为6.19,S1(SW6)为7.94,基本符合规范给出的范围,说明经合理设计的剪力墙其形成的塑性铰具有足够的塑性转动能力(图13)。
表5 各算例剪力墙性能对比
Table 5 Lateral-load-resisting and other performance of specimens

算例 初始刚度K/(kN·mm-1)屈服位移δy/mm屈服荷载Qy/kN极限承载力Qu/kN极限位移δu/mm延性系数μ曲率比φp/φy SW5 277.32 10.2 2186.76 2403.87 55.8 5.47 6.2 SW5-6 282.21 10.2 2227.79 2460.66 66.5 6.52 _SW6 330.56 10.4 2633.84 2919.55 134.1 12.89 7.9 SW8 434.93 10.5 3508.21 3924.65 >200 >19.05 18.22
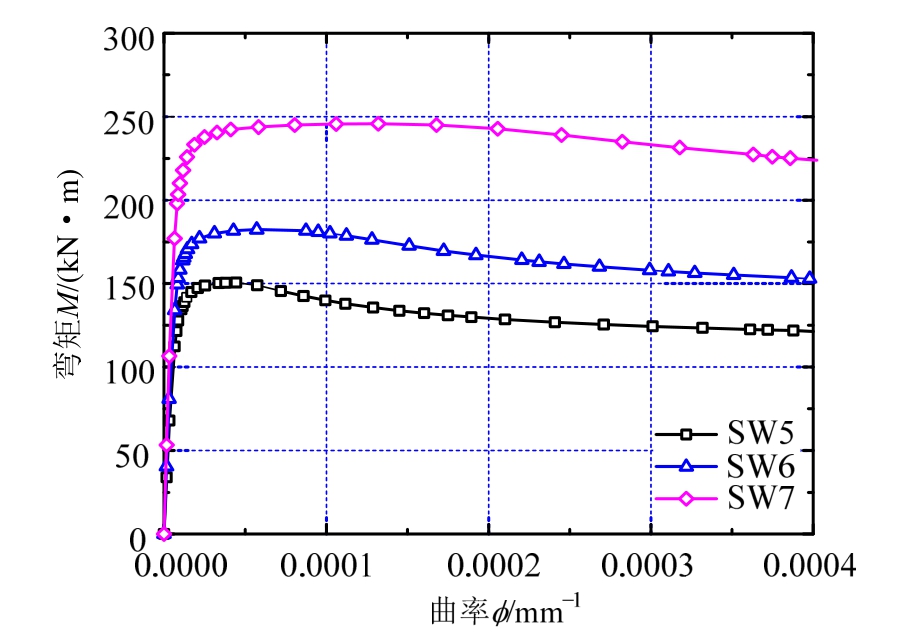
图13 弯矩-曲率曲线
Fig.13 Moment-curvature curves
表6中从用钢量S的角度对各算例的经济效益进行了简单分析,结果表明增大钢管的厚度,减小有提升,每单位用钢量的初始刚度K则基本相同。
表6 各算例经济性指标对比
Table 6 Efficiency of specimens
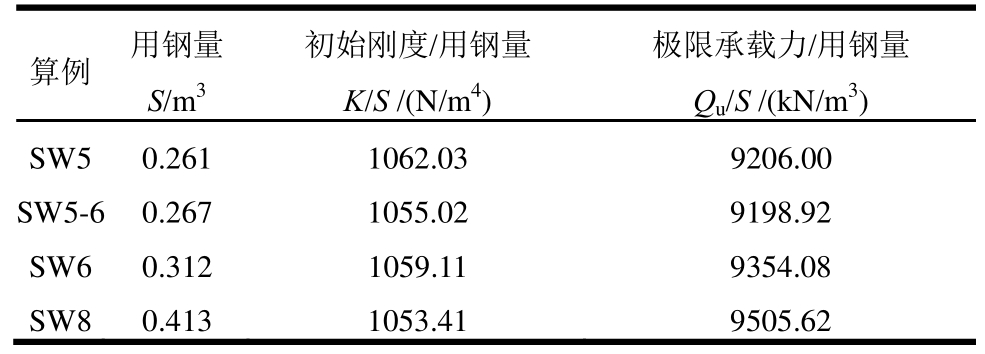
算例 用钢量S/m3初始刚度/用钢量K/S /(N/m4)极限承载力/用钢量Qu/S /(kN/m3)SW5 0.261 1062.03 9206.00 SW5-60.267 1055.02 9198.92 SW6 0.312 1059.11 9354.08 SW8 0.413 1053.41 9505.62
1.4.2 滞回性能及耗能能力
现有的研究表明,传统薄钢板剪力墙存在着滞回曲线捏缩的现象,带竖缝钢板剪力墙的滞回曲线虽然较为饱满,但在加载后期同样也可能出现捏缩的现象[19]。加劲钢板剪力墙的滞回曲线,如十字加劲[20]和交叉加劲钢板剪力墙[21],也可能出现较为明显的捏缩现象。本文通过对模型施加水平往复荷载,SW5、SW6和SW8的滞回曲线见图14。由图14可知,各算例的滞回曲线呈梭形,十分饱满,基本无捏缩现象,体现了非常优异的耗能能力。
为了对带竖缝钢板剪力墙和新型剪力的耗能能力进行比较,表7列出了两者的等效粘滞阻尼比,其中文献[22](带竖缝剪力墙)和新型剪力墙SW5,SW6和SW8模型的结果均来自数值分析。由表7可以看出,两种剪力墙的等效粘滞阻尼比均随着加载位移级别的增加而增加,在整个加载过程中,新型剪力墙的耗能能力均优于带竖缝剪力墙:带竖缝剪力墙的等效粘滞阻尼比由0.075逐渐增加至0.376;新型剪力墙则由0.1左右增加至0.4至0.5左右。
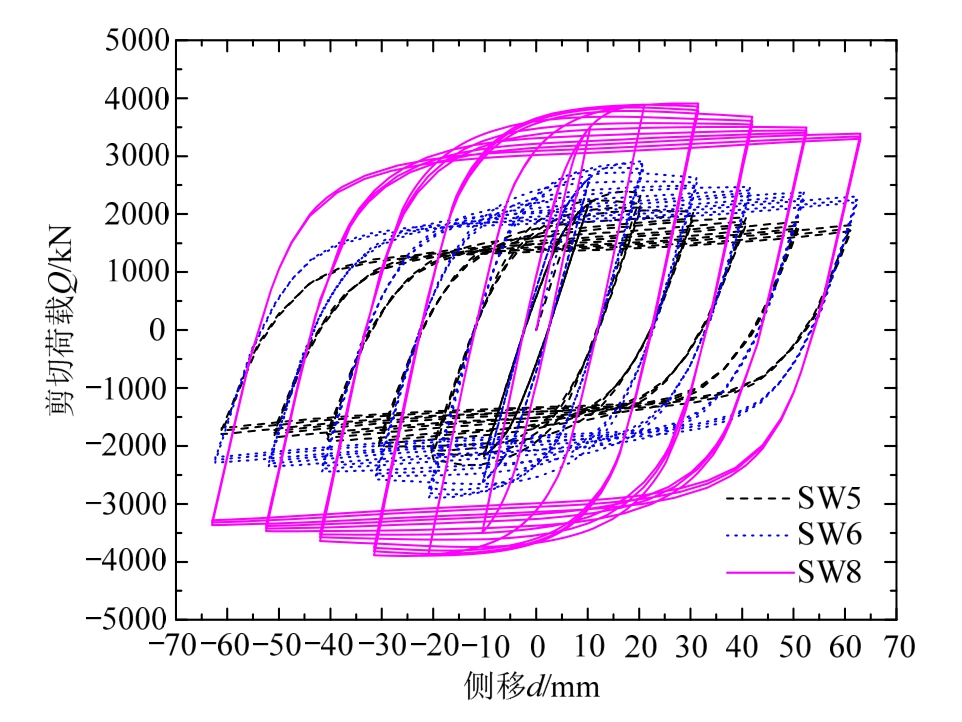
图14 新型剪力墙滞回曲线
Fig.14 Hysteresis loop of SSWS
表7 等效粘滞阻尼比
Table 7 Comparison of equivalent viscous damping ratio

等效粘滞阻尼比ζeq屈服位移δy 2倍屈服位移2δy 3倍屈服位移3δy 4倍屈服位移4δy 5倍屈服位移5δy 6倍屈服位移6δy算例SW5 0.113 0.330 0.398 0.413 0.4190.421新型剪力墙算例SW6 0.116 0.321 0.421 0.440 0.4460.448开缝钢板剪力墙 文献[8]0.395/0.385薄钢板文献[17]最大值0.342剪力墙 文献[20]最大值0.220文献[21]最大值0.239算例SW8 0.116 0.319 0.418 0.474 0.4850.488文献[22]0.075 0.194 0.251 0.292 0.3210.376文献[19]0.296/0.312加劲肋钢板剪力墙 文献[20]最大值0.208
文献[19]由试验得到的开竖缝钢板剪力墙的等效粘滞阻尼比为0.296和0.312,文献[8]对文献[19]的试件进行了改进,将开缝钢板剪力墙的等效粘滞阻尼比提高到了0.395(108 mm荷载级,4.78%)和0.385(90 mm荷载级,3.63%)。而新型剪力墙的最大等效粘滞阻尼比均超过了0.4,且这个最大值随着钢管壁厚的增加有所增加。这是因为新型剪力墙相比于带竖缝剪力墙避免了加载过程中缝间小柱的弯扭失稳。文献[17]对两侧边与柱连接的薄钢板剪力墙进行数值模拟,在位移达到40 mm(5.56δy)时获得了最大等效粘滞阻尼比为0.342。新型剪力墙相比于薄钢板剪力墙避免了拉力场的形成,故等效阻尼比明显提高。文献[21]对交叉加劲肋钢板剪力墙试件进行试验研究,在位移达到5δy时获得了最大值0.239。而文献[20]通过试验获得的薄钢板剪力墙等效粘滞阻尼比最大值仅为0.220,获得的十字加劲钢板剪力墙等效粘滞阻尼比最大值仅为0.208。因此,相比之下新型剪力墙的0.113~0.488的等效粘滞阻尼系数代表非常优异的耗能性能。
1.4.3 两侧与框架柱连接方式的影响
如前文所述,在薄钢板剪力墙的研究中,为避免将拉力场的作用传递到柱子,只将墙板的上下两边与钢框架梁相连[23-25],但这种做法易造成墙板的两侧位置发生平面外失稳破坏。在带竖缝钢板剪力墙的试验研究中也发现墙板两侧自由边发生失稳破坏[8]。考虑到新型剪力墙的特点,本文中通过典型算例对剪力墙和边柱采用不连接(SW6)、焊缝高度范围内连接(SW6a)、全高范围内连接(SW6b)3种连接形式对抗剪性能的影响进行研究(图15)。有限元分析中剪力墙和框架柱的连接通过tie命令将剪力墙边缘钢管腹板位置的节点与对应位置柱节点相连来实现。

图15 与柱连接方式示意图
Fig.15 Sketch of connection between column and SSWS
弹性屈曲分析表明,SW6、SW6a和SW6b的1阶模态均为局部屈曲(图16),临界荷载依次为9312.88 kN、4348.69 kN和4029.70 kN。这说明与柱相连后剪力墙的弹性屈曲临界荷载反而大幅下降,但两种连接方式对应的算例SW6a和SW6b差别不大。3个算例的局部屈曲均发生在边缘位置的钢管,屈曲的位置均较靠近端部位置,但SW6、SW6a和SW6b依次由端部位置向中间位置移动(图16)。


图16 剪力墙1阶屈曲模态
Fig.16 Buckling mode of specimens
需要说明的是,两侧边连接后剪力墙的弹性屈曲临界荷载反而降低,主要是因为所有试件的屈曲都是由板件的局部屈曲控制。同时,通过线性分析发现,在相同的侧向荷载下在屈曲位置附近SW6a和SW6b的局部压应力明显大于SW6,因此更容易发生局部失稳。
图17中显示了3个算例的弹塑性荷载-位移曲线,可以发现3个算例均具有优异抗侧性能,同时将剪力墙侧边与钢柱相连可以明显改善结构的抗侧性能。由表8可知,相比SW6、SW6a和SW6b在初始刚度、屈服荷载、极限荷载、极限位移和延性系数上均有了明显的提高。其中,延性系数更是从SW6的12.89提高到了SW6a和SW6b的20以上。因此,从弹塑性抗侧性能看,剪力墙与钢柱两侧相连是有利于结构的抗侧性能,这与前文弹性屈曲分析的结果相反。图18为算例SW6a的变形图,可以发现在加载后期,SW6a的边缘位置的钢管在角部区域形成了一个小的拉力场,部分侧向荷载通过这一局部拉力场传递至梁柱交点位置,这也是其后期承载能力要高于SW6的原因。
边钢管与柱之间连接焊缝的高度需满足两者之间的传力的要求。假定剪力墙的倾覆弯矩均由两侧的焊缝承受,因此每条焊缝的剪力为:
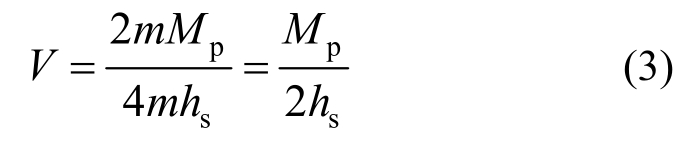
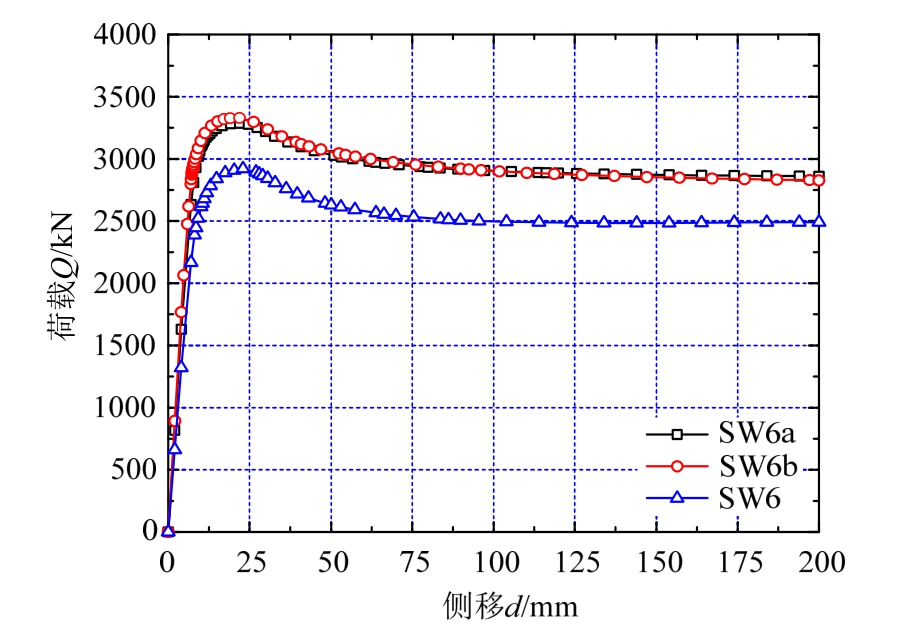
图17 荷载-位移曲线比较
Fig.17 Comparison of load-displacement curves
表8 各算例剪力墙性能对比
Table 8 Lateral-load-resisting and other performance of specimens

算例初始刚度K/ (kN·mm-1)屈服位移δy/mm屈服荷载Qy/kN极限承载力Qu/kN极限位移δu/mm延性系数μ SW6330.56 10.4 2633.84 2919.55 134.1 12.89 SW6a408.86 8.7 3021.63 3286.40 >200 >21.62 SW6b445.80 9.3 3043.89 3329.88 200 22.99
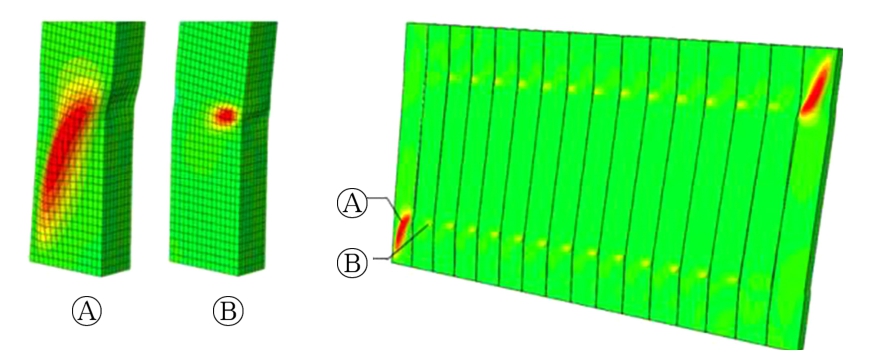
图18 SW6a面外变形图
Fig.18 Out-of-plane deformation of SW6a
其中,倾覆弯矩可由每个小柱端部的塑性铰弯矩之和近似获得。比较式(2)和式(3)可知,考虑倾覆弯矩的前提下,剪力墙两侧与柱的连接焊缝承受的剪力与相邻钢管之间的连接焊缝相同,因此两者取相同的高度可以满足承载能力要求。
同时,图17和表8中同时可以看出,SW6a和SW6b的结果基本一致,也就是说这两种连接方式对极限承载力的提高幅度基本一致,在实际中考虑经济性与施工方便,并不需要在全高范围内将剪力墙的边缘与柱相连,只需在焊缝高度范围内相连即可。
1.5 计算方法与构造措施
1.5.1 弹性抗侧刚度
弹性抗侧刚度是剪力墙正常使用极限状态的一个重要指标。在侧向荷载作用下,新型钢管排柱剪力墙变形主要由3部分组成,分别为缝间小柱高度范围内的弯曲变形、缝间小柱高度范围内的剪切变形以及连接焊缝高度范围内的剪切变形,这3部分引起的侧向位移分别用δb、δv1和δv2来表示,可得:

式中:Q为剪力墙所受侧向荷载;κ为截面剪切形状系数(对矩形钢管截面来说为1.2);E为钢材弹性模量;G为剪切模量;I为钢管截面惯性矩;m、t、hs和h的含义见图3。剪力墙的弹性抗侧刚度为:
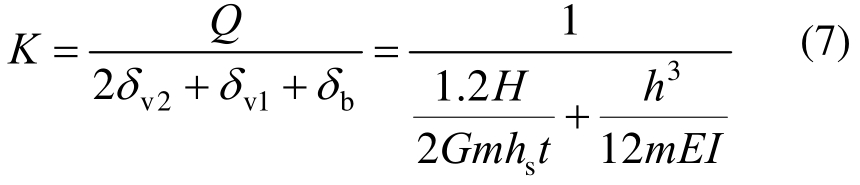
当边钢管壁厚与中部钢管不同时:

式中,I、m和t的下标1和2分别表示边缘钢管和中部钢管。
将算例SW6的有限元分析结果和根据式(4)~式(6)计算所得的位移值进行比较(图19),可见有限元结果与计算值较为符合。由图19可见,剪力墙的变形主要来自缝间小柱,根据有限元计算结果,在弹性阶段、极限荷载时和侧移为200 mm时,小柱的变形占总变形的比例分别为88.5%,91.6%和98.3%。这说明,在整个加载过程中小柱的变形均占绝对的主导地位,并且随着加载过程不断进行小柱部分的变形占比越来越高,后期的小柱变形的加剧主要由于端部塑性铰的转动。

图19 剪力墙沿高度关键节点的侧移量(算例SW6,荷载661.13 kN时)
Fig.19 Horizontal displacement of key points along the height direction (SW6, at load of 661.13 kN)
由式(7)和式(8)的计算结果(KEq.7,8)与有限元结果(KFEA)的比较见表9。由表9可知计算结果比有限元结果大8%~9%。实用中可以将式(7)或者式(8)的计算结果除以1.08的调整系数,调整后的结果(Km)与有限元非常吻合。
表9 初始刚度 /(kN/mm)
Table 9 Initial stiffness

算例 公式计算结果KEq有限元计算结果KFEA比值KEq/ KFEA调整后公式计算结果Km比值Km/KFEA SW8 468.64434.931.08 433.93 1.00 SW6 356.60330.561.08 330.19 1.00 SW5-6 306.48282.211.09 283.78 1.01 SW5 299.32277.321.08 277.15 1.00
1.5.2 屈服荷载
定义弯矩最大截面边缘纤维屈服时的弯矩来求解钢管排柱剪力墙的屈服荷载,则:
式中,截面抵抗矩![]()
由式(9)计算所得的计算值Qy,Eq与有限元结果Qy,FEA1的比较见表10。需要说明的是,本文有限元结果中的屈服荷载是通过作图法(即通用屈服弯矩法)[20]得到的,与式(9)基于的边缘纤维屈服的定义不完全一样,这也是两者差别较大的原因(约20%),但两者的变化规律是一致的。文献[26]通过分析构件和结构的试验数据得出其所提出的“最远点法”与建议的屈服定义具有一致性。采用“最远点法”[26]处理有限元结果所得到的屈服荷载值Qy,FEA2与计算值Qy,Eq的比较同样见表10。从表10的比较可以得知,除了SW8外,其他算例的有限元结果与计算值已十分相近,且式(9)的结果总是偏于安全。
表10 屈服荷载 /kN
Table 10 Yield load

算例公式计算结果Qy,Eq通用屈服弯矩法计算结果比值Qy,Eq /最远点法计算结果比值Qy,FEA1Qy,FEA1Qy,FEA2 Qy,Eq/Qy,FEA2 SW82824.15 3508.21 0.81 3475.03 0.81 SW62156.56 2633.84 0.82 2446.78 0.88 SW5-61856.17 2227.79 0.83 1978.39 0.94 SW51813.26 2186.76 0.83 1945.24 0.93
1.5.3 极限承载力
根据小柱端部达到全塑性弯矩可得钢管排柱剪力墙的极限承载力为:
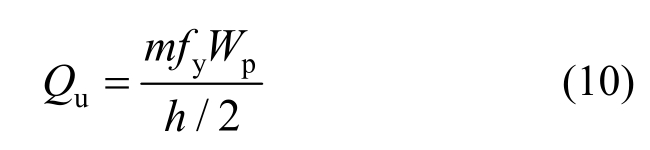
式中,Wp为小柱截面的塑性抵抗矩,![]()
式(10)的计算值Qu,Eq与有限元结果Qu,FEA的比较见表11与图20。由表11结果可知有限元分析得到的极限承载力略高于计算值(约10%),这是小柱端部的其它应力,如横向正应力和剪应力的存在,根据Mises屈服准则计算可知竖向应力会超过屈服应力235 MPa,因此合成的弯矩可能大于塑性铰弯矩。表11中还将式(10)的结果与有限元侧移为200 mm时的承载能力Qu,200进行了比较,发现对于宽厚比较小的SW8和SW6,两者的结果较为接近,误差不大于6%,但是对于宽厚比相对较大的SW5和SW5-6误差大约为10%。其中3个典型试件SW5,SW6和SW8的结果还可以由图20的荷载位移-曲线进行直观地比较。
表11 极限承载力 /kN
Table 11 Ultimate load

算例 公式计算结果Qu,Eq有限元计算结果Qu,FEA比值Qu,Eq/Qu,FEA侧移200 mm时承载力Qu,200比值Qu,Eq/Qu,200 SW8 3473.88 3924.65 0.89 3501.10 0.99 SW6 2643.85 2919.55 0.91 2491.89 1.06 SW5-6 2272.40 2460.66 0.92 2069.45 1.10 SW5 2219.34 2403.87 0.92 2011.61 1.10

图20 计算值与有限元结果比较
Fig.20 Comparison between solutions and FEA results
2 结论
本文通过有限元分析,对一种新型的钢结构剪力墙-带竖向缝隙的钢管排柱剪力墙的抗侧性能进行了研究,并在此基础上提出了各主要性能参数的计算方法。
(1)新型钢管排柱剪力墙的1阶弹性屈曲均为钢管壁的局部屈曲,且临界荷载远大于弹塑性极限承载力,因此通常情况下不会控制剪力墙的承载能力。对于新型剪力墙来说,加强边缘钢管对提高弹性临界荷载是非常有效的。
(2)通过典型算例可见,新型钢管排柱剪力墙具有优良的抗侧刚度、抗侧承载力和延性,以及优异的滞回性能。
(3)连接焊缝端部存在应力集中,受力较为复杂,可能成为薄弱环节,因此在实际工程中可进行一定的加固措施,如可在焊缝端部位置加一横向加强钢板条。
(4)将剪力墙侧边与钢柱相连可以明显改善结构的抗侧性能。在实际中考虑经济性与施工方便,并不需要在全高范围内将剪力墙的边缘与柱相连,只需在焊缝高度范围内相连即可。
(5)本文提出的初始刚度、屈服荷载、极限承载力的计算公式可为相关研究提供参考。
[1]张磊, 童根树.一种带竖向缝隙矩形钢管排剪力墙结构[P].中国: ZL201621490205.3, 2017.Zhang Lei, Tong Genshu.Steel-tube shear wall with slits[P].China: ZL201621490205.3, 2017.(in Chinese)
[2]郭彦林, 周明.钢板剪力墙的分类及性能[J].建筑科学与工程学报, 2009, 26(3): 1-13.Guo Yanlin, Zhou Ming.Categorization and performance of steel plate shear wall [J].Journal of Architecture and Civil Engineering, 2009, 26(3): 1―13.(in Chinese)
[3]Design guide 20: Steel plate shear walls [S].Chicago, IL,USA: American Institute of Steel Construction, 2007.
[4]陈国栋, 郭彦林, 范珍, 等.钢板剪力墙低周反复荷载试验研究[J].建筑结构学报, 2004, 25(2): 19―26.Chen Guodong, Guo Yanlin, Fan Zhen, et al.Cyclic test of steel plate shear walls [J].Journal of Building Structures, 2004, 25(2): 19―26.(in Chinese)
[5]CAN/CSA S16-01, limit states design of steel structures[S].Willowdale, Ontario, Canada: Canadian Standards Association, 2001.
[6]FEMA 450, NEHRP recommended provisions for seismic regulations for new buildings and other structures [S].Washington, DC: Building Seismic Safety Council for the Federal Emergency Management Agency,2004.
[7]JGJ 99―2015, 高层民用建筑钢结构技术规程[S].中国: 中国建筑工业出版社, 2015.JGJ 99―2015, Technical specification for steel structure of tall building [S].China: China Architecture & Building Press, 2015.(in Chinese)
[8]蒋路, 陈以一, 卞宗舒.足尺带缝钢板剪力墙低周往复加载试验研究II [J].建筑结构学报, 2009, 30(5):65―71.Jiang Lu, Chen Yiyi, Bian Zongshu.Experimental study on full scale steel plate shear wall with slits under low-frequency cyclic loads: Part II [J].Journal of Building Structures, 2009, 30(5): 65―71.(in Chinese)
[9]陈以一, 蒋路.带缝钢板剪力墙的承载力和开缝参数研究[J].建筑科学与工程学报, 2010, 27(3): 109―114.Chen Yiyi, Jiang Lu.Research on bearing capacity and slit parameters of steel plate shear wall with slits [J].Journal of Architecture and Civil Engineering, 2010,27(3): 109―114.(in Chinese)
[10]蒋路.带缝钢板剪力墙试验报告[R].上海: 同济大学,2008.Jiang Lu.Experiment report on steel plate shear wall with slits [R].Shanghai: Tongji University, 2008.(in Chinese)
[11]He L S, Togo T, Hayashi K, et al.Cyclic behavior of multirow slit shear walls made from low-yield-point steel[J].Journal of Structural Engineering, 2016, 142(11): 1―9.
[12]Gortes G, Liu J.Experimental evaluation of steel slit panel–frames for seismic resistance [J].Journal of Constructional Steel Research, 2011, 67(2): 181―191.
[13]Hitaka T, Matsui C.Experimental study on steel shear wall with slits [J].Journal of Structural Engineering,2003, 129(5): 586-595.
[14]GB 50017―2017, 钢结构设计规范[S].中国: 中国建筑工业出版社, 2017.GB 50017―2017, Standard for design of steel structures[S].China: China Architecture & Building Press, 2017.(in Chinese)
[15]JGJ 101―2015, 建筑试验抗震规程[S].中国: 中国建筑工业出版社, 2015.JGJ 101―2015, Specification for seismic test of buildings [S].China: China Architecture & Building Press, 2015.(in Chinese)
[16]陈以一, 宁燕琪, 蒋路.框架-带缝钢板剪力墙抗震性能试验研究[J].建筑结构学报, 2012, 33(7): 133―139.Chen Yiyi, Ning Yanqi, Jiang Lu.Experimental study on seismic behavior of frame-steel plate shear wall with slits[J].Journal of Building Structures, 2012, 33(7): 133―139.(in Chinese)
[17]曹正罡, 杜鹏, 邱星玮, 等.三类薄钢板剪力墙滞回性能及选型[J].哈尔滨工业大学学报, 2014, 46(10): 10―16.Cao Zhenggang, Du Peng, Qiu Xingwei, et al.Hysteretic performance study and lectotype suggestion for three types of thin steel plate shear walls [J].Journal of Harbin Institute of Technology, 2014, 46(10): 10―16.(in Chinese)
[18]王先铁, 刘立达, 杨航东, 等.方钢管混凝土框架内置两侧开洞薄钢板剪力墙的抗震性能研究[J].工程力学,2017, 34(3): 162―172.Wang Xiantie, Liu Lida, Yang Hangdong, et al Seismic study of concrete-filled square steel tubular framethin steel plate shear walls with two-side openings [J].Engineering Mechanics, 2017, 34(3): 162―172.(in Chinese)
[19]蒋路, 陈以一, 汪文辉, 等.足尺带缝钢板剪力墙低周往复加载试验研究I [J].建筑结构学报, 2009, 30(5):57―64.Jiang Lu, Chen Yiyi, Wang Wenhui, et al.Experimental study on full scale steel plate shear wall with slits under low-frequency cyclic loads: Part I [J].Journal of Building Structures, 2009, 30(5): 57―64.(in Chinese)
[20]李峰.钢板剪力墙抗震性能的试验与理论研究[D].西安: 西安建筑科技大学, 2011.Li Feng.Experimental and theoretical investigation to earthquake resistant behavior of steel plate shear walls[D].Xi’an: Xi’an University of Architecture and Technology, 2011.(in Chinese)
[21]李峰, 李慧, 李振敏, 等.交叉加劲肋钢板剪力墙低周反复荷载试验研究[J].西安建筑科技大学学报(自然科学版), 2009, 41(1): 57―62.Li Feng, Li Hui, Li Zhenmin, et al.Experimental study on diagonally stiffened steel plate shear wall under low-frequency cyclic loads [J].Journal Xi’an University of Architecture and Technology (Natural Science Edition), 2009, 41(1): 57―62.(in Chinese)
[22]李慎.开缝钢板剪力墙简化模型的性能研究[D].西安: 西安建筑科技大学, 2012.Li Shen.The study on behavior of simplified model of steel plate shear wall with slits [D].Xi’an: Xi’an University of Architecture and Technology, 2012.(in Chinese)
[23]缪友武.两侧开缝钢板剪力墙结构性能研究[D].北京: 清华大学, 2004.Miao Youwu.The investigation to structural behavior of steel plate shear wall slotted at two edges [D].Beijing:Tsinghua University, 2004.(in Chinese)
[24]郭彦林, 缪友武, 董全利.全加劲两侧开缝钢板剪力墙弹性屈曲研究[J].建筑钢结构进展, 2007, 9(3): 58―62.Guo Yanlin, Miao Youwu, Dong Quanli.Elastic buckling of stiffened steel plate shear walls slotted at two edges[J].Progress in Steel Building Structures, 2007, 9(3):58―62.(in Chinese)
[25]张爱林, 张勋, 刘学春, 等.钢框架-装配式两边连接薄钢板剪力墙抗震性能试验研究[J].工程力学, 2018,35(9): 54―63, 72.Zhang Ailin, Zhang Xun, Liu Xuechun, et al.Experimental study on seismic behavior of steel frame with prefabricated beam-only connected steel plate shear wall [J].Engineering Mechanics, 2018, 35(9): 54―63,72.(in Chinese)
[26]冯鹏, 强翰霖, 叶列平.材料、构件、结构的“屈服点”讨论[J].工程力学, 2017, 34(3): 36―46.Feng Peng, Qiang Hanlin, Ye Lieping.Discussion and definition on yield points of materials, members and structures [J].Engineering Mechanics, 2017, 34(3): 36―46.(in Chinese)