随着我国隧道工程的蓬勃发展，各类深埋长大隧道不断涌现，以复合式衬砌(结构形式主要为初期支护(简称“初支”)和二次衬砌(简称“二衬”)为主要支护手段的新奥法理念已广泛应用于隧道施工[1－4]。由于隧洞开挖过程中自稳能力通常较差，洞壁收敛变形明显，因此，工程施工中一般采用混凝土、锚杆、钢拱架等大刚度材料来限制围岩位移，然而，公路、铁路隧道设计规范对此类支护结构何时施加尚未给出明确建议，因此，有必要对该问题深入研究。
现阶段，隧洞支护时机的相关研究已经涌现诸多成果，研究手段多基于数值模拟、室内试验和现场监测，如Farias等[5]采用三维数值模拟研究了新奥法开挖隧道的位移控制问题；苏凯等[6]建立隧洞二维和三维数值模型，给出基于位移完成率的最佳初次支护时机选择方法；杨建平等[7]采用数值模拟手段开展了小净距隧道在不同荷载释放比例下支护时机对围岩稳定性影响的研究；王中文等[8]考虑隧道围岩蠕变特性，结合现场实测给出了二次衬砌的合理支护时机；来弘鹏等[9]通过模型试验研究了支护时机对软弱围岩公路隧道围岩压力、衬砌切向应力大小与分布规律的影响。然而，上述研究手段均为所建工程服务，其他工程借鉴有限，因此，必须在理论上有所突破。近几年，部分学者已经开展了对隧洞支护时机的理论研究，如张建海等[10]考虑开挖围岩的时效变形作用，提出了脆性围岩“适时支护”思维；Liu等[11]给出了不同支护时机和强度作用下寒区隧道的弹塑性解析解；王华宁等[12]考虑纵向推进和双层衬砌构筑过程，给出隧洞最佳支护时机的初步设计；但文献[10]未能体现“分步支护”的理念,即何时施加何种支护，文献[11―12]支护仅考虑衬砌作用，支护结构过于简单，因此，亟待开展隧洞分步支护时机的理论研究。为了使复合式衬砌分步支护力学解答更为精确，考虑到围岩本身具有一定的自承能力，则理论解答应引入围岩开挖过程中的“空间效应”，另外，复合式衬砌结构中混凝土一般浇筑后28 d达到设计强度，则理论解答应考虑混凝土的时效特性。
基于此，本文针对“初衬+锚杆+钢拱架+二衬”的复合式衬砌结构，将锚杆锚固远端置于弹性区，基于Mohr-Coulomb准则，考虑开挖“空间效应”、衬砌时效特性以及支护结构分步施加的时机，试图得到隧道开挖与支护过程中塑性区应力、洞壁收敛变形以及支护压力解析解，通过算例分析支护结构的分步支护时机是否妥当，若不妥当则优化隧洞开挖过程中的支护时机。
1 支护压力理论分析
1.1 力学模型建立
为了便于理论分析，建立圆形隧洞力学模型如图1所示。其中：① 围岩为均质、各向同性岩体；② 隧道埋深足够深且轴向长度足够长；③ 隧道处于静水应力场中，半径为R0，地应力为p0；④ 隧道开挖时产生塑性区，半径为Rp，支护时锚杆长度为L,锚固半径为RL且RL=R0+L,初衬、二衬内侧半径分别为R1、R2；⑤ 钢拱架采用20b工字钢材料，钢拱架位于初衬中(图1未给出)；⑥ 初衬、锚杆、钢拱架和二衬均处于弹性状态。
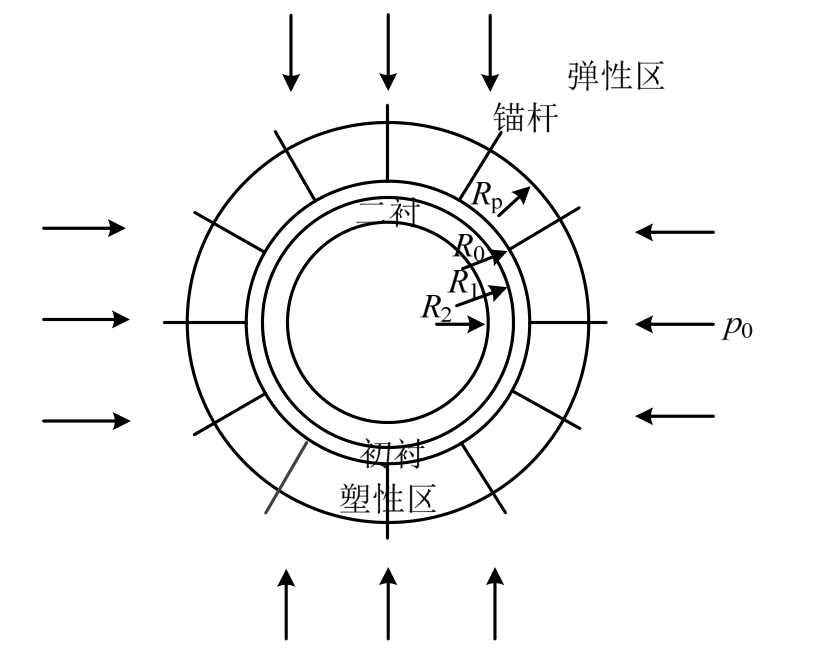
图1 力学模型
Fig.1 Mechanical model
1.2 基本方程及屈服准则
1) 平衡微分方程
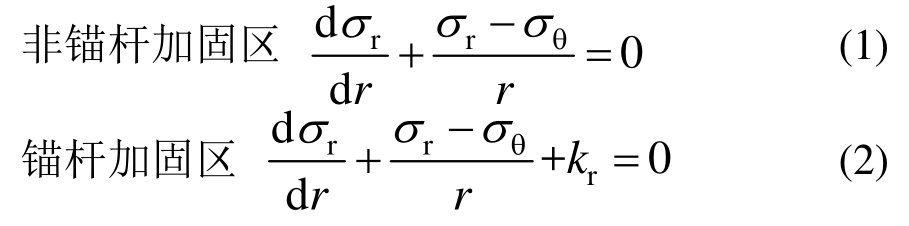
式中：σr、σθ分别为围岩径向应力、切向应力；kr为锚杆径向体积力，
其中A为锚杆横截面积，f1、f2分别为锚杆的间距、排距。采用Mohr-Coulomb屈服准则，有：
式中：ξ=(1+sinφ)/(1-sinφ)，φ为岩体内摩擦角；σc为岩体单轴抗压强度，σc=2ccosφ/(1-sinφ)，c为岩体粘聚力。
1.3 “空间效应”计算公式
隧道开挖过程中，地应力释放荷载并非立刻达到p0，根据文献[13]，其释放荷载随时间的变化可以表示为：
式中：m=3.15V/(2R0)，V为掌子面推进速度；t为开挖时间，记隧洞刚开挖时t=0。
则开挖过程中“虚拟支护力”为：
1.4 考虑分步支护时机的支护压力分析
支护过程中，各支护结构施加的顺序依次为初衬、锚杆和钢拱架(假定施加锚杆与钢拱架之间的时间差近似为0)、二衬，施加的时刻分别为t1、t2和t3。考虑初衬和二衬的时效特性，即初衬和二衬形成强度需要时间养护，另外，将锚杆与围岩形成锚固承载体，锚杆提供的支护压力仅考虑预紧力的作用。设初衬、锚杆、钢拱架和二衬提供的支护压力分别为p1(t)、p2、p3和p4(t)，则支护结构在各个时间段的支护压力pi(t)为：
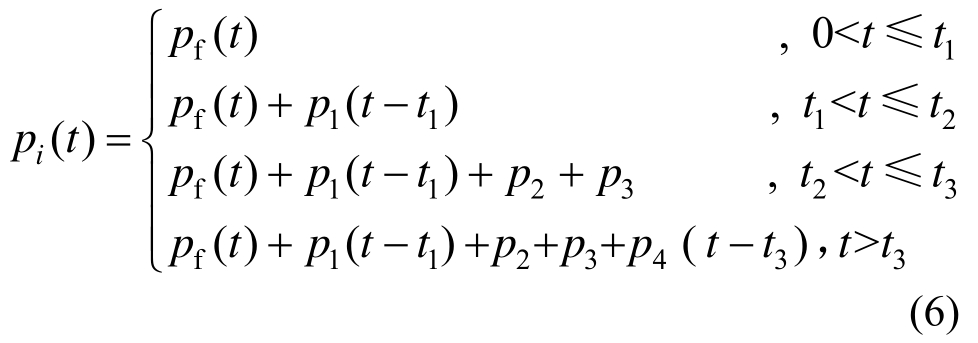
1.5 考虑分步支护时的塑性区围岩应力、洞壁位移及支护压力分析
1) 初衬施加之前
根据经典的洞室围岩理论，考虑“虚拟支护力”时，塑性区围岩应力为：
若不施加支护且不考虑“虚拟支护力”，洞壁在t=∞时的位移为：
式中：G为岩石的剪切模量，
μ分别为岩体的弹性模量、泊松比；
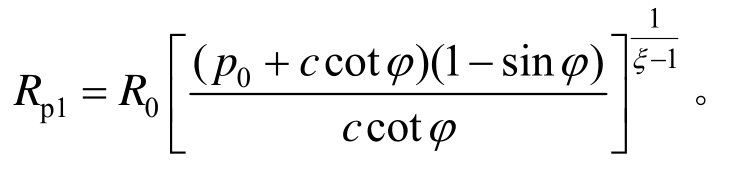
初衬开始施加时的洞壁位移为：
在t1时刻支护并考虑“虚拟支护力”时，洞壁位移为[14-15]：
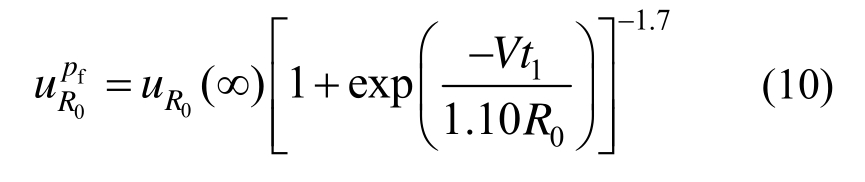
2) 施加初衬之后、锚杆和钢拱架之前
塑性区围岩应力有：
洞壁位移参考文献[16]，围岩与初衬相互作用下的解析方程为：
式中：
为初衬施加之后的洞壁位移；Kc1为初衬刚度，根据文献[17]，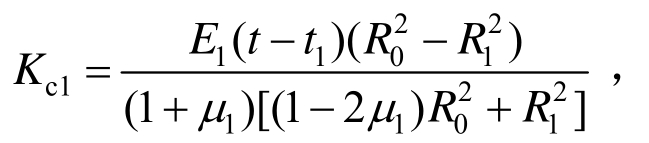
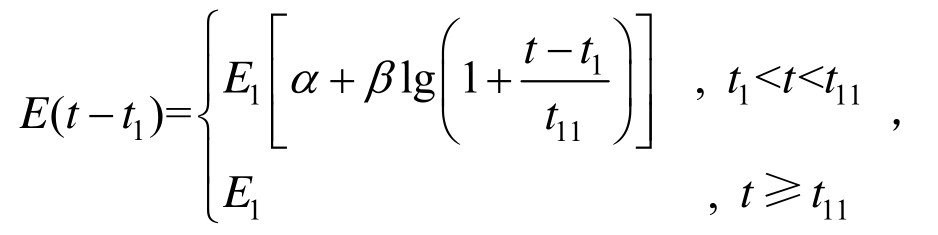α和β取值参考文献[18]，t11为混凝土达到设计强度的时刻。
式(12)可解出
则初衬提供的支护压力为：
3) 施加锚杆和钢拱架之后、二衬之前
施加锚杆、钢拱架时刻记为t2，若锚杆覆盖整个围岩区，则其塑性区径向应力为：
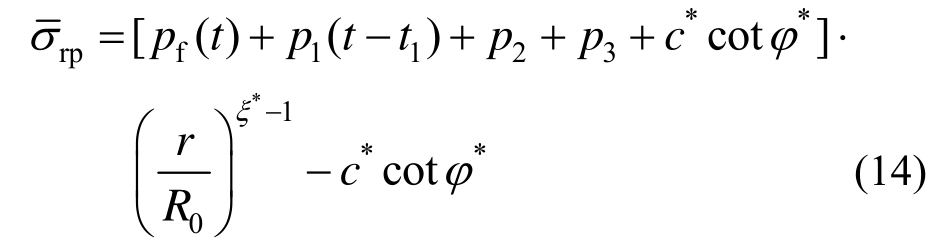
式中：c*、φ*分别锚固范围内的粘聚力、内摩擦角，根据文献[19―20]，将锚杆视作均匀化支护，有
根据文献[21]，锚杆密度因子定义为
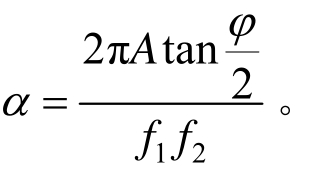
通过预测围岩塑性区选取合适的锚杆，使得锚杆远端超出塑性区一部分(为了覆盖塑性区)，而要求本文锚杆、钢拱架支护下的塑性区应力σrp3，则需对
修正。
锚杆、钢拱架支护时，将弹性区分为非锚固弹性区和锚固弹性区，则非锚固弹性区的径向应力为：
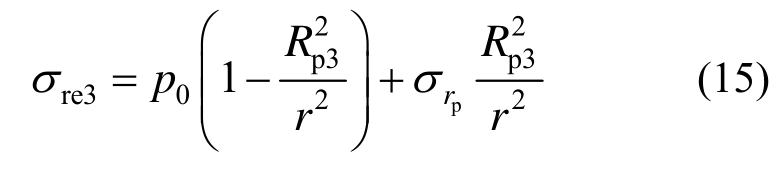
式中，Rp3为初衬、锚杆和钢拱架支护下的塑性区为：
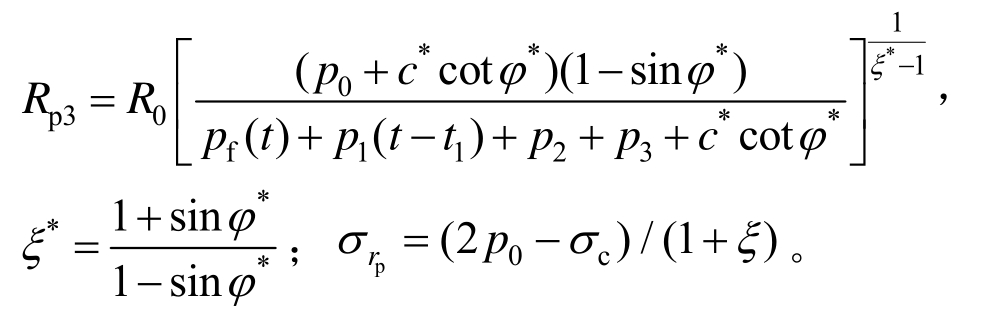
将式(3)代入式(2)，并在r=RL 处有
则锚固弹性区的径向应力为：
有
即将整个围岩视为锚固区时塑性区内径向应力比本文锚固情况下多出Δσ1，则锚杆、钢拱架支护时的围岩应力为：
围岩与初衬、锚杆和钢拱架共同作用下的塑性区位移解析方程为：
式中：
为锚杆和钢拱架施加之后的洞壁位移；
为初衬和钢拱架的刚度之和，Kc2为钢拱架刚度，
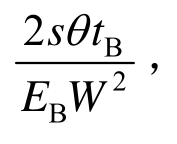其中s、Es、As、Is和W为钢拱架布置间距、弹性模量、横截面积、惯性矩和翼缘宽度；EB、tB分别为楔块的弹性模量和厚度；θ为相邻楔点之间夹角的一半。
式(18)可解出
锚杆和钢拱架提供的支护压力为：
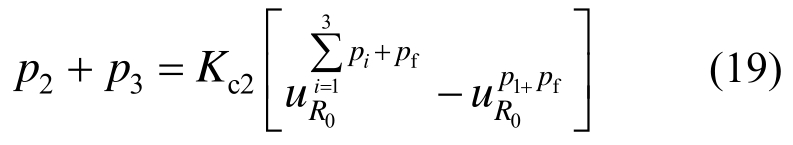
4) 施加二衬之后
施加二衬时刻记为t3，计算过程近似第3)部分若锚杆覆盖整个围岩区，则其塑性区径向应力为：
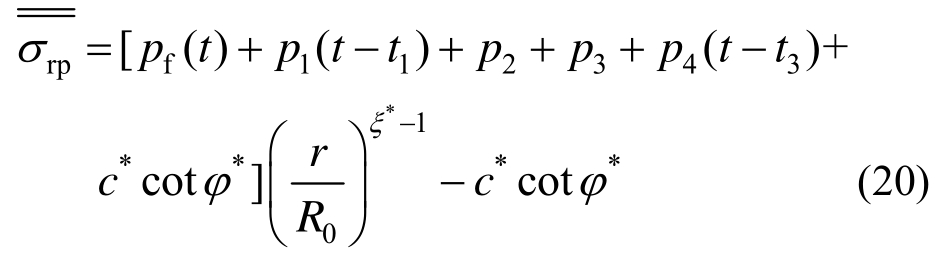
非锚固弹性区的径向应力为：
式中，Rp4为初衬、锚杆、钢拱架和二衬支护下的塑性区：
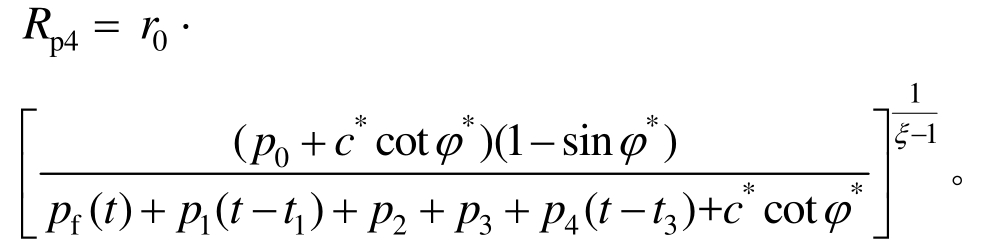
施加二衬后，将式(3)代入式(2)并在r=RL 处有
则：
有
即将整个围岩视为锚固区时塑性区内径向应力比本文锚固情况下多出Δσ2，则锚杆、钢拱架支护时的围岩应力为：
围岩与初衬、锚杆、钢拱架和二衬作用下的塑性区位移解析方程为：
式中：
为初衬、锚杆、钢拱架和二衬施加之后的洞壁位移；Kc3为二衬刚度，
求法同理E1(t-t1)。
式(24)可解出
二衬提供的支护压力为：
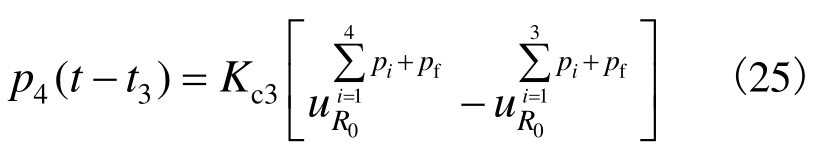
2 算例分析
深埋圆形隧道开挖半径R0=5 m，地应力p0=8 MPa，并在合理范围内选取围岩力学参数和支护材料参数，如表1、表2、表3和表4所示。
若不施加支护，塑性区半径Rp1=8.25 m，施加锚杆能覆盖塑性区且锚杆远端处于弹性区，满足本文理论部分设想。
隧道在t=0 d开始开挖，掘进平均进度为V=4 m/d；初衬在t=t1=5 d时开始施加，锚杆和钢拱架在t=t2=15 d时开始施加，二衬在t=t3=30 d开始施加，支护速度与掘进速度一致。
表1 围岩力学参数
Table 1 Mechanical parameters of surrounding rock
弹性模量E/MPa内摩擦角φ/(°)粘聚力泊松比ν c/MPa 1500 30 0.4 0.3
表2 锚杆材料参数
Table 2 Material parameters of bolt
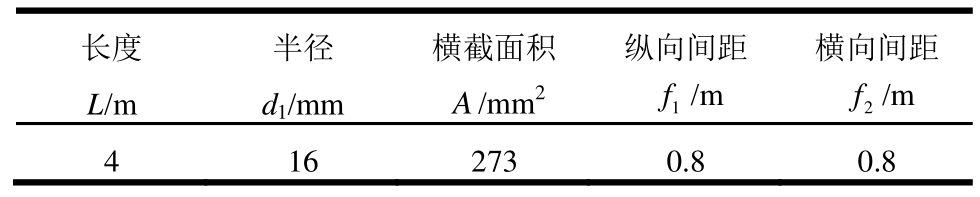
长度L/m半径d1/mm横截面积A/mm2纵向间距横向间距f/m 1 f/m 2 4 16 273 0.8 0.8
表3 钢拱架、楔块材料参数
Table 3 Material parameters of steel arch and wedge
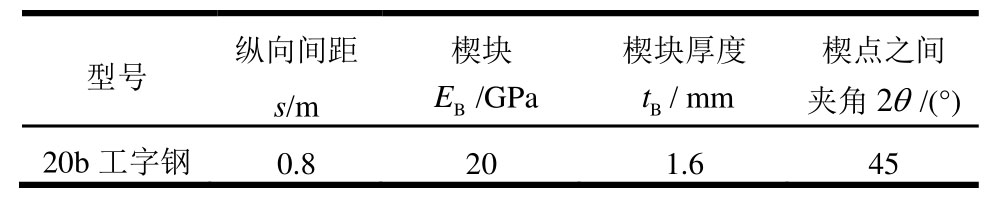
型号 纵向间距s/m楔块楔块厚度E/GPa B t/ mm B楔点之间夹角2θ/(°)20b工字钢0.8 20 1.6 45
表4 初衬、二衬材料参数
Table 4 Material parameters of initial lining and two lining
初衬 二衬弹性模量泊松比厚度a/m弹性模量E/GPa 1 E/GPa 泊松比 厚度b/m 2 20.5 0.2 0.16 25.3 0.17 0.4
采用FLAC3D有限差分软件对本文算例模拟，建立模型如图2所示，模型尺寸为60 m×140 m×40 m，共计60327个单元。支护结构如图3所示，初衬、锚杆和二衬分别为shell单元、cable单元和实体单元，对于钢拱架的模拟一般考虑增加初衬混凝土弹性模量，并有公式如下：
式中：
为钢拱架与初衬混凝土的等效弹性模量；Ag、Eg分别为钢拱架的横截面积和弹性模量。
图2 隧洞开挖示意图
Fig.2 Schematic of tunnel excavation
图3 支护结构示意图
Fig.3 Schematic diagram of supporting structure
以隧洞进尺0 m处断面为研究对象，将不同支护时刻的解析解洞壁位移与FLAC3D数值解进行对比，如表5所示。
表5 洞壁位移对比表
Table 5 Comparison table of wall displacement
时间/d 5 15 30 60位移/mm FLAC3D解 25.6 53.8 60.7 62.5本文解 27.6 57.7 65.4 67.6
表5显示，本文洞壁位移计算值较FLAC3D解略大，但总体误差在7.6%以内，吻合性较好，验证了本文理论解答的可行性。
2.1 隧洞应力、位移分析
图4显示开挖与支护过程中4个时刻的围岩应力。随着支护时间的推移，围岩塑性区的径向应力逐渐加强，切向应力峰区向洞壁转移，塑性区厚度减小了38.1%，塑性区围岩得到加固。另外，施加锚杆和钢拱架后，洞壁切向应力增速快于径向应力以及在锚固弹性区有段应力跌落的过程，揭示了锚杆和钢拱架使得塑性区径向应力显著加强。
图4 隧洞支护过程中的围岩应力
Fig.4 Stress of surrounding rock in tunnel supporting process
支护前后洞壁位移以及支护结构承受压力如图5所示。支护后洞壁围岩位移仅比未支护时减小18.6%，位移限制效果不佳，其原因是：开始支护时洞壁产生较大位移，占未支护时的55.4%，施加支护较迟。支护结构承受压力从大到小依次为锚杆与钢拱架、二衬、初衬，记二衬荷载分担比=(二衬与初支之间的压力)/(围岩与初支之间的压力)，则本文算例中二衬荷载分担比为39.1%，二衬分担压力较大，与隧规设计要求(二衬分担压力较小甚至作为安全储备)相悖，因此，有必要优化分步支护施加的时机。
图5 支护前后洞壁位移以及支护压力
Fig.5 Wall displacement before and after supporting and supporting pressure
部分成果对支护设计的优化局限于改变初衬、二衬厚度或换取支护刚度更大的材料，其必然影响隧洞运行空间或增加额外成本[22－23]。研究表明：钢拱架因具有较高的承载力在地下工程支护中广泛使用，但在支护过程中未能充分发挥钢拱架承载力而造成材料浪费的现象时有发生[24－25]。因此，笔者试图调整初衬、锚杆和钢拱架的支护时机以便减小二衬分担的压力，提高隧洞的安全性。
2.2 隧洞合理支护时机的确定
支护结构在不同时刻支护下的洞壁位移、二衬荷载分担比如图6、图7所示。为了尽快控制洞壁位移，将支护时刻提前。图6显示：支护时刻提前后，洞壁最大位移较支护前减少46.0%，围岩位移得到有效控制，初支提前时间越多，限制位移越明显，其中锚杆和钢拱架对围岩位移的限制起到决定性作用，而二衬由于支护顺序限制施加较迟，限制位移有限；图7显示：调整支护时刻后的二衬荷载分担比最大值较本文算例降低13.2%，尤其初支施加提前，使得初支成为主要受力结构，大大减小二衬荷载。
结合隧洞掘进速度，为了优化洞壁位移与二衬荷载分担比，本文算例中初衬、锚杆和钢拱架、二衬施加时机距开挖面距离不应超过8 m、24 m、64 m，其它深埋隧洞可依据其围岩条件、断面大小、支护材料、掘进与支护速度等因素参考本文理论解答给出所建隧洞支护材料的合理施加时机。
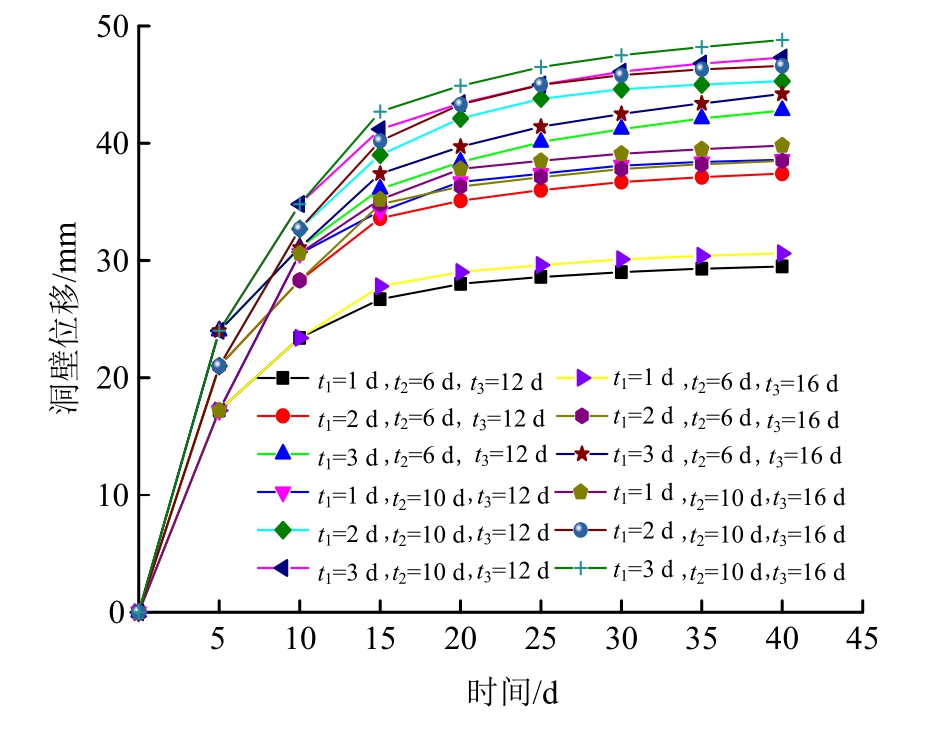
图6 支护结构在不同时刻支护下的洞壁位移
Fig.6 Displacement of retaining wall under different supporting time
图7 支护结构不同时刻支护下的二衬荷载分担比
Fig.7 Two lining load sharing ratio of support structure at different time supporting
3 结论
本文基于Mohr-Coulomb准则，通过考虑开挖“空间效应”、衬砌时效特性以及支护结构分步施加的时机，得到了深埋隧洞“初衬+锚杆+钢拱架+二衬”的复合式衬砌结构分步支护下的弹塑性解析解，并采用有限差分软件FLAC3D对该解析解进行了验证，得到以下主要结论：
(1)推导得到了隧洞开挖与支护过程中塑性区应力、洞壁位移以及支护结构所分担的支护压力理论解答，将不同支护时刻的洞壁位移与FLAC3D数值解对比分析，吻合性较好，验证了该方法的可靠性。
(2)支护结构施加过程中，围岩塑性区的径向应力逐渐加强，切向应力峰区向洞壁转移，塑性区厚度大幅降低，锚杆与钢拱架承受主要围岩压力。
(3)优化初支施加时机后，洞壁最大位移、二衬荷载分担比较算例相应减少，并给出了支护结构分步施加时刻的建议值，其它深埋隧洞可根据自身条件设计参考本文理论研究提出合理的支护结构分步支护时机。
[1]张顶立, 陈峰宾, 房倩.隧道初期支护结构受力特性及适用性研究[J].工程力学, 2014, 31(7): 78－84.Zhang Dingli, Chen Fengbin, Fang Qian.Study on mechanical characteristics and applicability of primary lining used in tunnel [J].Engineering Mechanics, 2014,31(7): 78－84.(in Chinese)
[2]孙振宇, 张顶立, 房倩.隧道锚固系统的协同作用及设计方法[J].工程力学, 2019, 36(5): 53－66, 75.Sun Zhenyu, Zhang Dingli, Fang Qian.The synergistic effect and design method of tunnel anchorage system [J].Engineering Mechanics, 2019, 36(5): 53－66, 75.(in Chinese)
[3]冯冀蒙, 仇文革, 王航.隧道复合式衬砌初期支护极限状态模型试验研究[J].岩土力学, 2012, 33(11):3345－3351.Feng Jimeng, Qiu Wenge, Wang Hang, et al.Model testing research on limit state of primary support in composite lining tunnels [J].Rock and Soil Mechanics,2012, 33(11): 3345－3351.(in Chinese)
[4]陈建勋, 欧阳院平, 王明年.公路隧道复合式衬砌结构数值计算及分析[J].中国公路学报, 2006, 19(2):74－79.Chen Jianxun, Ouyang Yuanping, Wang Mingnian.Numerical computing and analysis of highway tunnel composite lining structure [J].China Journal of Highway and Transport, 2006, 19(2): 74－79.(in Chinese)
[5]de Farias M M, Moraes A H, de Assis A P.Displacement control in tunnels excavated by the NATM: 3-D numerical simulations [J].Tunneling and Underground Space Technology, 2004, 19(3): 283－293.
[6]苏凯, 崔金鹏, 张智敏.隧洞施工开挖过程初次支护时机选择方法[J].中南大学学报(自然科学版), 2015,46(8): 3075－3082.Su Kai, Cui Jinpeng, Zhang Zhimin.Method of choosing initial supporting time during tunnel excavation [J].Journal of Central South University (Science and Technology), 2015, 46(8): 3075－3082.(in Chinese)
[7]杨建平, 陈卫忠.小净距公路隧道支护时机对围岩稳定性影响研究[J].岩土力学, 2008, 29(2): 483－490.Yang Jianping, Chen Weizhong.Effect of sup-porting time on stability of small spacing roadway tunnel [J].Rock and Soil Mechanics, 2008, 29(2): 483－490.(in Chinese)
[8]王中文, 方建勤.考虑围岩蠕变特性的隧道二衬合理支护时机确定方法[J].岩石力学与工程学报, 2010,29(增刊1): 3241－3246.Wang Zhongwen, Fang Jianqin.Determination method of supporting time for secondary lining in tunnel considering rock creep behaviors [J].Chinese Journal of Rock Mechanics and Engi-neering, 2010, 29(Suppl 1):3241－3246.(in Chinese)
[9]来弘鹏, 林永贵, 谢永利, 等.支护时机对软弱围岩公路隧道力学特征影响的试验研究[J].岩土工程学报,2009, 31(3): 390－395.Lai Hongpeng, Lin Yonggui, Xie Yongli, et al.Influence of supporting opportunity on stress characteristics of soft-weak surrounding rocks in highway tunnels [J].Chinese Journal of Geotechnical Engineering, 2009,31(3): 390－395.(in Chinese)
[10]张建海, 王仁坤, 周钟, 等.基于时效变形的脆性围岩最优支护时机研究[J].岩土工程学报, 2017, 39(10):1908－1914.Zhang Jianhai, Wang Renkun, Zhou Zhong, et al.Optimum support time of brittle underground cavern based on time-dependent deformation [J].Chinese Journal of Geotechnical Engineering, 2017, 39(10):1908－1914.(in Chinese)
[11]Liu W W, Feng Q, Fu S G.Elasto-plastic solution for cold-regional tunnels considering the compound effect of non-uniform frost heave, supporting strength and supporting time [J].Tunnelling and Ungerground Space Technology, 2018, 82(8): 293－302.
[12]王华宁, 李悦, 骆莉莎, 等.应变软化弹塑性岩体中TBM施工过程围岩力学状态的理论分析[J].岩石力学与工程学报, 2016, 35(2): 356－368.Wang Huaning, Li Yue, Luo Lisha, et al.Analytical research of mechanical response of TBM construction in strain-softening elasto-plastic rock [J].Chinese Journal of Rock Mechanics and Engineering, 2016, 35(2): 356－368.(in Chinese)
[13]赵光明, 彭瑞, 孟祥瑞, 等.软岩巷道开挖-支护过程承载结构稳定性分析[J].中国矿业大学报, 2017,46(4): 792－802.Zhao Guangming, Peng Rui, Meng Xiangrui, et al.Stability of bearing structure during soft roadway excavation-supporting [J].Journal of China University of Mining & Tech-nology, 2017, 46(4): 792－802.(in Chinese)
[14]孙钧.岩石流变力学及其工程应用研究的若干进展[J].岩石力学与工程学报, 2007, 26(6): 1081－1106.Sun Jun.Rock rheological mechanics and its advance in engineering applications [J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(6): 1081－1106.(in Chinese)
[15]Carranza T C, Fairhurst C.Application of the convergence-confinement method of tunnel design to rock masses that satisfy the Hoek-Brown failure criterion[J].Tunnelling and Underground Space Technology,2000, 15(2): 187－213.
[16]侯公羽, 李晶晶, 杨悦, 等.围岩弹塑性变形条件下锚杆、喷混凝土和U型钢的支护效果研究[J].岩土力学,2014, 35(5): 1357－1376.Hou Gongyu, Li Jingjing, Yang Yue, et al.Support effects of anchor bolt, shotcrete and U-steel in elastoplastic stage of surrounding rock [J].Rock and Soil Mechanics, 2014, 35(5): 1357－1376.(in Chinese)
[17]Bay J A, Stokoe II K H.Field determination of stiffness and integrity of PCC members using the SASW method [C]// Proceedings of the Nondestructive Evaluation of Civil Structures and Materials Conference.Boulder:University of Colorado, 1990: 71－86.
[18]Pan Y W, Dong J J.Time-dependent tunnel convergence-I formulation of the model [J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1991, 28(6): 469－475.
[19]孟强, 赵洪波, 茹忠亮, 等.锚杆支护圆形隧洞弹塑性解[J].工程力学, 2015, 32(7): 17－25.Meng Qiang, Zhao Hongbo, Ru Zhongliang, et al.Analytical solution for circular tunnels with rock bolts[J].Engineering Mechanics, 2015, 32(7): 17－25.(in Chinese)
[20]晏勤, 李树忱, 谢璨, 等.锚杆加固作用下圆形隧道复合岩体围岩特征曲线解析方法研究[J].岩石力学与工程学报, 2017, 36(12): 3021－3027.Yan Qin, Li Shuchen, Xie Can, et al.Analytical solution for ground characteristic curve of composite rock mass reinforced by bolts in circular tunnels [J].Chinese Journal of Rock Mechanics and Engineering, 2017,36(12): 3021－3027.(in Chinese)
[21]Indraratna B, Kaiser P K.Analytical model for the design of grouted rock bolt [J].International Journal for Numerical and Analytical Methods in Geomechanics,1990, 14(4): 227－251.
[22]邓斌, 饶和根, 廖卫平.软岩隧道支护结构优化研究[J].铁道科学与工程报, 2017, 14(10): 2203－2213.Deng Bin, Rao Hegen, Liao Weiping, et al.Optimization of the soft rock tunnel support structure [J].Journal of Railway Science and Engineering, 2017, 14(10): 2203－2213.(in Chinese)
[23]谷拴成, 黄荣宾, 苏培莉.考虑隧道围岩蠕变的复合式衬砌受力规律[J].交通运输工程学报, 2018, 18(2):53－60.Gu Shuancheng, Huang Rongbin, Su Peili.Force rule of composite lining considering creep of tunnel surrounding rock [J].Journal of Traffic an Transportation Engineering, 2018, 18(2): 53－60.(in Chinese)
[24]李树忱, 晏勤, 谢璨, 等.膨胀性黄土隧道钢拱架-格栅联合支护力学特性研究[J].岩石力学与工程学报,2017, 36(2): 446－456.Li Shuchen, Yan Qin, Xie Can, et al.The study on mechanical behavior of composite supports of steel-grid in loess tunnel [J].Chinese Journal of Rock Mechanics and Engineering, 2017, 36(2):446－456.(in Chinese)
[25]曲海锋, 朱合华, 黄成造, 等.隧道初期支护的钢拱架与钢格栅选择研究[J].地下空间与工程学报, 2007,3(2): 258－262.Qu Haifeng, Zhu Hehua, Huang Chengzao, et al.Study on selection of section-steel and grid-steel in primary support system of tunnel [J].Chinese Journal of Underground Space and Engineering, 2007, 3(2): 258－262.(in Chinese)