钢管混凝土不仅已被较广泛的应用在大型公共建筑、厂房、高层和超高层建筑中[1-2],其在我国的桥梁结构中也有许多应用实例[1,3]。由于钢管和混凝土之间的“组合作用”,使得钢管混凝土具有强度高、抗震性能好等优点[4],然而,实际结构构件往往存在初始缺陷,例如钢结构中的残余应力及初始几何缺陷等,钢管混凝土的主要缺陷形式为“脱空缺陷”。对于水平跨越的钢管混凝土结构(钢管混凝土拱、桁架等),因其在施工时首先架设空钢管,然后采用泵送顶升的方式浇灌混凝土,在浇灌过程中构件截面顶部出现的气腔以及后期混凝土沉降均有可能产生“圆弓形脱空缺陷”[5],如图1所示。脱空缺陷的存在可能导致钢管和混凝土在界面上发生分离,削弱钢管和混凝土之间的“组合作用”,从而导致结构存在安全隐患。而现有的技术补救措施(如灌浆补强等)仍无法完全消除其影响[6],因此有必要开展带缺陷的钢管混凝土构件力学性能研究。
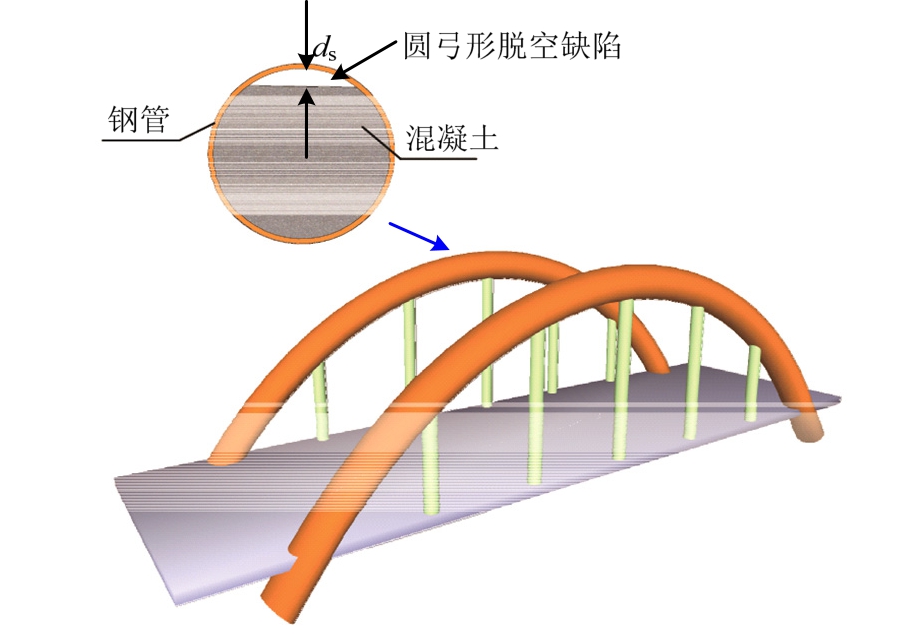
图1 圆弓形脱空缺陷示意图
Fig.1 Schematic diagram of CFST with a circular-segment gap
实际工作中,由于侧向水平风荷载或竖向荷载的作用下,管混凝土构件不仅处于轴压状态,往往也处于偏压或压弯状态[7],Liao等[5,8]进行了圆弓形脱空缺陷对钢管混凝土构件轴压和纯弯力学性能的影响研究,结果表明:圆弓形脱空会削弱钢管对混凝土的约束作用,使混凝土截面形成全约束区、半约束区以及无约束区,因而降低了构件的承载力。Han等[9]研究了不同脱空率(0.0%、2.2%、4.4%和6.6%)下圆弓形脱空缺陷对钢管混凝土构件压弯性能的影响,并在试验和理论研究的基础上提出了考虑脱空影响的压弯承载力简化计算公式。韩浩等[10]完成了带圆弓形脱空缺陷的钢管混凝土构件在压弯滞回荷载作用下的有限元分析。
然而,上述研究主要集中在圆弓形脱空缺陷对钢管混凝土压弯构件(包括轴压、偏压、纯弯和滞回)的力学性能的影响上。实际工程结构中,钢管混凝土构件还可能处于压弯扭等复杂受力状态。例如,钢管混凝土拱桥的拱肋跨度较大时,拱肋将承受较大的轴向压力,在水平地震荷载作用下,主拱也往往处于压弯扭复合受力状态[11]。以往关于钢管混凝土抗震性能的研究多以压弯构件为主,研究结果表明[12-22]:钢管混凝土构件在地震往复荷载作用下具有较高的后期承载力和较好的延性,轴压比和径(宽)厚比是影响钢管混凝土构件滞回性能的重要参数。在地震荷载作用下,钢管混凝土构件也会承受扭转作用,聂建国等[23]对钢管混凝土构件在纯扭和压扭荷载下的抗震性能进行了试验研究和理论分析。王宇航等[11]、Nie等[24]、Wang等[25-26]学者对钢管混凝土柱在压弯扭耦合作用下的滞回性能进行了试验研究和数值模拟,发现弯扭比是影响构件破坏模态和力学性能的重要因素,并由此发展出考虑扭转效应的纤维梁单元,用于分析钢管混凝土柱在往复扭矩作用下的抗震性能。
目前有关于带缺陷的钢管混凝土构件在压弯扭复合作用下滞回性能的研究尚未见有报道,脱空对此类工况下钢管混凝土力学性能的影响也尚不明确。因此,本文开展了带圆弓形脱空缺陷构件在压弯扭复合作用下的滞回性能试验研究,重点考察脱空率、轴压比和弯扭比对此类构件破坏模态、滞回特性、承载力、刚度、耗能以及应变发展的影响规律,研究结果可为实际钢管混凝土工程的安全评估提供参考。
1 试验概况
1.1 试验设计和制作
进行了16个试件在恒定轴压力和弯扭耦合反复荷载作用下的滞回试验,其中包括8个带圆弓形脱空缺陷的钢管混凝土试件、6个无脱空和2个空钢管对比试件。截面类型均为圆形,截面外径(D)均为180 mm,钢管壁厚(ts)均为4.8 mm,试件高度(H)均为900 mm。试验参数包括脱空率、弯扭比和轴压比,如表1所示。其中χ(=ds/D,ds为圆弓形脱空值,如图1所示)为脱空率[5];γ为弯扭比;n(=N0/Nu,其中N0为施加在试件上的恒定轴压力,Nu为采用文献[5]提出的带脱空缺陷的圆钢管混凝土轴压承载力公式计算所得的试件轴压承载力)为轴压比。其中,脱空率(χ)的取值为4.4%和6.6%,涵盖了实际工程中较为极端的情况[5,9]。对于弯扭比选取了γ=0.9和γ=1.8,轴压比则选取了n=0.25和n=0.5,目的在于考察压、弯、扭不同比例组合下脱空缺陷对钢管混凝土试件力学性能的影响规律。试件编号如表1所示,第1个字母C代表钢管混凝土试件;第2个字母中的N代表无脱空,S代表圆弓形脱空;第1个数字为脱空率,0代表脱空率为0.0%,4代表脱空率为4.4%,6代表脱空率6.6%;第2个数字代表轴压比取值,1代表取0.25,2代表取0.50;第3个数字代表弯扭比,1代表取弯扭比为0.9,2代表取弯扭比为1.8;表中空钢管试件编号第1个字母H代表空钢管试件;所有试件编号中最后1个字母代表试验参数相同的试件序号,a代表第1根试件,b代表第2根试件。例如,CS421-a代表带圆弓形脱空缺陷的,脱空率4.4%,轴压比为0.50,弯扭比为0.90的第1根钢管混凝土试件。
表1 试件信息表
Table1 Details of specimens
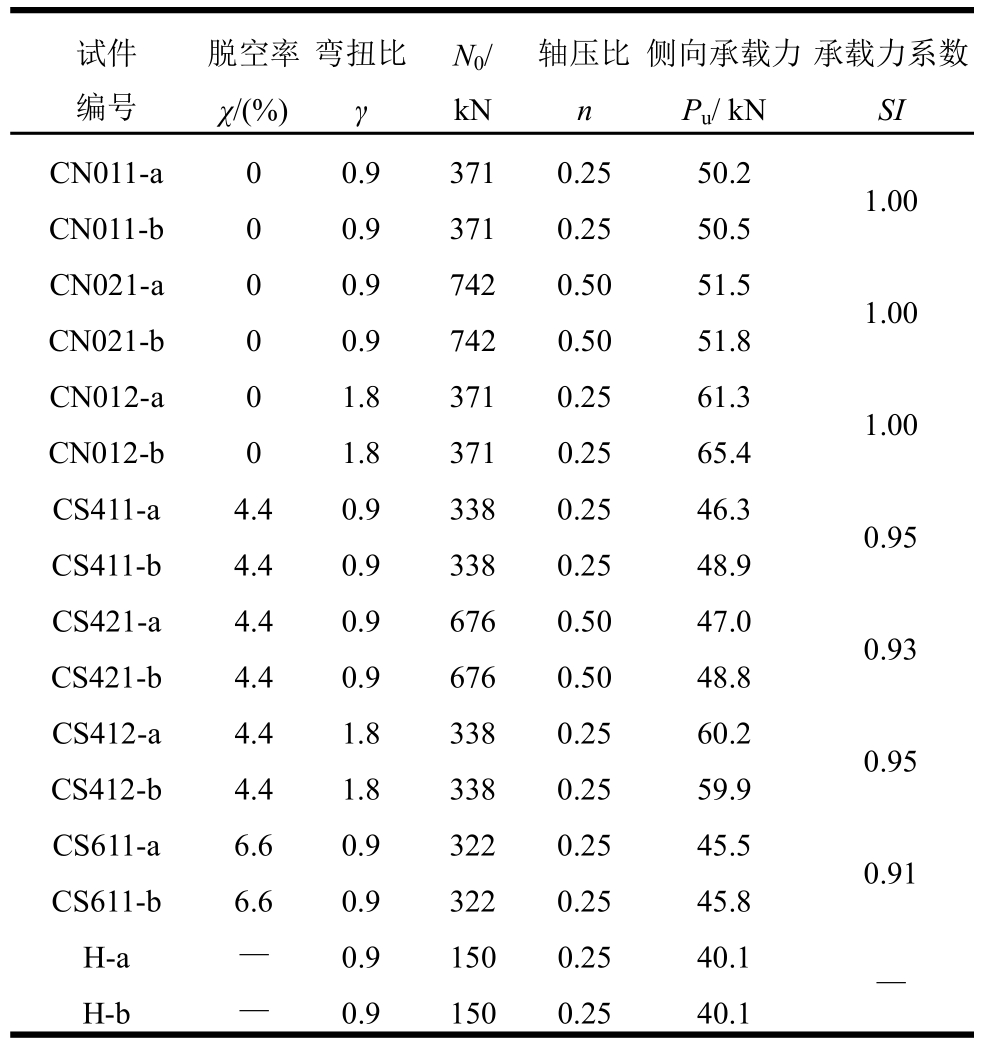
试件编号脱空率χ/(%)弯扭比γ N0/kN轴压比n侧向承载力Pu/ kN承载力系数SI CN011-b 0 0.9 371 0.25 50.5 CN021-a 0 0.9 742 0.50 51.5 1.00 CN021-b 0 0.9 742 0.50 51.8 CN012-a 0 1.8 371 0.25 61.3 1.00 CN012-b 0 1.8 371 0.25 65.4 CS411-a 4.4 0.9 338 0.25 46.3 0.95 CS411-b 4.4 0.9 338 0.25 48.9 CS421-a 4.4 0.9 676 0.50 47.0 0.93 CS421-b 4.4 0.9 676 0.50 48.8 CS412-a 4.4 1.8 338 0.25 60.2 0.95 CS412-b 4.4 1.8 338 0.25 59.9 CS611-a 6.6 0.9 322 0.25 45.5 0.91 CS611-b 6.6 0.9 322 0.25 45.8 H-a — 0.9 150 0.25 40.1 —H-b — 0.9 150 0.25 40.1 CN011-a 0 0.9 371 0.25 50.2 1.00
为精确制造圆弓形脱空缺陷,加工了厚度为3 mm的不锈钢条作为模具,并在其表面涂抹专用的脱模剂。在混凝土浇筑前,将不锈钢模具置于钢管中并临时固定,待混凝土初凝后抽出模具从而形成如图1所示的“圆弓形脱空缺陷”。试验中的无脱空对比试件则正常进行混凝土浇筑,待至养护时间后焊接上端板。典型缺陷试件的截面照片如图2所示。

图2 试件截面照片
Fig.2 Photo of section of specimen with gap
核心混凝土采用自密实混凝土,混凝土材料选用:42.5级普通硅酸盐水泥;Ⅱ级粉煤灰;中砂;玄武岩碎石,最大粒径为20 mm;普通自然水和TW-PS聚羧酸减水剂,其质量配合比为水泥:粉煤灰∶砂∶石∶水∶减水剂=263.67 kg/m3∶175.82 kg/m3∶759.94 kg/m3∶1013.26 kg/m3∶187.25 kg/m3∶4.40 kg/m3。混凝土强度由与试件同时浇筑,同条件养护下的3个边长为150 mm的立方体试块测得。试验时,实测其平均抗压强度(fcu)为44.3 MPa,弹性模量(Ec)为28.3 GPa,泊松比(νc)为0.2,坍落度为255 mm,扩展度为650 mm。通过拉伸实验测得外钢管的屈服强度(fy)、极限抗拉强度(fu)、弹性模量(Es)、泊松比(νs)和延伸率(δ)分别为362 MPa、434 MPa、200 GPa、0.27和30.0%。
1.2 试验装置与量测方案
试验装置如图3所示。试验过程中试件垂直放置,其顶端与加载横梁通过高强螺栓连接,底端与刚性底座固接。采用自带半球铰的100 t液压千斤顶对试件施加轴向压力。加载过程中通过油泵控制并随时补载以保持轴向力的恒定。为保证试件在受荷过程中轴压力始终保持竖直方向,竖向千斤顶与刚性梁之间通过滑轨连接。水平往复荷载由MTS伺服作动器施加在与之相连的加载横梁上。作动器和横梁之间通过8根高强螺栓连接。由于作动器自带球铰,因此在加载过程中可保证荷载始终和加载横梁保持垂直。试件与加载横梁刚接,通过MTS作动器的推拉力对试件施加成比例的弯矩和扭矩。

图3 试验装置
Fig.3 Test setup
荷载-位移关系数据由MTS系统自动采集,轴向变形和往复荷载作用方向的侧向位移利用位移计进行测量。此外,在构件的1/4处、1/2处和3/4处各架设1个位移计量测试件的侧向位移。由于在本试验施加的压弯扭复合荷载作用下,轴压力和扭矩沿试件轴线方向总体上均匀分布,而弯矩则从上至下线性增长,因此试件底部预期为应变发展最为充分的区域。但另一方面为了避免端部焊接区域的影响,故选取距试件底部200 mm处粘贴三向应变花,以量测试件在压-弯-扭加载过程中外钢管关键截面的横向、纵向和剪切应变发展,如图4所示。
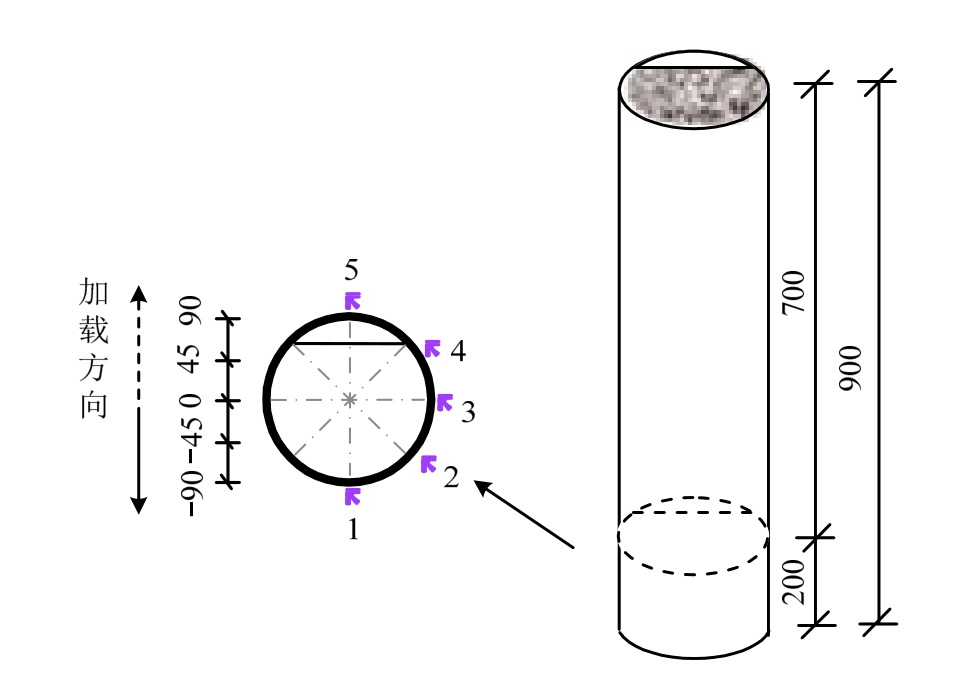
图4 应变片布置 /mm
Fig.4 Arrangements of strain gauges
1.3 加载方法
试验时首先施加轴向荷载并全程保持恒定,然后采用荷载-位移双控制方法施加水平荷载。在试件达到屈服强度前采用荷载分级控制加载,分别按0.25 Pmax、0.50 Pmax、0.70 Pmax进行加载,每级循环2次,其中Pmax为采用有限元方法预估的承载力,相关有限元模型在文献[10]和文献[27]中有详细描述,试件达到屈服强度后,采用位移控制加载,按1.0 Δy、1.5 Δy、2.0 Δy、3.0 Δy、5.0 Δy、7.0 Δy、8.0 Δy进行加载,前3级(1.0 Δy、1.5 Δy、2.0 Δy)均循3次,其余循环2次(其中Δy为试件的屈服位移,由0.7 Pmax来确定:Δy=0.7 Pmax/ Ksec,Ksec为荷载达到0.7 Pmax时荷载-变形曲线的割线刚度)。试验停机条件为作动器达到其最大运行范围。试验的加载制度如图5所示。
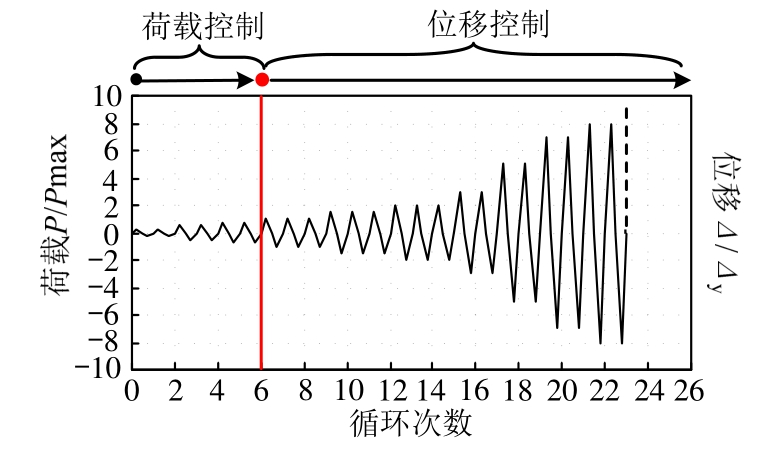
图5 加载制度示意图
Fig.5 Schematic view of loading protocol
试验的加载方法原理如图6所示,将水平作动器的荷载F对柱底截面进行简化,可以得到试件关键截面-柱底截面所受的弯矩和扭矩如下:
式中:H1为试件有效高度;L为加载点与试件几何中心距离;β为水平作动器与加载横梁的夹角。加载过程中,β值基本在90°,因而sinβ值均保持在1.0左右。弯扭比γ可简化定义如下:
由式(2)可知,不同弯矩和扭矩成比例加载可以通过变化H1/L的值来实现,H1为定值,通过改变加载位置L即可实现不同弯扭比值,弯扭比为0.9和1.8时,加载位置L分别为1000 mm和500 mm。
试件的扭转角(θ)与MTS作动器加载点位移以及试件柱顶位移的关系如下式所示:
式中:θ为构件的扭转角;Δ1为MTS作动器加载点位移;Δ2为构件柱顶位移。如图6(b)所示。
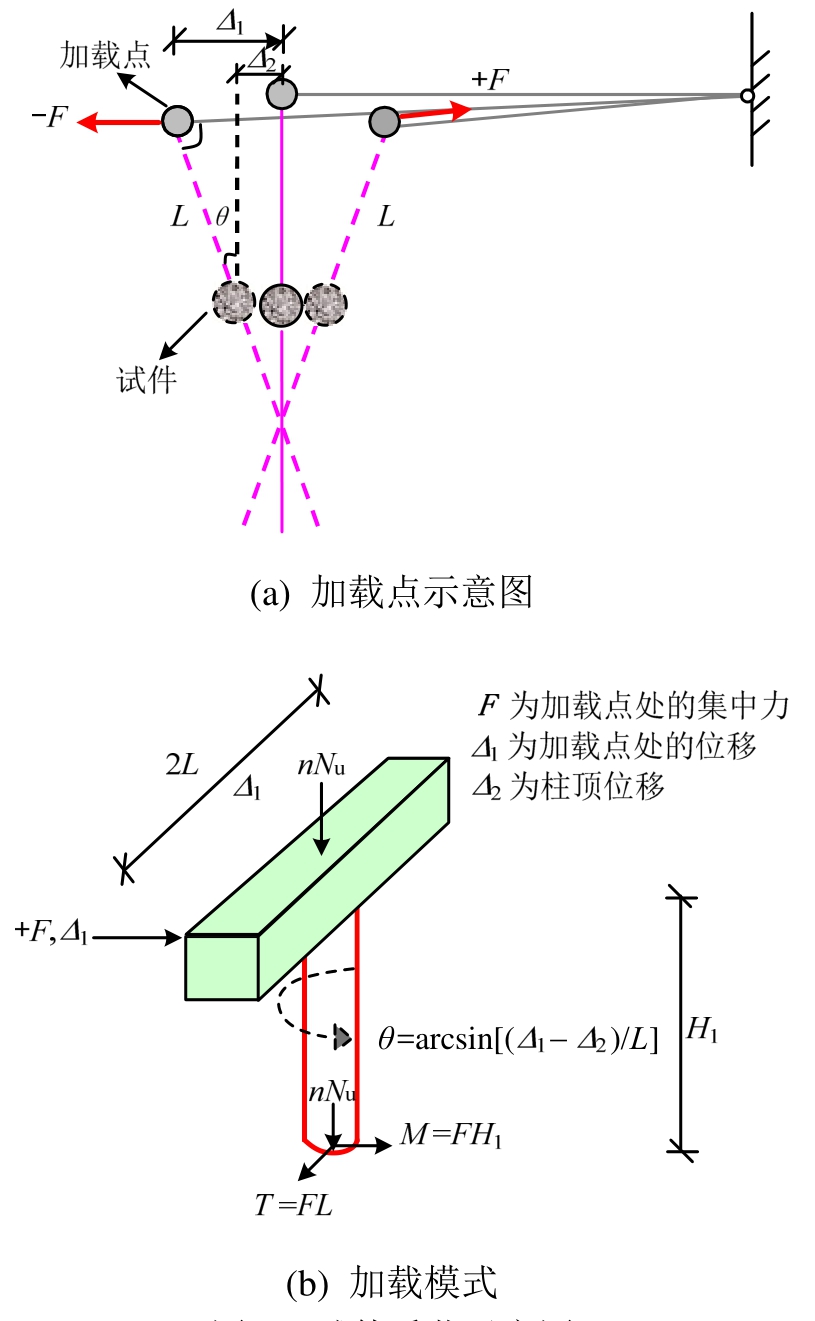
图6 试件受荷示意图
Fig.6 Schematic diagram of loading approach
2 试验结果与分析
2.1 破坏模态
所有试件均在作动器达到最大行程时停机。停机时,试件的侧向位移均超过100 mm,扭转角均超过0.08 rad,此时试件的荷载-变形关系曲线仍保持平缓上升,无下降段出现。典型试件的破坏模态如图7所示。对于空钢管试件,由于其钢管内无核心混凝土的支撑作用,因此在扭矩和弯矩耦合作用下试件钢管底部出现了较为明显的斜向鼓屈现象。而对于无脱空和带圆弓形脱空的试件,外钢管均未观察到有明显的破坏现象。试验结束后剖开钢管,其核心混凝土的破坏形态如图8所示,可见无脱空和带缺陷试件的核心混凝土均未见有明显的裂缝产生。由沿试件高度1/4、1/2和3/4处实测的侧向位移比较可知:试件越靠近底部的区域其侧向位移也相应越大,这主要是由于试件所承受的弯矩沿高度方向从上而下有增大的趋势。
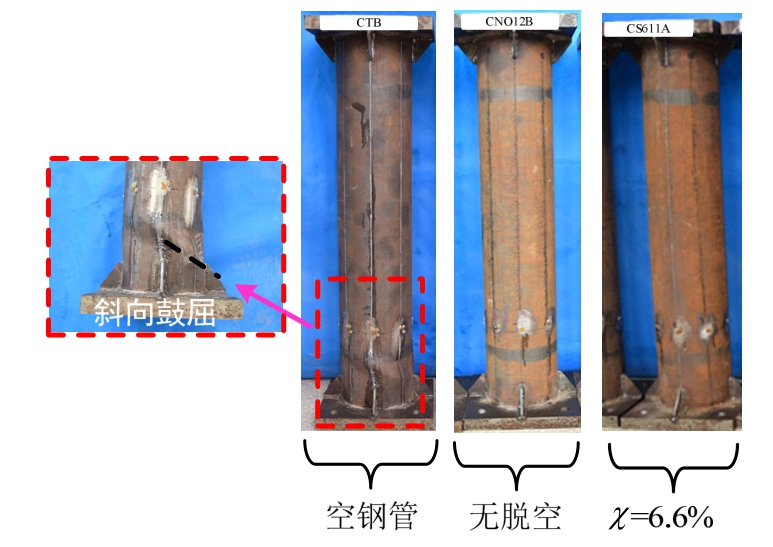
图7 典型试件破坏模态
Fig.7 Failure modes of typical specimens

图8 典型试件核心混凝土破坏形态
Fig.8 Failure modes of core concrete in typical specimens
2.2 滞回关系曲线
试验实测的侧向荷载(P)-侧向位移(Δ)滞回关系曲线如图9所示,扭矩(T)-扭转角(θ)扭转滞回关系曲线如图10所示(图中a和b代表试验参数相同的两根试件),其中扭矩(T)和扭转角(θ)为分别按照式(1b)和式(3)计算所得。由图9和图10可见:同组相同参数的两根试件其滞回关系曲线均较为接近。所有试件的滞回曲线均较为饱满,基本未观察到有“捏缩”现象,曲线的卸载刚度与弹性刚度基本一致。这是由于试件的圆形外钢管可为核心混凝土提供较强的约束作用,从而提高了混凝土的塑性性能;同时混凝土也为钢管提供支撑作用,从而延缓了钢管局部屈曲的发生。这种“组合作用”使钢管混凝土构件具有很好的耗能能力,其滞回曲线饱满,无捏缩现象发生。相较而言,小弯扭比(γ=0.9)的试件其滞回曲线比大弯扭比(γ=1.8)的试件更加饱满,表现出更好的耗能能力。这是由于:在试件有效高度(H1)不变的条件下,弯扭比减小则意味着扭转力臂(L)增大,从而在试件所承受的弯扭耦合作用中其扭转所占的比例相应增大。而相对与受弯作用,在扭转作用下钢管混凝土中的钢管对试件抗扭能力的贡献占了主导地位[1,27],比例大大超过核心混凝土,因此反映在试件的滞回曲线上则表现为滞回环更加饱满。总体而言,脱空缺陷对试件滞回曲线的形状影响不大。加载后期,钢管混凝土试件的荷载仍然保持着上升趋势,而空钢管试件的荷载则趋于平缓。
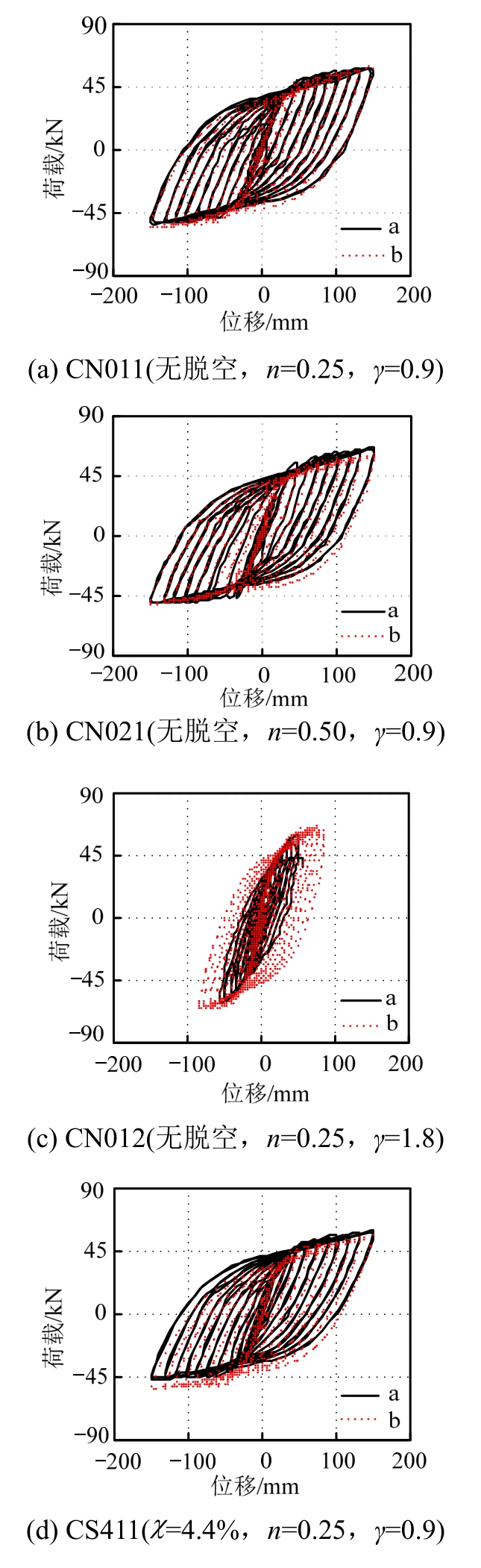
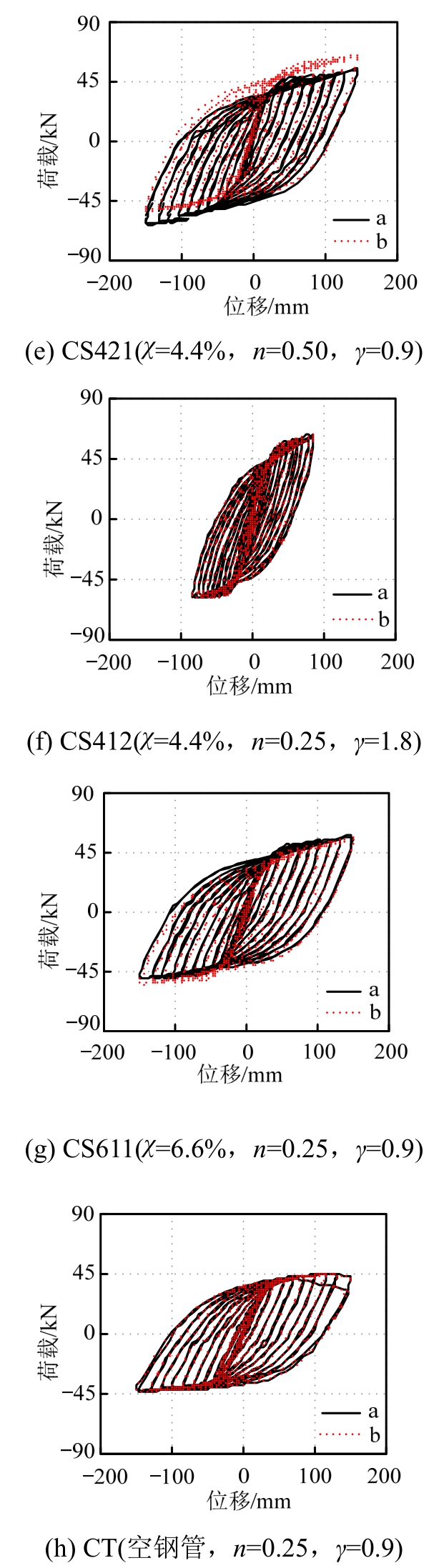
图9 侧向荷载(P)-侧向位移(Δ)滞回关系曲线
Fig.9 Lateral load (P)-Lateral displacement (Δ) hysteretic curves



图10 扭矩(T)-扭转角(θ)滞回关系曲线
Fig.10 Torsion moment (T)-torsion angle (θ) hysteretic curves
2.3 荷载-位移关系骨架曲线对比
试件的实测侧向荷载(P)-侧向位移(Δ)关系骨架曲线对比如图11所示,可见,所有试件的P-Δ骨架曲线均经历了弹性阶段、弹塑性阶段和强化(平缓)阶段等3个阶段。
图11(a)比较了无脱空试件、带缺陷试件和空钢管试件的P-Δ骨架曲线。可见,带缺陷试件的初始刚度与无脱空试件基本相同,而空钢管试件的初始刚度则明显低于钢管混凝土试件。在弹塑性阶段结束后,空钢管试件的荷载趋于平缓,而变形则急剧增大;无脱空试件由于核心混凝土和钢管间的“组合作用”,其P-Δ骨架曲线在加载后期具有显著的强化特征,荷载一直保持稳定上升直至试验停止;对于带缺陷试件,脱空缺陷的存在削弱了混凝土和钢管之间的“组合作用”,因此其曲线强化段的刚度较无脱空试件有所下降。随着脱空率的增大,试件刚度和承载力均有所降低。
由图11(a)和图11(b)比较可见,和无脱空试件相比,随着轴压比增大脱空缺陷对试件P-Δ骨架曲线的影响更加显著。这是由于脱空缺陷主要影响钢管混凝土试件的受压性能,而轴压比大的情况下,试件截面受压区面积相应较大,因此脱空影响则更为显著[5]。
由图11(a)和图11(c)比较可见,和无脱空试件相比,随着弯扭比增大脱空缺陷对试件P-Δ骨架曲线的影响同样有趋于显著的趋势。这是由于,钢管混凝土构件在受扭状态下主要依赖钢管和核心混凝土之间的粘结力来传递扭矩,而圆弓形脱空只是局部削弱二者之间的相互作用,对其整体扭矩传递的影响不大。但是在受弯状态下,当圆弓形脱空处于受压区时,其对构件受压性能的影响则较为显著,因此此类脱空缺陷对构件受弯性能的影响要更大一些。
由图11(d)可见,对于脱空率为4.4%的缺陷试件而言,在轴压比(n)为0.25时,随着弯扭比(γ)由0.9增大到1.8,缺陷试件的刚度和承载力都有所提升。这是由于:如式(2)所示,试件的γ取决于试件有效高度(H1)和加载点水平力臂(L)的比值,而在H1一定的情况下,提高弯扭比即意味着减小L值,因此试件底部所承受的弯矩和扭矩的耦合作用则相应较小,所以大弯扭比的试件其刚度和承载力较高。
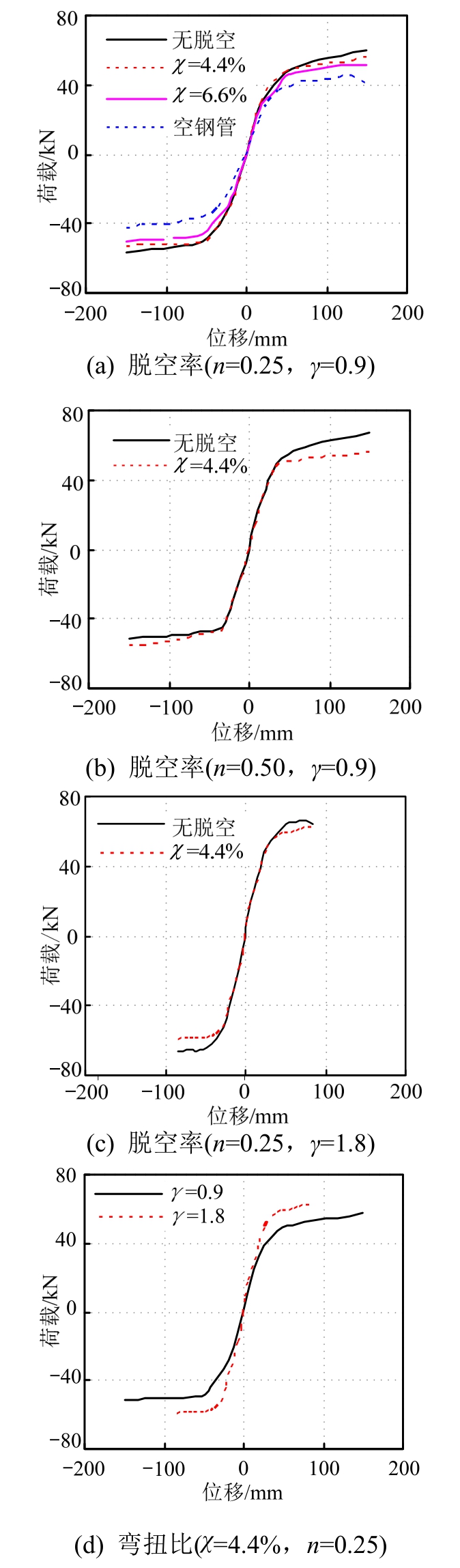
图11 侧向荷载(P)-侧向位移(Δ)关系骨架线比较
Fig.11 Comparisons of P-Δ envelope curves
2.4 抗侧和抗扭承载力比较
由于本文试验的钢管混凝土试件的荷载-位移关系曲线均没有出现下降段,因此参考文献[1]和文献[27]取试件的抗侧承载力(Pu)为构件截面边缘剪应变(即图4中的5号剪应变)达到10000 με时所对应的荷载值。这是由于:根据文献[27]对大量钢管混凝土受扭构件的全过程分析结果表明,当构件边缘剪应变达10000 με后,构件的扭矩-扭转角关系曲线变化趋于平缓,扭矩值增长不大,但构件变形则急剧增大。剪应变的计算公式如下:
式中:εa为测点的竖向正应变;εb为测点的水平环向正应变;εc为测点的斜向45°正应变。试件的抗扭承载力(Tue)可由对应的抗侧承载力通过式(1b)计算得到。
各试件抗侧承载力和抗扭承载力的对比如图12所示。由图12(a)可见:在轴压比(n)为0.25,弯扭比(γ)为0.9时,试件的抗侧承载力和抗扭承载力大小相等,表明作用于试件底部的弯矩作用和扭矩作用基本相当。随着脱空率的增大,试件的抗侧承载力和抗扭承载力均略有下降。文献[5]的研究结果表明:圆弓形脱空的存在会部分削弱钢管和核心混凝土之间的“组合作用”,混凝土截面依据离脱空位置的距离和受脱空影响程度可以分为无约束区、半约束区和全约束区。在压弯扭耦合作用下,脱空处的钢管和混凝土之间的荷载传递路径中断,二者在脱空区域内无法共同工作以抵抗扭矩作用,因此导致试件承载力随脱空率的增大而有所降低。
图12(b)所示为轴压比对带缺陷试件承载力的影响。可见,在脱空率(χ)为4.4%、弯扭比(γ)为0.9时,轴压比(n)由0.25增大至0.50,试件承载力略微有所提高,但总体变化不大。
由图12(c)可见随着弯扭比的增大,缺陷试件(χ=4.4%)的抗侧承载力有所增大,而抗扭承载力则有所降低。这是由于弯扭比(γ)由0.9变化为1.8时,由于扭转力臂减小,因此扭矩作用有所降低,而弯矩作用则相应有所提高。
2.5 承载力系数(SI)比较
为了便于分析不同轴压比和弯扭比组合下圆弓形脱空缺陷对钢管混凝土压弯扭试件抗侧承载力的影响,定义承载力系数(SI)如下:

式中:Pu为试件实测的抗侧承载力;Pu-no gap为对应试验参数相同的无脱空试件实测的抗侧承载力。

图12 承载力对比
Fig.12 Comparisons of bearing capacity
试件的SI值列于表1中,图13比较了不同参数对试件SI值的影响。可见,在轴压比(n)为0.25、弯扭比(γ)为0.9时,脱空率为4.4%的试件其承载力较无脱空试件降低了约5.0%,当脱空率增大为6.6%时承载力降幅增大为约9.0%。对于脱空率为4.4%的试件,当弯扭比为0.9、轴压比为0.50时,其承载力较无脱空试件降低了约7.0%;当弯扭比为1.8、轴压比为0.25时,其承载力较无脱空试件降低了约5.0%。由此可见,圆弓形脱空对试件承载力的影响随轴压比增大有更加显著的趋势,这可能是因为脱空主要影响试件的受压性能,而轴压比增大则使试件的受压区面积有所增大,因此受脱空的影响程度则相应更加明显。由图13还可见:带缺陷试件的承载力系数受弯扭比变化的影响并不显著。此外,在脱空率χ=4.4%和6.6%的情况下,其脱空面积(Agap)占试件横截面面积(Asc)的比例为1.5%和2.8%,而在本文试验参数范围内脱空缺陷试件的抗侧承载力较无脱空试件下降了5.0%~9.0%,由此可见圆弓形脱空对钢管混凝土压弯扭承载力的影响并不仅仅在于减小了混凝土截面积,也在于削弱了钢管和混凝土之间的“组合作用”。

图13 脱率对承载力系数(SI)的影响
Fig.13 The effect of gap ratio on the strength index (S I)
2.6 刚度退化
用滞回环峰值点等效刚度(割线刚度)来表示试件的刚度退化,其定义如下[28]:
式中:Ki为试件加载至第i级循环的等效刚度;Pi为试件加载至第i级时的峰值荷载;Δi为试件加载至第i级峰值荷载所对应的位移。
图14所示为各试件的刚度退化曲线比较。可见,试件的刚度随着加载位移增大而降低,且在加载后期其下降速度有减弱的趋势。由图14(a)可见:总体而言,脱空率对试件刚度退化趋势的影响并不显著。到试验停机时,脱空率为4.4%和6.6%的试件其等效刚度较无脱空试件降低了约7.1%和8.9%,而空钢管试件则降低了约26.2%。
由图14(b)可见:轴压比对带缺陷试件(χ=4.4%)的刚度退化速度影响较小;而随着弯扭比的增大,试件的刚度退化速度有增大的趋势。
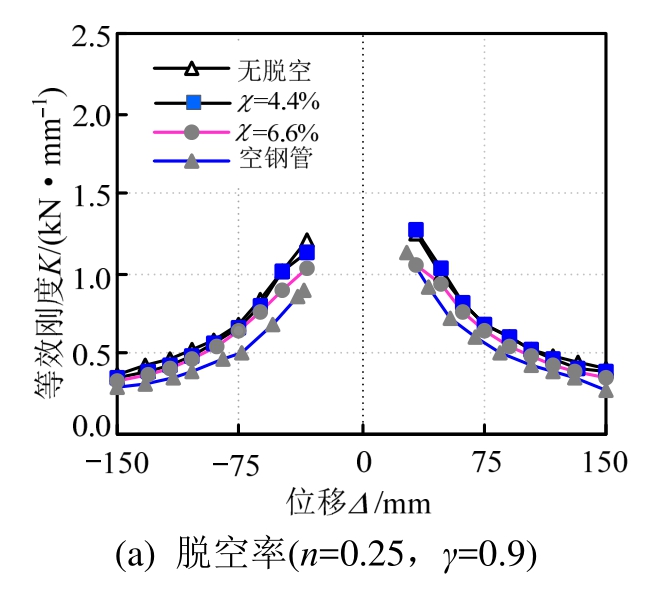
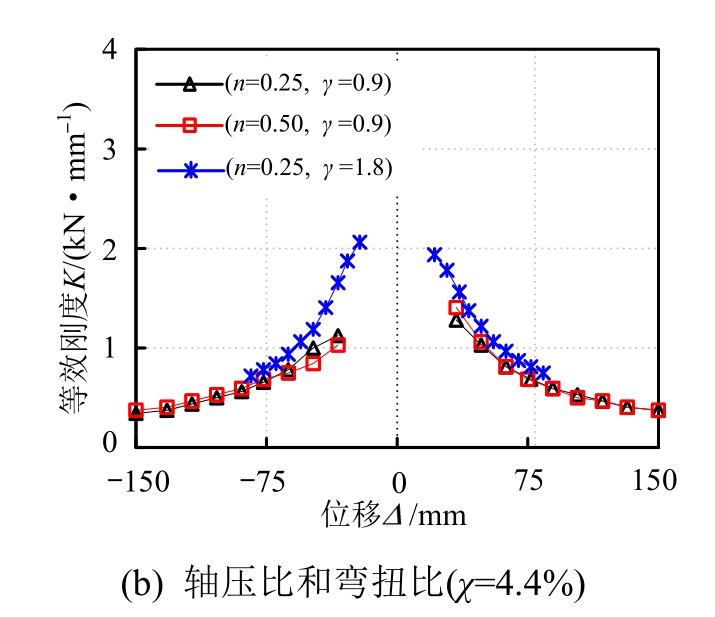
图14 试件等效刚度比较
Fig.14 Comparisons of the equivalent stiffness of specimens
2.7 耗能分析
采用等效粘滞阻尼系数来评估本文试件的耗能特性。等效粘滞阻尼系数的计算参考文献[29]。
如图15所示,等效粘滞阻尼系数hc可根据滞回环A-B-C-D的面积进行计算[29]:

式中:hc为等效粘滞阻尼系数;SADC和SABC分别为弧线ADC和ABC与坐标轴所围成的面积,二者之和为滞回环包含的实际面积;SDOF和SBOE分别为三角形(如图15所示阴影区域)面积,代表试件的弹性能。
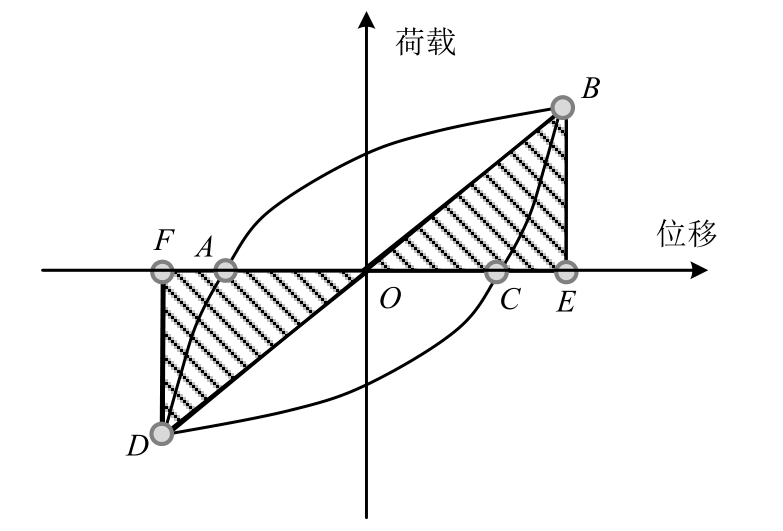
图15 荷载-位移滞回环
Fig.15 P-Δ hysteretic cycle
由式(7)计算所得的本文试件的等效粘滞阻尼系数在0.351~0.462之间,如图16所示。图16(a)可见,圆弓形脱空缺陷的存在不仅会降低钢管混凝土试件的承载力,也会影响其在地震作用下的耗能能力,如在轴压比(n)为0.25、弯扭比(γ)为0.9时,脱空率(χ)4.4%和6.6%的试件其等效粘滞系数较无无脱空试件降幅超过11%,而空钢管试件则降低了约15.8%。对于带缺陷的钢管混凝土试件,随着轴压比增大其等效粘滞阻尼系数略有降低,而弯扭比由0.9增至1.8时,带缺陷试件的等效粘滞系数则显著降低,降幅达到13.8%,如图16(b)所示。这表明相较于受扭,脱空缺陷对钢管混凝土受弯力学性能的影响更为显著。

图16 等效粘滞系数比较
Fig.16 Comparisons of the equivalent viscous damping coefficient
2.8 应变分析
图17比较了在轴压比(n)为0.25,弯扭比(γ)为0.9时,脱空对试件中截面轴向应变发展的影响,其中应变点1、应变点2、应变点3、应变点4和应变点5分别处于距试件截面中轴-90 mm、-45 mm、0 mm、45 mm、90 mm的位置。在图17中,0.2 Pu、0.6 Pu和0.8 Pu分别代表了荷载水平为极限承载力的20%、60%和80%时截面各点的轴向应变。可见,脱空缺陷对试件截面轴向应变发展的影响并不显著。在靠近中和轴位置,试件截面轴向应变值很小,而在远离中和轴位置,试件在弯矩作用下其轴向应变发展得较为充分。在荷载水平为0.2 Pu时,同一截面不同位置上的5个测点其轴向应变值基本呈线性分布,而当加载至0.6 Pu和0.8 Pu时,由于扭转作用的影响,试件截面的轴向应变表现出较为明显的非线性特征。

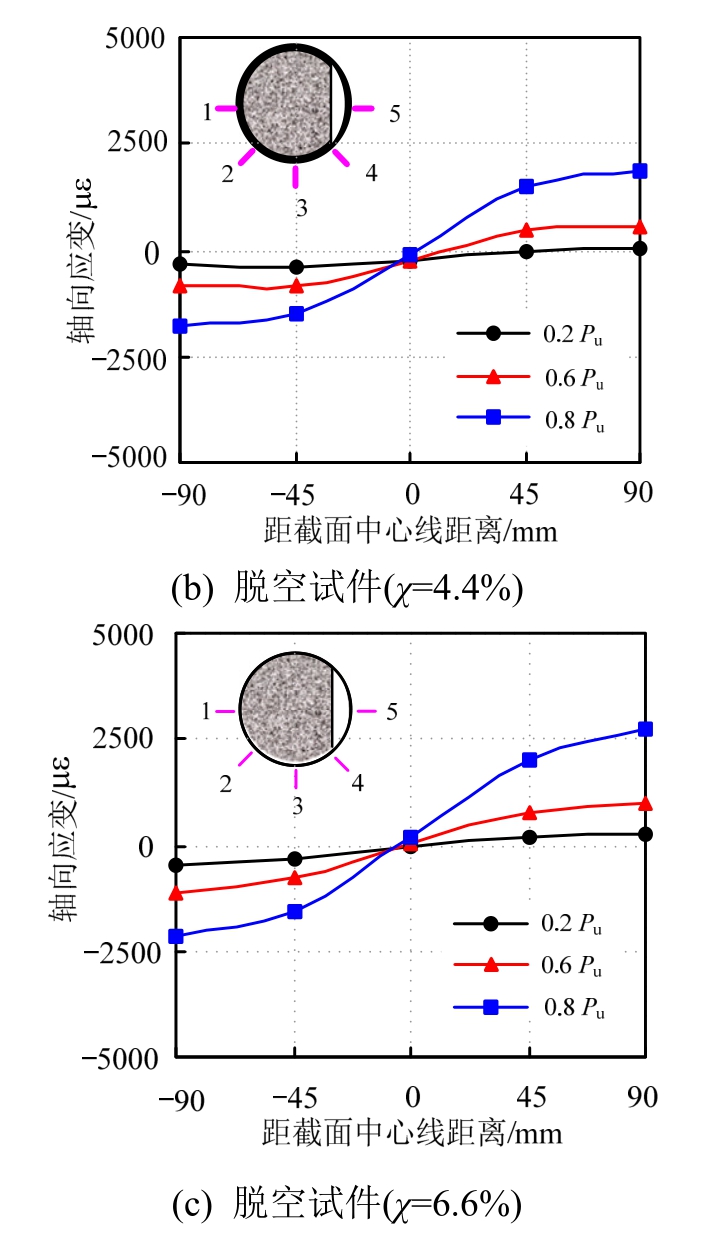
图17 不同荷载水平下轴向应变比较
Fig.17 Comparisons of axial strain strain of steel tube at different load levels
图18所示为不同荷载水平下钢管横向应变的发展比较。可见和无脱空试件相比,带缺陷试件在脱空处的横向应变(5号应变)发展更为充分,且随着脱空率的增大该趋势愈加显著。这主要是由于,脱空缺陷的存在导致外钢管所承担的扭矩在脱空处无法传递给核心混凝土,因此钢管在该位置的扭转变形发展较快,从而钢管的横向应变发展相应较为充分。


图18 不同荷载水平下钢管横向应变比较(n=0.25, γ=0.90)
Fig.18 Comparisons of transverse strain of steel tube at different load levels(n=0.25, γ=0.90)
图19比较了在轴压比(n)为0.25,弯扭比(γ)为0.90时,不同脱空率(χ=0.0%、4.4%和6.6%)下试件钢管表面5个测点在不同荷载水平下的剪应变分布,以分析脱空缺陷对于扭转作用所产生的钢管剪应变发展的影响规律。由图19(a)可见,对于无脱空试件其各点剪应变发展较为均匀,这与文献[24]中的研究结果一致。而对于带圆弓形脱空缺陷的钢管混凝土试件,在加载至0.2 Pu时其剪应变发展与无脱空试件十分接近。之后,随着荷载水平的增大,脱空处的钢管由于缺乏核心混凝土的支撑作用,在扭转作用下其剪应变发展更为迅速,在加载至0.8 Pu时,脱空处的剪应变值明显大于其他区域。
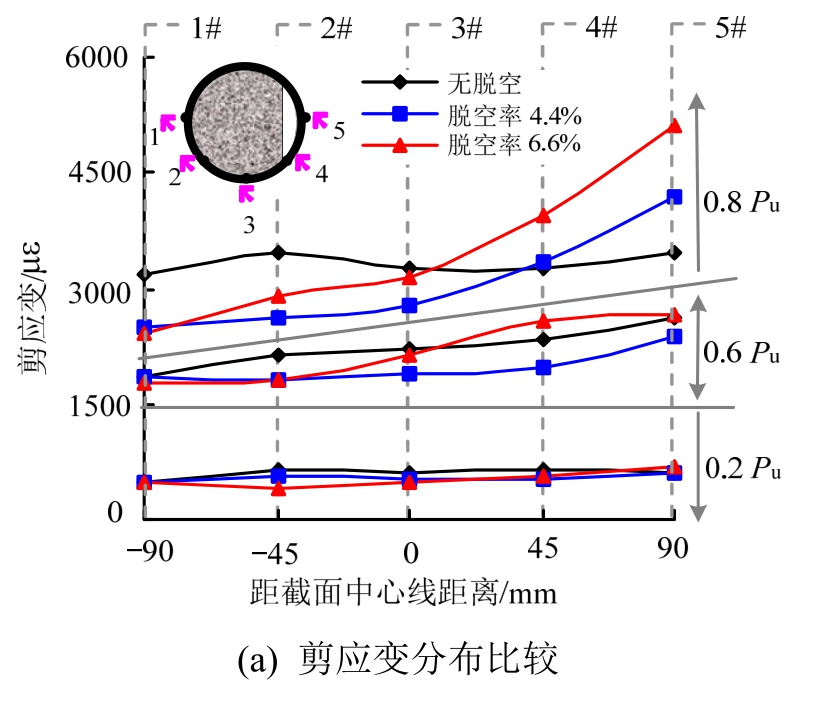
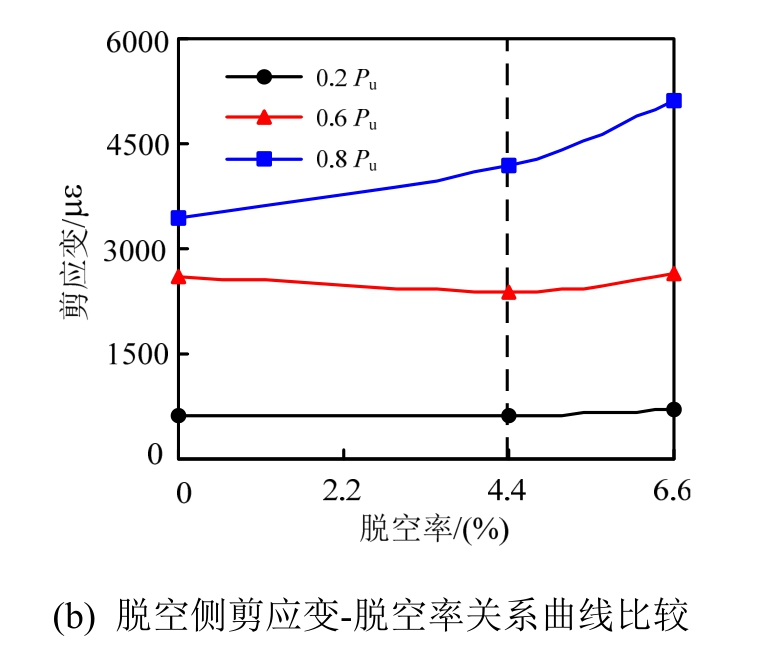
图19 不同荷载水平下的剪应变比较
Fig.19 Comparisons of shear strain of steel tube at different load levels
图19(b)给出了脱空处(5号应变)的剪应变-脱空率关系曲线比较,可见在荷载水平较低时(0.2 Pu或0.6 Pu),脱空率的改变对试件剪应变的影响并不明显,而当荷载水平达到0.8 Pu时,随着脱空率的增大,试件脱空处的剪应变有明显增大的趋势。
3 结论
本文完成了16个钢管混凝土试件在压弯扭复合受力作用下的滞回性能试验,在本文试验参数范围内可得到以下结论:
(1)空钢管试件由于缺少核心混凝土的有效支撑,钢管底部在弯矩和扭矩的共同作用下出现了斜向鼓屈现象,而带圆弓形脱空的试件和无脱空试件的破坏现象均不显著,其核心混凝土也未观察到有明显的破坏特征。
(2)总体而言,圆弓形脱空缺陷对钢管混凝土试件滞回曲线的形状影响不大,但是带缺陷试件的荷载—变形关系骨架线的强化段刚度较无脱空试件有所下降,且随着脱空率的增大,试件的刚度和承载力均有所降低。
(3)脱空缺陷的存在会削弱钢管和混凝土之间的“组合作用”,因此不仅使试件承载力有所降低,且导致其耗能能力下降,同时刚度退化加剧。与无脱空钢管混凝土压弯扭试件相比,脱空率为4.4%时,试件的极限承载力、等效刚度和等效粘滞阻尼系数分别降低了7.0%、7.1%和11.0%;脱空率为6.6%时,则分别降低了9.0%、8.9%和11.2%。
(4)变化轴压比(n=0.25, n=0.50)对带缺陷试件的极限承载力、等效刚度和耗能能力的影响并不明显。随着弯扭比的增大,脱空缺陷对试件极限承载力、等效刚度和耗能能力的影响有趋于显著的趋势,表明相较于受扭作用,脱空对钢管混凝土受弯性能的影响更为显著。
(5)脱空缺陷对试件截面轴向应变发展的影响并不显著,但随着荷载水平的增大,脱空处的钢管由于缺乏核心混凝土的支撑作用,其在扭转作用下横向应变和剪应变发展更为迅速,在较大荷载水平时脱空处的剪应变值明显大于其他区域。
本文的试验结果可为实际工程中钢管混凝土结构的安全评估提供参考,也为相关理论研究提供试验数据验证。
[1]韩林海.钢管混凝土结构-理论与实践[M].第三版.北京: 科学出版社, 2016: 30―66, 281―286.Han Linhai.Concrete filled steel tubular structurestheory and practice [M].3rd ed.Beijing: Science Press,2016: 30―66, 281―286.(in Chinese)
[2]史艳莉, 周绪红, 鲜威, 等.无端板矩形钢管混凝土构件基本剪切性能研究[J].工程力学, 2018, 35(12): 25―33.Shi Yanli, Zhou Xuhong, Xian Wei, et al.Research on basic shear performance of concrete filled rectangular steel tubular members without end-plate [J].Engineering Mechanics, 2018, 35(12): 25―33.(in Chinese)
[3]陈宝春, 韦建刚, 周俊, 等.我国钢管混凝土拱桥应用现状及展望[J].土木工程学报, 2017, 50(6): 50―61.Chen Baochun, Wei Jiangang, Zhou Jun, et al.Application of concrete filled steel tube arch bridges in China: current status and prospects [J].China Civil Engineering Journal, 2017, 50(6): 50―61.(in Chinese)
[4]柯晓军, 苏益声, 商效瑀, 等.钢管混凝土组合柱压弯性能试验及承载力计算[J].工程力学, 2018, 35(12):134―142.Ke Xiaojun, Su Yisheng, Shang Xiaoyu , et al.Strength calculation and eccentric compressive test of steel tube-reinforced concrete composite columns [J].Engineering Mechanics, 2018, 35(12): 134―142.(in Chinese)
[5]Liao F Y, Han L H, He S H.Behavior of CFST short column and beam with initial concrete imperfection:Experiments [J].Journal of Constructional Steel Research, 2011, 67(12): 1922―1935.
[6]邵志向, 任更锋, 房永祥.有脱空缺陷钢管混凝土补强技术分析[J].广西大学学报(自然科学版), 2018,43(1): 126―131.Shao Zhixiang, Ren Gengfeng, Fang Yongxiang.Reinforce technical analysis of concrete-filled steel tube with cementation deviating [J].Journal of Guangxi University (Natural Science Edition), 2018, 43(1): 126―131.(in Chinese)
[7]徐礼华, 宋杨, 刘素梅, 等.多腔式多边形钢管混凝土柱偏心受压承载力研究[J].工程力学, 2019, 36(4):135―146.Xu Lihua, Song Yang, Liu Sumeiet, et al.Study on the eccentric compressive bearing capacity of polygonal multi-cell concrete filled steel tubular columns [J].Engineering Mechanics, 2019, 36(4): 135―146.(in Chinese)
[8]Liao F Y, Han L H, Tao Z.Behavior of CFST stub columns with initial concrete imperfection: analysis and calculations [J].Thin-Walled Structures, 2013, 70(13):57―69.
[9]Han L H, Ye Y, Liao F Y.Effects of core concrete initial imperfection on performance of eccentrically loaded CFST columns [J].Journal of Structural Engineering,ASCE, 2016, 142(12): 04016132.
[10]韩浩, 廖飞宇, 李永进.脱空缺陷对钢管混凝土滞回性能的影响分析[J].工业建筑, 2017, 47(9): 146―151.Han Hao, Liao Feiyu, Li Yongjin.Effect of spherical-cap gap on hysteretic behaviour of concrete-filled steel tubular columns [J].Industrial Construction, 2017, 47(9):146―151.(in Chinese)
[11]王宇航, 郭一帆, 刘界鹏, 等.偏压荷载下钢管混凝土柱的抗扭性能试验研究[J].土木工程学报, 2017,50(7): 50―61.Wang Yuhang, Guo Yifan, Liu Jiepeng, et al.Experimental study on behaviour of concrete filled steel tube columns under torsion and eccentric compression[J].China Civil Engineering Journal, 2017, 50(7): 50―61.(in Chinese)
[12]马恺泽, 梁兴文, 李斌.高轴压比方钢管高强混凝土柱抗震性能研究[J].工程力学, 2010, 27(3): 155―162.Ma Kaize, Liang Xingwen, Li Bin.Aseismic behavior of high strength concrete-filled rectangular steel tubular columns with high axial load ratio [J].Engineering Mechanics, 2010, 27(3): 155―162.(in Chinese)
[13]Wang J F, Zhang L, Spencer J BF.Seismic response of extended end plate joints to concrete-filled steel tubular columns [J].Engineering Structures, 2013, 49(4): 876―892.
[14]Tu Y Q, Shen Y F, Zeng Y G, et al.Hysteretic behavior of multi-cell T-Shaped concrete-filled steel tubular columns [J].Thin-Walled Structures, 2014, 85(11):106―116.
[15]Liu C Y, Wang Y Y, Wang W, et al.Seismic performance and collapse prevention of concrete-filled thin-walled steel tubular arches [J].Thin-Walled Structures, 2014,80(6): 91―102.
[16]陈宗平, 张向冈, 薛建阳, 等.圆钢管再生混凝土柱抗震性能与影响因素分析[J].工程力学, 2016, 33(6):129―137.Chen Zongping, Zhang Xianggang, Xue Jianyang, et al.Analysis on aseismic performance and influence factors of recycled concrete filled circular steel-tube columns[J].Engineering Mechanics, 2016, 33(6): 129―137.(in Chinese)
[17]范重, 王倩倩, 李振宝, 等.大直径钢管混凝土柱抗震性能试验研究及承载力计算方法[J].建筑结构学报,2017, 38(11): 34―41.Fan Zhong, Wang Qianqian, Li Zhenbao, et al.Experimental study on seismic behavior of CFST columns with large diameter and calculation of bearing capacities [J].Journal of Building Structures, 2017,38(11): 34―41.(in Chinese)
[18]王成刚, 柳炳康, 周健, 等.方钢管再生混凝土中长柱抗震性能试验研究[J].工业建筑, 2017, 47(4):159―165.Wang Chenggang, Liu Bingkang, Zhou Jian, et al.Experimental research on seismic behavior of slender square steel tubular columns filled with recycled aggregate concrete [J].Industrical Construction, 2017,47(4): 159―165.(in Chinese)
[19]罗金辉, 李元齐, 张元植, 等.设分配梁与内环板传力构造的巨型钢管混凝土柱抗震性能试验研究[J].土木工程学报, 2018, 51(4): 34―44.Luo Jinhui, Li Yuanqi, Zhang Yuanzhi, et al.Experimental study on seismic performance of giant CFT columns with distributive beam and inner diaphragms as load-transfer detailing [J].China Civil Engineering Journal, 2018, 51(4): 34―44.(in Chinese)
[20]Tang Y C, Li L J, Feng W X, et al.Study of seismic behavior of recycled aggregate concrete-filled steel tubular columns [J].Journal of Constructional Steel Research, 2018, 148(9): 1―15.
[21]董宏英, 谢翔, 曹万林, 等.圆钢管再生混凝土柱抗震性能试验[J].天津大学学报(自然科学与技术版),2018, 51(10): 1096―1106.Dong Hongying, Xie Xiang, Cao Wanlin, et al.Experimental on seismic performance of recycled aggregate concrete filled circular steel tube columns [J].Journal of Tianjin University(Science and Technology),2018, 51(10): 1096―1106.(in Chinese)
[22]Wang J T, Sun Q, Li J X.Experimental study on seismic behavior of high-strength circular concrete-filled thin-walled steel tubular columns [J].Engineering Structures, 2019, 182(3): 403―415.
[23]聂建国, 王宇航, 樊建生.钢管混凝土柱在纯扭和压扭荷载下抗震性能研究[J].土木工程学报, 2014,47(1): 47―58.Nie Jiangguo, Wang Yuhang, Fan Jiansheng.Study on seismic behavior of concrete filled steel tube columns under pure torsion and compression-torsion combined action [J].China Civil Engineering Journal, 2014, 47(1):47―58.(in Chinese)
[24]Nie J G, Wang Y H, Fan J S.Experimental research on concrete filled steel tube columns under combined compression-bending-torsion cyclic load [J].ThinWalled Structures, 2013, 67(2): 1―14.
[25]Wang Y H, Zhou X H.Non-linear torsion behaviour of concrete filled steel tube columns [J].Materials and Structures, 2016, 49(12): 5227―5241.
[26]Wang Y H, Nie J G, Fan J S.Fiber beam-column element for circular concrete filled steel tube under axial-flexure-torsion combined load [J].Journal of Constructional Steel Research, 2014, 95(4): 10―21.
[27]尧国皇.钢管混凝土构件在复杂受力状态下的工作机理研究[D].福州: 福州大学, 2006: 195―202, 237―242.Yao Guohuang.Reasarch on behaiour of concrete-filled steel tubes subjected to complicated loading states [D].Fuzhou: Fuzhou University, 2006: 195―202, 237―242.(in Chinese)
[28]Liao F Y, Han L H, Tao Z.Behavior of composite joints with concrete encased CFST columns under cyclic loading: Experiments [J].Engineering Structures, 2014,59(2): 745―764.
[29]唐九如.钢筋混凝土框架节点抗震[M].南京: 东南大学出版社, 1989: 311―316.Tang Jiuru.Seismic Joints of concrete filled steel framework [M].Nanjing: Southeast University Press,,1989: 311―316.(in Chinese)