不锈钢优异的耐腐蚀性、全生命周期维护成本低、良好抗冲击性能和加工性能等优点使其在工程上的应用越来越广泛。在实际工程中,柱构件往往处于压弯状态,如偏心受压柱和水平荷载作用下的轴心受压柱以及由于制造误差等其他原因造成很多存在初始缺陷的轴心受压柱构件等,因此,本文将压弯构件的整体稳定承载性能作为研究重点。与普通钢相比,不锈钢材料具有非线性的应力-应变关系、较低的比例极限和明显的应变硬化特性[1-2],如果采用针对理想弹塑性钢材提出的设计计算方法存在明显的不合理性,因此,近年来国内外相关学者针对不锈钢压弯构件的整体稳定性能开展了一定的研究工作。舒赣平等[3]对比了国外不锈钢规范中压弯构件平面内稳定的设计方法,并结合不锈钢轴心受压构件稳定承载能力的研究成果,考虑不锈钢材料力学性能的离散性,提出不锈钢压弯构件平面内整体稳定的计算公式。员翔等[4]对奥氏体不锈钢冷弯方钢管进行了有限元研究,通过拟合得到了不锈钢方管偏心受压构件平面内整体稳定承载力的下限式及线性相关公式。Zheng等[5]进行了奥氏体不锈钢方管和焊接工字形压弯构件进行了试验研究,并将试验数据与现行的欧洲和美国规范 进行对比,提出了基于美国规范的改进方法。Lui等[6]对20个双相型不锈钢方管进行了偏心加载试验,将试验数据与美国和澳大利亚规范进行了对比,结果表明规范计算方法偏于保守。Huang和Young[7-8]进行了双相型不锈钢方管偏心加载试验和有限元研究。Zhao等[9-11]对不同截面形状和材料等级的不锈钢压弯构件进行了一系列的试验和数值研究,并对已有规范的计算方法进行了评估并提出了新的设计方法。但是,不锈钢压弯构件整体稳定性能的已有研究主要还是集中在冷成型不锈钢构件,对热轧焊接构件的研究较少。
目前,《不锈钢结构技术规程》(CECS 410―2015) [12]中关于压弯构件承载力的相关计算主要还是采用了我国冷弯薄壁型钢结构规范中的相关规定,计算公式中并未考虑构件的塑性发展。但是,相对于冷弯薄壁截面,焊接截面构件则可以组合较厚的板件以满足更大的承载力需求,且在受弯情况下截面通常有一定的塑性发展[13-14],因此需要进一步研究。
本文将在已有试验的基础上,利用有限元软件ANSYS对不锈钢焊接工字形和箱形截面压弯构件的整体稳定性能进行研究。利用验证的有限元模型开展参数分析,根据有限元分析结果对CECS 410―2015中计算方法的精确性进行评估,并提出改进的计算方法。
1 试验概况
本文进行的有限元研究基于已完成的试验研究[15],文献[15]开展了30个焊接不锈钢压弯构件静力加载试验,包括5个奥氏体型和5个双相型不锈钢焊接箱形截面柱,10个奥氏体型和10个双相型不锈钢焊接工字形截面柱。在试验之前对各构件的几何参数和整体缺陷进行实测;试验得到了不锈钢板材的拉伸试验应力-应变曲线、不锈钢压弯构件的失稳模态以及试验荷载-位移曲线。
构件的截面示意图如图1所示。试件实测尺寸如表1和表2所示,试件编号中的第一个字母S表示箱形截面,H或I分别代表工字型试件绕弱轴失稳和绕强轴失稳,304和2205分别代表奥氏体型和双相型不锈钢,2500代表试件设计长度,单位为mm,最后的数字1或2表示两试件偏心距不同;e为实测荷载偏心距,L为构件几何长度,Lt为构件端部单刀铰支座的转动中心距离(Lt=L+340),λ为长细比(λ=Lt/i,i为回转半径)。
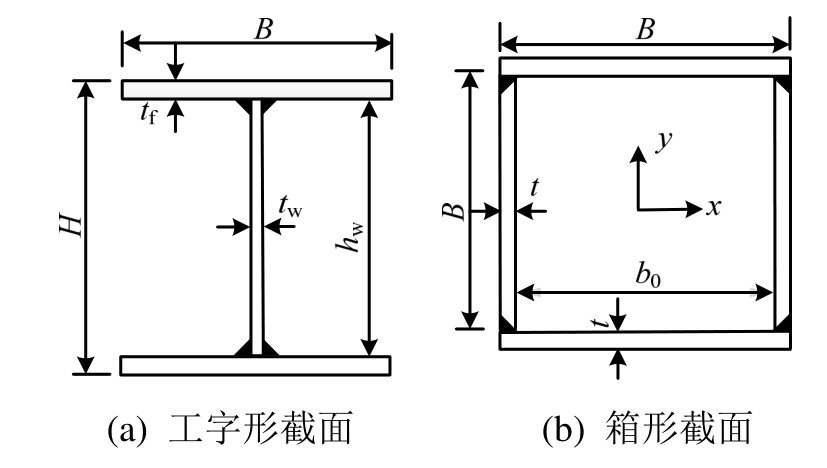
图1 构件截面尺寸符号示意图
Fig.1 Symbolic illustration for cross-sectional geometry of specimens
表1 工字形截面构件实测尺寸[15]
Table 1 Measurements of of I-section specimens

试件编号 B/mmH/mmtf/mm tw/mm e/mm L/mmLt/mm H304-2500 150140 10 6 57 24972837 H304-3000-1150140 10 6 49 29953335 H304-3000-2150140 10 6 70 29963336 H304-4000-1150140 10 6 50 39964336 H304-4000-2150140 10 6 57 39954335 H2205-2500150140 10 6 56 25012841 H2205-3000-1150140 10 6 50 29973337 H2205-3000-2150140 10 6 70 29963336 H2205-4000-1150140 10 6 49 39974337 H2205-4000-2150140 10 6 60 39994339 I304-2500 150140 10 6 41 24962836 I304-3000-1 150120 10 6 50 29963336 I304-3000-2 150120 10 6 71 29993339 I304-4000-1 150120 10 6 50 40164356 I304-4000-2 150120 10 6 61 40154355 I2205-2500 150120 10 6 58 24982838 I2205-3000-1150120 10 6 51 29983338 I2205-3000-2150120 10 6 70 29983338 I2205-4000-1150120 10 6 50 39964336 I2205-4000-2150120 10 6 56 39974337
表2 箱形截面构件实测尺寸[15]
Table 2 Measurements of box-section specimens

试件编号 B/mm t/ mme/ mm L/mm Lt/mm S304-2500 130.5 5.85 60.3 2497 2837 S304-3000-1 131.8 5.85 48.3 2993 3333 S304-3000-2 131.5 5.85 70.0 2992 3332 S304-4000-1 131.2 5.85 47.7 3994 4334 S304-4000-2 131.4 5.85 56.4 4012 4352 S2205-2500 131.7 5.87 58.0 2495 2835 S2205-3000-1 131.4 5.87 54.4 2999 3339 S2205-3000-2 131.0 5.87 70.6 2999 3339 S2205-4000-1 131.0 5.87 50.4 4017 4357 S2205-4000-2 131.5 5.87 58.6 4016 4356
2 有限元模型的建立与验证
2.1 有限元模型的建立
2.1.1 单元的选择和边界条件
采用Shell181单元进行建模,该单元属于平面壳单元,适合对薄壳和中等厚度的壳体结构进行分析。试验研究中采用单刀铰模拟两端铰接的约束条件,为了更准确地模拟试验过程,有限元模型中对相应的自由度进行释放。
2.1.2 不锈钢材料的本构模型
为了能够准确地模拟试验,有限元模型中的材料模型采用ANSYS提供的多线性随动强化模型(KINH),模型中输入的应力-应变曲线为文献[15]材性试验得到的平均值,如图2所示。

图2 不锈钢材料应力-应变曲线[15]
Fig.2 Stress-strain curves of stainless steel
2.1.3 构件的几何初始缺陷和残余应力分布
在有限元模型中考虑了几何初始缺陷和残余应力的影响。引入的残余应力模型为文献[16]提出的焊接不锈钢构件残余应力模型,残余应力分布模式如图3所示。在ANSYS使用命令INISTATE将残余应力数值施加到模型中。

图3 残余应力分布模式[16]
Fig.3 The distribution of residual stress
采用更新节点坐标的方法施加构件的几何初始缺陷,即根据压弯构件的第1阶特征值屈曲模态作为变形状态,根据文献[15]试件几何初始缺陷的实测值确定更新模型的比例系数,利用ANSYS中的UPGEOM命令将实测值作为一阶模态的最大位移添加在构件上。
2.2 有限元模型的验证
将有限元得到的构件承载力、荷载-位移曲线和失稳模态与试验结果分别进行比较。
图4为有限元失稳模态和试验结果对比,有限元和试验均为整体失稳,未发生扭转和局部失稳。
图5给出了部分构件的荷载-柱中水平位移曲线的试验和有限元结果对比情况,从图中可以看出有限元得到的荷载-位移曲线和试验曲线具有相同的发展趋势。表3为试验和有限元承载力Pexp和PFE对比结果,构件承载力的试验值和有限元值的误差均小于10%,平均误差在5%左右,说明该有限元模型能够较好地模拟不锈钢焊接工字形和箱形截面压弯构件的整体稳定承载性能。


图4 有限元失稳模态和试验结果对比
Fig.4 Comparison of FE and test failure modes
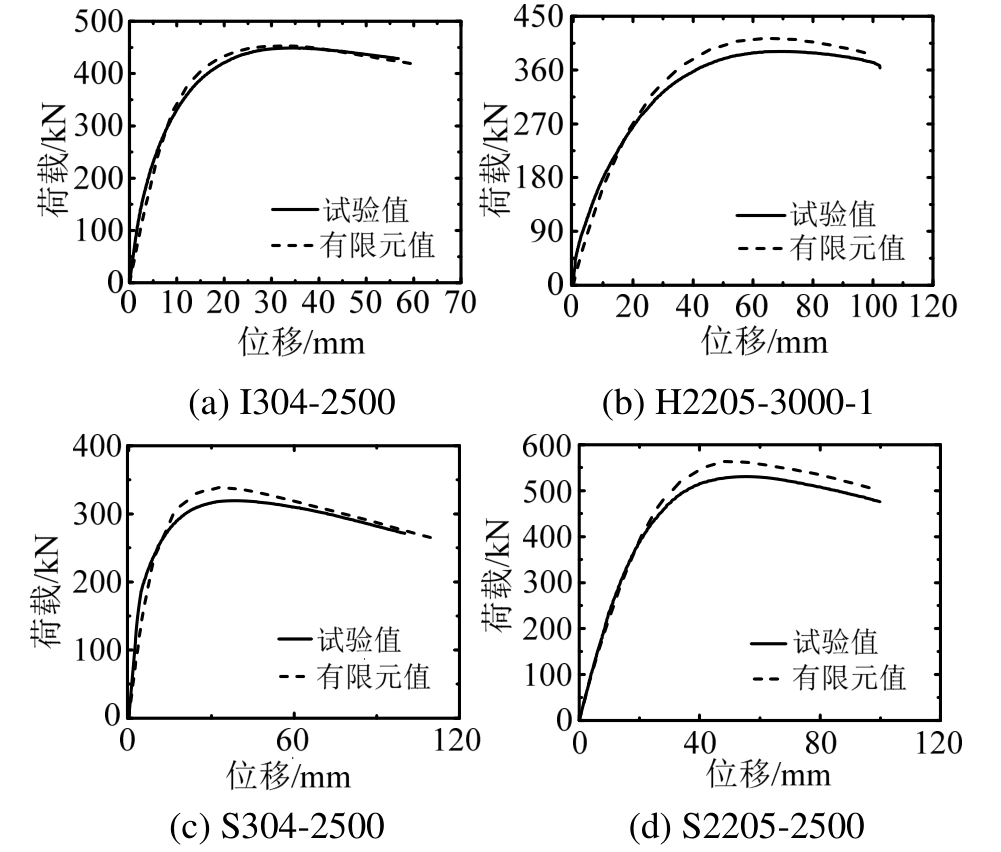
图5 试验和有限元荷载-水平位移曲线对比
Fig.5 Comparison of FE and test load-lateral deformation curves
3 试件整体稳定性能影响参数分析
利用验证的有限元模型开展参数分析,探究焊接残余应力和几何初始缺陷对不锈钢焊接工字形和箱形截面压弯构件整体稳定性能的影响。
3.1 焊接残余应力
通过84个算例分析研究焊接残余应力对不锈钢工字形和箱形截面压弯构件整体稳定承载性能的影响,结果如图6所示。图中横坐标表示构件正则化长细比,纵坐标表示考虑残余应力时构件的极限荷载Pr与不考虑残余应力的极限荷载P的比值。结果表明:随着长细比的变化,残余应力对构件的极限承载力的影响也随之改变;焊接残余应力对工字形截面构件绕弱轴失稳时的极限承载力影响大于绕强轴失稳,表明绕弱轴失稳时构件对残余应力更敏感;此外,从整体来看,残余应力对奥氏体型不锈钢构件承载力的影响要大于双相型不锈钢构件。
表3 试验和有限元承载力对比结果
Table 3 Comparison of FE and test ultimate resistances

试件编号 Pexp/kN PFE/kN Pexp/PFE 误差/(%)I304-2500 454.0 456.8 0.99 0.62 I304-3000-1 376.4 378.5 0.99 0.56 I304-3000-2 321.1 315.6 1.02 1.71 I304-4000-1 324.7 313.3 1.04 3.51 I304-4000-2 306.3 291.5 1.05 4.83 I2205-2500 649.5 702.7 0.92 8.19 I2205-3000-1 597.8 629.2 0.95 5.25 I2205-3000-2 516.6 529.7 0.98 2.54 I2205-4000-1 472.4 468.9 1.01 0.74 I2205-4000-2 439.2 440.2 1.00 0.23 H304-2500 269.4 282.8 0.95 4.97 H304-3000-1 262.0 262.4 1.00 0.15 H304-3000-2 217.7 214.8 1.01 1.33 H304-4000-1 210.3 205.3 1.02 2.38 H 304-4000-2 188.2 181.0 1.04 3.83 H2205-2500 428.1 438.4 0.98 2.41 H2205-3000-1 398.6 413.2 0.96 3.66 H2205-3000-2 324.7 332.8 0.98 2.49 H2205-4000-1 291.5 284.7 1.02 2.33 H2205-4000-2 269.4 270.4 1.00 0.37平均值 ― ― 1.00 2.61离散系数 ― ― 0.04 0.80 S304-2500 328.4 338.8 0.97 3.17 S304-3000-1 302.2 314.5 0.96 4.07 S304-3000-2 236.2 255.6 0.92 8.21 S304-4000-1 248.2 239.0 1.04 3.71 S304-4000-2 215.4 227.9 0.95 5.80 S2205-2500 535.1 563.4 0.95 5.29 S2205-3000-1 490.8 501.3 0.98 2.14 S2205-3000-2 413.3 428.7 0.96 3.73 S2205-4000-1 394.9 415.8 0.95 5.29 S2205-4000-2 365.4 398.6 0.92 9.09平均值 ― ― 0.96 5.05离散系数 ― ― 0.04 0.44
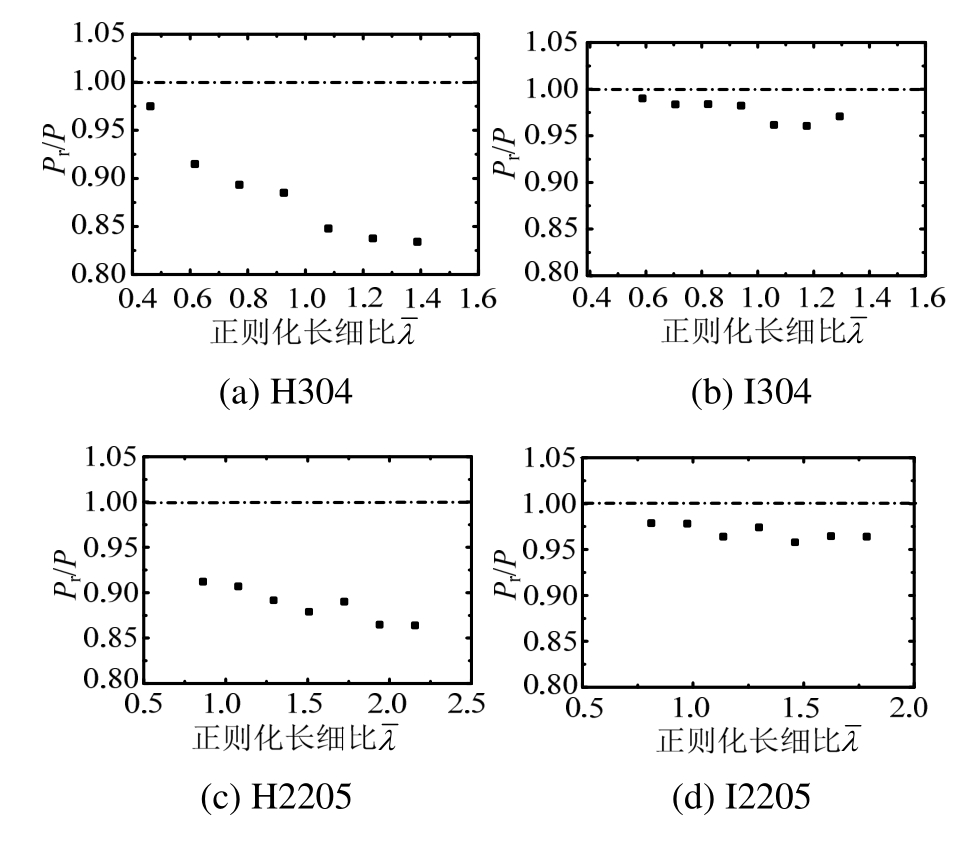
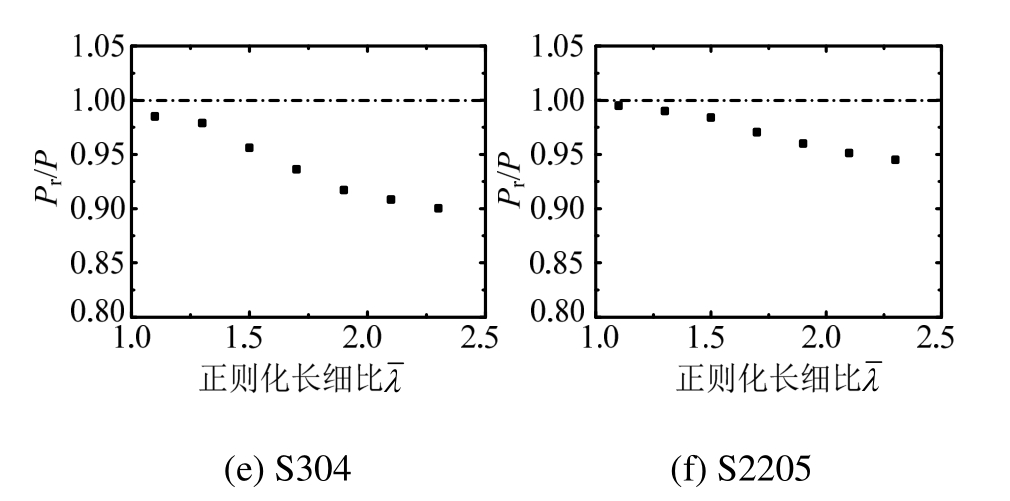
图6 焊接残余应力对试件的影响
Fig.6 Influence of residual stress on specimens
3.2 几何初始缺陷
通过126个算例来研究构件几何初始缺陷对不锈钢工字形截面和箱形截面压弯构件整体稳定承载力的影响。由于《钢结构工程施工质量验收规范》(GB 50205―2001) [17]规定受压构件的弯曲矢高不应大于L/1000和10 mm,故在不改变其他参数情况下,分别对几何初始缺陷值为0.001 L、0.0015 L和0.002 L时工字形截面和箱形截面压弯构件进行有限元分析,并将初始缺陷为0.0015 L和0.002 L时的极限荷载值与初始缺陷值为0.001 L时的极限荷载值进行对比,对比结果见图7。图中纵坐标表示极限荷载P0.0015、P0.002与极限荷载P0.001的比值。通过对比可知:初始缺陷的存在导致构件承载力降低,初始缺陷越大承载力下降越大;初始缺陷为0.0015 L时的极限荷载比初始缺陷为0.001 L的极限荷载降低2%左右,初始缺陷为0.002 L时的极限荷载比初始缺陷为0.001 L的极限荷载降低5%左右,且均随着长细比变化轻微波动。


图7 几何初始缺陷对试件的影响
Fig.7 Influence of initial geometric imperfections on specimens
4 CECS 410―2015中计算方法的评估和改进
为了评价CECS 410―2015中计算方法的精确性,共设计565个算例(包括两种截面形式和两种不锈钢材料),设计参数包括不同的板件宽厚比以覆盖不同的截面等级(欧洲规范(EN 1993-1-4) [18]中1类、2类和3类截面;《钢结构设计标准》(GB 50017―2017) [19]中S1级、S2级和S3级截面),不同的荷载偏心e(0 mm~200 mm),不同的正则化长细比![]() 所有分析试件的失稳形式均为平面内整体失稳。
所有分析试件的失稳形式均为平面内整体失稳。
4.1 CECS 410―2015 中计算方法的评估
根据CECS 410―2015,双轴对称截面的压弯构件平面内的稳定性可以按下式计算:

式中:M为计算弯矩;本试验试件的计算弯矩M为轴力N与试件荷载偏心距e的乘积;Ae为有效截面面积;βm为等效弯矩系数; 为欧拉临界力;φ为构件的整体稳定系数;We为对最大受压边缘的有效截面模量。
为欧拉临界力;φ为构件的整体稳定系数;We为对最大受压边缘的有效截面模量。
将有限元结果与按照CECS 410―2015中计算方法计算的承载力进行对比,结果列于表4。为了更为直观地比较,现将横坐标定义为受弯部分,纵坐标定义为受压部分,画出图8对比示意图。
从表4和图8可以看出,CECS 410―2015中的计算方法对于不锈钢焊接工字形和箱形截面压弯构件整体稳定承载力的预测整体偏于保守,对于弱轴失稳情况和当偏心距较大时,该情况更加明显。
4.2 计算方法的改进
《不锈钢结构技术规程》(CECS 410―2015)中关于压弯构件承载力的相关计算主要还是采用了我国冷弯薄壁型钢结构规范中的相关规定。计算公式中并未考虑构件的塑性发展,但是大多数压弯构件(欧洲规范EN 1993-1-4中1类和2类截面构件;《钢结构设计标准》(GB 50017―2017)中S1级、S2级和S3级截面构件)当受压最大边缘刚开始屈服时尚有较大的强度储备,既容许截面塑性深入;因此,现行的计算方法可能会低估上述等级截面构件的承载力。规程CECS 410―2015中的计算公式中的相关参数计算需要计算有效截面,为了简化构件的设计过程,将构件分为全截面有效构件和非全截面有效构件,但是,全截面有效构件板件宽厚比取值是根据规程CECS 410―2015第5.6节公式计算所得,缺乏一定的试验数据验证。现行国外不锈钢规范以及国内钢结构规范根据构件截面的性能对构件的截面等级进行分类,根据不同的截面等级选择相应的计算方法,而现行国内不锈钢规程在该方面可能还需要完善。针对CECS 410―2015中计算方法存在的问题,并考虑和GB 50017―2017中计算公式形式统一,提出改进的计算方法如下:
表4 有限元结果与CECS 410―2015预测值对比
Table 4 Comparison of FE results with predictions of CECS 410―2015

截面形式 不锈钢 PFE/PCECS平均值 离散系数奥氏体型 1.191 0.078强轴失稳双相型 1.207 0.101整体 1.198 0.089奥氏体型 1.330 0.182双相型 1.361 0.192整体 1.343 0.186强轴和弱轴整体 1.270 0.162 奥氏体型等边箱形 双相型工字形弱轴失稳1.260 1.235 0.119 0.127整体 1.248 0.123


图8 有限元结果和CECS 410―2015预测值对比
Fig.8 Comparison of FE results and predictions of CECS 410―2015
式中:βW=1,对于1类截面和2类截面,取1=We/Wp;对于3类截面,取We/Wp;η取值参考表5。
表5 系数η 取值
Table 5 Coefficient (η) values

截面形式 整体失稳 不锈钢材料 η双相型 0.20弱轴失稳 奥氏体型 0.20双相型 0.15等边箱形 整体失稳 奥氏体型 0.05强轴失稳 奥氏体型 0.30工字形双相型 0.10
式(2)只针对不锈钢焊接截面构件平面内整体稳定承载力的计算。公式中Wp为截面塑性模量,其中塑性发展的考虑参考了EN 1993-1-4。由于国内现行不锈钢规范中还未提出合理的截面分类,且刚实施的GB 50017―2017中提出的截面分类主要针对碳素钢和低合金钢,所以本公式中的截面分类采用的是欧洲不锈钢规范EN 1993-1-4中的截面分类。A为构件毛截面面积。公式中的其他参数定义同现行不锈钢规程CECS 410―2015。
将有限元结果和改进的计算方法计算的承载力进行对比,结果如表6和图9所示。
表6 有限元结果与改进的计算方法预测值对比
Table 6 Comparison of FE results with predictions of improved calculation method

截面形式 不锈钢PFE/Pimp平均值 离散系数奥氏体型 1.161 0.054强轴失稳双相型 1.175 0.085整体 1.167 0.069工字形弱轴失稳奥氏体型 1.135 0.122双相型 0.144 0.114整体 1.139 0.119强轴和弱轴整体 1.153 0.097等边箱形奥氏体型双相型1.172 1.148 0.091 0.087整体 1.160 0.089


图9 有限元结果和改进的计算方法预测值对比
Fig.9 Comparison of FE results with predictions of improved calculation method
从表6和图9可以看出,改进的计算方法对于不锈钢焊接工字形和箱形截面压弯构件整体稳定承载力能够给出较为合理的预测。对比表4和表6,工字形构件强轴和弱轴整体PFE/PCECS平均值为1.270,离散系数为0.162,而PFE/Pimp平均值为1.153,离散系数为0.097,说明改进的计算方法较CECS 410―2015中的计算方法能够更精确地预测不锈钢焊接工字形截面压弯构件的整体稳定承载力;且改进的计算方法对不锈钢焊接工字形截面压弯构件绕弱轴失稳时的整体稳定承载力的预测精度相比现行方法有明显的提高;箱形截面构件整体PFE/PCECS平均值为1.248,离散系数为0.123,而PFE/Pimp平均值为1.160,协方差为0.089,说明改进的计算方法较CECS 410―2015 中的计算方法能够更精确地预测不锈钢焊接箱形截面压弯构件的整体稳定承载力。
5 结论
本文在已有试验的基础上利用有限元软件ANSYS建立有限元模型对不锈钢焊接工字形和箱形截面压弯构件的整体稳定性能进行了数值模拟。利用验证的有限元模型开展参数分析,得到以下结论:
(1)本文建立的有限元模型能够较好地模拟不锈钢焊接工字形和箱形截面压弯构件的整体稳定性能。
(2)随着长细比的变化,残余应力对构件的极限承载力的影响也随之改变;焊接残余应力对工字形截面构件绕弱轴失稳时的极限承载力影响大于绕强轴失稳;残余应力对奥氏体型不锈钢构件承载力的影响要大于双相型不锈钢构件;初始缺陷的存在导致构件承载力降低,初始缺陷越大承载力下降越大。
(3)从有限元结果与CECS 410―2015中计算方法的对比情况可以看出,规程中的计算方法对于不锈钢焊接工字形和箱形截面压弯构整体稳定承载力的预测整体偏于保守,对于弱轴失稳情况和当偏心距较大时,该情况更加明显。
(4)考虑焊接截面的塑性发展,提出了整体稳定承载力改进计算方法,改进的计算方法能够更精确的预测不锈钢焊接工字形和箱形截面压弯构件的整体稳定承载力,且对于工字形截面的绕弱轴整体稳定承载力的预测精度明显提高。
[1]郑宝锋, 舒赣平, 沈晓明.不锈钢材料常温力学性能试验研究[J].钢结构, 2011, 26(5): 1―7.Zheng Baofeng, Shu Ganping, Shen Xiaoming.Experimental study on material properties of stainless steel at room temperature [J].Steel Construction, 2011,26(5): 1―7.(in Chinese)
[2]范圣刚, 郑家珵, 孙文隽, 等.S30408奥氏体不锈钢高温力学性能试验研究[J].工程力学, 2017, 34(4): 172―181, 191.Fan Shenggang, Zheng Jiacheng, Sun Wenjun, et al.Experimental investigation on mechanical properties of S30408 austenitic stainless steel at elevated temperatures[J].Engineering Mechanics, 2017, 34(4): 172―181, 191.(in Chinese)
[3]舒赣平, 郑宝锋, 沈晓明.不锈钢压弯构件平面内稳定承载力计算方法研究[J].工业建筑, 2012, 42(5):41―44.Shu Ganping, Zheng Baofeng, Shen Xiaoming.In-plane stability design method of stainless-steel beam-columns[J].Industrial Construction, 2012, 42(5): 41―44.(in Chinese)
[4]员翔, 赵果, 段宝山, 等.不锈钢方矩管压弯构件平面内稳定承载力理论研究[J].工业建筑, 2015, 45(3):150―155.Yuan Xiang, Zhao Guo, Duan Baoshan, et al.Theoretical research on in-plane stability capacity of RHS stainless steel beam-columns [J].Industrial Construction, 2015,45(3): 150―155.(in Chinese)
[5]Zheng B, Hua X, Shu G.Tests of cold-formed and welded stainless steel beam-columns [J].Journal of Constructional Steel Research, 2015, 111: 1―10.
[6]Lui W M, Ashraf M, Young B.Tests of cold-formed duplex stainless steel SHS beam–columns [J].Engineering Structures, 2014, 74: 111―121.
[7]Huang Y, Young B.Experimental investigation of cold-formed lean duplex stainless steel beam-columns[J].Thin-walled Structures, 2014, 76(3): 105―117.
[8]Huang Y, Young B.Design of cold-formed lean duplex stainless steel members in combined compression and bending [J].Journal of Structural Engineering, 2015, 141(5): 1―10.
[9]Liang Y, Zhao O, Long Y L, et al.Stainless-steel channel sections under combined compression and minor axis bending–Part 1: Experimental study and numerical modelling [J].Journal of Constructional Steel Research,2019, 152: 154―161.
[10]Zhao O, Gardner L, Young B.Buckling of ferritic stainless-steel members under combined axial compression and bending [J].Journal of Constructional Steel Research, 2016, 117: 35―48.
[11]Zhao O, Rossi B, Gardner L, et al.Behaviour of structural stainless-steel cross-sections under combined loading–Part I: Experimental study [J].Engineering Structures, 2015, 89: 236―246.
[12]CECS 410―2015, 不锈钢结构技术规程[S].北京: 中国计划出版社, 2015.CECS 410―2015, Technical specification for stainless steel structures [S].Beijing: China Planning Press, 2015.(in Chinese)
[13]杨璐, 赵梦晗, 班慧勇, 等.不锈钢焊接工形截面压弯构件试验研究[J].建筑结构学报, 2018, 39(5): 138―145.Yang Lu, Zhao Menghan, Ban Huiyong, et al.Experimental research on stainless steel welded I-section beam-columns [J].Journal of Building Structures, 2018,39(5): 138―145.(in Chinese)
[14]杨璐, 宁克洋, 班慧勇, 等.不锈钢焊接箱形截面压弯构件弯曲屈曲试验研究[J].工程力学, 2018, 35(12):143―150.Yang Lu, Ning Keyang, Ban Huiyong, et al.Experimental research on flexural buckling of stainless-steel welded box-section beam-columns [J].Engineering Mechanics, 2018, 35(12): 143―150.(in Chinese)
[15]赵梦晗.焊接不锈钢压弯构件静力承载性能研究[D].北京: 北京工业大学, 2017.Zhao Menghan.Research on static loading behavior of welded-section stainless steel beam-columns [D].Beijing: Beijing University of Technology, 2017.(in Chinese)
[16]Yuan H X, Wang Y Q, Shi Y J, et al.Residual stress distributions in welded stainless-steel sections [J].Thin-Walled Structures, 2014, 79 (2): 38―51.
[17]GB 50205―2001, 钢结构工程施工质量验收规范[S].北京: 中国计划出版社, 2002.GB 50205―2001, Code for acceptance of construction quality of steel structures [S].Beijing: China Planning Press, 2002.(in Chinese)
[18]EN 1993-1-4, Eurocode 3: Design of steel structures-Part 1-4: General rules: Supplementary rules for stainless steel [S].Brussels: European Committee for Standardization (CEN), 2015.
[19]GB 50017―2017, 钢结构设计标准[S].北京: 中国建筑工业出版, 2017.GB 50017―2017, Standard for design of steel structures[S].Beijing: China Architecture & Building Press, 2017.(in Chinese)