混凝土中的纵筋在受拉力作用下会与混凝土发生相对滑移，这种滑移现象发生在梁-柱或基础-柱界面处时，将导致构件的整体转动，这种转动会使构件的变形出现显著的增加。因此，在确定钢筋混凝土结构变形时，考虑钢筋滑移是很重要的。Sezen[1]测试的4根试验柱的结果表明，在某些情况下，钢筋滑移引起的变形可能与柱的弯曲变形一样大。这表明，如果在构件分析中忽略钢筋滑移引起的变形，其侧向变形能力可能会被低估。
纵筋的粘结滑移主要与混凝土与钢筋之间的粘结状态有关，由于钢筋与混凝土两者接触面相互作用的多变性和复杂性，相关的研究仍在不断发展。本质上根据钢筋与混凝土粘结段钢筋应变的积分可以计算出端部钢筋滑移量与钢筋应力的关系，但是这样做一般很难有理论上的解析表达式，除非粘结滑移本构进行了简化。Lehman和Moehle[2]、Sezen和Setzler[3]根据反复试验结果提出了钢筋和混凝土粘结强度在钢筋屈服前保持定值，屈服后粘结强度下降一半也保持定值的模型，据此可以推导出端部钢筋应力与滑移量的关系。Zhao和Sritharan[4]提供了另一种思路，在拉拔试验的基础上直接提出了端部钢筋拉应力-滑移量关系模型，并据此开发了应用于软件OpenSees[5]中的Bond-Slip模型，建模时将该模型应用在柱底零长度单元中来考虑钢筋的粘结滑移效应，给滑移量的计算带来了巨大的便利，目前已经得到广泛的应用。
在非线性计算中，滑移转角也可以通过弯矩-滑移转角模型来考虑，一般在界面处施加零长度的弹簧来模拟。Hachem等[6]和Haselton等[7]将弯矩-滑移转角关系赋予到柱底与节点区域的单元中，该弯矩-滑移转角模型均采用二折线模型直接计算钢筋滑移造成的界面转角，但是目前对于弯矩-滑移转角模型关键点的计算还没有明确直接的方法。
本文在理论推导和试验验证的基础上，提出了弯矩-滑移转角模型计算方法，可以直接用于计算滑移转角。
1 粘结滑移骨架曲线计算模型
粘结滑移转角关系如图1所示，在基础-柱界面处纵筋在拉应力的作用下与混凝土发生相对滑移，导致柱的整体转动，其转角可由最外侧纵筋滑移量(Ss)与纵筋到截面中和轴的距离(S′)计算得到。
为了建立粘结滑移骨架曲线计算模型，本文收集了Calderone等[8]、李贵乾[9]、Naito等[10]、Goodnight等[11]以及文献[2]的试验结果，图2为其中4根圆柱粘结滑移弯矩-转角试验结果，从试验结果可以看出，粘结滑移弯矩-转角骨架曲线基本呈现二折线型，这也证明了文献[6]与文献[7]中将粘结滑移弯矩-转角关系简化为二折线型是可行的。
二折线型粘结滑移弯矩-转角关系如图3所示，根据文献[2]，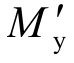
为截面首次屈服点弯矩，一般取最外侧受拉钢筋达到屈服时弯矩和最外侧混凝土受压应变达到0.002时弯矩中的较小值，在轴压较低时一般钢筋先达到受拉屈服。My为名义屈服点弯矩，一般取截面最外侧混凝土受压应交达到0.0035时弯矩。滑移转角θy,s取屈服点时钢筋滑移引起的转角。第二点弯矩取为极限点弯矩Mu，滑移转角取为与之对应的极限滑移转角θu,s。
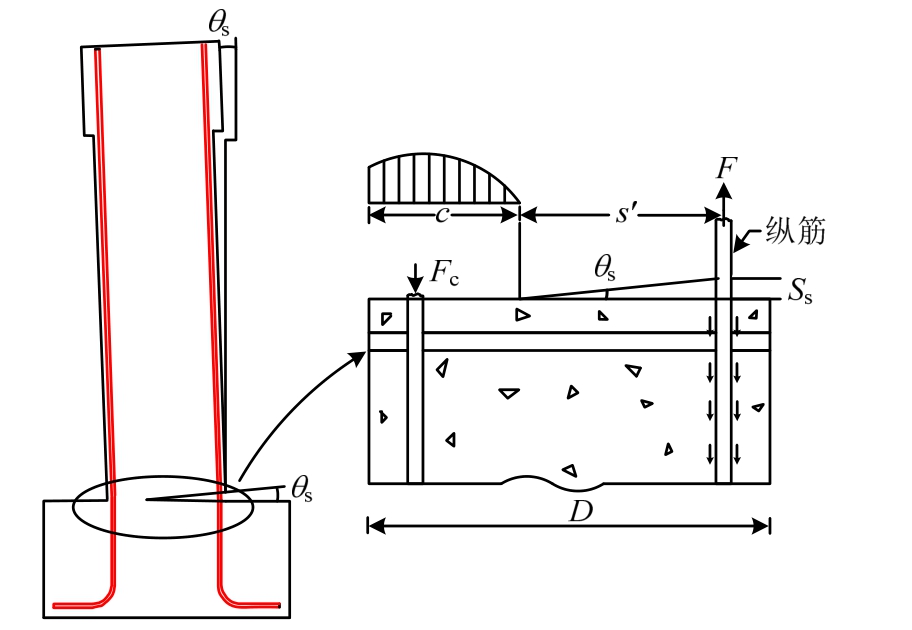
图1 粘结滑移转角关系图
Fig.1 Bond slip rotation diagram
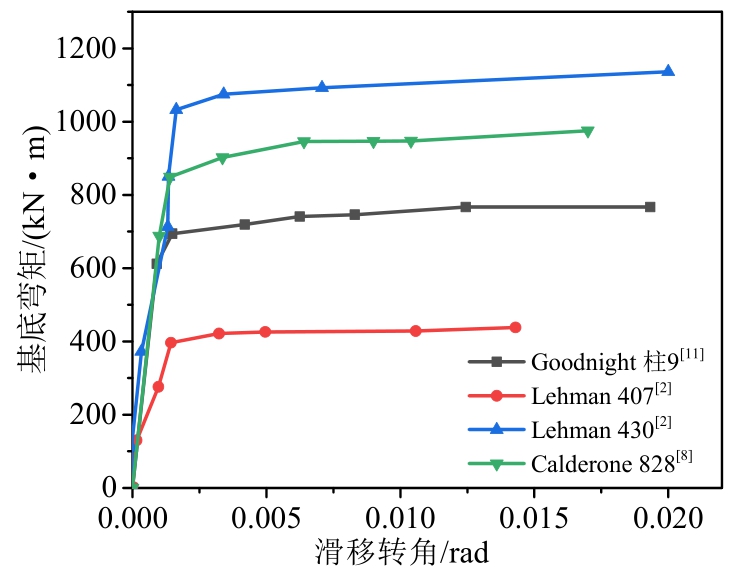
图2 试验粘结滑移弯矩-转角结果
Fig.2 Experimental slip moment-rotation
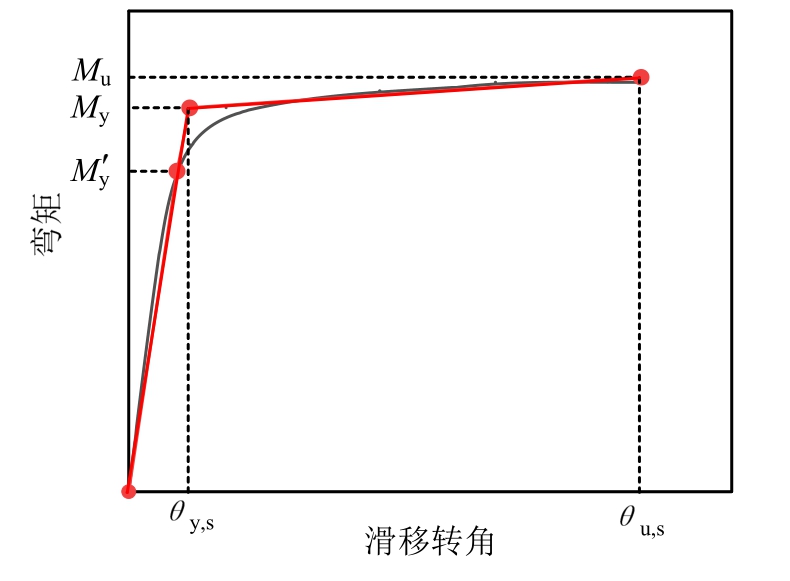
图3 柱底粘结滑移弯矩-转角简化计算图
Fig.3 Simplified calculation of moment-rotation of bond-slip
1.1 RC柱屈服时粘结滑移转角的确定
RC柱变形一般用等效塑性铰法进行计算。Priestley等[12]提出的塑性铰计算方法得到了广泛的应用，如图4所示，该塑性铰模型考虑柱底钢筋应变渗透影响，用附加长度(Lsp)来考虑。
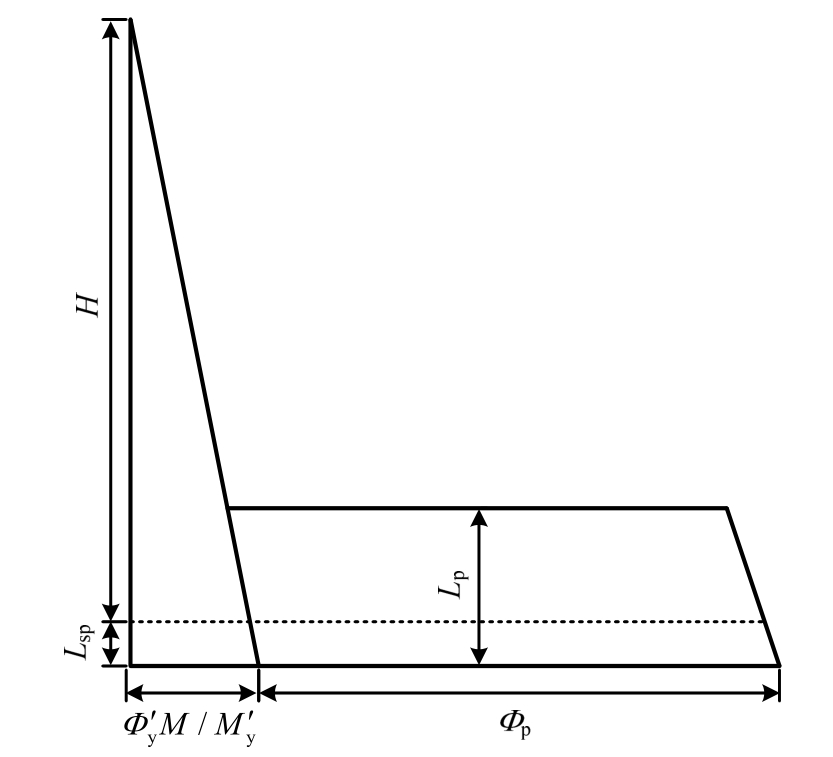
图4 等效曲率分布
Fig.4 Equivalent curvature distributions
根据Priestley等[12]的塑性铰计算方法，圆柱屈服曲率Φy、屈服位移Δy以及考虑应变渗透影响的固定塑性铰长度(Lsp)计算公式如下：
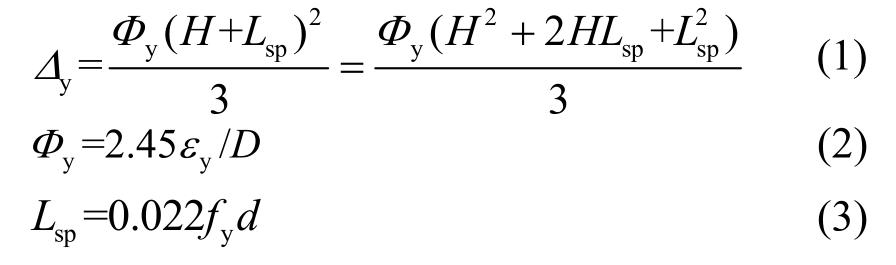
式中：H为柱高；εy为纵筋屈服应变；D为柱截面直径；fy为纵筋屈服强度；d为纵筋直径；由于Lsp与柱高H相比相对较小，常用的参数范围内比值在0.1左右，所以式(1)Δy计算展开式中
项与前两项相差一个量级，因此为了简化计算，省略式(1)的
项，可以得到：
对于屈服转角θy，则可由式(5)计算：
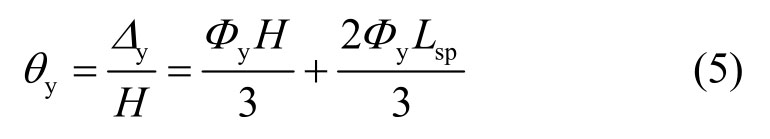
式(5)第一项是柱的弯曲变形造成的柱顶转角[13]，第二项是钢筋粘结滑移造成的转角θy,s。
1.2 RC柱破坏时粘结滑移转角的确定
RC柱最终破坏状态比较复杂，一般在试验滞回加载中，钢筋出现屈曲现象时RC柱承载力便开始下降，因此钢筋屈曲是判断RC柱是否进入破坏阶段的重要标志之一。由于钢筋屈曲后应力很难再有提高，钢筋粘结滑移量基本不再增加，因此可以认为钢筋进入屈曲状态时的粘结滑移转角即为RC柱破坏时的粘结滑移转角。
柱顶极限转角θu由屈服转角θy和塑性铰区塑性转角θp组成：
式中：Φp为塑性铰区塑性曲率；Lp为等效塑性铰长度；Φu为截面极限曲率。
根据参考文献[12]：
式(8)可以写成：
前一项为柱弯曲变形成分，后一项为钢筋滑移造成的转角：
故滑移造成的总转角为：
式中，θy,s可由式(6)得到。
截面极限曲率Φu可以根据钢筋屈曲时的应变计算得到，对于钢筋屈曲状态的计算，文献[13]中基于试验实测数据提出钢筋屈曲时的峰值拉应变εb计算方法如下：
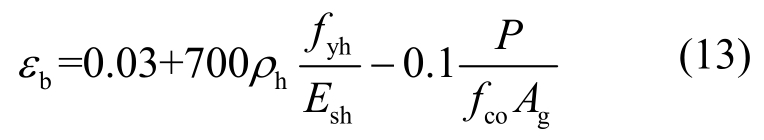
式中：ρh为体积配箍率；fyh为箍筋屈服强度；Esh为箍筋弹模；P为轴压力；fco为无约束混凝土圆柱体抗压强度；Ag为圆柱截面面积。
对于RC圆柱：ρh=4Asp/dssh ，其中，Asp为箍筋截面积；ds为同一截面箍筋中心间距；sh为箍筋竖向间距。
纵筋屈曲时截面极限曲率Φu：
式中：S为截面受拉区高度。顾冬生等[14]认为对于破坏时受拉区高度的计算，主要受轴压比(v)、配箍特征值(λh)和纵筋配筋特征值(λl)三个参数影响，并根据数值计算的结果进行回归，提出了受压区对应圆心角απ计算方法，具体计算方法如下：
式中：R为截面半径；轴压比v=P/fcoAg ；配箍特征值λh=ρhfyh/fco；纵筋配筋特征值λl=fyAs/Agf co ，其中，As为纵筋总面积。截面组成如图5所示。
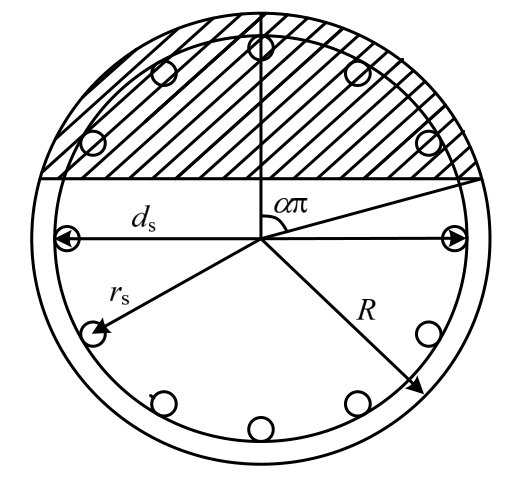
图5 截面组成
Fig.5 Section composition
2 模型验证
为了验证计算模型精度，计算结果需要与试验结果进行对比。在处理试验数据时，屈服点滑移转角取试件屈服时钢筋滑移引起的转角。极限点弯矩与滑移转角取为试验中报告钢筋出现屈曲现象时的试验值。考虑到文献[13]中建立钢筋屈曲时拉应变式(13)时，所采用的试验数据轴压比均不大于0.2的圆柱，本文在收集试验数据时，详细报告滑移测量数据的圆柱轴压比也在0.0～0.2。根据文献检索共收集了国内外24个大尺寸圆柱试验试件，试件直径均不小于400 mm。试件均报告了详细的滑移测量数据。
采用本文式(6)与式(12)对24根圆柱试件的粘结滑移屈服转角与极限转角进行计算，24根试件的主要参数、实测结果与计算结果均列于表1。根据统计，式(6)计算结果与试验结果比值的平均值为0.92，离散系数(COV)为19.5%。式(12)计算结果与试验结果比值的平均值为1.03,离散系数(COV)为20%，可以看出式(6)与式(12)均有很好的计算精度。
表1 试件主要参数及结果
Table 1 Details of test specimens
引用文献 试件编号 柱高H/mm柱截面直径D/mm纵筋直径d/mm轴压比v体积配箍率ρh试验计算/试验试验θ/rad式(6)θ/rad y,s y,s θ/rad u,s θ/rad 计算/试验式(12)u,s 407 2438.4 609.6 15.90 0.0720.0069 0.001420.00112 0.79 0.0143 0.0124 0.87文献[2]文献[8]415 2438.4 609.6 15.90 0.0720.0069 0.001500.00112 0.75 0.0158 0.0131 0.83 430 2438.4 609.6 15.90 0.0720.0069 0.001600.00121 0.76 0.0200 0.0140 0.70 328 1828.8 609.6 19.00 0.0910.0088 0.001000.00122 1.22 0.0203 0.0167 0.82 828 4876.8 609.6 19.00 0.0910.0088 0.001370.00122 0.89 0.0170 0.0167 0.98 1028 6096.0 609.6 19.00 0.0910.0088 0.001200.00133 1.11 0.0190 0.0167 0.88 5724 2300.0 400.0 18.00 0.10 0.0100 0.001630.00119 0.73 0.0209 0.0153 0.73文献[9]7015 2800.0 400.0 14.00 0.10 0.0150 0.001200.00133 1.11 0.0202 0.0168 0.83 7024 2800.0 400.0 18.00 0.20 0.0240 0.001360.00154 1.13 0.0201 0.0176 0.88 A1 2819.4 711.2 19.05 0.0440.0053 0.001160.00154 1.33 0.0183 0.0150 0.82文献[10]A2 2819.4 711.2 19.05 0.0420.0053 0.001420.00122 0.86 0.0120 0.0150 1.25 B1 2895.6 711.2 19.05 0.0580.0053 0.001490.00122 0.82 0.0144 0.0137 0.95 B2 2895.6 711.2 19.05 0.0560.0053 0.001070.00122 1.14 0.0110 0.0137 1.25 test 9 2438.4 609.6 19.05 0.0540.0100 0.001480.00133 0.90 0.0193 0.0175 0.91文献[11]test 13 2438.4 609.6 19.05 0.0620.0130 0.001570.00133 0.85 0.0155 0.0189 1.22 test 14 2438.4 609.6 19.05 0.0570.0050 0.001560.00133 0.85 0.0100 0.0133 1.33 test 15 2438.4 609.6 19.05 0.0520.0070 0.001630.00133 0.82 0.0123 0.0147 1.20 test 16 2438.4 609.6 19.05 0.0560.0130 0.001890.00133 0.70 0.0178 0.0184 1.03 test 20 2438.4 457.2 19.05 0.0500.0130 0.002400.00178 0.74 0.0184 0.0226 1.23 test 21 3352.8 457.2 19.05 0.0500.0130 0.001550.00178 1.15 0.0143 0.0175 1.22 test 23 3962.4 457.2 19.05 0.0500.0130 0.001940.00166 0.86 0.0154 0.0153 0.99 test 25 2438.4 609.6 22.23 0.0500.0100 0.002220.00177 0.80 0.0163 0.0213 1.31 test 29 2438.4 457.2 19.05 0.2000.0130 0.001860.00180 0.97 0.0143 0.0167 1.17 test 30 2438.4 457.2 25.40 0.1500.0130 0.002400.00193 0.80 0.0179 0.0221 1.23
对于RC柱屈服弯矩My与极限弯矩Mu计算方法的研究目前已经很成熟。顾冬生等[15]提出了一种正截面受弯承载力的计算方法。文献[14]通过理论分析并结合95个大比例试件试验结果，提出截面受弯承载力极限值计算方法，计算结果与试验结果吻合很好。文献[14]与文献[15]的弯矩计算方法均是在数值计算的基础上，通过理论分析并结合实验结果得到的，应用范围基本涵盖了工程参数常用范围，能直接应用于本文的骨架曲线计算中。对于屈服弯矩与极限弯矩具体计算公式，由于篇幅原因这里不进行细述，在计算时可参考上述文献。
综合上述粘结滑移骨架曲线计算，可以得到各试件粘结滑移骨架曲线，见图6，为了图示的简洁，这里仅给出四根圆柱的对比，通过对比可以看出计算与试验结果能够较好的吻合。一个值得强调的是，在应用这一骨架曲线时，在极限点后仍需按原直线斜率延长，如图7中线段1所示。在极限点之后如果按线段2水平设置时，当数值计算的弯矩大于Mu时会使得滑移转角不合理增大，出现变形的增加完全集中在滑移转角上的现象；按线段3设置时，如果侧向荷载出现下降段，可能按直线3卸载，转角逐渐增加，这和实际不符，弯矩下降转角不会增加，只能减小。
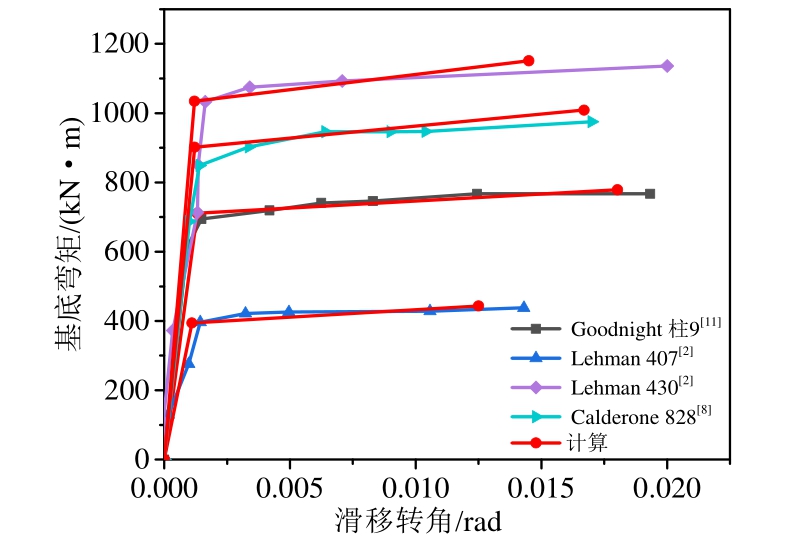
图6 粘结滑移弯矩-转角骨架曲线计算与试验结果
Fig.6 Analytical and test results of base moment-slip rotation envelope curve results
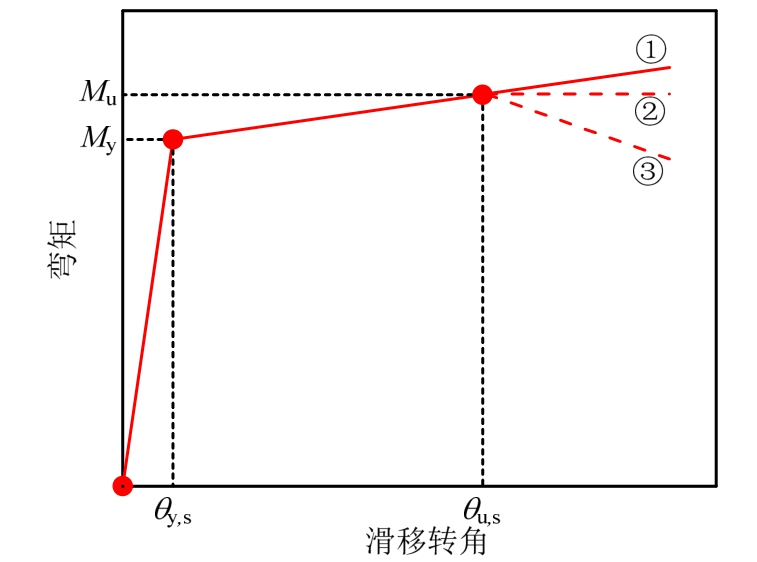
图7 极限点后骨架曲线设置方法
Fig.7 Method of setting envelope curve after limit point
3 数值模拟
3.1 低周反复数值分析
为了检验本文提出的粘结滑移弯矩转角计算模型的有效性，采用OpenSees对表1中试验结果进行了模拟，这里图示出文献[2]中试件407与415试验和计算结果。
计算模型如图8所示，柱截面采用纤维截面划分，弯曲变形采用基于力法的纤维单元模型进行模拟，其中混凝土本构采用单轴材料模型Concrete02 Material，箍筋约束混凝土采用Mander模型来确定，钢筋模型选用考虑纵筋疲劳与屈曲效应的Reinforcing Steel单轴材料，可以更好地反映出构件在大变形下的实际受力变形行为。考虑柱的剪切变形[16]，采用截面组装的方法将剪切变形与弯曲变形耦合。在柱底加入零长度转动弹簧单元用以考虑柱底的粘结滑移，采用单轴双线性滞回材料模型定义弯矩-滑移骨架曲线，骨架曲线采用本文的二折线模型，根据文献[6]，骨架曲线滞回规律采用Clough滞回规则。
试件顶点转角和侧向力滞回曲线模拟计算结果如图9和图10所示，通过与试验滞回曲线对比可以看出，模拟计算结果与试验结果吻合较好。由于篇幅关系，图11只列出了415柱底粘结滑移计算结果。试验中只报告了每级加载的滑移转角量，并没有给出相关的卸载段数据，所以计算结果和测量的骨架曲线进行了对比，可以看到计算结果和试验骨架曲线吻合较好。415柱试验中钢筋出现屈曲时，柱底滑移转角为0.0158，计算的转角为0.0178，比试验结果大11%。
图8 混凝土柱分析模型
Fig.8 Analysis model of concrete column
图9 407滞回曲线计算与试验结果
Fig.9 Hysteresis curve results of column 407
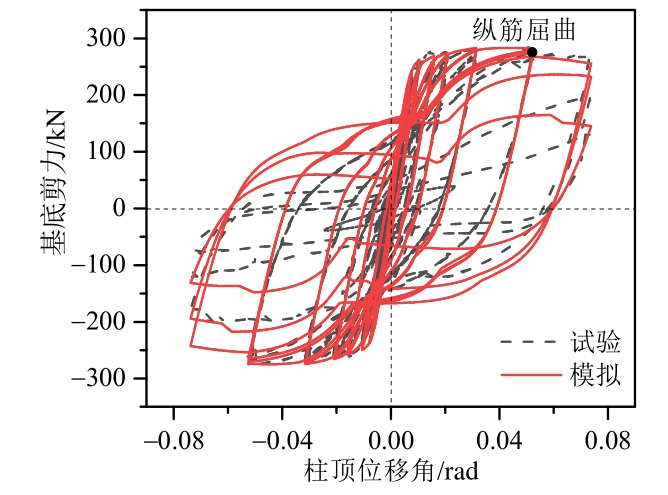
图10 415滞回曲线计算与试验结果
Fig.10 Hysteresis curve results of column 415
图11 415柱底粘结滑移弯矩-转角
Fig.11 Slip moment-rotation of column 415
3.2 时程分析
为了验证本文弯矩-滑移转角模型在时程分析中的有效性，需和试验结果进行比较。时程分析采用文献[6]RC圆柱振动台试验，该试验研究圆柱在单向和双向地震下的变形，本文对单向地震波下的时程曲线进行模拟。选取文中试件A1横向地震波加载试验，试验中通过对同一地震波调幅，对试验柱进行8次连续的地震波加载，其中第1次加载对应RC柱的屈服状态，对后续加载影响较小，本文直接对第2次、第3次加载进行模拟，这两次加载地震波基本对应我国的中震和大震量级。
纤维单元建模方法与材料选择均与上文一致，对于粘结滑移，分别采用本文的二折线模型与文献[4]的Bond-Slip模型[17―19]进行模拟计算。根据Petrini等[20]的研究，时程分析中定义瑞利阻尼跟切线刚度相关，阻尼比取为5%。根据Berry和Eberhand[21]的建议，将柱顶质量块的重量集中在柱顶的重心上，用刚臂将集中质量与柱顶连接，同时考虑质量块的转动惯量。
图12与图13分别为设计状态和最大地震波作用下柱顶位移角模拟与试验结果图，结果表明用弯矩-转角模型与Bond-Slip模型模拟钢筋滑移，柱顶位移角计算结果都能与试验结果吻合较好。图14列出了最大地震波加载时的柱底滑移结果，从图中对比结果可以看出弯矩-转角模型与Bond-Slip模型粘结滑移计算结果和试验实测结果也基本吻合。在试验中最大地震波第一次加载时纵筋未出现屈曲现象，实测与计算结果中滑移变形占总变形大约在20%~25%，试验在后续同样的最大地震波加载时纵筋屈曲，此时滑移变形占总变形的25%～30%。这些对比结果显示出本文粘结滑移弯矩-转角模型有较高的预测精度。
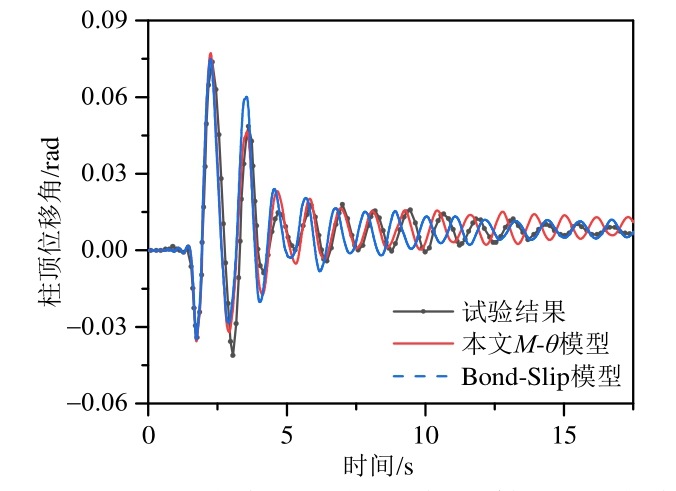
图12 设计地震波柱顶位移角计算与试验结果
Fig.12 Analytical and test results of drift ratio history at design earthquake level
图13 最大地震波柱顶位移角计算与试验结果
Fig.13 Analytical and test results of drift ratio history at maximum earthquake level
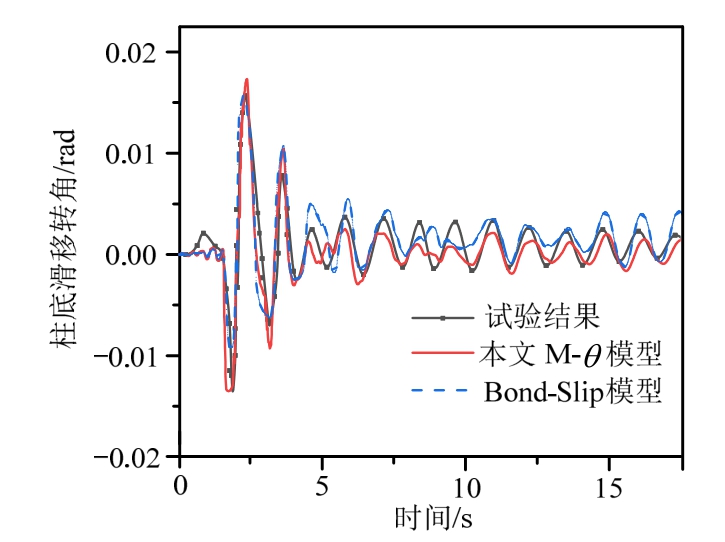
图14 最大地震波柱底滑移转角计算与试验结果
Fig.14 Analytical and test results of bottom slip ratio history at maximum earthquake level
值得一提的是，Bond-Slip模型应用于纤维截面时，钢筋的应力-应变关系曲线由滑移量与钢筋应力关系曲线来代替，而滑移量一般达到毫米级，所以对应的混凝土应变也会非常大，在数值计算时容易出现收敛性问题。而本文的粘结滑移弯矩-转角模型是截面上的力和变形关系，减少了从材料性能到截面性能的积分过程，在计算过程中数值稳定性有了较大提高，在截面较多和高非线性状态下应用有优势[22]。
4 参数分析
根据分析钢筋屈曲时的滑移量与轴压比、体积配箍率等因素有关，把415柱作为模型进行参数分析，计算在轴压比为0、0.1、0.2下，体积配箍率分别为0.0069、0.0104、0.0140时，钢筋达到屈曲应变，滑移转角与柱顶位移角的比值。一共9个模型用于计算，纵筋的屈曲应变采用式(13)计算。结果如图15所示，可以看到屈曲时滑移变形在总变形中的比例随轴压比增加而减小，随体积配箍率减小而减小，这与试验测量结果一致。在文献[2]中钢筋滑移转角占比随柱顶侧向变形增加而增加，表明柱子变形能力大时，滑移转角占比增加。大量的试验结果表明轴压比增加和配箍率下降都会造成柱子变形能力下降，因此滑移占比会下降。
图15 滑移占比计算结果
Fig 15 Calculation results of slip ratio
对于屈服状态的滑移，上述9个模型计算结果表明，在屈服状态滑移占比相对较小，约在20%，在屈服后滑移占比会随位移增加而增加，这与文献[21]的计算结论一致，并和文献[2]的试验结果吻合。
5 结论
通过理论分析、数据统计、数值模拟，本文对RC圆柱粘结滑移弯矩-转角骨架曲线计算方法进行研究，主要结论有：
(1)根据理论分析，提出了一种RC圆柱粘结滑移弯矩-转角骨架曲线简化计算模型计算方法。该模型为二折线型，计算简单，应用范围广，便于在数值计算中应用。
(2)根据数值模拟，从本文所建议的模型分析所得结果与试验结果的对比图中可以看出模拟计算结果与试验所测结果吻合较好，能够较准确地预测出柱底滑移量，验证了该模型的准确性。
(3)根据参数分析，纵筋屈曲时滑移占比随轴压比增加而下降，随体积配箍率下降而下降。钢筋滑移转角占比在屈服后会随柱顶位移的增加而增加。
由于高轴压比RC圆柱试验较少，本文主要对轴压比为0～0.2时的RC柱粘结滑移弯矩-转角计算方法进行研究，主要适用于桥墩柱，对于高轴压比下RC柱粘结滑移弯矩-转角计算方法还有待进一步探究。
[1]Sezen H.Seismic behavior and modeling of reinforced concrete building columns [D].Berkeley, USA:University of California, 2002.
[2]Lehman D E, Moehle J P.Seismic performance of well-confined concrete bridge columns [R].Berkeley:Pacific Earthquake Engineering Research Center, 1998.
[3]Sezen H, Setzler E J.Reinforcement slip in reinforced concrete columns [J].Aci Structural Journal, 2008, 105(3):280―289.
[4]Zhao J, Sritharan S.Modeling of strain penetration effects in fiber-based analysis of reinforced concrete structures[J].ACI Structural Journal, 2007, 104(2): 133―141.
[5]Mazzoni S, McKenna F.Open system for earthquake engineering simulation user command-language manual[R].Berkeley: Pacific Earthquake Engineering Research Center, 2006.
[6]Hachem M M, Mahin S A, Moehle J P.Performance of circular reinforced concrete bridge columns under bidirectional earthquake loading [R].Berkeley: Pacific Earthquake Engineering Research Center, 2003.
[7]Haselton C B, Goulet C A, Mitrani-Reiser J, et al.An assessment to benchmark the seismic performance of a code-conforming reinforced concrete moment-frame building [R].Berkeley: Pacific Earthquake Engineering Research Center, 2007.
[8]Calderone A, Lehman D E, Moehle J P.Behavior of reinforced concrete bridge columns having varying aspect ratios and varying lengths of confinement [R].Berkeley:Pacific Earthquake Engineering Research Center, 2000.
[9]李贵乾.钢筋混凝土桥墩抗震性能试验研究及数值分析[D].重庆: 重庆交通大学, 2010.Li Guiqian.Experimental study and numerical analysis on seismic performance of reinforced concrete bridge columns [D].Chongqing: Chongqing Jiaotong University,2010.(in Chinese)
[10]Naito C J, Moehle J P, Mosalam K M.Experimental and computational evaluation of reinforced concrete bridge beam-column connections for seismic performance [R].Berkeley: Pacific Earthquake Engineering Research Center, 2001.
[11]Goodnight J C, Feng Y, Kowalsky M J, et al.The effects of load history and design variables on performance limit states of circular bridge columns [D].Raleigh, USA:North Carolina State University, 2015.
[12]Priestley M J N, Calvi G M, Kowalsky M J.Displacement-based seismic design of structures [M].Pavia, Italy: IUSS Press, 2007.
[13]Goodnight J C, Kowalsky M J, Nau J M.Modified plastic-hinge method for circular RC bridge columns [J].Journal of Structural Engineering, ASCE, 2016,142(11):04016103-1―04016103-12.
[14]顾冬生, 吴刚, 吴智深.RC圆柱受弯承载力极限值计算方法研究[J].工程力学, 2012, 29(8): 227―235.Gu Dongsheng, Wu Gang, Wu Zhishen. Calculation of the ultimate flexural capacity of normal section of RC circular columns [J]. Engineering Mechanics, 2012, 29(8):227―235.(in Chinese)
[15]顾冬生, 吴刚, 吴智深.钢筋混凝土圆柱正截面受弯承载力计算方法研究[J].建筑结构, 2010, 40(10): 97―101.Gu Dongsheng, Wu Gang, Wu Zhishen.Analysis on calculation method for normal section flexural capacity of reinforced concrete circular columns [J]. Building Structure, 2010, 40(10): 97―101.(in Chinese)
[16]骆欢, 杜轲, 孙景江, 等.小跨高比钢筋混凝土连梁非线性剪切滞回和分析模型研究[J].工程力学, 2018,35(9): 161―169, 179.Luo Huan, Du Ke, Sun Jingjiang, et al.Hysteretic shear and analysis models for reinforced concrete coupling beams with small span-to-depth ratios [J].Engineering Mechanics, 2018, 35(9): 161―169, 179.(in Chinese)
[17]Su J, Dhakal R P, Wang J.Fiber-based damage analysis of reinforced concrete bridge piers [J].Soil Dynamics and Earthquake Engineering, 2017, 96(5): 13―34.
[18]Wu R Y, Pantelides C P.Concentrated and distributed plasticity models for seismic repair of damaged RC bridge columns [J].Journal of Composites for Construction, 2018, 22(5): 04018044-1―04018044-15.
[19]孙小云, 韩建平, 党育, 等.地震动持时对考虑梁柱节点区不同破坏模式RC框架的地震易损性影响[J].工程力学, 2018, 35(5): 193―203.Sun Xiaoyun, Han Jianping, Dang Yu, et al.Effect of ground motion duration on seismic fragility of RC frames with different beam-column joint failure modes [J].Engineering Mechanics, 2018, 35(5): 193―203.(in Chinese)
[20]Petrini L, Maggi C, Priestley M J N, et al.Experimental verification of viscous damping modeling for inelastic time history analyzes [J].Journal of Earthquake Engineering, 2008, 12(Suppl 1): 125―145.
[21]Berry M P, Eberhard M O.Performance modeling strategies for modern reinforced concrete bridge columns[R].Berkeley: Pacific Earthquake Engineering Research Center, 2007.
[22]Goulet C A, Haselton C B, Mitrani-Reiser J, et al.Evaluation of the seismic performance of a codeconforming reinforced-concrete frame building-from seismic hazard to collapse safety and economic losses [J]. Earthquake Engineering and Structural Dynamics, 2007,36(13): 1973―1997.