我国西南地区的水利和机场等工程建设发展很快[1-2],为节省耕地和满足净空要求,山区机场多选址在荒山荒放区,水利工程则常位于险峻的高山峡谷间。由于地形条件复杂,工程建设需要进行深挖和高填[3]。原地基中,经常分布厚度不等的软弱层,使得高填方边坡具有典型的二元结构[4]。而在高填方的填筑中,顺坡填筑无法避免。顺坡填筑是指填筑体边坡坡向与原地面坡向相同[5],与水平地基上的填方相比,顺坡填筑边坡稳定性较差。为了增强填筑体稳定性,减少挖方量,山区工程上经常采取原地基开挖台阶后再填筑的经验方法[6],这一方法也曾广泛应用在高速公路填方工程中[7-8],近几年,也陆续写入了山区高填方工程相关规范,例如当填筑区内原场地坡比大于1∶5时,应开挖台阶,并使用粗粒土料或土夹石混合料分层回填并使用强夯法处理[9],又如顺坡填筑时,应对原地基坡面的软弱覆盖层予以清除或加固处理,且宜将坡面做成台阶状[10]。但是,国内外目前对于台阶开挖提高边坡稳定性的机理研究较少,大多直接应用该工法[11],并通过长期动态监测验证方法有效性[12]。影响机理的研究手段有物理试验和数值试验两种,前者通过土工离心机模型试验,对在基-填界面设置台阶的模型边坡稳定性进行分析,以预测实际边坡的破坏[13-15],后者依据实际工程建模,采用有限元方法分析了不同台阶开挖方式对结构体稳定和变形的影响[7, 16]。也有研究者结合随机场进一步展开分析[17-18]。
为研究顺坡填筑情况下原地基-填方体界面开挖台阶后对边坡稳定性的影响规律和机理,文章从无限长边坡基-填界面开挖台阶情况出发,利用Bishop方法推导不同破坏模式下的安全系数公示,并计算理论解,对关键变量进行参数敏感性分析。然后,利用有限元软件Plaxis2D对简化后的有限长边坡平面应变模型在不开挖台阶、开挖小台阶和开挖大台阶三种情况下的稳定性进行计算比较。通过研究基-填界面剪应力的分布和基-填界面强度影响稳定性趋势解释开挖台阶增强稳定性的机理。最后以某西南山区高填方机场实际工程为例[19],在暴雨工况和地震工况[20]下对开挖台阶的贡献进行研究。研究情况逐渐复杂,对机理的解释逐渐具体。
1 无限长边坡基-填界面理论解与参数敏感性分析
为了解开挖台阶对边坡稳定性的影响,可从无限长边坡入手,先研究无限长边坡开挖台阶后安全系数的理论解(图1)。
1.1 理论模型与材料参数
图1中,B是一级台阶(包括平台段和倾斜段)水平投影的宽度,n是一级台阶平台段的宽度,α为原界面倾角,β为台阶倾角。一般而言,B越大、n越大,则开挖的工程量越大。若B的大小对安全系数影响不大,则可以将B取小一些、减少工程量。设置台阶后,最危险滑裂面可能仍然是一条直线(原界面),但其对应的安全系数提高了。原先此处是界面,计算安全系数时用界面强度。设置台阶后,该直线所在位置是填筑体,计算安全系数是用填筑体的强度。设置台阶,填筑体的最危险滑面也有可能是开挖形成的基-填界面,这是条折线。填筑体竖向厚度为H,容重为γ。cF、φF为填筑体强度参数,cI 、φI为填筑体与基岩界面强度。界面强度低于填筑体强度,cF≥cI,φF≥φI。利用Bishop方法计算安全系数。

图1 无限长边坡开挖台阶
Fig.1 Infinite long slope excavation steps
1.2 无限长边坡理论解与应用
无限长边坡理论解需要考虑多种情况:不开挖台阶安全系数、开挖台阶后不同滑坡模式的安全系数等,理论解如下。
若不开挖台阶,则滑裂面为界面处,安全系数为:

开挖台阶后,填筑体形状更复杂,可能的滑坡模式也更多。
1) 当顺坡填筑后,若边坡沿原界面所在位置滑动,安全系数为:
2) 当顺坡填筑后,若边坡在一个台阶内部出现局部滑坡,此时安全系数较难直接写出表达式。当Btanα ≥H时可能出现这种滑坡,此时B过大,不经济,不讨论。
3) 当顺坡填筑后,若边坡基-填界面滑动(滑裂面为台阶状),对于这种情况,其安全系数并没有现成的表达式。为计算这种情况的安全系数,取出一个台阶及其上方的填土,对其受力状态进行分析。简化Bishop法只考虑土条间的水平力,认为不存在切向力(图2)。
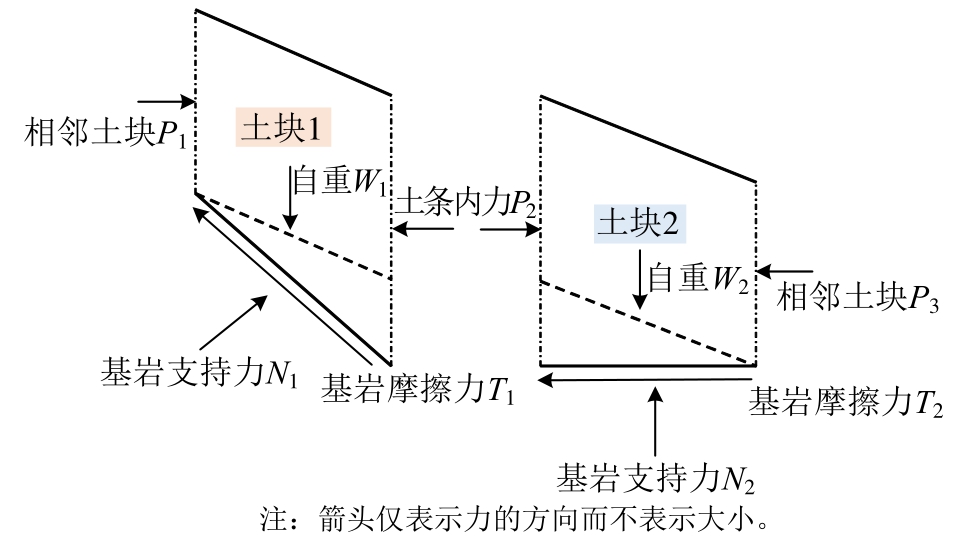
图2 无限长边坡受力分析
Fig.2 Stress analysis of infinite long slope
P1和P3为相邻土块提供水平力,P2为土块间水平内力,N1和N2为基岩对填方体土块的接触面支持力,T1和T2为基岩对填方体土块的接触面摩擦力,W1和W2为土块重力。列出两部分平衡方程

联立式(1)~式(5),推导出只含Fs的方程:
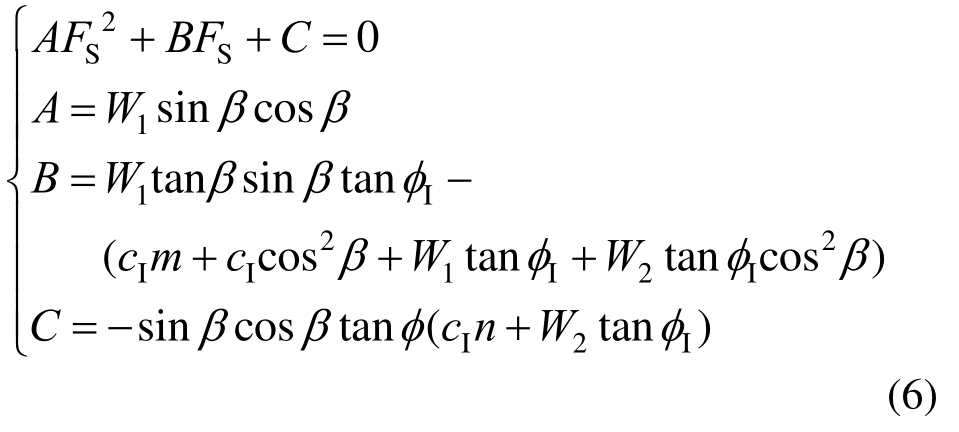
联立求解该方程,滑裂面为基-填界面时,无限长边坡的安全系数为:
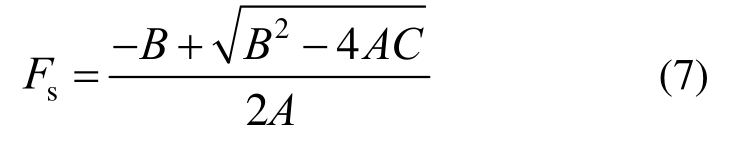
实际的安全系数是以上3种安全系数的最小值(一般第2种情况不会成为最小值),可写为:

应用无限长边坡理论解计算,参数见表1和表2。
表1 无限长边坡模型数据
Table 1 Unlimited long slope model data
数据基岩倾角α/(°)台阶倾角β/(°) 水平总长B/m 填方厚度H/m取值26.6 45 20 30
表2 无限长边坡材料参数
Table 2 Material parameters of infinite slope

材料填筑体cF/kPa φ°填筑体F/()界面cI/kPa φ°界面I/()填料γ/ (kN/m³)取值6.3 28.8 4.3 20.1 21.5
不同破坏情况下的安全系数如表3。开挖台阶后,沿基岩表面滑动的安全系数变大,但仍然小于滑裂面在填筑体内部时的安全系数。即开挖台阶增加安全系数,上限为填筑体内部破坏时安全系数。
表3 不同滑裂面对应的安全系数
Table 3 Safety factor corresponding to different slip surfaces

滑动破坏模式 安全系数不开挖台阶,沿界面处滑动,滑裂面为直线。0.75计算时所用强度为界面强度开挖台阶,沿原界面处滑动,滑裂面为直线。1.12计算时所用强度为填筑体强度开挖台阶,沿新界面处滑动,滑裂面为折线。0.90计算时所用强度为界面强度
理论解模型中B和β是关键参数,而填方体强度参数和界面强度参数的比值选取也会影响最终的破坏模式,所以应进行参数敏感性分析。
1.3 台阶尺寸B敏感性分析
保持其他参数不变,改变台阶宽度B,分析B的变化对安全系数的影响,如图3所示。B的变化对安全系数的影响不大,且B越小,沿基岩面滑动的安全系数越大,即说明在实际工程中,可以在适当范围内控制台阶宽度的大小,并减少工程量。
1.4 台阶倾角β敏感性分析
改变β的大小,即改变n与B的比值,计算结果如图4所示,两条水平参考线表示开挖台阶前后直线滑裂面对应的安全系数。从图4中可以看出,随着比值的增加,开挖形成的新界面(折线)对应的安全系数也逐渐增加。当n与B的比值<0.75时,其安全系数<1.12,最危险滑裂面为开挖形成的基岩-填筑体界面;当n与B的比值>0.75时,最危险滑裂面为开挖前的原界面直线,此时增大台阶倾角并不能提高边坡的安全系数。n与B的比值0.75为临界值。
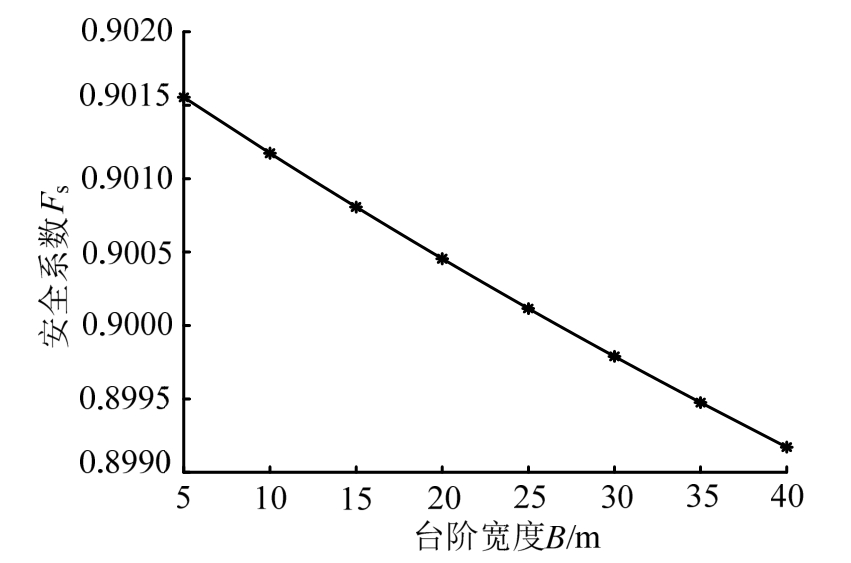
图3 台阶宽度对安全系数的影响
Fig.3 Effect of step width on safety factor

图4 台阶倾角对安全系数的影响
Fig.4 Influence of step inclination on safety factor
1.5 界面强度折减系数敏感性分析
对于不同的界面强度折减系数,n与B的比值临界值不同,界面强度折减系数越大,n与B的比值临界值越小,如图5所示。若界面强度与填筑体强度相同(不折减),则无论n与B的比值多大,开挖形成的折线界面的安全系数比原界面的安全系数都大,边坡会沿着原界面破坏,设置台阶没有作用。也就是说,若界面强度与填方体强度一致,是否开挖台阶不影响安全系数。
2 有限长边坡基-填界面有限元解与稳定性强化机理
无限长边坡理论解解释了台阶开挖的宏观规律,为研究影响机理,需进行有限长边坡研究。

图5 界面强度折减对有效上限的影响
Fig.5 The effect of interface reduction on the effective upper limit
2.1 有限元模型与材料参数
利用有限元方法,使用Plaxis计算软件,研究顺坡填筑的高填方边坡在基-填界面开挖台阶对提高其稳定性的贡献及机理。使用简化后平面应变模型。原基岩坡比为0.3,其上填筑体顶面宽120 m,边坡坡比为0.5,坡高为90 m。基-填界面不开挖台阶Plaxis计算模型如图6(a)所示。基-填界面开挖台阶,分为小台阶和大台阶两种情况,分别见图6(b)和图6(c)。小台阶平台宽21 m,台阶斜面宽9 m,高9 m;大台阶平台宽42 m,台阶斜面宽18 m,高18 m。

图6 简化台阶计算模型
Fig.6 Simplified step calculation model
填方体和基岩之间界面强度折减系数为0.8,以模拟工程中接触面的实际情况。材料参数如表4所示,强度符合摩尔-库伦准则,边坡安全系数计算采用有限元强度折减法[21]。
表4 基岩和填土材料参数表
Table 4 Bedrock and fill material parameter table

分类 重度γ/(kN/m³) 模量E/GPa 泊松比ν 粘聚力c/kPa 摩擦角φ/(°)填土岩石21.6 27 0.06 13 0.26 0.19 6.3 5000 28.8 38
2.2 基-填界面剪应力分布
基-填界面剪应力分布情况直接影响边坡稳定性,本研究引入相对剪应力的概念,即以实际剪应力和界面抗剪强度(摩尔-库伦准则)的比值。一般剪应力较大、发生滑坡的界面一般处于坡的中下部,本研究关注图6剪应力观测区中的界面。相对剪应力分布如图7所示。
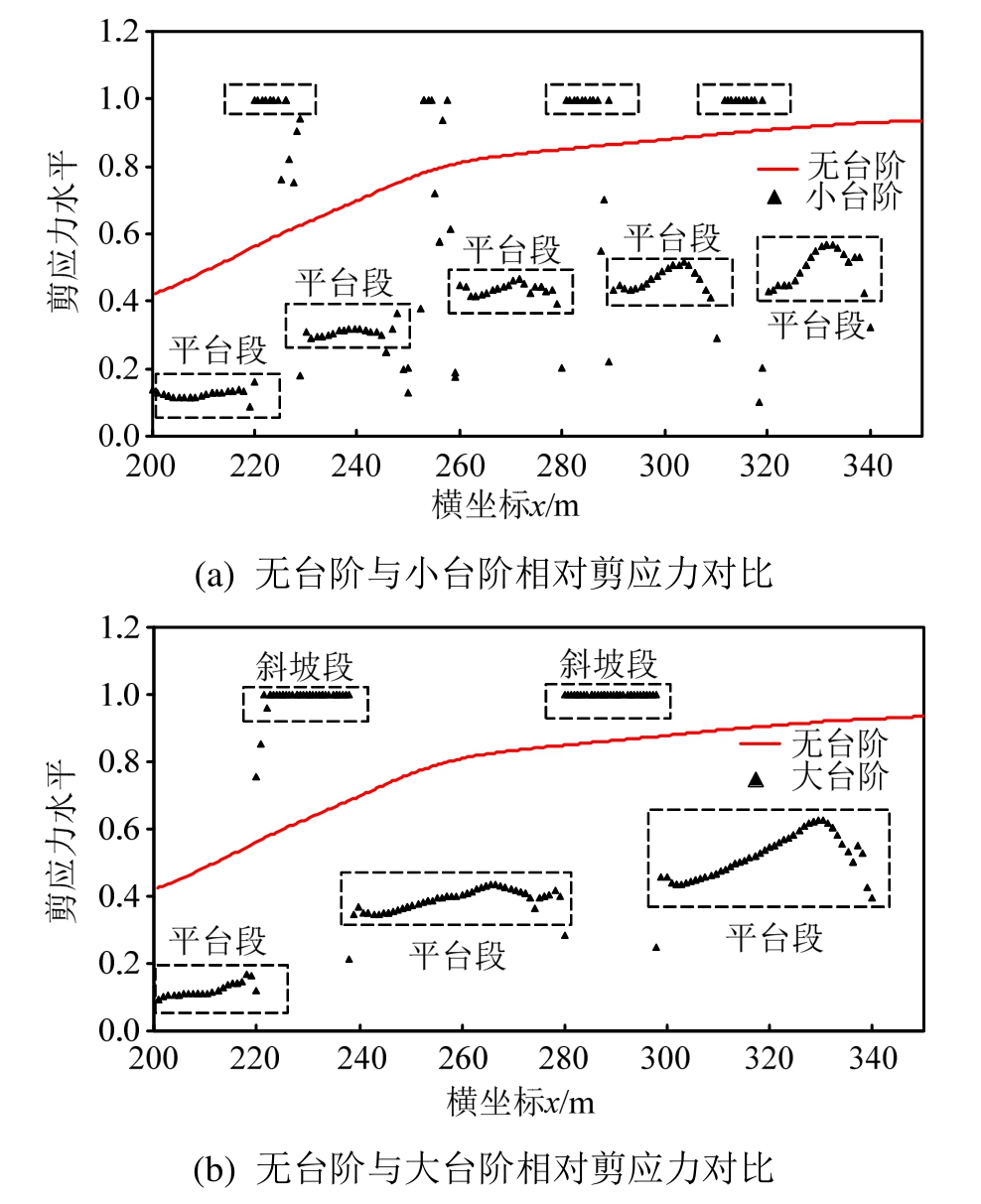
图7 基-填界面相对剪应力分布对比(局部)
Fig.7 Base-fill interface relative shear stress distribution comparison (partial)
对于无台阶模型,横坐标X越大,越靠近坡底,相对剪应力水平越高,从抗剪强度的40%增加到90%以上。若忽略黏聚力对抗剪强度的贡献,极限状态下剪应力与正应力的比值为0.385。岩层斜坡的坡率为1∶3,界面的正应力、剪应力与土的重力平衡,所以总的剪力为重力的0.3倍,平均的相对剪应力水平为0.78,与图7有限元计算的无台阶平均水平基本相同。
对于开挖台阶,对平台区和斜坡区分别分析,横坐标X越大,越靠近坡底,同样相对剪应力水平越高。另外,台阶斜坡的相对剪应力水平较大,剪应力基本达到了极限剪应力,而台阶平台的相对剪应力水平较小,处于10%~60%区间,且均小于无台阶界面相对剪应力水平。
取填方体台阶斜坡上土条,如图8所示,进行受力分析。W为土条自重,F为相邻土条作用力,N1和N2为基岩提供支持力,F1和F2为基岩提供抗滑力。水平应力和竖向应力比值理想化为侧限压缩的比值。故界面剪应力和正应力比值计算公式为:
式中:σ表示应力;下角标h表示水平;下角标v表示竖直;Δh表示基岩支持力N2涉及的三角高度;Δs 表示基岩支持力N1涉及的土条水平长度。
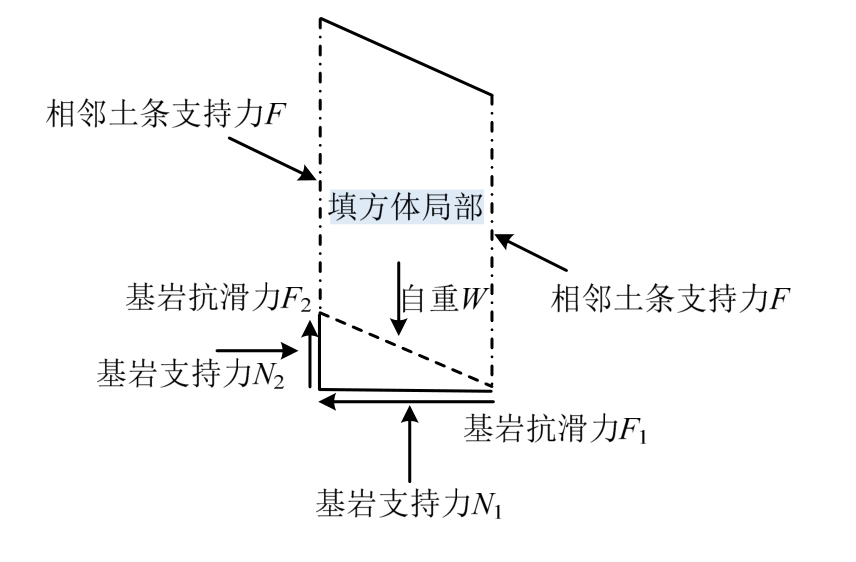
图8 简化分析模型
Fig.8 Simplified analysis model
平台的平均相对剪应力水平为0.46,与开挖台阶有限元模型计算的平均水平基本一致。这个值与无台阶开挖界面的平均相对剪应力水平0.78相比有很大的改善。
通过以上分析可以得出结论,对岩石开挖台阶平台可以明显减小界面的相对剪应力水平,使得界面上的安全储备更高;开挖台阶的大小对界面的安全储备影响不大。另外,对于大台阶模型,每延米填方体自重157464 kN,而台阶平台段提供的竖向反力合计为113784 kN,占比72.3%。可见,填方体所受重力荷载大部分由台阶平台段的竖向反力平衡。
2.3 基-填界面强度影响稳定性趋势
基础算例中,界面强度和填方体强度的比值为0.8。在实际工程中,受填筑质量的影响,有必要对该比值的变化对边坡的潜在滑裂面和安全系数的影响进行分析,结果如图9所示。

图9 基-填界面强度折减系数对滑裂面和安全系数的影响
Fig.9 Effect of Foundation-filled Interface Strength Reduction Factor on Sliding Surface and Safety Factor
随着基-填界面强度比值的降低,潜在滑裂面向深层发展,且有相当一部分直接就是薄弱的基-填界面,安全系数也随之降低。对于不开挖台阶边坡,基-填界面强度比值的增大,安全系数增大的趋势变缓(图10),此时的滑裂面也基本不通过该界面。即随着比值的增加,潜在滑裂面逐渐转移到填筑体内,不再受基-填界面是否开挖台阶的影响。开挖台阶的尺度对安全系数计算结果影响不大,小台阶相对大台阶更加安全,随着比值的增加,小台阶和大台阶的计算结果都增加且十分接近。当比值为1时,台阶开挖对整体稳定的提升已无作用,大台阶和小台阶的安全系数结果重合,与理论解中结论一致。

图10 边界安全系数与界面强度比值的关系
Fig.10 Relationship between boundary safety factor and interface strength ratio
3 暴雨地震环境作用中工程边坡稳定性
3.1 工程场地与边坡情况
以某西南山区机场工程典型断面为分析对象,模型如图11所示。仍使用Plaxis有限元软件计算。断面长210 m,高86.5 m,土层分布从上至下分为填土、强风化白云岩、中风化白云岩,参数如表5所示。

图11 案例分析模型
Fig.11 Case analysis model
表5 材料参数
Table 5 Material parameter
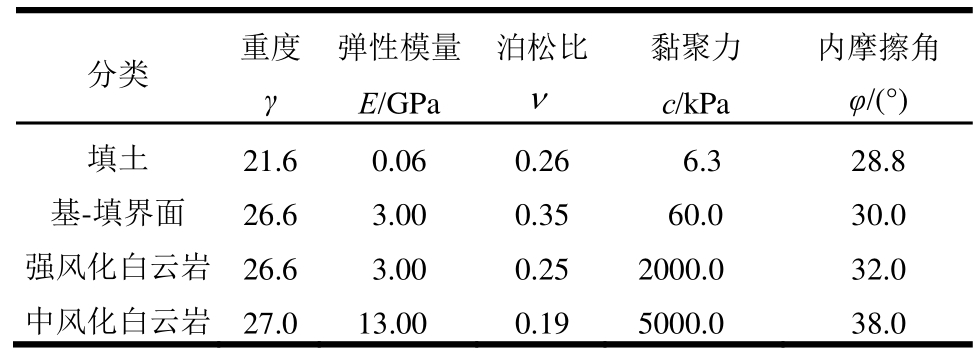
分类 重度γ弹性模量E/GPa泊松比ν黏聚力c/kPa内摩擦角φ/(°)填土基-填界面强风化白云岩中风化白云岩21.6 26.6 26.6 27.0 0.06 3.00 3.00 13.00 0.26 0.35 0.25 0.19 6.3 60.0 2000.0 5000.0 28.8 30.0 32.0 38.0
3.2 暴雨工况与边坡稳定
西部山区多雨且降雨较为集中,暴雨情况下,容易发生危险。有必要对暴雨工况下台阶开挖后的安全性进行分析。同时作为重要的山区战略机场,要具有在极端地质灾害中安全运行的能力,所以也要在地震工况下,对基-填界面台阶开挖后的填方边坡稳定性进行校核。
暴雨工况的破坏模式如图12所示,计算结果如表6所示。潜在滑裂面上部仍为圆弧形滑裂面,但是下部沿边界滑出。滑裂面加深,安全系数也明显下降,仅为1.170。

图12 暴雨情况下边坡破坏
Fig.12 Slope damage under heavy rain
3.3 地震工况与边坡稳定
该山区机场所在地设防烈度为6度以下,但按照政府要求,取6度为校核烈度。峰值加速度为0.05 g。地震工况分析时,采用拟静力法,水平加速度取峰值加速度的1/3[13],为0.01667 g。计算结果如表6所示,填土内部发生滑移,安全系数为1.254,也明显下降,但是好于暴雨工况。对比计算结果,暴雨工况和地震工况的安全系数仍高于不开挖台阶的天然工况,说明了台阶开挖的有效性。天然工况界面不折减,开挖台阶与否安全系数较接近。地震情况下边界破坏如图13所示。
表6 边坡安全系数计算结果汇总
Table 6 Slope safety factor calculation result summary

填方工法 界面折减系数为0.67 界面不折减天然工况 暴雨工况 地震工况 天然工况开挖台阶不开挖台阶1.311 1.156 1.170—1.254—1.367 1.372

图13 地震情况下边坡破坏
Fig.13 Slope damage under earthquake
4 结论
本研究通过简化Bishop方法和有限元方法对山区建设中经常采取的工程措施—在原地基和填方界面间开挖台阶后再填筑的机理和影响规律进行分析。提出了理论解法并解释了稳定性强化机理,并结合实际工程分析。填方体和原地基间的界面强度必定低于填筑体的强度,在这样的前提下,原地基开挖台阶总是能够增加整体稳定性。
研究以求解无限长边坡理论解为出发点,归纳边坡破坏类型,分三种情况求解安全系数并取最小值。理论解指出,顺坡填筑后边坡整体的稳定性与填筑质量,尤其是原地基与填方体界面的处理密切相关,当破坏面位于基-填界面时易发生危险。理论解中,台阶水平总长、台阶倾角和基-填界面相对填方体强度对最终结果有重要影响,进行敏感性分析,台阶水平总长越小,安全系数越高,但影响幅度小,即在实际工程中,可以在适当范围内控制台阶宽度的大小,并减少工程量。台阶倾角越大,安全性也随之上升,但有上限值,超过该值,增大倾角对稳定性提高无效。基-填界面相对填方体强度会影响稳定性的上限,比值越接近1,台阶能够发挥的作用越小。
为分析强化机理,进一步研究有限长边坡,通过基-填界面剪应力分布和基-填界面强度影响边坡稳定性趋势,指出台阶能够增加边坡稳定性主要是由于平台段将填方体重力荷载通过垂直反力平衡掉,从而降低了边坡的下滑力,降低了界面上相对剪应力的大小。使用台阶工法能够显著提高边坡稳定性50%以上,基-填界面相对填方体强度越小,其效果越明显。实际工程中,如不能充分保证基-填界面强度,务必在原地基表面施做台阶。
无论是暴雨工况还是地震工况,边坡稳定性都会降低,但是台阶的存在仍然能够提高边坡的稳定性。
[1]徐明, 陈金锋, 宋二祥.陡坡寺中微风化料的大型三轴试验研究[J].岩土力学, 2010, 31(8): 2496―2500.Xu Ming, Chen Jinfeng, Song Erxiang.Large scale triaxial testing of Douposi moderately-to-slightly weatherd fill materials [J].Rock and Soil Mechanics,2010, 31(8): 2496―2500.(in Chinese)
[2]徐则民, 张倬元, 许强, 等.九寨黄龙机场填方高边坡动力稳定性分析[J].岩石力学与工程学报, 2004,23(11): 1883―1890.Xu Zemin, Zhang Zhuoyuan, Xu Qiang, et al.Dynamic stability analysis of high fill slope of Jiu Zhai-Huang Long airfield [J].Chinese Journal of Rock Mechanics and Engineering, 2004, 23(11): 1883―1890.(in Chinese)
[3]黄佳昕.山区机场填方地基加强处理区域及顺坡填筑边坡稳定分析[D].北京: 清华大学, 2009.Huang Jiaxin.Slope stability of the improvement area in soft ground and fills on slope foundation in mountainous regions.[D].Beijing: Tsinghua University, 2009 (in Chinese)
[4]刘宏, 李攀峰, 张倬元, 等.山区机场高填方地基变形与稳定性系统研究[J].地球科学进展, 2004, 19(增刊1):324―328.Liu Hong, Li Panfeng, Zhang Zhuoyuan, et al.A systematic research on the deformation and stability of high embankment of airport in mountains area [J].Advance in Earth Sciences, 2004, 19(Suppl 1): 324―328.(in Chinese)
[5]陈金锋, 宋二祥, 徐明.山区顺坡填筑边坡稳定的强度折减有限元分析[J].工业建筑, 2012, 42(1): 103―109.Chen Jinfeng, Song Erxiang, Xu Ming.Application of FEM with strength reduction to stability analysis of filled slope on incline rock ground [J].Industrial Construction,2012, 42(1): 103―109.(in Chinese)
[6]吴红刚, 冯文强, 艾挥, 等.山区机场高填方边坡工程实践与研究[J].防灾减灾工程学报, 2018(2): 385―400.Wu Honggang, Feng Wenqiang, Ai Hui, et al.Engineering practice and research on High Fillslope of Mountainous Airport [J].Journal of Disaster Prevention and Mitigation Engineering, 2018(2): 385―400.(in Chinese)
[7]沈国印.高速公路新老路基拼接的台阶开挖效果分析[J].公路, 2012(7): 49―53.Shen Guoyin.Analysis of effect of step excavation in splicing between new and existing embankment of Expressway [J].Highway, 2012(7): 49―53.(in Chinese)
[8]李玉, 贾献卓.山前平原区高速公路路基加宽施工关键技术研究[J].公路交通科技(应用技术版), 2017(10):56―59.Li Yu, Jia Xianzhuo.Study on key technology of highway subgrade widening construction in piedmont plain [J].Highway Traffic Technology (Applied Technology Edition), 2017(10): 56―59.(in Chinese)
[9]GB 51254―2017, 高填方地基技术规范[S].北京: 中国建筑工业出版社, 2017.GB 51254―2017, Technical code for deep filled ground[S].Beijing: China Building Industry Press, 2017.(in Chinese)
[10]MH/T 5035―2017, 民用机场高填方工程技术规范[S].北京: 中国民航出版社, 2017.MH/T 5035―2017, Technical code for high filling engineering of airport [S].Beijing: China Civil Aviation Press, 2017.(in Chinese)
[11]Tian Chenglin, Ning Chunming, Liao Hongjian.Study on mechanical characteristics of micropiles in step-shaped slope [C].Proceedings of the inaugural World Transport Convention, Beijing, China, June 4―6, 2017.
[12]杨校辉, 朱彦鹏, 周勇, 等.山区机场高填方边坡滑移过程时空监测与稳定性分析[J].岩石力学与工程学报,2016(增刊2): 538―551.Yang Xiaohui, Zhu Yanpeng, Zhou Yong, et al.Time-space monitoring and stability analysis of high fill slope slip process at a airport in mountain region [J].Chinese Journal of Rock Mechanics and Engineering,2016(Suppl 2): 538―551.(in Chinese)
[13]徐光明, 邹广电, 王年香.倾斜基岩上的边坡破坏模式和稳定性分析[J].岩土力学, 2004, 25(5): 703―708.Xu Guangming, Zou Guangdian, Wang Nianxiang.Fail mode and stability analysis of soil slope on inclined bedrock [J].Rock and Soil Mechanics, 2004, 25(5):703―708.(in Chinese)
[14]刘欣欣, 唐春安, 龚斌, 等.基于DDD离心加载法的黑山铁矿西帮边坡稳定性研究[J].工程力学, 2018,35(1): 191―200.Liu Xinxin, Tang Chunan, Gong Bin, et al.Research on the stability of the west slope of the Heishan iron mine based on the DDD centrifugal loading method [J].Engineering Mechanics, 2018, 35(1): 191―200.(in Chinese)
[15]Gong B, Tang C A.Slope-slide simulation with discontinuous deformation and displacement analysis [J].International Journal of Geomechanics, 2016: E4016017.
[16]杨广庆, 张仲帆, 熊保林, 等.台阶开挖技术在高速公路路堤拓宽中的应用及研究[J].公路交通科技(应用技术版), 2015, 11(1): 68―72,123.Yang Guangqing, Zhang Zhongfan, Xiong Baolin, et al.Application and research of step excavation technology in widening of expressway embankment [J].Highway Traffic Technology (Applied Technology Edition), 2015,11(1): 68―72,123.(in Chinese)
[17]蒋水华, 姚池, 杨建华, 等.基于模型修正的空间变异边坡可靠度分析方法[J].工程力学, 2018, 35(8): 154―161.Jiang Shuihua, Yao Chi, Yang Jianhua, et al, Model correction factor method based approach for reliability analysis of spatially variable slopes [J].Engineering Mechanics, 2018, 35(8): 154―161.(in Chinese)
[18]Jiang S H, Li D Q, Cao Z J, et al.Efficient system reliability analysis of slope stability in spatially variable soils using monte carlo simulation [J].Journal of Geotechnical and Geoenvironmental Engineering, 2016,75: 18―27.
[19]郭振.茅台机场2号填方斜坡稳定性研究[D].成都:成都理工大学, 2013.Guo Zhen.Research on the stability of the NO.2 embankment slope of the MaoTai airport [D].Chengdu:Chengdu University of Technology, 2013.(in Chinese)
[20]郑颖人, 叶海林, 黄润秋, 等.边坡地震稳定性分析探讨[J].地震工程与工程振动, 2010, 30(2): 173―180.Zheng Yingren, Ye Hailin, Huang Runqiu, et al.Study on the seimic analysis of a slope [J].Journal of Earthquake Engineering and Engineering Vibration, 2010, 30(2):173―180.(in Chinese)
[21]宋二祥,孔郁斐,杨军.土工结构安全系数定义及相应计算方法讨论[J].工程力学, 2016, 33(11): 1―10.Song Erxiang, Kong Yufei, Yang Jun.Discussion of safety factor definitions and computation method for geotechnical structures [J].Engineering Mechanics,2016, 33(11): 1―10.(in Chinese)