我国广大的村镇建筑、城市老旧多层住宅楼均以砌体结构为主,传统砌体结构存在建筑能耗高、抗震性能差等突出问题[1-2]。自保温暗骨架承重墙[3-4]通过系列节能承重砌块实现自保温,通过内置的水平条带和竖向芯柱组成暗骨架,集抗震节能于一体,属于约束砌体。
带门洞、窗洞的各类砌体墙在建筑结构中广泛存在;伴随人民对居住条件改善的现实需求,在老旧多层住宅楼改造过程中较普遍存在拆除窗下墙。在上述背景下,开展窗下墙对抗震性能的影响研究引起学界关注。国内外学者[5-7]关于震害调查的结果表明,存在窗下墙可以延缓墙体裂缝发展,改善墙体耗能能力,提高建筑抗灾性能;郭猛等[8]为研究拆除窗下墙对粘土砖墙抗震性能的影响,进行了5片足尺砌体墙的低周往复荷载试验,结果表明拆除窗下墙显著影响墙体失效破坏模式、变形与承载能力等;信任等[9]通过两片实心标准砖墙体试件,研究了无筋砌体结构窗下墙的抗震性能,提出应充分考虑窗下墙的破坏模式与机理,建立其抗震设计方法尤为必要。范博等[10]利用数值模拟方法研究了窗下墙跨高比、开洞率以及高宽比对砌体结构地震破坏的影响;Tasnimi和Mohebkhak[11]通过低周往复荷载试验研究了开洞口砌体填充墙钢框架的抗震性能。针对窗下墙对自保温暗骨架承重墙抗震性能影响的研究鲜见公开报道。
本文旨在通过设计制作带窗洞、门洞的足尺自保温暗骨架承重墙试件,运用低周往复荷载试验研究窗下墙对自保温暗骨架承重墙抗震性能的影响;以试验研究为基础,建立该类墙体的开裂荷载和极限荷载计算方法,最终实现对窗下墙直接和间接参与抗震性能的定量影响评价。
1 试验概况
1.1 试件设计与制作
为探究窗下墙对自保温暗骨架承重墙抗震性能的影响,设计制作了两片足尺试件墙体,如图1(a)、图1(c)所示。两片墙体外形尺寸相同,均为宽×高×厚=2800 mm×2500 mm×240 mm,带窗洞、门洞的墙体分别编号为W1和W2,洞口高度分别为1.4 m、2.2 m,两片墙体的门窗洞口宽度均为0.81 m;二者不同之处是,墙体W1窗洞下方设有窗下墙,窗下墙高度0.8 m。两个墙体试件均由顶梁、墙体和底梁三部分组成,顶梁、底梁均由现浇钢筋混凝土浇筑而成,墙体采用图1(b)所示的全角型、半角型和水平条带三种砌块及强度等级为Mb7.5的砂浆砌筑而成;砌块强度等级为MU10,三种砌块的高度均为190 mm,长度分别为390 mm、190 mm、390 mm。两个试件均在墙体中布设4根竖向芯柱与2道水平条带组成暗骨架,4根竖向芯柱布置在墙体和门洞或窗洞两侧,两道水平条带分别布置在第4、8皮水平构造带模板砌块的凹槽处,间隔0.8 m,竖向芯柱与水平条带的截面尺寸均为160 mm×80 mm,并在其中分别内置1根14 mm的HRB335级钢筋,试件制作完成后养护28 d进行加载。
1.2 加载制度与数据采集
1.2.1 加载制度
为保证加载时试件底部不发生移动和转动,通过地脚螺栓和水平向千斤顶紧固底梁;低周往复荷载通过水平向MTS作动器施加,竖向荷载由两个竖向MTS作动器施加并保持不变至试验结束;为保证竖向荷载的分配和有效传递,通过在顶梁上放置刚性分配垫梁实现,为实现加载过程中墙体的侧向变形,在两根刚性垫梁之间设置滚轴支座。
图2所示为两个试件的试验加载现场,试验分为预加载和正式试验,通过预加载实现人机联调联试,检查机器设备运转情况;试验中利用两个竖向作动器分别提供55 kN的恒定荷载模拟典型四层村镇住宅底层墙体的竖向压力,对应轴压比为0.04;水平往复荷载通过水平作动器和反力墙提供。正式试验分为力控制和位移控制两个阶段,墙体开裂前通过力控制加载,采用逐级加荷方法,单次循环,以推为正向、拉为负向,墙体开裂后转为位移控制加载,取开裂荷载对应的位移为级差分别进行加载,每级循环3次,荷载下降至极限荷载的85%时停止试验。
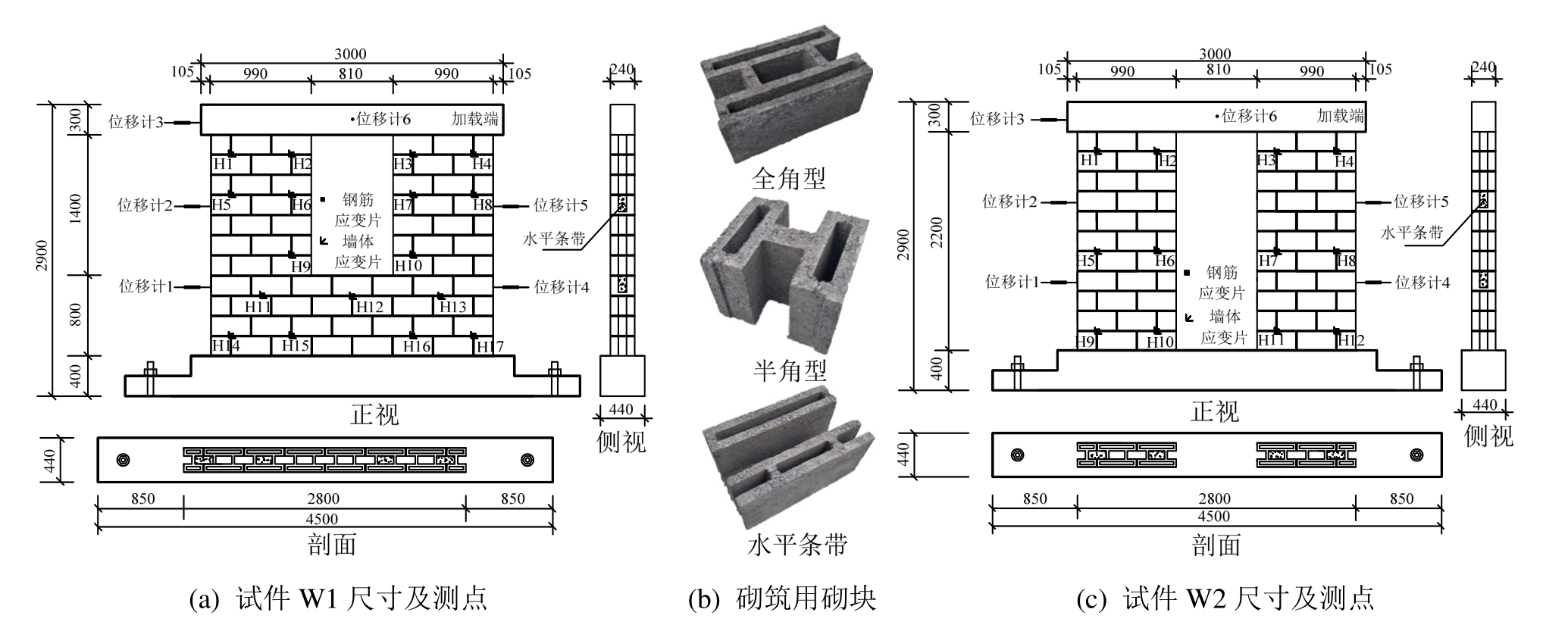
图1 试件设计与制作
Fig.1 Design and construct of the specimen

图2 加载现场
Fig.2 Loading site
1.2.2 数据采集
加载期间采集的数据类型主要包括应变、变形、力、裂缝等,相关测点布置方案详见图1(a)、图1(c)。其中,应变数据包括墙体表面及钢筋应变,均通过应变采集仪采集;出力大小直接由MTS加载系统自动采集;利用电测位移计实现墙体侧向变形的采集;墙体的失效过程以及裂缝观测由专门试验人员利用“ZBL-F103裂缝宽度观测仪”进行测试记录。
2 试验现象
2.1 力控制加载阶段
试件W1、试件W2在加载伊始,均无开裂现象;荷载分别增至140.655 kN、95.040 kN时,出现首条裂缝,即W1开裂荷载较W2提高48.06%。该阶段W1的破坏现象是:在窗下墙第3~4皮砌块(墙体皮数如图3、图4所示)水平灰缝处出现裂缝,缝宽约0.4 mm,对应水平侧向变形为4.211 mm,窗下第3皮砌块由中间砌块右侧向左下出现阶梯型裂缝,右侧窗间墙上部第10皮主砌块间出现竖向裂缝并向左下侧呈阶梯状发展,如图3(a)所示;W2的破坏现象是:在左侧墙肢的第2~3皮砌块间水平灰缝处出现第1条裂缝,缝宽0.4 mm左右,对应水平侧向变形为2.449 mm,如图4(a)所示。
2.2 位移控制加载阶段
根据开裂荷载对应的侧向变形实测值,将±4.0 mm、±2.5 mm分别作为试件W1、试件W2在位移控制加载阶段的第1荷载步。该阶段第1荷载步后,试件W1在窗洞左侧第5~6皮和第9~10皮砌块之间出现新的水平裂缝;试件W2的墙体裂缝没有进一步发展。
试件W1在侧向变形增至±8.0 mm时,第3、第4皮砌块间(对应水平条带下方)的水平裂缝贯通,窗洞左侧第6~7皮、第9~10皮砌块之间开始出现阶梯状裂缝,且窗下墙阶梯状裂缝进一步发展延伸至底梁;当侧向变形增至±12.0 mm时,窗下墙形成“X”形裂缝,且裂缝延伸至窗间墙根部,窗洞两侧墙体的裂缝在原有基础上进一步延伸形成4条明显的阶梯状裂缝;当侧向变形增至±14.0 mm时,在墙体左下角与右下角开始出现水平和竖向裂缝,且窗洞左、右两侧的墙体裂缝进一步发展;当侧向变形增至±16.0 mm时,墙体左下侧与右下侧分别形成阶梯状裂缝,整个墙体在水平条带与竖向芯柱所包围的各个小区域中,分别形成了阶梯状裂缝,砌块基本退出工作,由芯柱和水平条带组成的暗骨架演变为主要抗侧体系,对应荷载下降至极限荷载的85%,终止试验。

图3 墙体W1失效破坏过程
Fig.3 Failure process of W1

图4 墙体W2失效破坏过程
Fig.4 Failure process of W2
试件W2在侧向变形增至±5.0 mm时,左侧墙体第1、第2皮砌块出现阶梯状裂缝,在第3皮砌块及其上方灰缝处分别出现竖向和水平裂缝,墙体右侧第5~6皮砌块间出现水平裂缝并且延伸至右侧立面;当侧向变形增至±7.5 mm时,在左、右侧墙肢第2道水平条带的上部区域均出现对称阶梯状裂缝,同时在门洞右下角出现水平裂缝;侧向变形增至±10.0 mm时,在两侧墙肢第6、第7皮砌块出现水平与竖向裂缝,右侧墙肢根部水平裂缝基本贯通,左侧墙肢的根部区域自洞口边亦出现水平裂缝,右侧墙肢在第2、第3皮砌块形成阶梯状裂缝,两侧墙肢开裂状态基本呈对称分布;当侧向变形增至±12.5 mm时,两侧墙肢的上部和下部都形成了阶梯状裂缝,中部区域裂缝发展相对较轻;加载至±15.0 mm时,由芯柱和水平条带围合而成的各区域均基本形成了阶梯状斜裂缝;侧向变形增至±17.0 mm时,墙体裂缝数量没有进一步增多,但裂缝宽度显著增加,对应水平荷载降至极限荷载的85%,试验结束。
综上可知,试件W1和试件W2的最终破坏形态都是在水平条带和竖向芯柱所包围的区域形成了阶梯状裂缝,即可以推断两片墙体均在暗骨架包围的区域形成了斜压杆模型,后续关于墙体极限承载力的计算分析证明了此猜想;内置的暗骨架能有效阻止裂缝快速发展,延缓墙体失效破坏过程,提高墙体耗能能力。与试件W2相比,试件W1的裂缝发展更加充分,承载能力亦更高,说明窗下墙是墙体失效破坏过程稳定有序、各个构件充分发挥作用的重要组成部分,其有无直接影响自保温暗骨架承重墙的承载与耗能。
3 试验结果与分析
3.1 滞回曲线
图5为试件W1、试件W2的滞回曲线,可明显看出,试件W1的滞回曲线呈较为丰满的梭形,反映出试件具有良好的耗能特性和抗震能力;试件W2滞回曲线的饱满程度明显低于W1,二者的差异在后期更显著,直接反映出试件W2的耗能能力低于试件W1。两个试件的开洞位置、洞口宽度、暗骨架布置方式均相同,不同之处即有无窗下墙,故滞回曲线的差异能直接归因于窗下墙的影响。
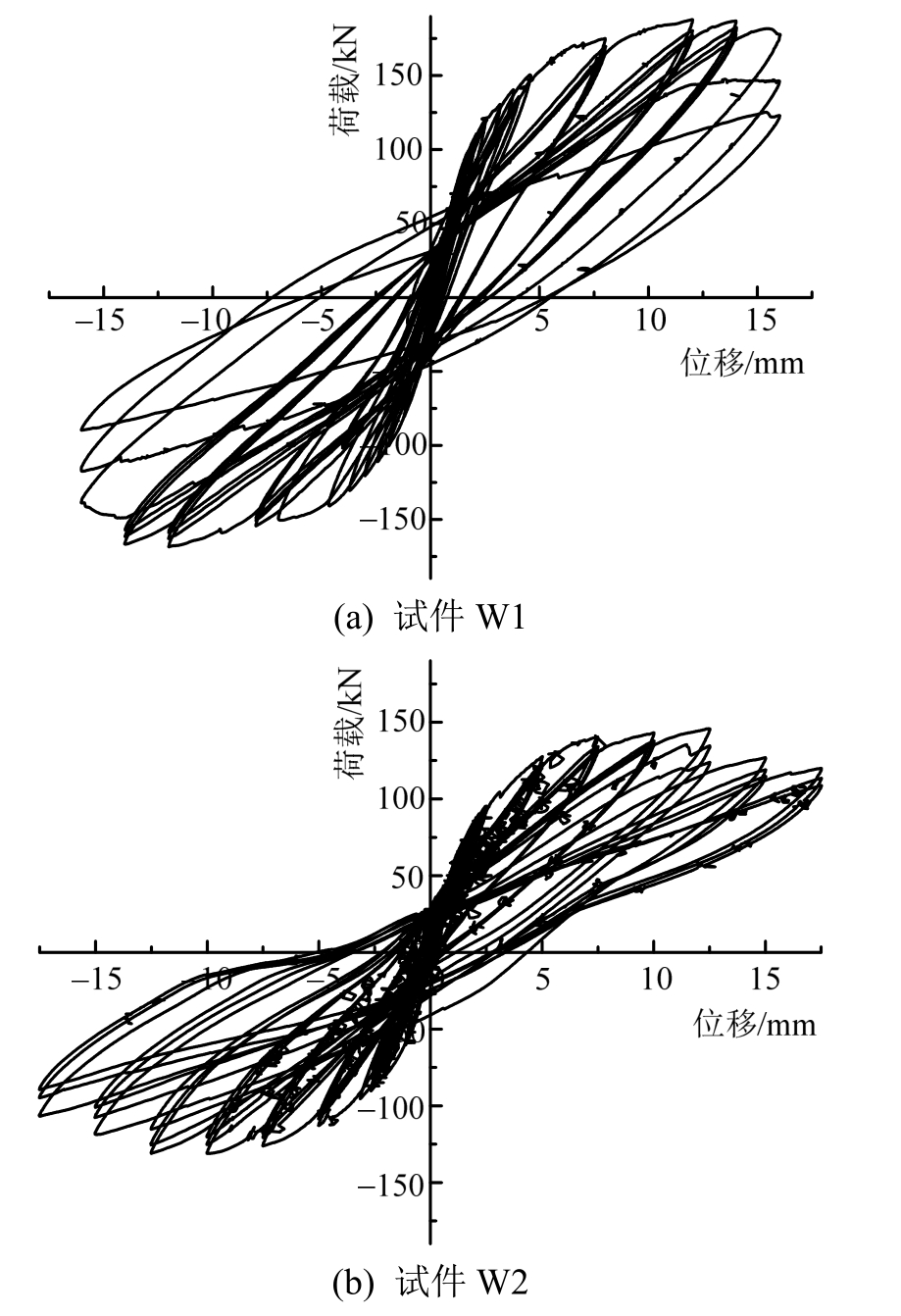
图5 试件滞回曲线
Fig.5 Hysteretic curve of the specimen
进一步分析可知,两个试件的滞回曲线均呈现三阶段特征,恰与我国抗震设防目标相对应,即:在开裂前,曲线斜率基本不变,加卸载曲线基本重合,即滞回环面积为零,说明墙体处于弹性阶段,对应抗震设防目标“小震不坏”;墙体开裂后对应的曲线斜率逐渐减小,即墙体刚度降低,但伴随侧向变形增加,2个试件的承载能力均不断提高,同时滞回环面积逐渐增加,卸载后墙体存在残余应变,此时墙体进入弹塑性阶段,但破坏程度相对较轻,对应“中震可修”阶段;极限荷载后,墙体的承载能力和刚度均降低,在同级侧向变形下伴随循环次数增加,试件的承载力、刚度均有一定程度退化,且墙体已出现不可修复的破坏,对应“大震不倒”阶段。
3.2 骨架曲线
图6为试件W1、试件W2的骨架曲线,反映不同阶段墙体的受力、变形特点,从中提取开裂点、峰值点、破坏荷载点等各特征点对应的荷载和变形列于表1。

图6 试件骨架曲线
Fig.6 Skeleton curve of the specimen
分析可知,试件W1的骨架曲线整体外包试件W2,即试件W1对应的抗侧刚度在各阶段均大于试件W2;试件W1、试件W2对应的极限荷载分别是178.153 kN、138.413 kN,前者较后者高28.71%,上述均可归因于窗下墙的影响。共同之处体现在:开裂前骨架曲线均近似为一条直线,说明墙体处于弹性工作阶段;开裂后,曲线斜率缓慢减小,说明试件刚度减小,但2个试件的抗侧承载力均伴随侧向变形增加而增加;峰值荷载后,曲线进入平缓下降段,伴随侧向变形增加承载力缓慢降低。
试件变形能力的大小还可以通过延性系数体现,即极限位移与屈服位移之比,延性系数越大说明试件变形能力越好;延性差的试件说明变形能力差,试件在极限荷载后更易发生脆性破坏。通过计算可得,试件W1、试件W2对应的延性系数分别为3.034、3.545,说明2试件均具有良好的延性性能,失效破坏模式同属延性破坏。
表1 荷载及位移特征值
Table 1 Load and displacement eigenvalues

试件编号 开裂荷载Vcr/kN 开裂位移Δcr/mm 屈服荷载Vy/kN屈服位移Δy/mm极限荷载Vmax/kN破坏荷载Vu/kN 极限位移Δu/mm W1 140.655 4.211 147.734 5.281 178.153 151.430 16.023 W2 95.040 2.449 100.878 4.936 138.413 113.414 17.500
3.3 承载力退化
通过承载能力退化系数λ评价试件的承载力退化情况,其值越大说明抗震性能越好。依据《建筑抗震试验规程》(JGJ/T 101―2015)[12],通过式(1)计算λi,试件W1、试件W2对应的计算结果分别见表2、表3。
表2 试件W1承载能力退化系数和平均残余变形率
Table 2 Bearing capacity degradation coefficient and average residual deformation rate of W1
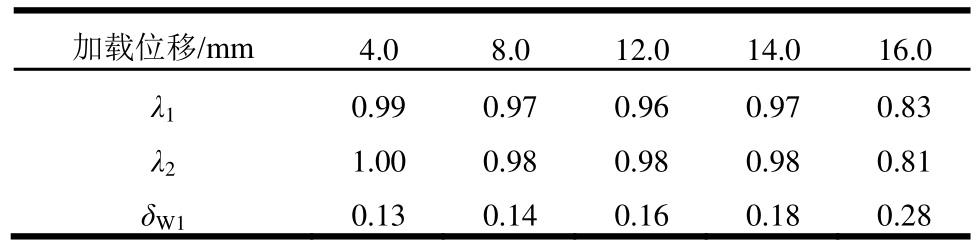
加载位移/mm 4.0 8.0 12.0 14.0 16.0 λ1 0.99 0.97 0.96 0.97 0.83 λ2 1.00 0.98 0.98 0.98 0.81 δW1 0.13 0.14 0.16 0.18 0.28
表3 试件W2承载能力退化系数和平均残余变形率
Table 3 Bearing capacity degradation coefficient and average residual deformation rate of W2
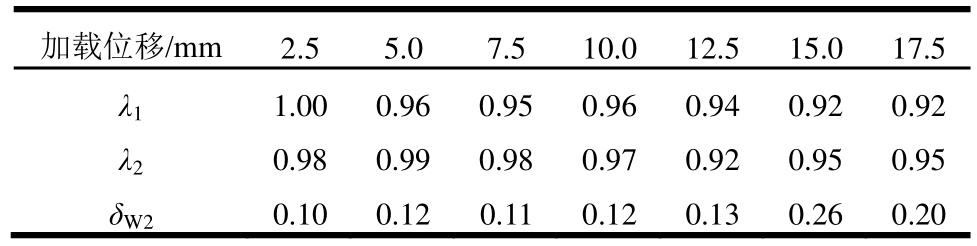
加载位移/mm 2.5 5.0 7.5 10.0 12.5 15.017.5 λ1 1.00 0.96 0.950.96 0.94 0.920.92 λ2 0.98 0.99 0.980.97 0.92 0.950.95 δW2 0.10 0.12 0.110.12 0.13 0.260.20

式中:λi为第i次循环对应的承载能力退化系数;![]() 分别表示第j次加载时第i、i-1次循环峰值点对应的荷载值。
分别表示第j次加载时第i、i-1次循环峰值点对应的荷载值。
分析表2、表3可知,试件W1、试件W2的承载能力退化系数平均值分别为0.95、0.96,说明二者抗震承载力退化不明显,均具有良好的承载能力,不会出现脆性破坏;墙体的承载能力还可以通过极限荷载与屈服荷载的比值体现,由表1经计算可知,试件W1、试件W2对应的比值分别为1.206、1.372,即二者的安全储备分别为20.6%、37.2%,再次验证二者均具有良好的承载能力。
3.4 残余变形率
结构的残余变形[13]不仅反映结构损伤程度,也体现结构的变形恢复能力。可通过式(2)得到试件W1、试件W2的平均残余变形率δ,计算结果见表2、表3。

式中:![]() 分别为试件每级加载位移的第1个循环在正负向荷载卸载时试件的残余变形
分别为试件每级加载位移的第1个循环在正负向荷载卸载时试件的残余变形![]() 分别为试件每级加载位移的第1个循环在正负向峰值时对应的位移。
分别为试件每级加载位移的第1个循环在正负向峰值时对应的位移。
由表2、表3可知,试件W1、试件W2的残余变形率基本均伴随加载位移的增加而增加,至达到破坏荷载后二者的残余变形率均在0.2以上,此时两个试件仍能达到“坏而不倒”,说明二者均具有良好的抗震性能。
3.5 刚度退化
通过每级正反向荷载绝对值之和与对应正、反向位移绝对值之和的比值计算试件对应的刚度,图7为试件W1、试件W2失效破坏全过程对应的刚度退化曲线。
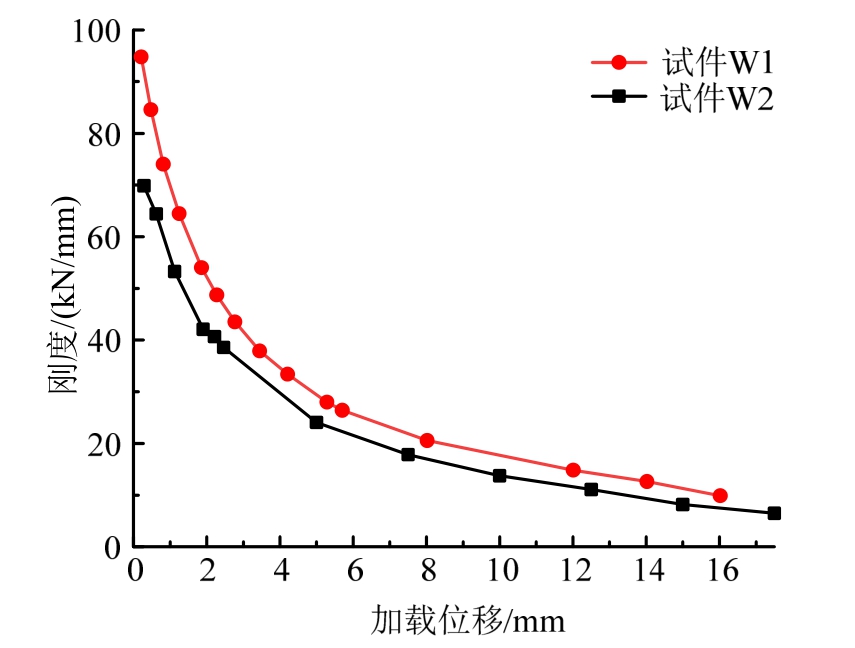
图7 刚度退化曲线
Fig.7 The curve of stiffness degradation
分析图7可知,二者刚度退化趋势基本相同,均体现为“先快后慢”,究其原因是:在前期加载位移较小时,墙体耗能主要通过砌块间的摩擦力与灰缝之间的粘结力;至加载后期,伴随侧向变形增加,墙内暗骨架逐渐代替砌块成为主要抗侧体系,刚度退化变得缓慢且均匀,体现为墙体结构在往复荷载作用下具有良好的延性。二者的不同则体现为相同侧移对应的抗侧刚度在失效破坏全过程均是试件W1大于试件W2,以初始刚度为例,试件W1较试件W2提高34.73%,上述差异可以推断为窗下墙的影响。
3.6 耗能能力
通过能量耗散系数E和等效粘滞阻尼系数ξeq[14]评价墙体耗能,其值越大说明耗能能力越好,即抗震性能越好。图8为试件W1、试件W2在每级加载位移第1次循环对应的E和ξeq,可明显看出二者的E和ξeq均伴随加载位移的增加而增加,并且在加载后期二者的ξeq均已超过0.1,说明二者均具有良好的耗能特性;侧移较小时二者的E和ξeq基本相同,但在加载后期试件W1显著高于试件W2,说明窗下墙的存在可以显著增加墙体耗能特性,利于提高墙体抗震性能。
3.7 墙体失效机制
图9为同一位置墙体表面与芯柱钢筋的应力对比,试件W1、试件W2所选的代表性测点分别是H10、H1(测点编号如图1),二者分别位于芯柱的根部和顶端。图9纵轴对应的应力由实测应变分别乘以砌块、钢筋的弹性模量得到,其弹性模量分别为9 GPa、200 GPa。
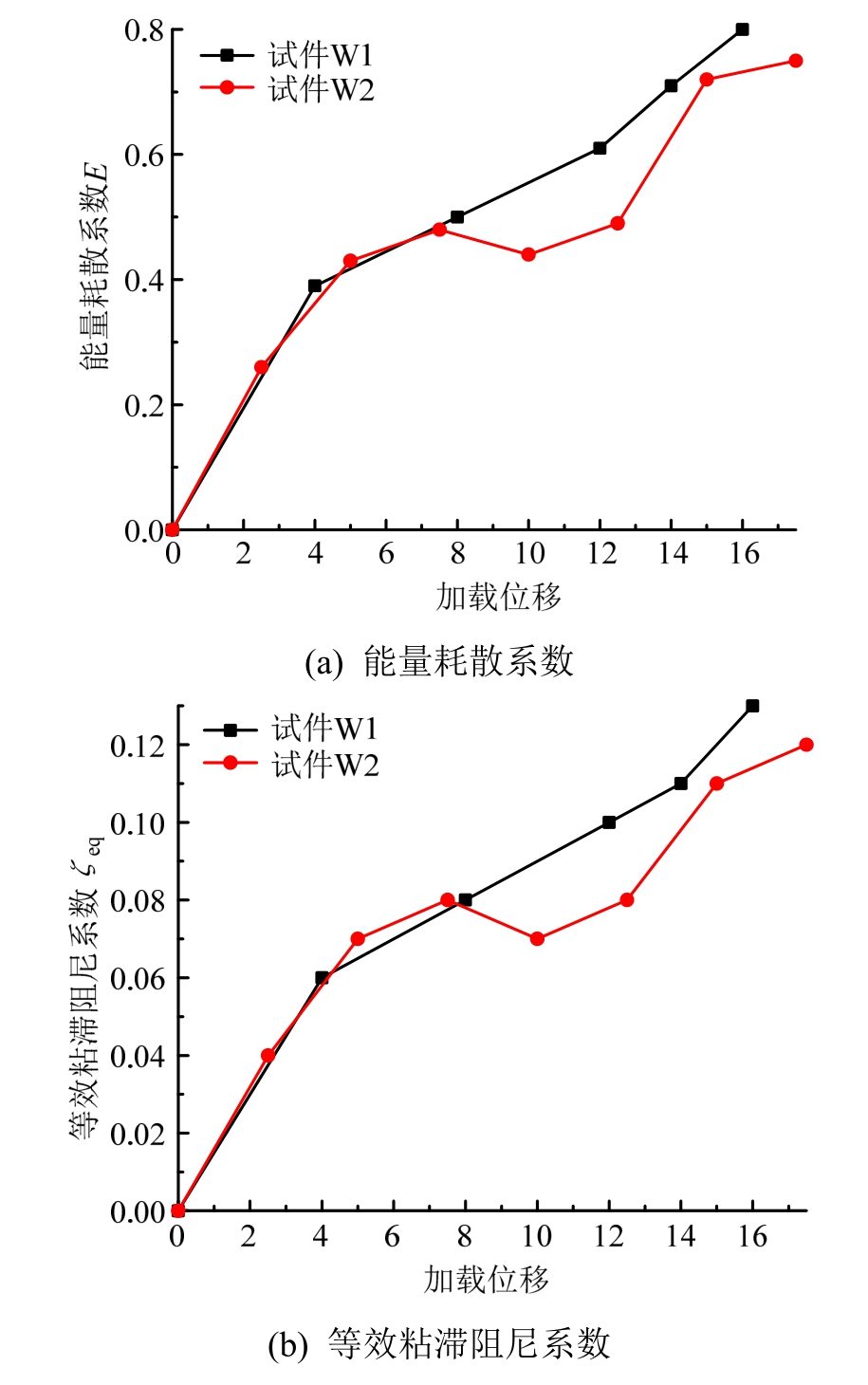
图8 试件耗能图
Fig.8 Energy dissipation diagram of specimen

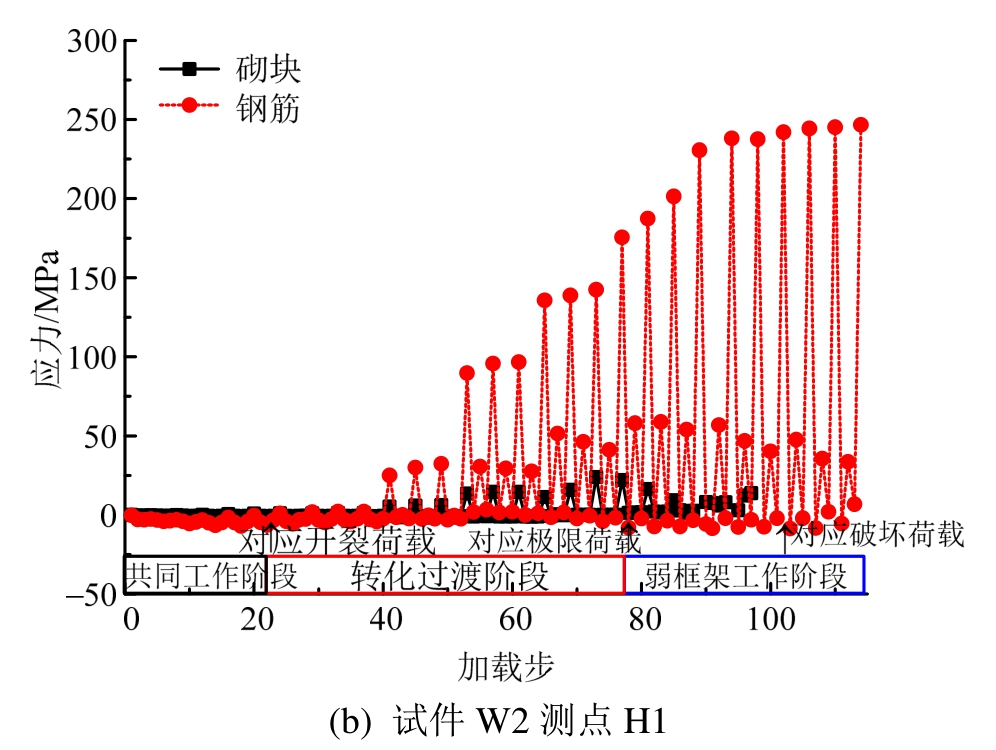
图9 砌块和钢筋的应力对比图
Fig.9 Comparison between block stress and steel stress
分析图9可知,根据砌块和芯柱的受力特性,可将该类墙体的失效破坏全过程分为共同工作、转化过渡和弱框架工作三个阶段。在开裂荷载之前砌块与钢筋应力基本相同,说明砌块与钢筋共同受力,墙体各组分处于共同工作阶段;开裂荷载至极限荷载阶段,钢筋应力迅速增加,砌块应力基本保持不变,即暗骨架逐渐演变为主要受力构件,此阶段定义为转化过渡阶段;极限荷载之后钢筋应力进一步增加,砌块退出工作,其表面测点基本失效,说明暗骨架已成为墙体主要的抗侧体系,演变为弱框架工作阶段。
4 抗震承载力计算方法与定量评价
4.1 基于等效弹性板模型的墙体开裂荷载计算
通过对上述试验结果的分析可知,在墙体开裂之前,墙体各组分处于共同工作阶段,砌块和暗骨架可作为一个整体受力构件,符合等效弹性板模型受力特征,其内力计算符合线性叠加原理,开裂荷载的计算可视为平面应力问题,对应的等效弹性板模型如图10所示。本文根据最大拉应力理论、双剪统一强度理论分别计算自保温暗骨架承重墙的开裂荷载,通过引入开洞率α、暗骨架约束系数η分别考虑门窗洞口、内置暗骨架对自保温暗骨架承重墙开裂荷载的影响。
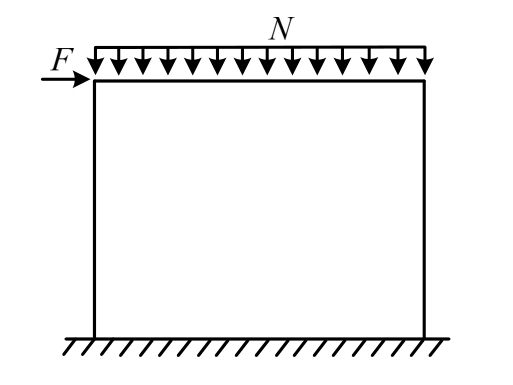
图10 等效弹性板模型
Fig.10 Equivalent elastic plate model
4.1.1 按最大拉应力理论计算开裂荷载
最大拉应力理论,即当自保温暗骨架承重墙中砌块的主拉应力达到其抗拉强度时,墙体开裂。根据最大拉应力理论[15]提出的公式,进行修正得到开裂荷载计算公式:
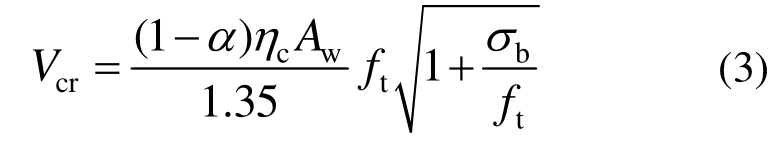
式中:ft为砌体抗拉强度,取值0.26 MPa;Aw为墙肢水平净截面面积;σb为砌块竖向压应力。
主要参数的确定如下。
由前文分析可知,墙体开裂前砌块与暗骨架处于共同工作阶段,所以可认为砌块与暗骨架竖向应变相同,即:

结合应力计算公式可得到式(5):
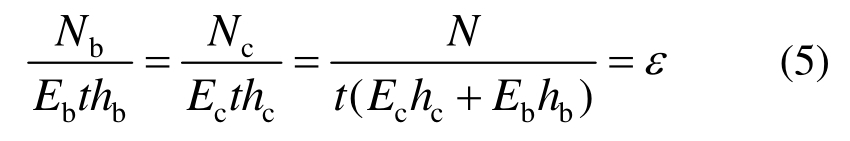
式(5)两侧同乘以Eb,经整理可得:

式中:hc、hb分别为墙体中混凝土和砌块的水平截面长度;Ec、Eb分别为混凝土和砌体的弹性模量;N为墙体承担的竖向压力。
暗骨架约束系数η,根据文献[15]修正可得:
式中,m、n分别为芯柱和水平条带的数量。
经计算,试件W1、试件W2的开裂荷载分别为134.220 kN、101.613 kN,与实测值140.655 kN、95.040 kN相比分别小4.58%、大6.92%。故二者均能与实测结果较好吻合,满足工程应用需要。
4.1.2 按双剪统一强度理论计算开裂荷载
通过对双剪统一强度理论所提出的公式[15]进行修正,可以得到开裂荷载计算公式:
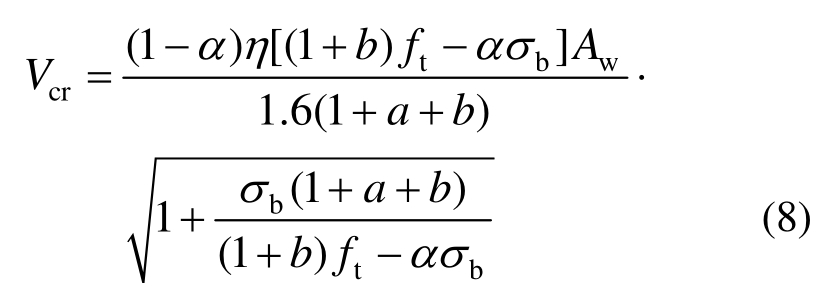
式中:a为拉压强度比,取值0.1;b为反映中间主切应力以及相应面上正应力对材料破坏程度影响的参数,取值0.5;σb通过式(6)计算。
经计算,试件W1、试件W2的开裂荷载分别为133.40 kN、100.99 kN,与实测值140.655 kN、95.040 kN相比分别小5.16%、大6.26%。显然,计算值与实测值亦吻合较好,满足工程应用需要。
对比可知,上述两种计算方法所得计算结果均能与实测结果较好吻合,且计算平均误差十分接近,即两种方法的计算精度基本相同;但从计算的简便性考虑,第一种方法优于第二种,故推荐使用按照最大拉应力理论计算开裂荷载。
4.2 基于抗剪抵抗机构的墙体极限荷载计算
结合自保温暗骨架承重墙的结构特点和失效特征,基于抗剪抵抗机构[16]思想提出刚架斜压杆模型;该模型是将暗骨架所围合的砌块用一个沿其对角线放置的等效斜压杆代替,整个墙体可简化为由暗骨架和与之铰接的等效斜压杆组合而成,即抗剪抵抗机构由墙内的水平钢筋、竖向钢筋、等效斜压杆共同组成,图11为试件W1、试件W2的刚架斜压杆模型。当等效斜压杆的应力达到有效抗压强度时,认为墙体达到极限承载力,此时钢筋屈服,依据叠加原理按照式(9)通过计算可得墙体的极限荷载Vmax。
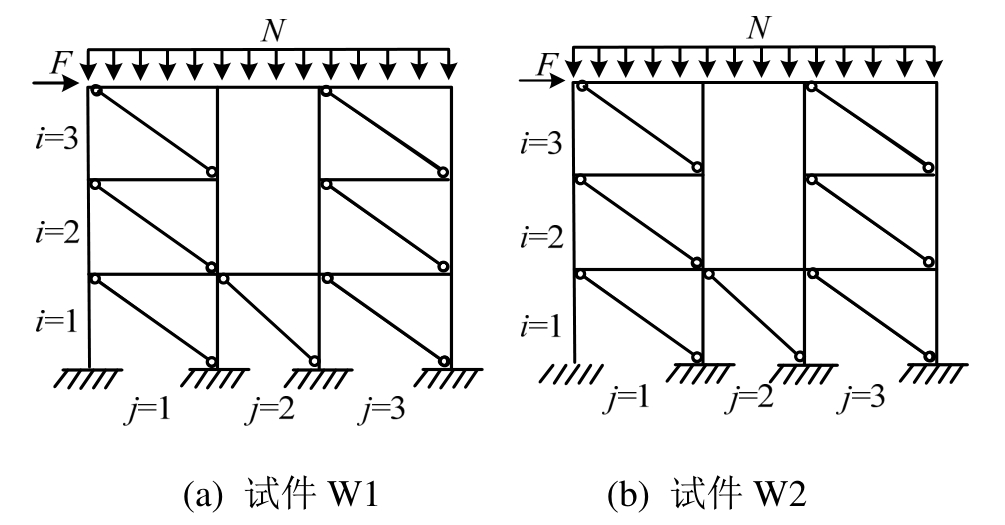
图11 刚架斜压杆模型
Fig.11 Rigid frame baroclinic model
式中:Vsv为竖向芯柱的销栓力;Vsh为水平钢筋的抗剪承载力;Vstr为等效斜压杆承担的抗剪承载力。
4.2.1 竖向芯柱销栓力Vsv
根据参考文献[17]修正可得:
式中:n为竖向芯柱钢筋的数量;d为钢筋直径;fc为混凝土抗压强度设计值;fy为钢筋抗拉强度设计值。
4.2.2 水平钢筋抗剪承载力Vsh
据《砌体结构设计规范》(GB 50003―2011)[18]第10.2.2条可得:
式中:ζs为钢筋参与工作系数,取值0.138;fyh为水平钢筋抗拉强度设计值;Ash为水平钢筋截面总面积。
4.2.3 等效斜压杆抗剪承载力Vstr
通过式(12)计算Vstr,即:
式中,σs为斜压杆有效抗压强度,根据文献[19]修正可得:
式中:γ为约束砌体有效抗压强度利用系数,取值0.073;fm为砌块砌体的抗压强度平均值,取值11.37 MPa。
Astr为斜压杆截面面积:
式中:t为墙体厚度;w为斜压杆的宽度,通过等效刚度法确定。
墙体开裂是其共同工作和转化过渡阶段的分界点,即等效弹性板模型和抗剪抵抗机构的分界点,可认为墙体在分界点刚度相同,即共同工作阶段的抗侧刚度Kt等于等效斜压杆模型的初始刚度Ks,据此可得到等效斜压杆的截面宽度w。
1) 共同工作阶段抗侧刚度Kt的确定
在计算墙体的层间侧向刚度Kt时,引入刚度折减系数β和开洞率α分别考虑墙体所用块材的孔洞和设置的门洞或窗洞,修正后的计算公式如式(15)所示,即:
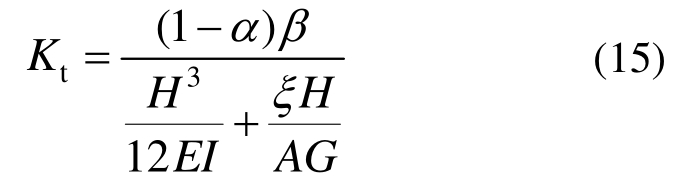
式中:H为墙高;A为墙体水平横截面面积;I为墙体截面惯性矩;β取值0.125;ξ为截面剪应力分布均匀系数,取值1.2;E为墙体弹性模量,通过式(16)计算:
式中:ηc为混凝土纤维修正系数,取0.7;Vc、Vb分别为墙体中混凝土和砌块的体积分数。G为墙体剪切模量,通过式(17)计算:
式中,Gc、Gb分别为墙体中混凝土和砌块的剪切模量。
通过计算可得,试件W1、试件W2的抗侧刚度分别为86.50 kN/mm、75.89 kN/mm,与实测值94.80 kN/mm、69.83 kN/mm相比分别小8.76%、大7.25%。显然,上述计算方法与实测结果吻合较好,能满足工程应用需要。
2) 等效斜压杆模型初始刚度Ks的确定
图12为单刚架斜压杆模型,假定水平集中力F使其产生单位侧向位移,则墙体抗侧刚度等于F与位移的比值,即在数值上水平力F等于其抗侧刚度。
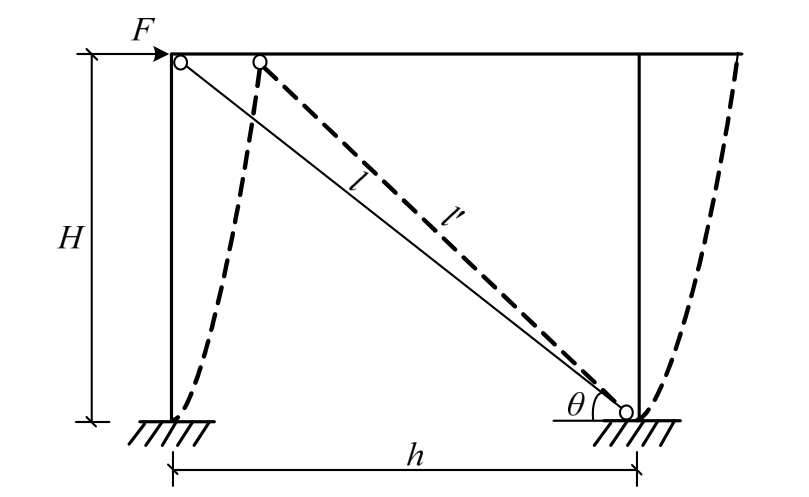
图12 单刚架斜压杆模型
Fig.12 Single rigid frame baroclinic model
分析可知,斜压杆的轴力为:
根据胡克定律可知:
式中:l为斜压杆初始长度;Δl=l-l′,l′为变形后的斜压杆长度;θ为斜压杆与水平面之间的夹角。
又![]() 联立式(18)、式(19),整理可得:
联立式(18)、式(19),整理可得:
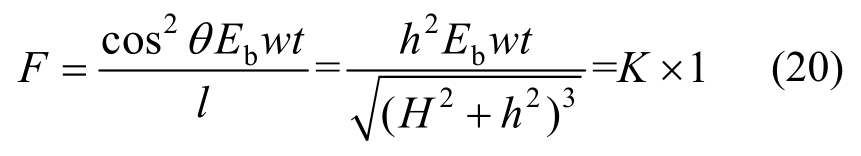
同理,可得到试件W1的抗侧刚度为:
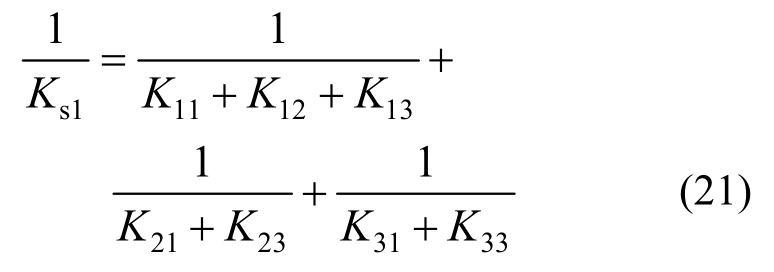
试件W2的抗侧刚度为:
式中:Kij代表图11所示计算模型中第i层第j跨的单个刚架抗侧刚度。
据上述方法计算可知,试件W1、试件W2的抗剪极限承载力分别为161.402 kN、145.799 kN,与实测值178.153 kN、138.413 kN相比分别小9.40%、大5.34%。计算值与实测结果吻合较好,满足工程应用需要。
综上可知,试件W2对应的开裂荷载与极限荷载计算值均略高于实测值,这是因为在计算时高估了试件W2两侧墙肢中部斜压杆参与抗剪工作的能力,该推断可通过该墙体的最终失效状态(图4)予以验证。
4.3 窗下墙对抗震承载力影响的定量评价
1) 直接作用:等效斜压杆抗剪承载力对比分析
据式(12)计算等效斜压杆抗剪承载力,由图11可知:试件W1的等效斜压杆抗剪承载力由窗间墙和窗下墙共同提供,其中窗间墙、窗下墙提供的等效斜压杆抗剪承载力分别为82.16 kN、11.84 kN,合计94.00 kN;试件W2的等效斜压杆抗剪承载力全部由门洞两侧墙肢提供,合计80.01 kN。对比可知,试件W1由于存在窗下墙,其等效斜压杆抗剪承载力较试件W2提高了17.49%,即窗下墙对墙体抗剪承载力具有显著影响。
2) 间接作用:窗下墙对窗间墙抗剪承载性能影响
据图3、图4的对比分析可明显看出,试件W2因缺少窗下墙,门洞两侧墙肢的中部区域并没有完全参与工作;与之形成显著对比,试件W1由暗骨架围合而成的各区域在最终均达到失效破坏状态,耗能更加充分。进一步通过定量计算可知,试件W1、试件W2两侧中部网格对应的等效斜压杆抗剪承载力分别为82.16 kN、80.01 kN,试件W1较试件W2提高了2.68%。上述抗剪承载力的差异与墙体失效破坏特征,均可归因于窗下墙的影响。
5 结论
(1)试验结果表明,带窗洞、门洞的自保温暗骨架承重墙抗震失效全过程可划分为共同工作、转化过渡和弱框架工作三个阶段,恰与我国现阶段抗震设防目标相对应;两片墙体均呈延性破坏,对应延性系数分别为3.034、3.545。
(2)基于等效弹性板模型,根据最大拉应力理论和双剪统一强度理论分别建立了开设门窗洞口的自保温暗骨架承重墙开裂荷载计算方法;基于抗剪抵抗机构思想提出刚架斜压杆模型,并利用等效刚度法明晰了斜压杆宽度的确定方法,最终建立了墙体极限荷载的计算方法;计算结果与实测值的比较分析表明,所建立的计算方法精度较高,均能满足工程应用需要。
(3)研究表明,窗下墙对自保温暗骨架承重墙的滞回曲线、骨架曲线、刚度及其退化、耗能能力等均存在显著影响,即窗下墙显著影响墙体抗震耗能;定量分析表明,窗下墙试件W1较等效斜压杆抗剪承载力试件W2直接提高17.49%,墙体两侧中部网格对应的等效斜压杆抗剪承载力试件W1较试件W2间接提高2.68%。
[1]清华大学、西南交通大学、北京交通大学土木工程结构专家组.汶川地震建筑震害分析[J].建筑结构学报,2008, 29(4): 1―9.Civil and Structural Groups of Tsinghua University,Xinan Jiaotong University and Beijing Jiaotong University.Analysis on seismic damage of buildings in the Wenchuan earthquake [J].Journal of Building Structures, 2008, 29(4): 1―9.(in Chinese)
[2]邓明科, 杨铄, 王露.高延性混凝土加固无筋砖墙抗震性能试验研究与承载力分析[J].工程力学, 2018,35(10): 101―111, 123.Deng Mingke, Yang Shuo, Wang Lu.Experimental and bearing capacity studies on the seismic behavior of unreinforced masonry walls strengthened with HDC layers [J].Engineering Mechanics, 2018, 35(10): 101―111, 123.(in Chinese)
[3]刘福胜, 王少杰.混凝土夹心秸秆砌块抗震节能生态宜居村镇建筑[M].北京: 中国建材工业出版社, 2018:168―179.Liu Fusheng, Wang Shaojie.Concrete sandwich straw block earthquake-resistant energy-saving ecological livable village and town buildings [M].Beijing: China Building Materials Press, 2018: 168―179.(in Chinese)
[4]Hou S D, Liu F S, Wang S J, et al.Coupled heat and moisture transfer in hollow concrete block wall filled with compressed straw bricks [J].Energy and Buildings,2017, 135: 74―84.
[5]Zhao B, Taucer F, Rossetto T.Field investigation on the performance of building structures during the 12 May 2008 Wenchuan earthquake in China [J].Engineering Structures, 2009, 31(8): 1707―1723.
[6]姚新强, 孙柏涛, 王明振, 等.我国农村典型砖砌体墙片拟静力试验研究[J].工程力学, 2017, 34(6): 198―209.Yao Xinqiang, Sun Baitao, Wang Mingzhen, et al.Study on the pseudo-static tests of typical brick masonry walls in rural China [J].Engineering Mechanics, 2017, 34(6):198―209.(in Chinese)
[7]Sharma K, Deng L, Noguez C C.Field investigation on the performance of building structures during the April 25, 2015, Gorkha earthquake in Nepal [J].Engineering Structures, 2016, 121: 61―74.
[8]郭猛, 徐福泉, 朱莹, 等.拆除窗下墙对砌体墙抗震性能影响的试验研究[J].建筑结构学报, 2014, 35(8):120―126.Guo Meng, Xu Fuquan, Zhu Ying, et al.Experimental research on seismic performance influence of masonry wall removed spandrel wall [J].Journal of Building Structures, 2014, 35(8): 120―126.(in Chinese)
[9]信任, 姚继涛, 吴梦溪, 等.无筋砌体结构窗下墙抗震性能拟静力试验研究[J].建筑结构, 2017, 47(7): 69―71, 51.Xin Ren, Yao Jitao, Wu Mengxi, et al.Quasi-static experimental study on seismic performance of unreinforced masonry spandrel walls [J].Building Structure, 2017, 47(7): 69―71, 51.(in Chinese)
[10]范博, 郭师虹, 庄稼铸.砌体结构窗下墙地震破坏研究[J].世界地震工程, 2017, 33(2): 186―191.Fan Bo, Guo Shihong, Zhuang Jiazhu.Study on earthquake damage to masonry structure window belly wall [J].World Earthquake Engineering, 2017, 33(2):186―191.(in Chinese)
[11]Tasnimi A A, Mohebkhah A.Investigation on the behavior of brick-infilled steel frames with openings,experimental and analytical approaches [J].Engineering Structures, 2011, 33(3): 968―980.
[12]JGJ/T 101―2015, 建筑抗震试验规程[S].北京: 中国建筑工业出版社, 2015.JGJ/T 101―2015, Specification for seismic test of buildings [S].Beijing: Building Industry Press of China,2015.(in Chinese)
[13]贾穗子, 曹万林, 任乐乐.装配式轻钢框架—带暗支撑轻墙体组合结构抗震性能试验研究[J].建筑结构学报, 2018, 39(11): 48―57.Jia Suizi, Cao Wanlin, Ren Lele.Experimental study on seismic performance of fabricated composite structure of lightweight steel frame-lightweight wall with concealed support [J].Journal of Building Structures, 2018, 39(11):48―57.(in Chinese)
[14]Quiroz L G, Maruyama Y, Zavala C.Cyclic behavior of Peruvian confined masonry walls and calibration of numerical model using genetic algorithms [J].Engineering Structures, 2014, 75: 561―576.
[15]黄炜, 陈国新, 姚谦峰, 等.基于统一强度理论的密肋复合墙体开裂荷载计算[J].工程力学, 2008, 25(7):94―99.Huang Wei, Chen Guoxin, Yao Qianfeng, et al.Calculation on cracking load of multi-ribbed composite wall based on twin shear unified strength theory [J].Engineering Mechanics, 2008, 25(7): 94―99.(in Chinese)
[16]Masao T, Norikazu O, Makoto M.Simplified maximum strength formula of framed walls with an opening and its analytical accuracy [J].Concrete Research and Technology, 2002, 13(1): 119―126.
[17]Tomazevic M.Earthquake-resistant design of masonry buildings [M].London: Imperial College Press, 1999:132―137.
[18]GB 50003―2011, 砌体结构设计规范[S].北京: 中国建筑工业出版社, 2011.GB 50003―2011, Code for design of masonry structures[S].Beijing: Building Industry Press of China, 2011.(in Chinese)
[19]张大长, 陈怀亮, 卢中强.基于抗剪抵抗机构的RC开洞剪力墙极限承载力分析[J].土木工程学报, 2008,41(11): 44―50.Zhang Dachang, Chen Huailiang, Lu Zhongqiang.Shear resistent mechanism analysis of the ultimate bearing capacity of RC shear walls with an opening [J].China Civil Engineering Journal, 2008, 41(11): 44―50.(in Chinese)