在抗震设防中，不规则地形因较差的地质条件以及临空面的存在使其地震场地效应受到重视[1―4]。许多研究者在阶梯地形场地反应分析方法和场地效应研究方面开展了工作，本文关注阶梯地形成层场地计算时的斜入射地震动输入问题，建立阶梯地形成层场地反应分析方法。
当震源较深或场地距离震中较近时，场地的输入地震动可以假定为竖直入射的平面体波。在竖直入射地震动作用下阶梯地形场地反应分析方法方面，一些工作[5―7]在计算模型的侧边界分别使用滚轴边界或黏性边界，底边界假定为刚性；George等[8]结合黏性边界考虑了侧边界自由场反应的输入。Naohiro[9]结合透射边界考虑自由场反应输入，建立了阶梯地形成层场地条件场地反应分析方法。
当震源较浅或场地距离震中适度远时，场地的输入地震动假定为倾斜入射的平面体波。一方面，针对水平地表均匀半空间场地，黄景琦[10]基于解析方法建立了场地反应分析方法，并对车站地震响应进行了分析[11]；针对水平地表成层半空间场地，在刘晶波等[12―14]提出的一维化时域有限元方法基础上，赵密等[15―16]提出了改进的方法，建立了场地反应分析方法，并应用于研究地震动斜入射对地铁车站地震反应的影响[17]。另一方面，针对阶梯地形地表均匀半空间场地，黄景琦[10]进一步建立了场地反应分析方法并应用于隧道洞口段地震反应分析；Ashford和Sitar[18]结合一致透射边界对SH波斜入射下阶梯地形的场地效应进行了分析；针对阶梯地形成层场地，丁海平和顾亮等[19―20]在文献[15]工作基础上，结合多次透射边界[21]，提出了一种场地反应分析方法，但文中仅给出均匀场地条件的算例。
本文在作者工作[15―16]基础上，结合黏性边界[22]，采用与文献[19―20]类似思路，给出了阶梯地形成层场地斜入射地震动输入方法，进而建立了相应场地反应分析方法。通过与参考解进行对比，进一步研究了人工边界位置、输入地震动、地震动入射角度、地表斜坡倾角及场地分层特性变化对该方法精度的影响。
1 地震动输入方法
地震动斜入射时阶梯地形成层场地问题如图1所示，引入人工边界将土体划分为无限域部分和有限域部分。无限域土体水平成层；有限域土体可考虑阶梯地形和非水平成层特征，采用有限元法模拟。
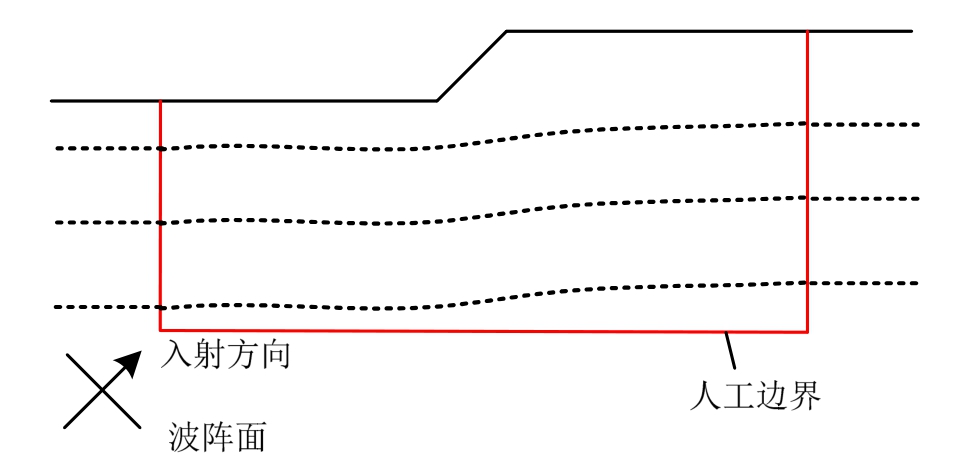
图1 地震动斜入射时阶梯地形成层场地问题示意图
Fig.1 Schematic diagram of layered step-shaped topography problem under seismic wave of oblique incidence
有限域的动力有限元方程可以写为：
式中：下标B和R分别表示人工边界和其余部分；u、
和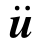
分别代表位移、速度和加速度；M、C和K分别表示质量、阻尼和刚度矩阵；fB是无限域对有限域的作用力。
人工边界处总反应分解为输入波场和其余部分：
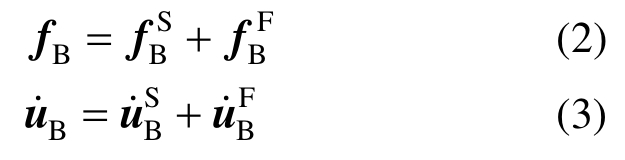
式中，上标F和S分别代表输入波场和其余部分。
采用黏性边界条件近似模拟除输入波场外的其余部分波场，黏性边界条件可以写为：
式中，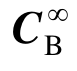
表示黏性边界阻尼矩阵，参数取值见文献[22]。
将式(3)代入式(4)，之后将结果代入式(2)，最终将结果代入式(1)，得：
其中，作用于人工边界处的等效地震荷载为：
对于式(6)，三个人工边界面采用各自的输入波场：两个侧面人工边界处采用各自高度水平成层场地自由场作为输入，该自由场采用文献[16]提出的一维化时域数值方法计算；底面人工边界处采用入射波场作为输入。对于阶梯地形成层场地，上述地震动输入方法是近似的，需要讨论方法的精度。
2 方法精度的算例研究
阶梯地形成层场地条件下，影响上述地震动输入方法精度的主要因素包括人工边界位置、输入地震动记录、地震动入射角度、地表斜坡倾角以及场地分层特性。下面通过数值算例讨论这些因素变化对地震动输入方法精度的影响。
计算模型如图2所示。选择一个基准模型，在此基础上研究每个因素变化对场地地震反应的影响。基准模型参数如下：B=110 m、H=60 m、h1=b2=10 m、θ=45°、b1=b3=50 m；采用均匀土体场地，土体的密度、弹性模量、泊松比分别为1980 kg/m3、498 MPa、0.26。考虑平面SV波从左下角点倾斜入射，输入的地震动时程曲线如图3所示。输出A点位移时程结果以及沿地表虚线的位移峰值变化。
图2 地震动斜入射时阶梯地形成层场地问题计算模型
Fig.2 Calculation model of layered step-shaped topography problem under seismic wave of oblique incidence
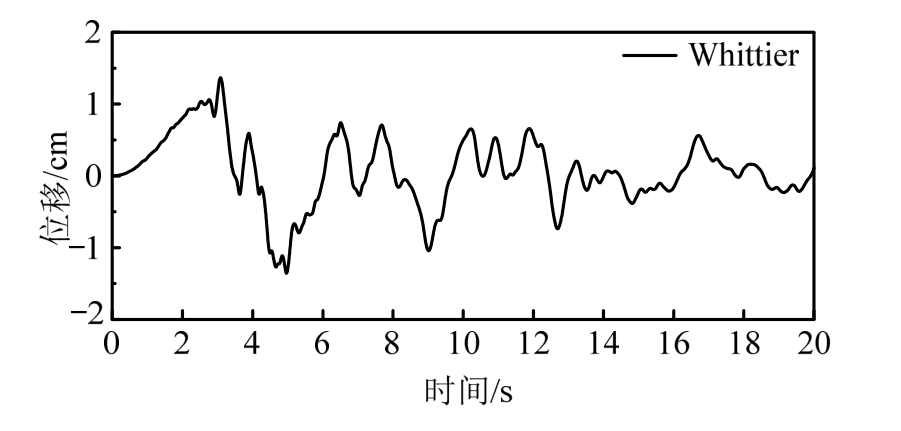
图3 输入的地震动时程曲线
Fig.3 Input displacement time history
参考解为“足够大”的有限元计算模型（后文简称“大模型”，模型尺寸长×高=4100 m×2100 m，其中2100 m是右侧高度）的计算结果，保证在有限分析时间内，经人工边界反射的虚假波动不会到达观测点。由于地震记录持时较长，大模型的计算代价过高，因此参考解仅给出从0时刻至位移峰值过后的结果。
定义衡量计算结果精度的峰值相对误差为：
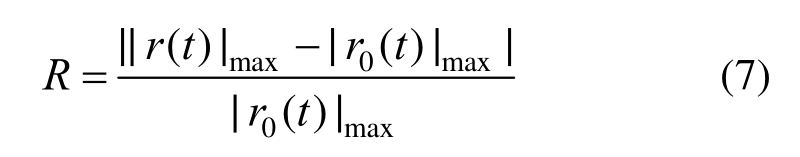
式中：r0(t)是参考解；r(t)是提出输入方法的计算结果；| |表示取绝对值；下标max表示取最大值。
2.1 人工边界位置的影响
在图2标准模型基础上再设置两组不同的边界位置，即将人工边界向内和向外分别移动30 m得到模型尺寸分别为B×H=50 m×30 m以及B×H=170 m×90 m。A点水平位移时程如图4所示，可以看到，三种人工边界位置模型的位移计算结果与参考解吻合较好。水平位移峰值沿地表变化及其误差如图5所示，可以看到，水平位移峰值随着地形起伏有明显的动力放大，三种人工边界位置下位移峰值误差均小于1%。
图4 三种人工边界位置下A点的水平位移时程
Fig.4 Horizontal displacement time histories of A point with three artificial boundary locations
2.2 地震动记录的影响
在图2标准模型基础上增加Sfern和Lytlecr两条地震记录，如图6所示。选取原则是与Whittier记录有频谱差异和峰值差异。A点水平位移时程如图7所示，标准模型在Whittier记录作用下的水平位移时程在2.1节已经展示过，因此不重复展示，2.3节同理。可以看到，两条地震记录下的位移计算结果与参考解吻合较好。水平位移峰值沿地表变化及其误差如图8所示，可以看到，虽然不同地震动作用下场地放大效应不同，但三种地震记录下位移峰值误差仍均小于1%。
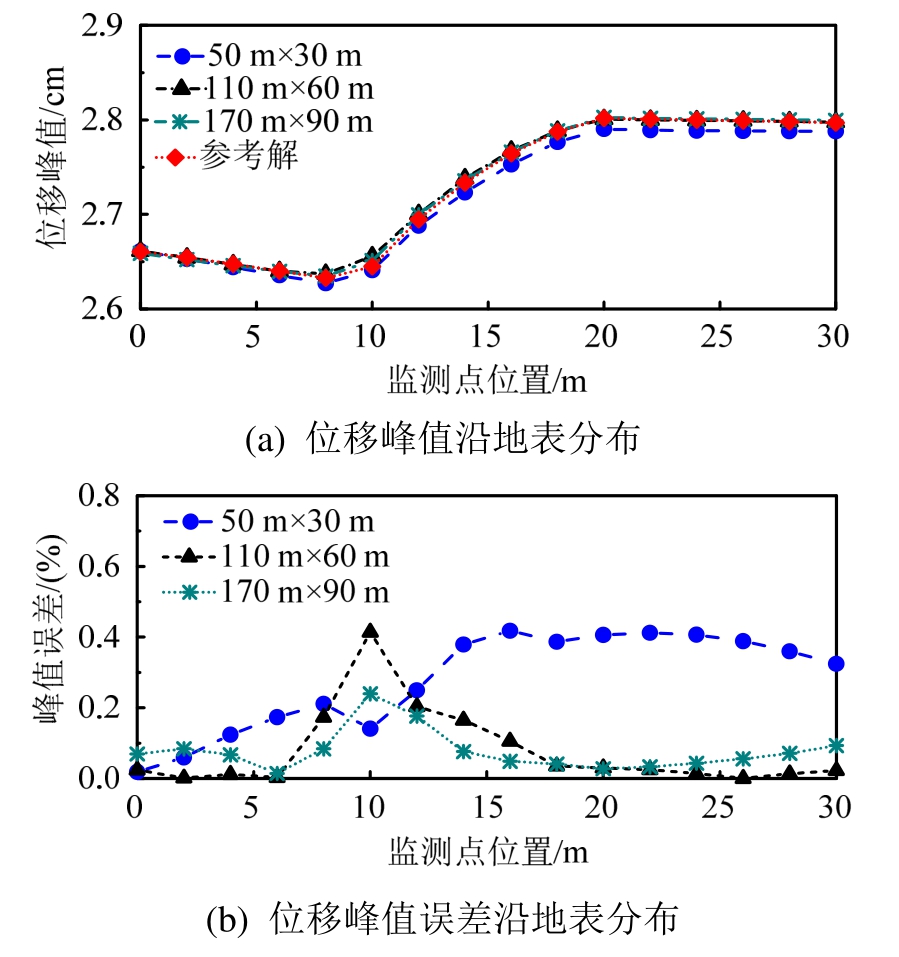
图5 水平位移峰值沿地表变化及其误差
Fig.5 The maximum responses and errors of horizontal displacements along slope surface
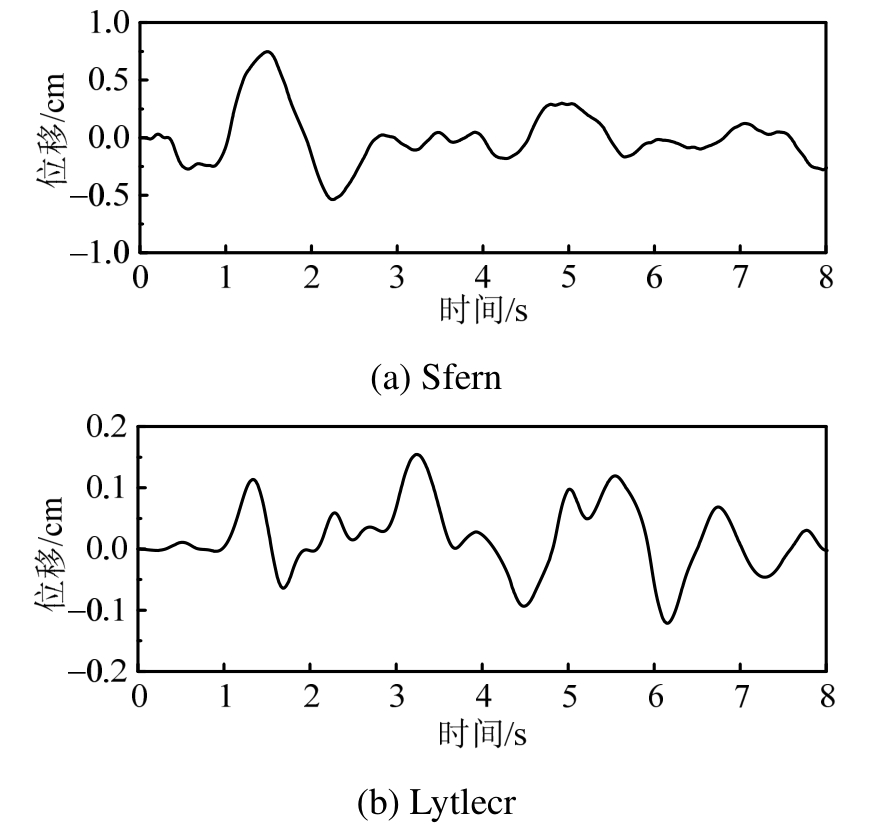
图6 输入的地震动时程曲线
Fig.6 Input displacement time histories
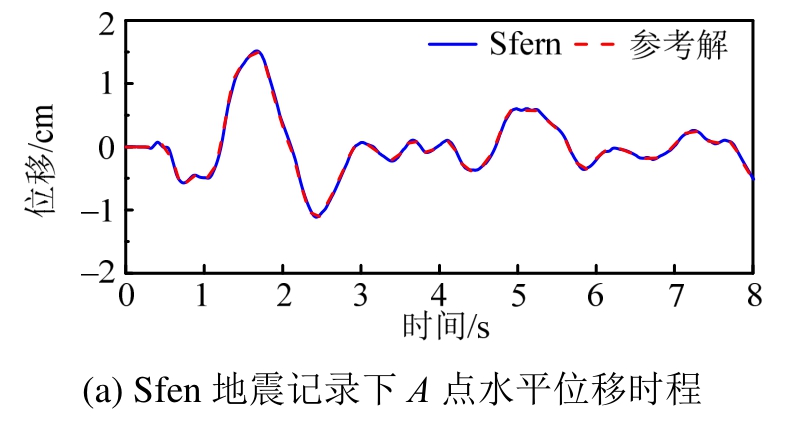
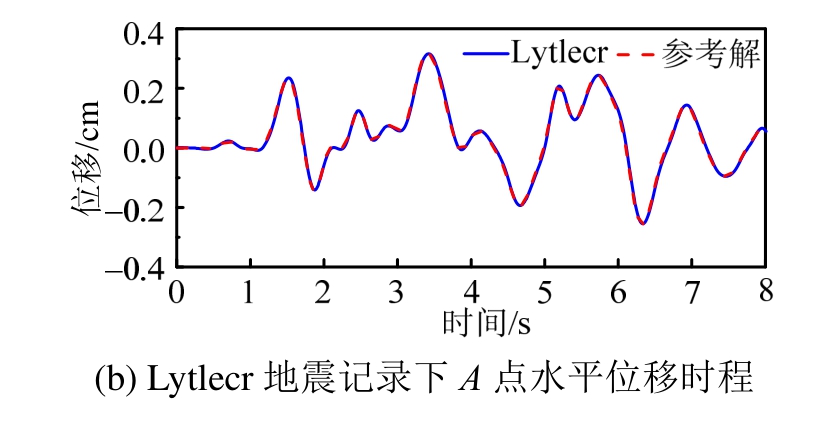
图7 二种地震记录下A点的水平位移时程
Fig.7 Horizontal displacement time histories of A point with two seismic records
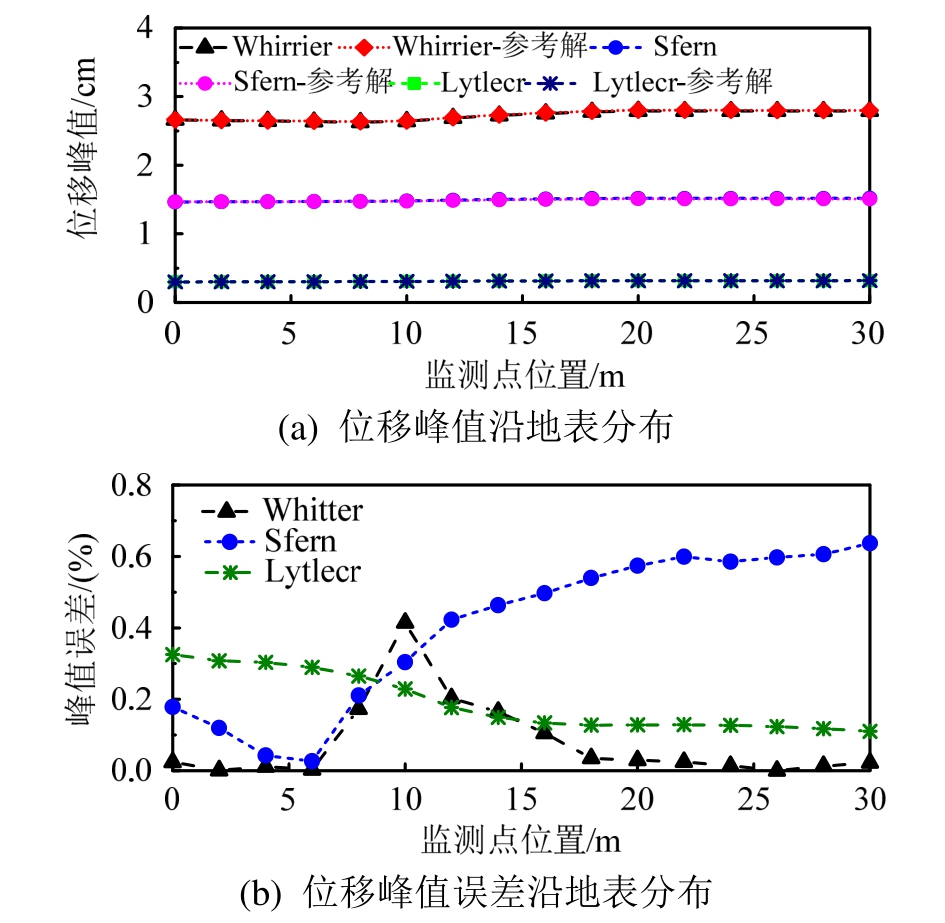
图8 水平位移峰值沿地表变化及其误差
Fig.8 The maximum responses and errors of horizontal displacements along slope surface
2.3 地震动入射角度的影响
在图2标准模型基础上再设置2组不同的入射角度和入射位置，即地震波从模型的左角点和右角点入射，角度均为10°和20°。从左角点入射时A点水平位移时程如图9，随着入射角度的增加，位移计算结果与参考解吻合程度降低。从右角点入射时A点水平位移时程如图10所示，位移计算结果与参考解吻合程度较好，计算精度明显高于左角点入射时的工况。右侧输入时，两个侧边界处的自由场反应更加接近于相应水平成层半空间场地反应；左侧输入时，自由场误差相对右侧输入大。水平位移峰值沿地表变化及其误差如图11所示，可以看到，地震波入射位置和角度发生变化基本不改变水平位移峰值随着地形起伏的动力放大效应，5种入射情况下位移峰值误差最高不大于5%，且从右角点入射时提出方法的计算精度更高。
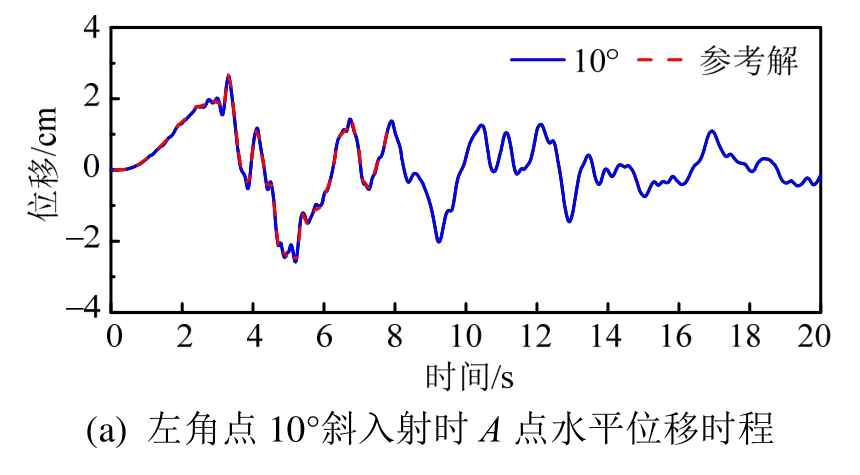
图9 左角点斜入射时A点的水平位移时程
Fig.9 Horizontal displacement time histories of A point under seismic wave of oblique incidence from the left corner
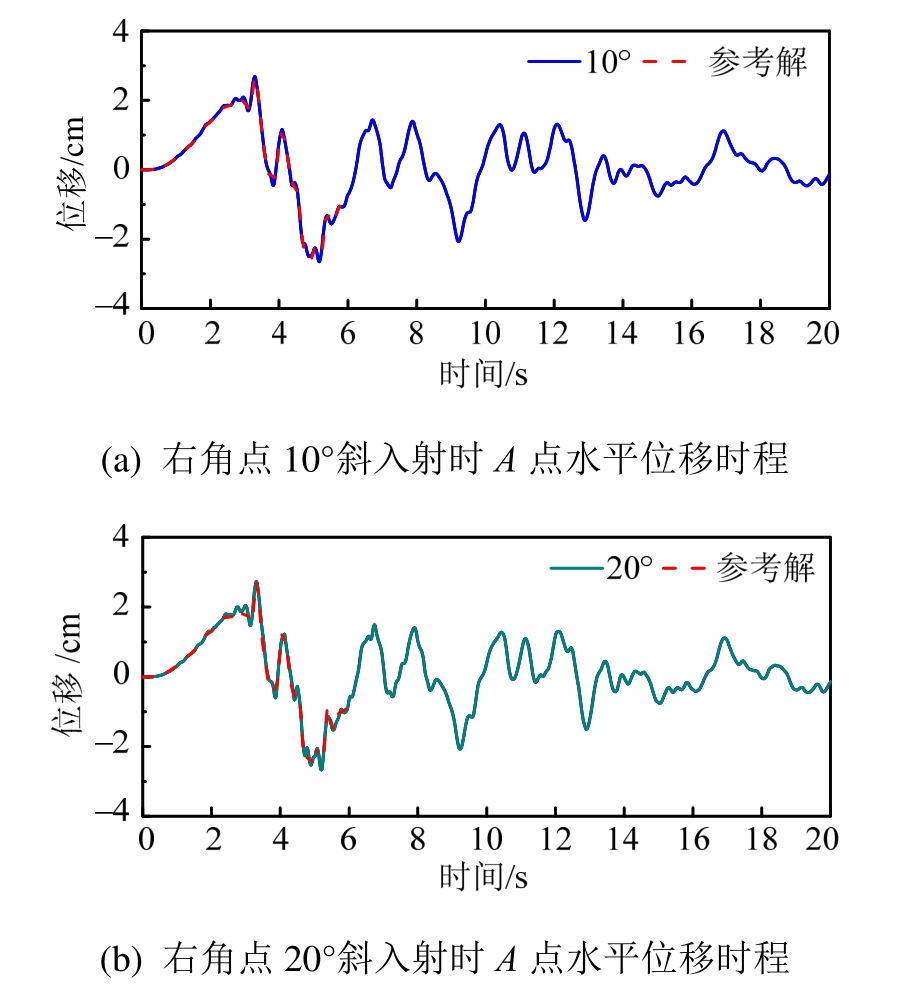
图10 右角点斜入射时A点的水平位移时程
Fig.10 Horizontal displacement time histories of A point under seismic wave of oblique incidence from the right corner
图11 水平位移峰值沿地表变化及其误差
Fig.11 The maximum responses and errors of horizontal displacements along slope surface
2.4 地表斜坡倾角的影响
在图2标准模型基础上再设置2组不同的斜坡倾角，将模型中的斜坡倾角分别增大和减小15°得到模型斜坡倾角分别为θ=60°以及θ=30°。在改变斜坡倾角的同时，保持斜坡的起始位置以及坡高不变，即通过改变坡顶距离右边界距离b2来使斜坡倾角发生变化。A点水平位移时程如图12，可以看到，新增2种斜坡倾角的位移计算结果与参考解吻合较好。水平位移峰值沿地表变化及其误差如图13，可以看到，三种工况下水平位移峰值在斜坡位置处有明显变化，这是因为倾角为30°时斜坡距离边界位置的距离减小，边界对斜坡的影响增大，而倾角为60°时斜坡变得很“陡”。三种斜坡倾角下位移峰值误差均小于2%。
图12 两种斜坡倾角下A点的水平位移时程
Fig.12 Horizontal displacement time histories of A point with two slop angles
图13 水平位移峰值沿地表变化及其误差
Fig.13 The maximum responses and errors of horizontal displacements along slope surface
2.5 场地分层特性的影响
将图2标准模型土体进行分层，对应图2中的h1=10 m、h2=10 m、h3=40 m，使用的模型土体参数见表1。A点水平位移时程如图14所示，可以看到，场地分层模型的位移计算结果与参考解吻合较好。水平位移峰值沿地表变化及其误差如图15所示，可见，分层土体比均匀土体的场地放大效应更为显著，两种工况下位移峰值误差均小于1%。
表1 土体参数
Table 1 Soil layer parameters
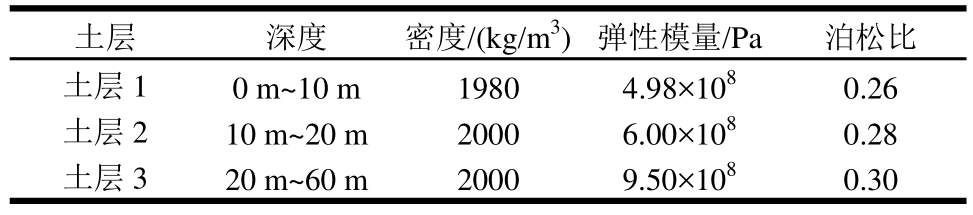
土层 深度 密度/(kg/m3) 弹性模量/Pa 泊松比土层1 0 m~10 m 1980 2000 2000土层2 10 m~20 m土层3 20 m~60 m 4.98×108 6.00×108 9.50×108 0.26 0.28 0.30
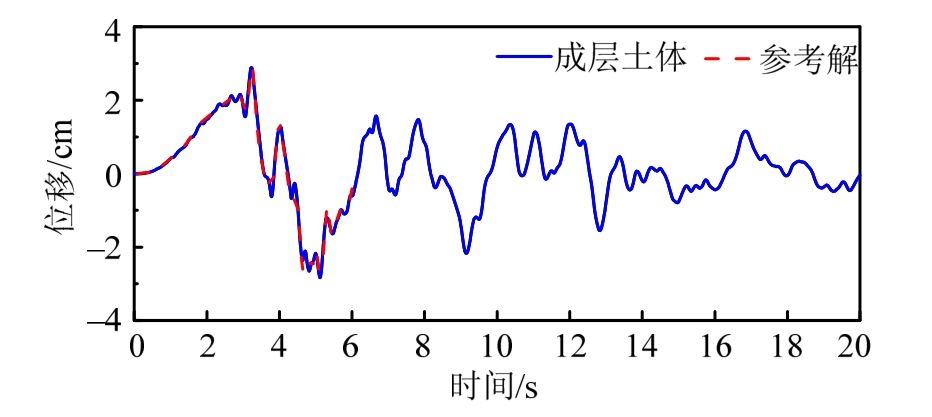
图14 场地分层时A点的水平位移时程
Fig.14 Horizontal displacement time history of A point with layered soil
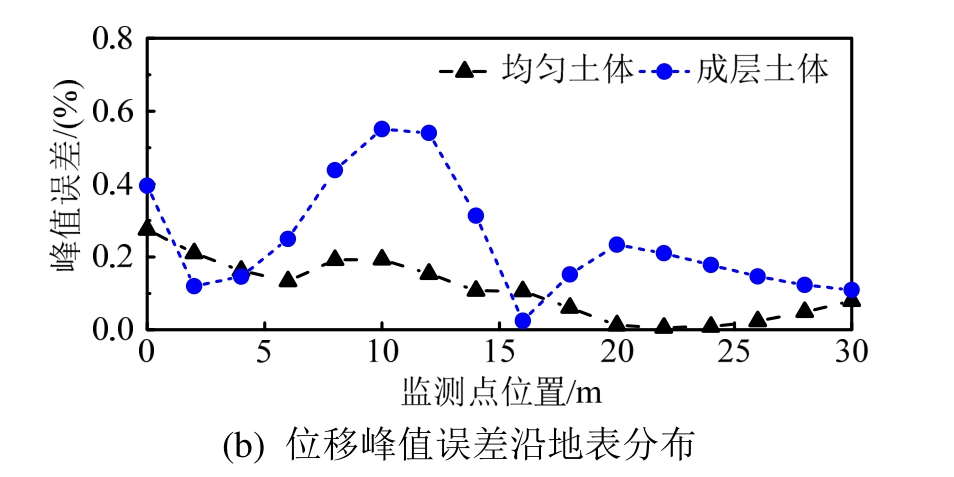
图15 水平位移峰值沿地表变化及其误差
Fig.15 The maximum responses and errors of horizontal displacements along slope surface
3 结论
本文基于黏性边界和地震动斜入射时水平成层场地反应计算方法发展了一种阶梯地形成层场地的斜入射地震动输入方法，并通过数值试验分析了人工边界位置、输入的地震动记录、地震动入射角度、地表斜坡倾角及场地成层特征变化对该方法精度的影响。结果显示，人工边界位置和地震动记录对计算精度的影响不大，位移误差都在1%以下；斜坡倾角对计算精度有影响，斜坡倾角为30°、45°和60°的位移峰值误差均小于2%；地震动入射角度对计算精度影响较大，随着入射角度增大地表水平位移峰值误差增加，但不超过5%；均匀场地的误差小于成层场地，成层场地的各观测点最大峰值误差均小于1%。总体看来，提出的输入方法精度较高，可用于地震斜入射下阶梯地形成层场地反应计算。
[1]蒋水华, 杨建华, 姚池, 等.考虑土体参数空间变异性边坡失稳风险定量评估[J].工程力学, 2018, 35(1):136―147.Jiang Shuihua, Yang Jianhua, Yao Chi, et al.Quantitative risk assessment of slope failure considering spatial variability of soil properties [J].Engineering Mechanics,2018, 35(1):136―147.(in Chinese)
[2]蒋水华, 姚池, 杨建华, 等.基于模型修正的空间变异边坡可靠度分析方法[J].工程力学, 2018, 35(8): 154―161.Jiang Shuihua, Yao Chi, Yang Jianhua, et al.Model correction factor method based approach for reliability analysis of spatially variable slopes [J].Engineering Mechanics, 2018, 35(8): 154―161.(in Chinese)
[3]Babak P, Arash F, Loukas F K.Seismic wave amplification by topographic features: A parametric study.[J].Soil Dynamics and Earthquake Engineering,2017, 92: 503―527.
[4]Valentin S G, Erik E, Jeffrey R M, et al.On the seismic response of deep-seated rock slope instabilities-Insights from numerical modeling.[J].Engineering Geology,2015, 193: 1―18.
[5]Panagiotis P, Anastasios B, Eleni P, et al.Surface topography and site stratigraphy effects on the seismic response of a slope in the Achaia-Ilia (Greece) 2008 Mw6.4 earthquake [J].Soil Dynamics and Earthquake Engineering, 2017, 100: 538―554.
[6]Samuela R, Ernesto C, Giovanni B.Coupling of topographic and stratigraphic effects on seismic response of slopes through 2D linear and equivalent linear analyses [J].Soil Dynamics and Earthquake Engineering,2014, 67: 66―84.
[7]Tripe R, Kontoe S, Wong T K C.Slope topography effects on ground motion in the presence of deep soil layers [J].Soil Dynamics and Earthquake Engineering,2013, 50: 72―84.
[8]George D Bouckovalas, Achilleas G Papadimitriou.Numerical evaluation of slope topography effects on seismic ground motion [J].Soil Dynamics and Earthquake Engineering, 2005, 25: 547―558.
[9]Naohiro N.Two-dimensional energy transmitting boundary in the time domain [J].Earthquakes and Structures, 2012, 3(2): 97―115.
[10]黄景琦.岩体隧道非线性地震响应分析[D].北京: 北京工业大学, 2015.Huang Jingqi.Study on nonlinear seismic response of rock tunnels [D].Beijing: Beijing University of Technology, 2015 (in Chinese)
[11]黄景琦, 杜修力, 田志敏, 等.斜入射SV 波对地铁车站地震响应的影响[J].工程力学, 2014, 31(9): 81―88,103.Huang Jingqi, Du Xiuli, Tian Zhimin, et al.Effect of the oblique incidence of seismic SV waves on the seismic response of subway station structure [J].Engineering Mechanics, 2014, 31(9): 81―88, 103.(in Chinese)
[12]刘晶波, 王艳.成层介质中平面内自由波场的一维化时域算法[J].工程力学, 2007, 24(7): 16―22.Liu Jingbo，Wang Yan.A 1D time—domain method for inplane wave motion of free field in layered media [J].Engineering Mechanics, 2007, 24(7); 16―22.(in Chinese)
[13]王艳.非一致地震动场数值方法研究及在结构动力分析中的应用[D].北京: 清华大学, 2007.Wang Yan.Research on the numerical method for asynchronous seismic wave motions and its application in dynamic analysis of structures [D].Beijing: Tsinghua University, 2007.(in Chinese)
[14]刘晶波, 王艳.成层半空间出平面自由波场的一维化时域算法[J].力学学报, 2006, 38(2): 219―225 Liu Jingbo, Wang Yan.A 1-D time-domain method for 2-D wave motion in elastic layered half-space by antiplane wave oblique incidence [J].Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(2): 219―225.(in Chinese)
[15]赵密, 杜修力, 刘晶波, 等.P-SV波斜入射时成层半空间自由场的时域算法[J].地震工程学报, 2013, 35(1):84―90.Zhao Mi, Du Xiuli, Liu Jingbo, et al.Time-domain method for free field in layered half space under P-SV waves of oblique incidence [J].China Earthquake Engineering Journal, 2013, 35(1): 84―90.(in Chinese)
[16]Zhao M, Yin H Q, Du X L, et al.1D finite element artificial boundary method for layered half space site response from obliquely incident earthquake [J].Earthquakes and Structures, 2013, 9(1): 173―194.
[17]Zhao M, Gao Z D, Wang L T, et al.Obliquely incident earthquake input for soil-structure interaction in layered half space [J].Earthquakes and Structures, 2017, 13(6):573―588.
[18]Ashford S A, Sitar N.Analysis of topographic amplification of inclined shear waves in a steep coastal bluff [J].Bulletin of the Seismological Society of America, 1997, 87(3): 692―700.
[19]丁海平, 于彦彦, 郑志法.P波斜入射陡坎地形对地面运动的影响[J].岩土力学, 2017, 38(6): 1716―1724,1732.Ding Haiping, Yu Yanyan, Zheng Zhifa.Effects of scarp topography on seismic ground motion under inclined P waves [J].Rock and Soil Mechanics, 2017, 38(6):1716―1724, 1732.(in Chinese)
[20]顾亮, 丁海平, 于彦彦.SV波斜入射陡坎地形对地面运动的影响[J].自然灾害学报, 2017, 26(4): 39―47.Gu Liang, Ding Haiping, Yu Yanyan, Effects of scarp topography on seismic ground motion under inclined SV waves [J].Journal of Natural Disasters, 2017, 26(4):39―47.(in Chinese)
[21]廖振鹏.工程波动理论导论[M].北京: 科学出版社,2002: 173―177.Liao Zhenpeng.Introduction to wave motion theories for engineering [M].Beijing: Science Press, 2002: 173―177.(in Chinese)
[22]Lysmer J, Kuhlemeyer R L.Finite dynamic model for infinite media [J].Journal of the Engineering Mechanics Division, 1969, 95(4): 859―878.