轴向运动结构广泛存在于工程实际中，比如加工机床类主轴、传送带和流体输送管道等都属于轴向运动结构。复合材料又是由两种或多种不同性质的材料用物理和化学方法在宏观尺度上组成的具有新性能的材料，且正交各向异性叠层板具有较高的比强度和比刚度，常常被做成薄壁结构。尤其对于轴向运动叠层板，外加载荷作用会导致其发生共振、分叉及混沌等复杂的非线性动力学现象。由此可见，针对轴向运动复合材料板非线性振动问题的研究具有理论和实际意义。
对于复合材料结构的振动和弯曲问题，国内外学者开展了较为丰富的研究。Crabtree等[1]对复合材料层合薄板的非线性高阶谐波共振进行了分析；陈万吉和任鹤飞[2]对基于新修正偶应力理论的Mindlin层合板的自由振动进行了研究；Xue等[3－4]研究了面内载荷作用下复合材料层合板的非线性行为，并应用多尺度法研究了纤维增强复合材料的非线性振动问题；Armagan和Metin[5]研究了各向同性复合材料夹层梁在轴向变化面内载荷和对应边界条件下的弹性屈曲行为。Krzysztof[6]研究了热环境下复合材料轴向移动夹层梁的振动问题；杨永宝和危银涛[7]研究了弹性基础上的正交各向异性圆柱壳的自由振动问题。近些年，轴向运动系统的研究成为动力学领域关注的课题。Marynowski[8]研究了具有对边简支对比自由轴向运动弹性板的动力学行为；Chen等[9]研究了具有内共振现象轴向移动梁的非线性振动问题；胡宇达等[10－11]针对横向磁场中轴向变速运动矩形板的参数振动和两平行导线间轴向运动载流梁的非线性主共振的问题进行了研究；Hu等[12]对磁场环境中周期外载作用下轴向运动导电条形板的非线性振动及混沌运动问题进行了研究；Ding和Chen[13－14]通过微积分法研究了轴向加速粘弹性梁横向运动的非线性动力学行为，分析了面内振动固有频率变化规律；叶康生和殷振炜[15]研究了面内运动平面曲梁的自由振动问题；Banichuk等[16]研究了轴向移动弹性带的横向振动及稳定性问题；Saurabh等[17]针对轴向运动功能梯度非均匀板的非线性强迫振动问题进行了研究；Zhang等[18]研究了基于Jacobi多项式的轴向功能梯度梁的自由振动问题。另外，针对随动载荷作用下系统振动问题的研究，王忠民等[19－20]对随从力作用下功能梯度矩形板的非线性振动和粘弹性矩形板的动力稳定性进行了研究；戎艳天和胡宇达[21]研究了横向磁场中移动载荷作用下轴向运动载流梁的参强联合共振问题；Mehdi等[22]研究了非线性弹性地基上轴向功能梯度梁在移动载荷作用下的非线性动力响应问题。
综上，针对复合材料结构的动力学问题已有较多研究，但对于其在轴向运动及其复杂载荷作用下非线性力学性能的研究相对较少，且是目前学者们关注的问题。本文基于已有文献工作，在考虑轴向运动条件及其确定随从力作用下研究复合材料叠层板的非线性共振问题，得到不同阶模态下谐波共振的幅频响应方程，讨论激励幅值、板厚、材料、层数等对系统共振特征的影响效应，确定共振激发的临界值问题。
1 轴向运动叠层板横向振动方程
如图一所示正交各向异性叠层板上作用有随板一起运动的随从荷载Q，速度为V，合力为：
式中，
为单位阶跃函数。叠层板板厚为h，密度为ρ，长为a，F0x为轴向拉力。建立空间直角坐标系，Oxy为板的中面，z轴为法向。
图1 随从力作用下轴向运动叠层板
Fig.1 Axial moving laminate under the follower force
根据叠层板的动能、势能表达式并应用哈密顿原理，可以得到正交各向异性叠层条形板的横向非线性振动方程为：
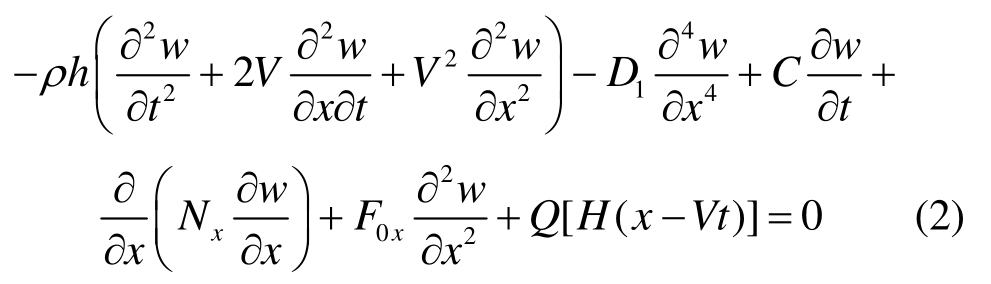
式中：w为横向位移；t为时间变量；C为阻尼系数，纤维沿x轴方向；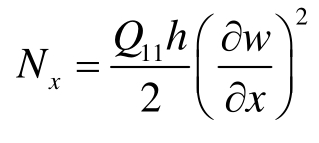
为叠层板的中面内力；
为弹性主向的弯曲刚度，
为叠层板层数；
为纵向弹性模量，ν12和ν21为泊松比，且
2 亚谐波共振问题求解
2.1 振动微分方程
正交各向异性叠层条形板的边界条件为对边简支(x=0,a)，考虑三阶模态，则位移函数取为：
式中，p1(t)、p2(t)和p3(t)分别为对应阶模态的时间响应函数。
为研究系统弱非线性振动，可引入小参数ε，并将式(3)代入式(2)，应用伽辽金法进行离散，可推得由随从力简协激发的关于时间变量的无量纲化非线性振动微分方程组：
式中：
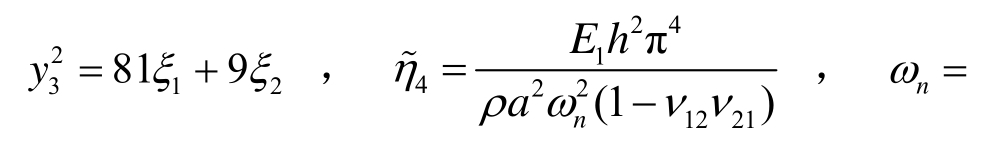
2.2 多尺度法求解
下面运用多尺度法求解外激励频率满足Ω1≈3y1、Ω2≈3y2和Ω3≈3y3的1阶、2阶和3阶不同共振情形的亚谐波共振问题。
将式(4)～式(6)的近似解表示为：
式中：j=(1,2,3)，新自变量，T0=τ，T1=ετ。
将式(7)代入式(4)～式(6)展开后令两边ε的同次幂相等，得到各阶近似方程：
关于ε0的近似方程：
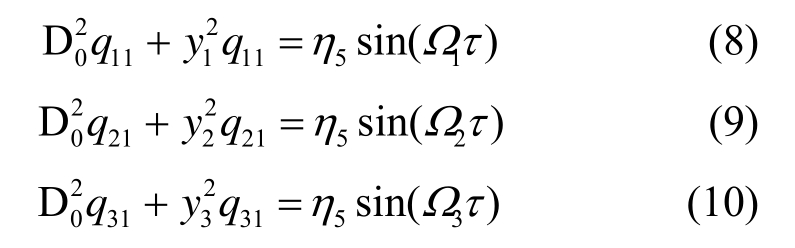
关于ε1的近似方程：
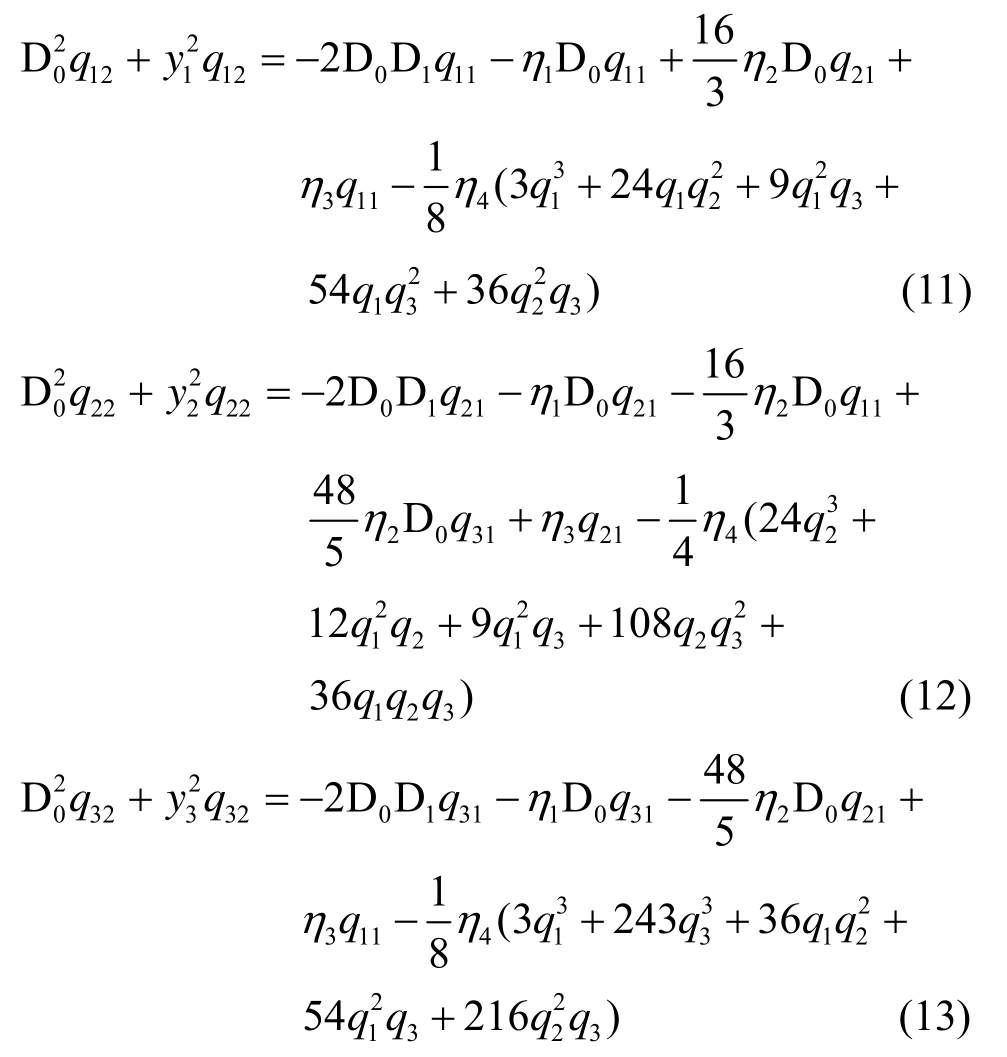
式中，
设式(8)～式(10)的通解形式为：
式中，
“横杠”表示其对应项的共轭，i2=-1(j=1,2,3)。
下面首先考虑外激励力频率满足Ω1≈3y1的亚谐波共振。引入调谐参数σ，并令Ω1=3y1+εσ。由此分析知，速度V与调谐值εσ为线性关系，即通过改变速度可以改变激励频率。将式(14)代入式(11)～式(13)中，为避免久期项，可以得到关于Bj满足的关系式：
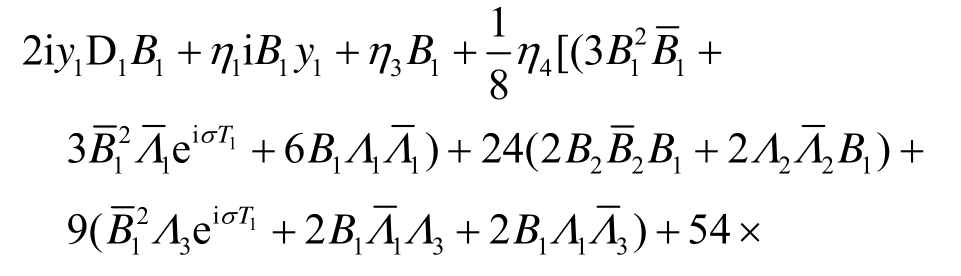
式中，B1、B2、B3可以表示为指数形式：
将式(18)代入式(15)~式(17)，进行实部与虚部分离，并令γ1=σT1-3β1，得到：
由式(19)~式(24)可见，幅值b2、b3都将衰减，表明此时2阶、3阶振动不会被激发。因此，对于系统的稳态运动情况，可令b1′=0和γ1′=0，然后消去γ1，最终得到关于幅值b1的幅频响应方程为：
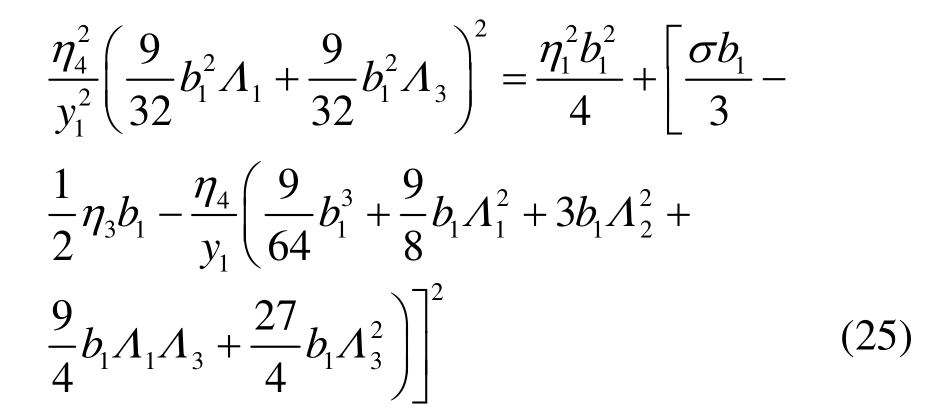
同理，可以得到关于外激励频率满足Ω2=3y2+εσ和Ω3=3y3+εσ的关于幅值b2、b3的幅频响应方程分别为：
根据一元二次方程根的判别式可判定幅频响应方程非平凡解的存在情况。通过判定可知，式(25)~式(27)均存在两个不相等的实根，即系统的1阶、2阶和3阶共振情形均能被激发。
进一步应用Lyapunov稳定性理论和Routh-Hurwitz判据，可判定三种共振情形下定常稳定解需满足的条件。
3 算例分析
下面针对叠层条形板的亚谐波共振问题给出数值算例。参数取为：板长a=0.3m，轴向拉力F0x=10kN/m ；材料属性见表1。
表1 几种复合材料参数
Table 1 Several composite parameters
材料参数 E1/GPaE2/GPa ν12 /(kg/m3)ρ[B4/5505]204.1 18.5 0.23 2000[T300/5280]181.1 10.3 0.28 1600[A5/3501]141 9.1 0.3 1600
图2~图4分别给出了不同材料、层数、激励幅值等参量影响下的1阶、2阶、3阶共振的振幅-调谐值特性曲线图。图中曲线均为封闭的月牙形双值光滑曲线，并分为上支曲线和下支曲线。其中，1阶共振振幅最明显，振幅较大，2阶和3阶振幅则越来越小；不同材料、层数、激励幅值、阻尼对于共振有显著影响。由图2可以看出，不同材料可以影响振幅的大小。由图3可以看出，在相同板厚的情况下，随着层数的增加，上支和下支曲线整体下移，呈现减小的趋势。由图4可以看出，在一定范围内，随着激励幅值的增加，曲线整体下移。为分析稳定性，如图2(a)所示，取A、B两点值进行判定可知，A点为对应判别值大于零的稳定解，即该点处于稳定性吸引域中，而B点为对应判别值小于零的不稳定解。
图5给出了与图4相对应的激发共振双值解临界点变化曲线。可以看出，调谐值、激励幅值取特定值时才会激发共振，产生非零解的共振振幅。图5中曲线中间部分为共振区域，曲线两侧为非共振区域；且随着激励幅值和调谐值的变化，激发共振的临界点也随之改变。同时可以看出，1阶、2阶左侧激发共振双值解的临界点随着激励幅值增大，调谐值在增大；右侧激发共振双值解的临界点随着激励幅值增大，调谐值在减小；3阶共振情形时，右侧激发共振的临界点同1阶、2阶共振情形有相似规律。
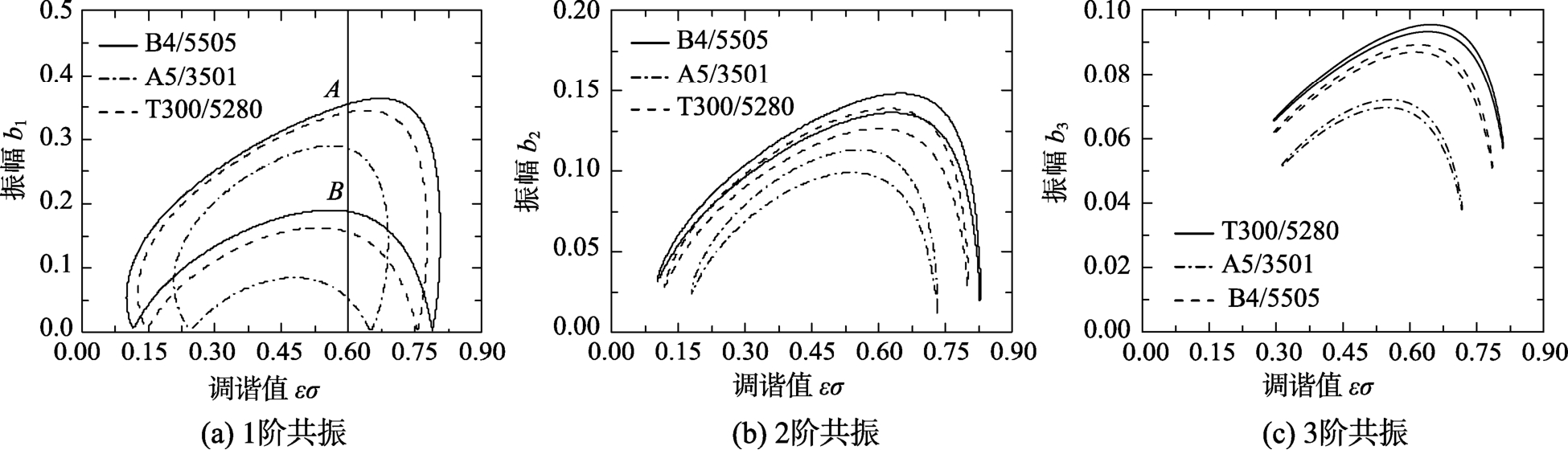
图2 振幅-调谐值特性曲线(不同材料)(Q=3kN/m, n=1, h=4mm)
Fig.2 Amplitude-detuning characteristic curves (different materials)(Q=3kN/m, n=1, h=4mm )
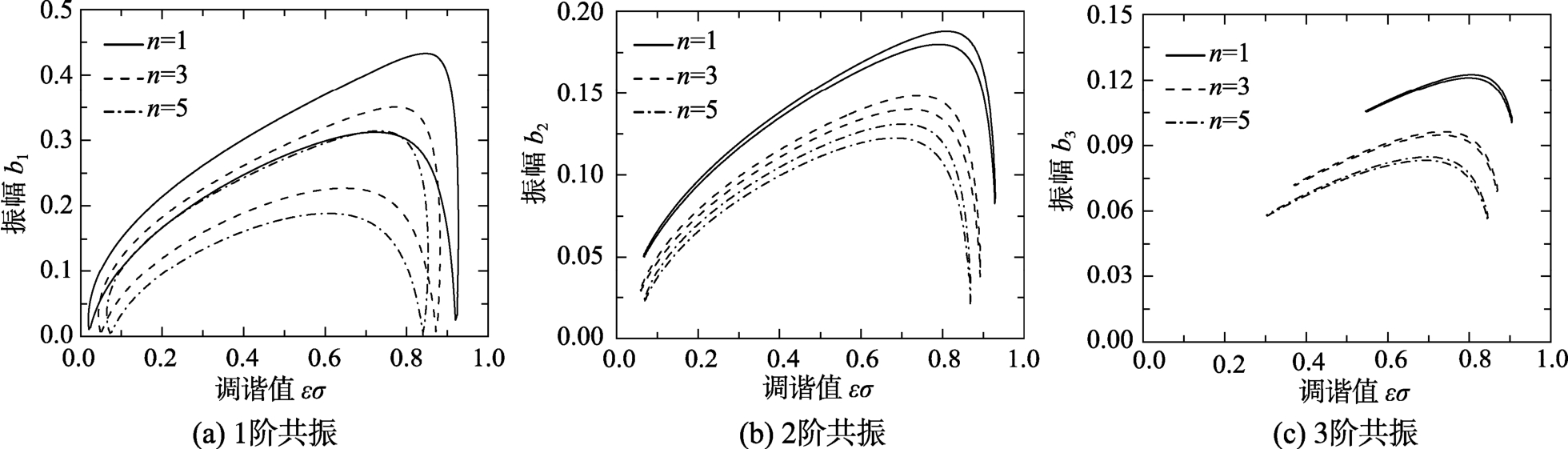
图3 振幅-调谐值特性曲线(不同层数)(Q=3kN/m , h=4mm, B4/5505)
Fig.3 Amplitude-detuning characteristic curves (different layers)(Q=3kN/m, h=4mm, B4/5505)
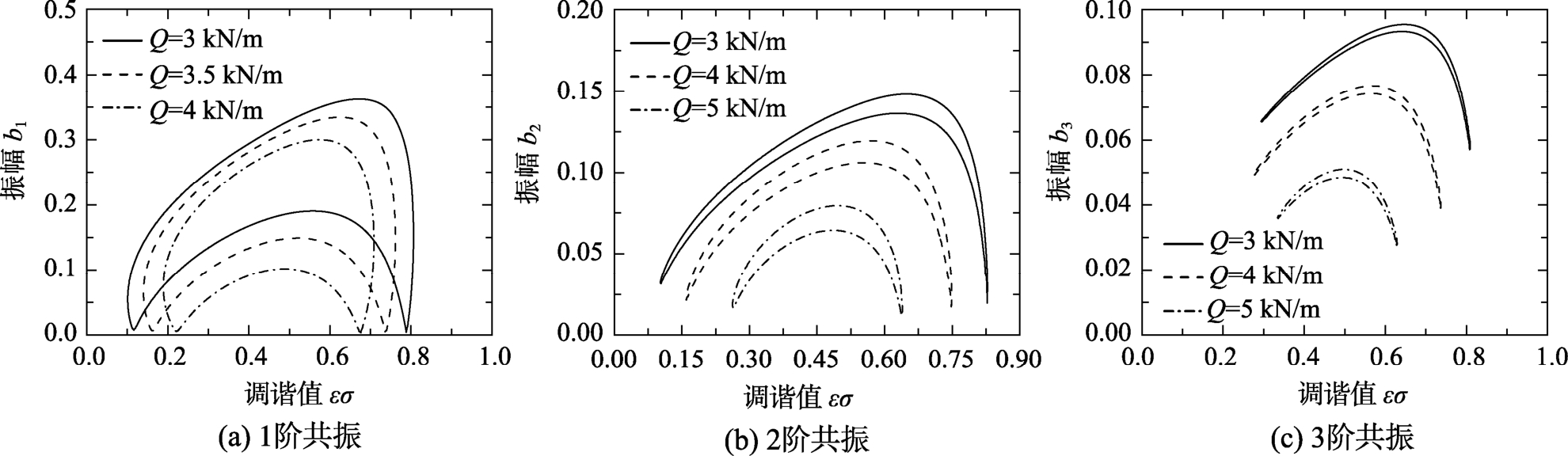
图4 振幅-调谐值特性曲线(不同激励幅值)(h=4mm, n=1, B4/5505)
Fig.4 Amplitude-detuning characteristic curves (different excitation amplitudes)(h=4mm, n=1, B4/5505)
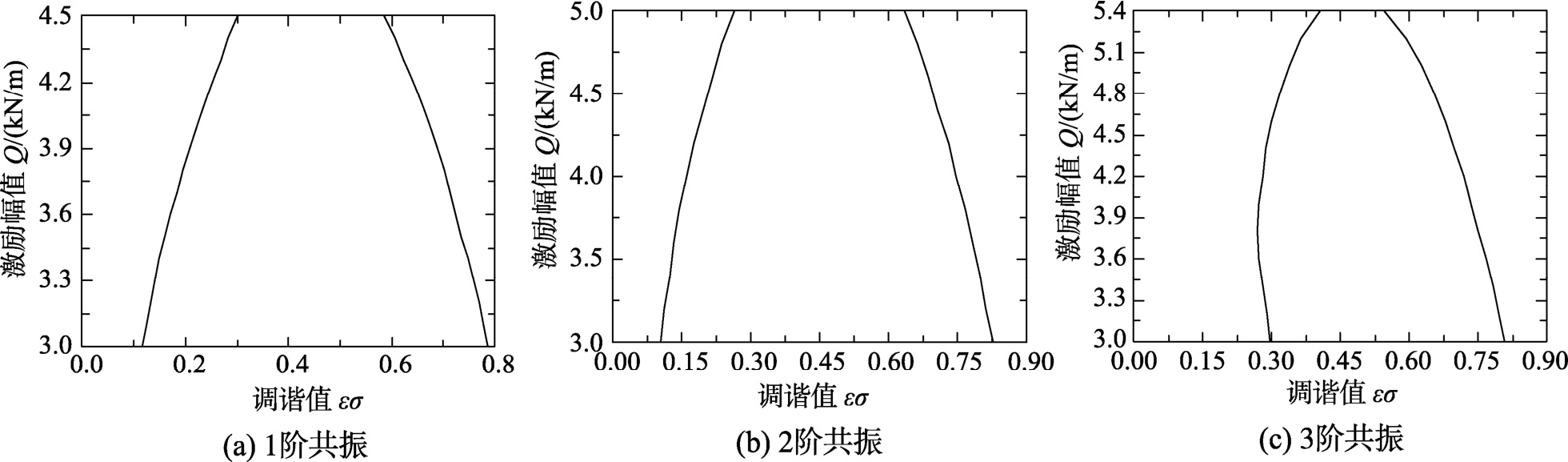
图5 激发共振双值解临界点变化曲线(h=4mm,n=1, B4/5505)
Fig.5 Excitation resonance double value solution critical point curve (h=4mm , n=1, B4/5505)
图6~图8分别给出了与图2~图4相对应的不同材料、层数、激励幅值的1阶、2阶、3阶共振情形下的振幅-速度特性曲线图。由图6~图8可以同样看出，所有曲线均为封闭月牙形双值曲线，且分为上支曲线和下支曲线，因此同一激励频率对应于振幅的两个不同值；1阶共振系统情形时，共振最明显，振幅较大，2阶、3阶振幅则越来越小；不同系统参数对于共振有显著影响。由图6可以看出不同材料可以影响振幅的大小。由图7可以看出，在相同板厚的情况下随着层数的增加，曲线整体下移。由图8可以看出，在一定范围内，随着激励幅值的增加，曲线整体下移。由于速度V与调谐值εσ为线性关系，且速度V与调谐值εσ的关系式中y1、y2、y3含有材料、板厚、层数这三个参量，不包含参量激励幅值Q，可以得出图6~图7中振幅值不完全对应图2~图3曲线振幅值，而图8完全对应于图4中振幅值。同样，以图6(a)为例进行稳定性分析，取A、B两点值进行判定可知，A点为对应判别值大于零的稳定解，即该点处于稳定性吸引域中，而B点为不稳定解。
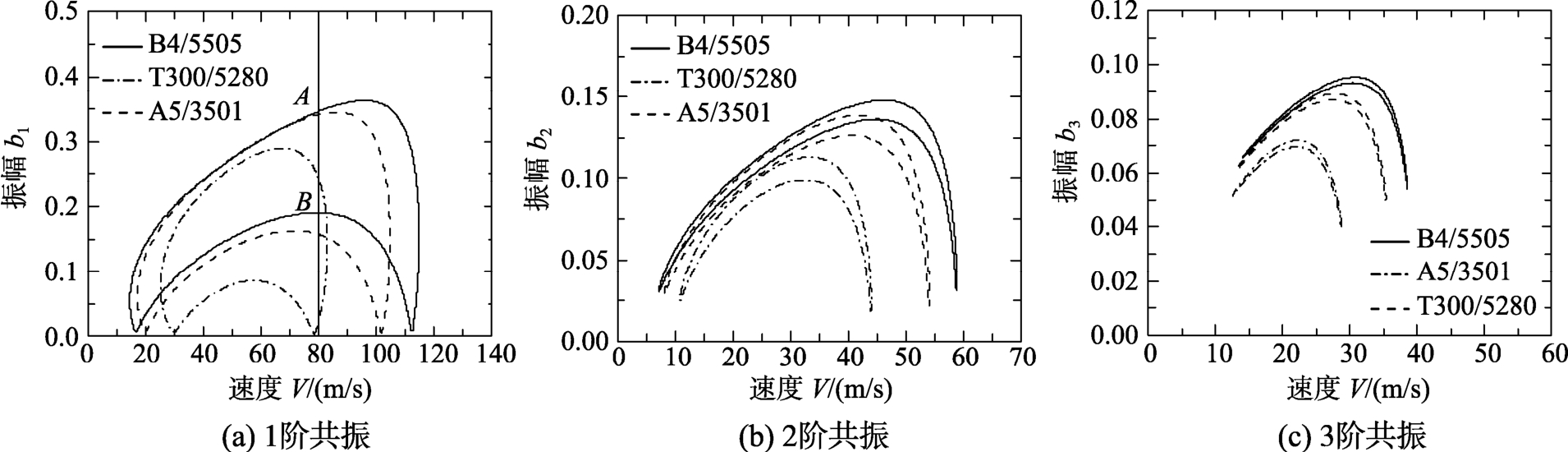
图6 振幅-速度特性曲线(不同材料)(Q=3kN/m , n=1, h=4mm)
Fig.6 Amplitude-speed characteristic curves (different materials)(Q=3kN/m, n=1, h=4mm )
图7 振幅-速度特性曲线(不同层数)(Q=3kN/m , h=4mm, B4/5505)
Fig.7 Amplitude-speed characteristic curves (different layers)(Q=3kN/m, h=4mm, B4/5505)
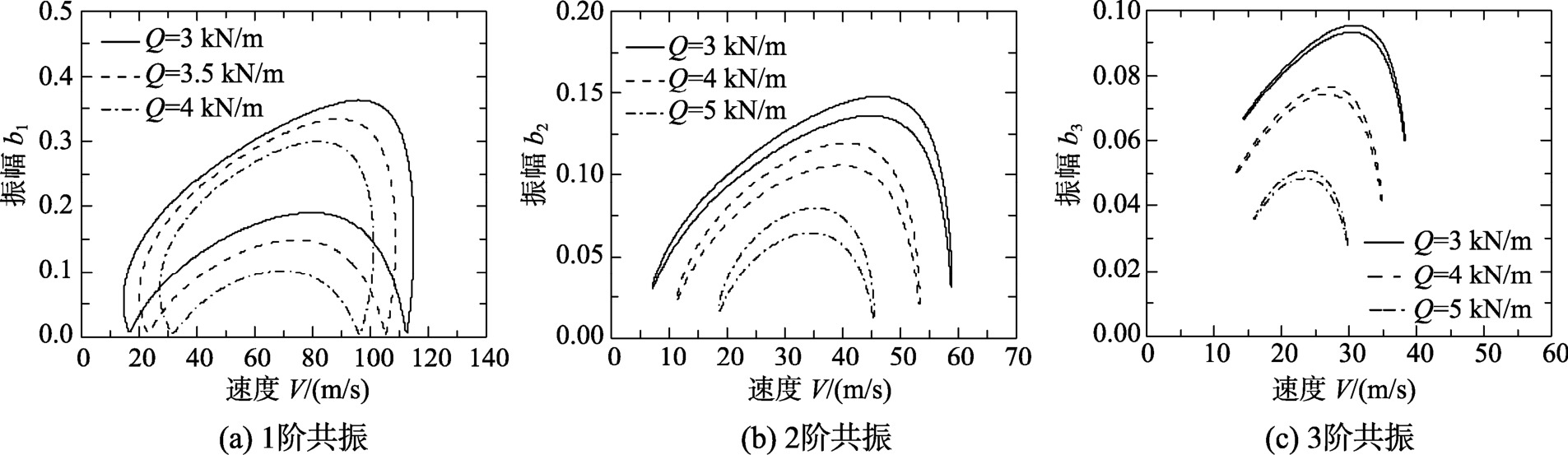
图8 振幅-速度特性曲线(不同激励幅值)(h=4mm, n=1, B4/5505)
Fig.8 Amplitude-speed characteristic curves (different excitation amplitudes)(h=4mm , n=1, B4/5505)
图9给出了与图8相对应的激发共振双值解的临界点变化曲线。图9表示不同激励幅值下图8中左右激发共振多值临界点的变化曲线。结果表明，当速度、激励幅值取特定值时才会激发共振，产生非零解的共振振幅，且曲线中间为共振区域，曲线两侧为非共振区域；由于速度与调谐值呈现线性关系，可以得出，图9中曲线同图5呈现相似的规律。
图9 激发共振双值解临界点变化曲线(h=4mm,n=1, B4/5505)
Fig.9 Excitation resonance double value solution critical point curve (h=4mm,n=1, B4/5505)
图10～图12给出了不同材料、层数、调谐值下的振幅-激励幅值特性曲线。其中图10(a)、图11(a)、图12(a)为月牙形封闭的双值曲线，图10(b)、图10(c)、图11(b)、图11(c)、图12(b)、图12(c)为狭窄月牙形封闭双值曲线。由图10～图12可以看出，曲线均随着激励振幅的增加，共振振幅呈现减小的趋势；通过改变材料、层数、调谐值等参量可以改变共振振幅；2阶、3阶相对于1阶的共振区域越来越细窄。同样，以图10(a)为例进行稳定性分析可知，A点为稳定性吸引域内的稳定解，B点为不稳定解。
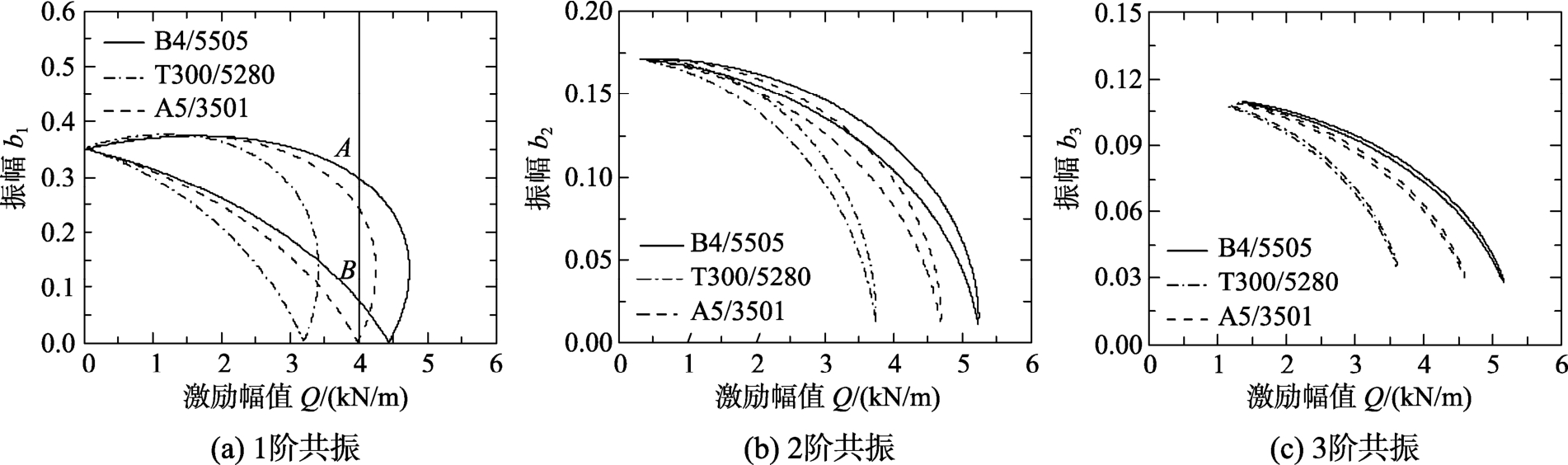
图10 振幅-激励幅值特性曲线(不同材料)(εσ=0.6, n=1, h=4mm)
Fig.10 Amplitude-excitation amplitude characteristic curves (different materials)(εσ=0.6, n=1, h=4mm )
图11 振幅-激励幅值特性曲线(不同层数)(εσ=0.6, h=4mm, B4/5505)
Fig.11 Amplitude-excitation amplitude characteristic curves (different layers)(εσ=0.6, h=4mm , B4/5505)
图12 振幅-激励幅值特性曲线(不同调谐值)(h=4mm, n=1, B4/5505)
Fig.12 Amplitude-excitation amplitude characteristic curves (different detunings)(h=4mm, n=1, B4/5505)
4 结论
本文研究随从力作用轴向运动正交各向异性叠层板的亚谐共振问题，得到叠层板的非线性幅频响应方程并进行了算例分析。计算结果表明：
(1)随从力随板一起运动时将以简协激励力的形式作用于板上，并随着板速改变，激励力频率也在发生改变，从而激发共振。
(2)亚谐波共振振幅均为封闭的双值光滑曲线，且分为上支和下支；调谐值与速度存在线性关系，且随着调谐值和速度的增大，振幅均出现先增大而后减小的趋势从而出现极值点。
(3)1阶共振情形振幅明显，2阶、3阶共振有明显减弱；随着激励幅值的增大，振幅封闭曲线整体均呈下移的趋势；激发共振双值解的左右临界点有不同变化规律。
[1]Crabtree O I, Mesarovic S D, Richards R F, et al.Nonlinear vibrations of a pre-sressed laminated thin plate[J].International Journal of Mechanical Sciences, 2006,48(4): 451―459.
[2]陈万吉, 任鹤飞.基于新修正偶应力理论的Mindlin层合板自由振动分析[J].工程力学, 2016, 33(12): 31―37, 43.Chen Wanji, Ren Hefei.Free vibration analysis of Mindlin laminates based on new modified couple stress theory [J].Engineering Mechanics, 2016, 33(12): 31―37, 43.(in Chinese)
[3]Xue J H, Jin F S, Zhang J W, et al.Post-buckling induced delamination propagation of composite laminates with bi-nonlinear properties and anti-penetrating interaction effects [J].Composites Part B, 2019, 166(1):148―161.
[4]Xue J H, Xia F, Ye J, et al.Multiscale studies on the nonlinear vibration of delaminated composite laminates-global vibration mode with micro buckles on the interfaces [J].Scientific Reports, 2017, 7(1): 44―68.
[5]Armagan K, Metin A.Buckling of laminated composite and sandwich beams due to axially varying in-plane loads[J].Composite Structures, 2019, 210: 391―408.
[6]Krzysztof M.Vibration analysis of an axially moving sandwich beam with multiscale composite facings in thermal environment [J].International Journal of Mechanical Sciences, 2018, 146/147:116―124.
[7]杨永宝, 危银涛.弹性基础上正交各向异性圆柱壳的自由振动[J].工程力学, 2018, 35(4): 24―32.Yang Yongbao, Wei Yintao.Free vibration of orthotropic cylindrical shells on elastic foundation [J].Engineering Mechanics, 2018, 35(4): 24―32.(in Chinese)
[8]Marynowski K.Free vibration analysis of the axially moving Levy-type viscoelastic plate [J].European Journal of Mechanics-A/Solids, 2010, 29(5): 879―886.
[9]Chen S H, Huang J L, Sze K Y.Multidimensional Lindstedt-Poincaré method for nonlinear vibration of axially moving beams [J].Journal of Sound & Vibration,2007, 306(1): 1―11.
[10]胡宇达, 孙建涛, 张金志.横向磁场中轴向变速运动矩形板的参数振动[J].工程力学, 2013, 30(9): 299―304.Hu Yuda, Sun Jiantao, Zhang Jinzhi.Parametric vibration of an axially variable motion rectangular plate in transverse magnetic field [J].Engineering Mechanics, 2013,30(9): 299―304.(in Chinese)
[11]胡宇达, 张明冉.两平行导线间轴向运动载流梁的非线性主共振[J].工程力学, 2018, 35(10): 238―248.Hu Yuda, Zhang Mingran.Nonlinear magnetic resonance of axial moving bearing beam between two parallel lines[J].Engineering Mechanics, 2018, 35(10): 238―248.(in Chinese)
[12]Hu Y D, Hu P, Zhang J Z.Strongly nonlinear subharmonic resonance and chaotic motion of axially moving thin plate in magnetic field [J].Journal of Computational and Nonlinear Dynamics, 2015, 10(2):021010.
[13]Ding H, Chen L Q.Nonlinear dynamics of axially accelerating viscoelastic beams based on differential quadrature [J].Acta Mechanica Solida Sinica, 2009,22(3): 267―275.
[14]Ding H, Chen L Q.Galerkin methods for natural frequencies of high-speed axially moving beams [J].Journal of Sound & Vibration, 2010, 329(17):3484―3494.
[15]叶康生, 殷振炜.平面曲梁面内自由振动有限元分析的p型超收敛算法[J].工程力学, 2019, 36(5): 28―36, 52.Ye Kangsheng, Yin Zhenwei.P-type superconvergence aigorithm for finite element analysis of free vibration in plane curved beam [J].Engineering Mechanics, 2019,36(5): 28―36, 52.(in Chinese)
[16]Banichuk N, Anichuk J, Jeronen P, et al.On the instability of an axially moving elastic plate [J].International Journal of Solids and Structures, 2009, 47(1): 91―99.
[17]Saurabh K, Anirban M, Haraprasad R.Forced vibration response of axially functionally graded non-uniform plates considering geometric nonlinearity [J].International Journal of Mechanical Sciences, 2017,128-129, 194―205.
[18]Zhang X F, Ye Z, Zhou Y J J.A Jacobi polynomial based approximation for free vibration analysis of axially functionally graded material beams [J].Composite Structures, 2019, 225: 111070.
[19]赵凤群, 王忠民. 随从力作用下功能梯度矩形板的非线性振动[J].振动与冲击, 2011, 30(3): 53―59.Zhao Fengqun, Wang Zhongmin.Nonlinear vibration of functionally graded rectangular plates subjected to subsequent forces [J].Journal of Vibration and Shock,2011, 30(3): 53―59.(in Chinese)
[20]王砚, 王忠民.线性变厚度粘弹性矩形板在随从力作用下的动力稳定性[J].固体力学学报, 2008, 29(1):41―51.Wang Yan, Wang Zhongmin.Dynamic stability of linear variable weight flexural structures under rarticle load [J].Chinese Journal of Solid Mechanics, 2008, 29(1): 41―51.(in Chinese)
[21]戎艳天, 胡宇达.移动载荷作用下轴向运动载流梁的参强联合共振[J].应用数学和力学, 2018, 39(3):266―277.Rong Yantian, Hu Yuda.Combined parametric and forced resonance of axially moving and current-carrying beams under moving loads [J].Applied Mathenatics and Mechanics, 2018, 39(3): 266―277.(in Chinese)
[22]Mehdi A, Mehdi S, Sattar M E.Nonlinear dynamic response of an axially functionally graded (AFG) beam resting on nonlinear elastic foundation subjected to moving load [J].Nonlinear Engineering, 2019, 8(1):250―260.