数值积分是有限元、边界元以及弱形式求积元法等工程分析数值计算方法中必不可少的工具。使用简单准确的积分公式一直是人们在实际工程计算中所希望的。弱形式求积元分析[1-2]中,需要采用含端点的数值积分公式。尽管笔者曾倡导过在弱形式求积元分析中采用克伦肖-柯蒂斯(Clenshaw-Curtis)等积分公式[3-4],由于洛巴托(Lobatto)积分的高效和准确性,目前洛巴托积分在弱形式求积元分析中仍是应用最广泛的数值积分公式。虽然,原则上闭区间的牛顿-科茨(Newton-Cotes)积分形式简单方便被弱形式求积元分析选用,但其高阶积分的数值不稳定性以及较低的代数精度,使得其很难在实际计算中得以广泛应用。数值积分的准确性就是要有足够高的代数精度;简单性则体现在积分公式中积分点或积分权系数的确定和表达形式上。在众多一维问题的数值积分公式中,切比雪夫(Chebyshev)等权积分公式无疑是形式简单的。对于任意区间[a,b],切比雪夫等权系数积分公式[5]可表示为:
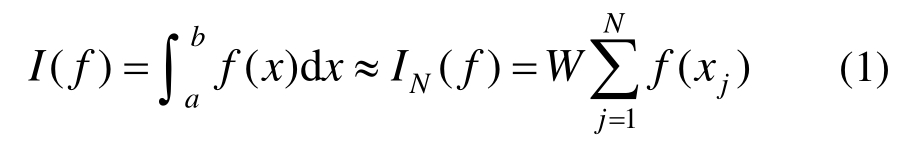
其中,唯一权系数W=(b-a)/N;积分节点xj(j=1,2,…,N)可以调整以取得至少N阶代数精度。然而,Bernstein[6]证明了只有在N =1~7以及N =9时,解得的积分节点值全为实数,因此,切比雪夫等权系数积分公式在实际应用中受到了限制。另外,由于它是开区间的积分并不适用于弱形式求积元分析。为了扩大其应用范围,本文将推出含端点的切比雪夫积分公式,给出相应的积分点和权系数表,并将所提出的积分公式应用到梁杆的线性和非线性弱形式求积元分析中。结果表明,修正后的切比雪夫公式,简单准确,可以作为弱形式求积元等数值方法中选择的一个有效工具。
1 修正切比雪夫积分公式
不失一般性,现考虑标准域[-1,1]上的积分公式,将切比雪夫等权积分公式修正为:

可以看到,修正切比雪夫积分公式仅需两个积分权系数:对应两个端点的权系数W0以及区间所有内部积分点对应的权系数W。除两个端节点x1=-1及xN=1指定外,内部积分节点xj(j=2,3,…,N -1)可以调节以取得最大可能的代数精度。
若没有内节点,即N=2,此时的含端点的切比雪夫积分公式将退化为梯形公式:W0=1。若N=3,即仅有一个内部节点,令式(2)对xj-1(j=1,2,3)都成立,可得方程组:
解得:x2=0,W0=1/3,W=4/3;显然,此时的含端点切比雪夫积分公式实为标准区间的辛普森(Simpson)积分公式。事实上,内部节点x2=0可由节点分布的对称性确定。若有两个内部节点(此时N=4),由节点分布的对称性可知,内部节点x2=-x3,此时有方程组:
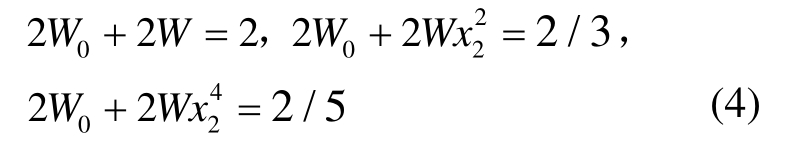
成立,解得:
更高阶的修正切比雪夫积分的节点和权系数可以同法确定。表1中给出了确保15位有效数字的标准区间内修正切比雪夫积分的节点和权系数。
表1 修正切比雪夫积分节点与权系数
Table 1 Abscissas and weights of modified Chebyshev quadrature

注:权系数栏中第一行为对应端点x=±1的权系数W0,第二行为对应内部节点的权系数W。
积分点数N节点±xj 权系数W0、W 2 1.00000 00000 000000 1.00000 00000 00000 3 1.00000 00000 000000 0.00000 00000 000000 0.33333 33333 33333 1.33333 33333 33333 4 1.00000 00000 000000 0.44721 35954 999580 0.16666 66666 66667 0.83333 33333 33333 5 1.00000 00000 000000 0.59586 15826 865180 0.00000 00000 000000 0.12659 86323 71090 0.58226 75784 19273 6 1.00000 00000 000000 0.70267 88767 179800 0.21066 78141 794960 0.08792 08719 419910 0.45603 95640 29004 7 1.00000 00000 000000 0.36348 13812 031770 0.75301 31207 930610 0.00000 00000 000000 0.07451 24083 568479 0.37019 50366 57261 8 1.00000 00000 000000 0.79928 10155 620700 0.45380 69551 328610 0.17744 34249 802640 0.05825 75694 955839 0.31391 41435 01472 9 1.00000 00000 000000 0.82408 62572 741140 0.53193 08398 874450 0.27802 08799 163910 0.00000 00000 000000 0.05173 56036 598948 0.27093 26846 68601 10 1.00000 00000 000000 0.84957 06409 632470 0.58021 39068 747370 0.38473 04842 254100 0.08426 51561 907727 0.04299 23896 244564 0.23925 19025 93886 11 1.00000 00000 000000 0.86421 07094 323440 0.62831 95290 619120 0.44090 44218 951050 0.20397 28810 084500 0.00000 00000 000000 0.03918 60825 913568 0.21351 42038 68587 12 1.00000 00000 000000 0.88023 26997 806640 0.65718 58799 886830 0.51456 30836 789710 0.20950 81939 921310 0.18630 85149 740190 0.03379 32922 259506 0.19324 13415 54810 13 1.00000 00000 000000 0.88984 69613 223420 0.69032 42176 239600 0.54880 85389 687410 0.32749 24036 312800 0.19486 87508 516400 0.00000 00000 000000 0.03131 72345 739724 0.17612 41391 683690
与开区间的切比雪夫等权系数积分公式只有N=1~7和N=9存在实数值节点比,修正的切比雪夫积分对于N=2~13时都可以获得实数值节点,其精度至少是N阶代数精度,且所有权系数都为正值,确保了其积分的数值稳定性。特别是,当N为偶数,即有偶数个积分点,由于此时对于xN+1积分式(2)自然成立,修正的切比雪夫积分公式可以达到N+1阶的代数精度。
2 算例
下面给出三个数值算例,以检验修正的切比雪夫积分公式在数值积分、求解梁杆的线性与非线性问题时的适用性和收敛特性。
2.1 计算积分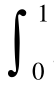 f(x)dx
f(x)dx
此时,精确解[7]为:

为利用修正的切比雪夫数值积分,做区域变换,得到标准区域的积分表达:
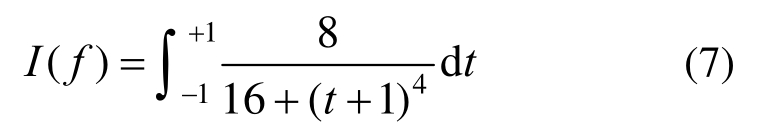
不同积分点数得到的结果如下。
N=2时(对应梯形公式):
其中,式后的括号中给出了按下式定义的相对误差:
N=3时(对应辛普森公式):
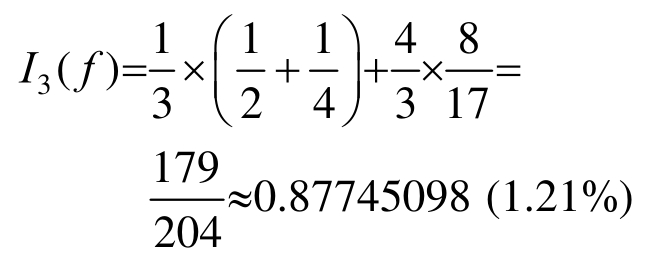
N=4时:

N=5时:
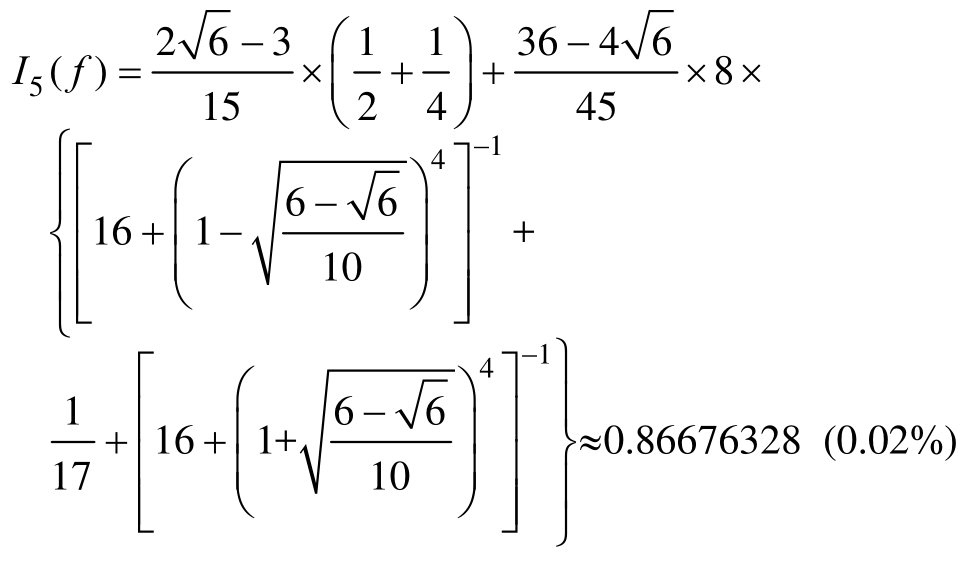
N=6时:
N=7时:
表2中同时列出洛巴托积分与修正的切比雪夫积分公式的结果。
表2 算例2.1中两种数值积分计算结果
Table 2 Results of example 2.1 using two quadrature rules

注:括号中给出的是结果的相对误差。
积分点数N修正切比雪夫积分公式 洛巴托积分公式3 0.87745098 (1.21%) 0.87745098(1.21%)4 0.86626092 (0.08%) 0.86626092(0.08%)5 0.86676328 (0.02%) 0.86699546(0.00%)6 0.86698688 (0.00%) 0.86697516(0.00%)7 0.86697969 (0.00%) 0.86697242(0.00%)
可以看出,修正的切比雪夫积分公式可以获得准确的数值积分,与洛巴托积分公式的结果对比差异细微,且此例中二者在同等阶次条件下的结果的误差几乎相同。
2.2 受到温度荷载作用的固支杆
本算例讨论修正的切比雪夫积分公式在受到温度荷载作用的两端固支杆的应用。一根长l的均匀杆两端固支,其温升沿杆长变化如下:

由虚功原理可得:
其中:

式中:E为弹性模量;α为线膨胀系数。取ξ为定义在[-1,1]标准区域上的标准化坐标。
可得:
此处采用弱形式求积元法对问题进行分析。弱形式求积元分析中,需先利用数值积分将其中的积分计算出来,再利用微分求积法则[8]将数值微分表示出来。以一维函数u(ξ)为例,它的m阶导数在第i个离散点上的值可表示为:

式中:N为离散点总数;u(ξj)为函数在各离散点上的值;![]() 为m阶导数的微分求积权系数。
为m阶导数的微分求积权系数。![]() 的显示表达[9]为:
的显示表达[9]为:

其中:
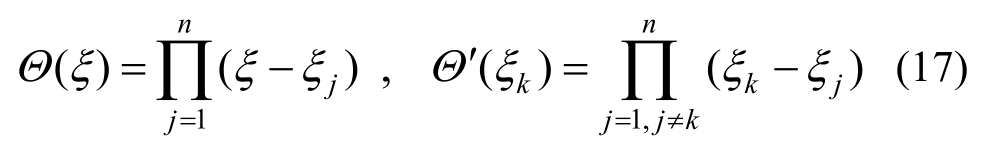
高阶导数和低阶导数相应的微分求积权系数之间存在着递推关系[10]:
其中,C(1)、C(m-1)和C(m)是由相应的微分求积权系数![]() 组成的矩阵。取整个杆为一个弱形式求积单元,将式(10)表示为:
组成的矩阵。取整个杆为一个弱形式求积单元,将式(10)表示为:

其中:
则可得:
其中:

注意,式(22)中积分权系数:
引入边界条件,便可求解线性方程组式(21)得到节点位移向量。
对于一个两端固支的均匀杆,温升引起的轴向位移的解析解为:

杆中点的无量纲位移解析解为:

用修正的切比雪夫积分公式与洛巴托积分公式计算得到杆中点的位移值。当积分点为偶数时,可利用拉格朗日插值:
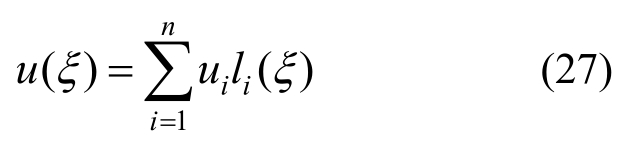
得到中点位移值;其中,li(ξ)为拉格朗日插值基函数:
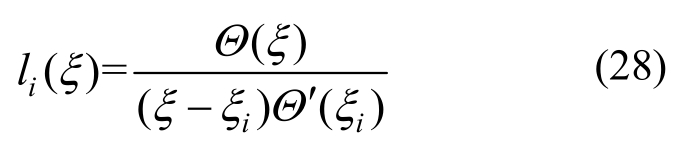
式中,Θ(ξ)和Θ′(ξi)的表达式见式(17)。杆中点位移的计算结果见表3。
表3 杆中点无量纲位移
Table 3 Non-dimensional midpoint displacement of rod
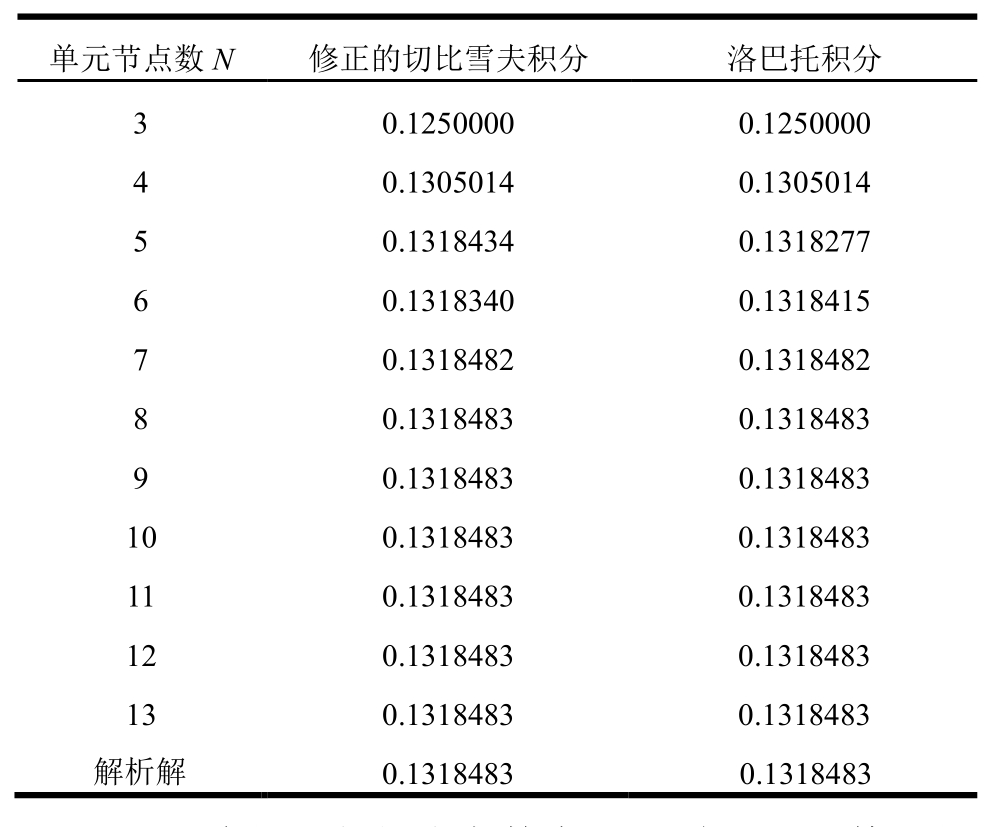
单元节点数N 修正的切比雪夫积分 洛巴托积分3 0.1250000 0.1250000 4 0.1305014 0.1305014 5 0.1318434 0.1318277 6 0.1318340 0.1318415 7 0.1318482 0.1318482 8 0.1318483 0.1318483 9 0.1318483 0.1318483 10 0.1318483 0.1318483 11 0.1318483 0.1318483 12 0.1318483 0.1318483 13 0.1318483 0.1318483解析解 0.1318483 0.1318483
可以看出,当积分点数大于3时,运用修正切比雪夫积分公式和洛巴托积分公式得到的数值解的相对误差都降到了1%。当积分点数大于6时,二者都可以获得六位有效数字的计算结果。可见运用修正的切比雪夫积分结果的收敛速度并不比运用洛巴托积分的慢。
2.3 受到集中力偶作用的悬臂梁
下面将修正的切比雪夫积分公式应用于基于几何精确模型的梁的强非线性弱形式求积元分析。如图1所示,一根初始长度为L的等截面悬臂梁受到杆端弯矩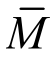 作用,相关参数:EA=ksGA=104,EI=102,L=10,和Simo[11]采用数据完全一致。
作用,相关参数:EA=ksGA=104,EI=102,L=10,和Simo[11]采用数据完全一致。

图1 受到集中力偶作用的等截面悬臂梁
Fig.1 Pure bending of a uniform cantilever beam
以初始构型为参考,建立完全拉格朗日格式的弱形式求积元列式。平面几何精确梁模型在初始和变形后的构型示意图如图2所示,建立直角坐标系,其中X轴和梁初始构型轴线重合。引入平动位移u、v和转动角度β来描述相应的变形,位移向量为ζT=(u,v,β),其内力虚功![]() 的表达式为[12]:
的表达式为[12]:

图2 梁的初始和变形后的构型
Fig.2 Initial and deformed configurations of beam
式中:χ为Reissner应变向量;N为等效截面力向量;外力虚功![]() 的表达式为:
的表达式为:
其中,![]() 分别代表其单元分布荷载向量和单元集中荷载向量,其弱形式求积元离散表达式为:
分别代表其单元分布荷载向量和单元集中荷载向量,其弱形式求积元离散表达式为:

式中,![]() 分别表示的是梁单元的两个端点处的集中荷载向量。可由虚功原理建立平衡方程:
分别表示的是梁单元的两个端点处的集中荷载向量。可由虚功原理建立平衡方程:
与增量方程:
式中:Gint、Gext分别为节点内力和节点荷载;R为残差向量;KT为切线刚度矩阵。通过迭代求得荷载位移曲线。更详尽的公式表达和求解步骤见文献[12]。
该问题解析解[13]表明,在受到杆端弯矩作用时,梁内部只有弯曲变形,变形后梁的轴线是一段圆弧,相应的曲率为:
当![]() 时,弯矩作用使得梁完全弯成一个整圆。采用1个弱形式求积单元进行计算,将采用修正切比雪夫积分公式与洛巴托积分公式的计算结果[12]进行对比,见表4。
时,弯矩作用使得梁完全弯成一个整圆。采用1个弱形式求积单元进行计算,将采用修正切比雪夫积分公式与洛巴托积分公式的计算结果[12]进行对比,见表4。
表4 等截面悬臂梁的端点位移
Table 4 Solution of end displacement components for cantilever beam subject to an end moment
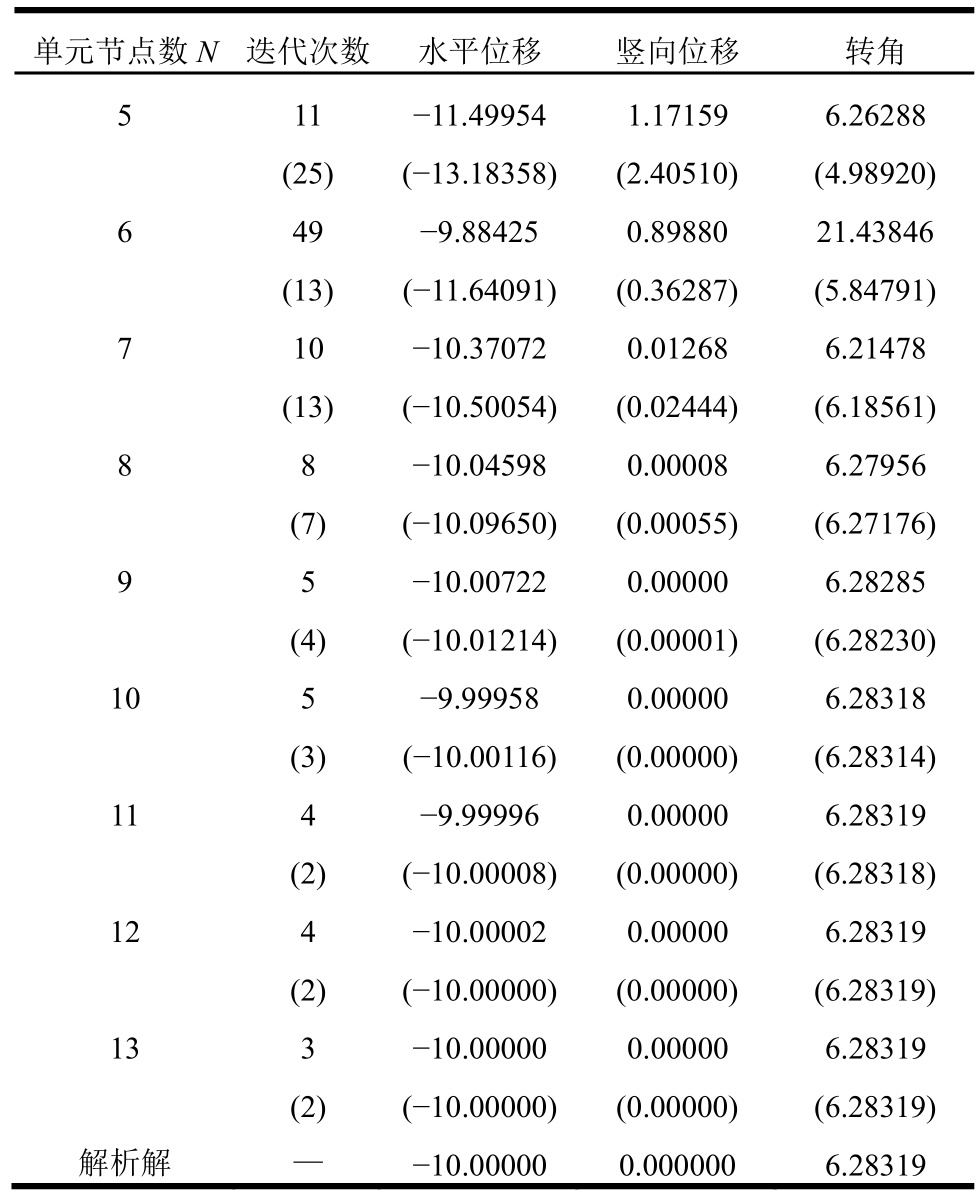
注:括号中数据为利用洛巴托积分公式计算结果。
单元节点数N迭代次数水平位移 竖向位移 转角5 11 -11.49954 1.17159 6.26288(25) (-13.18358) (2.40510) (4.98920)6 49 -9.88425 0.89880 21.43846(13) (-11.64091) (0.36287) (5.84791)7 10 -10.37072 0.01268 6.21478(13) (-10.50054) (0.02444) (6.18561)8 8 -10.04598 0.00008 6.27956(7) (-10.09650) (0.00055) (6.27176)9 5 -10.00722 0.00000 6.28285(4)(-10.01214) (0.00001) (6.28230)10 5 -9.99958 0.00000 6.28318(3)(-10.00116) (0.00000) (6.28314)11 4 -9.99996 0.00000 6.28319(2)(-10.00008) (0.00000) (6.28318)12 4 -10.00002 0.00000 6.28319(2)(-10.00000) (0.00000) (6.28319)13 3 -10.00000 0.00000 6.28319(2)(-10.00000) (0.00000) (6.28319)解析解 — -10.00000 0.000000 6.28319
可以看出,随着单元内节点数目的增加,梁端各个位移分量都趋于收敛,且达到误差限所需的迭代次数也在减小。修正切比雪夫积分公式和洛巴托积分公式在获得准确有效数字位数上几无差别。当单元节点数N增加到9时,二者与解析解水平位移和转角的相对误差都小到了0.1%以下。此外,从计算结果的收敛性与迭代次数的减少来看,洛巴托积分均略好于修正的切比雪夫积分,但二者的差异随着节点数的增加变得越来越小。这个算例说明,所提出的修正的切比雪夫积分公式对于存在大位移大转动的强非线性问题的数值分析也是准确可靠的。
3 结论
提出了一种修正的切比雪夫积分公式并将其应用于数值积分和求解梁杆的线性与非线性问题。计算结果与解析解及运用洛巴托积分公式所得结果进行了对比,证实了提出的修正的切比雪夫积分公式的实用价值与利用之取得的令人满意的计算结果。
[1]Zhong H, Yu T.Flexural vibration analysis of an eccentric annular Mindlin plate [J].Archive of Applied Mechanics, 2007, 77(4): 185―195.
[2]Zhong H, Yu T.A weak form quadrature element method for plane elasticity problems [J].Applied Mathematical Modelling, 2009, 33(10): 3801―3814.
[3]Zhang R, Zhong H.Weak form quadrature element analysis of geometrically exact shells [J].International Journal of Non-Linear Mechanics, 2015, 71: 63―71.
[4]Zhong H, Gao M.Quadrature element analysis of planar frameworks [J].Archive of Applied Mechanics, 2010,80(12): 1391―1405.
[5]Squire W.Integration for engineers and scientists [M].New York: American Elsevier Publication Company,1970: 132―133.
[6]Bernstein S N.Sur les formules de quadrature de Cotes et Tchebychef [J].Doklady Akademii Nauk SSSR, 1937,14(2): 323―326.
[7]Davis P J, Rabinowitz P.Methods of numerical integration [M].Orlando: Academic Press, 1984: 2.
[8]Bellman R, Casti J.Differential quadrature and long-term integration [J].Journal of Mathematical Analysis & Applications, 1970, 34(2): 235―238.
[9]Quan J R, Chang C T.New insights in solving distributed system equations by the quadrature method - I.Analysis[J].Computers & Chemical Engineering, 1989, 13(7):779―788.
[10]Shu C, Richards B E.Parallel simulation of incompressible viscous flows by generalized differential quadrature [J].Computing System in Engineering, 1992,3(1/2/3/4): 271―281.
[11]Simo J C, Vu-Quoc L.A three-dimensional finite-strain rod model.Part II: Computational aspects [J].Computer Methods in Applied Mechanics and Engineering, 1986,58(1): 79―116.
[12]Xiao N, Zhong H.Nonlinear quadrature element analysis of planar frames based on geometrically exact beam theory [J].International Journal of Non-Linear Mechanics, 2012, 47(5): 481―488.
[13]Love A E H.A Treatise on the mathematical theory of elasticity [M].4th ed.New York: Dover, 1944: 402―406.